
Lesson: Triangles
Exercise 6.1 (3)
Question: 1
Fill in the blanks using the correct word given in
brackets:
(i) All circles are ______. (congruent, similar)
(ii) All squares are ______. (similar, congruent)
(iii) All _____triangles are similar. (isosceles,
equilateral)
(iv) Two polygons of the same number of sides are
similar, if (a) their corresponding angles are
____and (b) their corresponding sides are
______. (equal, proportional)
Solution
(i) Similar
(ii) Similar
(iii) Equilateral
(iv)
(a) Equal
(b) Proportional
Question: 2
Give two different examples of pair of
(i) similar figures
(ii) non-similar figures
Solution
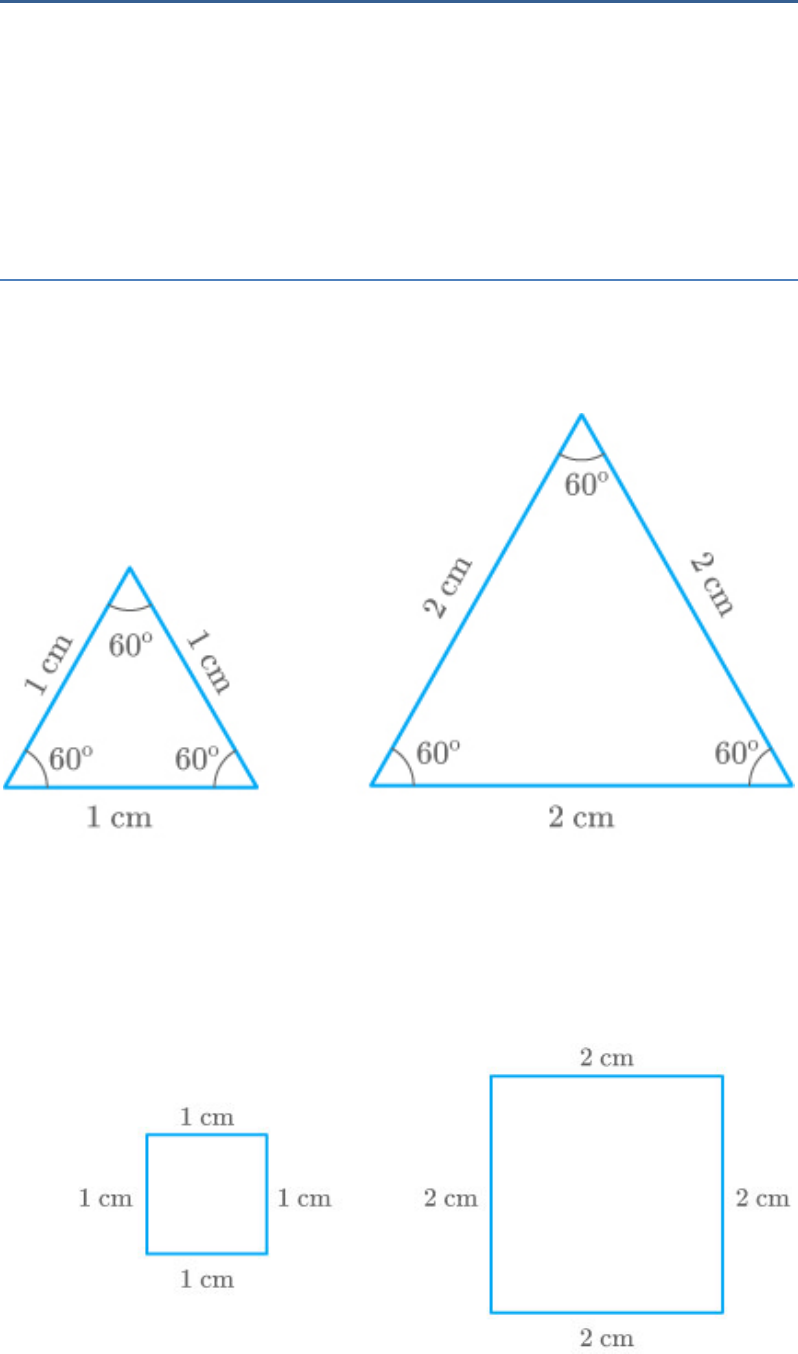
(i) Two equilateral triangles having sides 1 cm and
2 cm.
Fig. Exc_6.1_2 [i(a)]
Two squares having sides 1 cm and 2 cm.
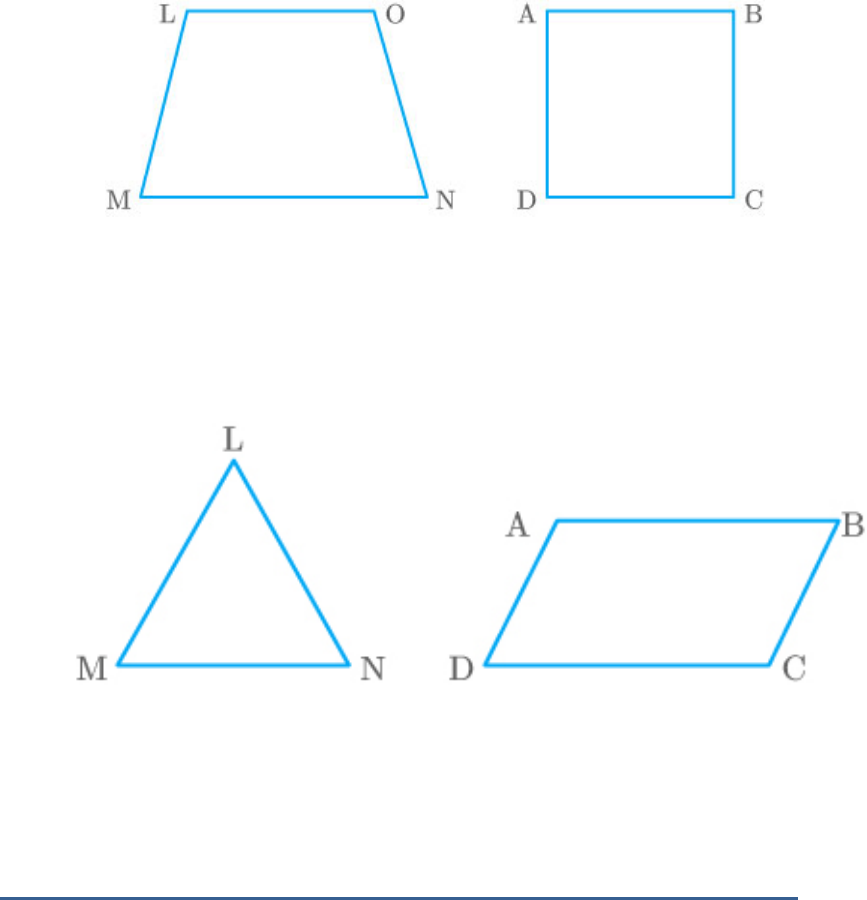
Fig. Exc_6.1_2 [i(b)]
(ii) Trapezium and square
Fig. Exc_6.1_2 [ii(a)]
Triangle and parallelogram
Fig. Exc_6.1_2 [ii(b)]
Question: 3
State whether the following quadrilaterals are similar
or not:

Fig. Exc_6.1_3
Solution
The corresponding sides of quadrilateral PQRS and
ABCD are proportional, but their corresponding
angles are not equal.
Hence, quadrilateral PQRS and ABCD are not
similar.
Exercise 6.2 (10)
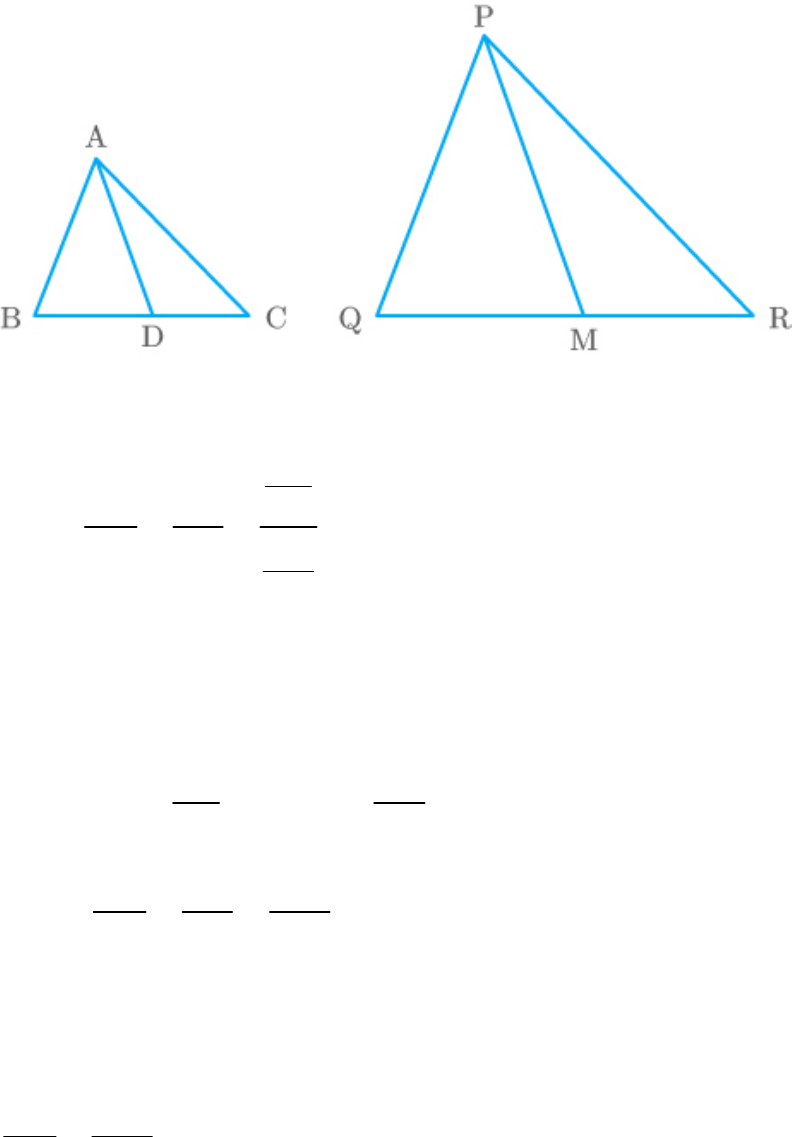
Question: 1
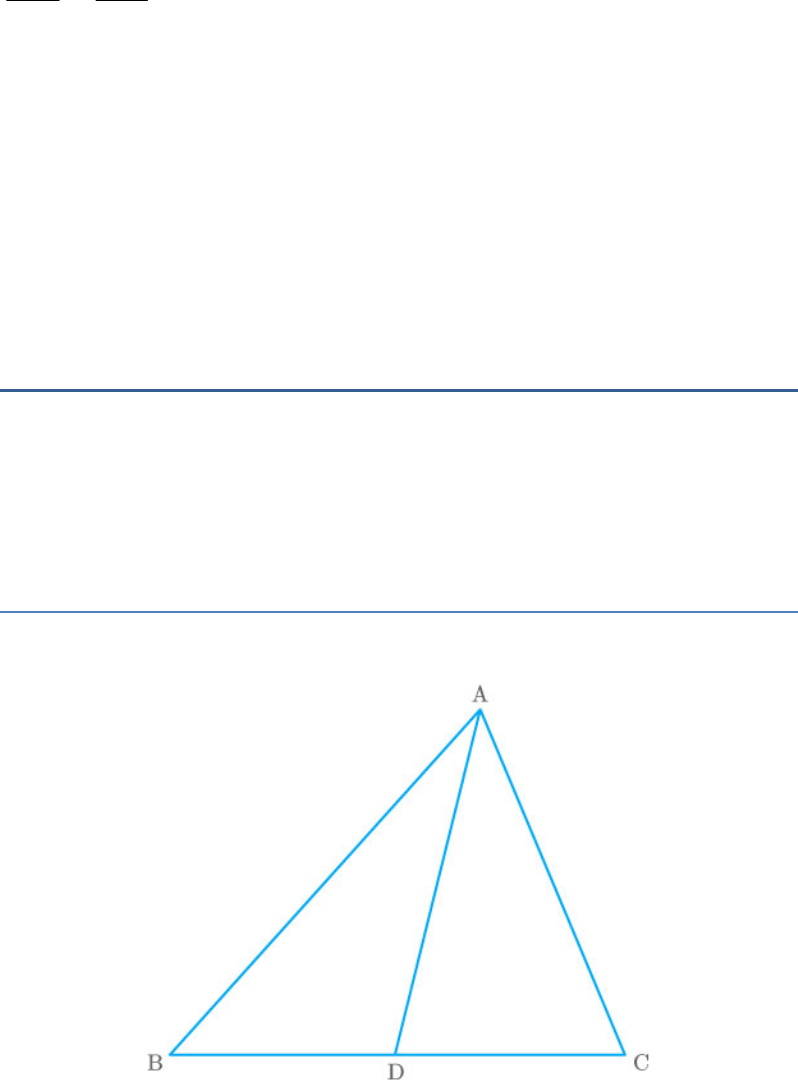
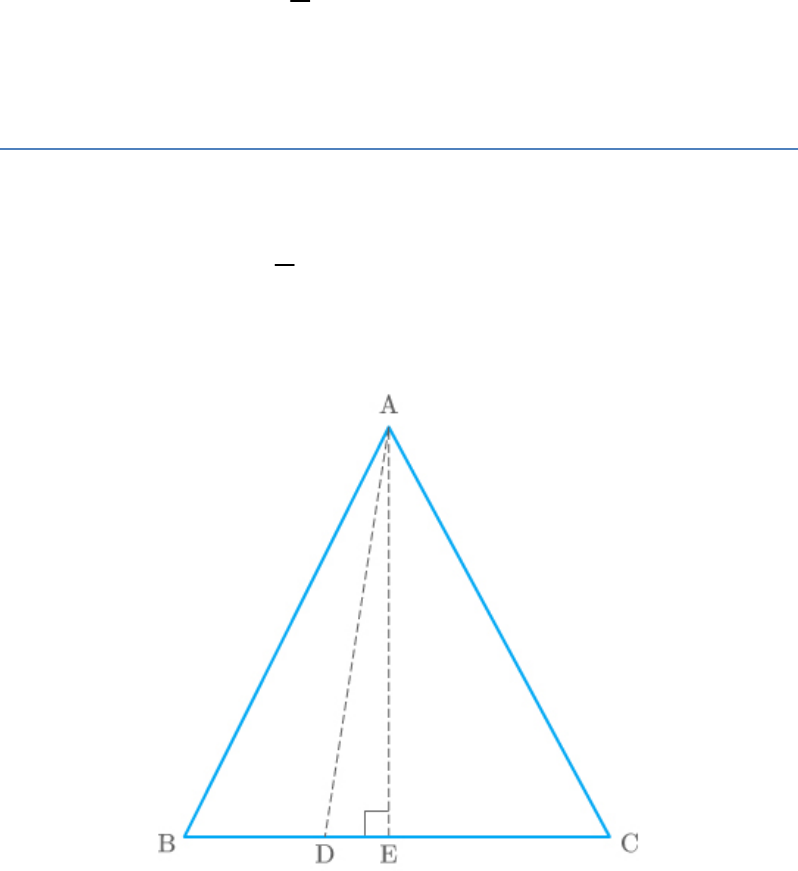
In the given figure, DE
||
BC. Find EC in (i) and AD in
(ii).
Fig. Exc_6.2_1

Solution
(i) Let
EC a cm
Given: .
DE||BC
By basic proportionality theorem,
AD AE
DB EC
1.5 1
3 a
3 1
a
1.5
a 2
Hence,
EC 2cm
(ii) Let
AD a cm
Given: .
DE||BC
By basic proportionality theorem,
AD AE
DB EC
a 1.8
7.2 5.4
1.8 7.2
a
5.4
a 2.4
Hence,
AD 2.4cm
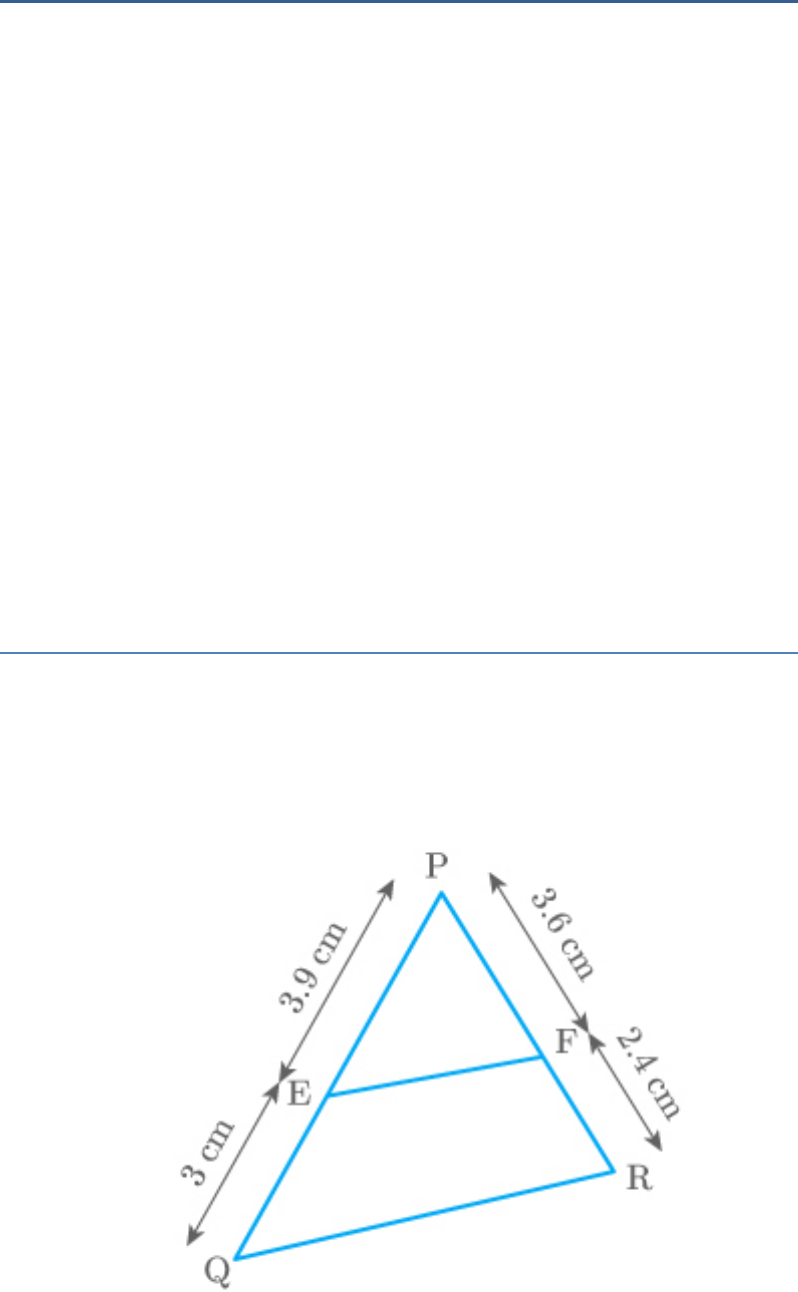
Question: 2
E and F are points on the sides PQ and PR
respectively of a PQR. For each of the following
cases, state whether EF QR:
:
(i) PE 3.9 cm, EQ 3 cm, PF 3.6 cm and FR
2.4 cm
(ii) PE 4 cm, QE 4.5 cm, PF 8 cm and RF 9
cm
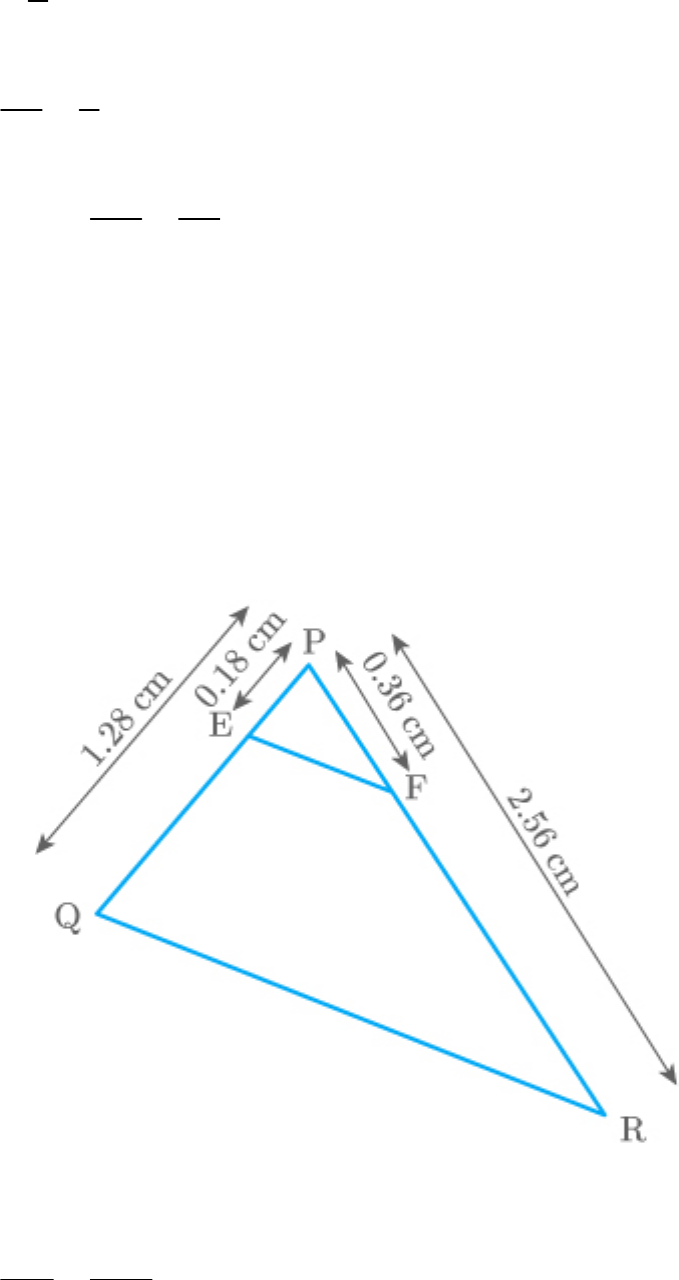
(iii) PQ 1.28 cm, PR 2.56 cm, PE 0.18 cm and
PF 0.36 cm
Solution
(i) Given:
PE 3.9 cm, EQ 3 cm, PF 3.6 cm and FR
2.4 cm
Fig. Exc_6.2_2 (i)
PE 3.9
EQ 3
1.3
PF 3.6
FR 2.4
1.5
Thus,
PE PF
EQ FR
Hence, EF is not parallel to QR.
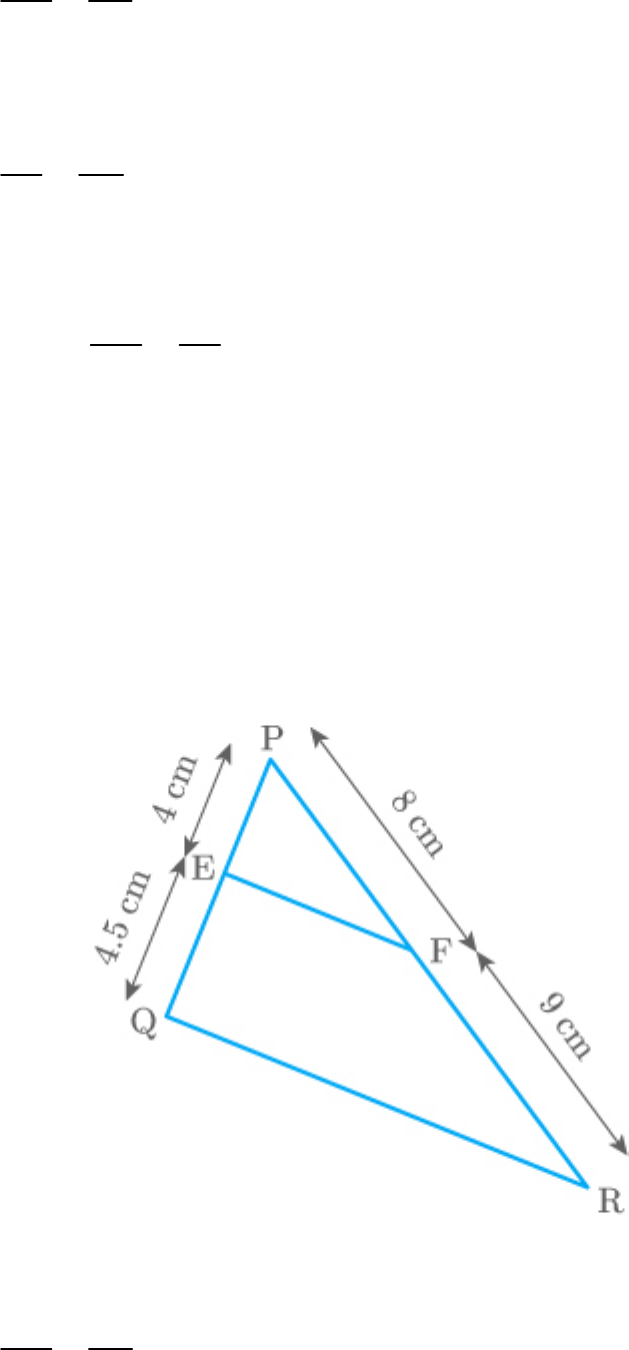
(ii) Given:
PE 4 cm, QE 4.5 cm, PF 8 cm and RF 9
cm
Fig. Exc_6.2_2 (ii)
PE 4
EQ 4.5
8
9
PF 8
FR 9
Thus,
PE PF
EQ FR
Hence, .
EF||QR
(iii) Given:
PQ 1.28 cm, PR 2.56 cm, PE 0.18 cm and
PF 0.36 cm
Fig. Exc_6.2_2 (iii)
PE 0.18
PQ 1.28
9
64
PF 0.36
PR 2.56
9
64
Thus,
PE PF
PQ PR
Hence, .
EF||QR
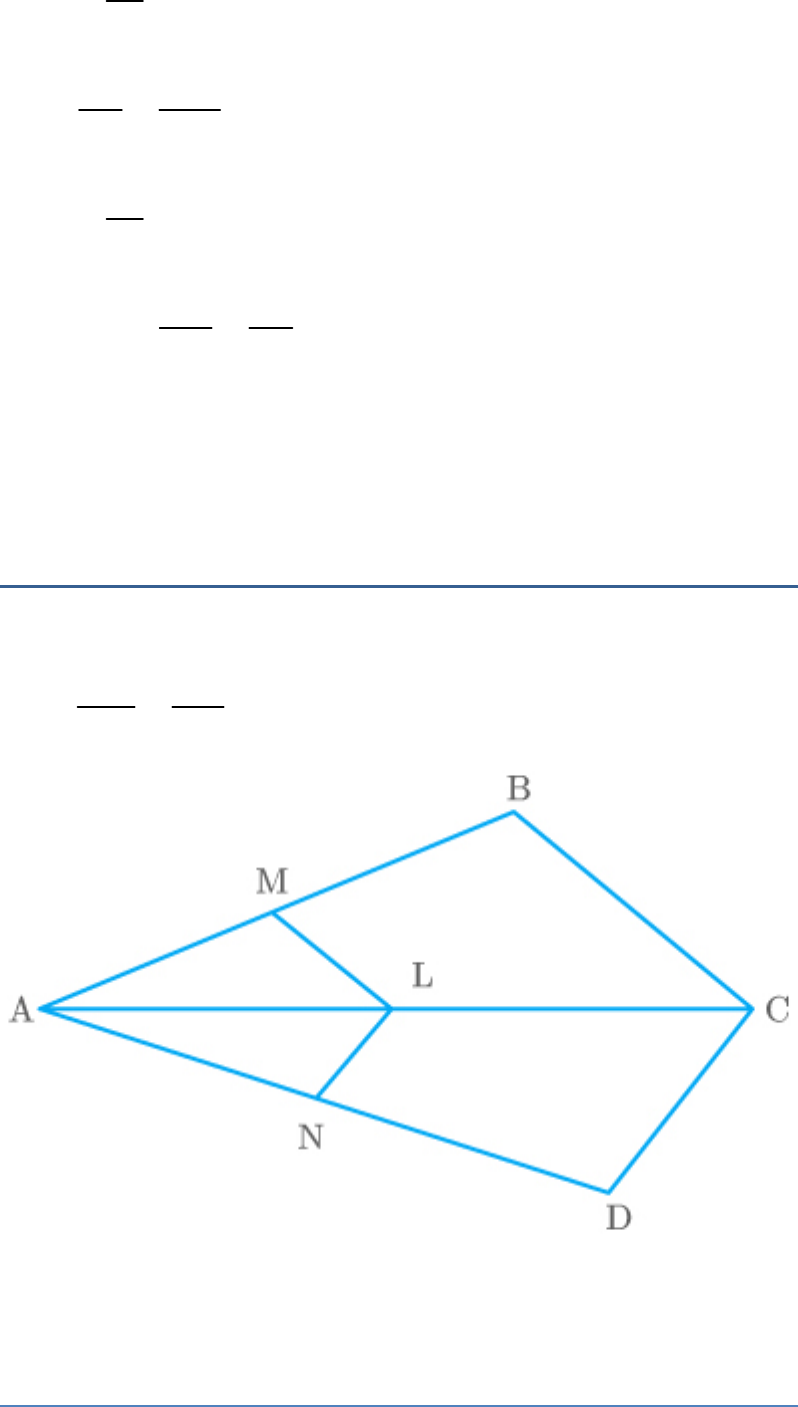
Question: 3
In the given figure, if LM
||
CB and LN
||
CD, prove
that .
AM AN
AB AD
Fig. Exc_6.2_3
Solution
Given: LM || CB.
By basic proportionality theorem,
AM AL
......(1)
AB AC
Also, given: LN || CD.
By basic proportionality theorem,
AN AL
......(2)
AD AC
From equations (1) and (2).
AM AN
AB AD
Hence proved.
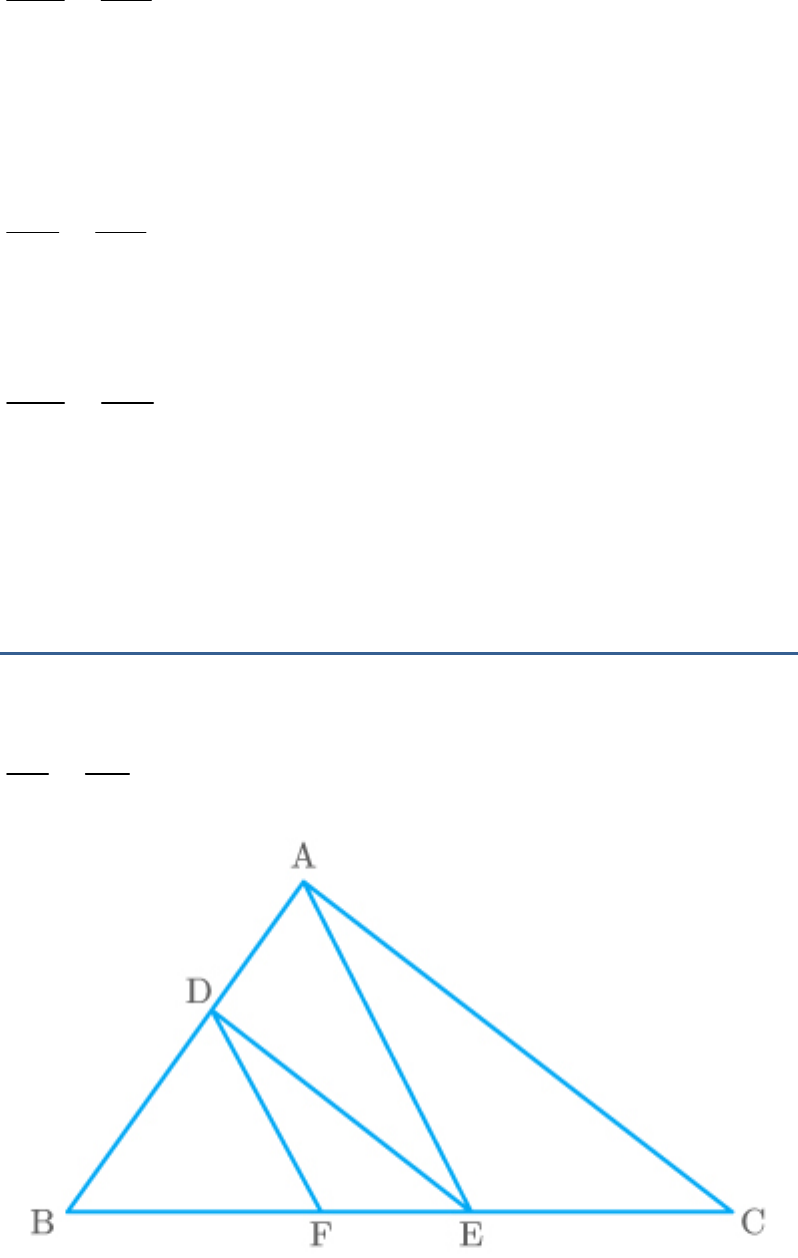
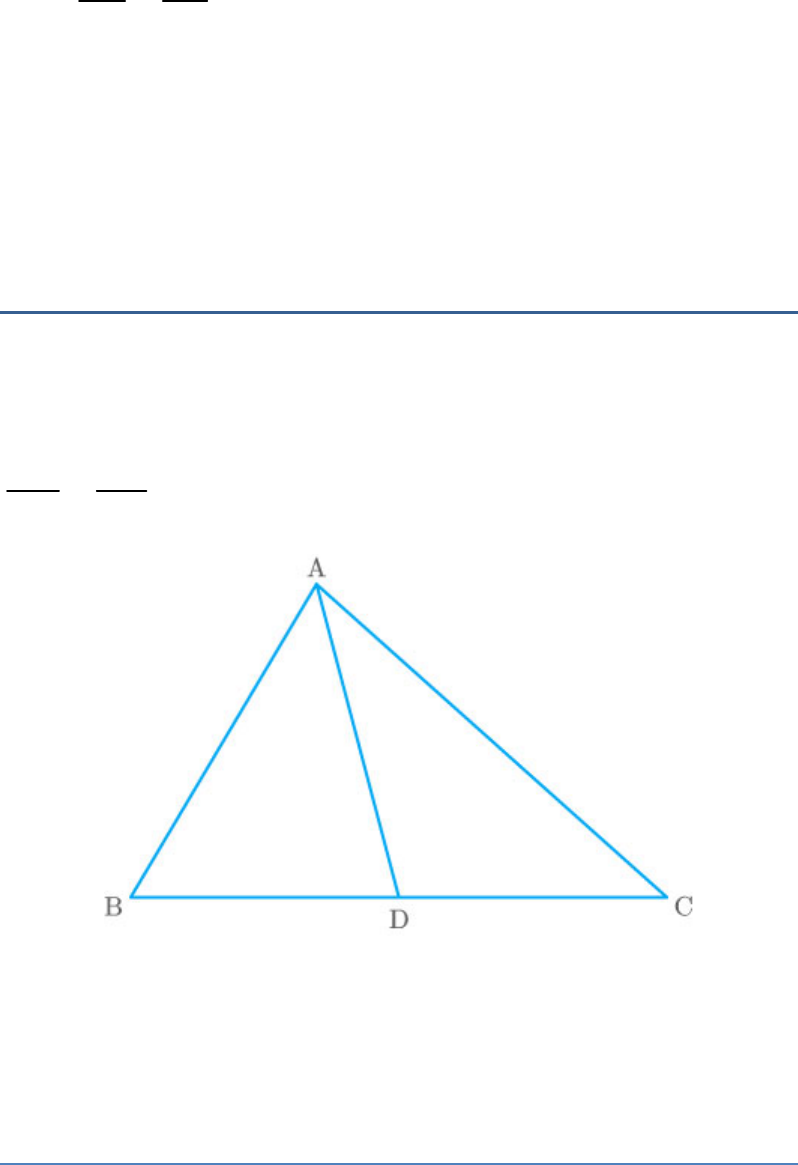
Question: 4
In the given figure, DE || AC and DF
||
AE. Prove that
.
BF BE
FE EC
Fig. Exc_6.2_4
Solution
Given: DE || AC.
By basic proportionality theorem,
BD BE
......(1)
DA EC
Also, given: DF || AE.
By basic proportionality theorem,
BD BF
......(2)
DA FE
From equations (1) and (2).
BF BE
FE EC
Hence proved.
Question: 5
In the given figure, DE || OQ and DF || OR. Show that
EF || QR.
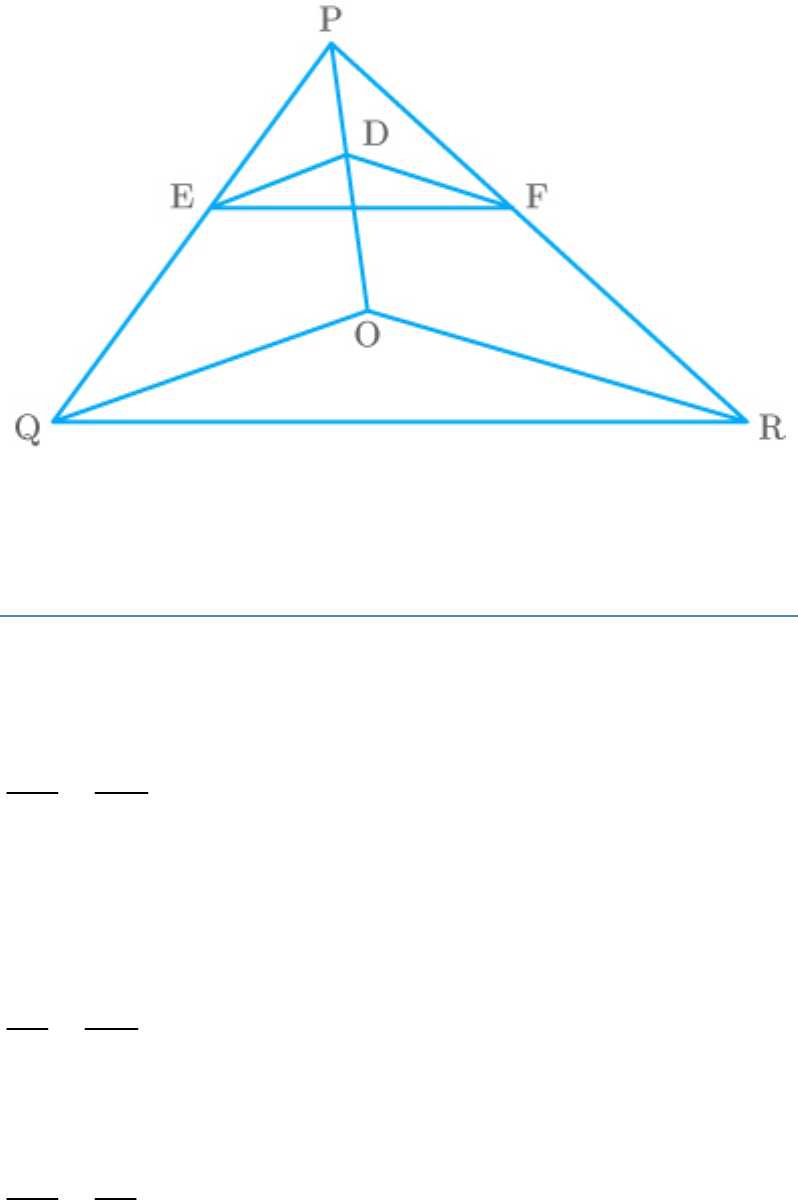
Fig. Exc_6.2_5
Solution
Given: DE || OQ.
By basic proportionality theorem,
PE PD
......(1)
EQ DO
Also, given: DF || OR.
By basic proportionality theorem,
PF PD
......(2)
FR DO
From equations (1) and (2).
PE PF
EQ FR
By converse of basic proportionality theorem,
EF
||
QR.
Hence proved.
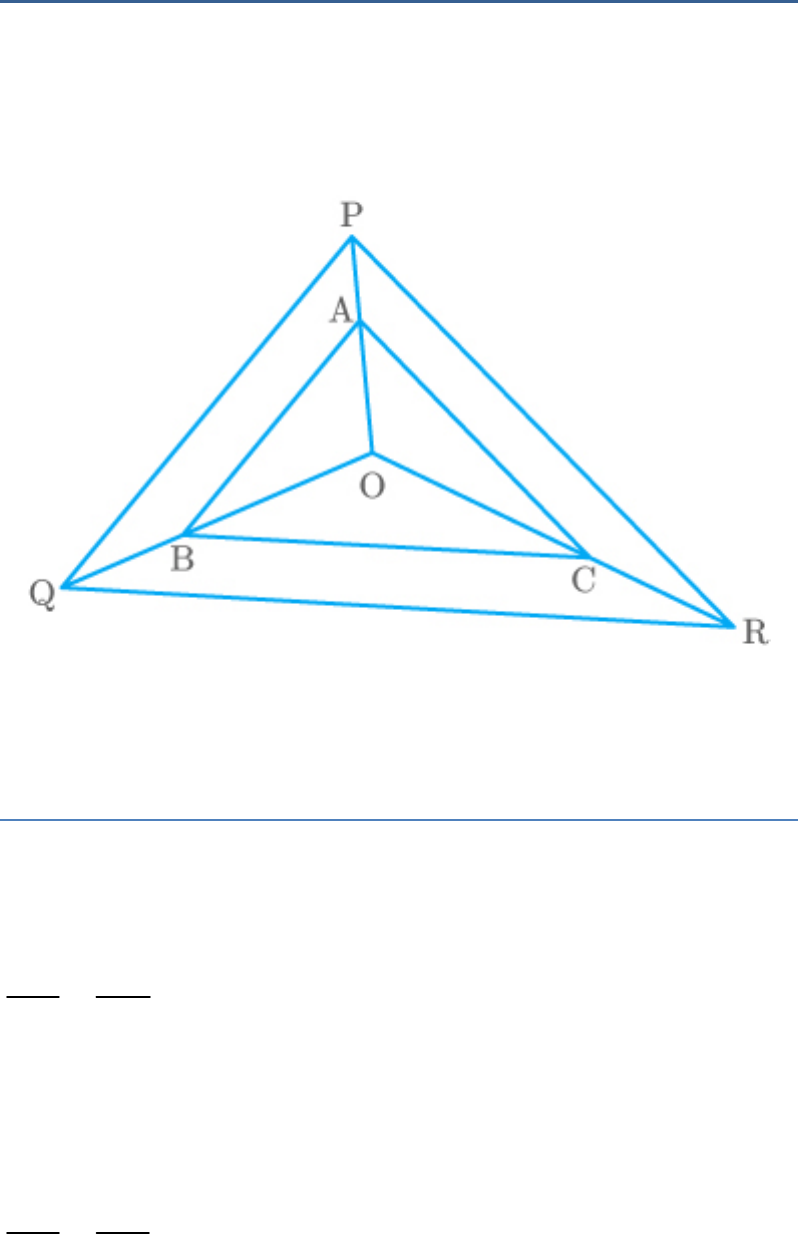
Question: 6
In the given figure, A, B and C are points on OP, OQ
and OR respectively such that AB || PQ and AC || PR.
Show that BC || QR.
Fig. Exc_6.2_6
Solution
Given: AB || PQ.
By basic proportionality theorem,
OA OB
......(1)
AP BQ
Also, given: AC || PR.
By basic proportionality theorem,
OA OC
......(2)
AP CR
From equations (1) and (2).
OB OC
BQ CR
By converse of basic proportionality theorem,
BC || QR.
Hence proved.
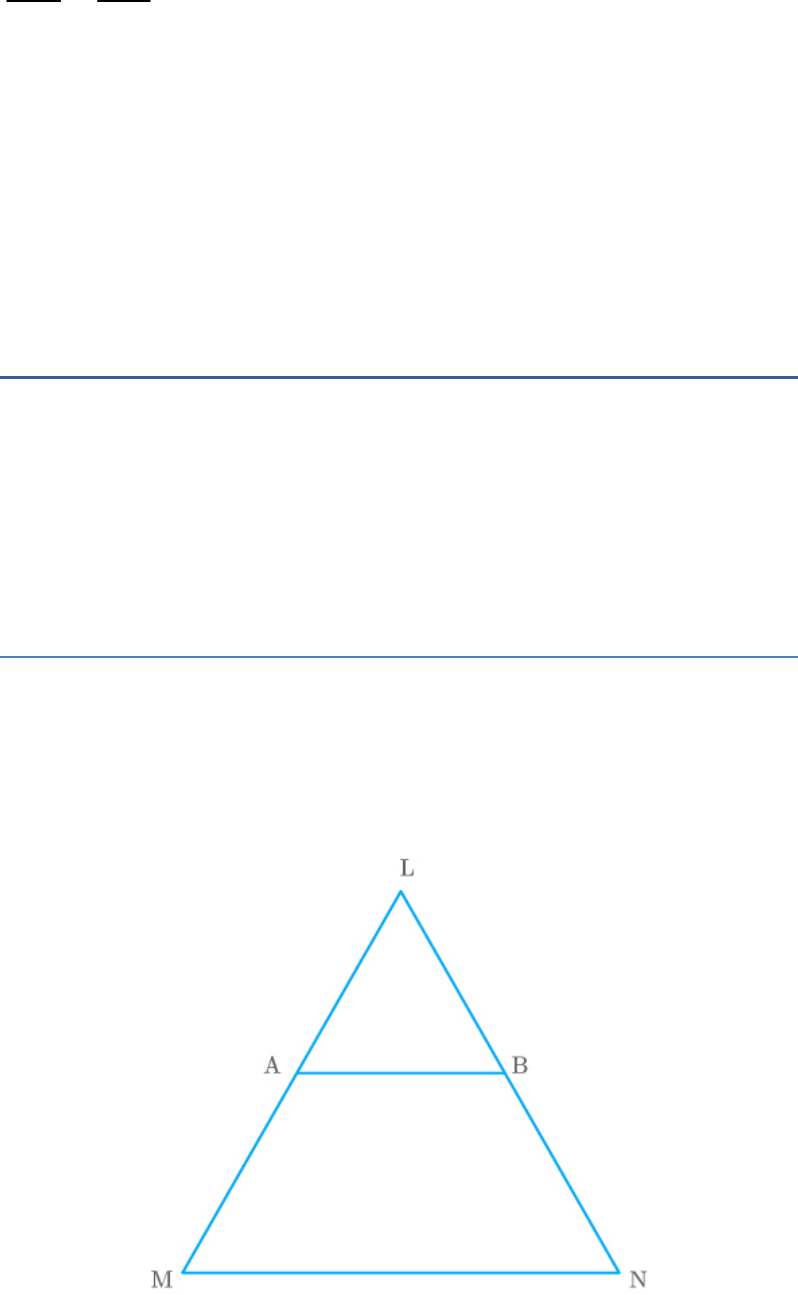
Question: 7
Using Theorem 6.1, prove that a line drawn through
the mid-point of one side of a triangle parallel to
another side bisects the third side.
Solution
Let LMN be a triangle and the line AB is drawn
through the mid-point A of LM.
Also, .
AB||MN
Fig. Exc_6.2_7

By basic proportionality theorem,
LB LA
BN AM
LB
1
BN
LA AM
LB BN
Thus, B is the mid-point of LN.
Hence, AB bisects LN at point B.
Question: 8
Using Theorem 6.2, prove that the line joining the
mid-points of any two sides of a triangle is parallel to
the third side.
Solution
Let LMN be a triangle and the line AB is drawn
through the mid-point A of LM to the mid-point B of
LN.
Thus, and
LA AM
LB BN
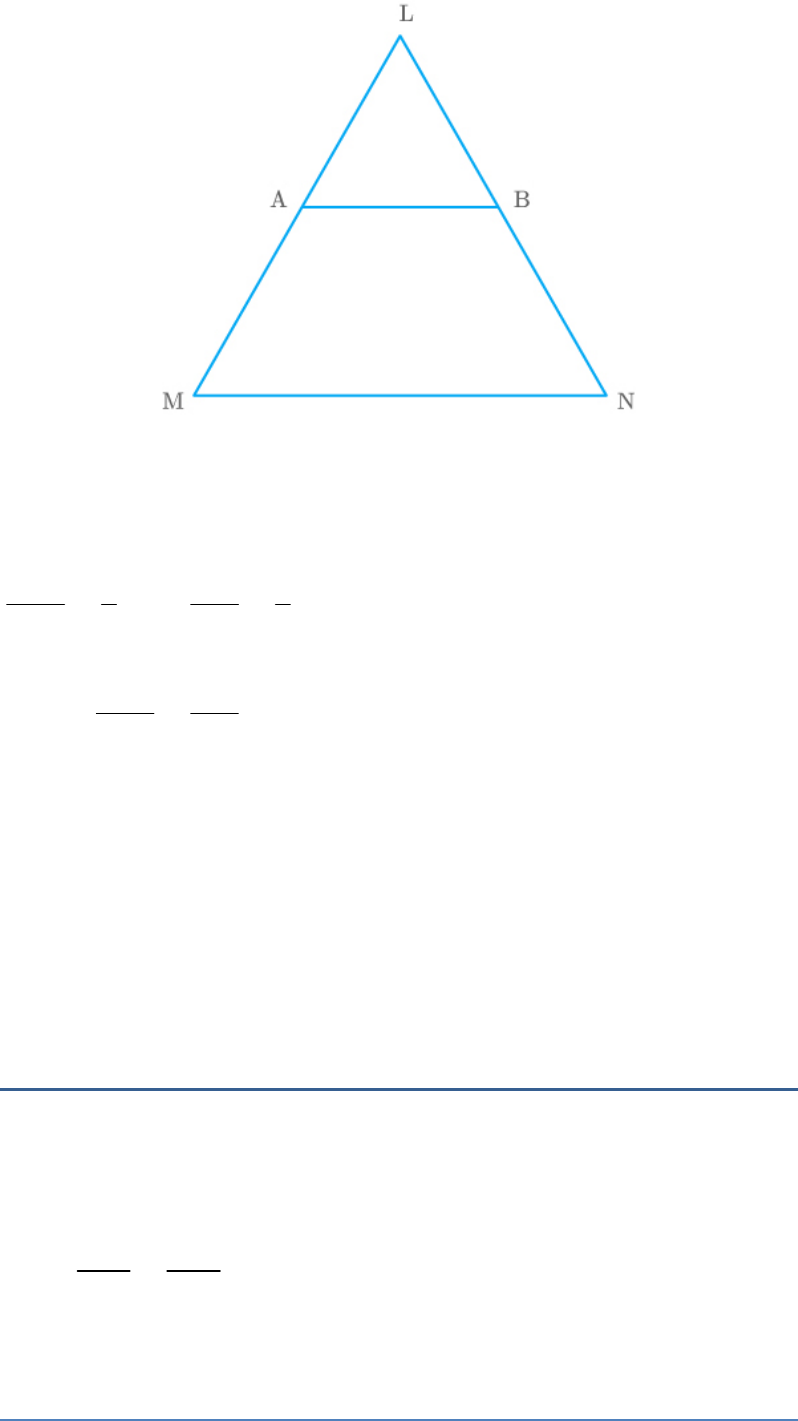
Fig. Exc_6.2_8
From the above results,
and
LA 1
AM 1
LB 1
BN 1
Thus,
LA LB
AM BN
By the converse of basic proportionality theorem,
AB||MN
Hence proved.
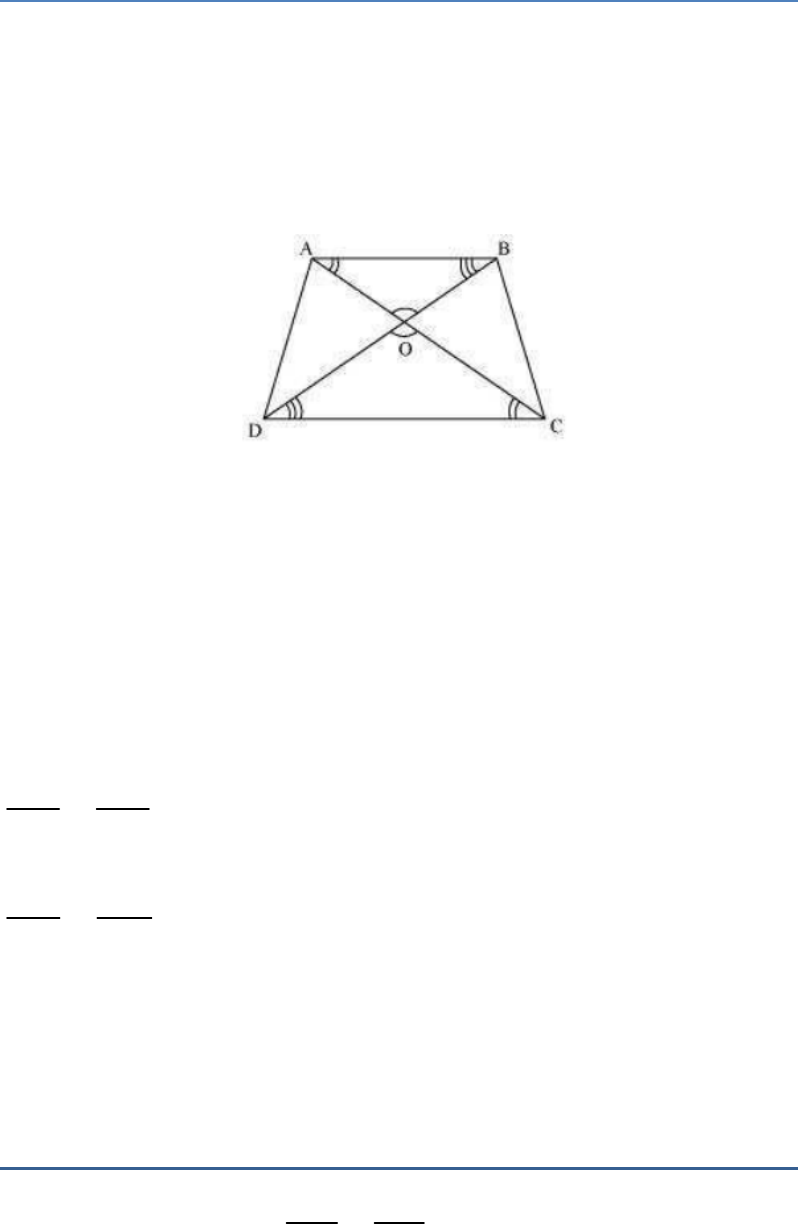
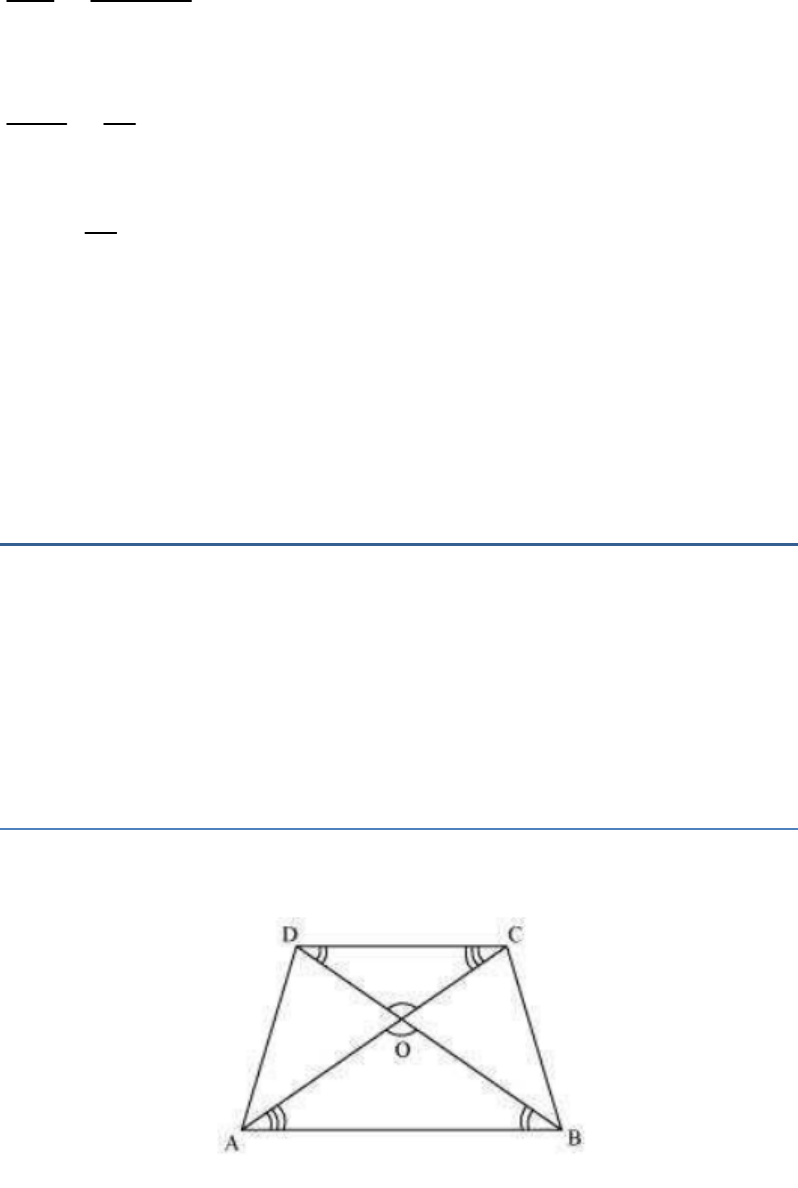
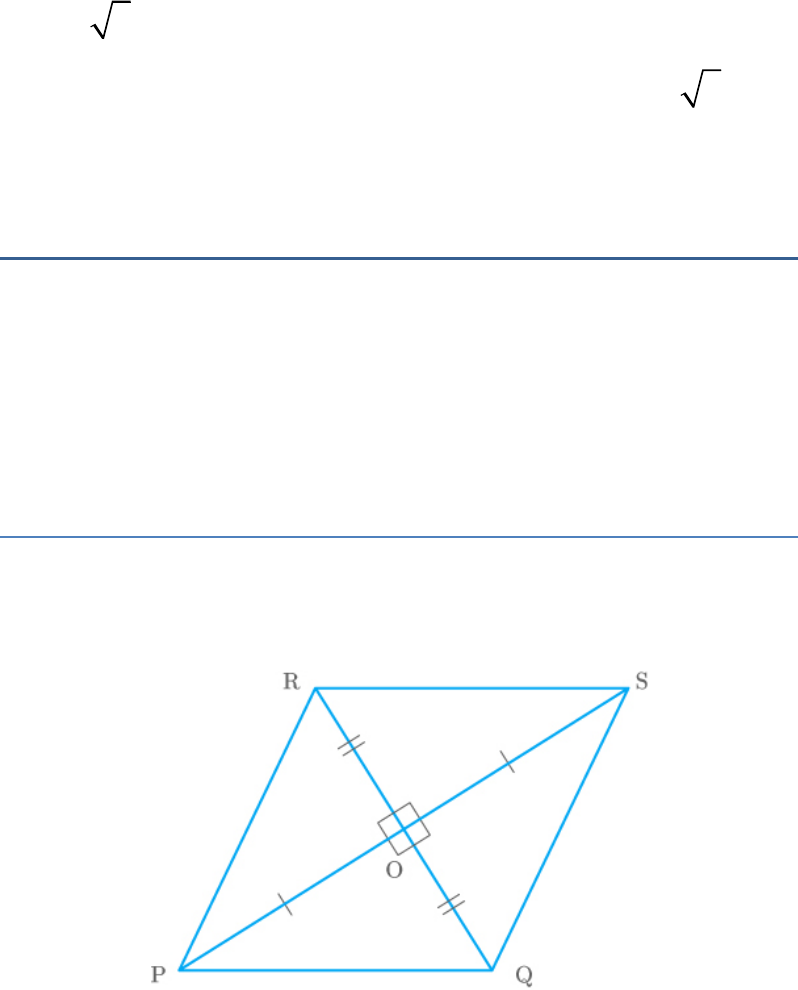
Question: 9
ABCD is a trapezium in which AB
||
DC and its
diagonals intersect each other at the point O. Show
that .
AO CO
BO DO
Solution
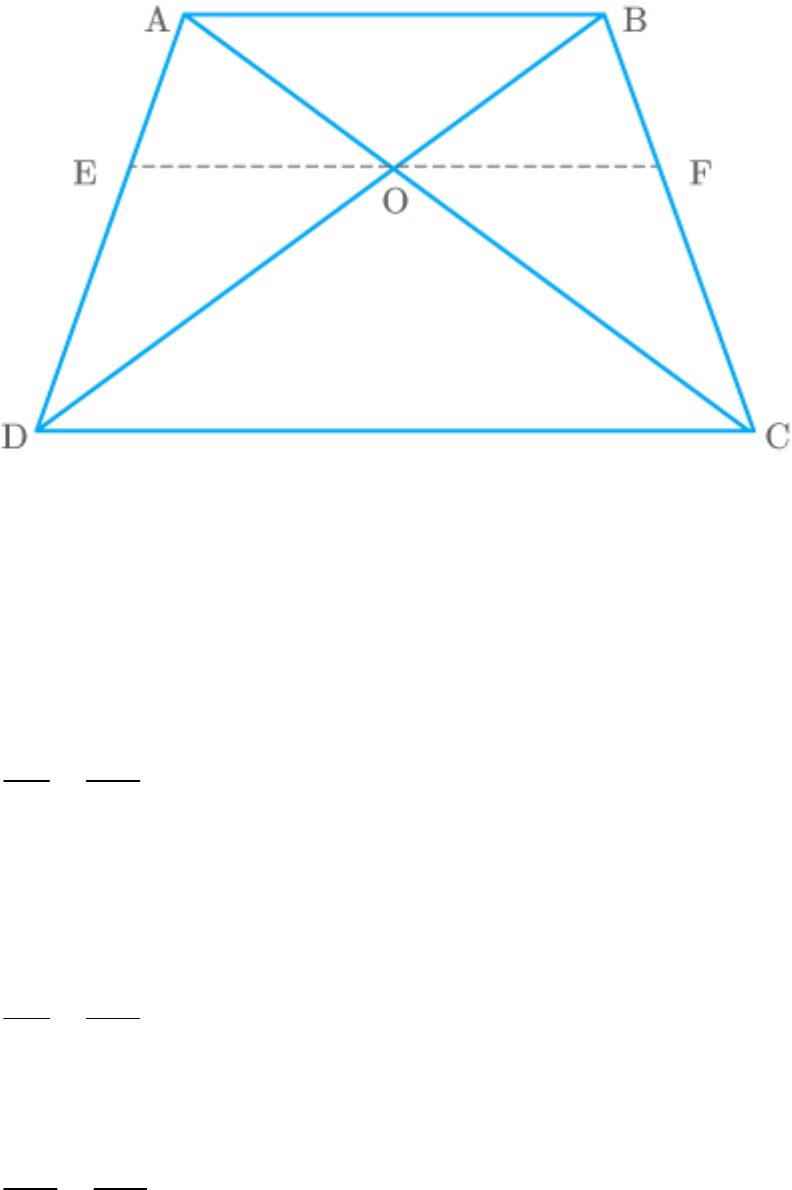
Given: A trapezium ABCD in which AB
||
DC and
diagonals of the trapezium intersect each other at
the point O.
Fig. Exc_6.2_9
Draw through O.
EF||CD
In , .
ADC
EO||CD
By the basic proportionality theorem,
)
AE AO
......(1)
ED CO
In , .
ABD
OE||AB
By the basic proportionality theorem,
AE BO
......(2)
ED DO
From equations (1) and (2).
AO BO
CO DO
AO CO
BO DO
Hence proved.
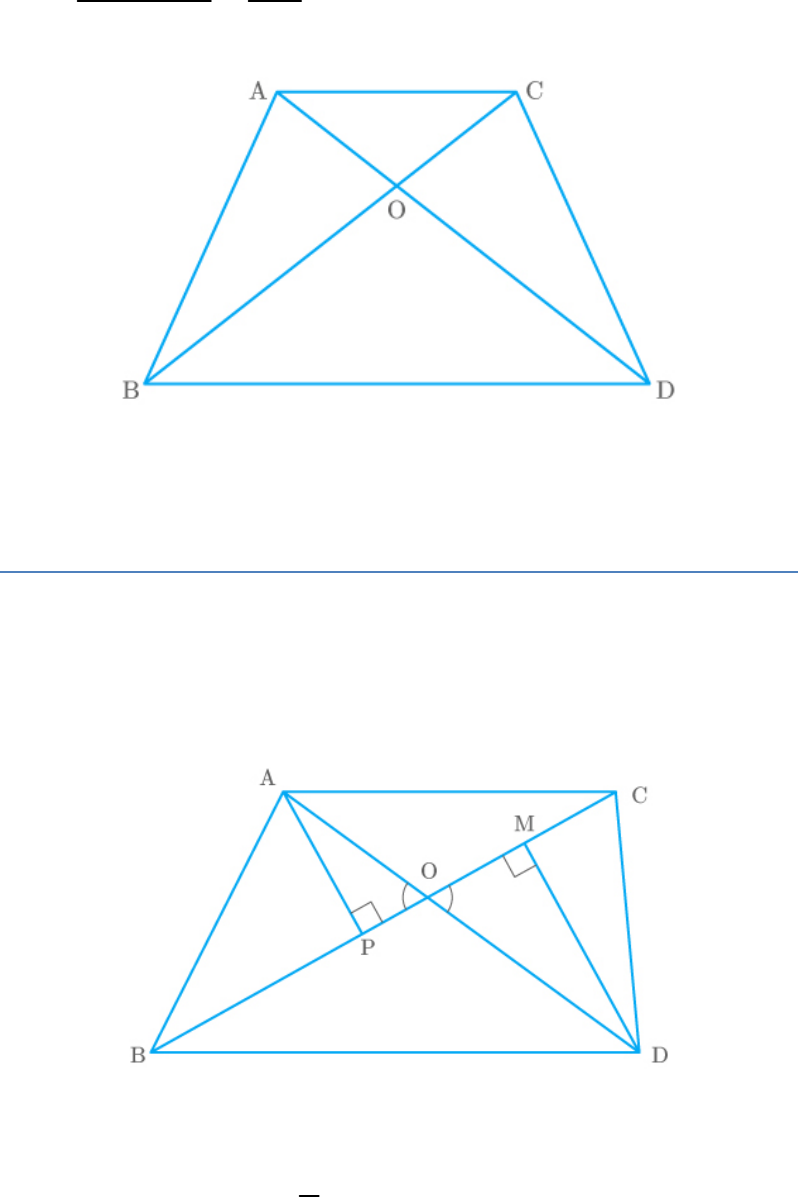
Question: 10
The diagonals of a quadrilateral ABCD intersect each
other at the point O such that . Show that
AO CO
BO DO
ABCD is a trapezium.
Solution
Given: A quadrilateral ABCD in which diagonals
intersect each other at the point O such that
.
AO CO
BO DO
Fig. Exc_6.2_10

Draw .
OE||AB
In ABD, OE || AB.
By the basic proportionality theorem,
AE BO
......(1)
ED DO
Given:
AO CO
BO DO
AO BO
......(2)
CO DO
From equations (1) and (2).
AE AO
ED CO
By the converse of basic proportionality theorem,
EO||DC
AB||EO||DC
AB||CD
Hence, ABCD is a trapezium.
Exercise 6.3 (16)
Question: 1
State which pairs of triangles in the given figure are
similar. Write the similarity criterion used by you for
answering the question and also write the pairs of
similar triangles in the symbolic form:
(i)
Fig. Exc_6.3_1 (i)
(ii)
Fig. Exc_6.3_1 (ii)
(iii)
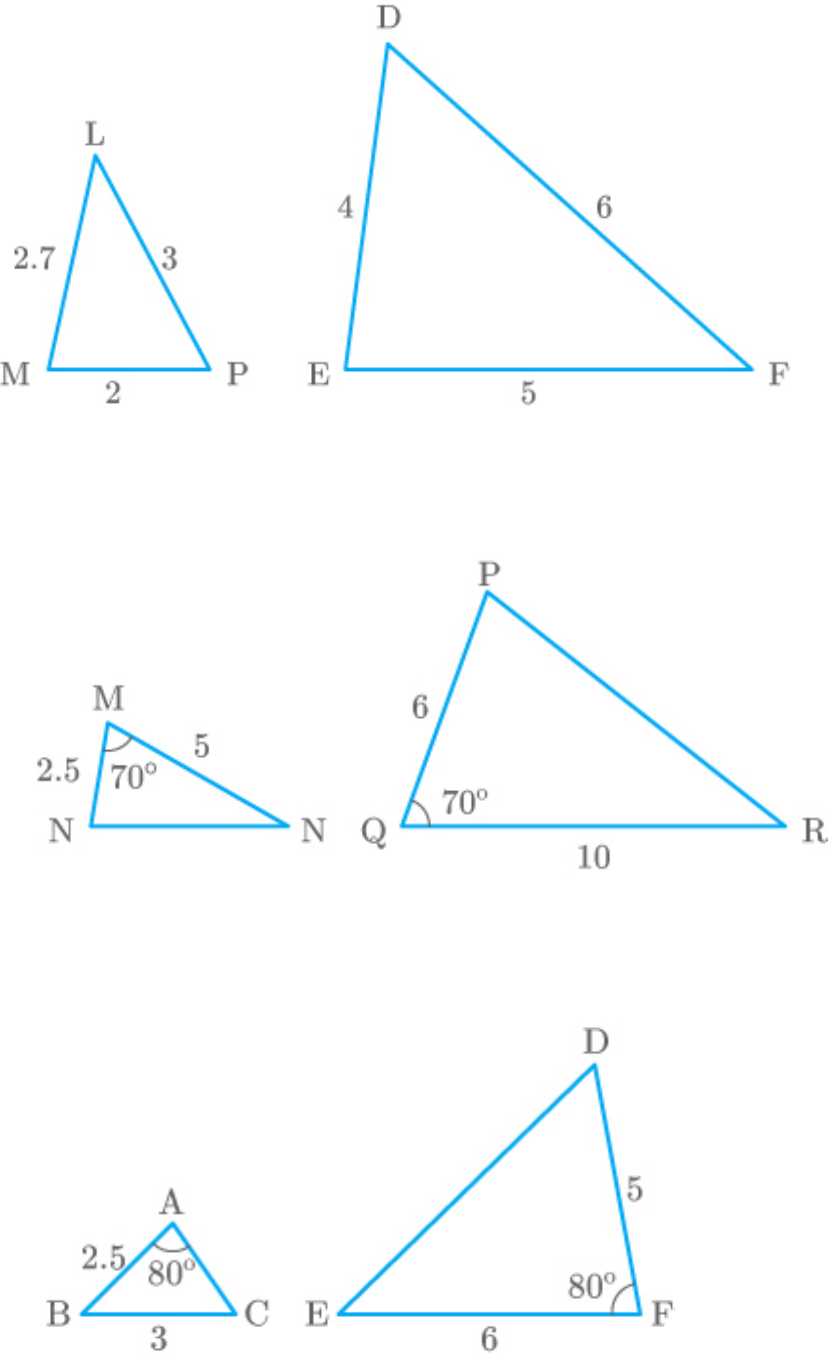
Fig. Exc_6.3_1 (iii)
(iv)
Fig. Exc_6.3_1 (iv)
(v)
Fig. Exc_6.3_1 (v)

(vi)
Fig. Exc_6.3_1 (vi)
Solution
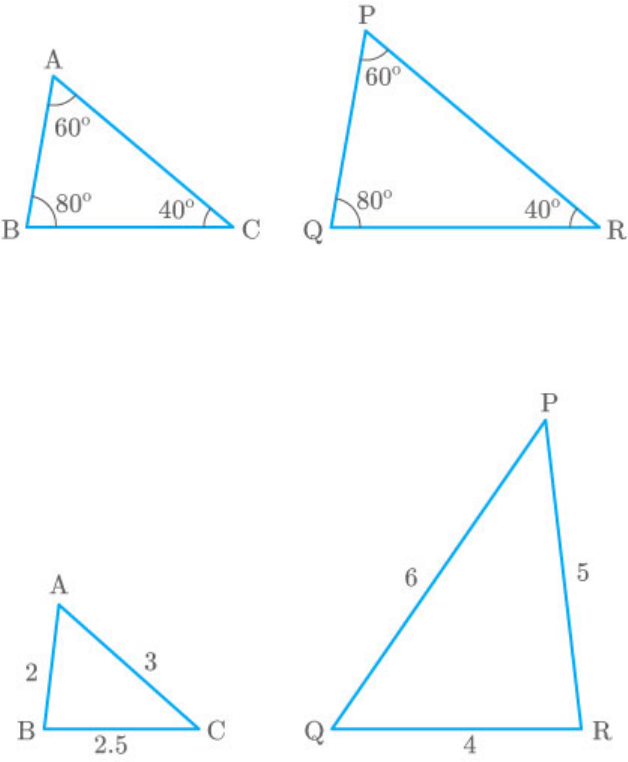
(i) From the figure,
A P 60
B Q 80
C R 40
Thus,
By AAA similarity crABC|| itePQR rion
AB BC CA
QR RP PQ
(ii) From the figure,
AB 2 1
QR 4 2
CA 3 1
PQ 6 2
BC 2.5 1
RP 5 2
Thus,

AB CA BC
QR PQ RP
Hence,
By SSS similarity crABC|| itePQR rion
(iii) From the figure,
The corresponding sides of the triangles are not
proportional.
Hence, the given triangles are not similar.
(iv) From the figure,
The corresponding sides of the triangles are not
proportional.
Hence, the given triangles are not similar.
(v) From the figure,
The corresponding sides of the triangles are not
proportional.
Hence, the given triangles are not similar.
(vi) We know that the sum of the interior angles of
a triangle is .
180
Thus, in ,
DEF
D E F 180
70 80 F 180
F 30
Similarly, in ,
PQR
P Q R 180
P 80 30 180
P 70
In and ,
DEF
PQR
D P
E Q
F R
Hence,
By AAA similarity crDEF|| itePQR rion
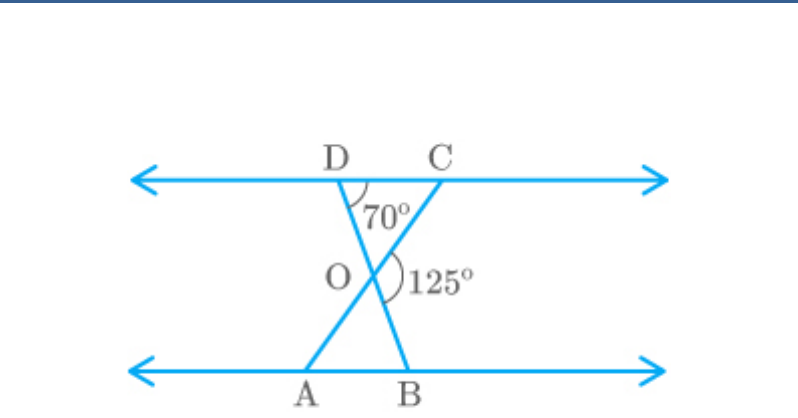
Question: 2
In the given figure, , and
ODC|| OBA
BOC 125
. Find , and .
CDO 70
DOC
DCO
OAB
Fig. Exc_6.3_2

Solution
From the figure,
The line DOB is straight.
Thus,
DOC COB 180
DOC 180 125 55
We know that the sum of the interior angles of a
triangle is .
180º
In ,
DOC
DCO CDO DOC 180
DCO 70 55 180
DCO 55
Given: .
ODC|| OBA
Thus,
OAB DCO Corresponding angles
Hence, .
OAB 55
Question: 3
Diagonals AC and BD of a trapezium ABCD with
intersect each other at the point O. Using a
AB||DC
similarity criterion for two triangles, show that
.
OA OB
OC OD
Solution
From the figure,
CDO ABO
Alternate interior angles
DCO BAO
Alternate interior angles
DOC BOA
Vertically opposite angles
Fig. Exc_6.3_3
Thus,
DOC|| BOA By AAA similarity criterion
Thus,
DO OC
BO OA
OA OB
OC OD
Hence proved.
Question: 4
In the given figure, and . Show
QR QT
QS PR
1 2
that .
PQS TQR:
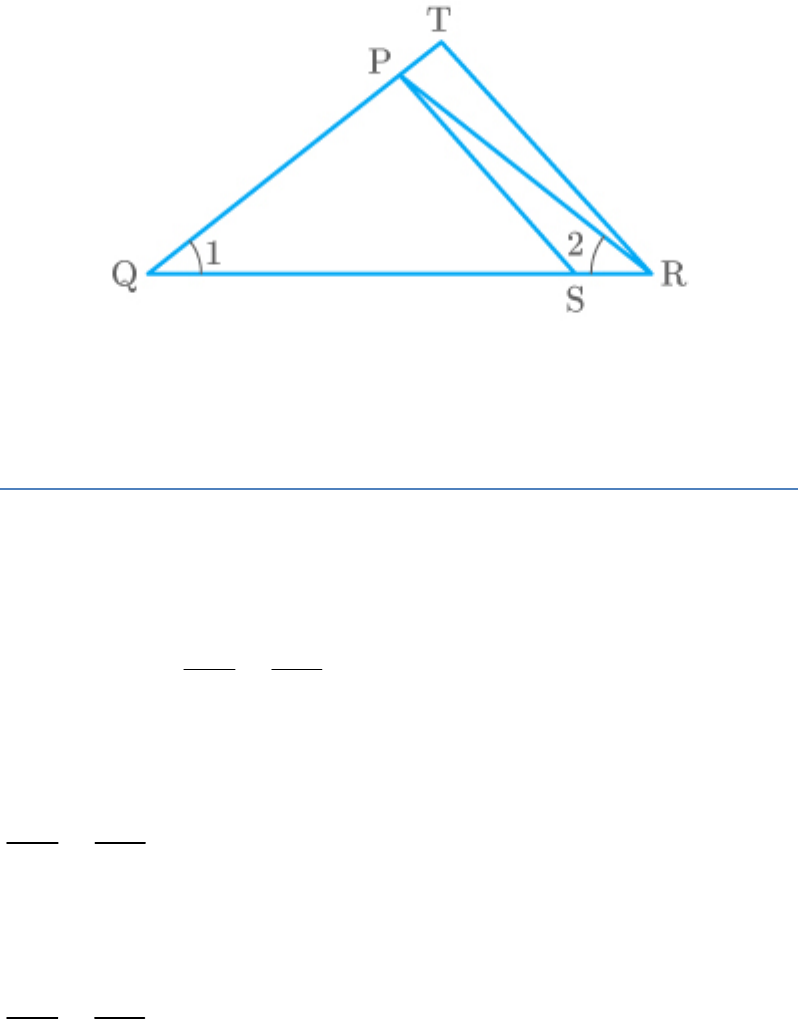
Fig. Exc_6.3_4
Solution
Given:
1 2
Thus,
.....PQ PR .(1)
Also, given:
QR QT
QS PR
From equation (1),
QR QT
......(2)
QS QP
In and ,
PQS
TQR
QR QT
QS QP
So, Q Q
Thus,
PQS|| TQR By SASsimilarity criterion
Hence proved.
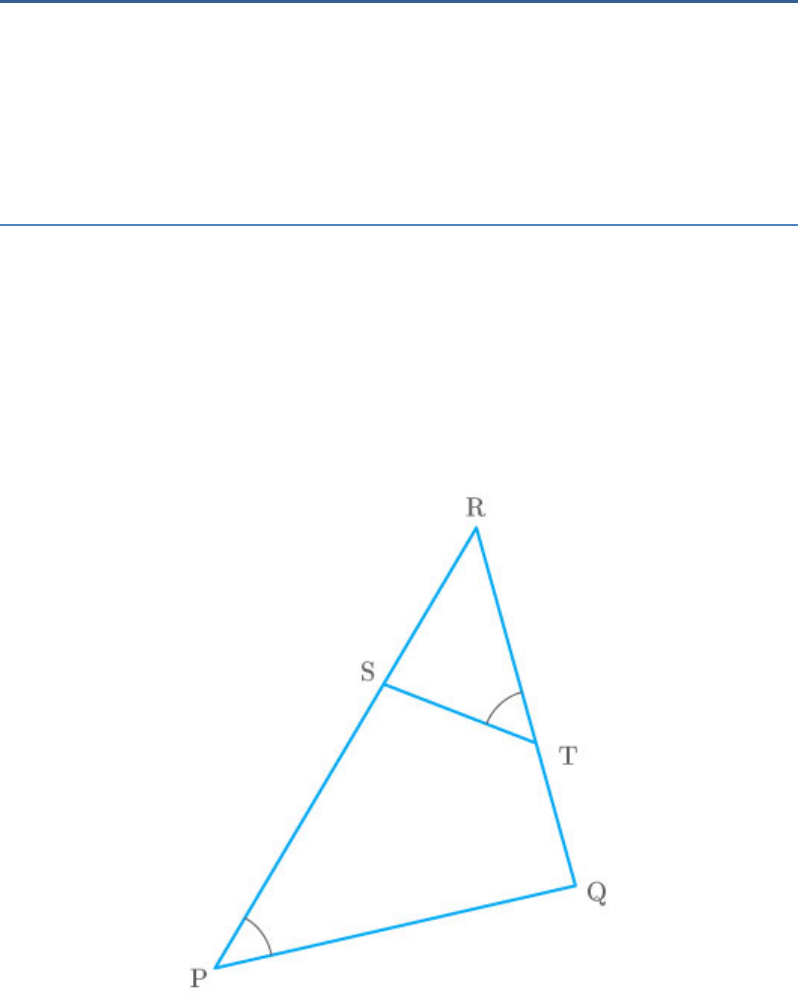
Question: 5
S and T are points on sides PR and QR of such
PQR
that . Show that .
P RTS
RPQ|| RTS
Solution
From the figure,
In and ,
RPQ
RST
RTS QPS
R R
Common angle
Fig. Exc_6.3_5
Thus,
RPQ|| RTS By AA similarity criterion
Hence proved.
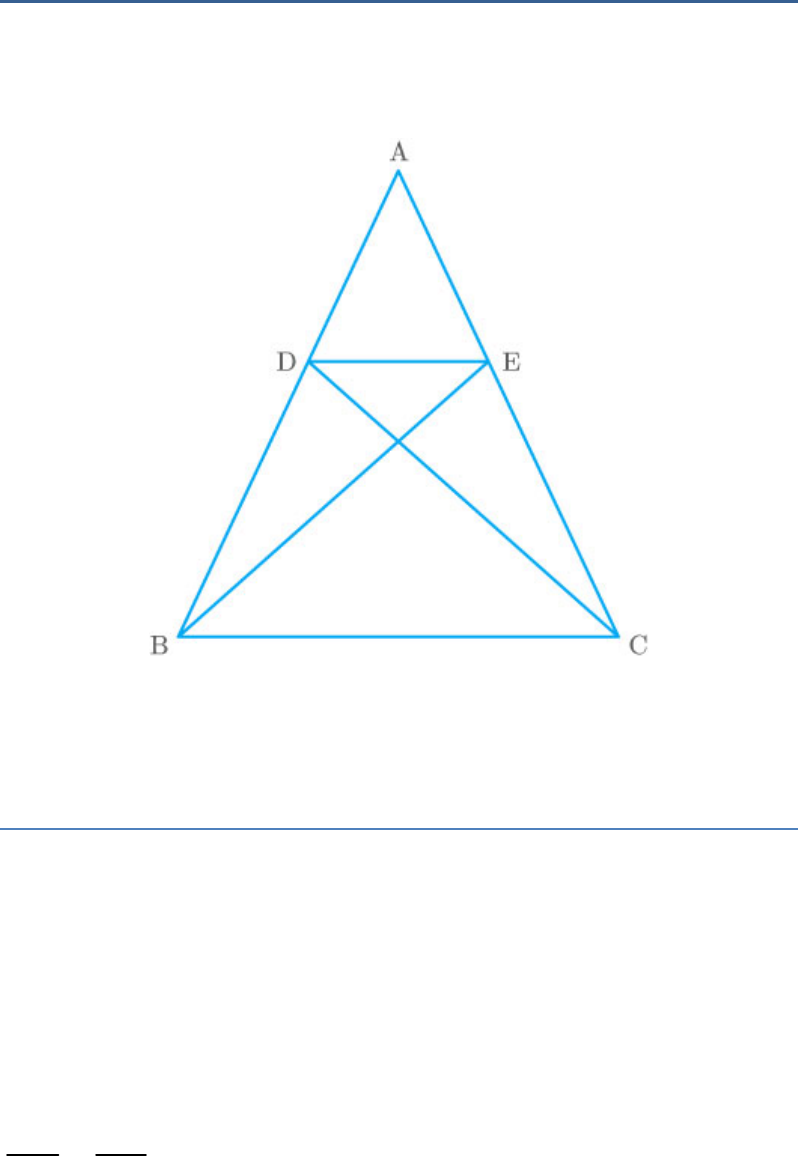
Question: 6
In the given figure, if , show that
ABE ACD
.
ADE|| ABC
Fig. Exc_6.3_6
Solution
Given:
ABE ACD
AB AC By CPCT ......(1)
By CPCT .....AD AE .(2)
Divide equation (2) by (1).
AD AE
AB AC
In and ,
ADE
ABC
A A
Common angle
AD AE
AB AC
Thus,
ADE|| ABC By SAS similarity criterion
Hence proved.
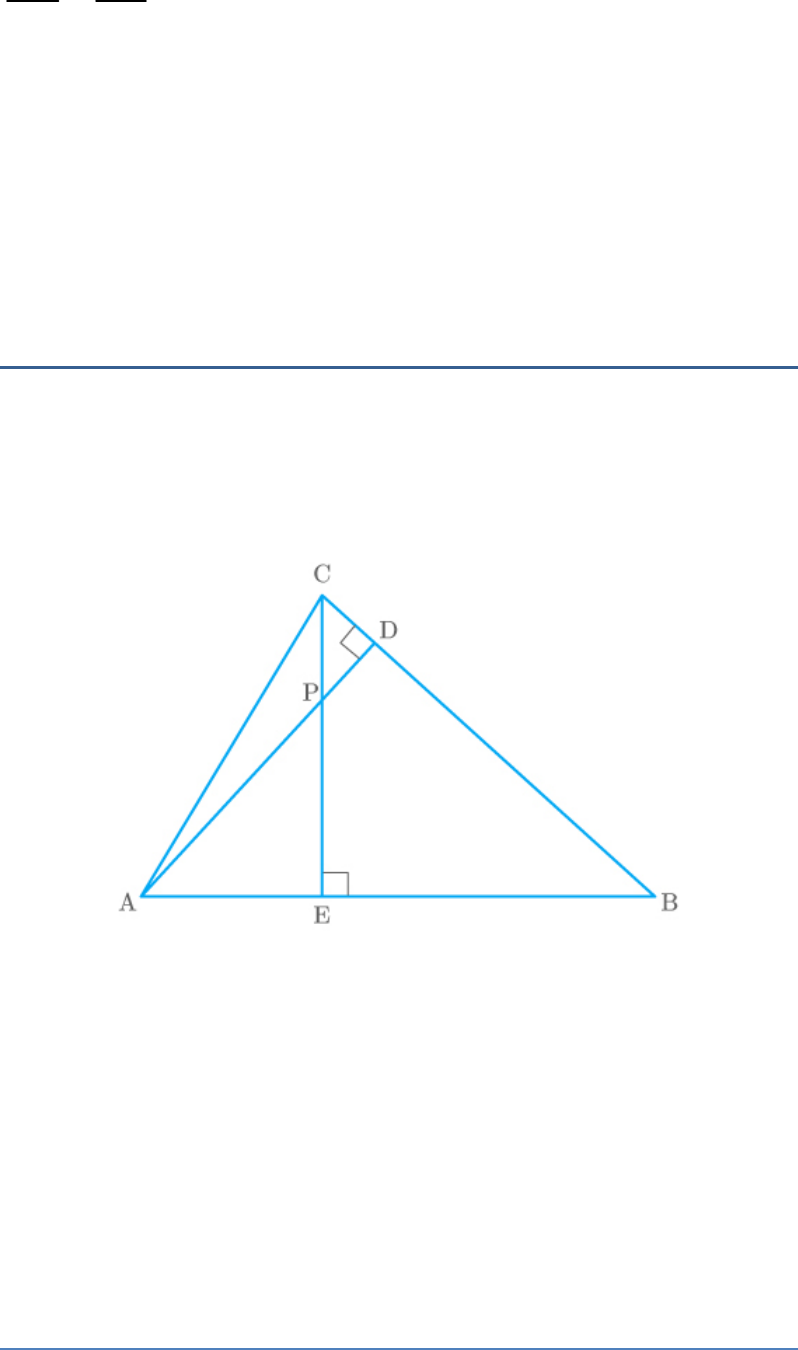
Question: 7
In the given figure, altitudes AD and CE of
ABC
intersect each other at the point P.
Fig. Exc_6.3_7
Show that:
(i)
AEP|| CDP
(ii)
ABD|| CBE
(iii)
AEP|| ADB
(iv)
PDC|| BEC

Solution
(i)
AEP|| CDP
In and ,
AEP
CDP
AEP CDP
Each angleisof 90
APE CPD
Vertically opposite angles
Hence,
AEP|| CDP AA similarity criterion
(ii)
ABD|| CBE
In and ,
ABD
CBE
ADB CEB
Each angleisof 90
ABD CBE
Common
Hence,
ABD|| CBE By AA similarity criterion
(iii)
AEP|| ADB
In and ,
AEP
ADB
AEP ADB
Each angleisof 90
PAE DAB
Common
Hence,
AEP|| ADB By AA similarity criterion
(iv)
PDC|| BEC
In and ,
PDC
BEC
PDC BEC
Each angleisof 90
PCD BCE
Common angle
Hence,
PDC|| BEC By AA similarity criterion
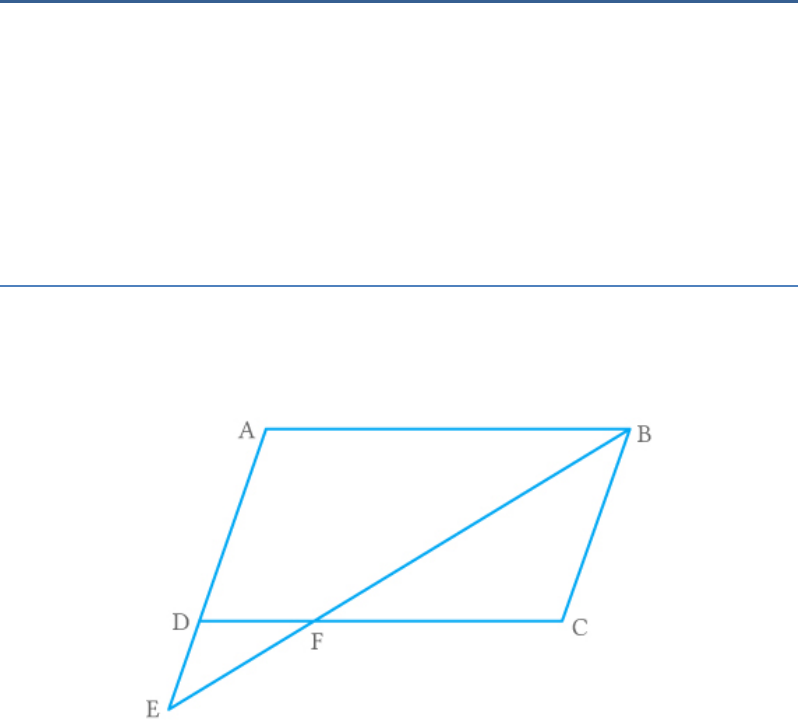
Question: 8
E is a point on the side AD produced of a
parallelogram ABCD and BE intersects CD at F.
Show that .
ABE|| CFB
Solution
From the figure,
In and ,
ABE
CFB
Fig. Exc_6.3_8
A C
Opposite angles of a parallelogram
Thus,
AEB CBF
Alternate interior angles
ABE|| CFB
By AA similarity criterion

Question: 9
In the given figure, ABC and AMP are two right
triangles, right angled at B and M respectively.
Fig. Exc_6.3_9
Prove that:
(i)
ABC|| AMP
(ii)
CA BC
PA MP
Solution
(i) To Prove:
ABC|| AMP
In and ,
ABC
AMP
ABC AMP
Each angleisof 90
A A
Common
Thus,
ABC|| AMP By AA similarity criterion

(ii) To Prove:
CA BC
PA MP
We have proved that .
ABC|| AMP
We know that the corresponding sides of similar
triangles are proportional.
Thus, in and ,
ABC
AMP
CA BC
PA MP
Hence, proved.
Question: 10
CD and GH are respectively the bisectors of
ACB
and such that D and H lie on sides AB and FE
EGF
of ABC and EFG respectively. If ,
ABC FEG:
show that:
(i)
CD AC
GH FG
(ii)
DCB|| HGE
(iii)
DCA|| HGF
Solution

Fig. Exc_6.3_10
Given: .
ABC|| FEG
Thus,
A F
B E
ACB FGE
Now,
ACD FGH Angle bisector
DCB HGE Angle bisector
(i) To Prove:
CD AC
GH FG
In and ,
ACD
FGH
A F
ACD FGH
ACD|| FGH By AA similarity criterion
Thus,
CD AC
GH FG

(ii) To Prove:
DCB|| HGE
In and ,
DCB
HGE
DCB HGE
B E
Thus,
DCB|| HGE By AA similarity criterion
(iii) To Prove:
DCA|| HGF
In and ,
DCA
HGF
ACD FGH
A F
Thus,
DCA|| HGF By AA similarity criterion
Question: 11
In the given figure, E is a point on side CB produced
of an isosceles triangle ABC with AB AC. If AD
BC and EF AC, prove that .
ABD|| ECF
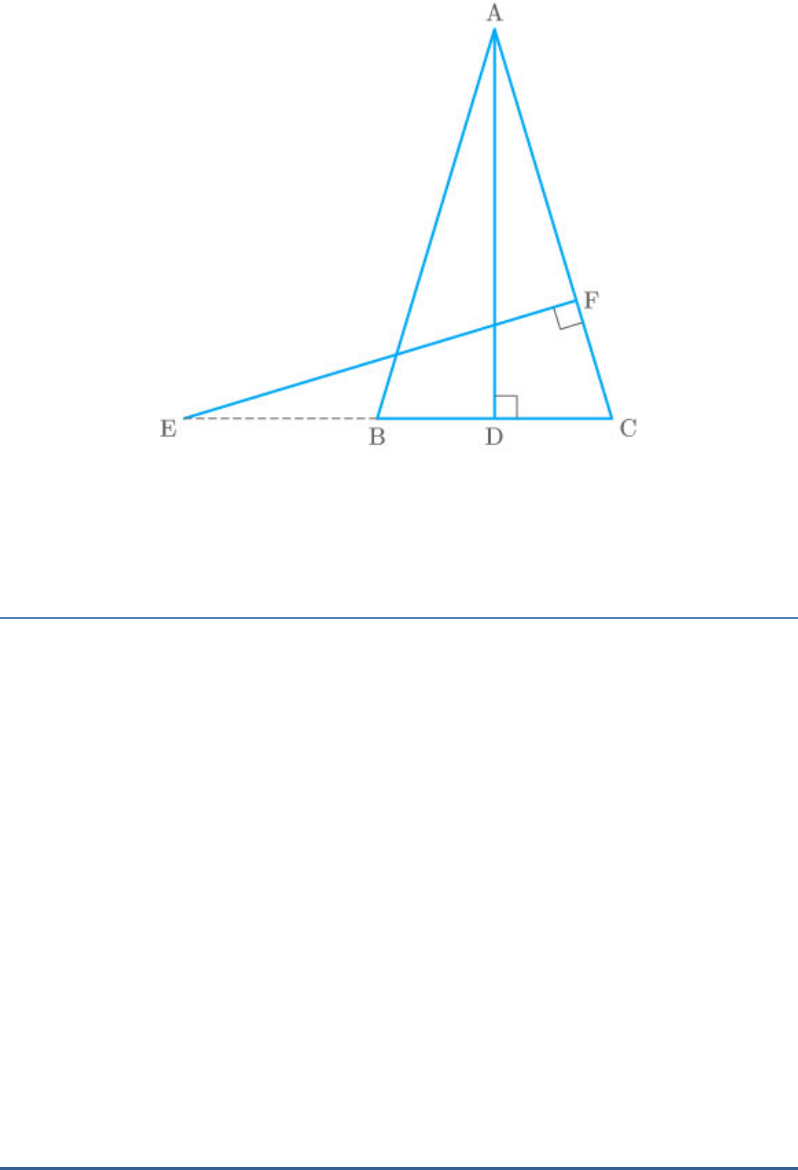
Fig. Exc_6.3_11
Solution
Given: An isosceles triangle ABC.
AB AC
Thus, .
ABD ECF
In and ,
ABD
ECF
ADB EFC Each angleisof 90
BAD CEF
Thus,
ABD|| ECF By AA similarity criterion
Question: 12
Sides AB and BC and median AD of a triangle ABC
are respectively proportional to sides PQ and QR and
median PM of . Show that
PQR
ABC|| PQR

Fig. Exc_6.3_12
Solution
Given:
AB BC AD
PQ QR PM
BC
AB AD
2
QR
PQ PM
2
We know that the median of a triangle divides the
opposite side.
Thus, and
BC
BD
2
QR
QM
2
Thus,
AB BD AD
PQ QM PM
In and ,
ABD
PQM
AB BD AD
PQ QM PM
Thus,
ABD|| PQM By SSS similarity criterion
ABD PQM Corresponding angles
In and ,
ABC
PQR
ABD PQM Corresponding angles
AB BC
PQ QR
Thus,
ABC|| PQR By SAS similarity criterion
Hence proved.
Question: 13
D is a point on the side BC of a triangle ABC such
that . Show that .
ADC BAC
2
CA CB.CD
Solution
Given:
ADC BAC
Fig. Exc_6.3_13

In and ,
ADC
BAC
ADC BAC
ACD BCA Common angle
Thus,
ADC|| BAC By AA similarity criterion
In similar triangles, corresponding sides are in
proportion.
Thus,
CA CD
CB CA
2
CA CB CD
Hence proved.
Question: 14
Sides AB and AC and median AD of a triangle ABC
are respectively proportional to sides PQ and PR and
median PM of another triangle PQR. Show that
.
ABC|| PQR
Solution
Given:
AB AC AD
PQ PR PM
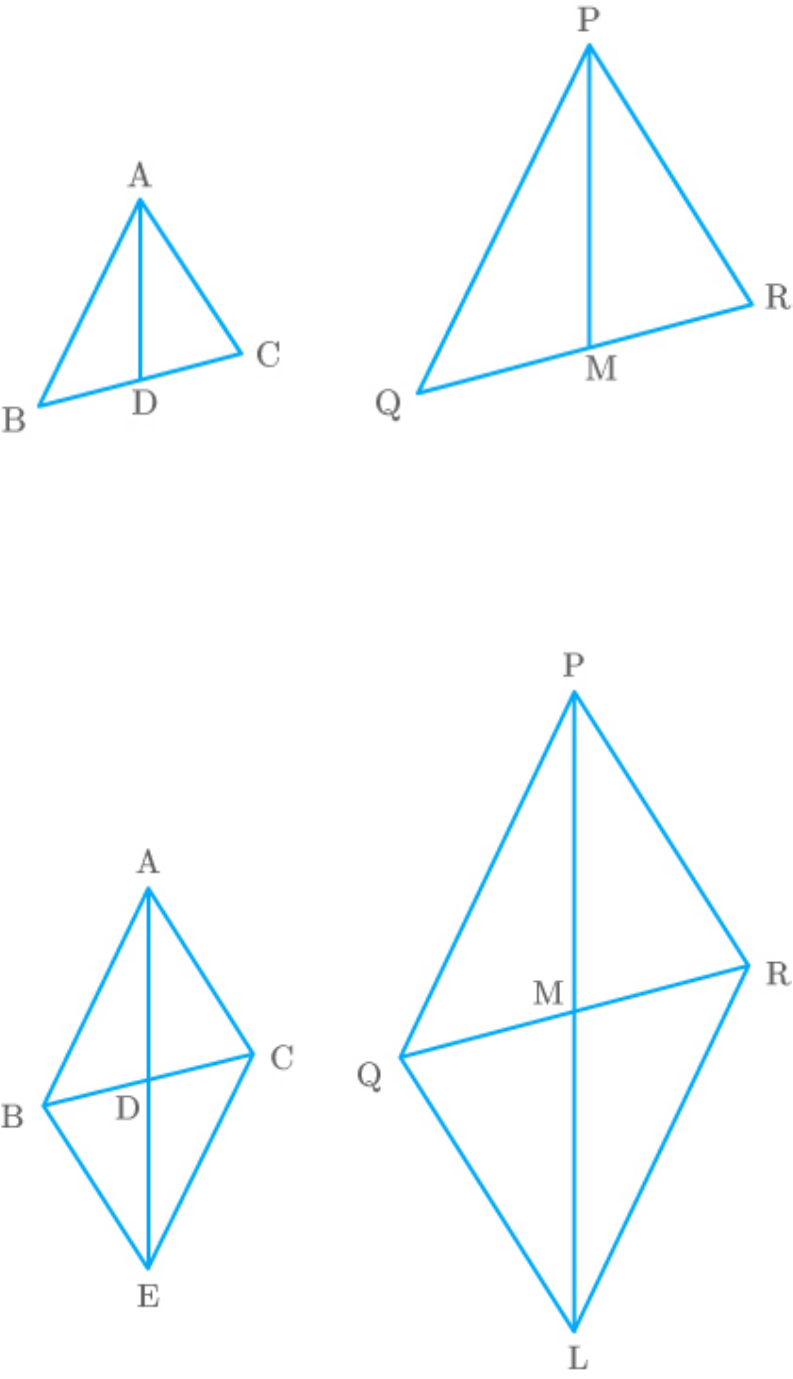
Fig. Exc_6.3_14 (i)
Expand AD and PM to the points E and L such that
AD DE and PM ML

Fig. Exc_6.3_14 (ii)
Join B to E, C to E, Q to L, and R to L.
Since median of a triangle divides the opposite side.
So,BD DC
QM MR
AD DE By construction
PM ML By construction
Diagonals AE and BC of quadrilateral ABEC, bisect
each other at point D.
Thus, ABEC is a parallelogram.
AC BE Opposite sides of a parallelogram
AB EC Opposite sides of a parallelogram
Similarly,
Quadrilateral PQLR is a parallelogram.
Thus,
PR QL
PQ LR
Given:
AB AC AD
PQ PR PM
AB AC 2AD
PQ PR 2PM
From the figure,
and
2AD AE
2PM PL
Thus,
AB AC AE
PQ PR PL
Thus,
ABE|| PQL By SSS similarity criterion
Similarly,
AEC|| PLR
BAE QPL Corresponding angles ......(1)
CAE RPL Corresponding angles ......(2)
Add equations (1) and (2).
BAE CAE QPL RPL
CAB RPQ ......(3)
In ABC and PQR,
AB AC
PQ PR
CAB RPQ
Thus,
ABC|| PQR By SAS similarity criterion
Hence proved.
Question: 15
A vertical pole of length 6 m casts a shadow 4 m long
on the ground and at the same time a tower casts a
shadow 28 m long. Find the height of the tower.
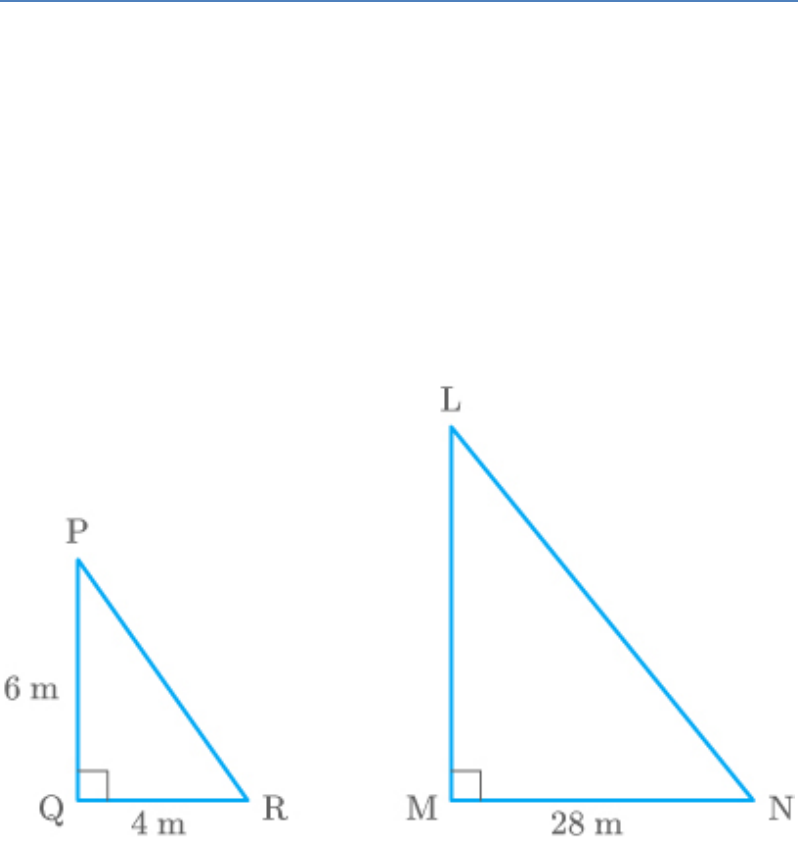
Solution
Let LM be a tower and PQ be a pole of length 6 m.
Let MN and QR be the shadow of LM and PQ
respectively.
MN 28m
PQ 6m
QR 4m
Fig. Exc_6.3_15
The rays of the sun falls on the tower and the pole at
the same time and at the same angle.
So, from the figure
QPR MLN
QRP MNL
(Tower and pole are standing
PQR LMN
vertically on the ground)

Thus,
|| By AAA similarity critPQR LMN erion
LM MN
PQ QR
LM 28
6 4
28
LM 6
4
LM 42
Hence, the height of the tower is 42 m.
Question: 16
If AD and PM are medians of triangles ABC and
PQR, respectively where , prove that
ABC|| PQR
.
AB AD
PQ PM
Solution
Given: .
ABC|| PQR
Since, the corresponding sides of similar triangles
remain in proportion.
AB AC BC
PQ PR QR
A P
B Q
C R
Fig. Exc_6.3_16
Also, .
BC
AB AC
2
QR
PQ PR
2
We know that medians divide their opposite sides
equally.
Thus, and
BC
BD
2
QR
QM
2
Thus,
AB AC BD
PQ PR QM
In ABD and PQM,
AB BD
PQ
B Q
QM
Thus,
ABD|| PQM By SAS similarity criterion
Thus,
AB BD AD
PQ QM PM
Hence proved.
Exercise 6.4 (9)
Question: 1
Let and their areas be, respectively, 64
ABC|| DEF
and 121 . If EF 15.4 cm, find BC.
2
cm
2
cm
Solution
Given: .
ABC|| DEF
Thus,
2 2 2
ar ABC
AB BC AC
ar DEF DE EF DF
Also, given:
EF 15.4 cm
2
ar ABC 64cm
2
ar DEF 121cm
2
ar ABC
BC
ar DEF EF
2
2
BC
64
121
15.4
BC 8
15.4 11
8
BC 15.4
11
BC 11.2
Hence, cm
BC 11.2
Question: 2
Diagonals of a trapezium ABCD with AB DC
||
intersect each other at the point O. If AB 2CD, find
the ratio of the areas of triangles AOB and COD.
Solution
Given: A trapezium ABCD with AB DC.
||
Fig. Exc_6.4_2
In and ,
AOB
COD

AOB COD Vertically opposite angles
OAB OCD Alternate interior angles
OBA ODC Alternate interior angles
Thus,
AOB|| COD By AAA similarity criterion
Thus,
2
ar AOB
AB
ar COD CD
Given: AB 2CD
Thus,
2
ar AOB
2CD
ar COD CD
2
ar AOB
2
ar COD 1
ar AOB
4
ar COD 1
Hence, the ratio of the areas of triangles AOB and
COD is .
4:1
Question: 3
In the given figure, ABC and DBC are two triangles
on the same base BC. If AD intersects BC at O, show
that .
ar ABC
AO
ar DBC DO
Fig. Exc_6.4_3 (Ques.)
Solution
Given: Two triangles ABC and DBC on the same
base BC and AD intersects BC at O.
Draw two perpendiculars AP and DM on BC.
Fig. Exc_6.4_3 (Sol)
Area of a triangle
1
base height
2

1
BC AP
ar ABC
AP
2
1
ar DBC DM
BC DM
2
......(1)
In and ,
APO
DMO
APO DMO Each angleisof 90
AOP DOM Vertically opposite angles
Thus,
APO DMO By AA similarity criterion:
So,
..
AP AO
D
...
M DO
.(2)
From (1) and (2),
ar ABC
AO
ar DBC DO
Hence proved.
Question: 4
If the areas of two similar triangles are equal, prove
that they are congruent.
Solution
Let ABC and XYZ be two similar triangles.
2 2 2
ar ABC
AB BC AC
ar PQR XY Y
....
Z XZ
..(1)

Given:
ar ABC ar XYZ
ar ABC
1 .....
ar XYZ
.(2)
From equations (1) and (2).
2 2 2
AB BC AC
1
XY YZ XZ
Thus,
AB XY
BC YZ
AC XZ
Thus,
ABC XYZ By SSScongruencecriterion
Hence proved.
Question: 5
D, E and F are respectively the mid-points of sides
AB, BC and CA of ABC. Find the ratio of the areas
of DEF and ABC.
Solution
Given: A triangle ABC in which D and E are the mid-
points of AB and BC.
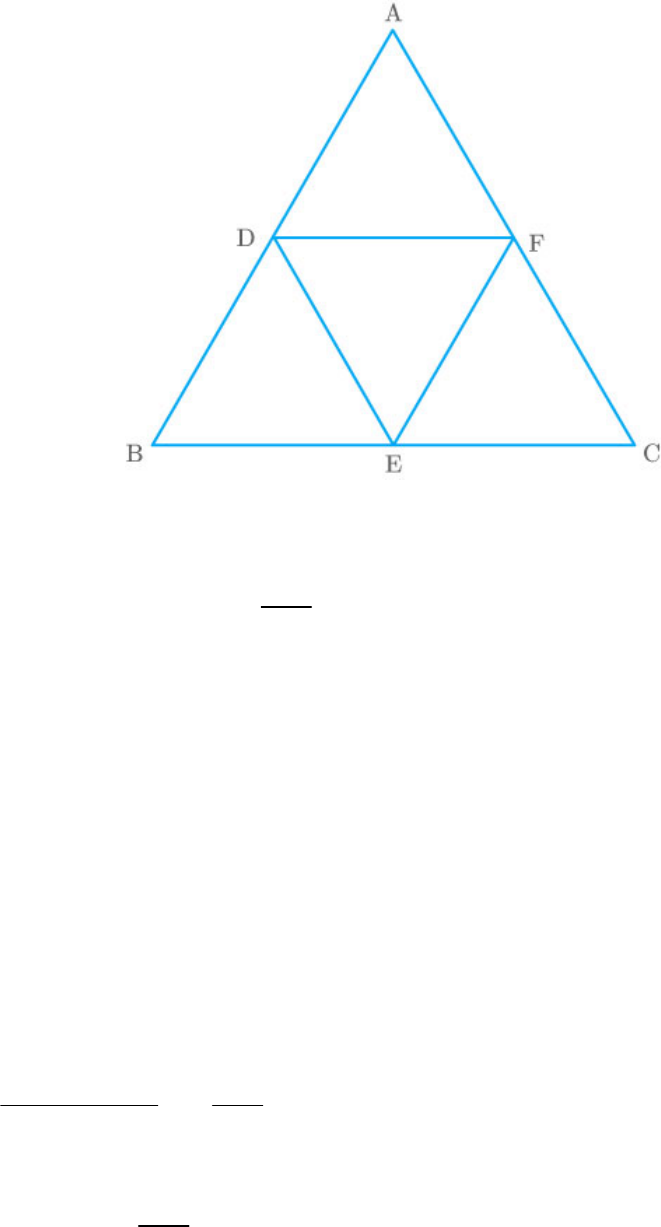
Fig. Exc_6.4_5
and
DE||AC
AC
DE
2
In and ,
BED
BCA
BED BCA Corresponding angles
BDE BAC Corresponding angles
EBD CBA Common angles
Thus,
BED BCA By AAA similarity crite|| rion
2
ar BED
DE
ar BCA AC
Put in above expression.
AC
DE
2
2
AC
ar BED
2
ar BCA AC
ar BED
1
ar BCA 4
1
ar BED ar BC ....A
4
..(1)
Similarly,
1
ar CFE ar CB ....A
4
..(2)
1
ar ADF ar AB ....C
4
..(3)
ar DEF ar ABC ar BED ar CFE ar ADF
From equations (1), (2) and (3).
3
ar DEF ar ABC ar ABC
4
1
ar DEF ar ABC
4
ar DEF
1
ar ABC 4
Question: 6
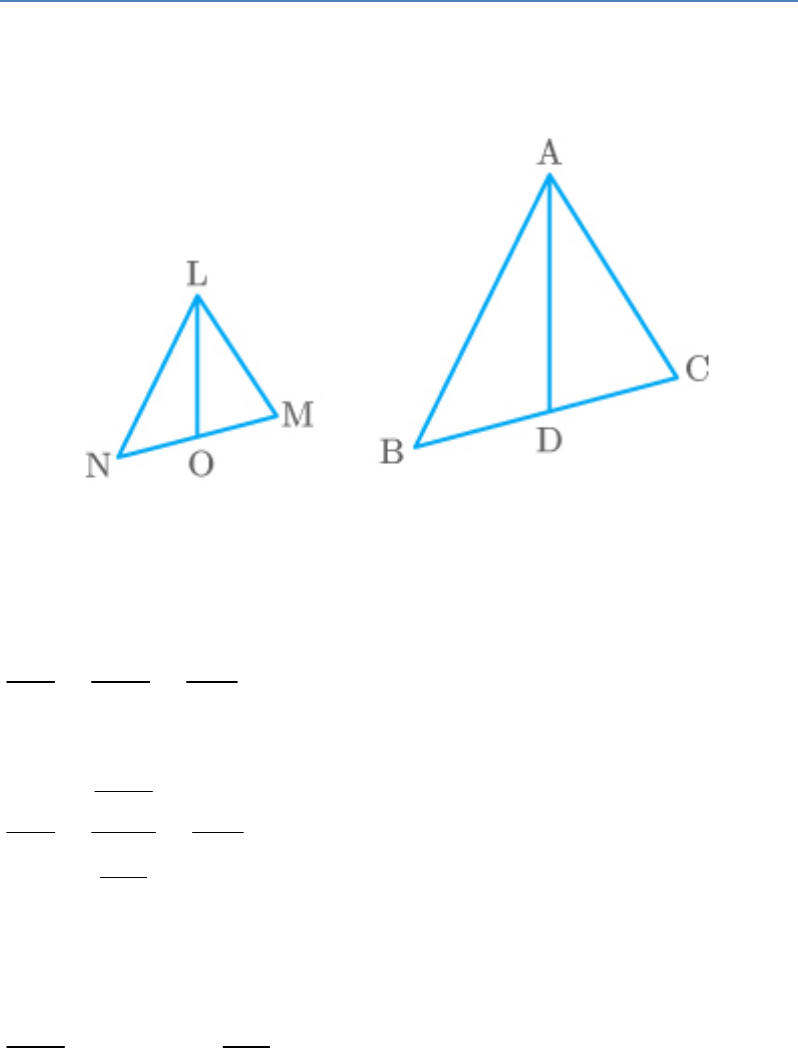
Prove that the ratio of the areas of two similar
triangles is equal to the square of the ratio of their
corresponding medians.
Solution
Let LMN and ABC be two similar triangles with
medians LO and AD respectively.
Fig. Exc_6.4_6
Since ,
||LMN ABC
LN NM LM
AB BC AC
NM
LN L
.
M
2
..
BC
AB
..
AC
2
.(1)
Since LO and AD are medians,
and
NM
NO
2
BC
BD
2
Thus,
LN NO LM
AB BD AC
From the figure,
L A
N B
M C
In and ,
LNO
ABD
N B
LN NO
AB BD
|| By SAS similarity critLNO ABD erion
Thus,
LN NO LO
....
A
.
B BD AD
.(2)
2 2 2
ar LMN
LN NM LM
ar ABC AB BC AC
From equations (1) and (2).
LN NM LM LO
AB BC AC AD
Thus,
2
ar LMN
LO
ar ABC AD
Hence proved.
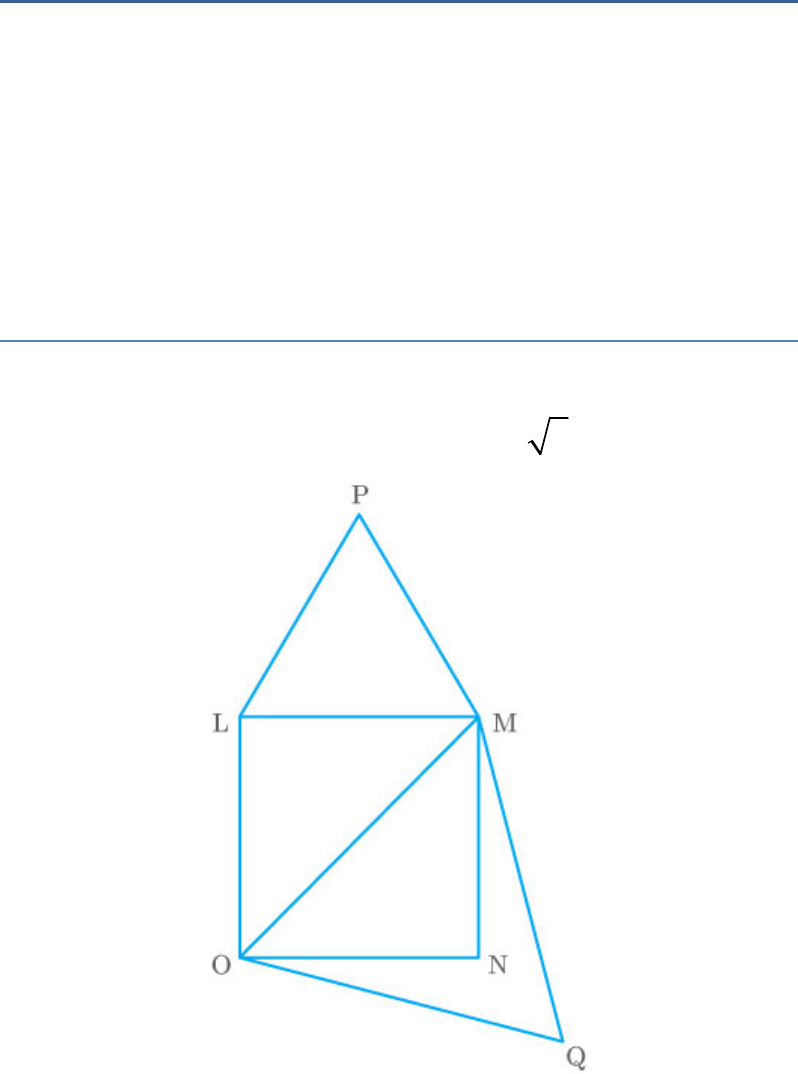
Question: 7
Prove that the area of an equilateral triangle
described on one side of a square is equal to half the
area of the equilateral triangle described on one of its
diagonals.
Solution
Let LMNO be a square of side .
k
The length of diagonal of LMNO
2k
Fig. Exc_6.4_7
LMP is an equilateral triangle described on one of
the sides of the square and OMQ is an equilateral

triangle described on one of the diagonals of the
square.
Length of the side of LMP
k
Length of the side of OMQ
2k
All equilateral triangles have sides of the same length
and their angles as .
60
Thus, equilateral triangles are similar to each other.
Now, find the ratio between the areas of LMP and
OMQ
2
ar
k 1
a
LMP
r
2
OMQ 2
k
Thus, the ration between the areas of LMP and
OMQ is .
1:2
Question: 8
Tick the correct answer and justify:
ABC and BDE are two equilateral triangles such that
D is the mid-point of BC. Ratio of the areas of
triangles ABC and BDE is
(A)
2:1
(B)
1:2
(C)
4:1
(D)
1:4
Solution
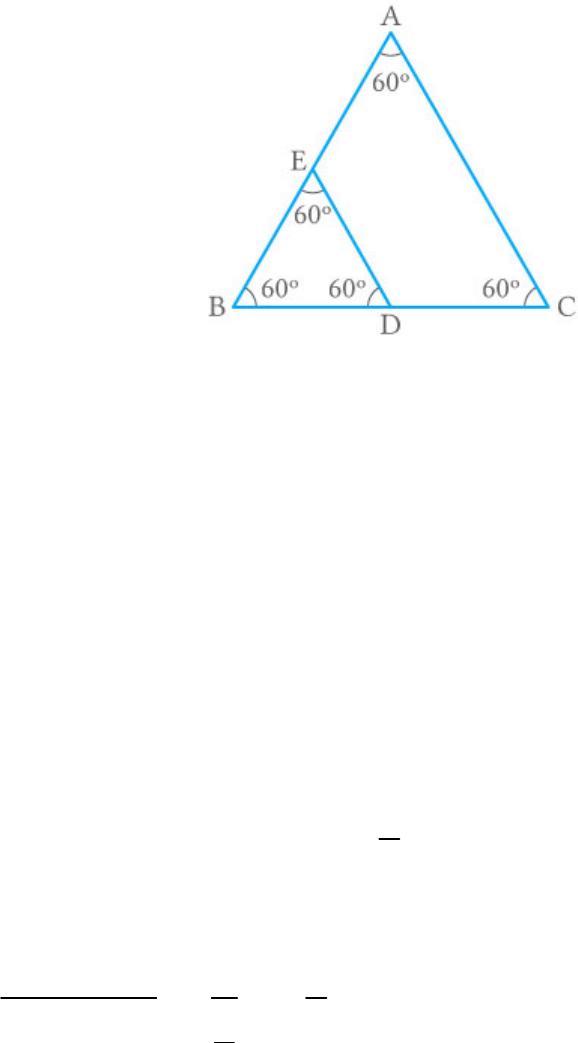
(C) Given: Two equilateral triangles ABC and BDE
such that D is the mid-point of BC.
Fig. Exc_6.4_8
The sides of equilateral triangles are of same length
and all the angles are of .
60
Thus, equilateral triangles are similar to each other.
Thus, the ratio of the areas of equilateral triangles is
equal to the square of the ratio of their sides.
Let us consider the side of ABC be .
x
Thus, the side of BDE =
x
2
2
ar ABC
x 4
x
ar BDE 1
2
Hence, the ratio of the areas of triangles ABC and
BDE is 4 : 1.

Question: 9
Tick the correct answer and justify:
Sides of two similar triangles are in the ratio .
4:9
Areas of these triangles are in the ratio
(A)
2:3
(B)
4:9
(C)
81:16
(D)
16:81
Solution
(D)
Given: Sides of two similar triangles in the ratio
.
4:9
In similar triangles, the ratio of the areas is
equal to the square of the ratio of the
corresponding sides.
The ratio of the areas of given triangles
2
4
9
16
81
Thus, the ratio is 16 : 81.
Exercise 6.5 (17)
Question: 1

Sides of triangles are given below. Determine which
of them are right triangles. In case of a right triangle,
write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Solution
(i) Given: 7 cm, 24 cm, 25 cm
Let us consider the lengths of the sides ,
a 7
, and
b 24
c 25
2 2
2 2
a b 7 24
2 2
a b 49 576
2 2
.....a b 625 .(1)
Now
2
2
c 25
2
c 625
From equations (1) and (2),
2 2 2
a b c
This satisfies the Pythagoras theorem.
Thus, the given triangle is a right triangle with
hypotenuse 25 cm.
(ii) Given: 3 cm, 8 cm, 6 cm
Let us consider the lengths of the sides ,
a 3
, and
b 6
c 8
2 2
2 2
a b 3 6
2 2
a b 9 36
2 2
.....a b 45 .(1)
Now
2
2
c 8
2
c 64
From equations (1) and (2),
2 2 2
a b c
This does not satisfy the Pythagoras theorem.
Thus, the given triangle is not a right triangle.
(iii) Given: 50 cm, 80 cm, 100 cm
Let us consider the lengths of the sides ,
a 50
, and
b 80
c 100
2 2
2 2
a b 50 80
2 2
a b 2500 6400
2 2
a b 8900 ......(2)
Now
2
2
c 100
2
c 10000
From equations (1) and (2),

2 2 2
a b c
This does not satisfy the Pythagoras theorem.
Thus, the given triangle is not a right triangle.
(iv) Given: 13 cm, 12 cm, 5 cm
Let us consider the lengths of the sides ,
a 5
, and
b 12
c 13
2 2
2 2
a b 5 12
2 2
a b 25 144
2 2
.....a b 169 .(1)
Now
2
2
c 13
2
c 169
From equations (1) and (2),
2 2 2
a b c
This satisfies the Pythagoras theorem.
Thus, the given triangle is a right triangle.
Question: 2
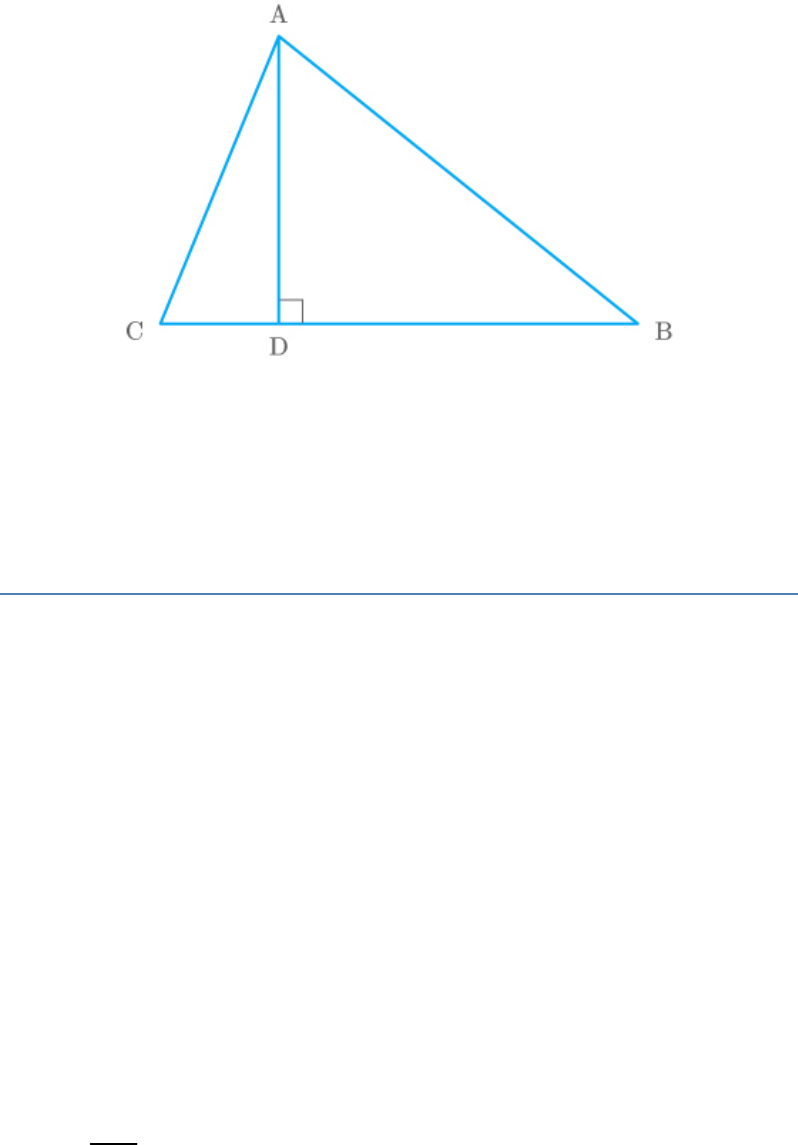
PQR is a triangle right angled at P and M is a point
on QR such that PM QR. Show that
.
2
PM QM.MR
Solution
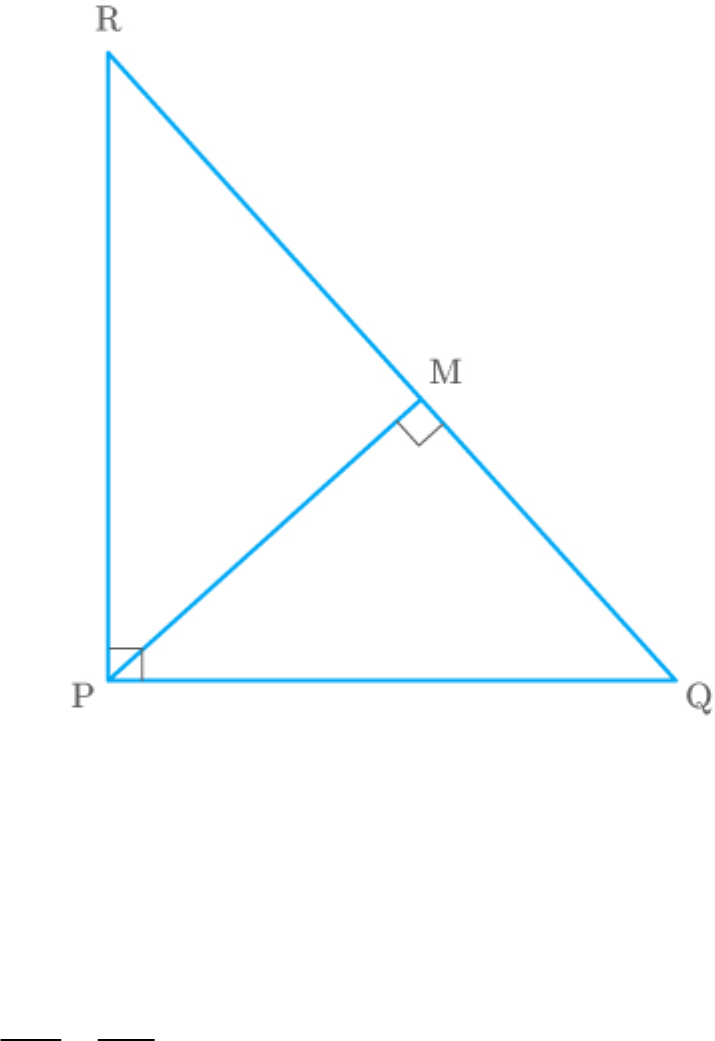
Given: A triangle PQR right angled at P and M is a
point on QR such that PM QR.
Fig. Exc_6.5_2
To prove:
2
PM QM.MR
Proof: It is given that PM QR.
Thus, .
PQM|| PRM
PM MR
QM PM
2
PM QM.MR
Hence proved.
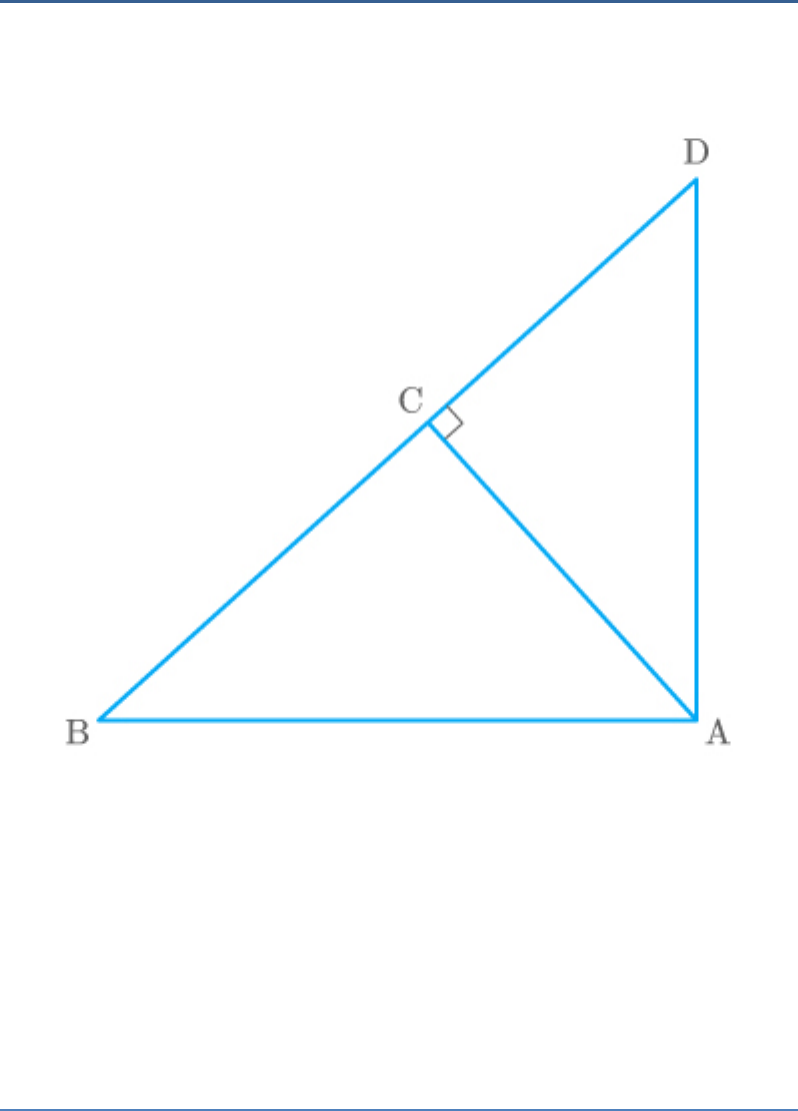
Question: 3
In the given figure, ABD is a triangle right angled at
A and AC BD.
Fig. Exc_6.5_3
Show that
(i)
2
AB BC.BD
(ii)
2
AC BC.DC
(iii)
2
AD BD.CD
Solution
Given: A triangle ABD, right angled at A and AC
BD.
(i) To Prove:
2
AB BC.BD
It is given that AC BD.
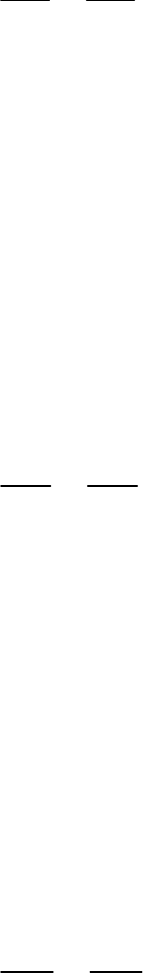
Thus,.
||ABC ABD
So,
AB BC
BD AB
2
AB BC.BD
Hence proved.
(ii) To Prove:
2
AC BC.DC
From equation (1),
||ABC ADC
AC DC
BC AC
2
AC BC.DC
Hence proved.
(iii) To Prove:
2
AD BD.CD
From equation (2),
||ADC ABD
AD BD
CD AD
2
AD BD.CD
Hence proved.
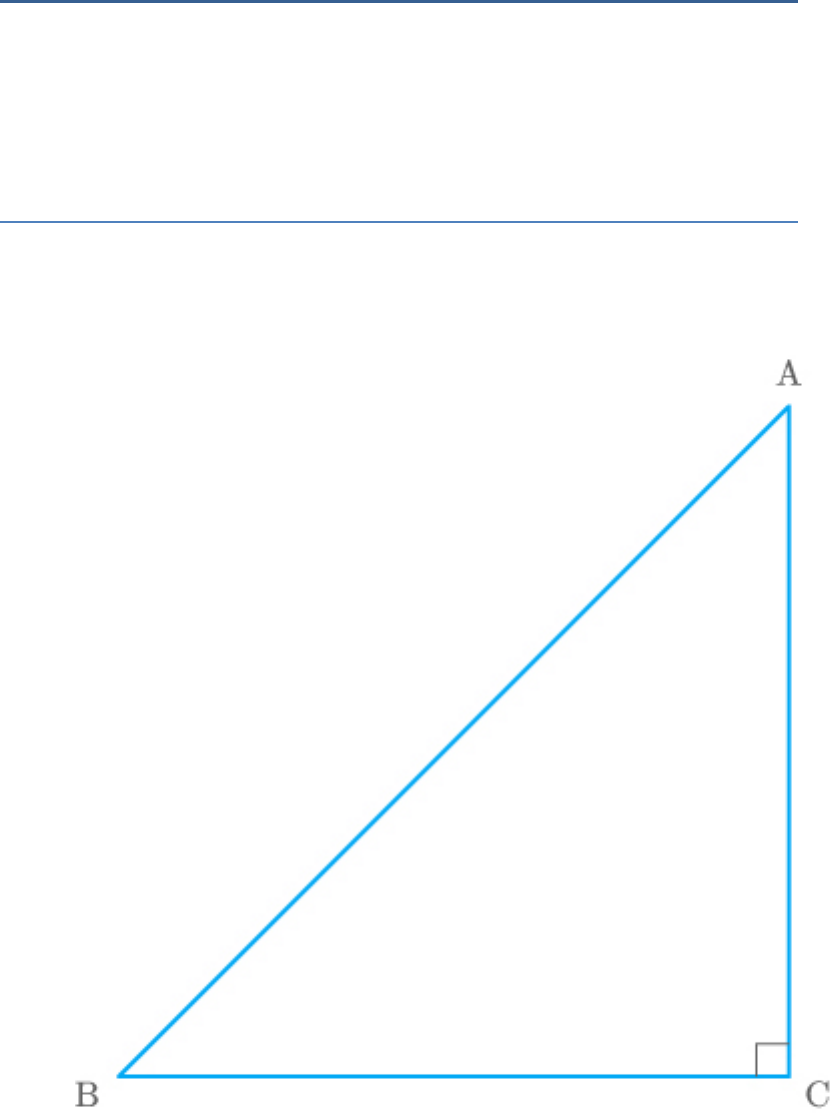
Question: 4
ABC is an isosceles triangle right angled at C. Prove
that .
2 2
AB 2AC
Solution
Given: An isosceles triangle ABC, right angled at C
and
AC BC
Fig. Exc_6.5_4
By the Pythagoras theorem,
2 2 2
AB AC BC
2 2 2
AB AC AC AC BC
2 2
AB 2 AC
Hence proved.
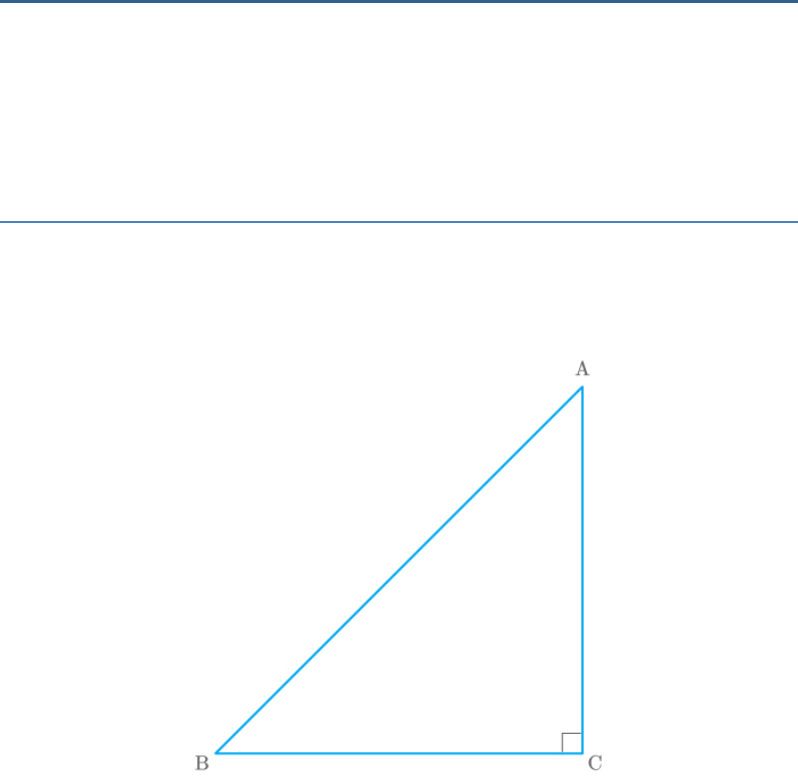
Question: 5
ABC is an isosceles triangle with . If
AC BC
, prove that ABC is a right triangle.
2 2
AB 2AC
Solution
Given: An isosceles triangle ABC such that
AC BC
and .
2 2
AB 2AC
Fig. Exc_6.5_5
2 2
AB 2AC
2 2 2
AB AC AC
2 2 2
AB AC B ACC BC
Thus, by Pythagoras theorem, ABC is a triangle,
right angled at C.
Hence proved.
Question: 6
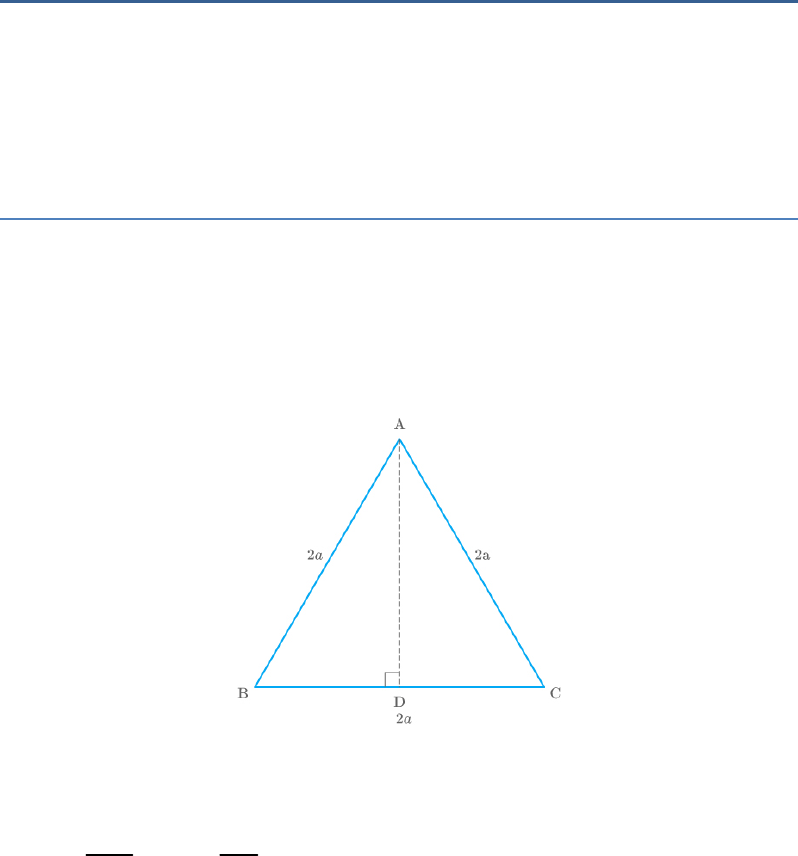
ABC is an equilateral triangle of side . Find each
2a
of its altitudes.
Solution
Given: An equilateral triangle ABC with side .
2a
Thus,
AB BC CA 2a ......(1)
Draw AD BC such that D be the mid-point of BC.
Fig. Exc_6.5_6
BC
BD
2
2a
BD
2
.....BD a .(2)
In right triangle ABD, by the Pythagoras theorem,
2 2 2
AB AD BD
From equations (1) and (2).
2
2 2
2a AD a
2 2
AD 3a
AD 3a
Hence, each of the altitudes of the triangle is .
3a
Question: 7
Prove that the sum of the squares of the sides of a
rhombus is equal to the sum of the squares of its
diagonals.
Solution
Let PQRS be a rhombus with diagonals PS and QR
that intersect each other at O.
Fig. Exc_6.5_7
We know that, the diagonals of a rhombus, bisect
each other at right angles.
Thus,

POQ QOS SOR ROP 90
and
PO SO
QO OR
Now, by Pythagoras theorem in right triangle POQ,
2 2 2
PQ PO QO
2 2
2
PS QR
PQ
2 2
2 2 2
4 PQ PS QR ......(1)
Similarly,
2 2 2
4 QS PS QR ......(2)
2 2 2
4 SR PS QR ......(3)
2 2 2
4 RP PS QR ......(4)
Add equations (1), (2), (3), and (4).
2 2 2 2 2 2
4 PQ QS SR RP 4 PS QR
2 2 2 2 2 2
PQ QS SR RP PS QR
Hence proved.
Question: 8
In the given figure, O is a point in the interior of a
triangle ABC, OD BC, OE AC and OF AB.
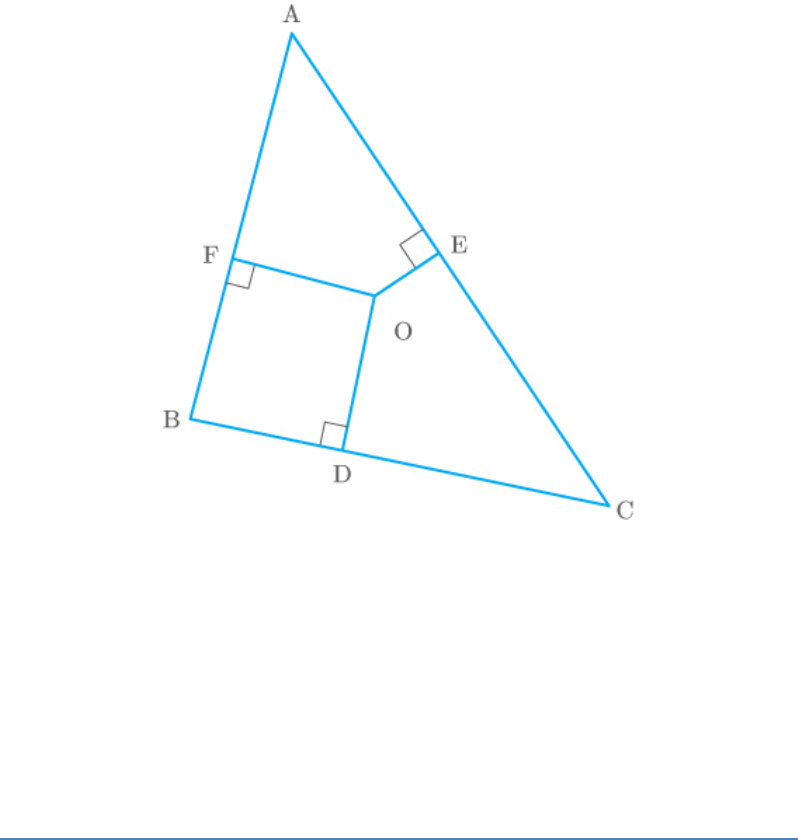
Fig. Exc_6.5_8 (Ques.)
Show that
(i)
2 2 2 2 2 2 2 2 2
OA OB OC – OD – OE – OF AF BD CE
(ii)
2 2 2 2 2 2
AF BD CE AE CD BF
Solution
Given: A triangle ABC such that OD BC, OE AC
and OF AB.
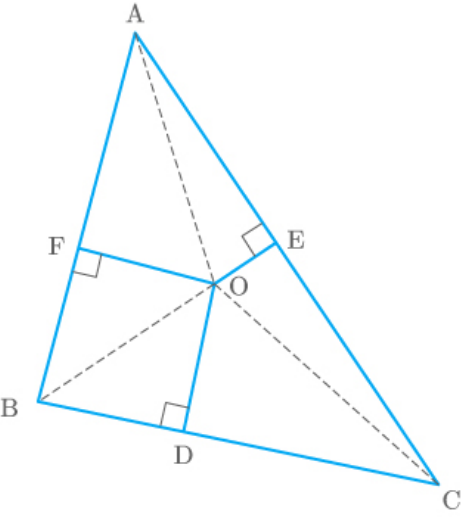
Fig. Exc_6.5_8 (Sol.)
Join AO, BO and CO.
(i)
2 2 2 2 2 2 2 2 2
OA OB OC – OD – OE – OF AF BD CE
By Pythagoras theorem in right triangles OFA,
ODB and OEC.
2 2 2
....OA AF OF ..(1)
2 2 2
....OB BD OD ..(2)
2 2 2
....OC CE OE ..(3)
Add equations (1), (2), and (3),
2 2 2 2 2 2 2 2 2
OA OB OC AF OF BD OD CE OE
2 2 2 2 2 2 2 2 2
OA OB OC – OD – OE – OF AF BD CE
Hence proved.
(ii)
2 2 2 2 2 2
AF BD CE AE CD BF

By Pythagoras theorem in right triangles ODB
and ODC.
2 2 2
....OB BD OD ..(1)
2 2 2
....OC OD CD ..(2)
Subtract equation (2) from (1).
2 2 2 2
OB OC BD C .....D .(3)
Similarly,
2 2 2 2
OC OA CE A .....E .(4)
2 2 2 2
OA OB AF B .....F .(5)
Add equations (3), (4), and (5),
2 2 2 2 2 2 2 2 2 2 2 2
OB OC OC OA OA OB BD CD CE AE AF BF
2 2 2 2 2 2
BD CD CE AE AF BF 0
2 2 2 2 2 2
AF BD CE AE CD BF
Hence proved.
Question: 9
A ladder 10 m long reaches a window 8 m above the
ground. Find the distance of the foot of the ladder
from base of the wall.
Solution
Let LM be a ladder that reaches the window and MN
be the wall.

and
LM 10m
MN 8m
Fig. Exc_6.5_9
From the figure,
LMN is a right triangle, right angled at N.
Now, by Pythagoras theorem in triangle LMN,
2 2
2
10 LN 8
2
LN 100 64
2
LN 36
LN 6m
Hence, the distance of the foot of the ladder from
base of the wall is 6 m.
Question: 10
A guy wire attached to a vertical pole of height 18 m
is 24 m long and has a stake attached to the other
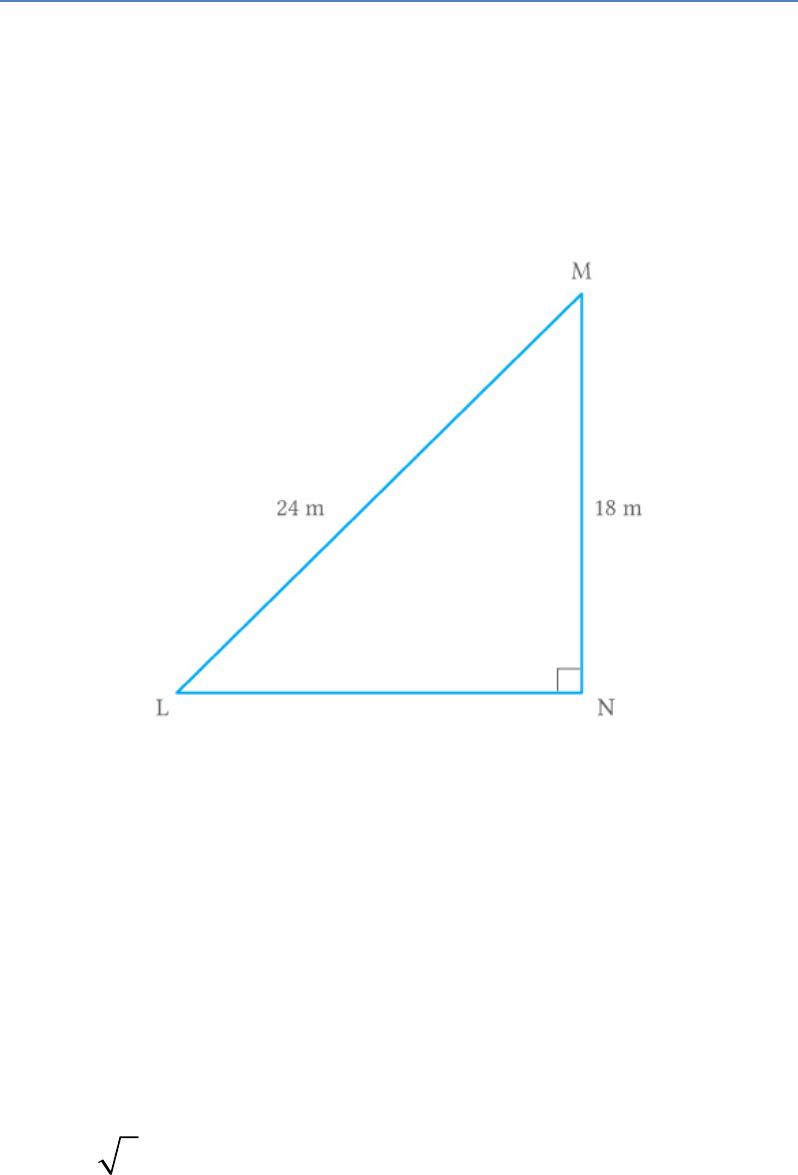
end. How far from the base of the pole should the
stake be driven so that the wire will be taut?
Solution
Let LM be a guy wire and MN be a vertical pole.
Let the wire is fixed to a stake at L to keep the wire
taut.
LM 24m andMN 18m
Fig. Exc_6.5_10
Now, by Pythagoras theorem in right triangle LMN.
2 2 2
LM LN MN
2 2
2
24 LN 18
2
LN 576 324
2
LN 252
LN 6 7

Thus, the stake should be driven at a distance of
6 7
m from the base of the pole so that the wire will be
taut.
Question: 11
An aeroplane leaves an airport and flies due north at
a speed of 1000 km per hour. At the same time,
another aeroplane leaves the same airport and flies
due west at a speed of 1200 km per hour. How far
apart will be the two planes after hours?
1
1
2
Solution
Let the first aeroplane leaves the airport from M at a
speed of 1000 km per hour and goes upto N towards
north.
Fig. Exc_6.5_11
We know that
Distance speed time
Thus,
1
MN 1000 1
2
3
MN 1000
2
MN 1500km
Let the second aeroplane leaves the airport from M
at a speed of 1200 km per hour and goes upto L
towards north.
1
LM 1200 1
2
3
LM 1200
2
LM 1800km
Now, by Pythagoras theorem in triangle LMN,
2 2 2
LN LM MN
2 2
2
LN 1800 1500
2
LN 3240000 2250000
2
LN 5490000
LN 300 61
Hence, the two planes will be at a distance of
300 61
km after hours.
1
1
2
Question: 12
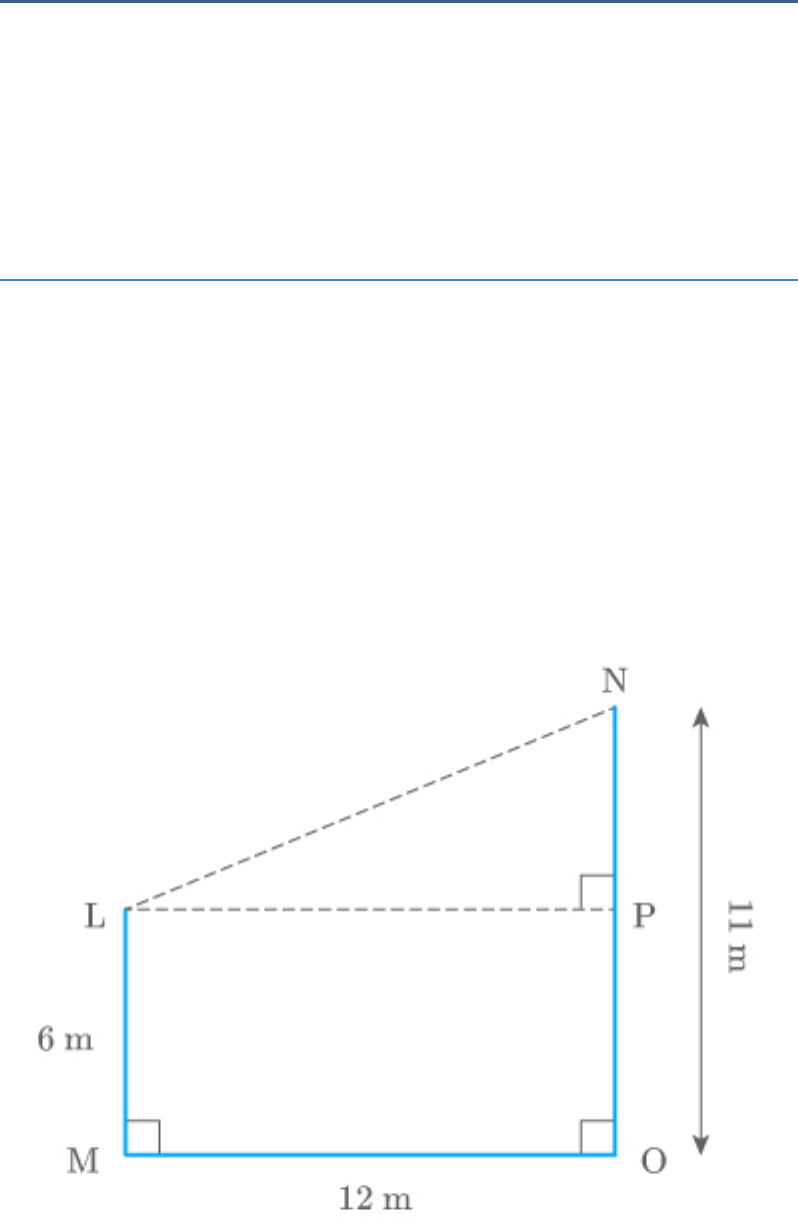
Two poles of heights 6 m and 11 m stand on a plane
ground. If the distance between the feet of the poles
is 12 m, find the distance between their tops.
Solution
Let LM and NO be the two poles at a distance of 12
m.
LM 6m
NO 11m
MO 12m
Draw and join LN.
LP NO
Fig. Exc_6.5_12
From the figure,

LP MO 12m
LM PO 6m
NP NO PO
NP 11 6
NP 5m
Now, by Pythagoras theorem in .
LNP
2 2 2
LN LP NP
2 2
2
LN 12 5
2
LN 144 25
2
LN 169
LN 13
Hence, the tops of the two poles are 13 m apart.
Question: 13
D and E are points on the sides CA and CB
respectively of a triangle ABC right angled at C.
Prove that .
2 2 2 2
AE BD AB DE
Solution
Given: A triangle ABC right angled at C with points
D and E on the sides CA and CB respectively.
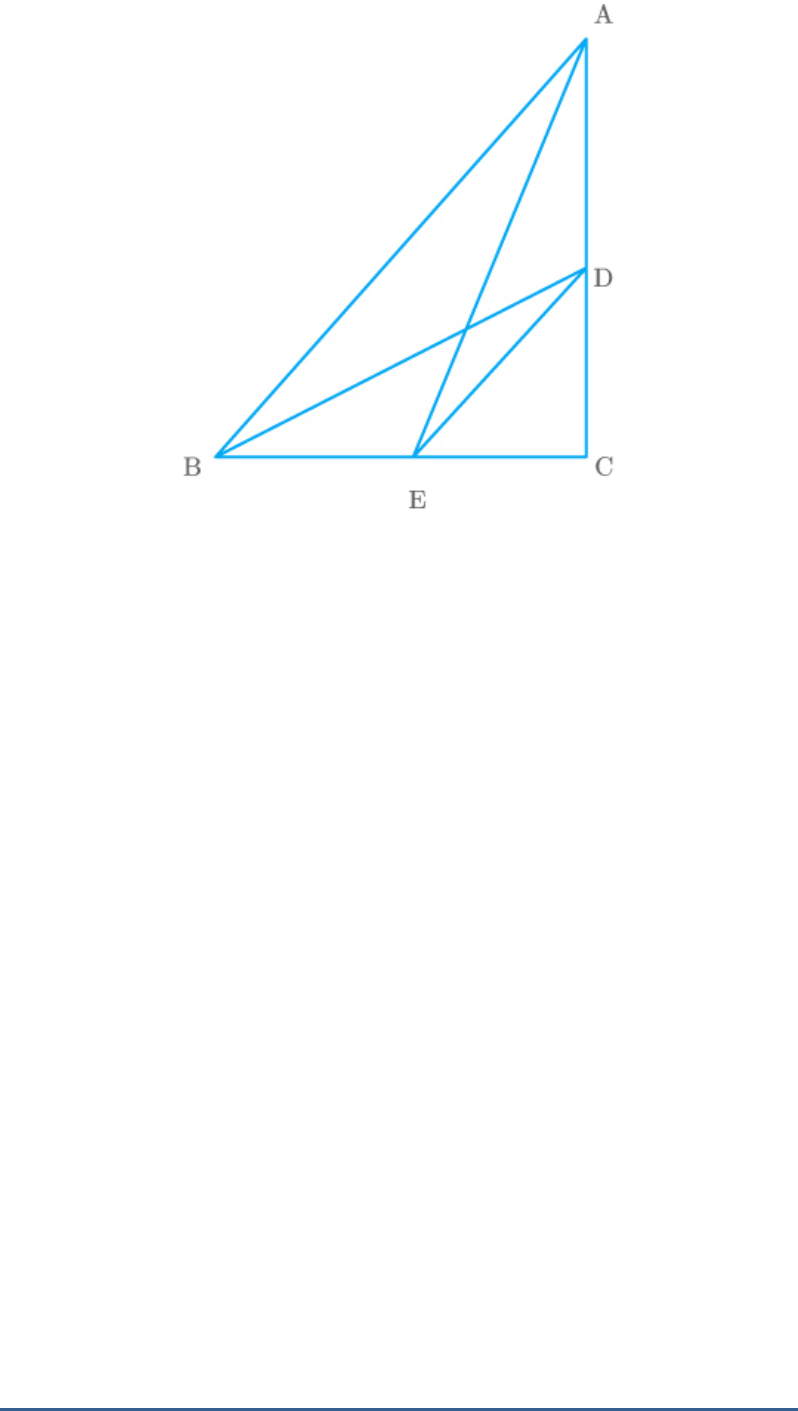
Fig. Exc_6.5_13
By Pythagoras theorem in triangles ACE and DCB.
2 2 2
....AE AC CE ..(1)
2 2 2
....BD DC BC ..(1)
Add equations (1) and (2).
2 2 2 2 2 2
AE BD AC CE DC BC
2 2 2 2 2 2
AE BD AC BC D ....C CE ..(1)
Again by Pythagoras theorem,
and
2 2 2
AC BC AB
2 2 2
DC CE DE
Put the above result in equation (3).
So,
2 2 2 2
AE BD AB DE
Hence proved.
Question: 14
The perpendicular from A on side BC of a ABC
intersects BC at D such that DB 3 CD (see the
given figure).
Fig. Exc_6.5_14
Prove that .
2 2 2
2AB 2AC BC
Solution
Given: A ABC, in which perpendicular from A on
BC intersects BC at D.
And,
.....DB 3CD .(1)
From the figure,
BC DB CD
From equation (1),
BC 3CD CD
BC 4CD
.....
BC
CD
4
.(2)
From equation (1),
DB 3CD
3BC
DB ......(3)
4
By Pythagoras theorem in ,
ABD
2 2 2
....AB AD DB ..(4)
Similarly, in ,
ACD
2 2 2
....AC AD CD ..(5)
Subtract equation (5) from (4).
2 2 2 2 2 2
AB AC AD DB AD CD
2 2 2 2
AB AC DB CD
From equations (2) and (3).
2 2
2 2
3 1
AB AC BC BC
4 4
2 2 2
9 1
AB AC BC
16 16
2 2 2
1
AB AC BC
2
2 2 2
2AB 2AC BC
2 2 2
2AB 2AC BC
Hence proved.
Question: 15
In an equilateral triangle ABC, D is a point on side
BC such that . Prove that .
1
BD BC
3
2 2
9AD 7AB
Solution
Given: An equilateral triangle ABC with a point D on
side BC and
1
BD BC
3
Join AD and draw .
AE BC
Fig. Exc_6.5_15
In triangles AEB and AEC,
Equilateral trianglepropAB AC erty
AEB AEC Each angleisof 90
AE AE Common
Thus,
By SASsimilarity criAEB A teE nC rio:

So,
BE EC
Thus,
and
BC
BD ,
3
2BC
DC ,
3
...
BC
BE EC
2
...(1)
We know that in an equilateral triangle, all angles
are of .
60
Thus, .
C 60
So, is an acute angle triangle.
ADC
2 2 2
AD AC DC 2DC EC
From equation (1).
2
2 2
2 2 1
AD AC BC 2 BC BC
3 3 2
2 2 2 2
4 2
AD AC BC BC
9 3
2 2 2 2
4 2
AD AB AB AB AB BC AC
9 3
2 2
7
AD AB
9
2 2
9AD 7AB
Hence proved.
Question: 16
In an equilateral triangle, prove that three times the
square of one side is equal to four times the square
of one of its altitudes.
Solution
Let PQR be an equilateral triangle such that,
.
PS QR
Fig. Exc_6.5_16
In triangles PQS and PSR,
PQ PR Given
Q R 60 Given
PSQ PSR Each angleisof 90
Thus,
By RHS criterion of congrPSQ PSR uence
Thus,
QS SR
QR
QS SR
2
By Pythagoras theorem in ,
PQS
2 2 2
PQ PS QS
2
2 2
QR
PQ PS
2
2
2 2
PQ
PQ PS QR PQ
2
2
2 2
PQ
PQ PS
4
2 2 2
4PQ PQ 4PS
2 2
3PQ 4PS
Hence proved.
Question: 17
Tick the correct answer and justify: In ΔABC,
cm, AC 12 cm and BC 6 cm. The angle
AB 6 3
B is:
(A)
120
(B)
60
(C)
90
(D)
45
Solution
(C)
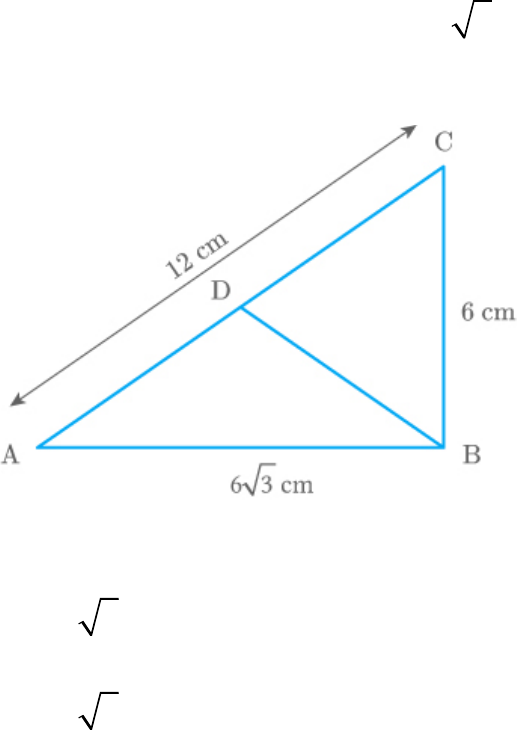
Given: A triangle ABC, in which, cm, AC
AB 6 3
12 cm and BC 6 cm
Fig. Exc_6.5_17
2
2
2 2
AB BC 6 3 6
2
2
2 2
AB BC 6 3 6
2 2
AB BC 144 ......(1)
2
2
AC 12
2
.....AC 144 .(2)
From equations (1) and (2).
2 2 2
AB BC AC
Thus, by Pythagoras theorem, triangle ABC is a right
triangle.
Thus,
B 90
Exercise 6.6 (10)(Optional)
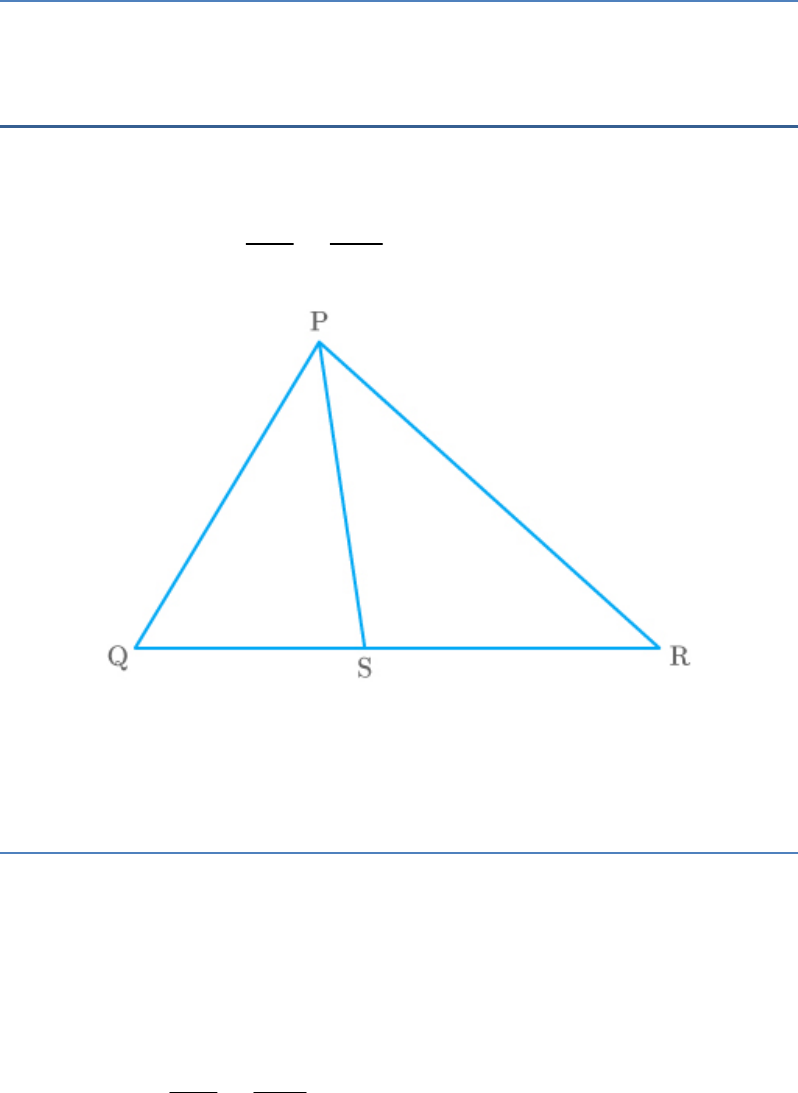
Question: 1
In the given figure, PS is the bisector of of
QPR
PQR. Prove that .
QS PQ
SR PR
Fig. Exc_6.6_1 (Ques.)
Solution
Given: A triangle PQR with PS as the internal
bisector of .
QPR
QPS SPR
To prove:
QS PQ
SR PR
Construction:
Extend QP and draw RT parallel to SP, such that it
intersects the extended part of QP at T.
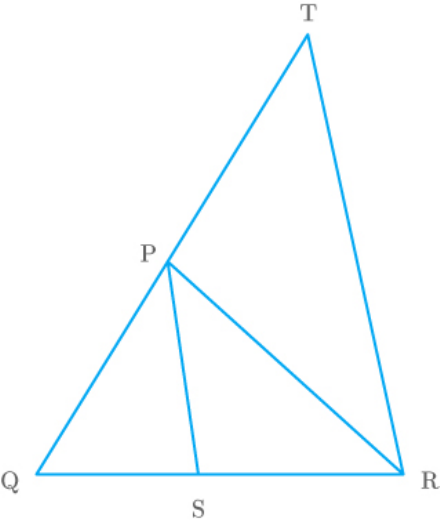
Fig. Exc_6.6_1 (Sol.)
Proof:
… (1)
SPR PRT Alternateangles
… (2)
QPS PTR Corresponding angles
Given that, … (3)
QPS SPR
From equations (1), (2), and (3),
PRT PTR
We know that, the opposite sides of equal angles are
equal.
Thus, … (4)
PT PR
In ,
QRT
RT SP By constru|| ction
Thus, by Thales theorem,
QS PQ
SR PT
From equation (4),
QS PQ
SR PR
Hence proved.
Question: 2
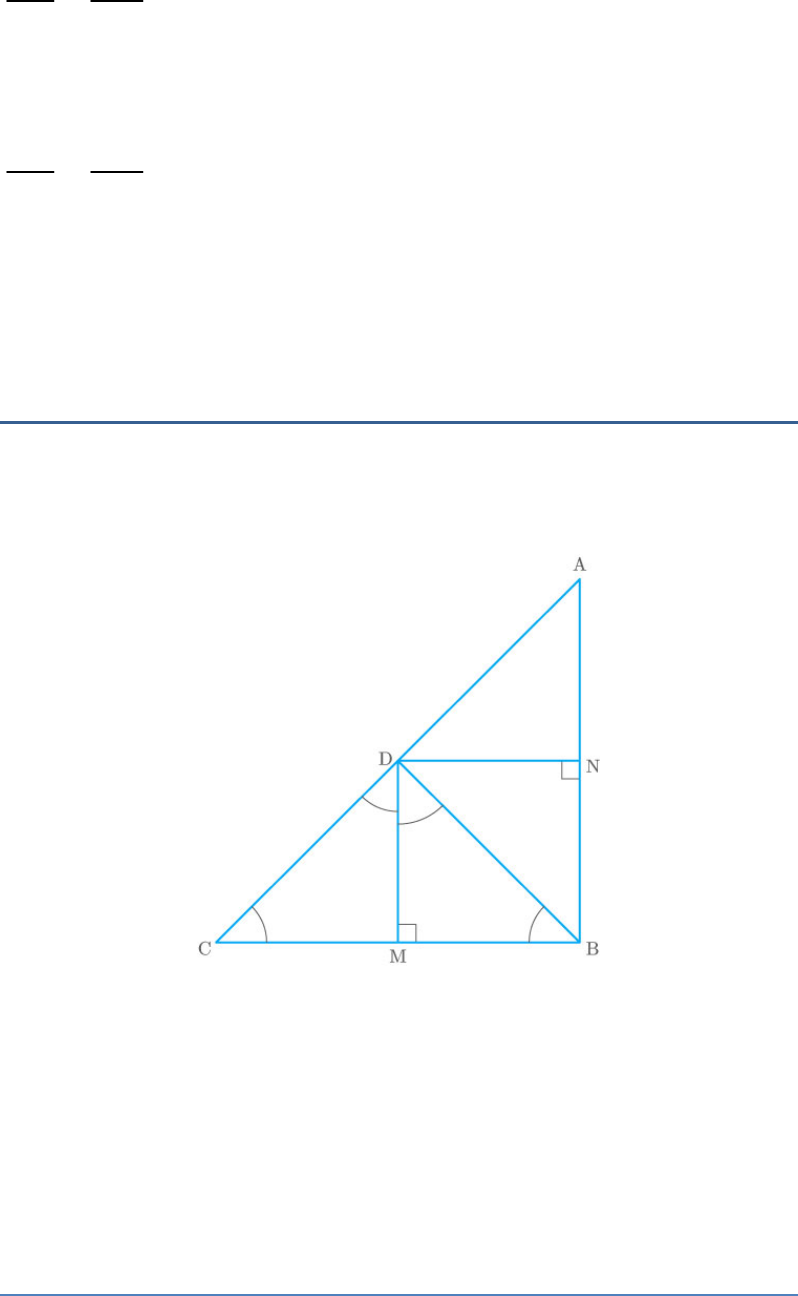
In the given figure, D is a point on hypotenuse AC of
ABC, DM BC and DN AB.
Fig. Exc_6.6_2 (Ques.)
Prove that:
(i)
2
DM DN.MC
(ii)
2
DN DM.AN
Solution
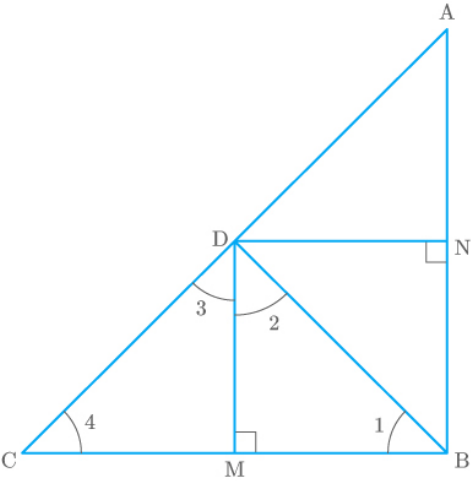
Given: A triangle ABC in which, D is a point on
hypotenuse.
DM BC and DN AB.
Fig. Exc_6.6_2 (Sol.)
AB BC
DM BC
Thus, .
AB DM:
Similarly,
BC AB
DN AB
Thus,
BC DN:
So, the quadrilateral BMDN forms a rectangle.
Thus,
BM ND
(i) To prove:
2
DM DN.MC

We know that the sum of all the interior angles
in a triangle is .
180
Thus, in ,
BMD
1 BMD 2 180
1 90 2 180
1 2 180 90
… (1)
1 2 90
Similarly, in ,
DMC
… (2)
3 4 90
From the figure,
BD AC
Thus, … (3)
2 3 90
From equations (1) and (3).
1 2 2 3
1 3
From equations (2) and (3).
3 4 2 3
4 2
In triangles BMD and DMC,
and
1 3
4 2
Thus, .
BMD DMC:
BM MD
DM MC
DN DM
BM DN
DM MC
2
DM DN.MC
Hence proved.
(ii) To prove:
2
DN DM.AN
Similarly, as in first part,
BND DNA:
Thus,
BN DN
DN NA
DM DN
BN DM
DN AN
2
DN DM.AN
Hence proved.
Question: 3
In the given figure, ABC is a triangle in which
and AD CB produced.
ABC 90
Fig. Exc_6.6_3
Prove that .
2 2 2
AC AB BC 2BC.BD

Solution
Given: A triangle ABC such that and
ABC 90
AD CB produced.
To prove:
2 2 2
AC AB BC 2BC.BD
Proof: By Pythagoras theorem in ,
ADB
… (1)
2 2 2
AB AD BD
Now by Pythagoras theorem in ,
ADC
2 2 2
AC AD DC
2
2 2
AC AD BD BC DC BD BC
2 2 2 2
AC AD BD BC 2BD BC
From equation (1),
2 2 2
AC AB BC 2BD BC
2 2 2
AC AB BC 2BC.BD
Hence proved.
Question: 4
In the given figure, ABC is a triangle in which
and AD BC.
ABC 90

Fig. Exc_6.6_4
Prove that .
2 2 2
AC AB BC 2BC.BD
Solution
Given: A triangle ABC such that and
ABC 90
AD CB.
To prove:
2 2 2
AC AB BC 2BC.BD
Proof: By Pythagoras theorem in ,
ADB
… (1)
2 2 2
AB AD BD
Now, by Pythagoras theorem in ,
ADC
2 2 2
AC AD DC
2
2 2
AC AD BC BD DC BC BD
2 2 2 2
AC AD BD BC 2BD BC
From equation (1),
2 2 2
AC AB BC 2BD BC
2 2 2
AC AB BC 2BC.BD
Hence proved.
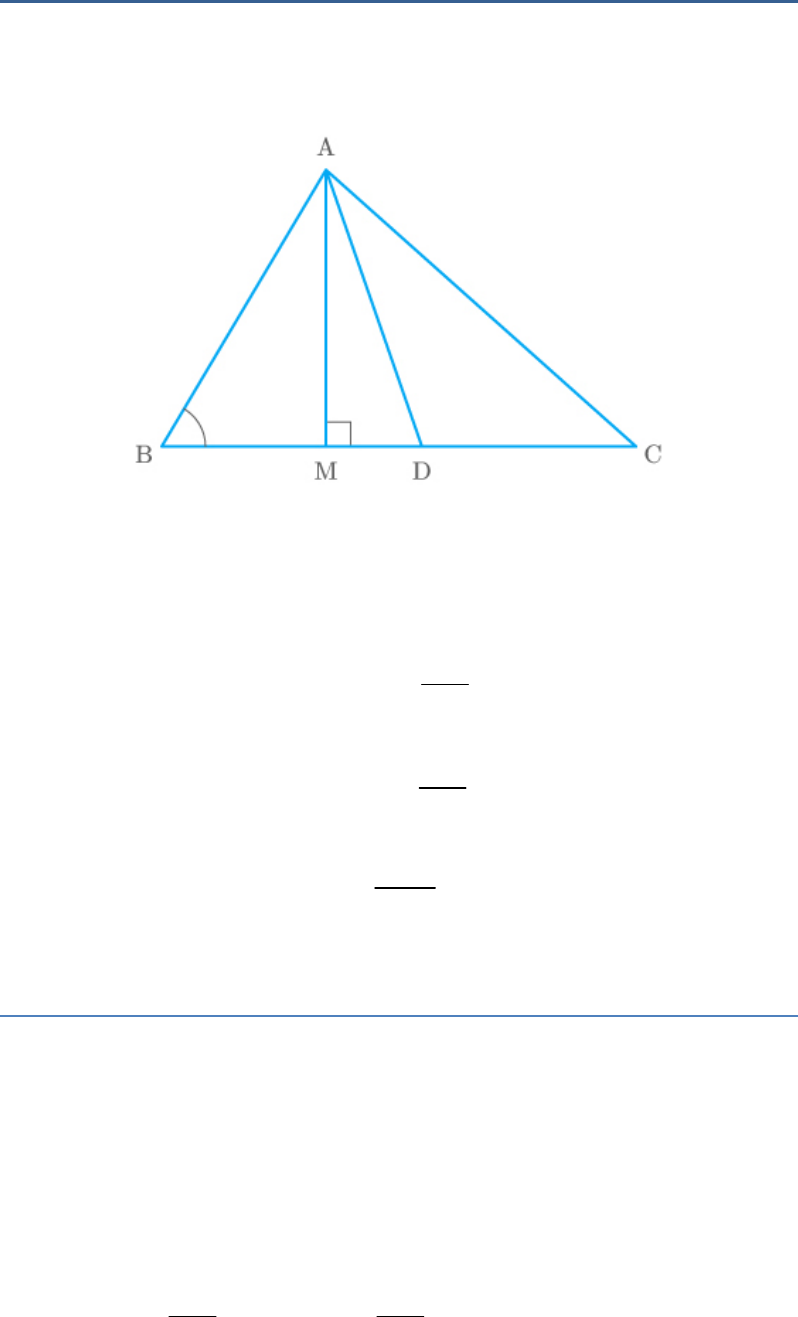
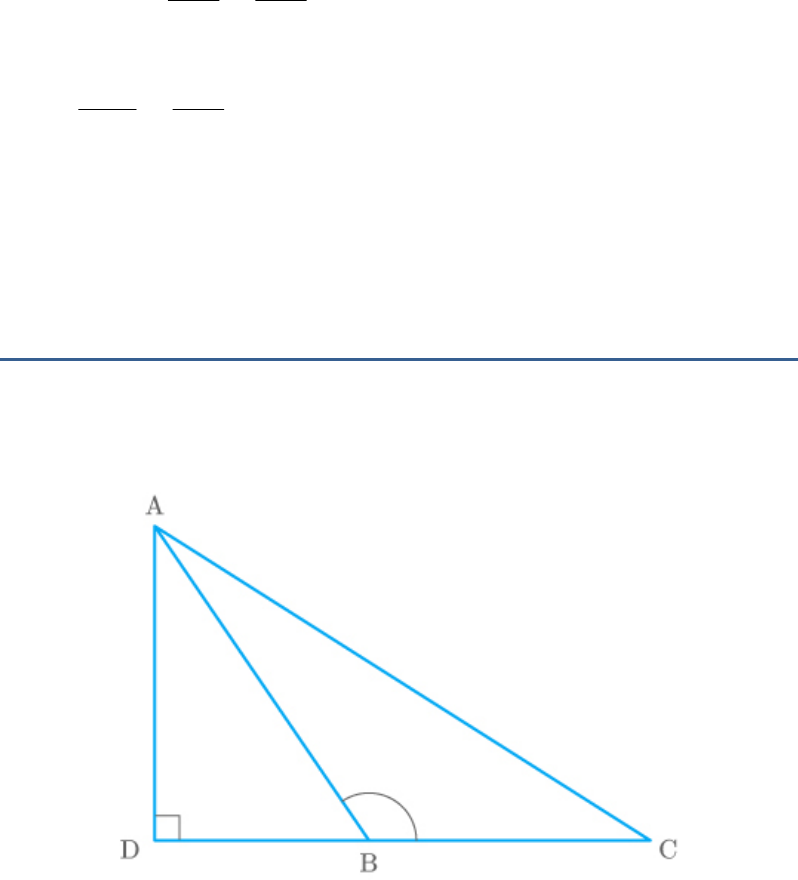
Question: 5
In the given figure, AD is a median of a triangle ABC
and AM BC.
Fig. Exc_6.6_5
Prove that:
(i)
2
2 2
BC
AC AD BC.DM
2
(ii)
2
2 2
BC
AB AD BC.DM
2
(iii)
2
2 2 2
BC
AC AB 2AD
2
Solution
Given: A triangle ABC with median AD and AM
BC.
AMD 90
AD is a median on BC.
Thus, and
BC
DC
2
BC
BD
2
Thus, and .
ADM 90
ADC 90
(i) Since ,
ADC 90
In ,
ADC
2 2 2
AC AD DC 2DC.DM
2
2 2
BC BC BC
AC AD 2 .DM DC
2 2 2
2
2 2
BC
AC AD BC.DM
2
2
2 2
BC
AC AD BC.DM
2
Hence proved.
(ii) Since ,
ADM 90
2 2 2
AB AD BD 2BD.DM
2
2 2
BC BC BC
AB AD 2 .DM BD
2 2 2
2
2 2
BC
AB AD BC.DM
2
2
2 2
BC
AB AD BC.DM
2
Hence proved.
(iii) From above two proofs,
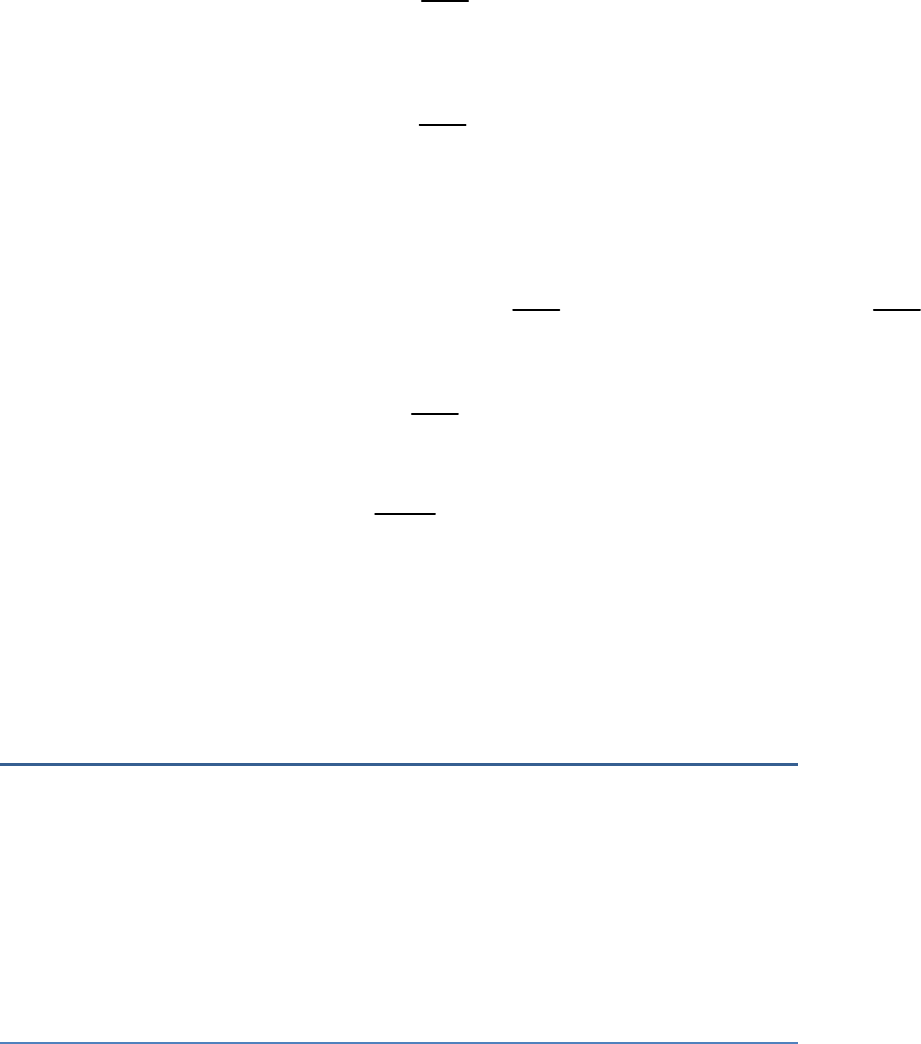
… (1)
2
2 2
BC
AC AD BC.DM
2
… (2)
2
2 2
BC
AB AD BC.DM
2
Add equations (1) and (2).
2 2
2 2 2 2
BC BC
AC AB AD BC.DM AD BC.DM
2 2
2
2 2 2
BC
AC AB 2AD 2
2
2
2 2 2
BC
AC AB 2AD
2
Hence proved.
Question: 6
Prove that the sum of the squares of the diagonals of
parallelogram is equal to the sum of the squares of
its sides.
Solution
Let PQRS be a parallelogram with diagonals PR and
QS.

Fig. Exc_6.6_6
PS is a median of .
PQR
Thus, .
2
2 2 2
QR
PQ PR 2PS
2
The medians of triangles PQR and PSR are QO and
SO because diagonals in a parallelogram bisect each
other
Thus,
… (1)
2 2 2 2
1
PQ QR 2QO PR
2
… (2)
2 2 2 2
1
PS RS 2SO PR
2
Add equations (1) and (2).
2 2 2 2 2 2 2 2
1 1
PQ QR PS RS 2QO PR 2SO PR
2 2
2 2 2 2 2 2 2
PQ QR PS RS 2 QO SO PR
2 2
2 2 2 2 2
QS QS QS
PQ QR PS RS 2 PR QO SO
2 2 2
2
2 2 2 2 2
2QS
PQ QR PS RS 2 PR
4
2 2 2 2 2 2
PQ QR PS RS QS PR
Hence proved.
Question: 7
In the given figure, two chords AB and CD intersect
each other at the point P.
Fig. Exc_6.6_7
Prove that:
(i)
APC|| DPB
(ii)
AP.PB CP.DP
Solution

(i) To prove:
APC|| DPB
In triangles APC and DPB,
APC DPB Vertically oppositeangles
CAP BDP Anglesin samesegment
Thus,
APC|| DPB By AA similarity criterion
Hence proved.
(ii) To prove:
AP.PB CP.DP
From the first part,
APC|| DPB
Thus,
AP CP
DP PB
AP.PB CP.DP
Hence proved.
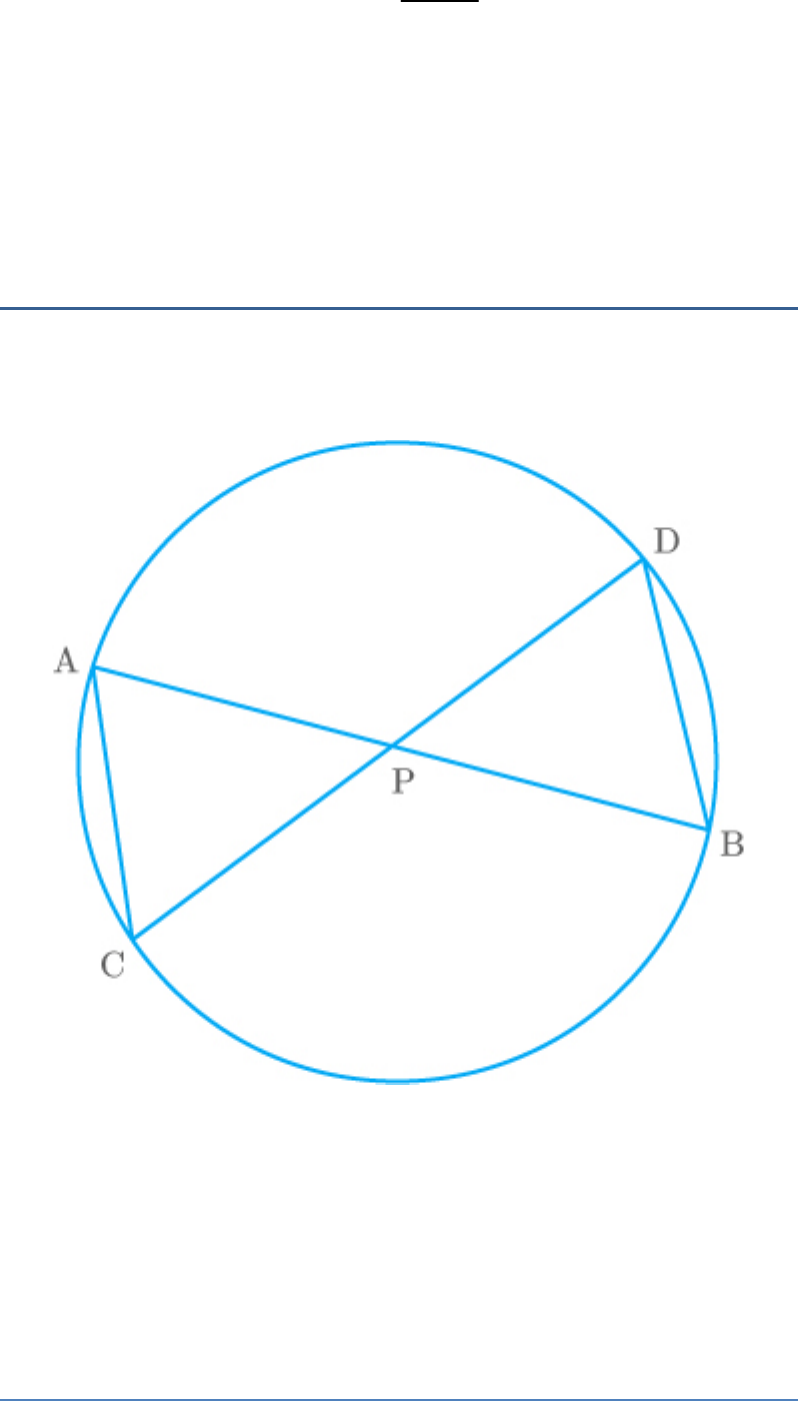
Question: 8
In the given figure, two chords AB and CD of a circle
intersect each other at the point P (when produced)
outside the circle.
Fig. Exc_6.6_8
Prove that
(i)
PAC PDB:
(ii)
PA.PB PC.PD
Solution
(i)
PAC|| PDB
In triangles PAC and PDB,
APC DPB Common
… (1)
BAC 180 PAC
PDB CDB 180 BAC
From equation (1),
PDB CDB 180 180 PAC
PDB PAC
Thus,
PAC|| PDB By AA similarity criterion
Hence proved.
(ii)
PA.PB PC.PD
From the first part,
PAC|| PDB
Thus,
PA PC
PD PB
PA.PB PC.PD
Hence proved.
Question: 9
In the given figure, D is a point on side BC of ABC
such that
.
BD AB
CD AC
Fig. Exc_6.6_9 (Ques.)
Prove that AD is the bisector of .
BAC
Solution
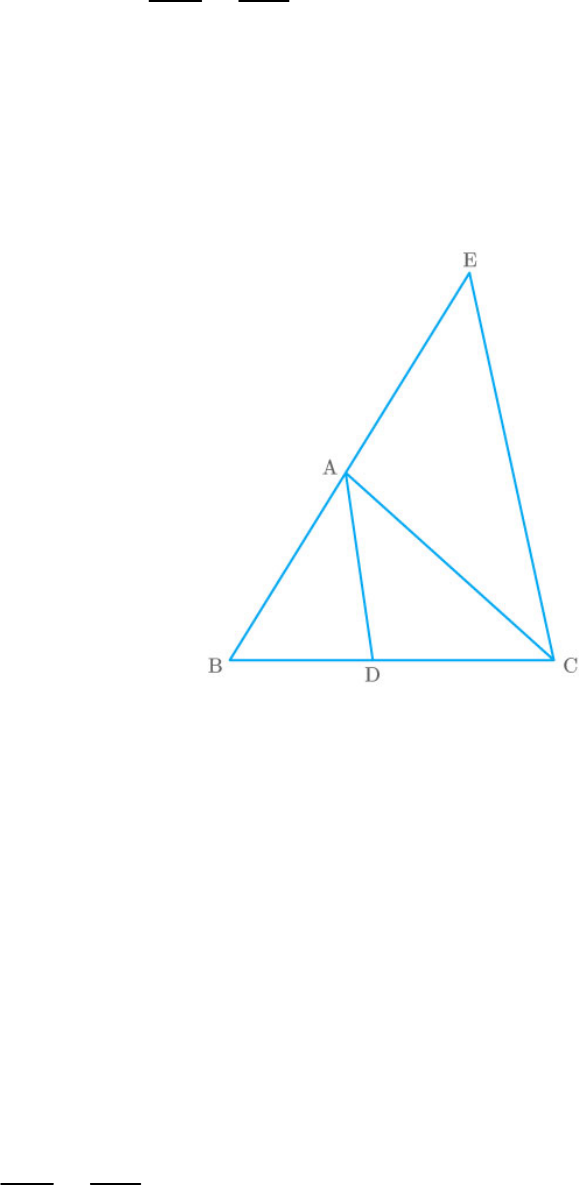
Given: A ABC in which D is a point on side BC
such that .
BD AB
CD AC
To prove: AD is the bisector of .
BAC
Construction: Extend BA to a point E such that,
and join CE.
AE AC
Fig. Exc_6.6_9 (Sol.)
Proof: In ,
AEC
AE AC
We know that the opposite angles of equal sides in a
triangle are equal.
Thus, … (1)
AEC ACE
Given that,
BD AB
CD AC

BD AB
AC AE
CD AE
By the converse of basic proportionality theorem,
DA CE:
… (2)
BAD AEC Corresponding angles
… (3)
DAC ACE Alternateangles
From equations (2) and (3),
BAD DAC
AEC ACE
Thus, AD is the bisector of .
BAC
Hence proved.
Question: 10
Nazima is fly fishing in a stream. The tip of her
fishing rod is 1.8 m above the surface of the water
and the fly at the end of the string rests on the water
3.6 m away and 2.4 m from a point directly under the
tip of the rod. Assuming that her string (from the tip
of her rod to the fly) is taut, how much string does
she have out (see given figure)? If she pulls in the
string at the rate of 5 cm per second, what will be the
horizontal distance of the fly from her after 12
seconds?
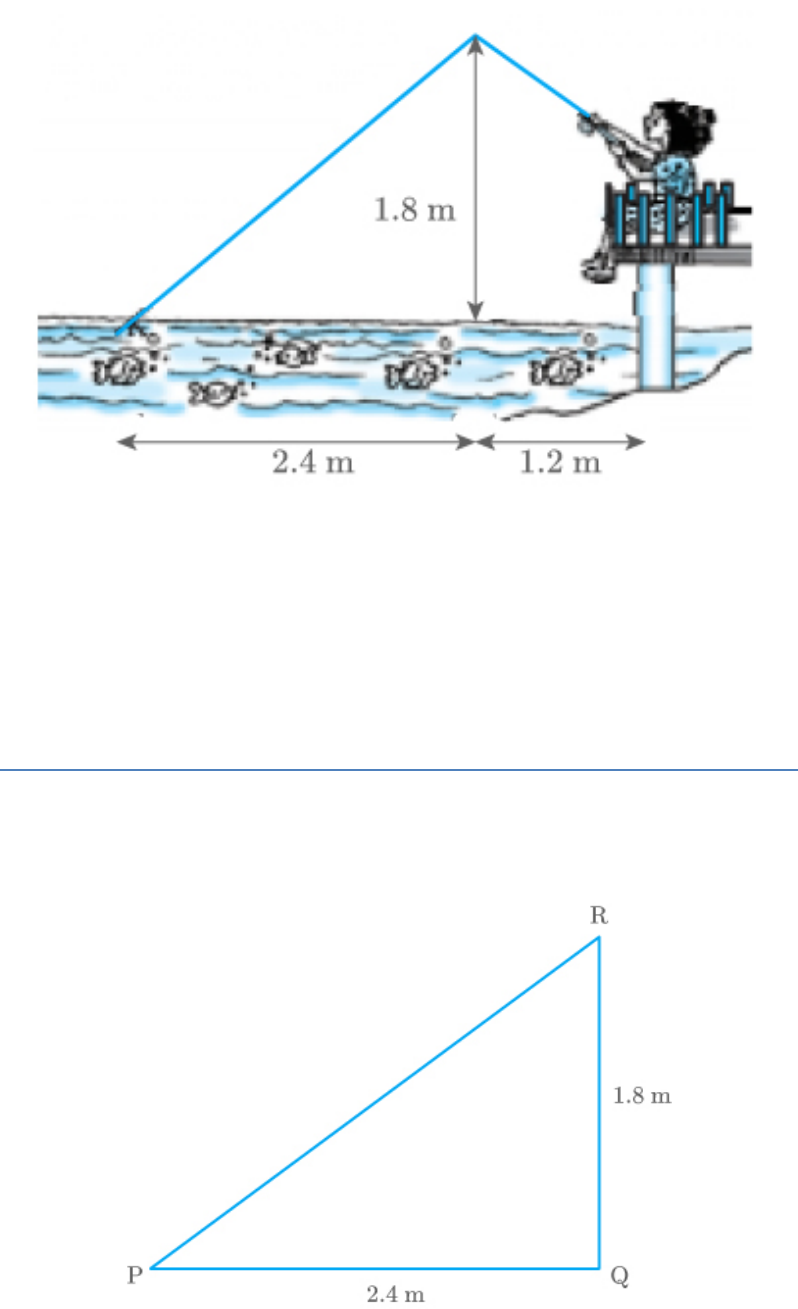
Fig. Exc_6.6_10 (Ques.)
Solution
Let R be the tip of the fishing rod and the fly at the
end of the string rests on point P.
Fig. Exc_6.6_10 (Sol.) (i)
From the figure,
PQ 2.4m
QR 1.8m
By Pythagoras theorem in ,
PQR
2 2 2
PR PQ QR
2 2 2
PR 2.4 1.8
2
PR 5.76 3.24
2
PR 9
PR 3
Thus, length of the string out of the water is 3 m.
Length of the string that is pulled
in 12 seconds at the rate of 5 cm / sec
5 12
60 cm
0.60 m 1 m 100 cm
The remaining part of the string left out 3 0.6
2.4 m
Now, find the horizontal distance of the fly from
Nazima after 12 seconds.
AR be the remaining part of the string after 12
seconds.
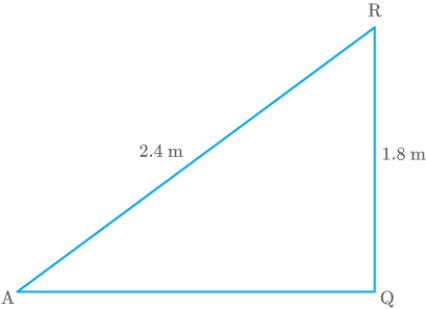
Fig. Exc_6.6_10 (Sol.) (ii)
By Pythagoras theorem in triangle AQR,
2 2 2
AR AQ QR
2 2 2
AR AQ QR
2
AQ 5.76 3.24
2
AQ 2.52
AQ 1.59
Thus,
The horizontal distance of the fly
1.59 1.2
from Nazima after 12 seconds
2.79 m
Hence, the horizontal distance of the fly from
Nazima is 2.79 m.