
Lesson: Area related to circles
Exercise 12.1 (5)
Question: 1
The radii of two circles are 19 cm and 9 cm
respectively. Find the radius of the circle which has
circumference equal to the sum of the
circumferences of the two circles.
Solution:
1
st
circle radius
1
r 19cm
2
nd
circle radius
2
r 9cm
Assume, the radius of the 3
rd
circle be .
r
Now, find the circumference of the 1
st
circle.
1
Circumference 2πr
2π 19
38π
Now, find the circumference of the 2
nd
circle.
2
Circumference 2πr
2π 9
18π

Now, find the circumference of 3
rd
circle.
Circumference 2πr
According to the statement,
rd st nd
Circumference Circumference Circumference
of 3 circle of 1 circle of 2 circle
2πr 38π 18π
2πr 56π
56π
r
2π
r 28
Thus, the radius of the circle is cm.
28
Question: 2
The radii of two circles are 8 cm and 6 cm
respectively. Find the radius of the circle having
area equal to the sum of the areas of the two
circles.
Solution:
1
st
circle Radius
1
r 8cm
2
nd
circle Radius
2
r 6cm
Let the 3
rd
circle radius be .
r
Now, find the Area of the 1
st
circle.

2
1
Area πr
2
π 8
64π
Now, find the Area of the 2
nd
circle.
2
2
Area πr
2
π 6
36π
Now, find the Area of the 3
rd
circle.
Area πr
According to the statement,
rd st nd
Area of Area of Area of
3 circle 1 circle 2 circle
2 2 2
1 2
πr πr πr
2
πr 64π 36π
2
πr 100π
2
r 100
r 10
But, radius cannot be negative.
Thus, the radius of the circle is cm.
10
Question: 3
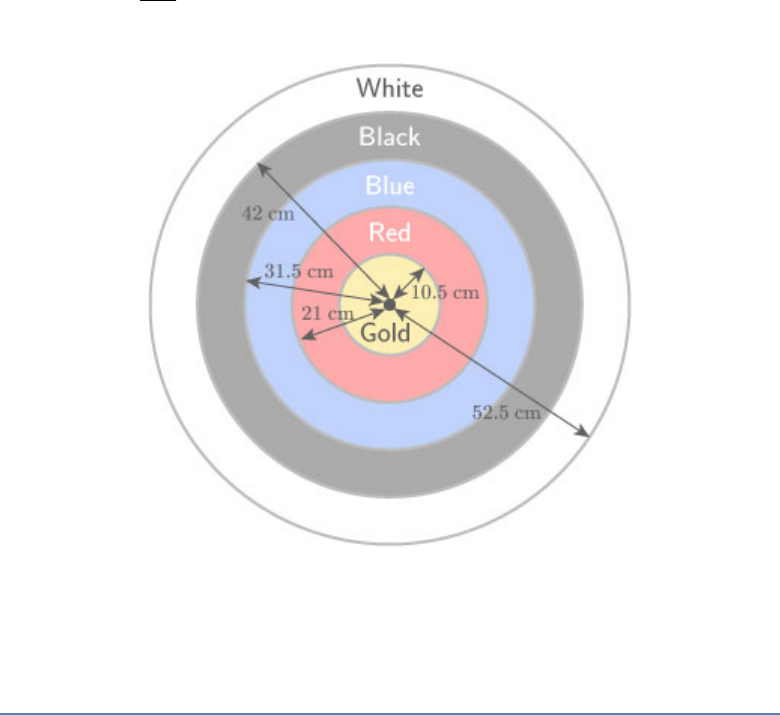
Given figure depicts an archery target marked with
its five scoring areas from the centre outwards as
Gold, Red, Blue, Black and White. The diameter of
the region representing Gold score is 21 cm and
each of the other bands is 10.5 cm wide. Find the
area of each of the five scoring regions.
[Use ]
22
π
7
Fig. Exc_12.1_3 (Ques.)
Solution:
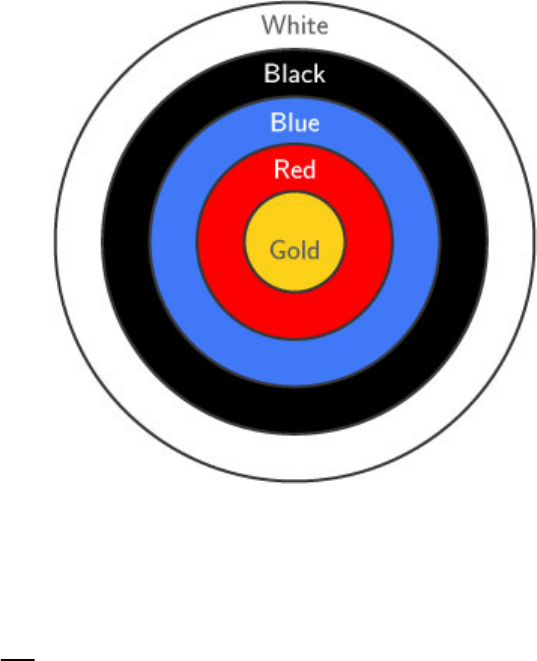
Fig. Exc_12.1_3 (Ans.)
First, find the 1
st
circle Radius (gold region)
1
(r )
1
21
r
2
10.5cm
According to the statement,
Each circle is 10.5 cm wider than the previous circle.
Thus,
2
nd
circle radius
2
(r )
10.5cm 10.5cm
21cm
3
rd
circle Radius
3
r
21cm 10.5cm
31.5cm
4
th
circle Radius
4
r
31.5cm 10.5cm
42cm
5
th
circle Radius
5
r
42cm 10.5cm

52.5cm
st
Area of gold region Area of 1 circle
2
1
πr
2
10.5
.
22
10 5 0 5
7
.1
346.5
2
cm
nd st
Area of Area of
Area of
red region
circle circle
2 1
2 2
2 1
πr πr
2 2
π(21) π(10.5)
441π 110.25π
22
330.75
7
2
1039.5cm
rd nd
Area of Area of
Area of
blue region
3 circle circle2
2 2
3 1
πr πr
2 2
π(31.5) π(21)
992.25π 441π
22
551.25
7

2
1732.5cm
th rd
Area of Area of
Area of
black region
4 circle 3 circle
2 2
4 3
πr πr
2 2
π(42) π(31.5)
1764π 992.25π
22
771.75
7
2
2425.5cm
th th
Area of Area of
Area of
whiteregion
5 circle 4 circle
2 2
5 4
πr πr
2 2
π(52.5) π(42)
2756.25π 1764π
22
992.25
7
2
3118.5cm
Thus, the areas of gold, red, blue, black and white
regions are
2
346 5cm ,
2
1039 5cm ,
2
1732 5cm ,
and respectively.
2
2425 5cm
2
3118 5cm

Question: 4
The wheels of a car are of diameter 80 cm each.
How many complete revolutions does each wheel
make in 10 minutes when the car is travelling at a
speed of 66 km per hour?
Solution:
Diameter of car’s wheel
80cm
Radius of car’s wheel
40cm
Circumference of wheel
2πr
2π 40
80π
Speed of car
66 km / hour
66 100000
cm / min
60
110000 cm / min
Car’s travel distance in 10 minutes
110000 10
1100000cm
Let be the number of revolutions of the wheel of
n
the car.
n Distance travelled
Distance travelled
in 1 revolution
in 10 minutes
that is, circumference
n 80π 1100000

1100000 7
n
80 22
4375
Thus, each wheel of the car will make 4375
revolutions.
Question: 5
Tick the correct answer in the following and justify
your choice: If the perimeter and the area of a circle
are numerically equal, then the radius of the circle
is:
(A) 2 units
(B) units
π
(C) 4 units
(D) 7 units
Solution:
(A)
Let be the radius of the circle.
r
We know that,
Circumference of circle
2πr
Area of circle
2
πr
Given: The area of circle & the circumference of
circle are equal.
2
2πr πr
2 r
Thus, the radius of the circle is 2 units.
Exercise 12.2 (14)
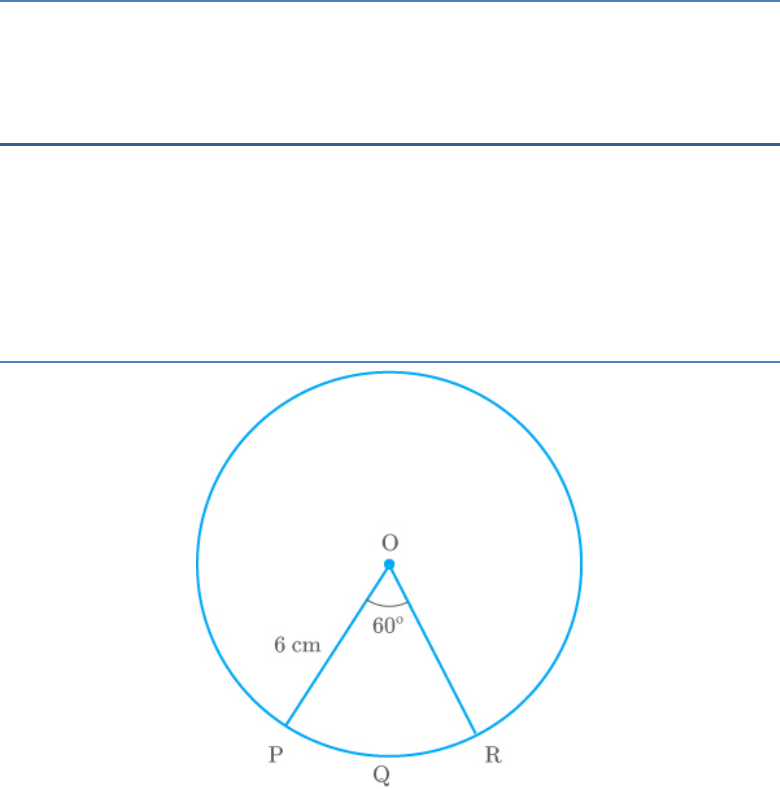
Question: 1
Find the area of a sector of a circle with radius 6 cm
if angle of the sector is .
60
Solution:
Fig. Exc_12.2_1
Assume OPQR be a sector of the circle making
angle at point O in the circle.
60
2
θ
Area of sector of angle θ πr
360
Now, calculate the area of the sector OPQR.
2
60 22
Area of sector OPQR (6)
360 7
1 22
6 6
6 7
2
132
cm
7
Thus, the area of the sector of the circle is .
2
132
cm
7
Question: 2
Find the area of a quadrant of a circle whose
circumference is 22 cm.
Solution:
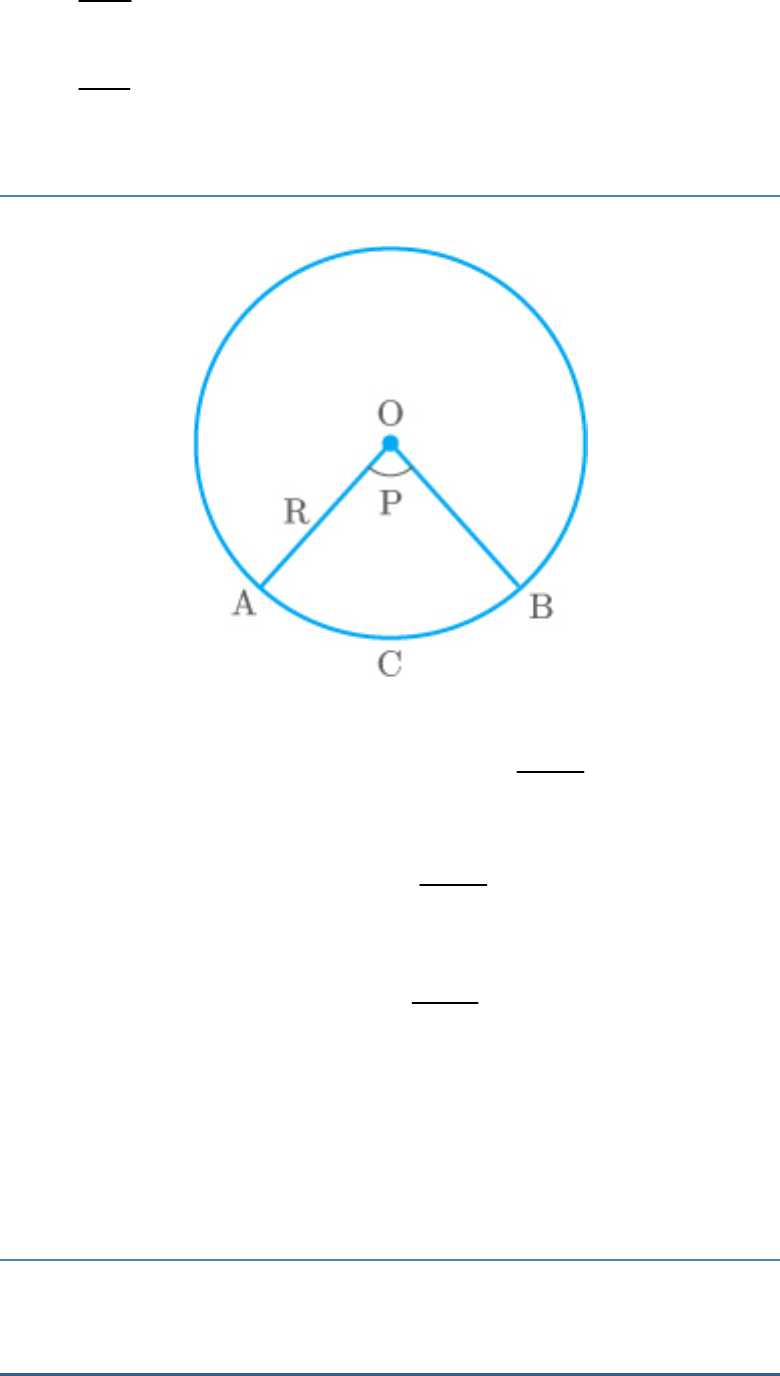
Fig. Exc_12.2_2

Let be the radius of the circle.
r
Circumferenceof circle 22cm
2πr 22
22
r
2π
11
r
π
Circle quadrant will subtend angle at the centre
90
of the circle.
2
90
Area of such circle quadrant= πr
360
2
1 11
π
4 π
121
4
121 7
4 22
2
77
cm
8
Thus, the area of the quadrant is .
2
77
cm
8
Question: 3
The length of the minute hand of a clock is 14 cm.
Find the area swept by the minute hand in 5
minutes.
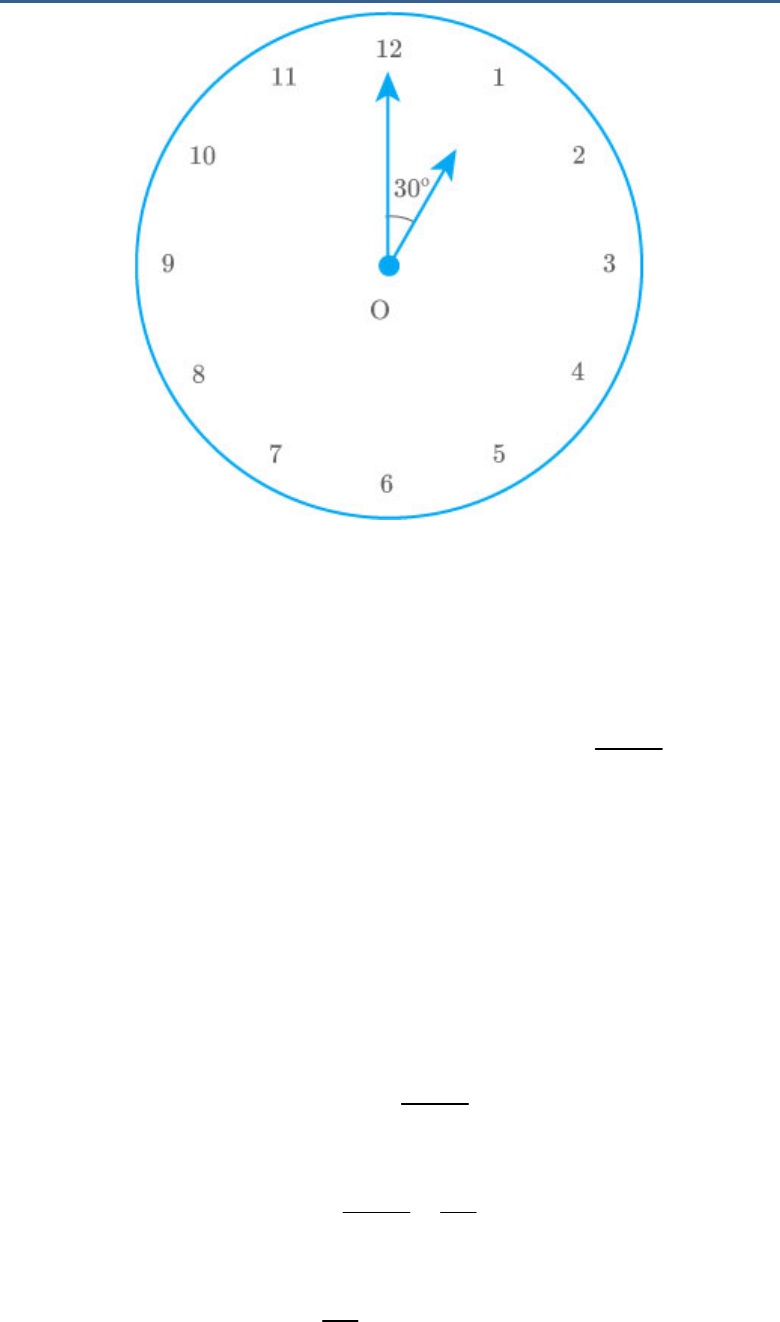
Solution:
Fig. Exc_12.2_3
In 1 hour (60 minutes), the minute hand rotates
.
360
In 5 minutes, minute hand will rotate
360
5
60
30
Thus, in 5 minutes, area covered by the minute
hand, will be the equal to the area of a sector of
30
in a circle whose radius is 14 cm.
2
θ
Area of sector of angle θ r
360
30 22
Area of sector of 30 14 14
360 7
22
2 14
12

11 14
3
2
154
cm
3
Thus, the area is .
2
154
cm
3
Question: 4
A chord of a circle of radius 10 cm subtends a right
angle at the centre. Find the area of the
corresponding:
(i) Minor segment
(ii) Major sector
[Use ]
π 3 4.1
Solution:
Fig. Exc_12.2_4

Let PR be the chord of the circle subtending at
90
the centre O of the circle.
Firstly, we will calculate the major sector.
(ii) Find the area of the major sector OPSR.
2
Area of major
sector OPSR
360 90
π r
360
2
270
π r
360
3
3 14 10 10
4
.
2
235.5cm
Now, calculate the area of the minor sector OPQR.
2
Area of minor
secto
90
π r
3
r
6
OP R
0
Q
1
3 14 10 10
4
.
2
78.5cm
Now, find the area of .
OPR
1
Area of OPR OP OR
2
1
10 10
2
2
50cm

(i) Calculate the area of the minor segment PQR.
Area of minor Area of minor Area of
segment PQR sector OPQR OPR
78.5 50
2
28.5cm
Question: 5
In a circle of radius 21 cm, an arc subtends an angle
of at the centre. Find:
60
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the
corresponding chord
Solution:
Radius of circle
r
21cm
Angle subtends by the given arc
60
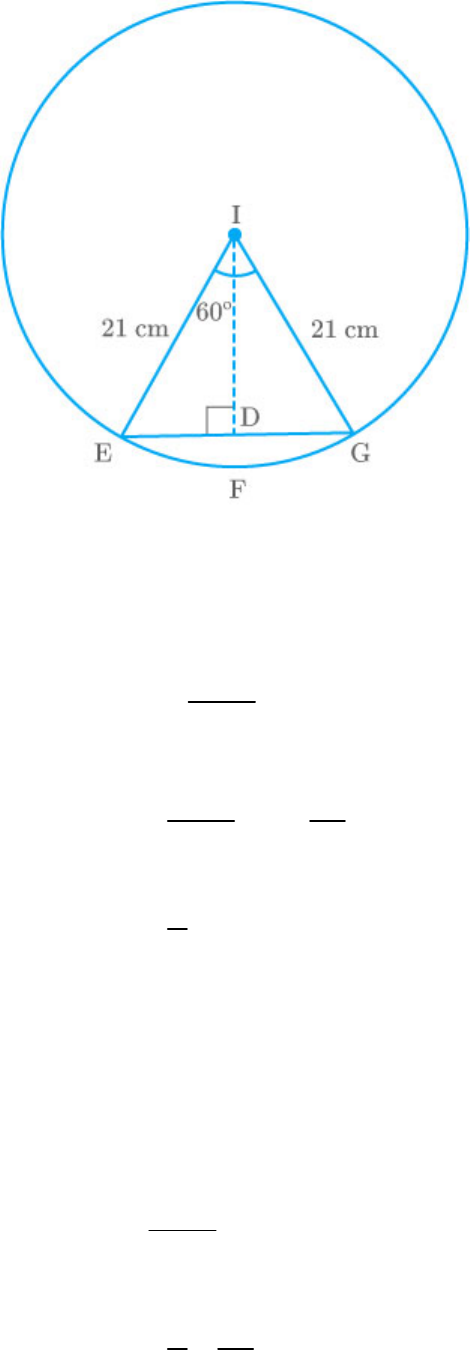
Fig. Exc_12.2_5
(i) Find the length of the arc EFG.
Length of the
arc E
θ
F
2πr
360
G
60 22
2 21
360 7
1
2 22 3
6
22cm
(ii) Find the area of the arc IEFG.
2
Area of the
arc IEF
60
36
G
πr
0
1 22
21 21
6 7
2
231cm
In ,
IEG
IEG IGE (As IE IG)
IEG EIG IGE 180
2 IEG 60 180
2 IEG 60 180
IEG 60
Thus, is an equilateral triangle.
IEG
So,
2
3
Area of IEG (Side)
4
2
3
(21)
4
2
441 3
cm
4
(iii) Now, find the area of segment EFG.
Area of Area of Area of
segment EFG segment IEFG IEG
2
441 3
231 cm
4
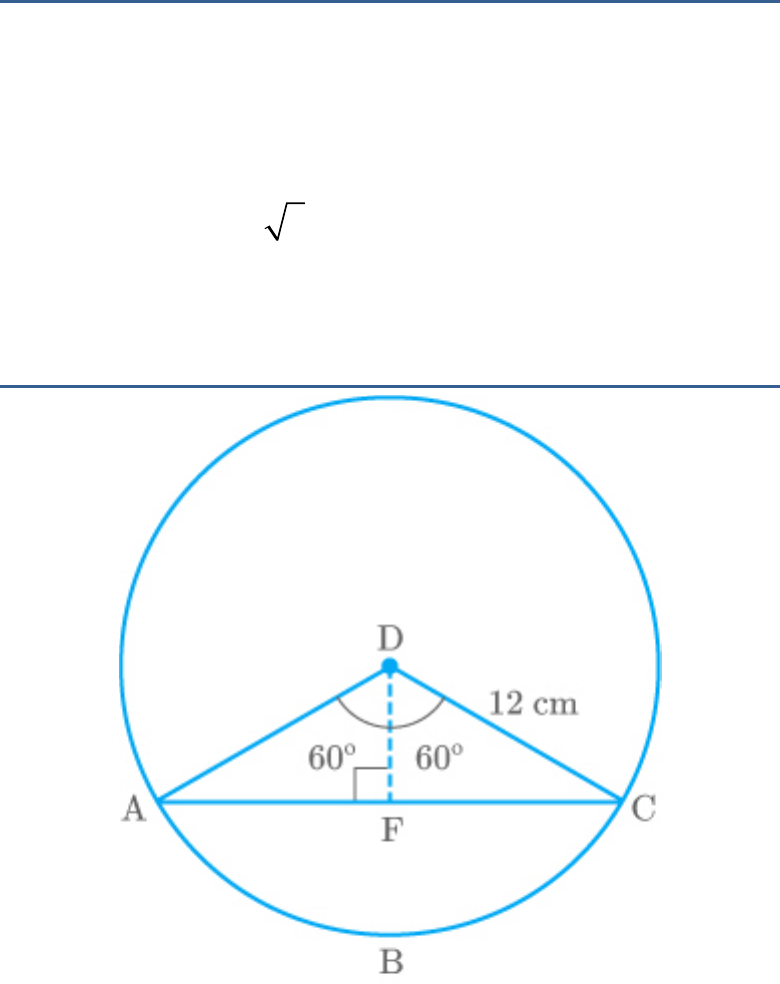
Question: 6
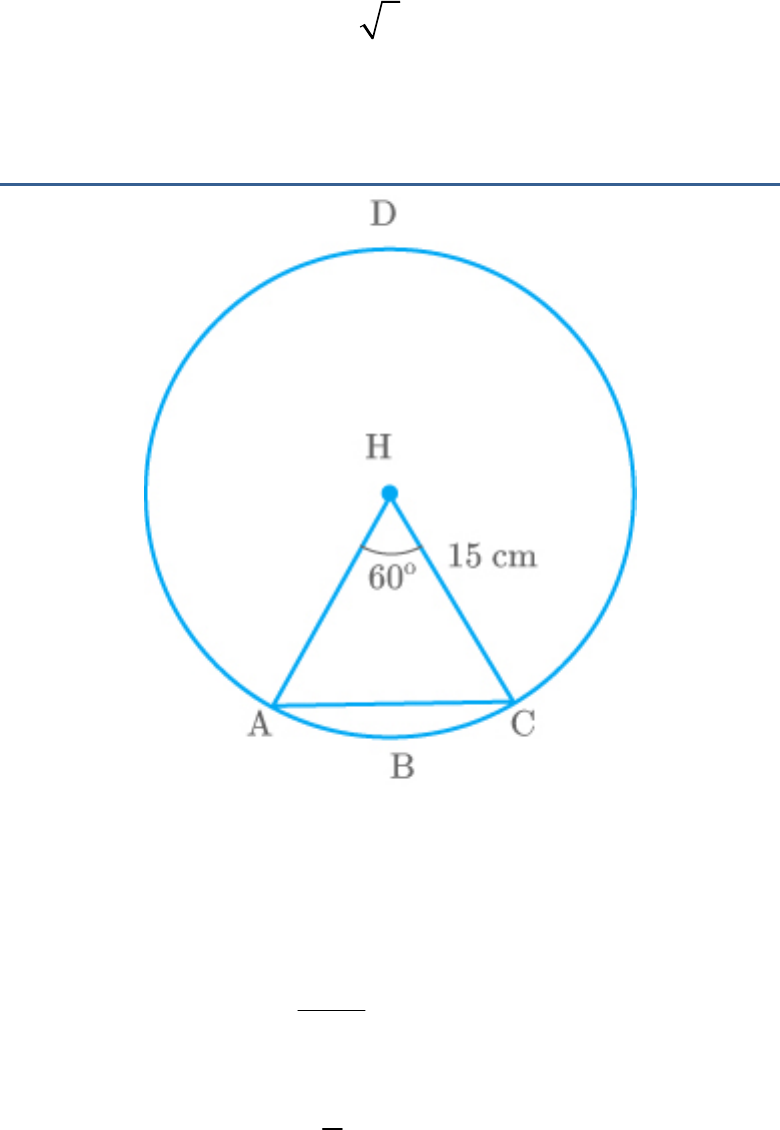
A chord of a circle of radius cm subtends an
15
angle of at the centre. Find the areas of the
60
corresponding minor and major segments of the
circle.
Useπ 3 14and 3 1 73. .
Solution:
Fig. Exc_12.2_6
Let be the radius of circle.
r
Radius
15cm
2
Area of
segment HAC
60
π r
360
B
2
1
3.14 (15)
6
2
117.75cm
In ,
HAC
HAC HCA (As HA HC)
HAC HCA AHC 180
HAC HAC 60 180
2 HAC 120
HAC 60
Thus, is an equilateral triangle.
HAC
We know that,
2
3
Area of HAC (side)
4
2
3
(15)
4
2
225 3
cm
4
2
56.25 3 cm
2
97.3125cm
Area of Area of Area of
sector ACB sector HABC sector HAC
117.75 97.3125
2
20.4375cm
Area of major Area of Area of
sector ADC circle sector ABC
2
π(15) 20.4375
3.14 225 20.4375
706.5 20.4375
2
686.0625cm
Question: 7
A chord of a circle of radius 12 cm subtends an
angle of 120° at the centre. Find the area of the
corresponding segment of the circle.
Useπ 3 14and 3 1 73. .
Solution:
Fig. Exc_12.2_7
Construction: Draw a perpendicular DF on chord
AC.
This bisects the chord AC in two parts.
AF FC
In
DFA,
DF
cos60
DA
DF 1
12 2
DF 6cm
AF
sin60
AD
Given: and
AD 12cm
3
sin60
2
AF 3
12 2
AF 6 3 cm
AC 2AF
2 6 3
12 3 cm
Now, find the area of .
DAC
1
Area of DAC AC DF
2
1
12 3 6
2
36 3
36 1.73

2
62.28cm
Now, find the area of sector DABC.
2
120
Area of sector DABC π r
360
2
120
3.14 (12)
360
1
3.14 144
3
2
150.72cm
Area of Area of Area of
sector ABC sector DAFC DAC
150.72 62.28
2
88.44 cm
Hence, the area of the corresponding segment of
the circle is .
2
88.44 cm
Question: 8
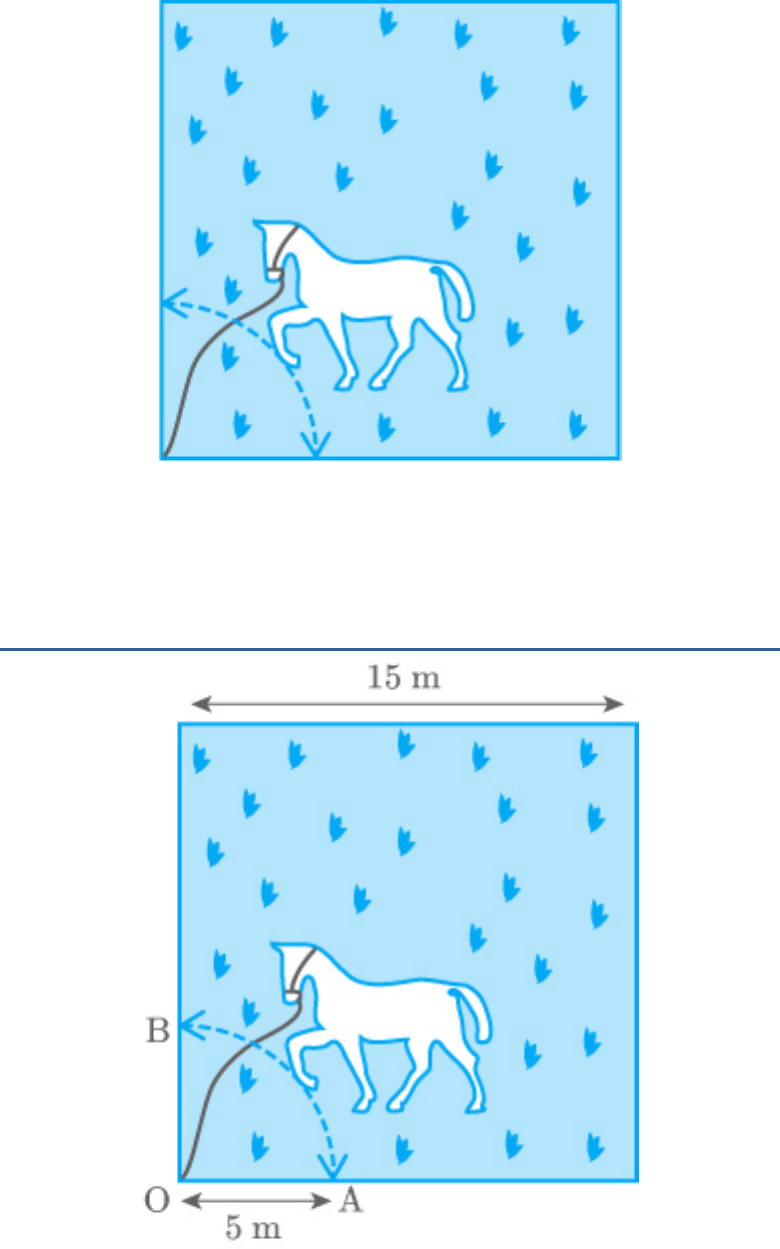
A horse is tied to a peg at one corner of a square
shaped grass field of side 15 m by means of a 5 m
long rope (see the given figure). Find:
(i) The area of that part of the field in which the
horse can graze.
(ii) The increase in the grazing area of the rope
were 10 m long instead of 5 m.
[Use ]
π 3 14
Fig. Exc_12.2_8 (Ques.)
Solution:
Fig. Exc_12.2_8 (Ans.)

From the figure, observe that the horse can graze a
sector of in a circle of 5 m radius.
90
(i) Area of that part of the field, in which the
horse can graze area of sector OACB
Area of sector OACB
2
90
πr
360
2
1
3.14 (5)
4
3.14
25
4
2
19.625m
Area of that part of the field, in which the
horse can graze, if the length of the rope is 10
m
2
90
πr
360
2
1
3.14 (10)
4
2
78.5m
(ii) Now, calculate the increase in the grazing area
of the rope.
Increase in the
grazing
7
a
8
re
.5
a
19.625
2
58.875m
Question: 9
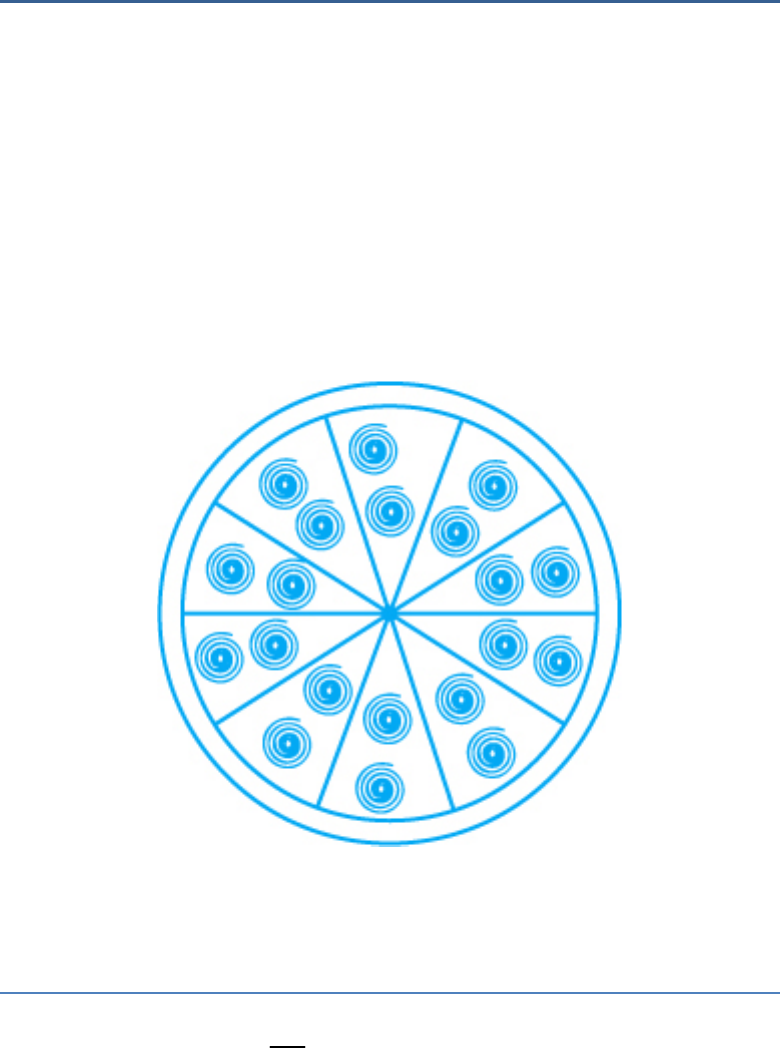
A brooch is made with silver wire in the form of a
circle with diameter 35 mm. The wire is also used in
making 5 diameters which divide the circle into 10
equal sectors as shown in figure. Find.
(i) The total length of the silver wire required.
(ii) The area of each sector of the brooch.
Fig. Exc_12.2_9
Solution:
Radius of circle
35
2
17.5mm
Circumference of brooch
2πr

22 35
2
7 2
110mm
(i) Length of the silver wire required
110 5 35
285mm
Observe, that each 10 sectors of the circle are
subtending at the center of the circle.
36
(ii) Now, find the area of each sector of the
brooch.
2
36
Area of each sector πr
360
2
1 22 35
10 7 2
2
1 22
17.5
10 7
2
96.25mm
Thus, the area of each sector of the brooch is
.
2
96.25mm
Question: 10
An umbrella has 8 ribs which are equally spaced
(see figure). Assuming umbrella to be a flat circle of
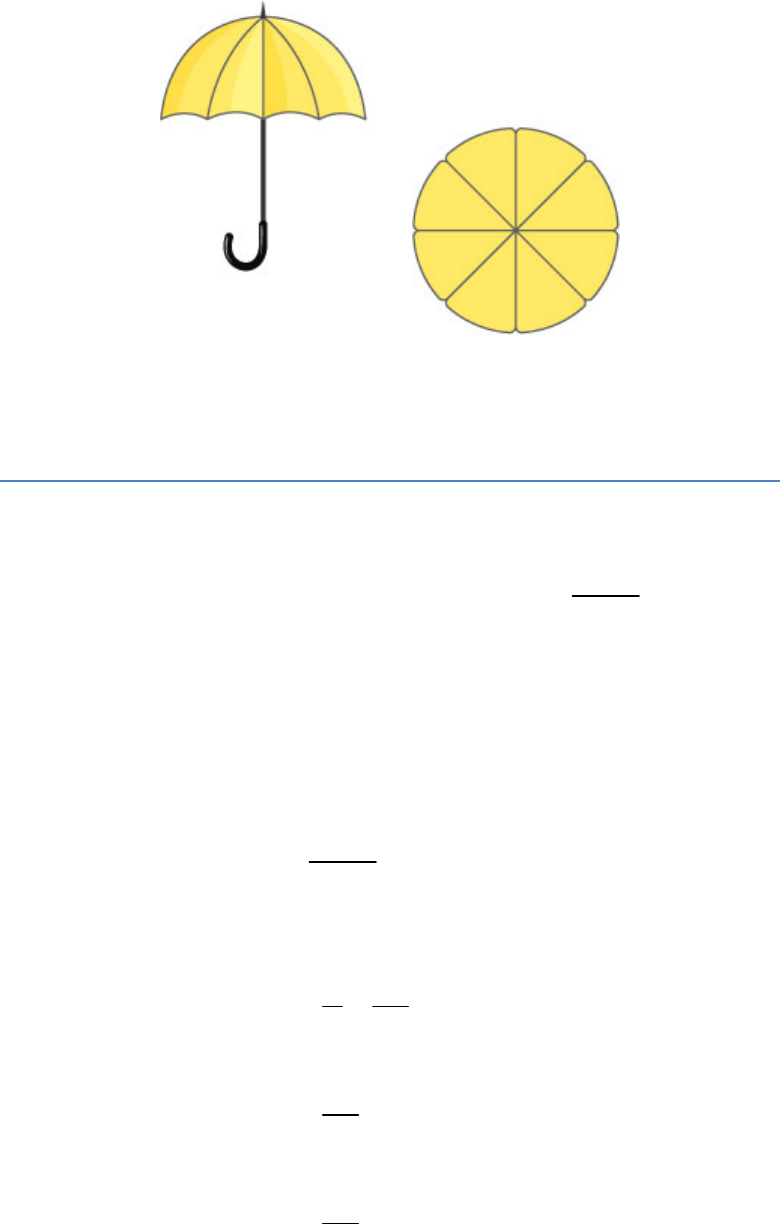
radius 45 cm, find the area between the two
consecutive ribs of the umbrella.
Fig. Exc_12.2_10
Solution:
Ribs in Umbrella
8
Angle between two consecutive ribs
360
8
45
Now, calculate the area.
2
Area between
two consecutive
ribs o
45
π r
f cir
360
cle
2
1 22
45
8 7
11
2025
28
11
2025
28
22275
28
2
795.54 cm
Thus, the area between two consecutive ribs of the
circle is .
2
795.54 cm
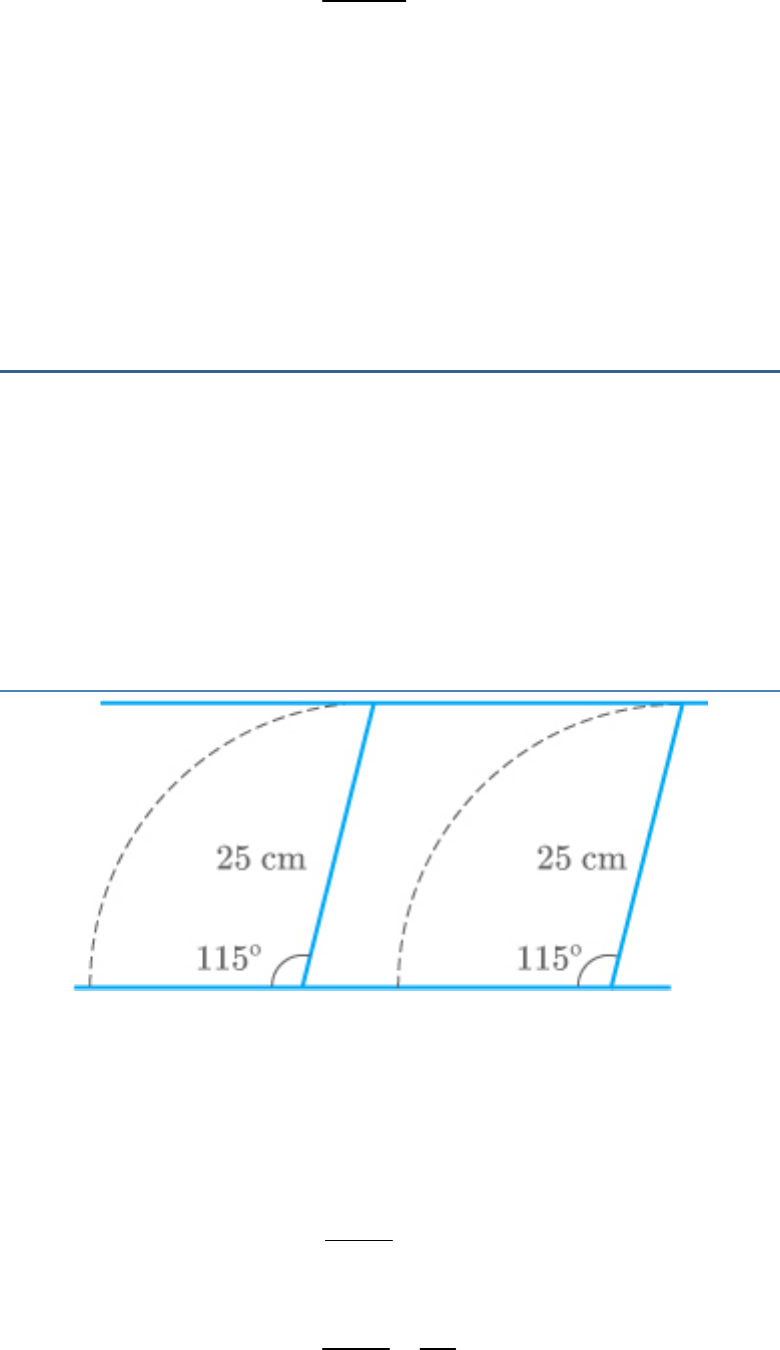
Question: 11
A car has two wipers which do not overlap. Each
wiper has blade of length 25 cm sweeping through
an angle of . Find the total area cleaned at each
115
sweep of the blades.
Solution:
Fig. Exc_12.2_11
From the figure, each blade of wiper will sweep an
area of in a circle of 25 cm radius.
115
2
115
Area of such sector π r
360
2
115 22
25
360 7

23 22
25 25
72 7
23 22
25 25
72 7
2
627.48cm
Area swept by 2 bl
158
ade
12
5
s
5
2
2 2
158125
126
2
1254.9603cm
Thus, the area swept by 2 blades is .
2
1254.9603cm
Question: 12
To warn ships for underwater rocks, a lighthouse
spreads a red coloured light over a sector of angle
to a distance of 16.5 km. Find the area of the
80
sea over which the ships warned. [Use ]
π 3 14
Solution:

Fig. Exc_12.2_12
The above figure shows that the lighthouse spreads
light across a sector of in a circle of 16.5 km
80
radius.
2
80
Area of sector OPQR r
360
2
80
3.14 16.5
360
2
2
3.14 16.5
9
2
189.97km
Thus, the area of the sector is .
2
189.97km
Question: 13
A round table cover has six equal designs as shown
in figure. If the radius of the cover is 28 cm, find the
cost of making the designs at the rate of Rs. 0.35 per
cm
2
. [Use ]
3 1 3.7
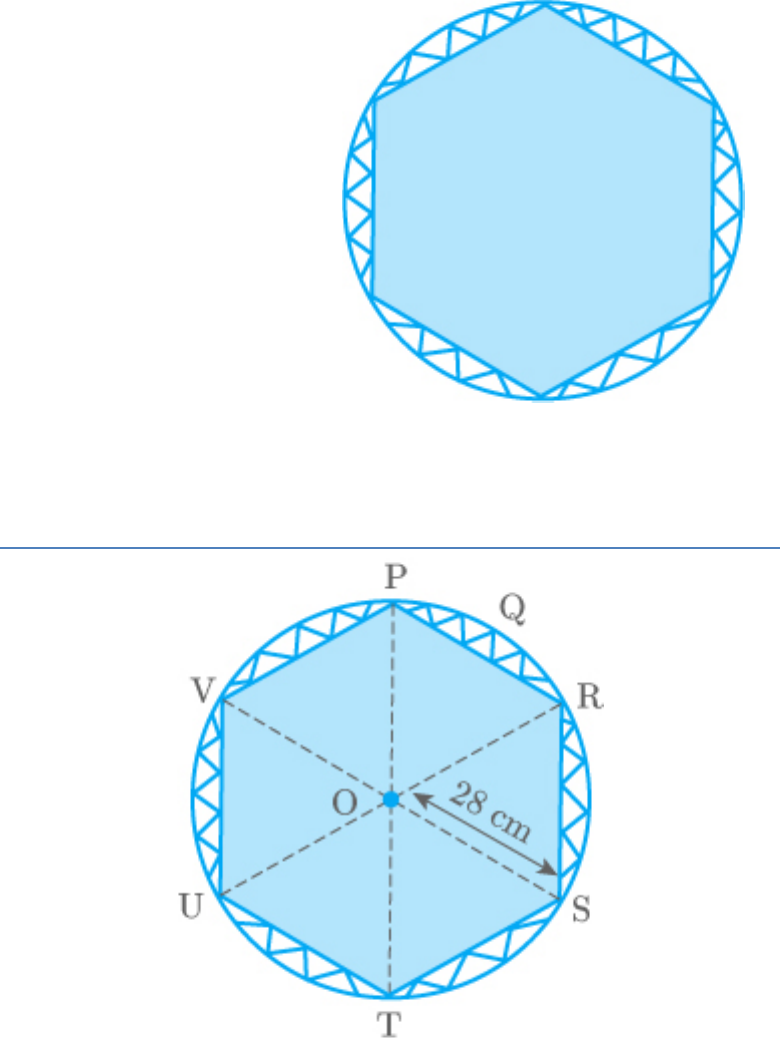
Fig. Exc_12.2_13 (Ques.)
Solution:
Fig. Exc_12.2_13 (Ans.)
Observe that these designs are the segments of the
circle.
Take segment PQR.
Chord PR is one side of the hexagon.
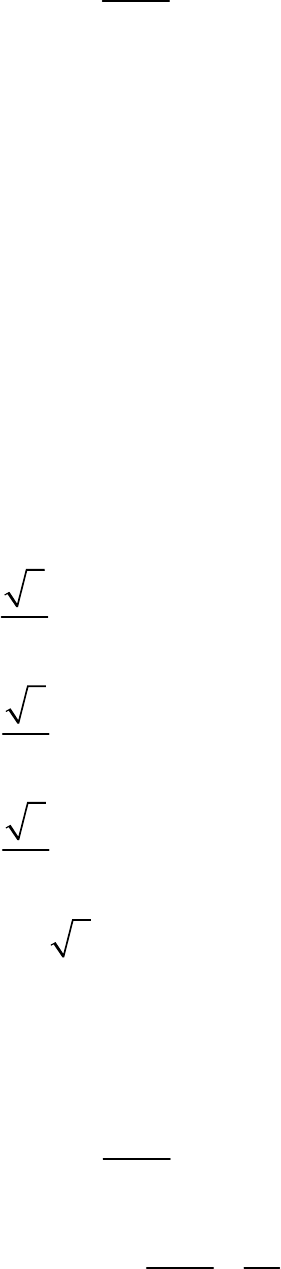
Substitute every chord at the center of
360
60
6
the circle.
In
OPR,
OPR ORP (As OP OR)
POR 60
OPR ORP POR 180
2 OPR 180 60 120
OPR 60
Thus,
OPR is an equilateral triangle.
2
3
Area of OPR side
4
2
3
28
4
3
784
4
196 3
196 1.7
2
333.2cm
2
60
Area of sector OPQR r
360
2
60 22
28
360 7

1 22
28 28
6 7
2
410 67cm
Area of Area of Area of
sector PQR sector OPQR OPR
410 667 333.2
2
77.467cm
Area of designs
77 76 .46
2
464 8cm
Making cost of designs
2
1cm
Rs 0.35
Making cost of designs
2
464.8cm
464.8 0.35
Rs.162.68
Thus, the making cost of such designs is Rs. .
162.68
Question: 14
Tick the correct answer in the following: Area of a
sector of angle (in degrees) of a circle with radius
p
is:
R
(A)
p
2πR
180
(B)
2
p
2πR
180
(C)
p
2πR
360
(D)
2
p
2πR
720
Solution:
(D)
Fig. Exc_12.2_14
The area of the sector of angle
2
θ
θ πR
360
2
p
Area of sector of angle p πR
360
2
o
p
2πR
720
Thus, the correct option is (D).
Exercise 12.3 (16)
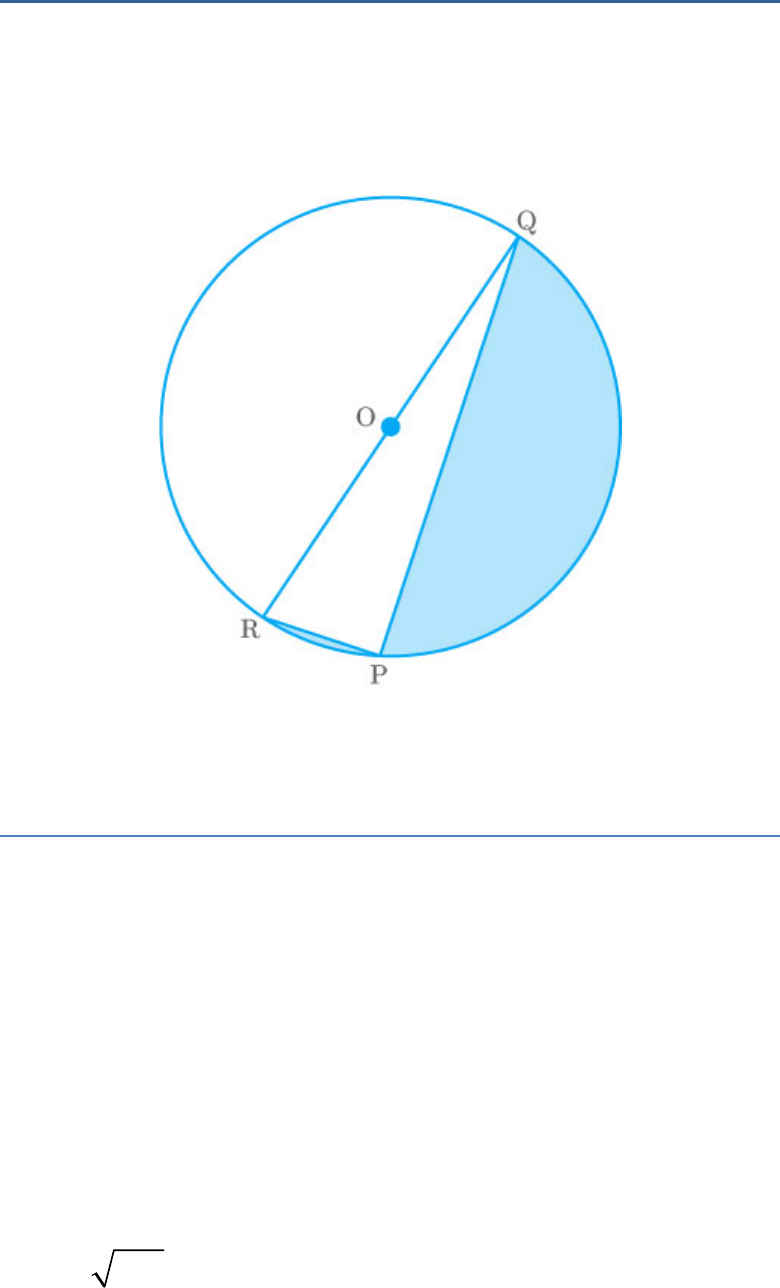
Question: 1
Find the area of the shaded region in the given
figure, if PQ = 24 cm, PR = 7 cm and O is the centre
of the circle.
Fig. Exc_12.3_1
Solution:
From the figure, observe that diameter of the circle
is RQ.
By applying Pythagoras theorem in PQR,
2 2 2
RQ RP PQ
2 2
2
RQ 7 24
2
RQ 49 576
RQ 625
RQ 25
Radius of circle , OR .
r
RQ 25
12.5
2 2
We know that, diameter of a circle divides circle in
two equal parts, so RQ is the diameter of the circle
that divides it in two equal parts.
2
1
Area of semi-circle RPQOR π r
2
2
1 22 25
2 7 2
1 22 625
2 7 4
6875
28
2
245.54 cm
1
Area of PQR PQ PR
2
1
24 7
2
2
84 cm
Area of Area of semi-Circle Area of
shadedregion RPQOR PQR
6875
84
28
6875 2352
28
4523
28
2
161.54 cm
Thus, the area of the shaded region is .
2
161.54 cm
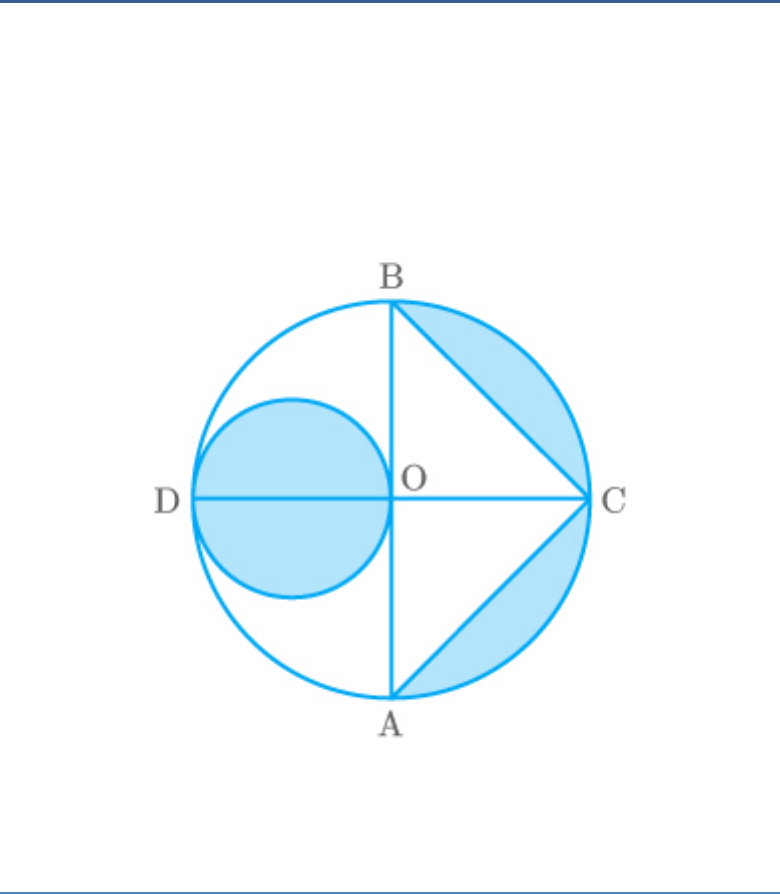
Question: 2
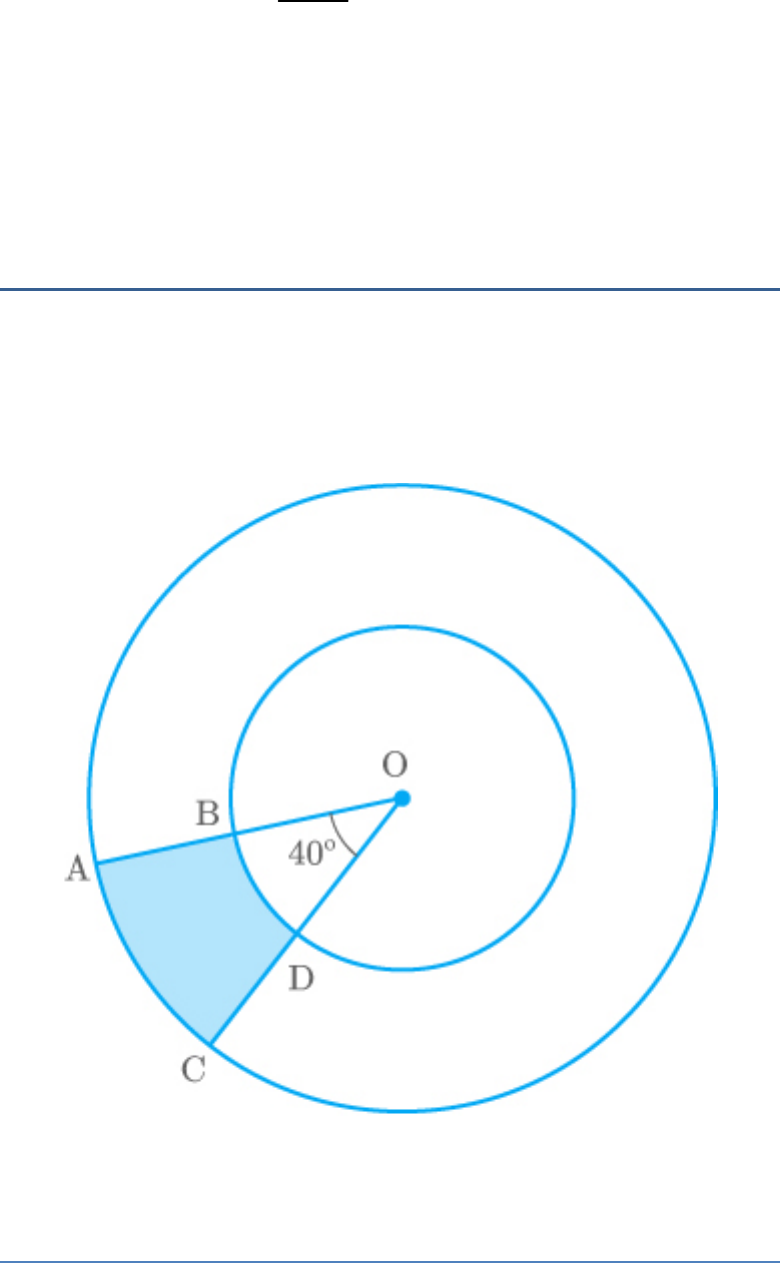
Find the area of the shaded region in given figure, if
radii of the two concentric circles with centre O are
7 cm and 14 cm respectively and .
AOC 40
Fig. Exc_12.3_2 (Ques.)
Solution:
Inner circle radius = 7 cm
Outer circle radius = 14 cm
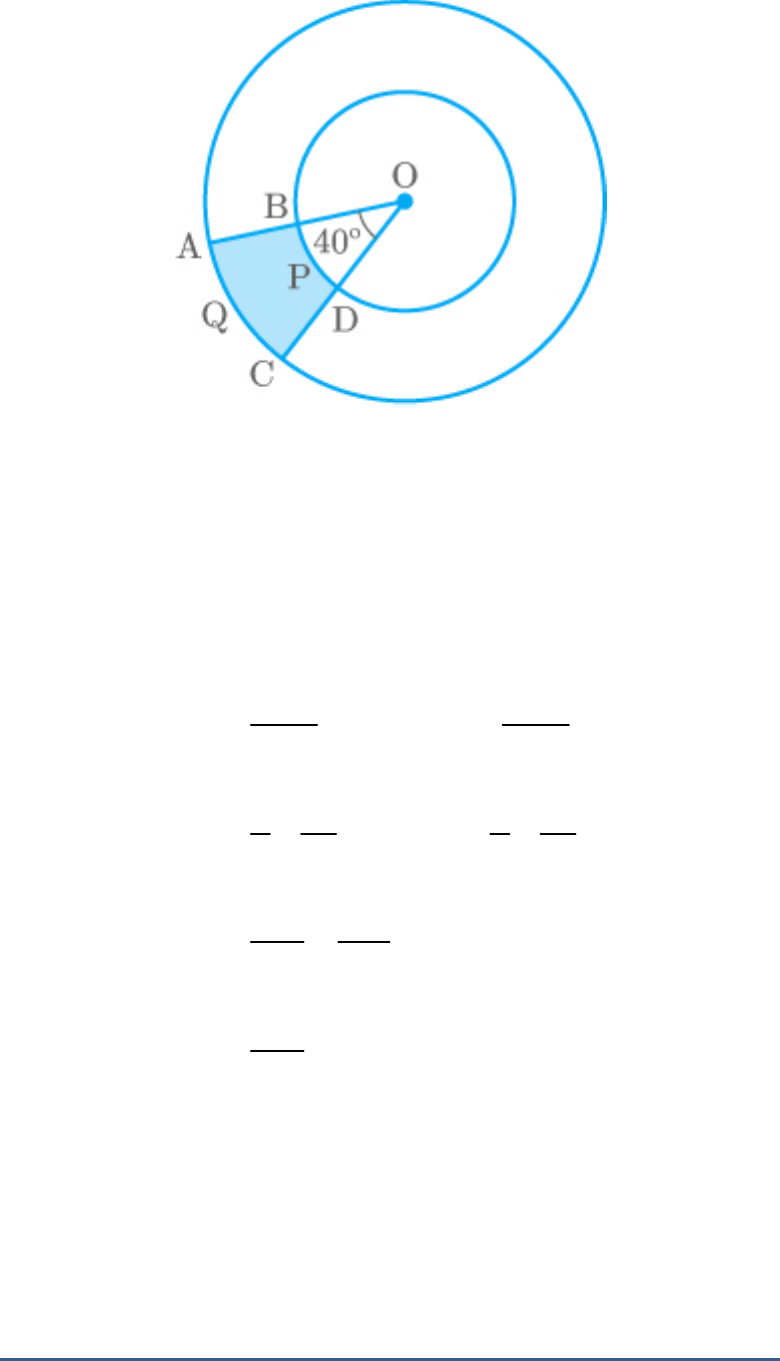
Fig. Exc_12.3_2 (Ans.)
Area of Area of Area of
shadedregion sector OAQC sector OBPD
o
2 2
40 40
π 14 π 7
360 360
1 22 1 22
14 14 7 7
9 7 9 7
616 154
9 9
462
9
2
51.33cm
Thus, the area of the shaded region is .
2
51.33cm
Question: 3
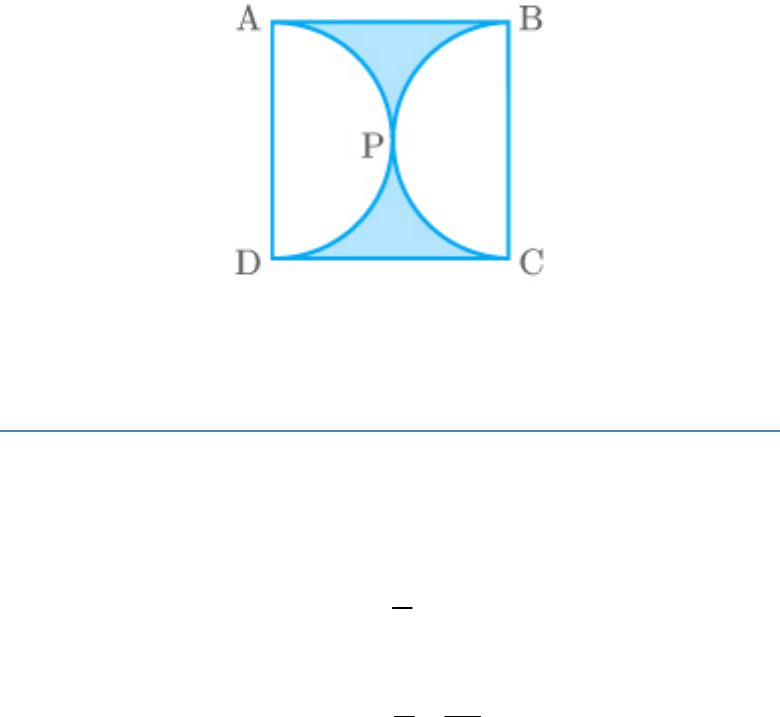
Find the area of the shaded region in the given
figure, if ABCD is a square of side 14 cm and APD
and BPC are semicircles.
Fig. Exc_12.3_3
Solution:
From the given figure, observe that the radius of
every semi-circle is 7 cm.
2
1
Area of each semi circle πr
2
2
1 22
7
2 7
11 7
2
77cm
Now, find the area of square.
2
Area of square ABCD 14
2
196cm
Area of Area of Area of Area of
shadedregion square ABCD semi-circleAPD semi-circleBPC
196 77 77
2
42cm
Thus, the area of the shaded region is .
2
42cm
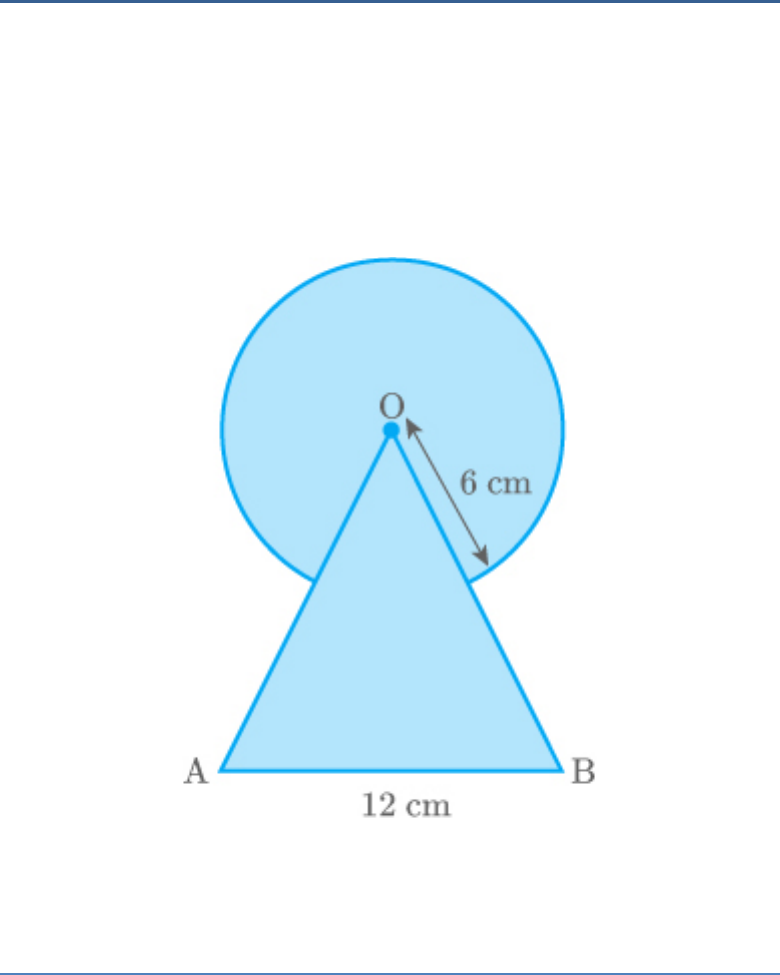
Question: 4
Find the area of the shaded region in the given
figure, where a circular arc of radius 6 cm has been
drawn with vertex O of an equilateral triangle OAB
of side 12 cm as centre.
Fig. Exc_12.3_4 (Ques.)
Solution:
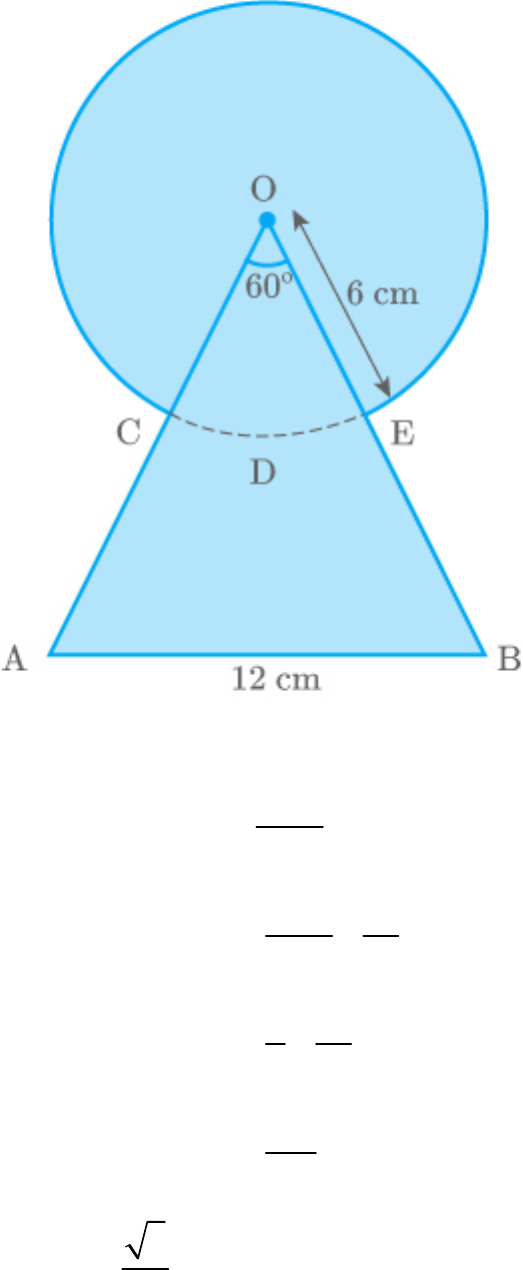
Each interior angle of an equilateral triangle is of
.
60
Fig. Exc_12.3_4 (Ans.)
2
60
Area of segment OCDE r
360
2
60 22
6
360 7
1 22
36
6 7
2
132
cm
7
2
3
Area of AOB 12
4
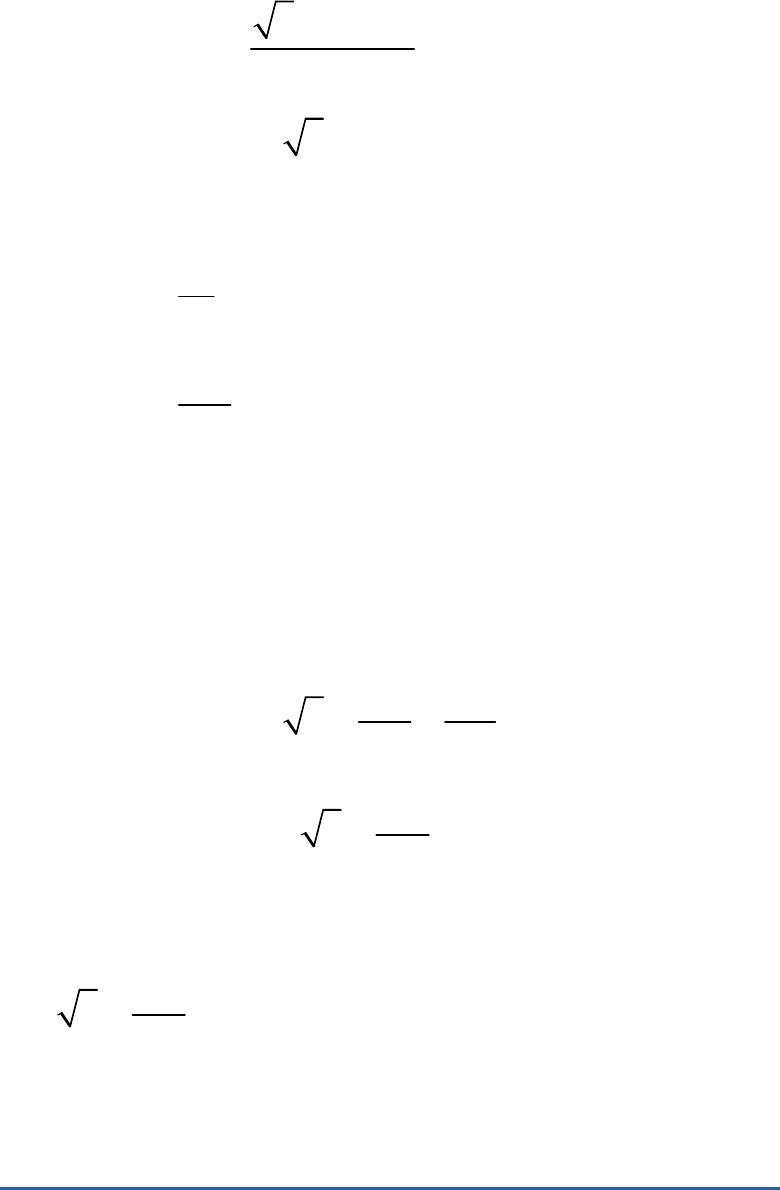
3 12 12
4
36 3
2
Area of circle πr
2
22
6
7
2
792
cm
7
Area of Area of Area of Area of
shadedregion OAB Circle sector OCDE
792 132
36 3
7 7
2
660
36 3 cm
7
Thus, the area of the shaded region is
.
2
660
36 3 cm
7
Question: 5
From each corner of a square of side 4 cm a
quadrant of a circle of radius 1 cm is cut and also a
circle of diameter 2 cm is cut as shown in the given
figure. Find the area of the remaining portion of the
square.
Fig. Exc_12.3_5 (Ques.)
Solution:
Fig. Exc_12.3_5 (Ans.)
Each quadrant is a sector of in a circle having
90
radius of 1 cm.

Area of each quadrant
2
90
πr
360
2
1 22
1
4 7
2
22
cm
28
2
Area of square PQRS 4
2
16cm
Area of Area of Area of Area of
4
shadedregion square circle quadrant
22 22
16 4
7 28
22 22
16
7 7
44
16
7
112 44
7
2
68
cm
7
Thus, the area of the shaded portion is .
2
68
cm
7
Question: 6
In a circular table cover of radius 32 cm, a design is
formed leaving an equilateral triangle ABC in the
middle as shown in the given figure. Find the area
of the design (shaded region).
Fig. Exc_12.3_6 (Ques.)
Solution:
Fig. Exc_12.3_6 (Ans.)
Radius of circle
r
32cm
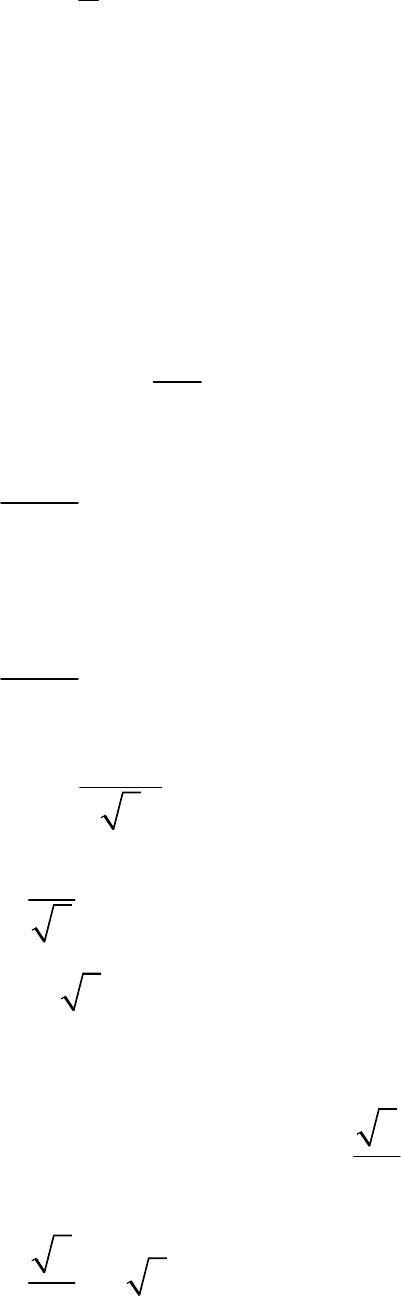
In , AP is the median.
ABC
3
AP 32
2
48cm
In ,
ABP
2 2
2
AB AP BP
2
2
AB
48
2
2
2
3AB
48
4
That is,
2
2
3AB
48
4
48 2
AB
3
96
3
32 3 cm
Now, calculate the area of the equilateral triangle.
2
Area of equilateral
3
AB
triangle ABC
4
2
3
32 3
4

3
32 32 3
4
96 8 3
2
768 3 cm
2
Area of circle πr
2
22
32
7
2
22528
cm
7
Area of Area of Area of
–
design circle ABC
2
22528
768 3 cm
7
Thus, the area of the design is
2
22528
768 3 cm
7
.
Question: 7
In the adjoining figure, ABCD is a square of side 14
cm. With centres A, B, C and D, four circles are
drawn such that each circle touch externally two of
the remaining three circles. Find the area of the
shaded region.
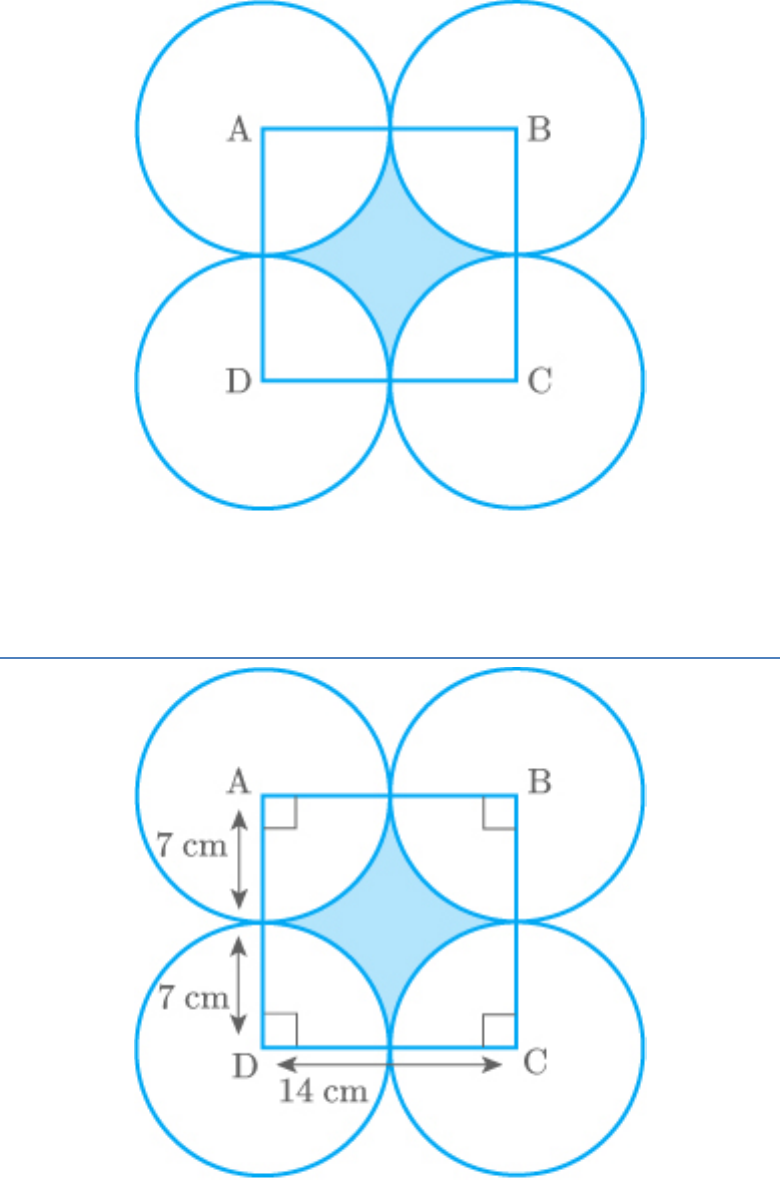
Fig. Exc_12.3_7 (Ques.)
Solution:
Fig. Exc_12.3_7 (Ans.)
In the figure, area of each sector is equal & in a
circle the sector is of having radius of 7 cm.
90

2
90
Area of each sector πr
360
2
90 22
7
360 7
1 22
49
4 7
2
38.5cm
2
Area of squareABCD Side
2
14
2
196cm
Area of Area of Area of
4
shadedregion square ABCD each sector
77
196 4
2
196 154
2
42cm
Thus, the area of the shaded portion is .
2
42cm
Question: 8
The given figure depicts a racing track whose left
and right ends are semi-circular.
The distance between the two inner parallel line
segments is 60 m and they are each 106 m long. If
the track is 10 m wide, find:
(i) the distance around the track along its inner
edge.
(ii) the area of the track.
Fig. Exc_12.3_8 (Ques.)
Solution:
Fig. Exc_12.3_8 (Ans.)
Distance around the track
AB arcBEC CD arcDFA
along its inner edge
1 1
106 2πr 106 2πr
2 2
1 22 1 22
212 2 30 2 30
2 7 2 7
22
212 2 30
7
212 188.57
400.57m
Area of the track = (Area of GHIJ − Area of ABCD)
+ (Area of semi-circle HKI − Area of semi-circle
BEC) + (Area of semi-circle GLJ − Area of semi-
circle AFD)
2 2
2 2
106 80 106 60
1 22 1 22
40 30
2 7 2 7
1 22 1 22
40 30
2 7 2 7
2 2
22 22
106 80 60 40 30
7 7
2 2
22
106 20 40 30
7
22
2120 10 70
7
2120 2200
2
4320m
Thus, the area of the track is 4320 m
2
.
Question: 9
In the given figure, AB and CD are two diameters of
a circle (with centre O) perpendicular to each other
and OD is the diameter of the smaller circle. If OA =
7 cm, find the area of the shaded region.
Fig. Exc_12.3_9 (Ques.)
Solution:

Fig. Exc_12.3_9 (Ans.)
From the figure, observe that,
Radius of larger circle = 7 cm
1
r
Radius of smaller circle =
2
r
7
cm
2
2
1
Area of smaller circle πr
22 7 7
7 2 2
77
2
2
38.5cm
2
2
1
Area of semi-circle AECFB πr
2
2
1 22
7
2 7

11
49
7
2
77cm
1
Area of ABC AB OC
2
1
14 7
2
2
49cm
Area of
smaller Circle
Area of Area of
shadedregion semi-circleAECFB
Area of
ABC
77
77 49
2
77
28
2
38.5 28
2
66.5cm
Thus, the area of the shaded region is 66.5 cm
2
.
Question: 10
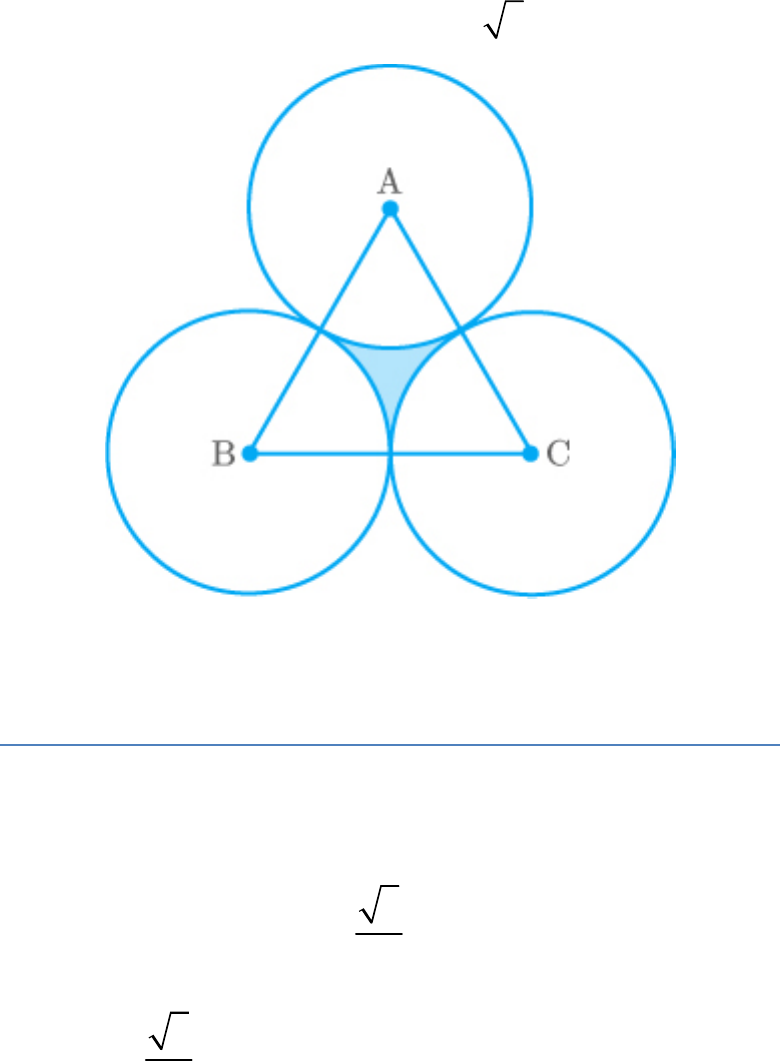
The area of an equilateral triangle ABC is 17320.5
cm
2
. With each vertex of the triangle as centre, a
circle is drawn with radius equal to half the length
of the side of the triangle. Find the area of the
shaded region. (Use and )
π 3 4.1
3 1 73205
Fig. Exc_12.3_10 (Ques.)
Solution:
Let be the side of an equilateral triangle.
a
Area of equilateral triangle is 17320.5
2
cm
2
Area of
equilateral triangl
3
e
a
4
2
3
17320.5 a
4
2
1.73205
17320.5 a
4
2
a 4 10000
a 200cm
Fig. Exc_12.3_10 (Ans.)
Each segment is a measure of 60°.
2
Area of
60
π r
segment ADEF
360
2
1
= π 100
6
3.14 10000
6
2
5233.33cm
Area of Area of Equilateral Area of each
shadedregion triangle segment
17320.5 3 5233.33
17320.5 15700
2
1620.5cm
Thus, the area of the shaded region is 1620.5 cm
2
.
Question: 11
On a square handkerchief, nine circular designs
each of radius 7 cm are made. Find the area of the
remaining portion of the handkerchief.
Fig. Exc_12.3_11 (Ques.)
Solution:
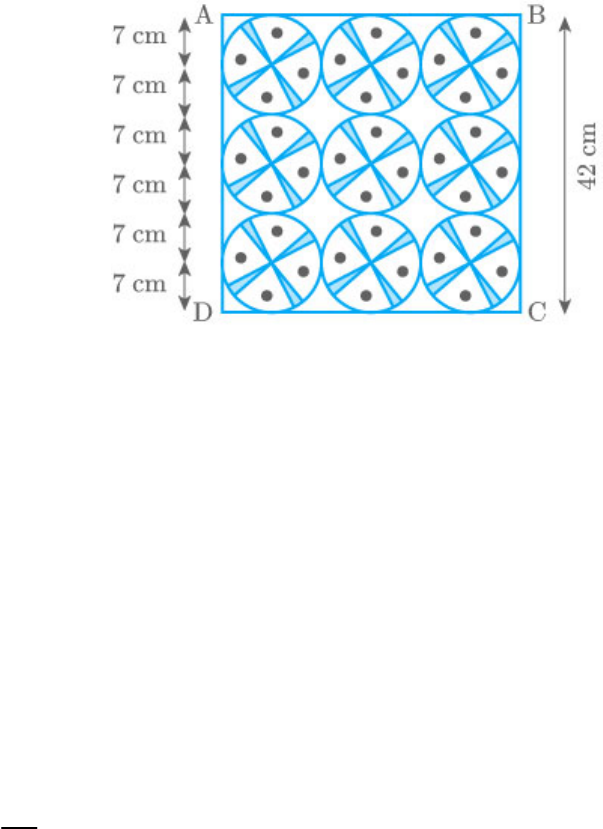
Fig. Exc_12.3_11 (Ans.)
From the figure, observe that the side of the square
is 42 cm.
2
Area of square Side
2
42
2
1764 cm
2
Area of each circle πr
2
22
7
7
2
154 cm
Area of 9 circles 9 154
2
1386cm
Handkerchief remaining portion area:
Area of remaining portion
1764 1386
of handkerchief
2
378cm
Thus, the area of the shaded region is 378 cm
2
.
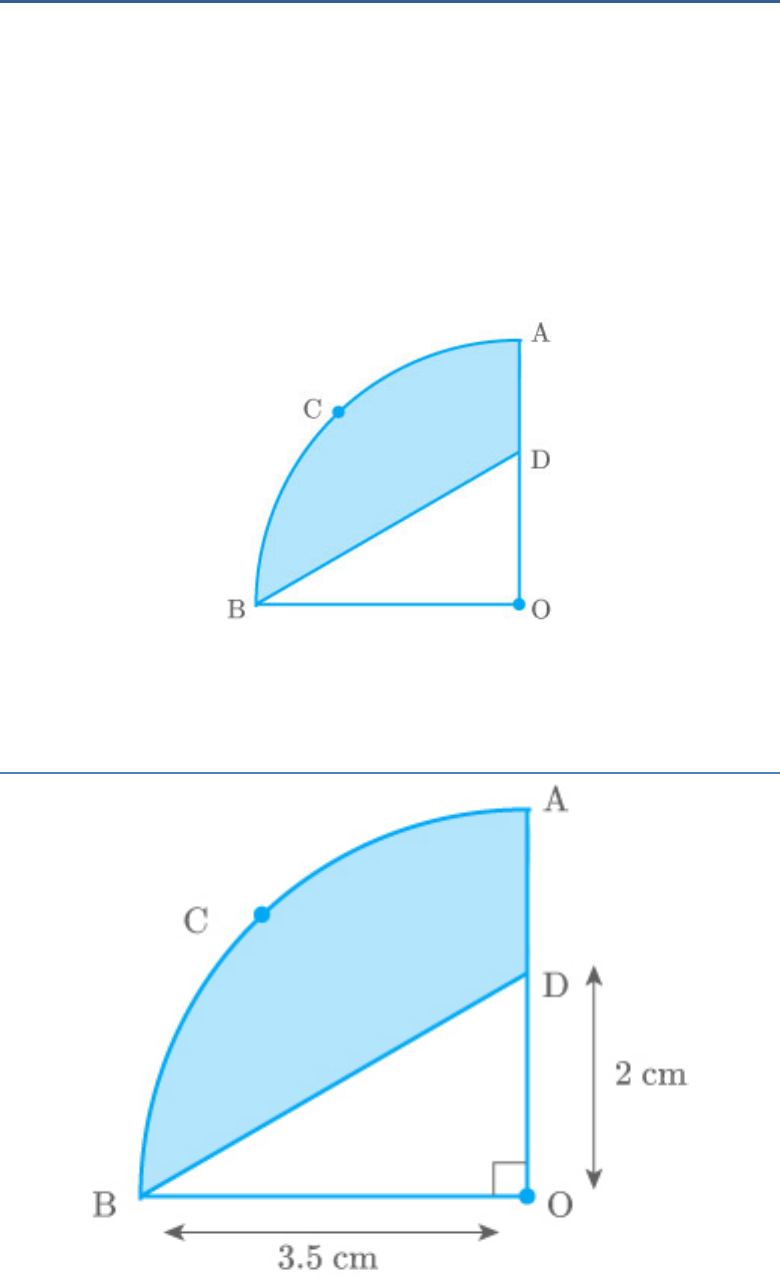
Question: 12
In the given figure, OACB is a quadrant of a circle
with centre O and radius 3.5 cm. If OD = 2 cm, find
the area of the
(i) quadrant OACB
(ii) shaded region
Fig. Exc_12.3_12 (Ques.)
Solution:
Fig. Exc_12.3_12 (Ans.)
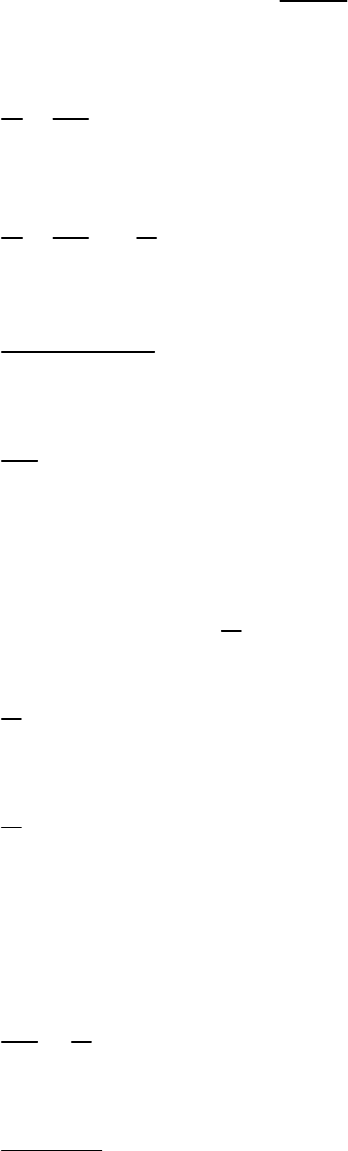
(i) Since OACB is a quadrant, it will subtend 90°
angle.
area:
2
quadrant OACB
Area of
90
πr
360
2
1 22
3.5
4 7
2
1 22 7
4 7 2
11 7 7
2 7 2 2
2
77
cm
8
(ii)
1
Area of OBD OB OD
2
1
3.5 2
2
2
7
cm
2
Area of Area of Area of
shadedregion quadrant OACB OBD
77 7
8 2
77 28
8
2
49
cm
8
Thus, the area of the shaded region is .
2
49
cm
8
Question: 13
In the given figure, a square OABC is inscribed in a
quadrant OPBQ. If OA = 20 cm, find the area of the
shaded region. (Use )
π 3 4.1
Fig. Exc_12.3_13 (Ques.)
Solution:
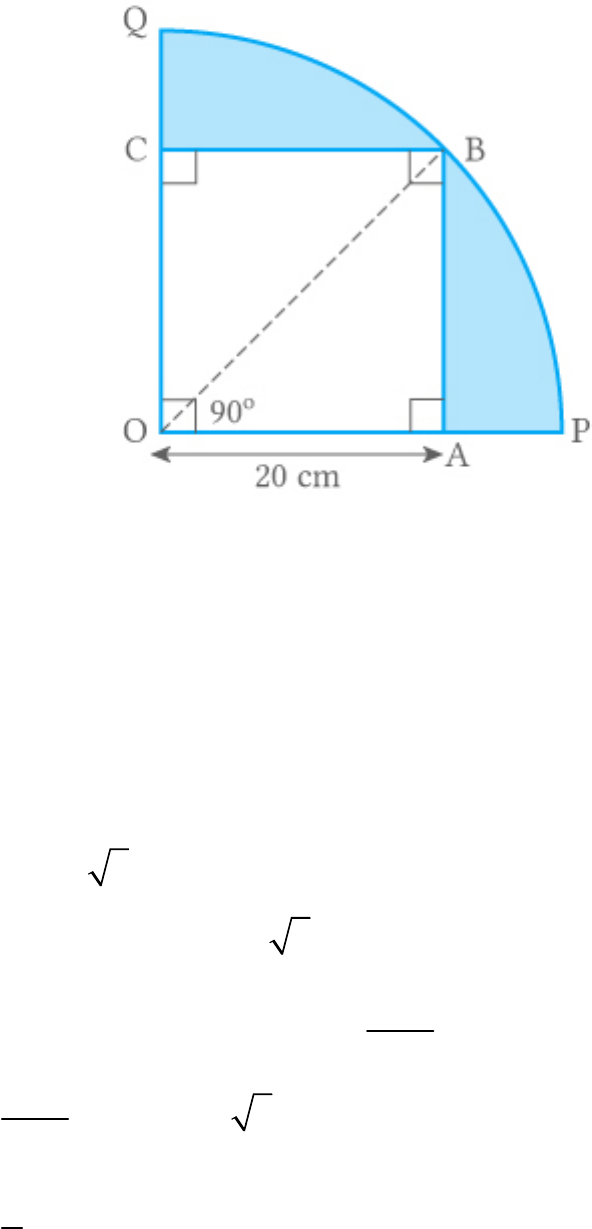
Fig. Exc_12.3_13 (Ans.)
In ,
OAB
2 2 2
OB OA AB
2 2
2
OB 20 20
2
OB 400 400
OB 20 2
Radius of circle
20 2 cm
2
90
Area of quadrant OPBQ π r
360
2
90
3.14 20 2
360
1
3.14 800
4
2
628cm
Area of Area of Area of
shadedregion quadrant OPBQ OABC
628 400
2
288cm
Thus, the area of the shaded region is 288 cm
2
.
Question: 14
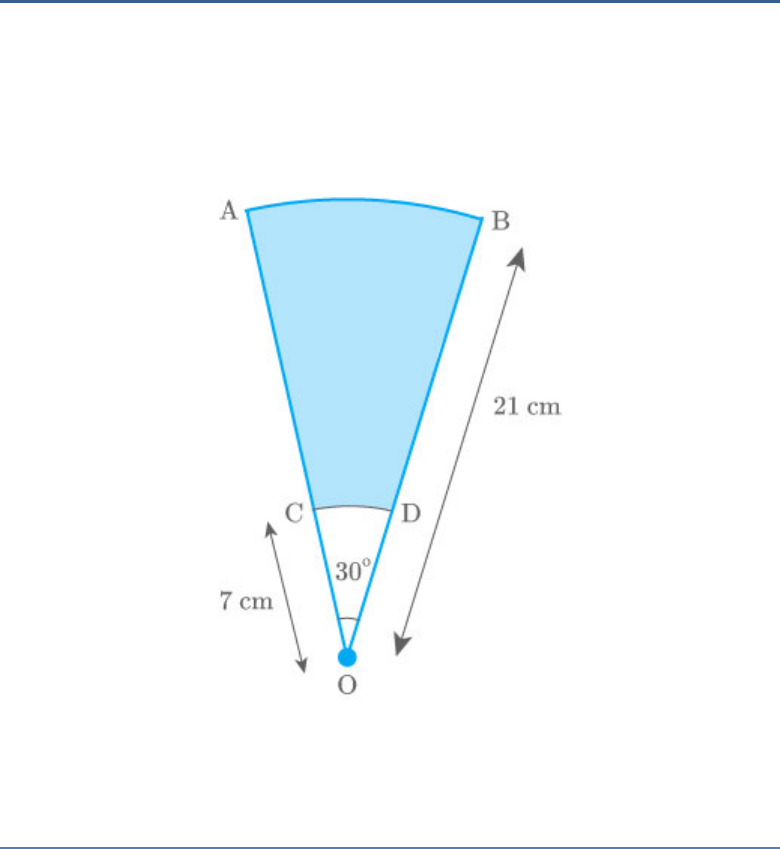
AB and CD are respectively arcs of two concentric
circles of radii 21 cm and 7 cm and centre O. If
AOB = 30°, find the area of the shaded region.
Fig. Exc_12.3_14 (Ques.)
Solution:
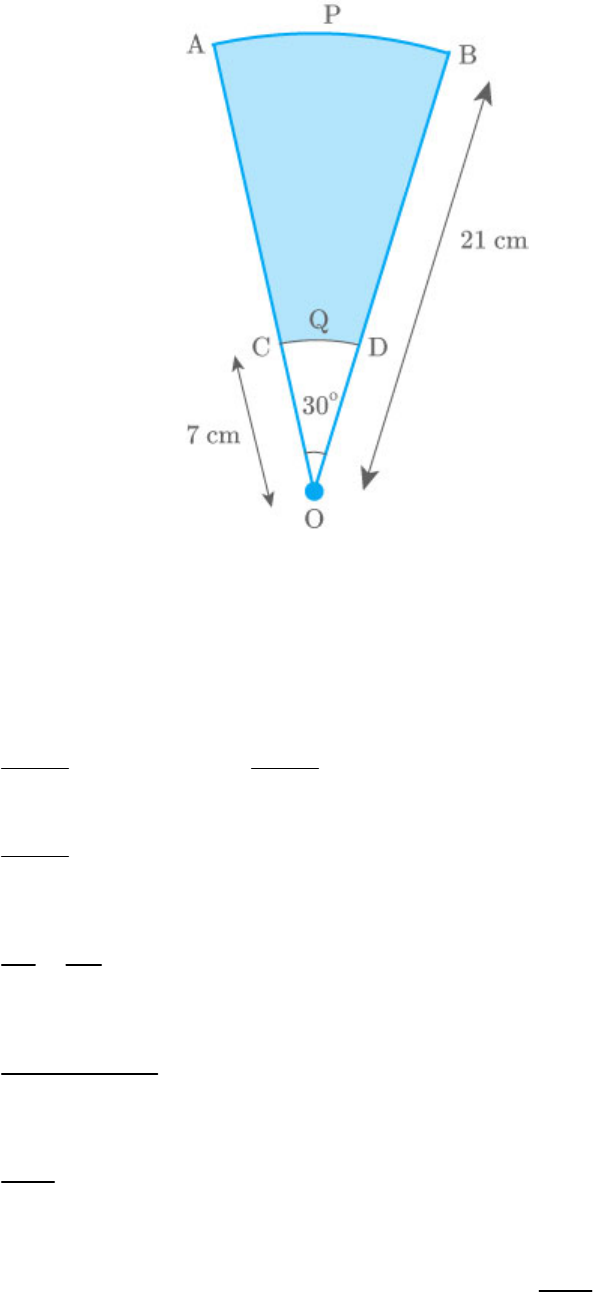
Fig. Exc_12.3_14 (Ans.)
Area of Area of Area of
shadedregion segment OAPB segment OCQD
2 2
30 30
π 21 π 7
360 360
2 2
30
π 21 7
360
1 22
21 7 21 7
12 7
22 14 28
12 7
2
308
cm
3
Thus, the area of the shaded region is .
2
308
cm
3
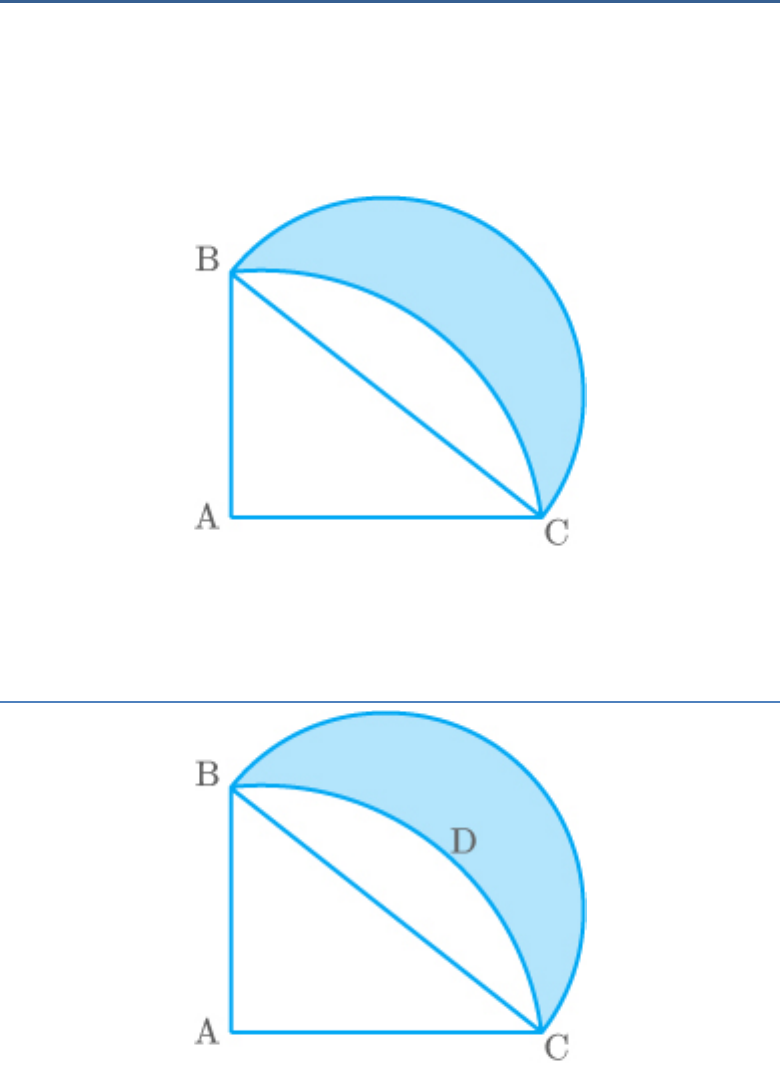
Question: 15
In the given figure, ABC is a quadrant of a circle of
radius 14 cm and a semicircle is drawn with BC as
diameter. Find the area of the shaded region.
Fig. Exc_12.3_15 (Ques.)
Solution:
Fig. Exc_12.3_15 (Ans.)
From the figure, observe that ABC is the quadrant
of the circle, is right-angle.
BAC
In ,
ABC
2 2 2
BC AC AB
2 2
2
BC 14 14
BC 14 2
1
14 2
Radius r of semi-circle drawn on BC
2
7 2 cm
1
Area of ABC AB AC
2
1
14 14
2
98cm
2
90
Area of sector ABCD π r
360
2
90 22
14
360 7
1 22
196
4 7
2
154 cm
2
1
Area of semi-circle
drawn
1
π
on B
r
2
C
2
1 22
7 2
2 7
1 22
98
2 7
2
154 cm
Area of
Semi-circle
Area of Area of
shadedregion segment ABCD
Area of
ABC
154 154 98
2
98cm
Thus, the area of the shaded region is 98 cm
2
.
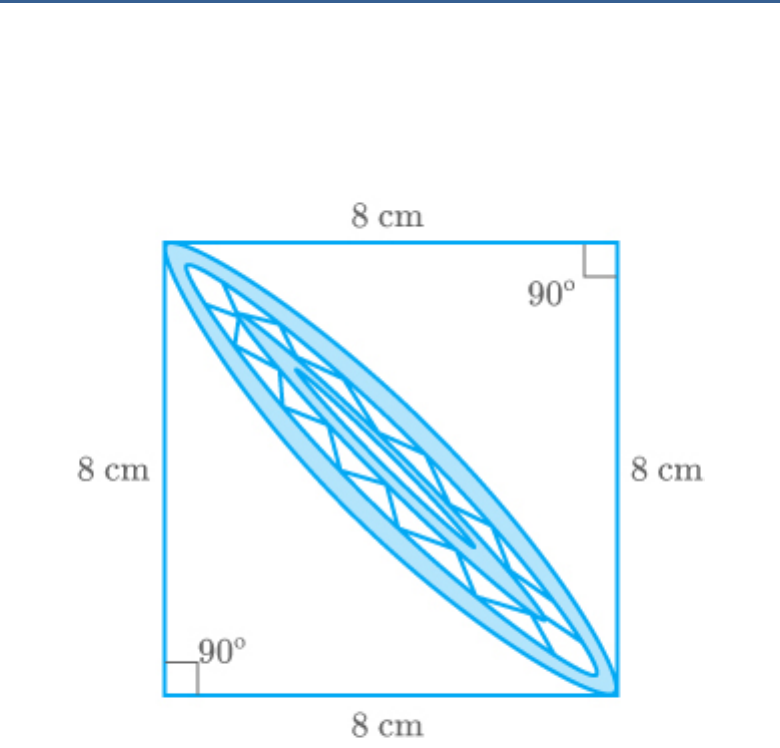
Question: 16
Calculate the area of the designed region in the
given figure common between the two quadrants of
circles of radius 8 cm each.
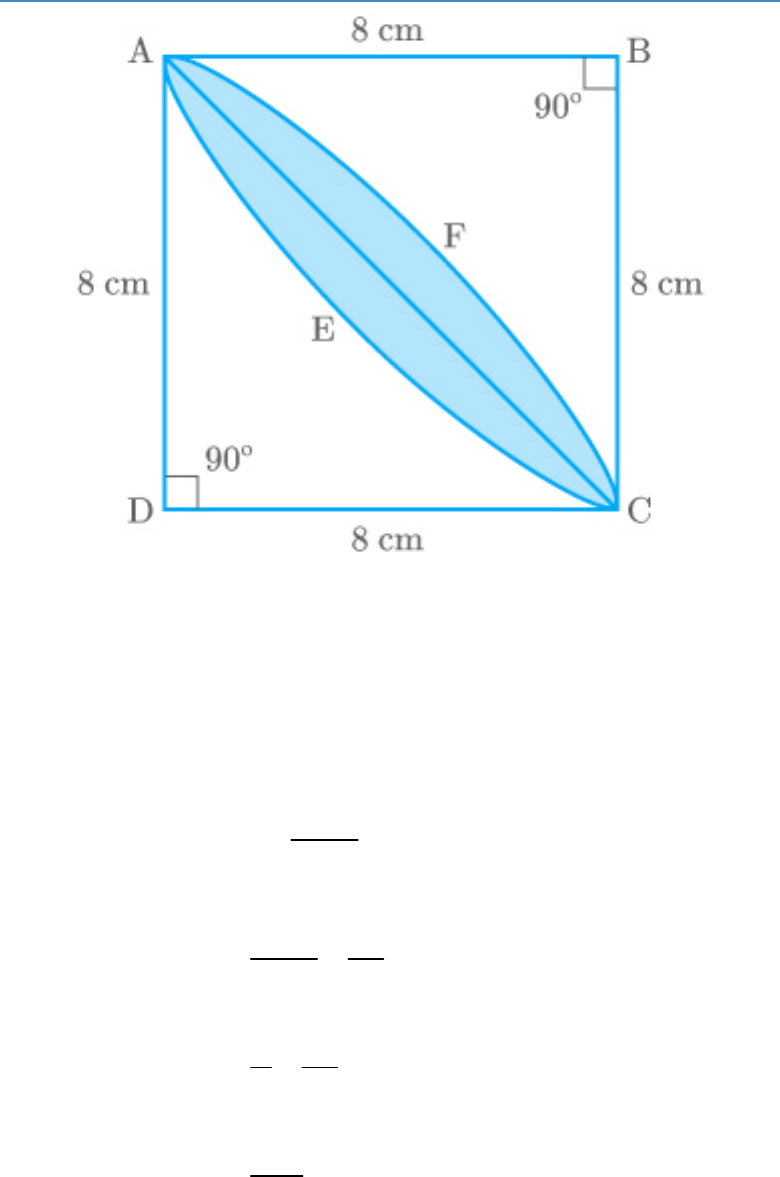
Fig. Exc_12.3_16 (Ques.)
Solution:
Fig. Exc_12.3_16 (Ans.)
Find the designed area between two segments
BAEC & DAFC.
Segment BAEC area:
2
Area of
90
π r
segment BAEC
360
2
90 22
8
360 7
1 22
64
4 7
2
352
cm
7

1
Area of BCA BA BC
2
1
8 8
2
2
32cm
Designed region area:
Area of Area of
2
designedregion segment AEC
Area of Area of
2
segment BAEC BAC
352
2 32
7
352 224
2
7
2 128
7
2
256
cm
7
Thus, the area of the designed region is .
2
256
cm
7