
Lesson: Constructions
Exercise 11.1 (7)
Question: 1
Draw a line segment of length 7.6 cm and divide it
in the ratio . Measure the two parts.
5:8
Solution:
The steps for construction are as follows:
1. Draw a line segment of length 7.6 cm.
RS
2. Draw a ray making an acute angle with
RX
RS
.
3. Mark 13 points along . The points will be
RX
such that .
1
R ,
2
R ,
3
R ,
13
,R
1 1 2 2 3
RR RR R R
4. Join point with point .
S
13
R
5. Through the point , draw a line parallel to
5
R
by making an angle equal to at
13
R S
13
RR S
5
R
. This line meets at a point .
RS
P
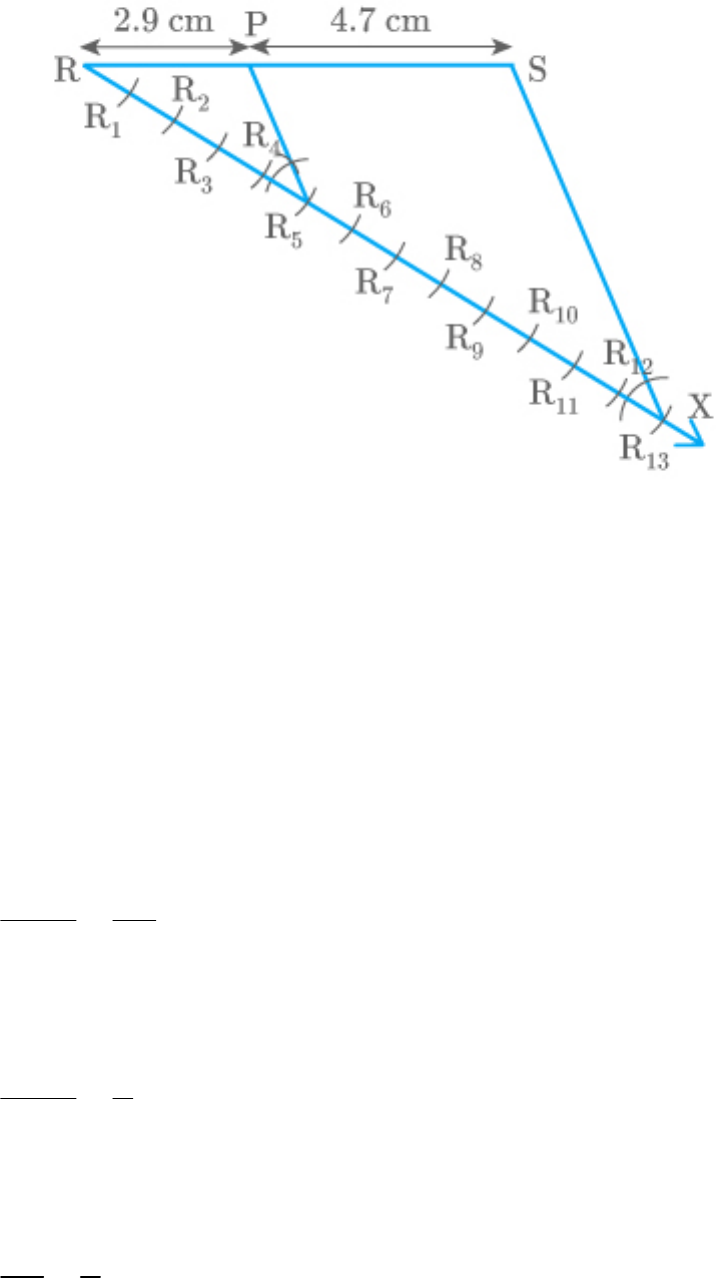
Fig. Exc_11.1_1
Thus, the point is the required point which
P
divides line internally in the ratio of .
RS
5:8
Justification:
In triangle , .
13
RSR
5 13
RP||R S
Thus, by the Proportionality Theorem
-
5
5 13
RR RP
...... 1
RR PS
By the above construction,
5
5 13
RR 5
...... 2
RR 8
By equations (1) and (2),
RP 5
PS 8
Hence,

RP:PS 5:8
Therefore, divides the line in the ratio of .
P
RS
5:8
Question: 2
Construct a triangle of sides 4 cm, 5 cm and 6 cm
and then a triangle similar to it whose sides are
2
3
of the corresponding sides of the first triangle.
Solution:
Construct a triangle in which
LMN
LM 4 cm,
and .
MN 5cm
LN 6cm
The following steps should be followed:
1. Draw a line segment LM of length .
4 cm
2. With L as centre and radius equal to ,
6cm
draw an arc.
3. With M as centre, draw another arc of radius
, cutting the previous arc at N.
5cm
4. Join LN and MN.
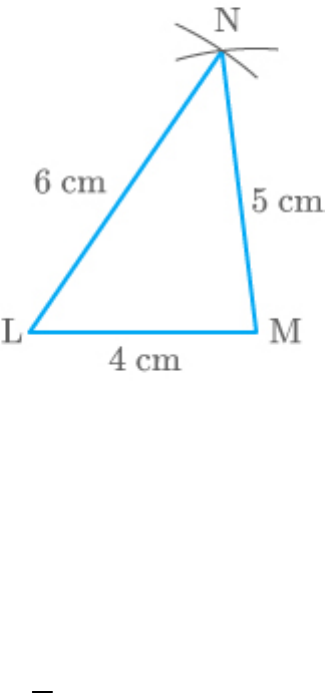
Fig. Exc_11.1_2 Sol (i)
Hence, is the required triangle.
LMN
The following steps are involved in the
construction of a triangle similar to the ,
LMN
with scale factor .
2
3
1. Draw the given .
LMN
2. Take any side of the triangle as base. For
instance, let be the base of the .
LM
LMN
3. Draw acute at the point below the
MLX
L
base .
LM
4. Mark off points along the line
3
1
L ,
2
L ,
3
L
LX
such that,
1 1 2 2 3
LL L L L L
5. Join .
3
L M
6. Beginning from , reach a point on and
L
3
L
LX
draw that touches at .
2 3
L M ||L M
LM
M
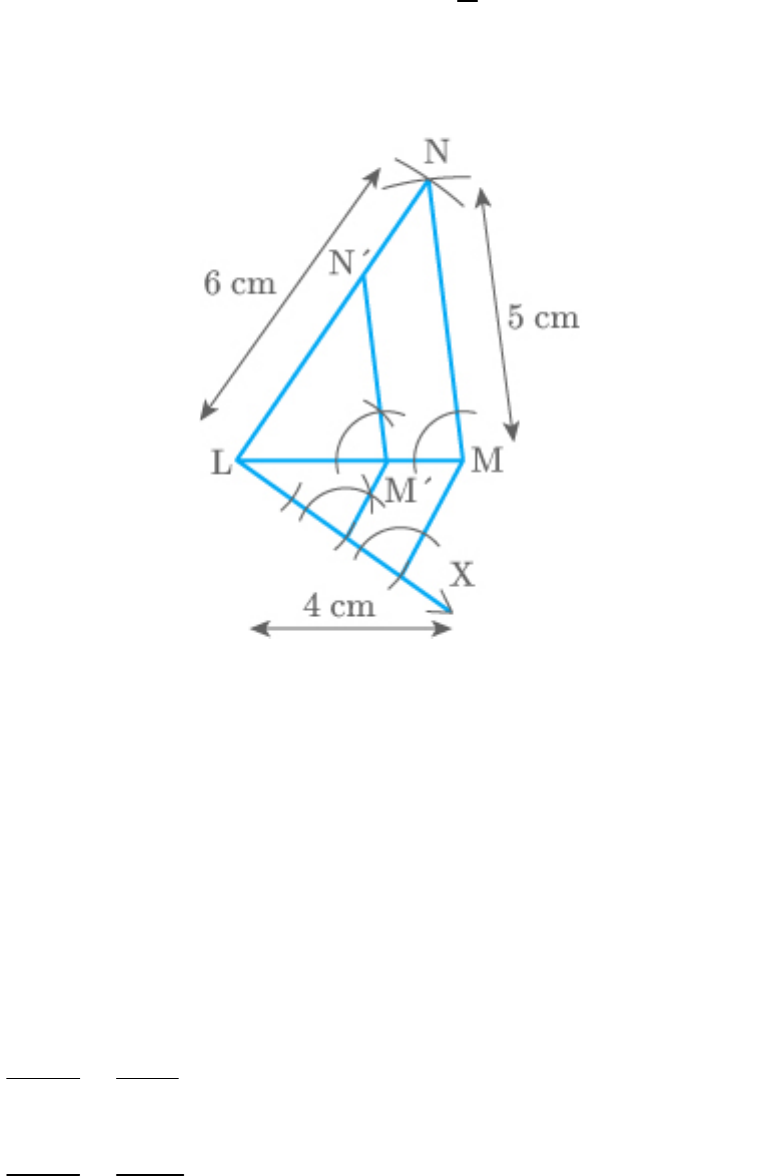
7. Draw that touches at .
M N ||MN
LN
N
8. is the required triangle similar to
LM N
, whose sides are of the
LMN
rd
2
3
corresponding sides of .
LMN
Fig. Exc_11.1_2 Sol (ii)
Justification: The construction of the triangle
similar to the given triangle can be verified as
follows.
M N ||MN
Therefore,
2
2 3
LM LL
proportionality theorem
M M L L
LM 2
M M 3 2
M M 3 2
...... 1
LM 2
Now,
LM LM M M
LM LM
LM M M
1
LM LM
From equation (1).
LM 3 2
1
LM 2
LM 2 3 2
LM 2
LM 3
LM 2
LM 2
...... 2
LM 3
In and ,
LMN
LM N
MLN M LN
LMN LM N
Hence,
LMN|| LM N similarity criterion
Hence,
LM M N LN
LM MN LN
From equation (2).

LM M N LN
LM MN LN
2
3
Hence, and are similar, and the
LM N
LMN
sides of are of the corresponding
LM N
rd
2
3
sides of .
LMN
Question: 3
Construct a triangle with sides 5 cm, 6 cm and 7 cm
and then another triangle whose sides are of the
7
5
corresponding sides of the first triangle.
Solution:
1. Draw a line segment LM of 5 cm. Taking L and
M as centre, draw arcs of 6 cm and 7 cm radius
respectively. Let these arcs intersect each other
at point N.
is the required triangle.
LMN
2. Draw a ray LX making acute angle with line
LM on the opposite side of vertex N.
3. Locate 7 points, on line LX
1
L ,
2
L ,
3
L ,
4
L ,
5
L ,
6
L ,
7
L
such that
1 1 2 2 3 3 4 4 5
LL L L L L L L L L
.
5 6 6 7
L L L L
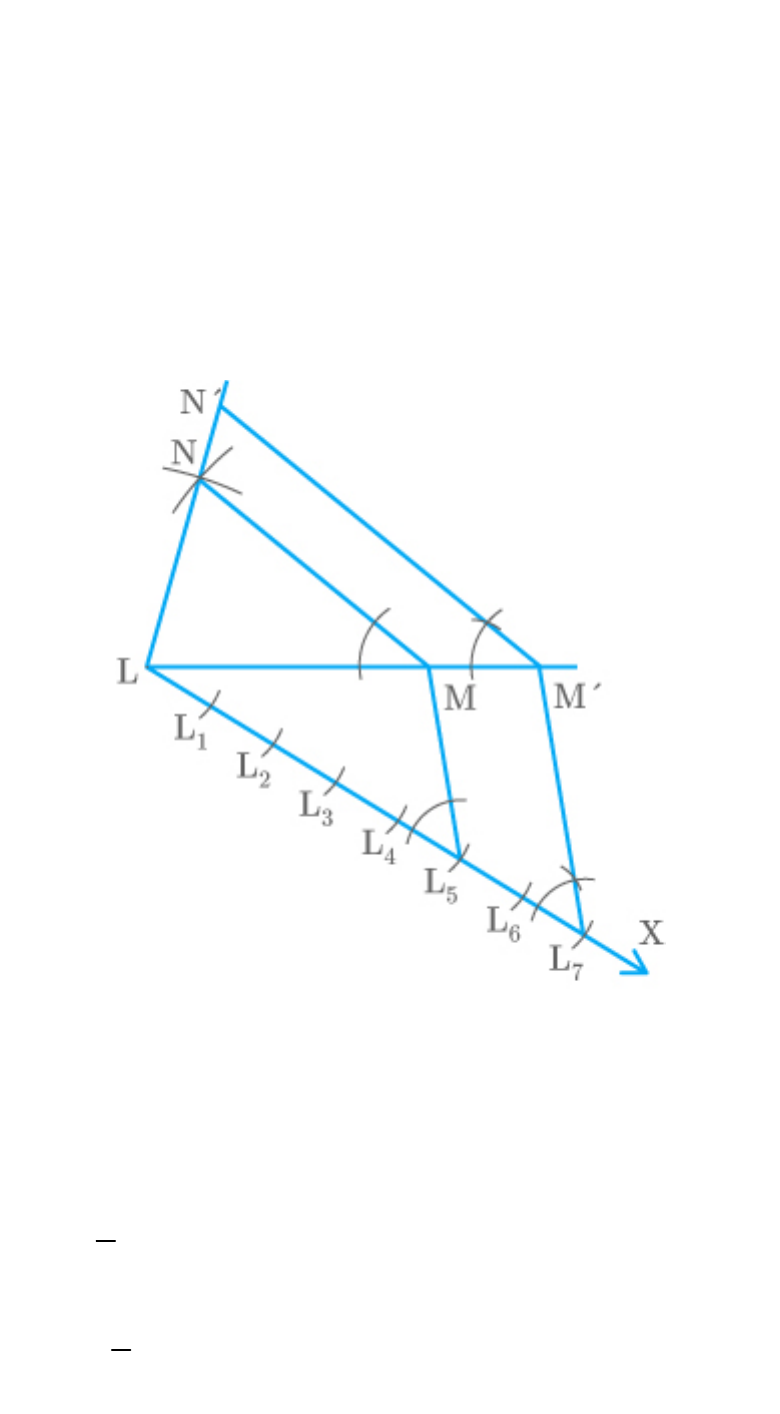
4. Join and draw a line through parallel to
5
ML
7
L
to intersect extended line segment LM at
5
ML
point .
M
5. Draw a line through parallel to MN
M
intersecting the extended line segment LN at
. is the required triangle.
N
LM N
Fig. Exc_11.1_3
Justification:
The construction can be justified by proving,
7
LM LM,
5
7
M N MN,
5

7
LN LN
5
In and ,
LMN
LM N
(corresponding angles)
LMN LM N
(common)
MLN M LN
Thus, (by the similarity criterion)
LMN|| LM N
LM MN LN
...... 1
LM M N LN
In and ,
5
LL M
7
LL M
(common)
5 7
L LM L LM
(corresponding angles)
5 7
LL M LL M
Thus, (by the similarity criterion)
5 7
LL M LL M:
5
7
LM LL
LM LL
LM 5
...... 2
LM 7
Compare equations (1) and (2),
LM MN LN 5
LM M N LN 7
7
LM LM
5
7
MN MN
5

7
LN LN
5
Hence, the construction is justified.
Question: 4
Construct an isosceles triangle whose base is 8 cm
and altitude 4 cm and then another triangle whose
sides are times the corresponding sides of the
1
1
2
isosceles triangle.
Solution:
Let us assume that is an isosceles triangle
LMN
having NL and NM of equal lengths, base LM of 8
cm, and NP is the altitude of 4 cm.
A whose sides are times of
LM N
1 3
1
2 2
LMN
can be drawn as follows:
1. Draw a line segment LM of length 8 cm. Draw
arcs of same radius on both sides of the line
segment while taking points L and M as its
centre. Let these arcs intersect each other at O
and O'. Join OO'. Let OO' intersect LM at P.
2. Taking P as centre, draw an arc of 4 cm radius
which cuts the extended line segment OO' at
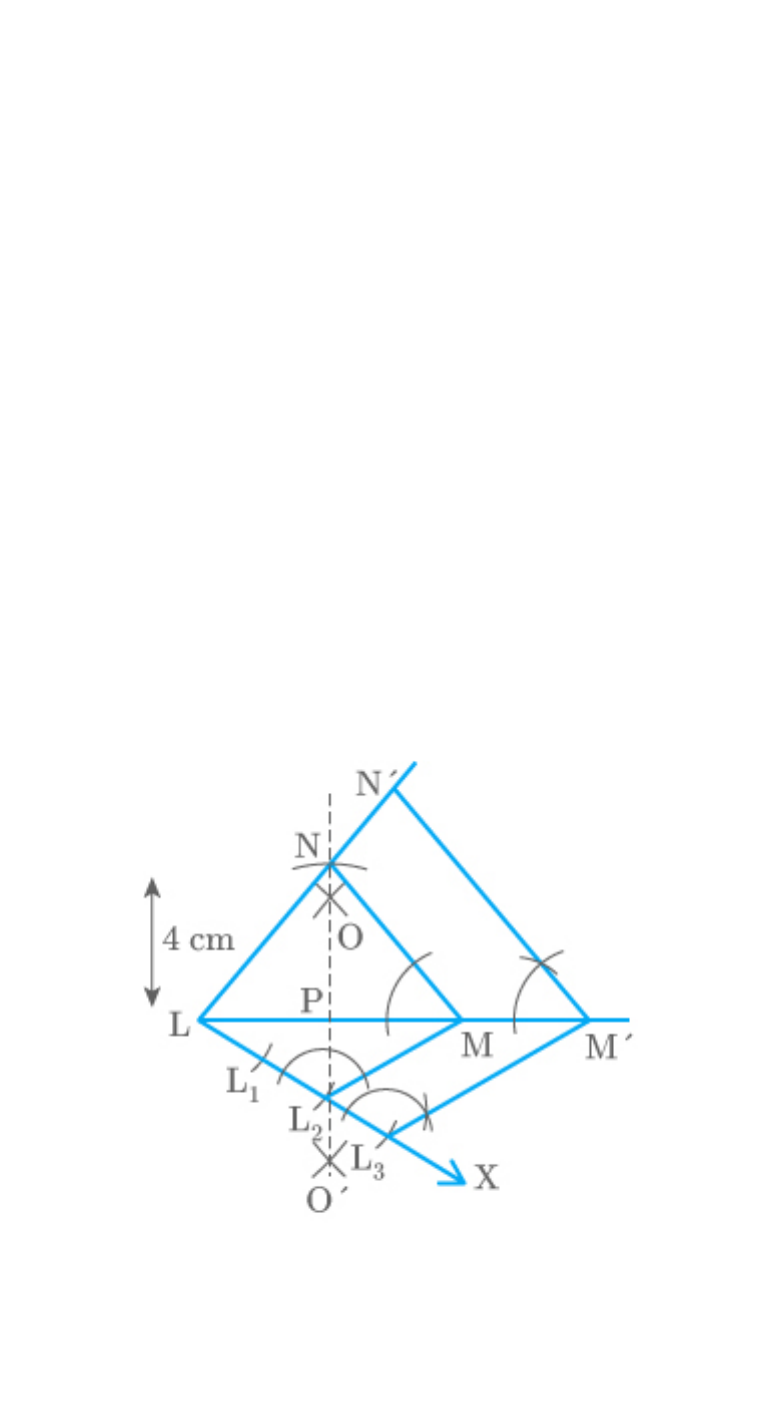
point N. An isosceles is formed, having
LMN
NP (altitude) as 4 cm and LM (base) as 8 cm.
3. Draw a ray LX making an acute angle with line
segment LM on the opposite side of vertex N.
4. Locate 3 points on LX such that
1
L ,
2
L ,
3
L
.
1 1 2 2 3
LL L L L L
5. Join and draw a line through parallel to
2
ML
3
L
to intersect extended line segment LM at
2
ML
point M'.
6. Draw a line through M' parallel to MN
intersecting the extended line segment LN at
N'. is the required triangle.
LM N
Fig. Exc_11.1_4
Justification:
The construction can be justified by proving,
3
LM LM
2
3
M N MN
2
3
LN LN
2
In ,
LMN and LM N
(corresponding angles)
LMN LM N
(Common)
MLN M LN
Thus, (by the similarity criterion)
LMN LM N:
LM MN LN
...... 1
LM M N LN
In and ,
2
LL M
3
LL M
(Common)
2 3
L LM L LM
(Corresponding angles)
2 3
LL M LL M
Thus, (by the similarity criterion)
2 3
LL M||LL M
2
3
LM LL
LM LL
LM 2
...... 2
LM 3
Compare equations (1) and (2).
LM MN LN 2
LM M N LN 3

3
LM LM
2
3
M N MN
2
3
LN LN
2
Hence, the construction is justified.
Question: 5
Draw a triangle ABC with side BC cm, AB
6
5
cm and . Then construct a triangle
ABC 60
whose sides are of the corresponding sides of the
3
4
triangle ABC.
Solution:
The steps for construction are as follows:
1. Draw a triangle ABC such that. ,
BC 6cm
and .
AB 5cm
ABC 60
2. Draw an acute below BC.
CBX
3. Mark four points along BX such
1,
B
2,
B
3,
B
4
B
that .
1 1 2 2 3 3 4
BB BB B B B B
4. Join
4
B C
5. Draw that meets BC at .
3 4
B C ||B C
C
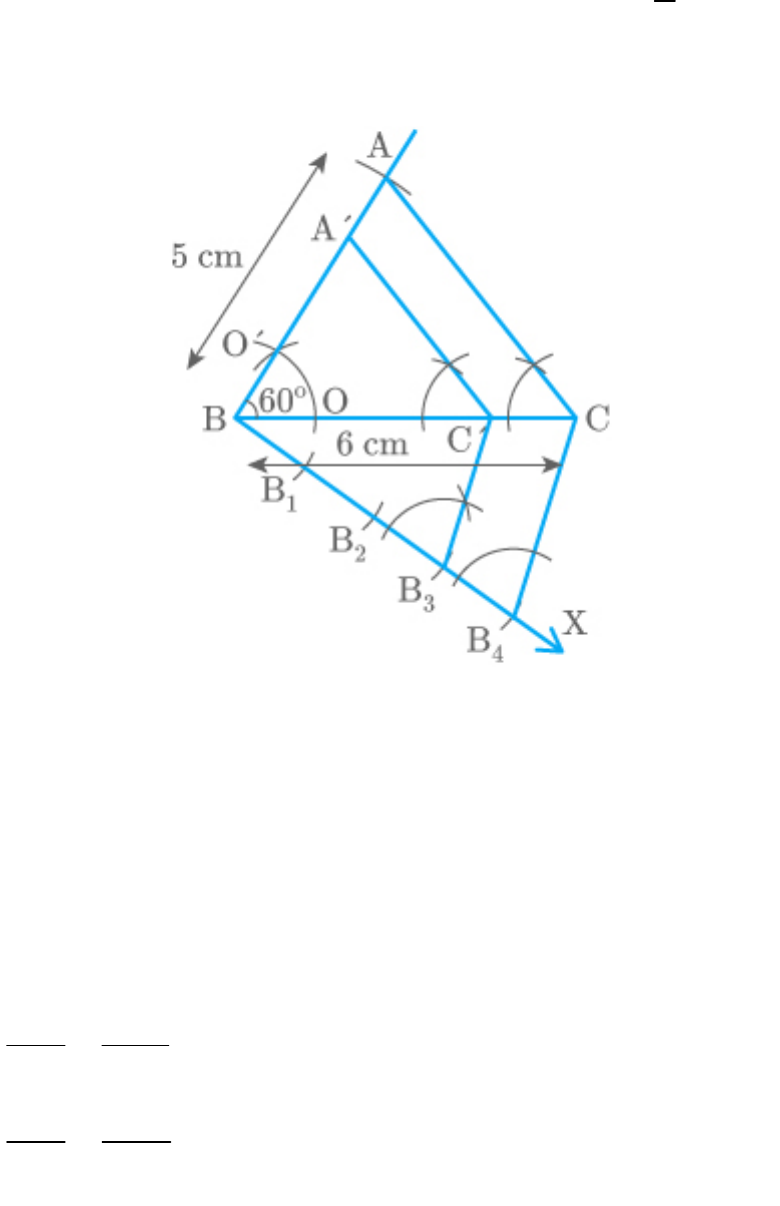
6. Draw that meets AB at
C A ||CA
A
7. is the required triangle similar to
A BC
and and each side of is of the
ABC
A BC
3
4
corresponding side of .
ABC
Fig. Exc_11.1_5
Justification: The construction of similar to
A BC
can be verified as follows.
ABC
A C AC:
Therefore,
3
3 4
BC BB
Proportionality theorem
C C B B
BC 3
C C 4 3

CC 4 3 1
...... 1
BC 3 3
Now,
BC BC C C
BC BC
BC C C
1
BC BC
From (1).
BC 1
1
BC 3
BC 3 1
BC 3
BC 4
BC 3
BC 3
...... 2
BC 4
In and ,
ABC
A BC
CBA C BA
BCA BC A
Thus,
ABC|| A BC Similarity criterion
Hence,
BC C A A B
BC CA AB
From (2),

BC C A A B 3
BC CA AB 4
Hence, and are similar and the sides of
ABC
A BC
are of the corresponding sides of
A BC
3
4
ABC
.
Question: 6
Draw a triangle ABC with side BC cm,
7
, . Then, construct a triangle
B 45
A 105
whose sides are times the corresponding sides of
4
3
.
ABC
Solution:
Given: BC cm, , and
7
B 45
A 105
Sum of all three interior angles
180
Thus,
A B C 180
105 45 C 180
C 180 105 45
C 30
The steps for construction are as follows:
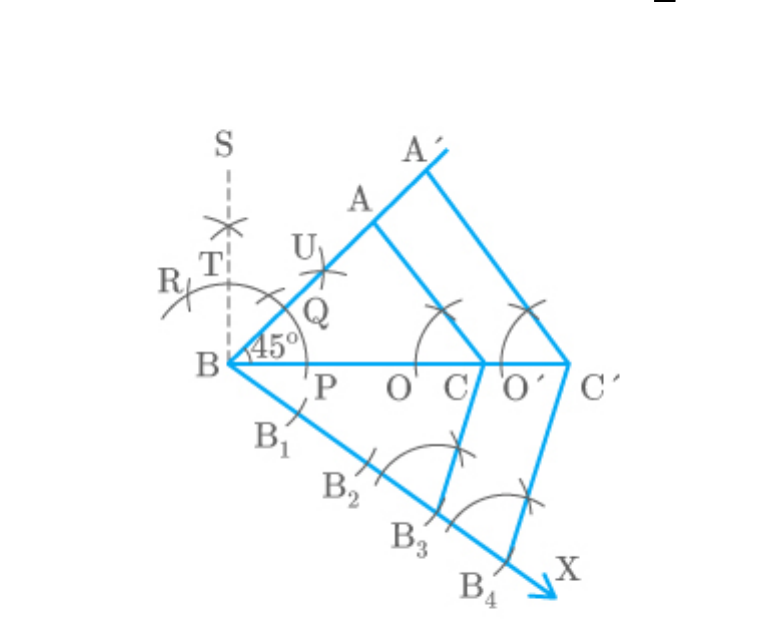
1. Draw a triangle ABC such that ,
BC 7cm
and .
B 45
C 30
2. Draw an acute below BC.
CBX
3. Mark four points along BX such
1,
B
2,
B
3,
B
4
B
that .
1 1 2 2 3 3 4
BB BB B B B B
4. Join
3
B C
5. Draw that meets at .
4 3
B C ||B C
BC
C
6. Draw that meets at
C A ||CA
A B
A
7. is the required triangle similar to
A BC
and and each side of is of the
ABC
A BC
4
3
corresponding side of .
ABC
Fig. Exc_11.1_6
Justification: The construction of similar to
A BC
can be verified as follows.
ABC

A C ||AC
Therefore,
4
3 4
BC BB
Proportionality theorem
C C B B
BC 4
C C 4 3
CC 4 3 1
...... 1
BC 4 4
Now,
BC BC C C
BC BC
BC C C
1
BC BC
From (1),
BC 1
1
BC 4
BC 4 1
BC 4
BC 3
BC 4
BC 4
...... 2
BC 3
In and ,
ABC
A BC
CBA C BA
BCA BC A

Thus,
ABC|| A BC Similarity criterion
Hence,
BC C A A B
BC CA AB
From (2),
BC C A A B 4
BC CA AB 3
Hence, and are similar and the sides
ABC
A BC
of are of the corresponding sides of
A BC
4
3
.
ABC
Question: 7
Draw a right triangle in which the sides (other than
hypotenuse) are of lengths 4 cm and 3 cm. Then
construct another triangle whose sides are times
5
3
the corresponding sides of the given triangle.
Solution:
The steps for construction are as follows:
1. Draw a triangle LMN such that. ,
LM 4 cm
and .
L 90
LN 3cm
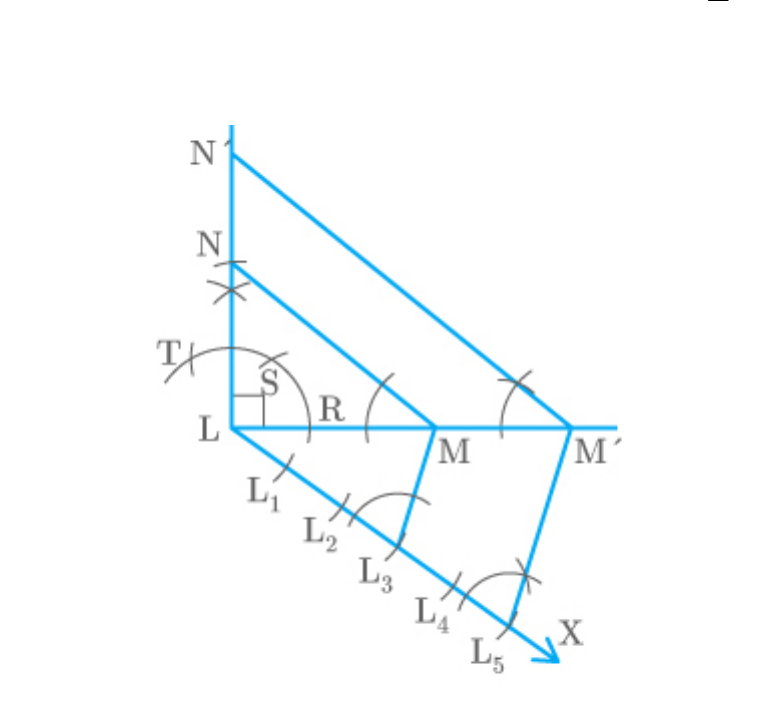
2. Draw an acute below LM.
MLX
3. Mark four points along LX such
1,
L
2,
L
3,
L
4
L ,
5
L
that .
1 1 2 2 3 3 4 4 5
LL L L L L L L L L
4. Join
3
L M
5. Draw that meets at .
5 3
L M ||L M
LM
M
6. Draw that meets at
M N ||MN
LN
N
7. is the required triangle similar to
LM N
and and each side of is of
LMN
LM N
5
3
the corresponding side of .
LMN
Fig. Exc_11.1_7
Justification: The construction of similar
LM N
to can be verified as follows.
LMN
M N MN:

Therefore,
5
3 5
LM LL
proportionality theorem
M M L L
LM 5
M M 5 3
M M 5 3 2
...... 1
LM 5 5
Now,
LM LM M M
LM LM
LM M M
1
LM LM
From (1).
LM 2
1
LM 5
LM 5 2
LM 5
LM 3
LM 5
LM 5
...... 2
LM 3
In and ,
LMN
LM N
MLN M LN
LMN LM N

Hence,
LMN|| LM N similarity criterion
Hence,
LM M N LN
LM MN LN
From (2).
LM M N LN 5
LM MN LN 3
Hence, and are similar, and the
LM N
LMN
sides of are of the corresponding sides
LM N
5
3
of .
LMN
Exercise 11.2 (7)
In each of the following, give also the justification
of the construction:
Question: 1
Draw a circle of radius 6 cm. From a point 10 cm
away from its centre, construct the pair of tangents
to the circle and measure their lengths.
Solution:
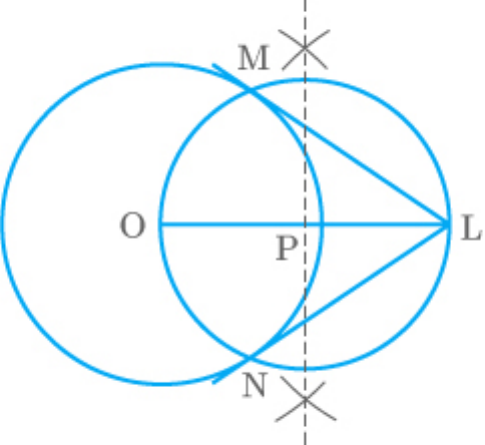
The following steps are to be followed in the
construction of the tangents to the circle.
Steps of construction:
1. Draw a circle with centre and radius .
O
6cm
2. Take a point in the exterior of the circle
L
such that .
OL 10cm
3. Join the centre and the point and bisect
O
L
at the mid-point .
OL
P
4. Draw a circle as origin and radius that
P
OP
intersects the previous circle at points and
M
.
N
5. Join and .
LM
LN
The required tangents are and .
LM
LN
Fig. Exc_11.2_1
Justification:

If we join and then,
O
M
OML 90 anglein a semicircle
.
Hence,LM OM
From the figure, is the radius of the circle.
OM
Hence, is a tangent to the circle from the point
LM
.
L
Similarly, is a tangent to the circle from the
LN
point .
L
Given: and
OL 10
OM 6
By the Pythagoras theorem,
2 2 2
OL OM LM
2 2
2
10 6 LM
2
LM 100 36
2
LM 64
LM 8
Hence, the lengths of the tangents and are
LM
LN
.
8cm
Question: 2
Construct a tangent to a circle of radius 4 cm from
a point on the concentric circle of radius 6 cm and

measure its length. Also verify the measurement by
actual calculation.
Solution:
The following steps are to be followed in the
construction of the tangents to the circle.
Steps of construction:
1. Draw a circle with centre and radius .
O
4 cm
2. Draw a circle with centre and radius .
O
6cm
3. Find a point L on the circle of radius 6 cm and
join OL.
4. Find a point P on the bisector of the line OL.
5. With P as the centre and OP as the radius,
draw a circle that intersects the given circle at
the points M and N.
6. Join LM and LN.
7. LM and LN are the required tangents.
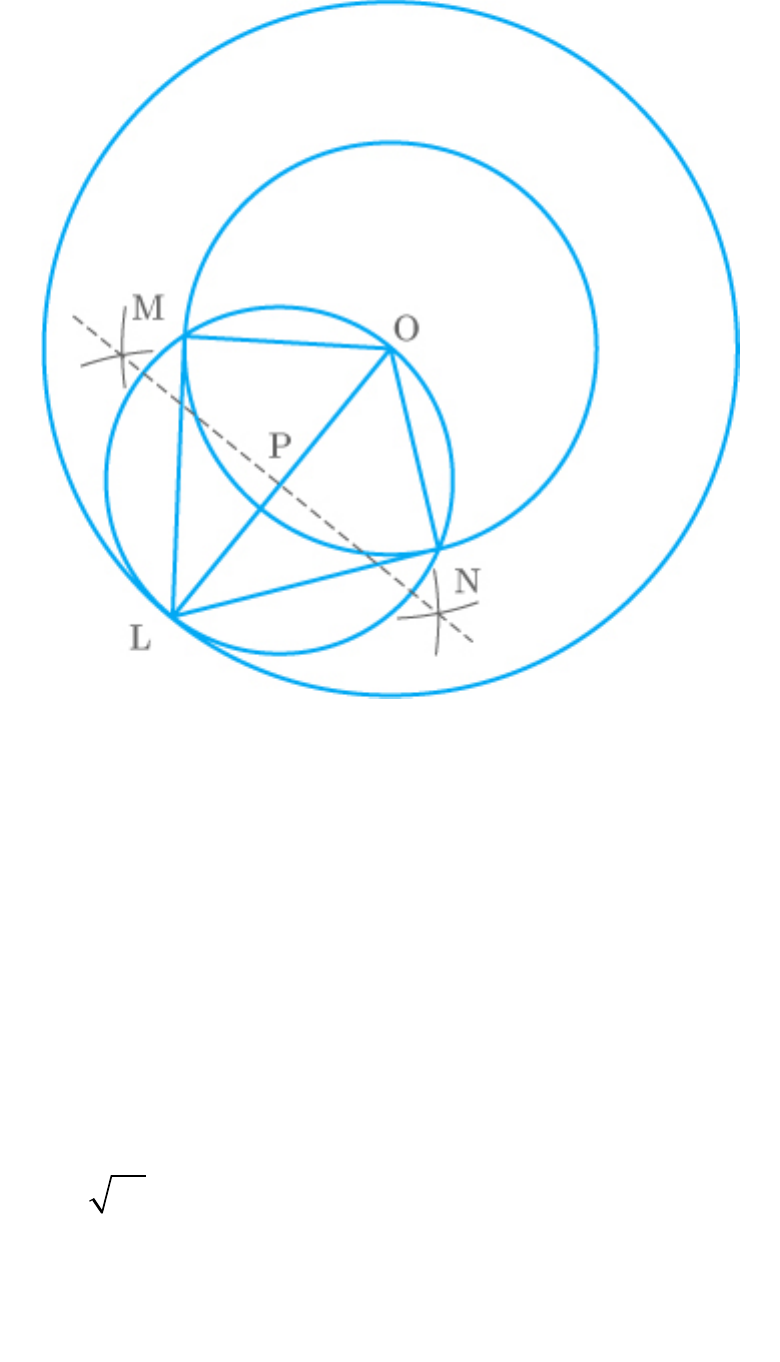
Fig. Exc_11.2_2
Given: and
OM 4
OL 6
By the Pythagoras theorem in ,
LMO
2 2 2
OL OM LM
2 2
2
6 4 LM
2
LM 36 16
2
LM 20
LM 20
LM 4.47cm
Justification:
If we join and then,
O
M

OML 90 anglein a semicircle
.
Hence,LM OM
From the figure, is the radius of the circle.
OM
Hence, is a tangent to the circle from the point
LM
.
L
Similarly, is a tangent to the circle from the
LN
point .
L
Question: 3
Draw a circle of radius 3 cm. Take two points P and
Q on one of its extended diameter each at a
distance of 7 cm from its centre. Draw tangents to
the circle from these two points P and Q.
Solution:
The following steps are to be followed in the
construction of the tangents to the circle.
Steps of construction:
1. Draw a circle with centre and radius .
O
3cm
2. On one of its extended diameters, RS, locate
two points such that
PO OQ 7cm
3. Bisect OP and OQ at the points T and U
respectively.
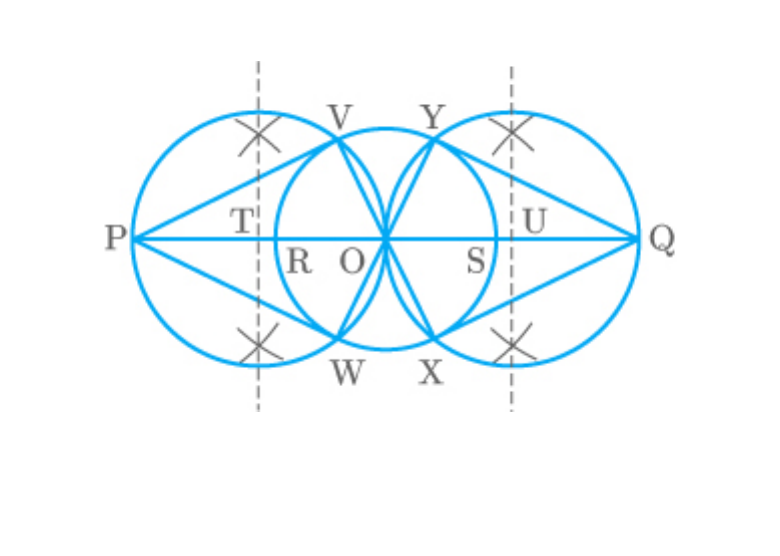
4. Draw two circles with centres T and U and
radius TO and UO respectively. Let the two
circles intersect the circle at point V, W, X, Y
respectively.
5. Join PV, PW, QX, and QY. These are the
required tangents.
Fig. Exc_11.2_3
Justification:
If we join and then,
O
V
OVP 90 anglein a semicircle
.
Hence,PV OV
From the figure, is the radius of the circle.
OV
Hence, is a tangent to the circle from the point
PV
.
P
Similarly, is a tangent to the circle from the
QY
point .
Q

Question: 4
Draw a pair of tangents to a circle of radius 5 cm
which are inclined to each other at an angle of 60°.
Solution:
The following steps are to be followed in the
construction of the tangents to the circle.
Steps of construction:
1. Draw a circle with centre and radius .
O
5cm
2. Locate a point M on the circumference of the
circle and join OM. Draw a line at point M
perpendicular to OM.
3. Draw a line ON equal to the radius of the
circle that makes an angle of
120 180 60
with OM.
4. At point N, draw a line perpendicular to ON.
Let the intersection point of both the
perpendiculars is L. LM and LN are the
desired tangents at an angle of 60°.
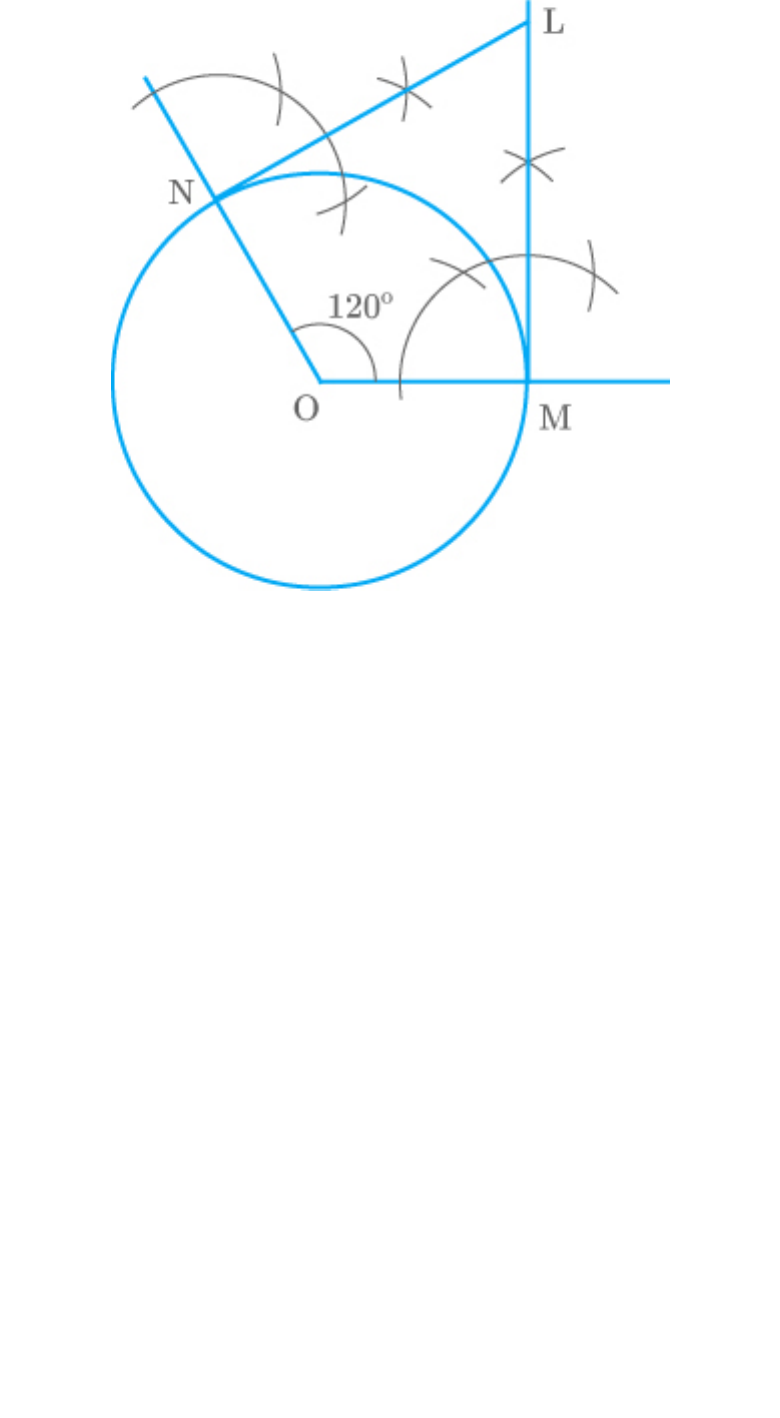
Fig. Exc_11.2_4
Justification:
To justify construction, we are to prove that
MLN
is .
60
By the construction,
OML 90
ONL 90
MON 120
The sum of all the angles of a quadrilateral is .
360
OML MLN MON ONL 360
90 MLN 120 90 360
MLN 360 120 90 90
MLN 60
Thus,

.
MLN 60
Hence, the construction is justified.
Question: 5
Draw a line segment AB of length 8 cm. Taking A as
centre, draw a circle of radius 4 cm and taking B as
centre, draw another circle of radius 3 cm.
Construct tangents to each circle from the centre of
the other circle.
Solution:
The following steps are to be followed in the
construction of the tangents to the circle.
Steps of construction:
1. Draw a line of length 8 cm and draw two
circles with centres A and B and radius 4 and
3 cm respectively.
2. Bisect AB at the point C
3. Draw a circle as origin C and radius AC that
intersects the circles at points P, Q, R, and S.
4. Join BP, BQ, AS, and AR.
The required tangents are BP, BQ, AS and AR.
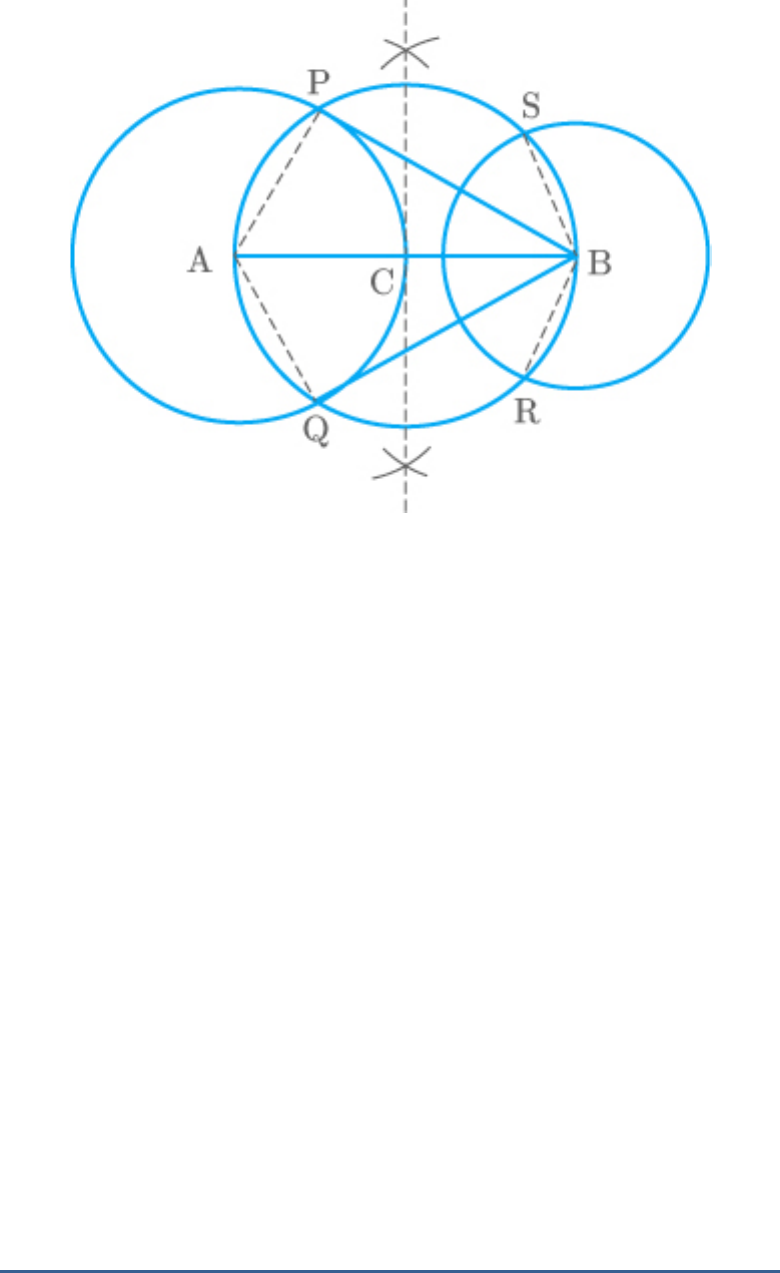
Fig. Exc_11.2_5
Justification:
If we join and then,
A
P
APB 90 anglein a semicircle
.
Hence,BP AP
From the figure, is the radius of the circle.
AP
Hence, is a tangent to the circle from the point
BP
.
L
Similarly, and are the tangents to the
BQ,
AS
AR.
circles.
Question: 6
Let ABC be a right triangle in which
AB 6cm,
and . BD is the perpendicular
BC 8cm
B 90

from B on AC. The circle through B, C, D is drawn.
Construct the tangents from A to this circle.
Solution:
Let a circle be drawn through the points B, D, and
C. Let BC be the diameter of the circle
BDCis90
and the centre E of this circle is the mid-point of
BC.
The following steps are to be followed in the
construction of the tangents to the circle.
Steps of construction:
1. Join AE and bisect AE at the point F.
2. Draw a circle with F as centre and FE as the
radius that intersects the previous circle at
points B and G.
3. Join AG
The required tangents are AB and AG.
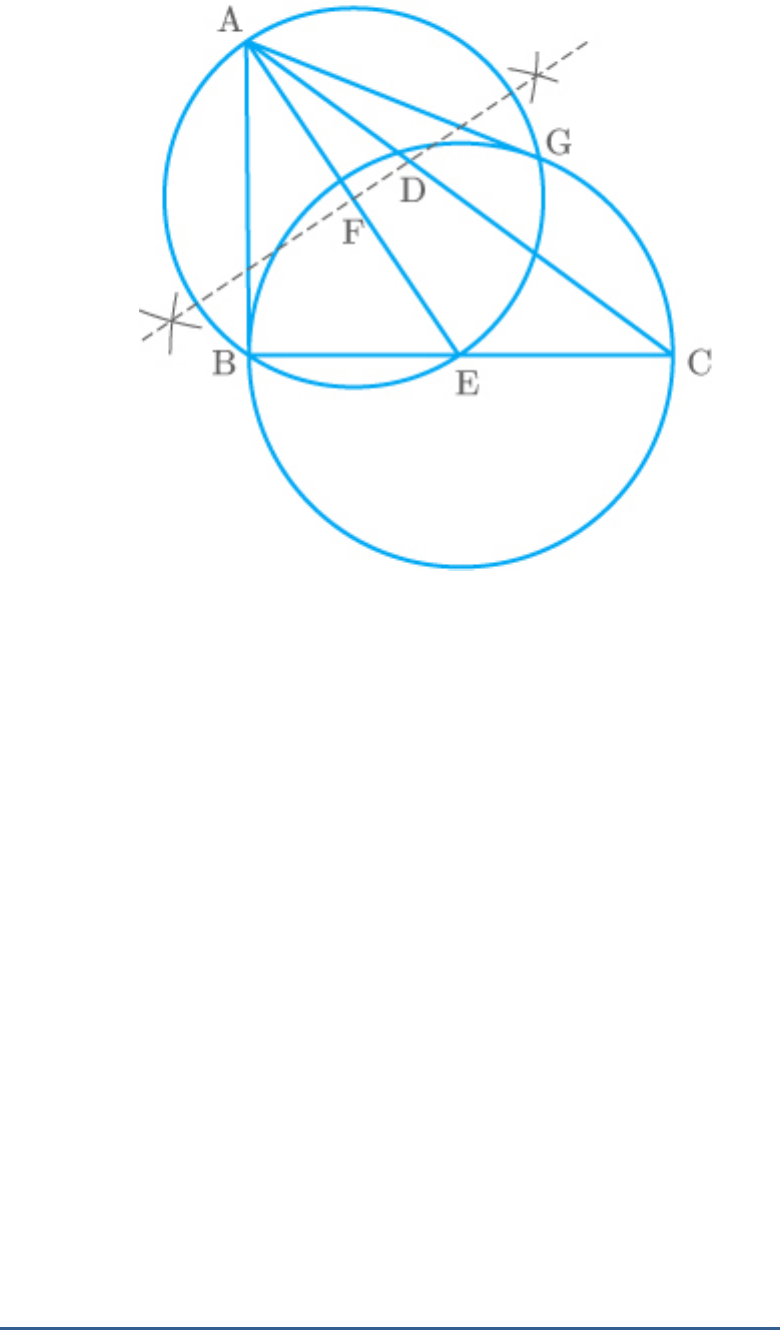
Fig. Exc_11.2_6
Justification:
If we join and then,
E
G
AGE 90 anglein a semicircle
.
Hence, AG GE
From the figure, is the radius of the circle.
GE
Hence, is a tangent to the circle from the point
AG
.
A
Similarly, is the tangent to the circle from the
AB
point A.
Question: 7

Draw a circle with the help of a bangle. Take a
point outside the circle. Construct the pair of
tangents from this point to the circle.
Solution:
The following steps are to be followed in the
construction of the tangents to the circle.
Steps of construction:
1. Draw a circle using a bangle.
2. Take two chords AB and CD of the circle and
draw their perpendicular bisectors that
intersect each other at point O.
3. Take a point L outside the circle and join OL.
4. Bisect OL at the mid-point P.
5. Draw a circle with centre P and radius OP that
intersects the previous circle at M and N.
6. Join LM and LN.
The required tangents are LM and LN.
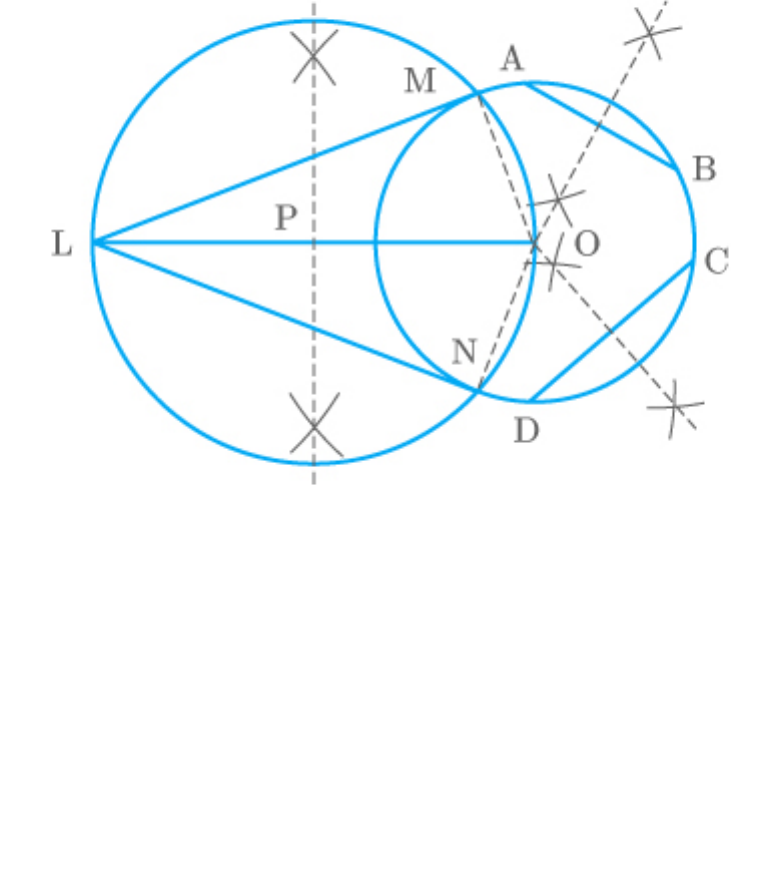
Fig. Exc_11.2_7
Justification:
A chord’s perpendicular bisector passes through the
centre of the circle.
Thus, the intersection point O of the perpendicular
bisectors of the two chords AB and CD is the centre
of the circle.
If we join and then,
O
M
LMO 90 anglein a semicircle
.
Hence,LM OM
From the figure, is the radius of the circle.
OM
Hence, is a tangent to the circle from the point
LM
.
L
Similarly, is a tangent to the circle from the
LN
point L.