Lesson: Circles

Exercise 10.1 (4)

Question: 1

How many tangents can a circle have?

Solution

A circle can have infinite number of tangents.

Question: 2

Fill in the blanks:

(i) A tangent to a circle intersects it in _____ point

(s).

(ii) A line intersecting a circle in two points is called

a ______.

(iii) A circle can have ______ parallel tangents at the

most.

(iv) The common point of a tangent to a circle and

the circle is called ______.

Solution

(i) One

(ii) Secant

(iii) Two

(iv) Point of contact

Question: 3

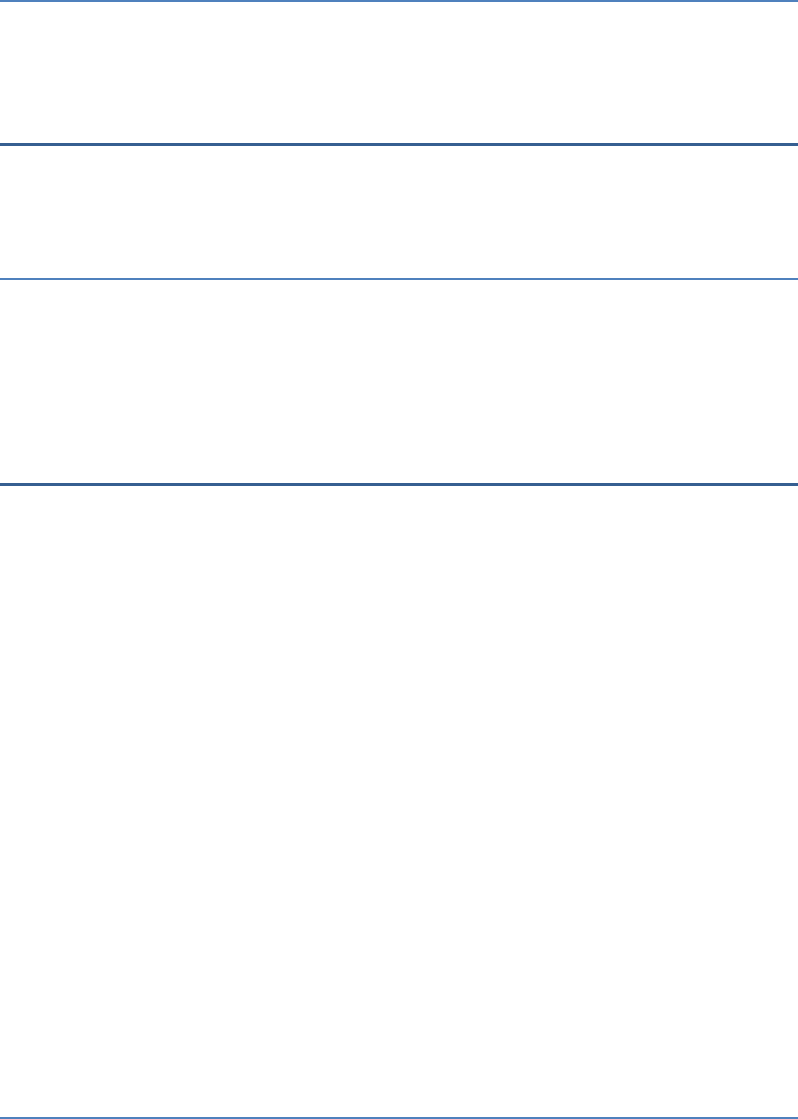
A tangent PQ at a point of a circle of radius 5 cm

meets a line through the centre O at a point Q so

that OQ 12 cm. Length PQ is:



a. 12 cm

b. 13 cm

c. 8.5 cm

d. cm

119

Solution

(d)

Draw a circle with radius 5 cm as shown in the figure

below.

Fig. Exc_10.1_3

The line from the centre to the tangent is

perpendicular to the tangent.

Thus, .

OP PQ

In , by Pythagoras theorem,

OPQ

 

2 2 2

OQ OP PQ

   

 

2 2

12 5 PQ

 

PQ 144 25



PQ 119

PQ 119

Thus, the length of PQ is .

119

Question: 4

Draw a circle and two lines parallel to a given line

such that one is a tangent and the other, a secant to

the circle.

Solution

Step 1: Draw a line .

Step 2: Set the compass to the desired radius of the

circle.

Step 3: Put the needle point of the compass at the

circle’s centre.

Step 4: Turn the compass through and draw

360

the circle above the line.

Step 5: Draw a line parallel to the given line such

that it intersects the circle at two points. It is a

secant of the circle.

Step 6: Draw a line parallel to the given line such

that it touches the circle at one point only. It is a

tangent of the circle.

Fig. Exc_10.1_4

Exercise 10.2 (13)

In Q.1 to 3, choose the correct option and give

justification.

Question: 1

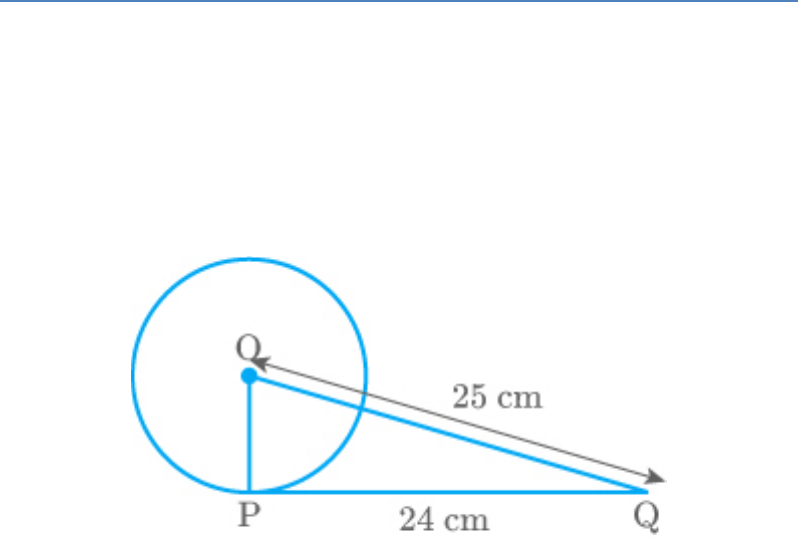
From a point Q, the length of the tangent to a circle

is 24 cm and the distance of Q from the centre is 25

cm. The radius of the circle is

a. 7 cm

b. 12 cm

c. 15 cm

d. 24.5 cm

Solution

(a)

Let the centre of the circle be O.

Given: OQ 25 cm and PQ 24 cm



In a circle, radius is perpendicular to the tangent.

Fig. Exc_10.2_1

Thus, OP PQ



By Pythagoras theorem in OPQ,



 

2 2 2

OP PQ OQ

   

 

2 2

OP 24 25

 

OP 625 576



OP 49

OP 7

Hence, the radius of the circle is 7 cm.

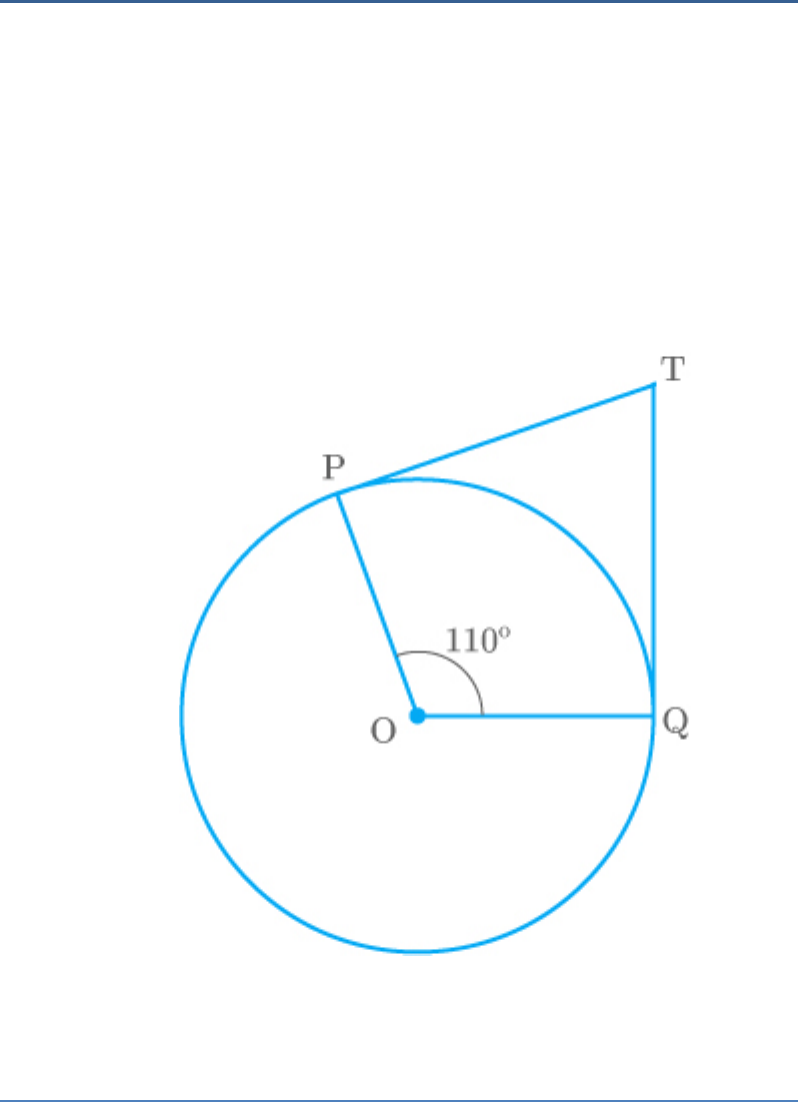
Question: 2

If TP and TQ are the two tangents to a circle with

centre O so that , then is equal

  POQ 110

PTQ

60

70

80

90

Fig. Exc_10.2_2

Solution

(b)

The tangents to the circle are TP and TQ.

Radius of a circle is perpendicular to the tangents.

Therefore, OP TP and OQ TQ



  OPT 90

  OQT 90

The sum of interior angles in quadrilateral POQT is

360

        OPT POQ OQT PTQ 360

         90 110 90 PTQ 360

  PTQ 70

Hence,

  PTQ 70

Question: 3

If tangents PA and PB from a point P to a circle with

centre O are inclined to each other at angle of ,

80

then is equal to

POA

50

60

70

80

Solution

(a)

Given: and are tangents.

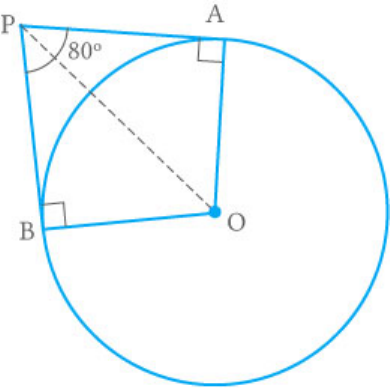
Fig. Exc_10.2_3

Thus, the radius and are perpendiculars to

the tangents.

Thus, and .

OA PA

OB PB

and

  OBP 90

  OAP 90

In quadrilateral ,

AOBP

Sum of all interior angles

 360

So,

        OAP APB PBO BOA 360

        90 80 90 BOA 360

    BOA 360 260

  BOA 100

In ,

 OPBand OPA

[Tangents from a point]

AP BP

[Radii of the circle]

OA OB

[Common side]

OP OP

Thus,

[By SSS congruence criterion]

  OPB OPA

Thus, [By CPCT]

  POB POA

Also,

  

POA AOB



 

100

= 50

Hence,

  POA 50

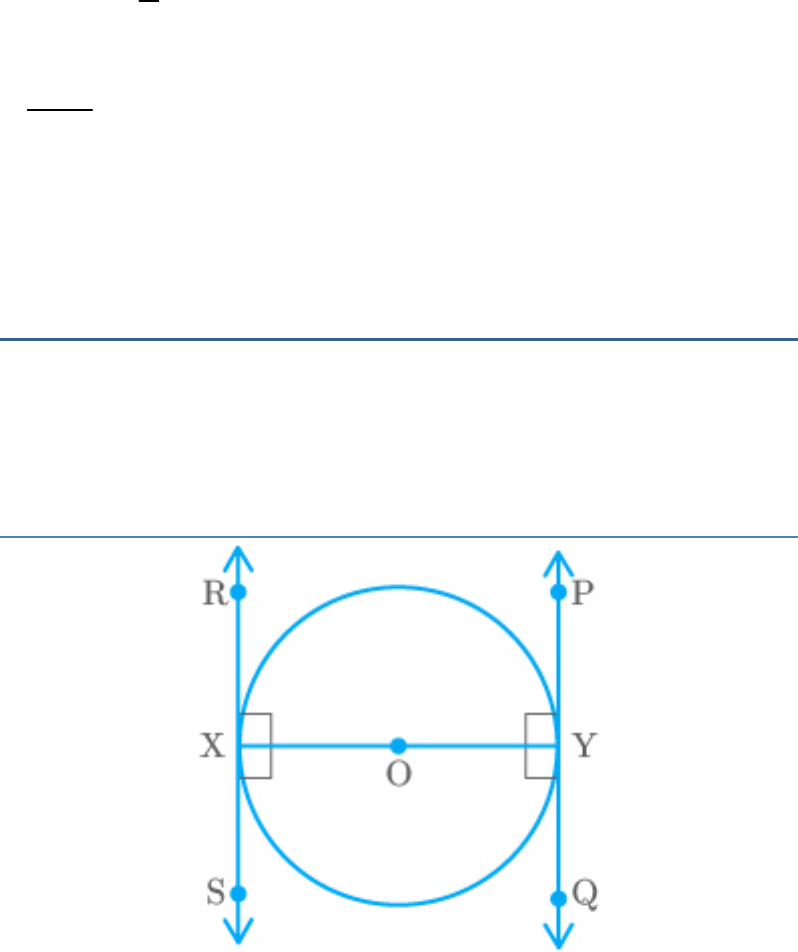
Question: 4

Prove that the tangents drawn at the ends of a

diameter of a circle are parallel.

Solution

Fig. Exc_10.2_4

Let the diameter of the circle be .

At point , two tangents are

Xand Y

PQ andRS

drawn.

So, and .

OX RS

OY PQ

    OXR 90 OXS

    OYP 90 OYQ

Observe that,

[Alternate interior angles]

  OXR OYQ

[Alternate interior angles]

  OXS OYP

Alternate interior angles are equal. So, lines

are parallel.

PQ andRS

Question: 5

Prove that the perpendicular at the point of contact

of the tangent to a circle passes through the centre.

Solution

Let be the centre of circle and be a tangent

that touches the circle at point .

We have to prove that the line perpendicular to

at passes through the point .

We will prove this by a contradiction.

Let the perpendicular to at do not pass

through the centre .

Let it is passes through another point .

Join and .

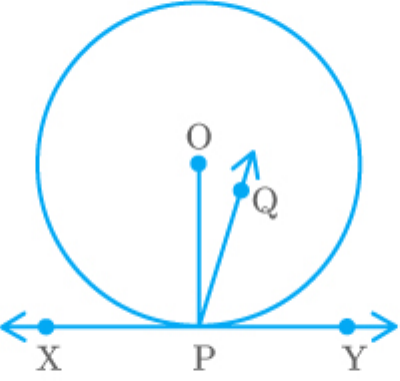
Fig. Exc_10.2_5

Perpendicular to at passes through .

Thus,

 

  QPY 90 ...... 1

According to the figure, the centre of the circle is

and the point of contact is .

So,

 

  OPY 90 ...... 2

By equation (1) and (2),

 

  QPY OPY ...... 3

From the figure, observe that

 

  QPY OPY ...... 4

Thus, is not possible.

  QPY OPY

It is possible only when the lines and QP

coincide.

Thus, perpendicular to XY through P, passes through

the centre O.

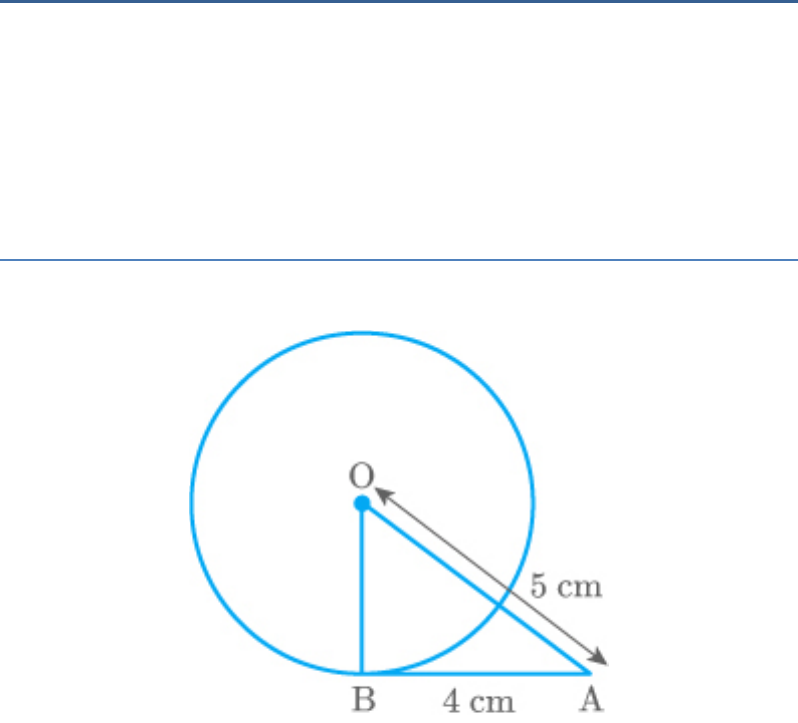
Question: 6

The length of a tangent from a point A at distance 5

cm from the centre of the circle is 4 cm. Find the

radius of the circle.

Solution

Let O as a centre of a circle.

Fig. Exc_10.2_6

From point A, AB tangent is drawn on the circle.

Given: and

OA 5cm

AB 4 cm

In ,

ABO

OB AB

Apply, Pythagoras theorem in ,

ABO

     

 

2 2 2

AB BO OA

     

 

2 2 2

4 BO 5

 

 

16 BO 25

 



BO 9

BO 3

Thus, radius of the circle is cm.

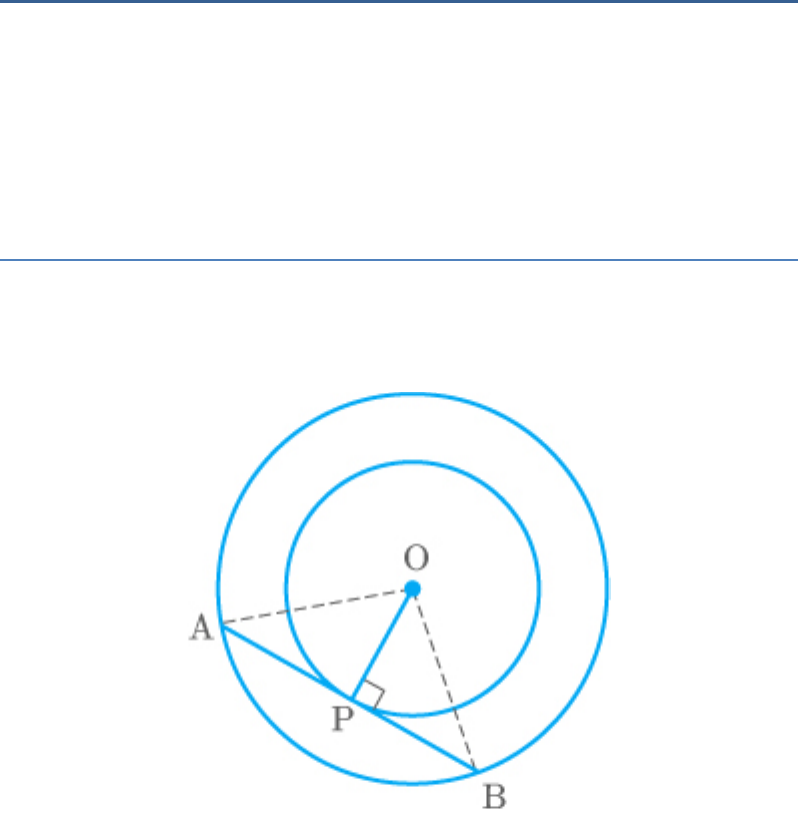
Question: 7

Two concentric circles are of radii 5 cm and 3 cm.

Find the length of the chord of the larger circle

which touches the smaller circle.

Solution

Let the point O be the centre of two concentric

circles.

Fig. Exc_10.2_7

Also, chord of the larger circle is AB and touches the

smaller circle at point P.

Thus, AB becomes the tangent to the smaller circle.

[ is radius of smaller circle]

OP AB

OP

Apply Pythagoras theorem in ,

OAP

     

 

2 2 2

OP AP OA

 

 

2 2

3 AP 5

 

 

AP 25 9

 



AP 16

AP 4

In ,

OAB

OP AB

AP PB

 

 

 

Perpendicular from thecentre

of thecirclebisectsthechord

Now,

AB 2AP

 2 4

 8

Thus, length of the chord is cm.

Question: 8

A quadrilateral ABCD is drawn to circumscribe a

circle. Prove that .

  AB CD AD BC

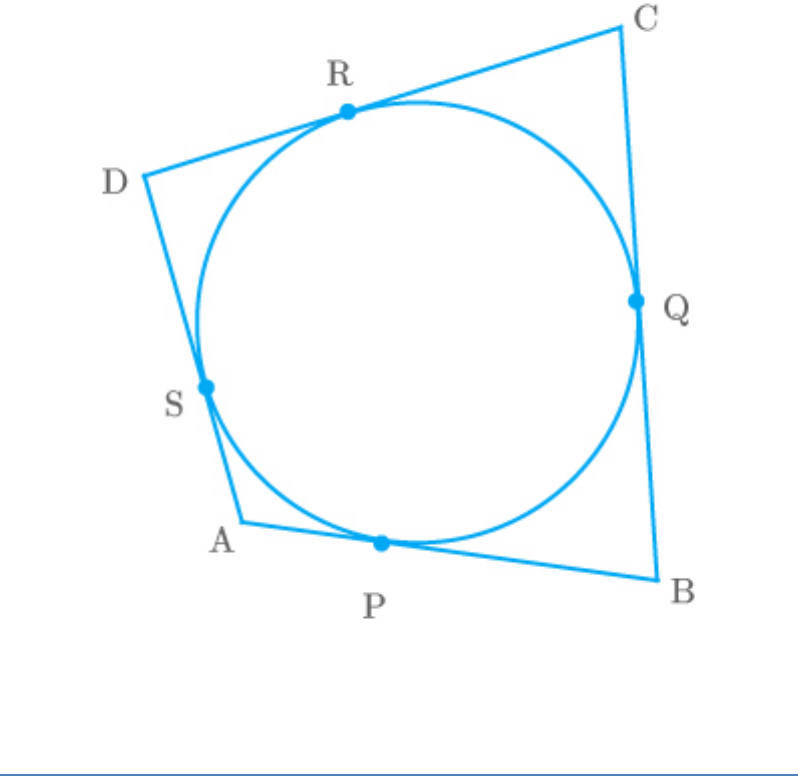
Fig. Exc_10.2_8

Solution

Let ABCD be a quadrilateral.

Observe that,

DR DS

 

 

 

Tangentsfrom point

D on thecircle

 

...... 1

CR CQ

 

 

 

Tangentsfrom point

C on thecircle

 

...... 2

BP BQ

 

 

 

Tangents from point

Bon thecircle

 

...... 3

AP AS

 

 

 

Tangents from point

A on thecircle

 

...... 4

Add all these equations.

      DR CR BP AP DS CQ BQ AS

       

      DR CR BP AP DS AS CQ BQ

  CD AB AD BC

Hence proved.

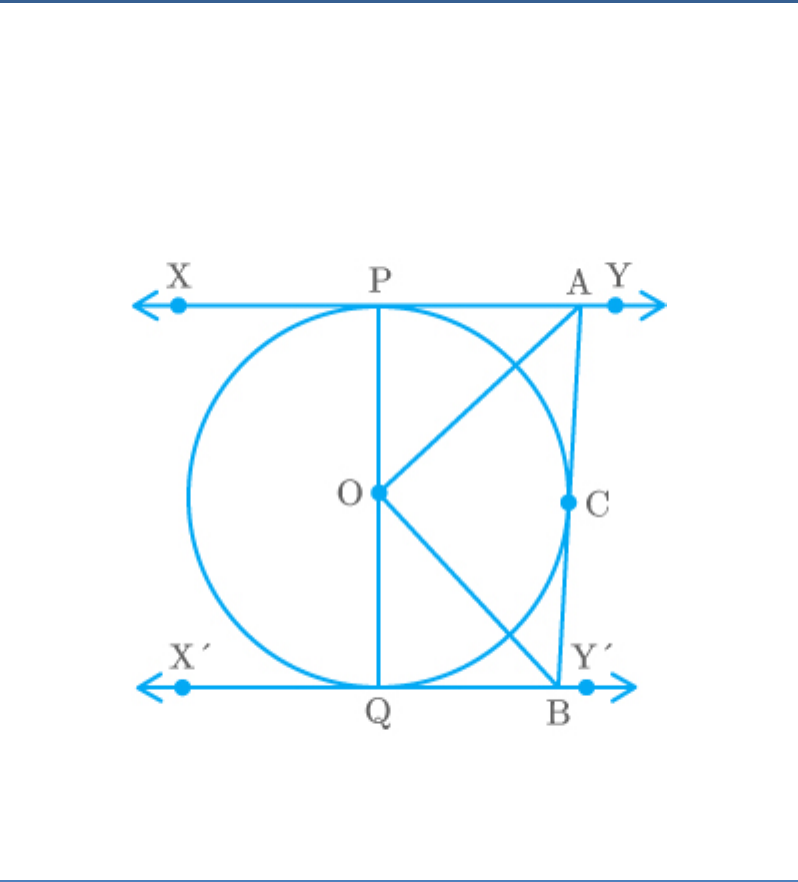
Question: 9

XY and are two parallel tangents to a circle with

 

centre O and another tangent AB with point of

contact C intersecting XY at A and at B. Prove

 

that .

  AOB 90

Fig. Exc_10.2_9(Ques.)

Solution

Join point O to C.

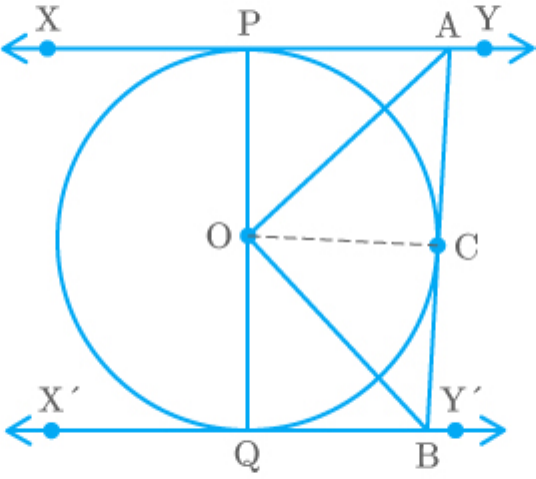
Fig. Exc_10.2_9(Sol.)

In and ,

OPA

OCA

[radii of same circle]

OP OC

AP AC

 

 

 

Tangents from point

A on thecircle

[Common side]

AO AO

[By SSS congruence criterion]

  OPA OCA

 

  POA COA ...... 1

Similarly,

  OQB OCB

 

  QOB COB ...... 2

The diameter POQ of the circle is a straight line.

Thus,

        POA COA COB QOB 180

From equations (1) and (2),

        POA COA COB QOB 180

        COA COA COB COB 180

    2 COA 2 COB 180

    COA COB 90

  AOB 90

Hence proved.

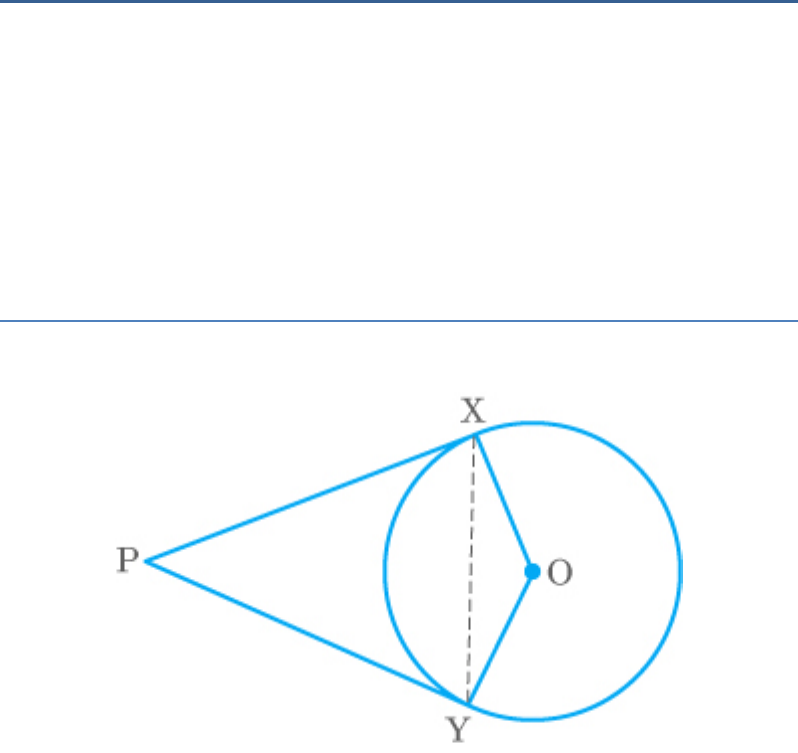
Question: 10

Prove that the angle between the two tangents

drawn from an external point to a circle is

supplementary to the angle subtended by the line-

segment joining the points of contact at the centre.

Solution

Let O be the centre of the circle.

Fig. Exc_10.2_10

Let P be the external point and PX and PY are the

two tangents.

XY is the line segment.

Observe that .

OX PX

Thus,

  OXP 90

Similarly, .

OY PY

  OYP 90

In quadrilateral ,

OXPY

        OXP XPY PYO YOX 360

        90 XPY 90 YOX 360

      XPY YOX 360 180

    XPY YOX 180

Hence, the angle between the two tangents drawn

from an external point to a circle is supplementary to

the angle subtended by the line-segment joining the

points of contact at the centre.

Question: 11

Prove that the parallelogram circumscribing a circle

is a rhombus.

Solution

Given: Let ABCD be a parallelogram.

 

AB CD ...... 1

 

BC AD ...... 2

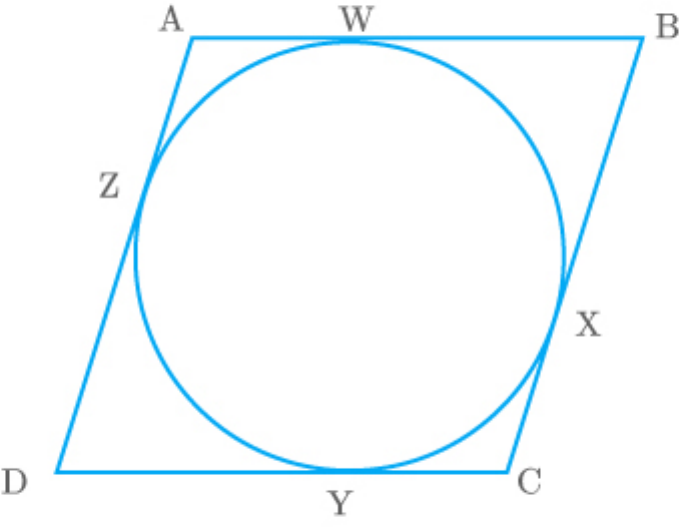
Fig. Exc_10.2_11

Observe that,

AW AZ

 

 

 

Tangents from point

A on thecircle

BW BX

 

 

 

Tangents from point

Bon thecircle

CY CX

 

 

 

Tangents from point

C on thecircle

DY DZ

 

 

 

Tangents from point

D on thecircle

Add the above equations.

      DY CY BW AW DZ CX BX AZ

       

      DY CY BW AW DZ AZ CX BX

  DC AB AD BC

From equations (1) and (2),

  DC AB AD BC

2AB 2BC

 

AB BC ...... 3

Compare equations (1), (2) and (3),

  AB BC CD DA

Hence, ABCD is a rhombus.

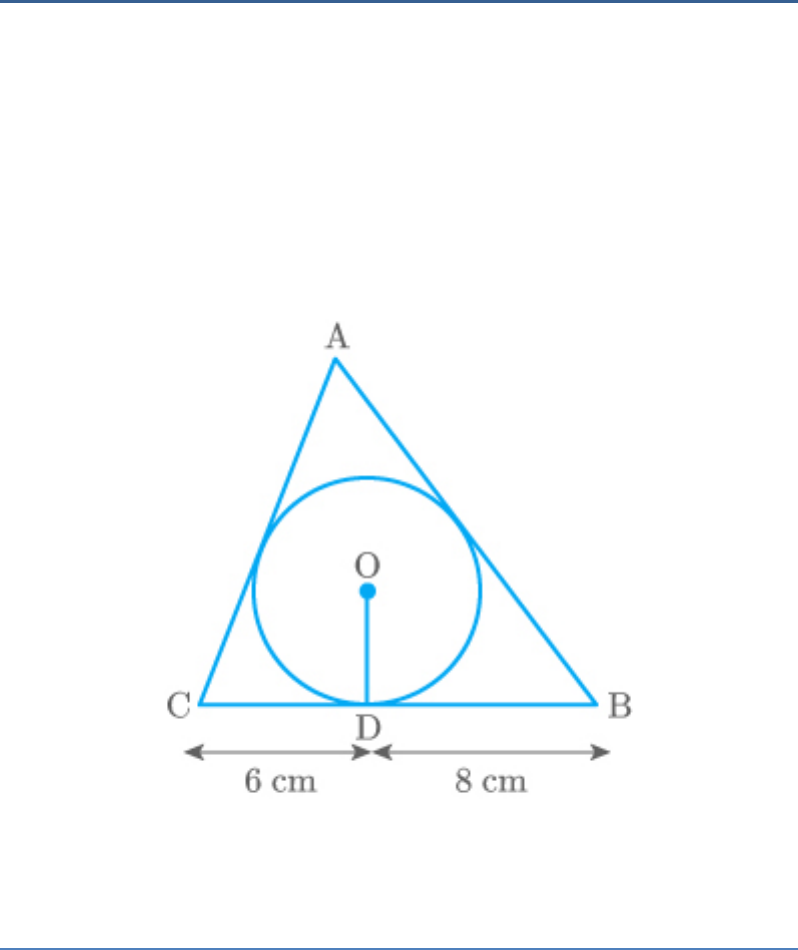
Question: 12

A triangle ABC is drawn to circumscribe a circle of

radius 4 cm such that the segments BD and DC into

which BC is divided by the point of contact D are of

lengths 8 cm and 6 cm respectively. Find the sides

AB and AC.

Fig. Exc_10.2_12(Ques.)

Solution

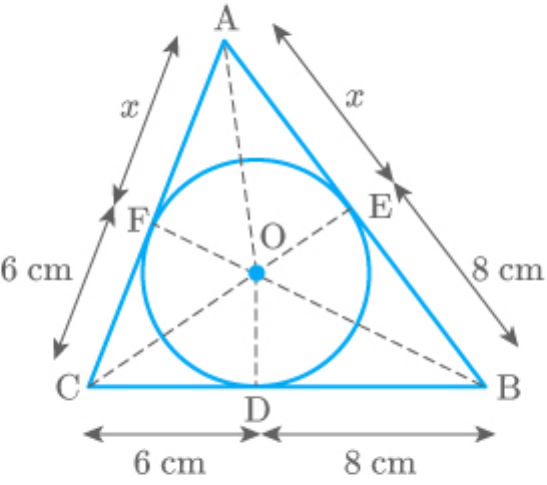
Sides AB and AC touch the circle at point E and F

respectively.

Let the length of AF be .

In ,

ABC

 CF CD 6cm

 

 

 

Tangents from point

C on thecircle

 BE BD 8cm

 

 

 

Tangents from point

Bon thecircle

 AF AE x

 

 

 

Tangents from point

A on thecircle

Fig. Exc_10.2_12(Sol.)

Now,

   AB AE EB x 8

 BC BD DC

 8 6

14

 CA CF FA

 6 x

By the Hero’s formula,

  2s AB BC CA

    2s x 8 14 6 x

 2s 28 2x

 s 14 x

   

    ABC s s a sArea o b sf c

    

 

         14 x 14 x 14 14 x 6 x 14 x 8 x

    

         14 x 14 x 14 14 x 6 x 14 x 8 x

    

 14 x x 8 6

 

 

4 3 14x x

   

OBCAre Oa

f Do BC

  

4 14

 28

   

OCAAre Oa

f Fo AC

 

   

4 6 x

 12 2x

OABAr OE AB

ea of    

 

4 8

x   

16 2x 

Now, find the value of .

Area of ABC Area of OBC  

Area of OCA 

Area of OAB 

 

4 3 14 28 12 2 16 2x x x x     

 

4 3 14 56 4x x x  

 

3 14 14x x x  

 

3 14 14x x x  

2 2

42 3 196 28x x x x   

2 14 196 0x x  

7 98 0x x  

Solve the quadratic equation.

7 98 0x x  

14 7 98 0x x x   

   

14 7 14 0x x x   

  

14 7 0x x  

14,7x  

Length is always positive so, is rejected.

14

Thus,

7x 

Hence, cm

AB 8 7 8 15x    

cm.

CA 6 6 7 13x    

Question: 13

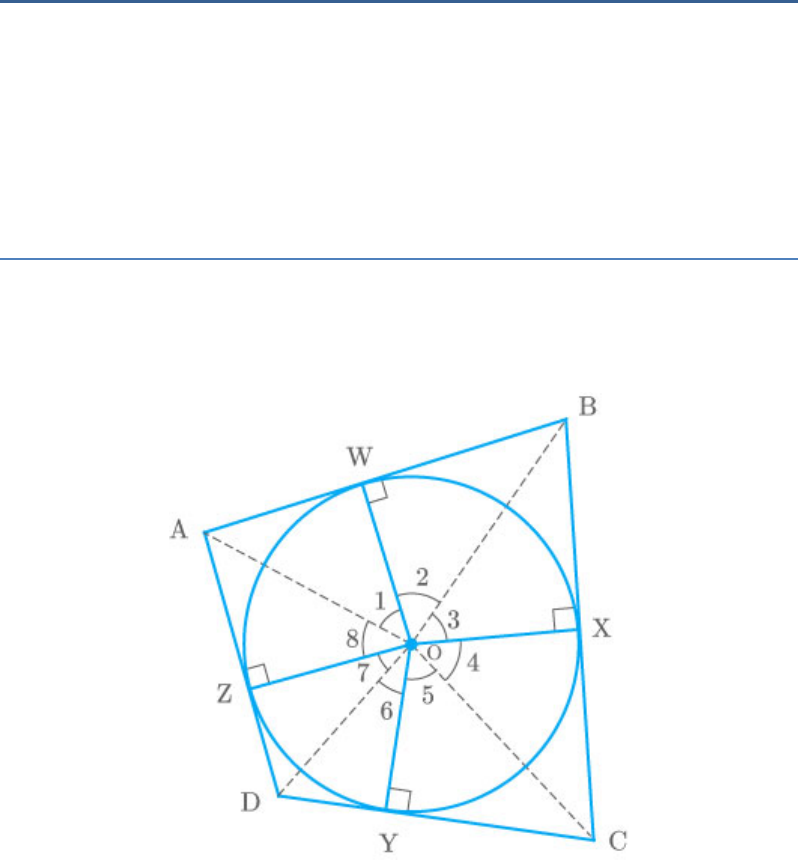
Prove that the opposite sides of a quadrilateral

circumscribing a circle subtend supplementary

angles at the centre of the circle.

Solution

Let O be the centre of circle and quadrilateral ABCD

touches the circle at points .

W X Y Z, , ,

Fig. Exc_10.2_13

Join the vertices of the quadrilateral with the centre

of the circle.

In and ,

OAW

OAZ

AW AZ

Tangents from point

A on thecircle

 

 

 

[radii of same circle]

OW OZ

[common side]

OA OA

[SSS congruence criterion]

OAW OAZ  

Thus,

WOA AOZ  

1 8  

Similarly,

2 3  

4 5  

6 7  

Now,

1 2 3 4 5 6 7 8 360                

       

1 8 2 3 4 5 6 7 360                

2 1 2 2 2 5 2 6 360        

   

2 1 2 2 5 6 360        

   

1 2 5 6 180        

AOB COD 180    

Similarly,

BOC DOA 180    

Thus, the opposite sides of a quadrilateral

circumscribing a circle subtend supplementary

angles at the centre of the circle.