
Lesson: Introduction to Trigonometry
Exercise 8.1 (15) (Multiple Choice Questions and
Answers)
Choose the correct answers from the given four
options:
Question: 1
If , then the value of is
4
cosA
5
tanA
a.
3
5
b.
3
4
c.
4
3
d.
5
3
Solution
(b)
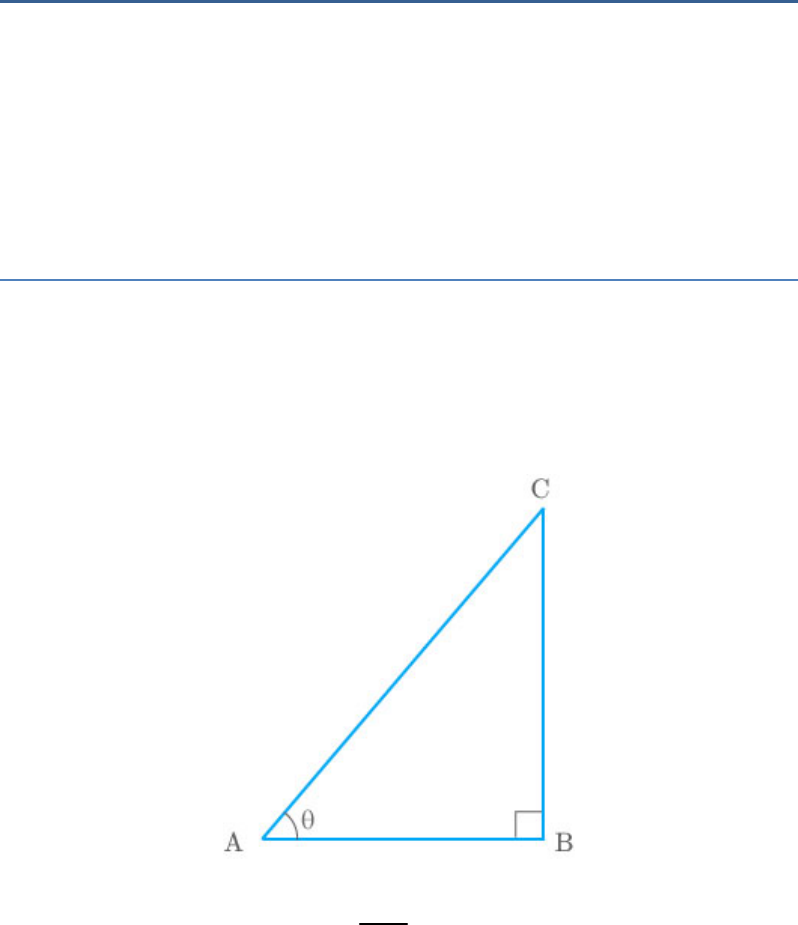
Let ABC be a triangle, right-angled at B.
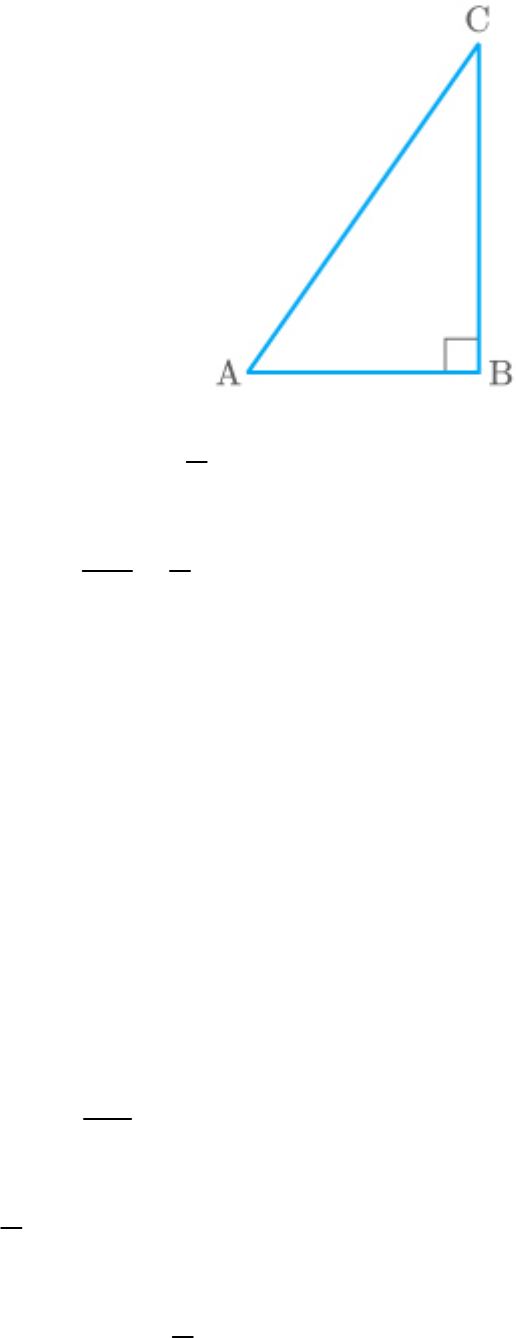
Given:
4
cosA
5
AB 4
cosA
AC 5
In , by the Pythagoras theorem,
ABC
2 2 2
AC AB BC
2 2 2
AC AB BC
2
BC 25 16
2
BC 9
BC 3
BC
tanA
AB
3
4
Thus, .
3
tanA
4
Question: 2
If , then the value of cot A is
1
sinA
2
a.
3
b.
1
3
c.
3
2
d.
1
Solution
(a)
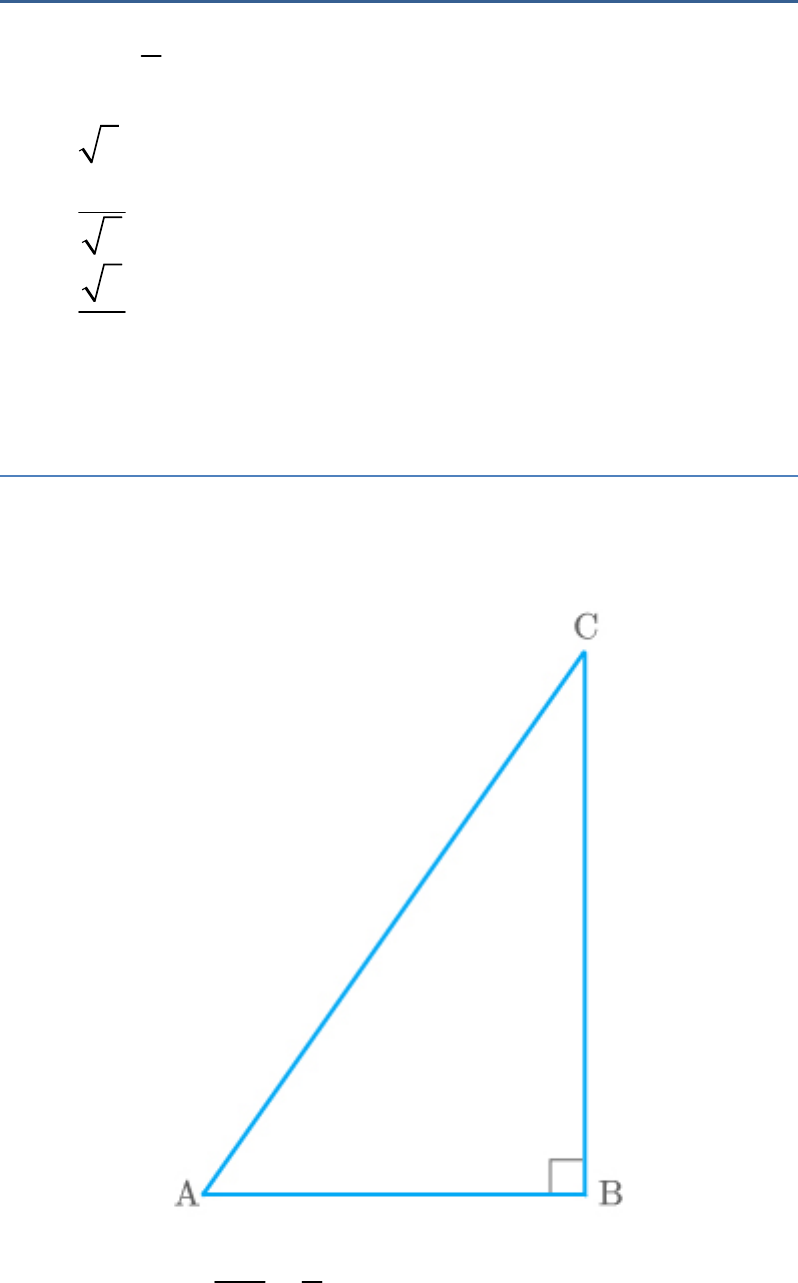
Let ABC be a triangle right-angled at B.
Given:
BC 1
sinA
AC 2
In , by the Pythagoras theorem,
ABC
2 2 2
AC AB BC
2
2 2
2 AB 1
2
AB 4 1
2
AB 3
AB 3
AB 3
cot A
BC 1
Hence, .
cot A 3
Question: 3
The value of the expression
cosec 75 θ sec 15 θ tan 55 θ cot 35 θ
is
a. -1
b. 0
c. 1
d.
3
2
Solution
(a)

Given:
cosec 75 θ sec 15 θ tan 55 θ cot 35 θ
Simplify the above expression.
cosec 75 θ sec 15 θ tan 55 θ cot 35 θ
cosec 75 θ sec 90 75 θ
tan 55 θ cot 90 55 θ
cosec 75 θ cosec 75 θ
tan 55 θ tan 55 θ
0
Hence,
cosec 75 θ sec 15 θ
0
tan 55 θ cot 35 θ
Question: 4
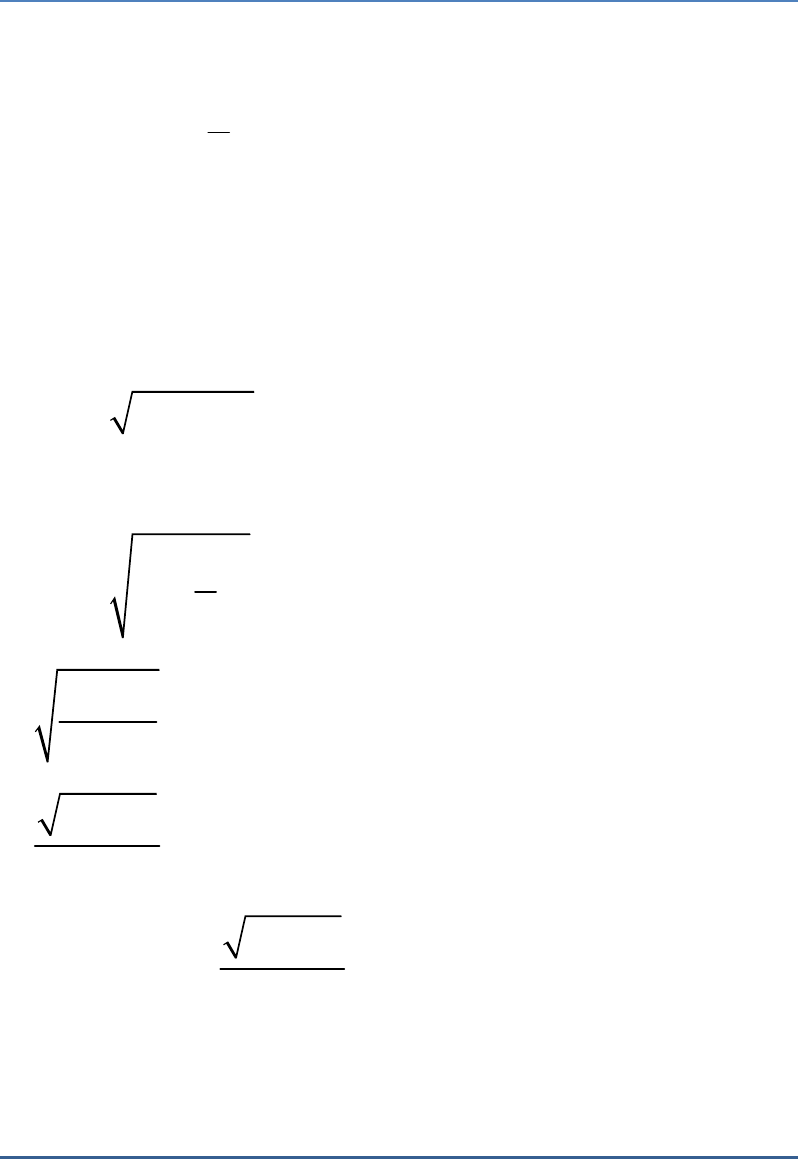
Given that , then is equal to
a
sinθ
b
cosθ
a.
2 2
b
b a
b.
b
a
c.
2 2
b a
b
d.
2 2
a
b a
Solution
(c)
Given:
a
sinθ
b
We know that .
2 2
sin θ cos θ 1
2 2
sin θ cos θ 1
2 2
cos θ 1 sin θ
2
cosθ 1 sin θ ...... 1
Put the value of in equation (1).
sinθ
2
a
cosθ 1
b
2 2
2
b a
b
2 2
b a
b
Hence, .
2 2
b a
cosθ
b
Question: 5
If , then can be reduced to
cos 0
sin
a.
cos
b.
cos2
c.
sin

d.
sin2
Solution
(b)
Given:
cos 0
We know that .
cos90 0
Thus,
cos cos90
90
90
Put the value of in .
sin
sin sin 90
sin 90 2
cos2
Hence, .
sin cos2
Question: 6
The value of is
tan1 tan2 tan3 ...tan89
a. 0
b. 1
c. 2
d.
1
2

Solution
(b)
Given:
tan1 tan2 tan3 ...tan89
Now, solve the expression.
tan1 tan2 tan3 ...tan89
tan1 tan89 tan2 tan88 ... tan45 tan45
tan1 tan 90 1 tan2 tan 90 2
...tan45 tan 90 45
tan1 tan 90 1 tan2 tan 90 2
...tan45 tan 90 45
tan1 cot1 tan2 cot 2 ...tan45 cot 45
1 1 1
tan1 tan2 ...tan45
tan1 tan2 tan45
1 1 1 1 1
1
Thus, .
tan1 tan2 tan3 ...tan89 1
Question: 7
If , then the value of
cos9 sin and 9 90
is
tan5
a.
1
3
b.
3
c. 1
d. 0
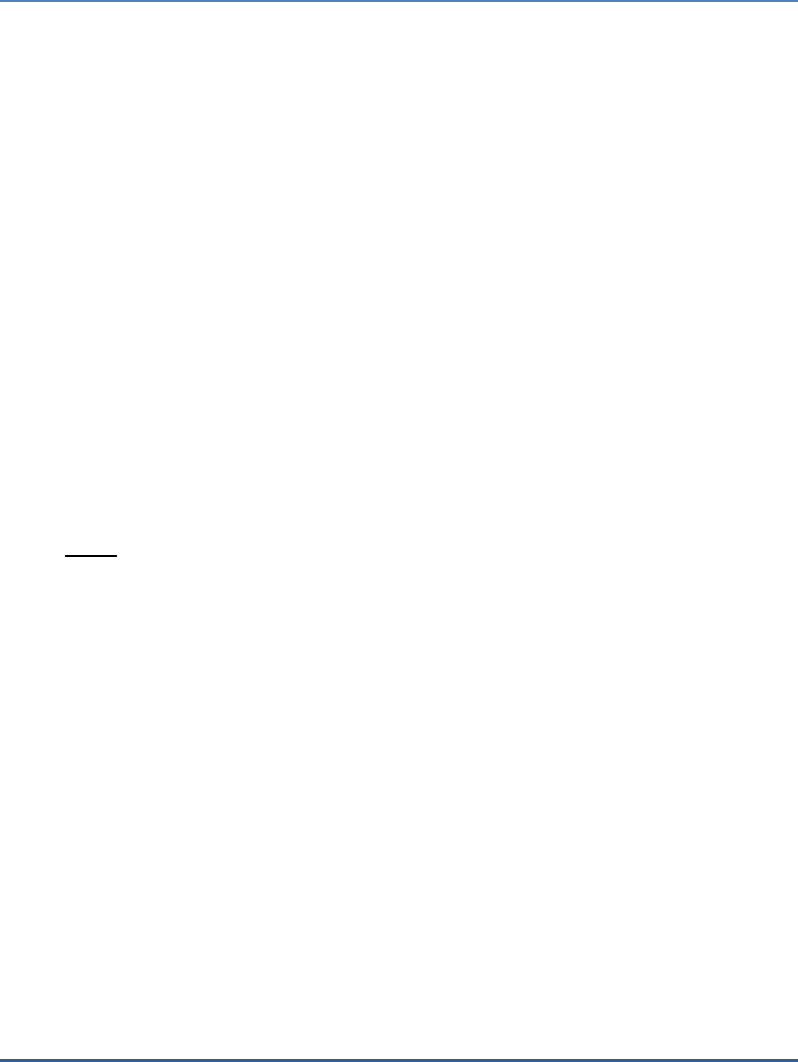
Solution
(c)
Given:
cos9 sin
Now, solve the expression.
cos9 sin
sin 90 9 sin
90 9
9 90
10 90
90
10
9
Now,
tan5 tan 5 9
tan45
1
Hence, .
tan5 1
Question: 8
If is right-angled at C, then the value of
ABC
is
cos A B
a. 0
b. 1

c.
1
2
d.
3
2
Solution
(a)
Given:
C 90
By the angle-sum property of a triangle,
A B C 180
A B 90 180
A B 180 90
A B 90
Now,
cos A B cos90
0
Thus, .
cos A B 0
Question: 9
If , then the value of the expression
2
sinA sin A 1
is
2 4
cos A cos A
a. 1
b.
1
2

c. 2
d. 3
Solution
(a)
Given:
2
sinA sin A 1
2
sinA sin A 1
2
sinA 1 sin A
2 2 2
sinA cos A 1 sin A cos A
Now, find the value of .
2 4
cos A cos A
2 4 2 2
cos A cos A cos A 1 cos A
2
sinA 1 sinA cos A sinA
2
sinA sin A
1
Hence, .
2 4
cos A cos A 1
Question: 10
Given that and , then the value of
1
sin
2
1
cos
2
is
a.
0
b.
30
c.
60
d.
90

Solution
(d)
Given:
1
sin
2
1
sin sin30
2
sin sin30
30
Also, given
1
cos
2
1
cos cos60
2
cos cos60
60
Now,
30 60
90
Thus, .
90
Question: 11
The value of the expression
is
2 2
2
2 2
sin 22 sin 68
sin 63 cos63 sin27
cos 22 cos 68
a. 3

b. 2
c. 1
d. 0
Solution
(b)
Given:
2 2
2
2 2
sin 22 sin 68
sin 63 cos63 sin27
cos 22 cos 68
Now, solve the expression.
2 2
2
2 2
sin 22 sin 68
sin 63 cos63 sin27
cos 22 cos 68
2 2
2 2
2
sin 22 sin 90 22
cos 22 cos 90 22
sin 63 cos63 sin 90 63
2 2
2
2 2
sin 22 cos 22
sin 63 cos63 cos63
cos 22 sin 22
2 2
1 sin 63 cos 63
2 2
1 1 sin 63 cos 63 1
2
Thus,
2 2
2
2 2
sin 22 sin 68
sin 63 cos63 sin27 2
cos 22 cos 68
Question: 12

If , then is equal to
4tanθ 3
4sinθ cosθ
4sinθ cosθ
a.
2
3
b.
1
3
c.
1
2
d.
3
4
Solution
(c)
Given:
4tanθ 3
So, .
3
tanθ
4
Now, calculate the value of .
4sinθ cosθ
4sinθ cosθ
Multiply and divide numerator and denominator by
.
cosθ
4sinθ cosθ
4sinθ cosθ
cosθ cosθ
4sinθ cosθ
4sinθ cosθ
cosθ cosθ
4tanθ 1
4tanθ 1
Put in the above expression.
3
tanθ
4

4sinθ cosθ 4tanθ 1
4sinθ cosθ 4tanθ 1
3
4 1
4
3
4 1
4
3 1
3 1
2
4
1
2
Thus, .
4sinθ cosθ 1
4sinθ cosθ 2
Question: 13
If , then the value of is
sinθ cosθ 0
4 4
sin θ cos θ
a. 1
b.
3
4
c.
1
2
d.
1
4
Solution
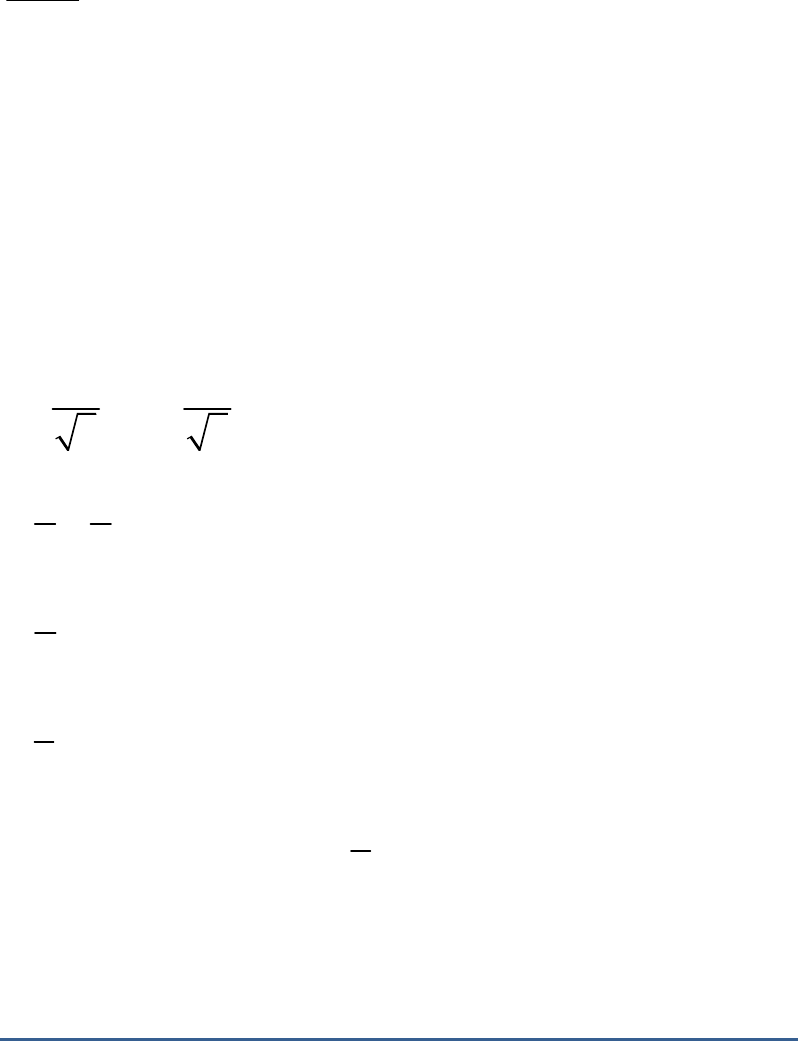
(c)
Given:
sinθ cosθ 0
sinθ cosθ
sinθ
1
cosθ
tanθ 1
θ 45
Now, find at .
4 4
sin θ cos θ
θ 45
4 4 4 4
sin θ cos θ sin 45 cos 45
4 4
1 1
2 2
1 1
4 4
2
4
1
2
Thus, .
4 4
1
sin θ cos θ
2
Question: 14
is equal to
sin 45 θ cos 45 θ

a.
2cosθ
b. 0
c.
2sinθ
d. 1
Solution
(b)
Given:
sin 45 θ cos 45 θ
sin 45 θ cos 45 θ sin 45 θ cos 90 45 θ
sin 45 θ sin 45 θ
0
Thus, .
sin 45 θ cos 45 θ 0
Question: 15
A pole 6 m high casts a shadow m long on the
2 3
ground, then the Sun’s elevation is
a.
60
b.
45
c.
30
d.
90
Solution
(a)
Let AB is a pole and BC is its radius.
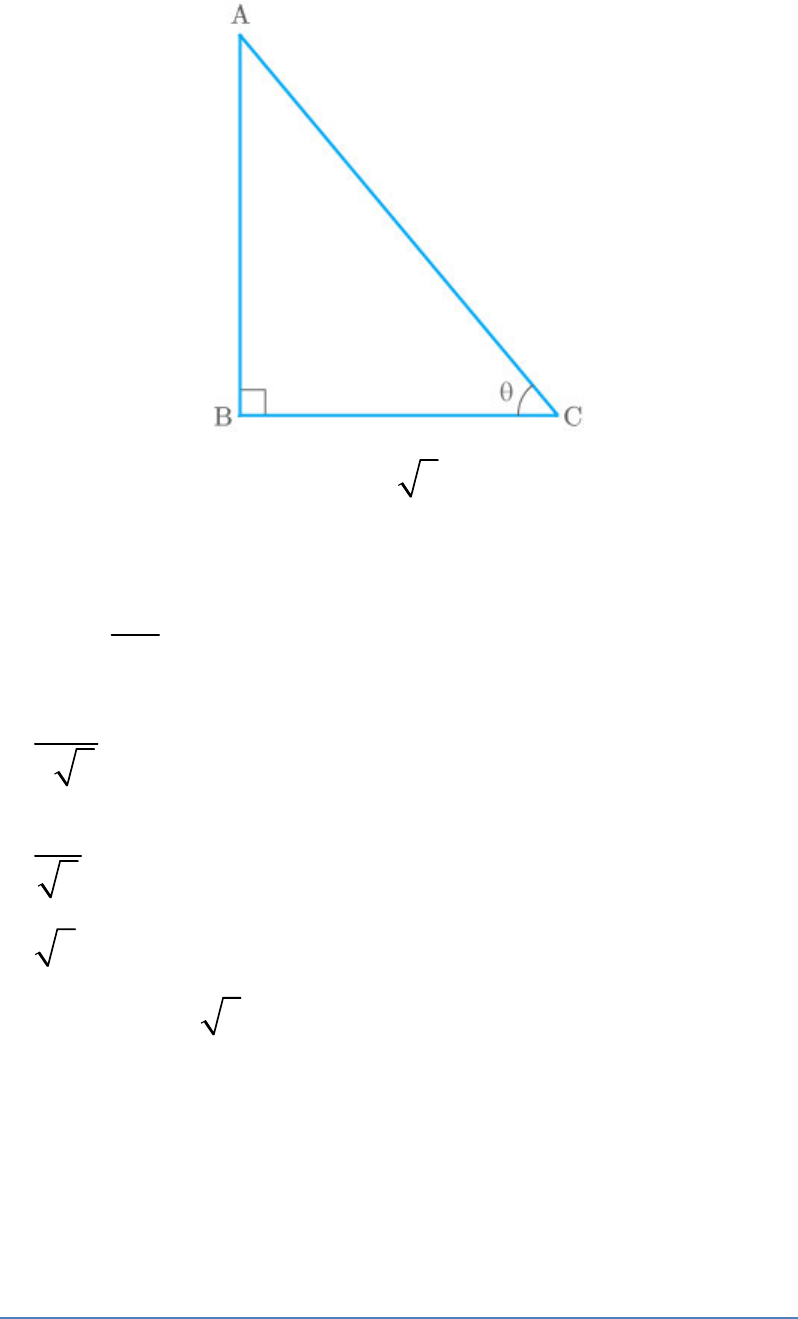
Given: and
AB 6m
BC 2 3 m
In triangle ABC,
AB
tanθ
BC
6
2 3
3
3
3
Thus,
tanθ 3 tan60
Thus, .
θ 60
Hence, the Sun’s elevation is .
60
Exercise 8.2 (12)

Write ‘True’ or ‘False’ and justify your answer in
each of the following:
Question: 1
tan47
1
cot 43
Solution
True.
Given
tan47
1
cot 43
LHS
tan 90 43
tan47
cot 43 cot 43
cot 43
cot 43
1
RHS
Hence proved.
Question: 2
The value of the expression is
2 2
cos 23 sin 67
positive.

Solution
False.
Given:
2 2
cos 23 sin 67
2 2 2 2
cos 23 sin 67 cos 90 67 sin 67
2 2
sin 67 sin 67
0
Thus, the value of the expression is not positive.
Question: 3
The value of the expression is
sin80 cos80
negative.
Solution
False.
Given:
sin80 cos80
sin80 cos80 sin80 cos 90 10
sin80 sin10
We know that the value of increases as
sinθ
θ
increases.
Thus, is positive.
sin80 cos80
Question: 4
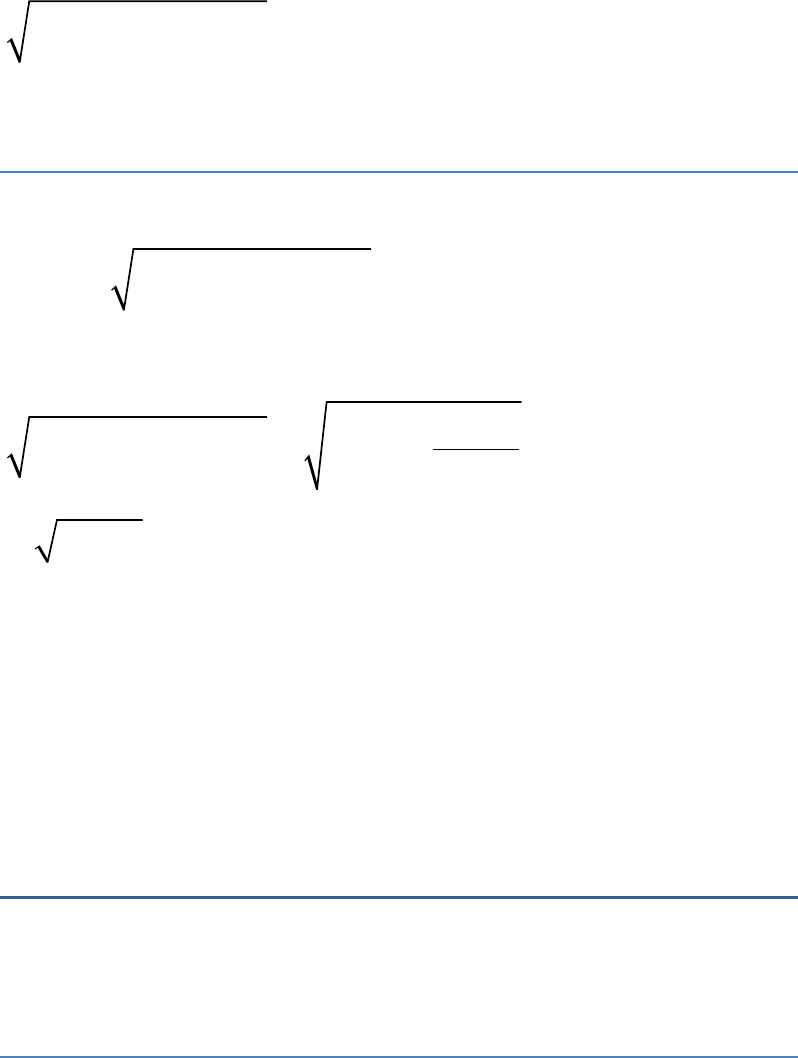
2 2
1 cos θ sec θ tanθ
Solution
True.
Given:
2 2
1 cos θ sec θ tanθ
LHS
2 2 2
2
1
1 cos θ sec θ sin θ
cos θ
2
tan θ
tanθ
RHS
Thus, LHS = RHS.
Question: 5
If , then .
2
cosA cos A 1
2 4
sin A sin A 1
Solution
True.
Given:
2
cosA cos A 1
2
cosA cos A 1
2
cosA 1 cos A
2
cosA sin A ...... 1

Now, solve the expression .
2 4
sin A sin A 1
LHS
2 4 2 2
sin A sin A sin A 1 sin A
From equation (1).
2 4 2 2
sin A sin A sin A 1 sin A
cosA 1 cosA
2
cosA cos A
1
RHS
Thus, LHS = RHS.
Question: 6
2
tanθ 2 2tanθ 1 5tanθ sec θ
Solution
False.
Given:
2
tanθ 2 2tanθ 1 5tanθ sec θ
LHS
2
tanθ 2 2tanθ 1 2tan θ tanθ 4tanθ 2
2
2tan θ 5tanθ 2
2 2
1 tan θ 1 tan θ 5tanθ
2 2 2 2
sec θ sec θ 5tanθ 1 tan θ sec θ
2
2sec θ 5tanθ
RHS
Thus, LHS RHS.
Question: 7
If the length of the shadow of a tower is increasing,
then the angle of elevation of the sun is also
increasing.
Solution
False.
Let BC is a tower and AB is its shadow and is the
θ
angle of elevation.
From the figure, .
BC
tanθ
AB
If AB increases, the value of decreases and thus
tanθ
the value of decreases.
θ
Hence, if the length of the shadow of a tower is
increasing, then the angle of elevation of the sun is
decreases.
Question: 8
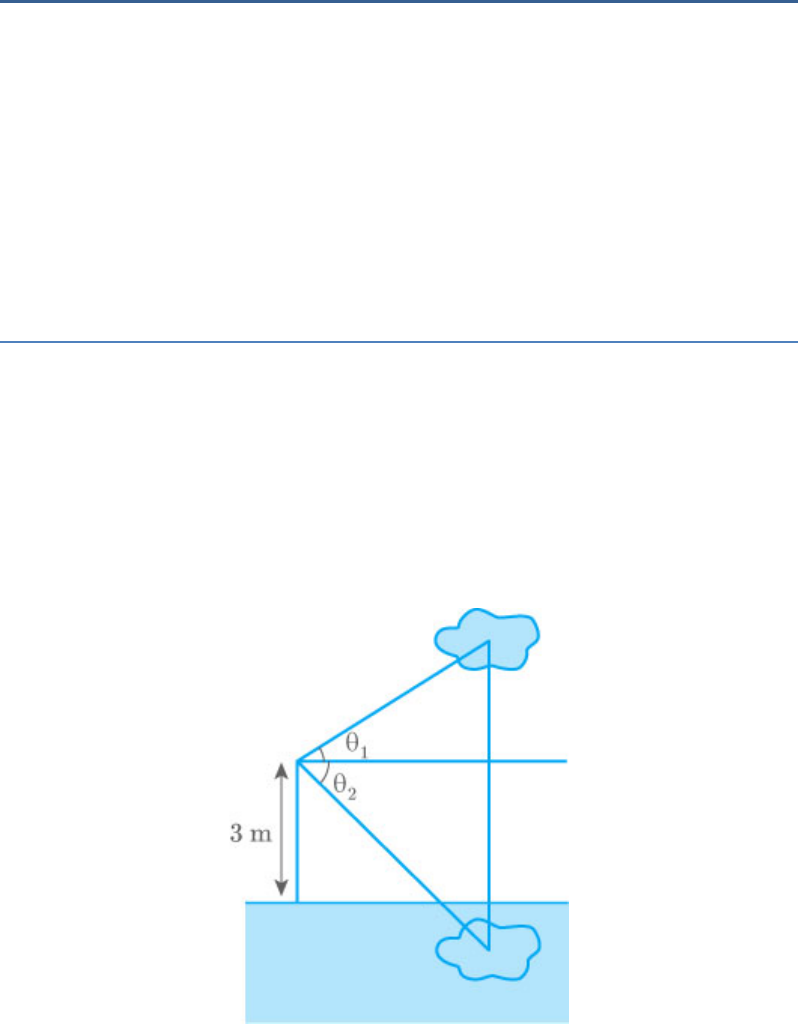
If a man standing on a platform 3 metres above the
surface of a lake observes a cloud and its reflection in
the lake, then the angle of elevation of the cloud is
equal to the angle of depression of its reflection.
Solution
False.
From the figure,
The angle is the angle of elevation of the cloud
1
θ
and is angle of depression of its reflection.
2
θ

It is observed that the height of the cloud from the
surface is more than the depth of its reflection in
water.
Thus, .
1 2
θ θ
Hence, the angle of elevation of the cloud is not
equal to the angle of depression of its reflection.
Question: 9
The value of can be , where is a
2sinθ
1
a
a
a
positive number, and .
a 1
Solution
False.
Let and find .
a 2
1
a
a
1 1
a 2
a 2
4 1
2
5
2
If , then .
5
2sinθ
2
5
sinθ
4
But the maximum value of is 1.
sinθ

Hence, the value of cannot be .
2sinθ
1
a
a
Question: 10
, where and are two distinct
2 2
a b
cosθ
2ab
a
b
numbers such that .
ab 0
Solution
False.
2 2
a b
cosθ
2ab
2
a b 2ab
2ab
2
a b
2ab
2ab 2ab
2
a b
1
2ab
The value of the above expression is more than 1.
But we know that the maximum value of is 1.
cosθ
Hence, cannot be equal to .
cosθ
2 2
a b
2ab
Question: 11
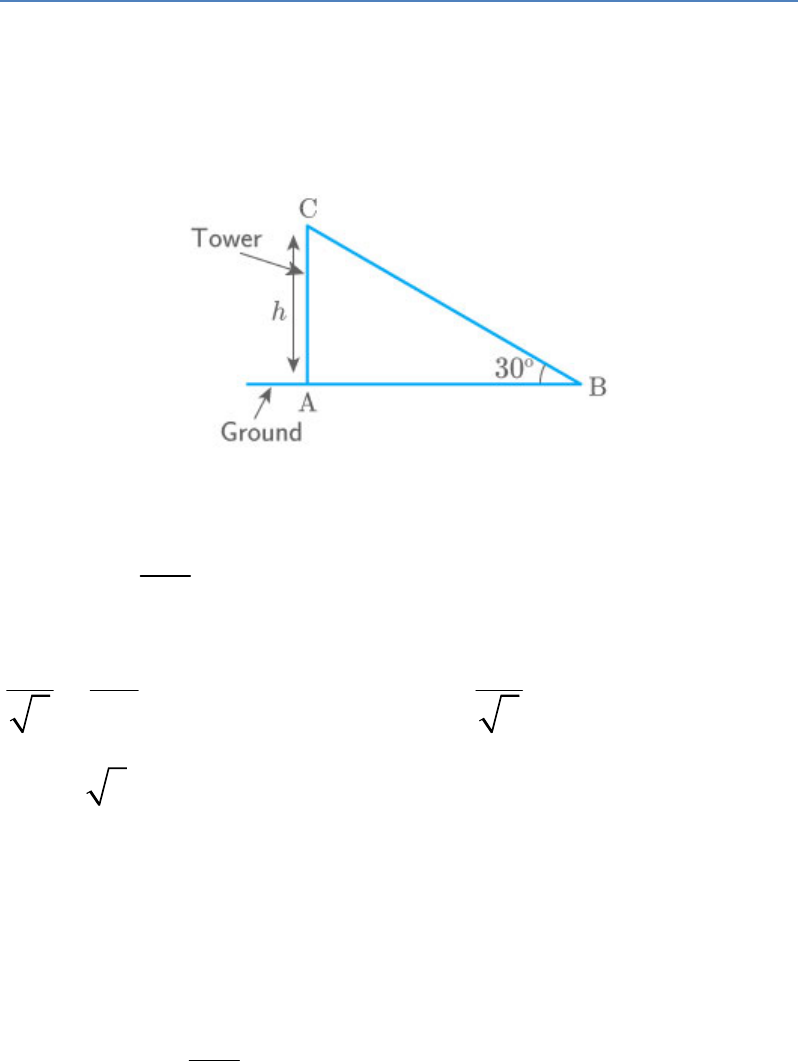
The angle of elevation of the top of a tower is . If
30
the height of the tower is doubled, then the angle of
elevation of its top will also be doubled.
Solution
False.
Let AC be a tower of height and the angle of
h
elevation is .
θ
In triangle ABC,
AC
tan30
AB
1 h 1
tan30
AB
3 3
AB 3h
Now, if the height of the tower is doubled,
AC 2h
In triangle ABC,
AC
tan CBA
AB
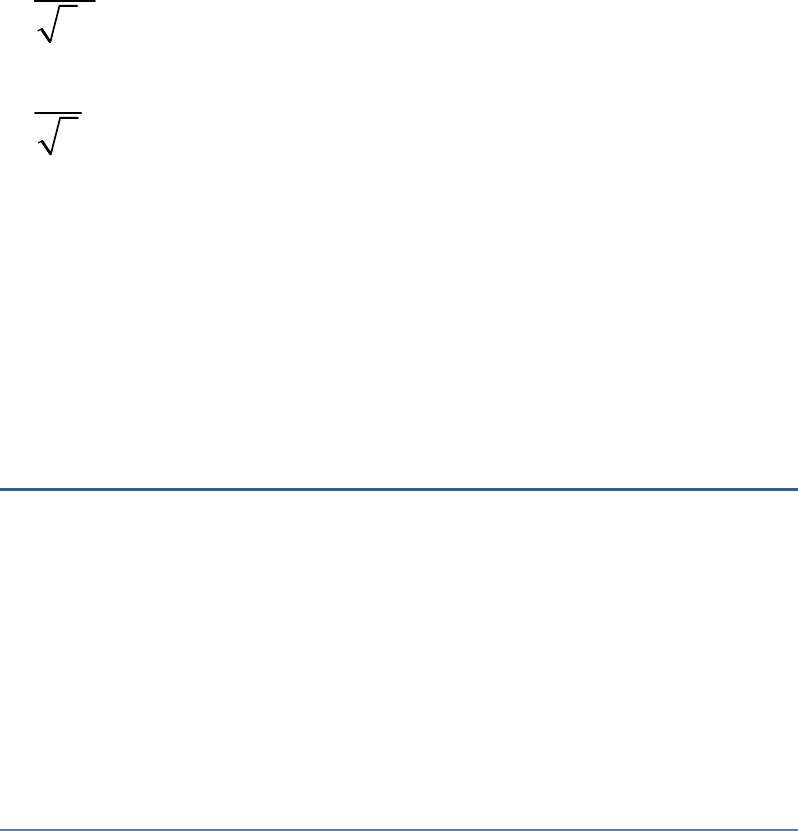
2h
3h
2
3
Thus, the angle CBA cannot be .
60
Hence, if the height of the tower is doubled, then the
angle of elevation of its top will not be doubled.
Question: 12
If the height of a tower and the distance of the point
of observation from its foot, both, are increased by
, then the angle of elevation of its top remains
10%
unchanged.
Solution
True.
Let BC be a tower and AB be the distance of the
point of observation from its foot.
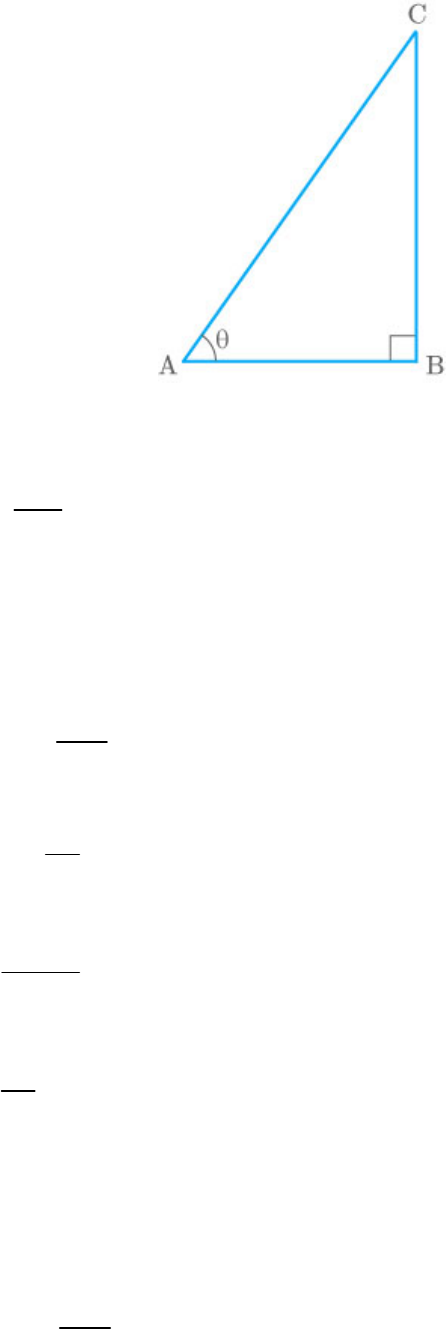
In triangle ABC,
BC
tanθ ...... 1
AB
Now after increasing BC by .
10%
New BC will be:
10
BC BC
100
1
BC 1
10
10 1
BC
10
11
BC
10
Now after increasing AB by .
10%
New AB will be:
10
AB AB
100

1
AB 1
10
10 1
AB
10
11
AB
10
Let after these increments, the angle of elevation be
.
Now,
In triangle ABC,
BC
tan
AB
11BC
10
11AB
10
BC
...... 2
AB
From equations (1) and (2).
tan tanθ
θ
Hence, the angle of elevation of the top remains
unchanged.
Exercise 8.3 (15)

Prove the following (from Q.1 to Q.7):
Question: 1
sinθ 1 cosθ
2cosecθ
1 cosθ sinθ
Solution
Given:
sinθ 1 cosθ
2cosecθ
1 cosθ sinθ
LHS
2
2
sin θ 1 cosθ
sinθ 1 cosθ
1 cosθ sinθ sinθ 1 cosθ
2 2
sin θ cos θ 1 2cosθ
sinθ 1 cosθ
2 2
1 1 2cosθ
sin θ cos θ 1
sinθ 1 cosθ
2 2cosθ
sinθ 1 cosθ
2 1 cosθ
sinθ 1 cosθ
2
sinθ
2cosecθ
RHS
Hence proved.

Question: 2
tanA tanA
2cosecA
1 secA 1 secA
Solution
Given:
tanA tanA
2cosecA
1 secA 1 secA
LHS
tanA tanA 1 1
tanA
1 secA 1 secA 1 secA 1 secA
1 secA 1 secA
tanA
1 secA 1 secA
2
2secA
tanA
1 sec A
2 2
2
2secA
tanA 1 sec A tan A
tan A
2secA
tanA
2
cosA
sinA
cosA
2
sinA
2cosecA
RHS
Hence proved.
Question: 3
If , then .
3
tanA
4
12
sinAcosA
25
Solution
Given: .
3
tanA
4
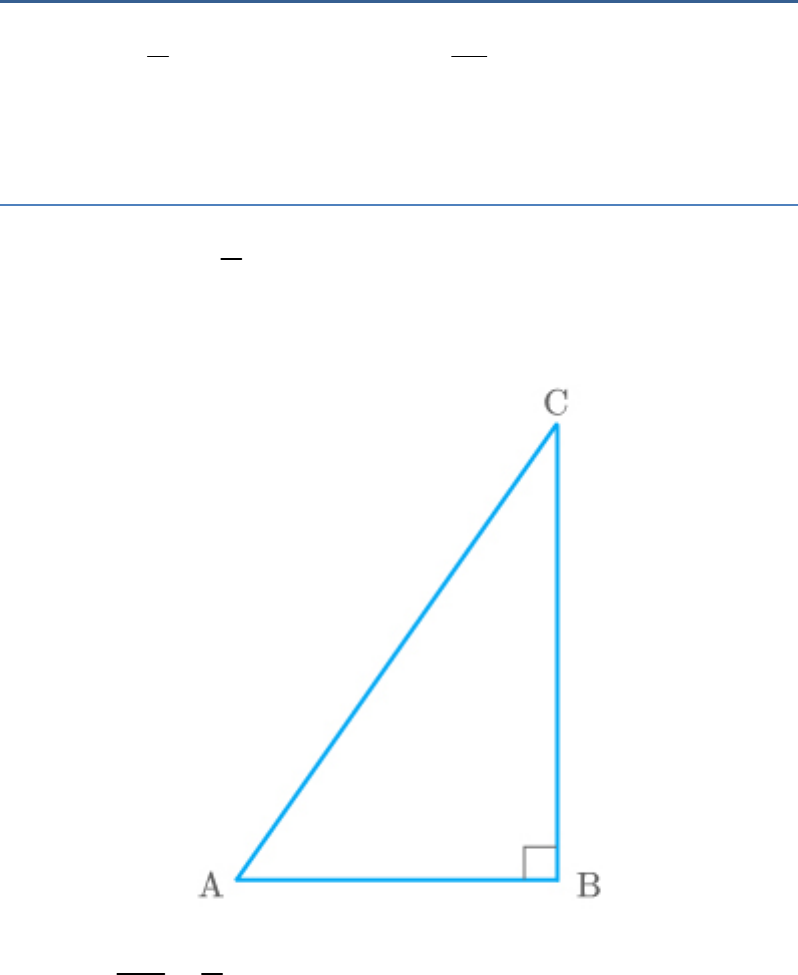
Let ABC be a triangle, right-angled at B.
BC 3
tanA
AB 4
Let .
BC 3a and AB 4a
In , by the Pythagoras theorem,
ABC
2 2 2
AC AB BC
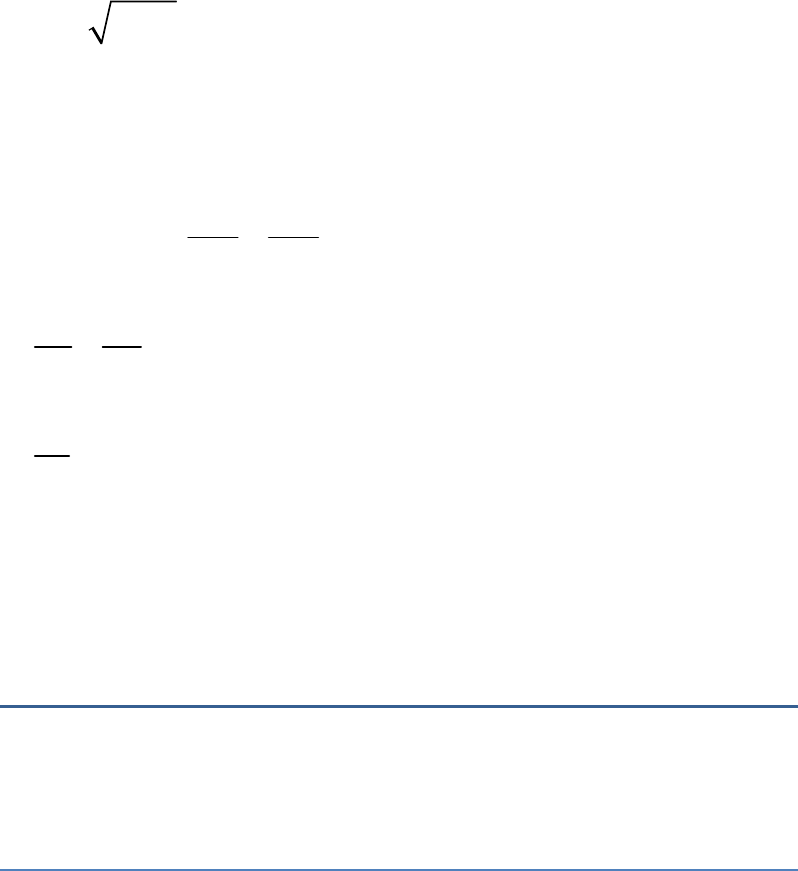
2 2 2
AC 4a 3a
2
2 2
AC 16a 9a
2
2
AC 25a
2
AC 25a
AC 5a
Now, calculate the value of .
sinAcosA
BC AB
sinAcosA
AC AC
3a 4a
5a 5a
12
25
Hence proved.
Question: 4
.
sin cos tan cot sec cosec
Solution
Given:
sin cos tan cot sec cosec
LHS
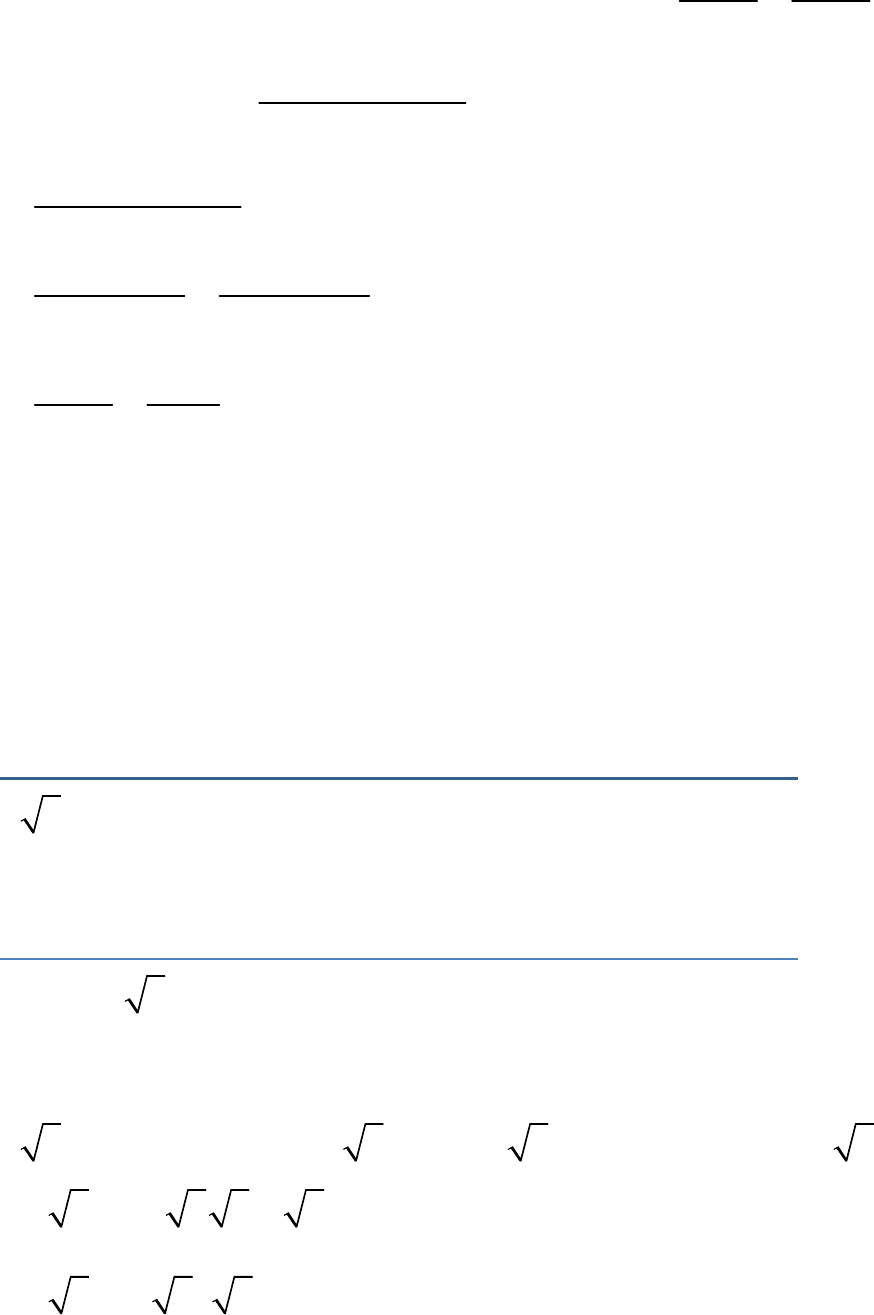
sin cos
sin cos tan cot sin cos
cos sin
2 2
sin cos
sin cos
sin cos
2 2
sin cos
sin cos 1
sin cos
sin cos
sin cos sin cos
1 1
cos sin
sec cosec
RHS
Hence proved.
Question: 5
.
3
3 1 3 cot 30 tan 60 2sin60
Solution
Given:
3
3 1 3 cot 30 tan 60 2sin60
LHS
3 1 3 cot 30 3 1 3 3 cot 30 3
3 1 3 3 3
3 1 3 3 1
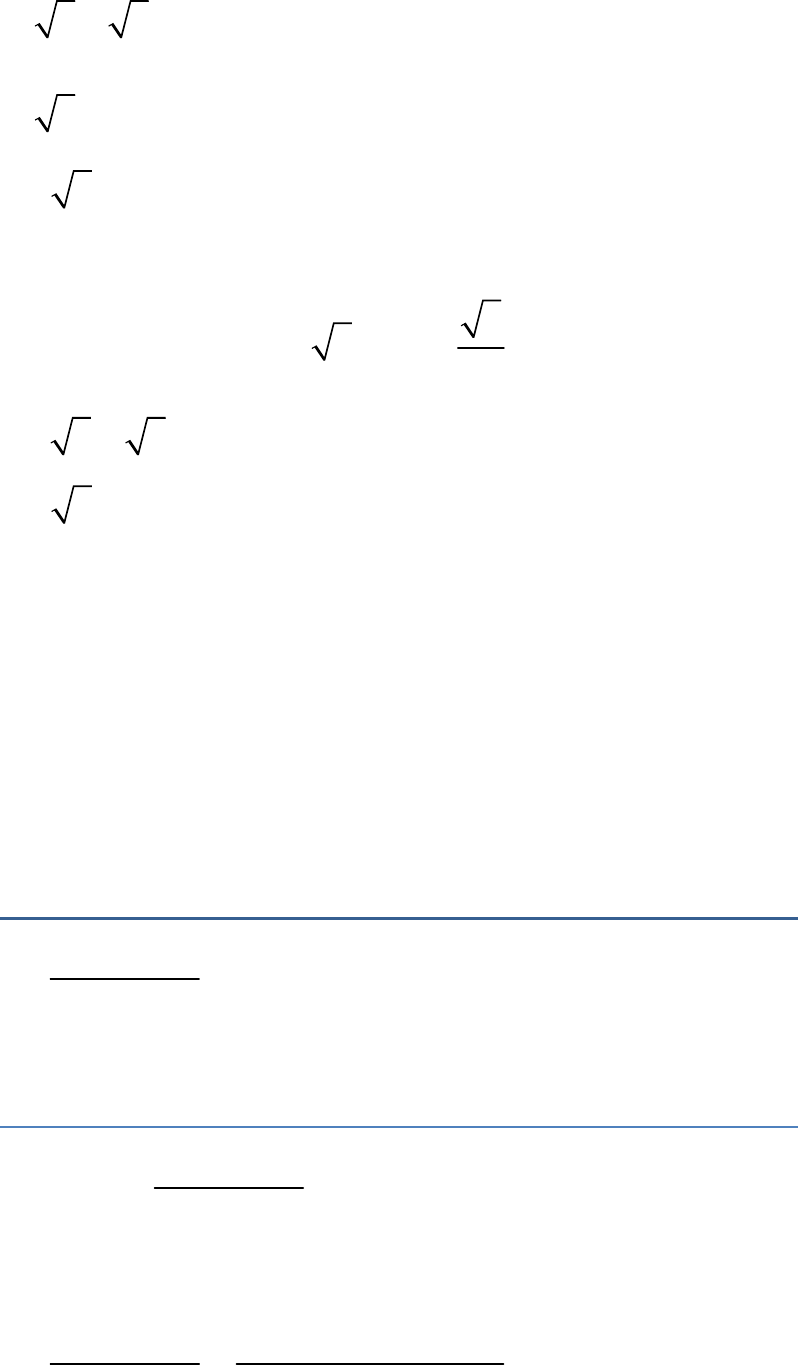
2
2
3 3 1
3 3 1
2 3
Now, take RHS.
3
3
3
tan 60 2sin60 3 2
2
3 3 3
2 3
Thus, LHS = RHS.
Hence proved.
Question: 6
2
cot
1 cosec
1 cosec
Solution
Given:
2
cot
1 cosec
1 cosec
LHS
2 2
cot 1 cosec cot
1
1 cosec 1 cosec

2
2 2
cosec cosec
1 cot cosec
1 cosec
cosec 1 cosec
1 cosec
cosec
RHS
Hence proved.
Question: 7
tanθ tan 90 θ secθsec 90 θ
Solution
Given:
tanθ tan 90 θ secθsec 90 θ
LHS
tanθ tan 90 θ tanθ cot θ tan 90 θ cot θ
sinθ cosθ
cosθ sinθ
2 2
sin θ cos θ
sinθcosθ
2 2
1
sin θ cos θ 1
sinθcosθ
secθ cosecθ
secθ sec 90 θ
RHS
Hence proved.
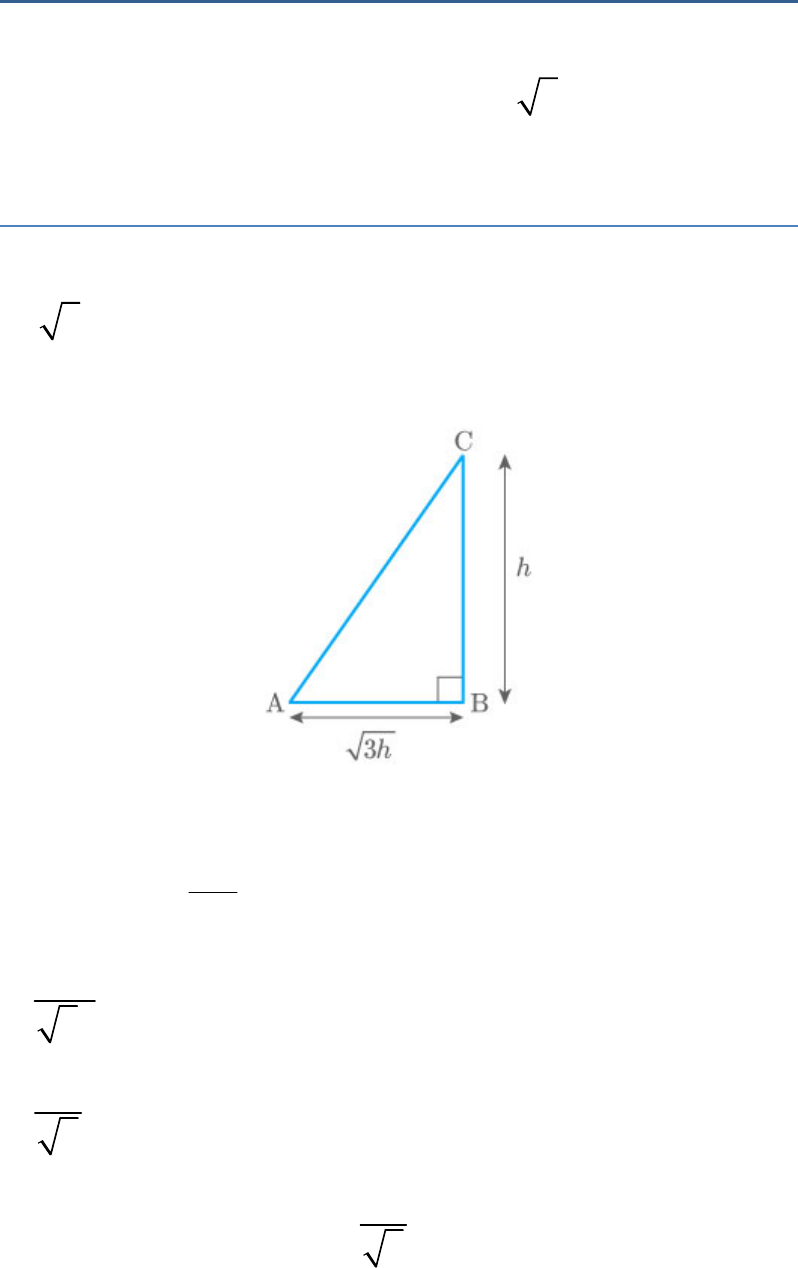
Question: 8
Find the angle of elevation of the sun when the
shadow of a pole metres high is metres long.
h
3h
Solution
Let BC be a pole of height , AB be its shadow which
h
is metres long and be the angle of
3h
CAB
elevation.
In the triangle ABC,
BC
tan CAB
AB
h
3h
1
3
We know that .
1
tan30
3
Thus, .
tan CAB tan30
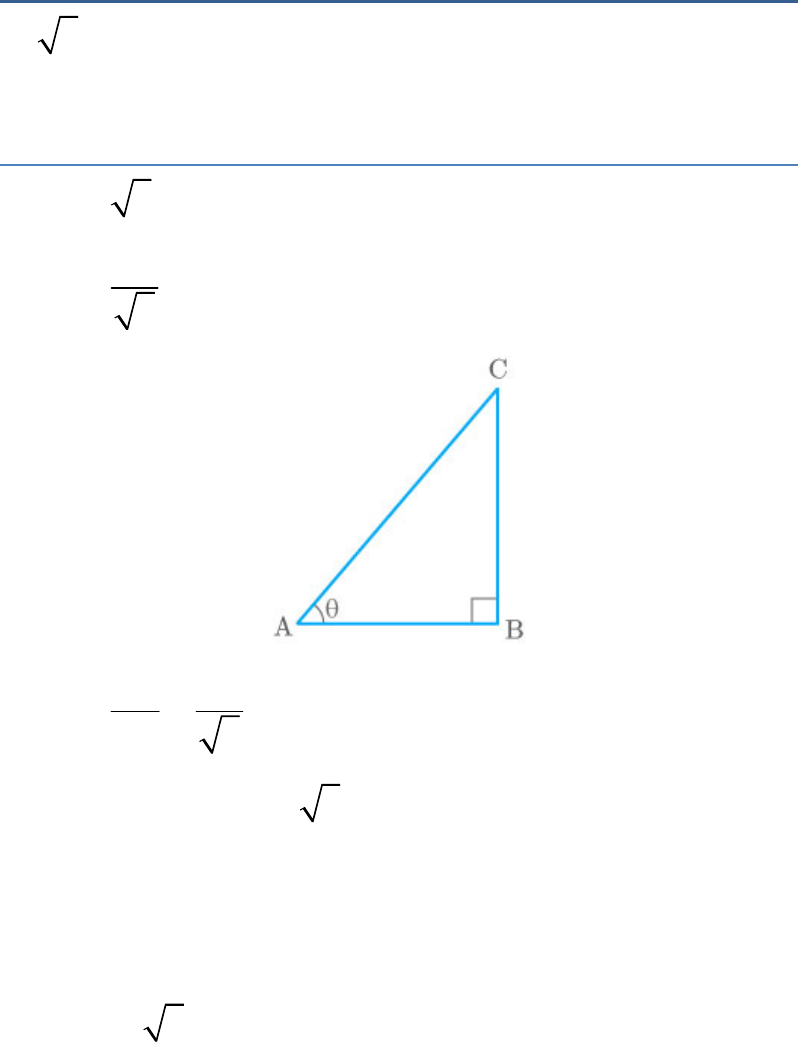
Thus, .
CAB 30
Hence, the angle of elevation of the sun is .
30
Question: 9
If , then find the value of .
3tanθ 1
2 2
sin θ cos θ
Solution
Given:
3tanθ 1
1
tanθ
3
BC 1
tanθ
AB
3
Let and .
BC a
AB 3a
By the Pythagoras theorem in triangle ABC,
2 2 2
AC AB BC
2
2 2
AC 3a a
2
2 2
AC 3a a
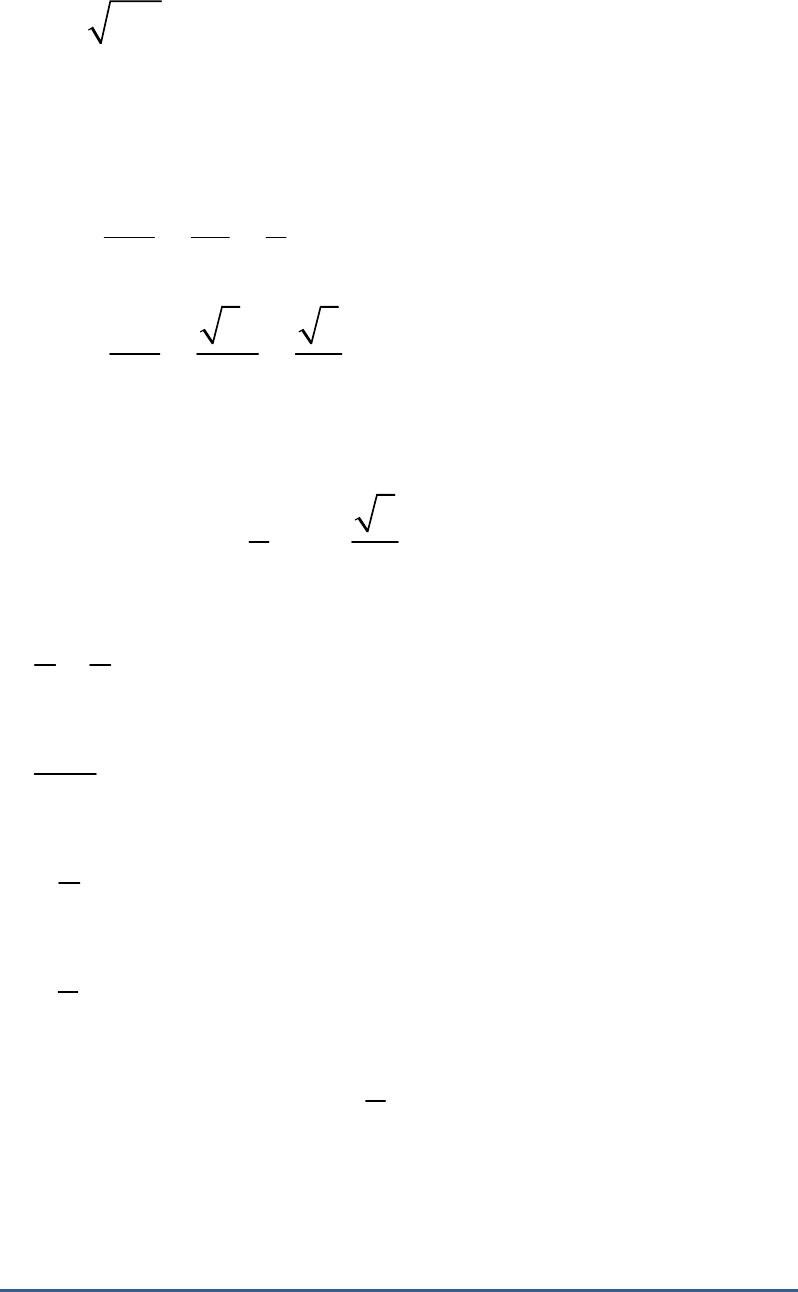
2
2
AC 4a
2
AC 4a
AC 2a
Now, in triangle ABC,
BC a 1
sinθ
AC 2a 2
AB 3a 3
cosθ
AC 2a 2
Now,
2
2
2 2
1 3
sin θ cos θ
2 2
1 3
4 4
1 3
4
2
4
1
2
Hence, .
2 2
1
sin θ cos θ
2
Question: 10
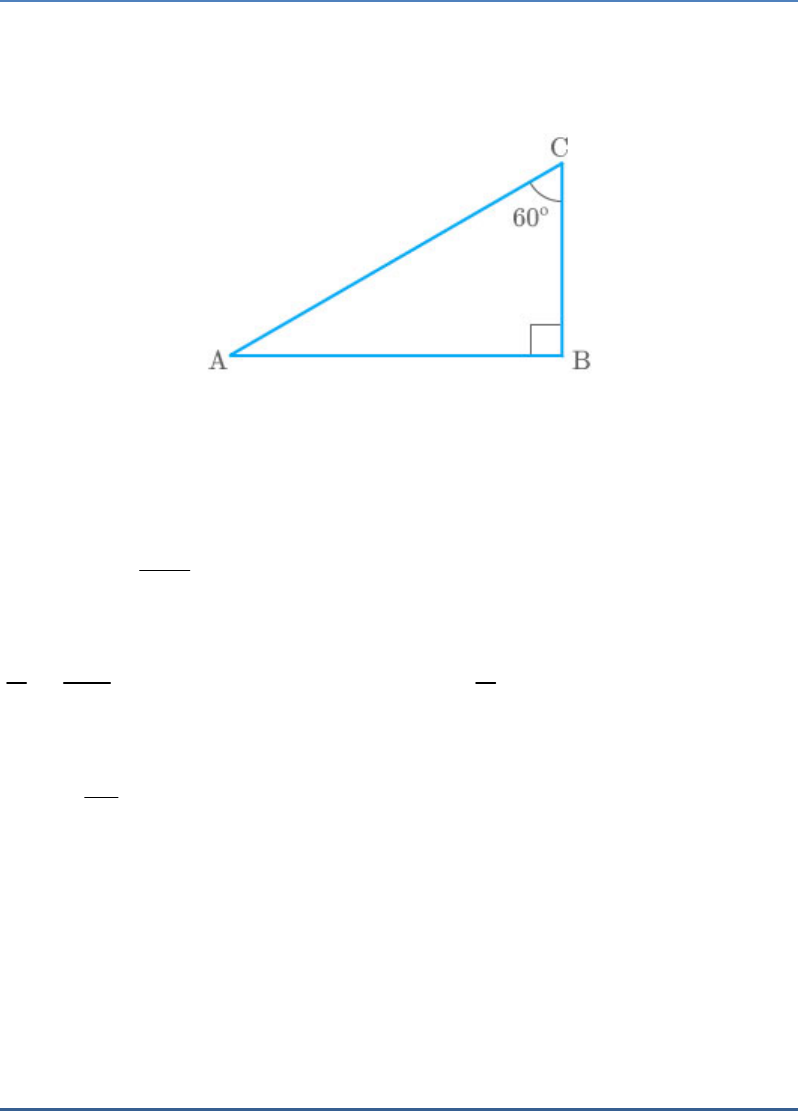
A ladder 15 metres long just reaches the top of a
vertical wall. If the ladder makes an angle of
60
with the wall, find the height of the wall.
Solution
Let AC be a ladder making an angle of with the
60
wall BC.
Given: .
AC 15m
In triangle ABC,
BC
cos60
AC
1 BC 1
cos60
2 15 2
15
BC
2
BC 7.5
Hence, the height of the wall is m.
7.5
Question: 11

Simplify
2
1 tan θ 1 sinθ 1 sinθ
Solution
Given: .
2
1 tan θ 1 sinθ 1 sinθ
Now, solve the expression.
2 2 2
1 tan θ 1 sinθ 1 sinθ 1 tan θ 1 sin θ
We know that
2 2 2 2
1 tan θ sec θand 1 sin θ cos θ
Thus,
2 2 2
1 tan θ 1 sinθ 1 sinθ sec θcos θ
2
2
1 1
sec θ cosθ
sec θ secθ
1
Hence,
2
1 tan θ 1 sinθ 1 sinθ 1
Question: 12
If , then find the value of .
2 2
2sin θ cos θ 2
θ
Solution
Given:
2 2
2sin θ cos θ 2
2 2
2sin θ cos θ 2
2 2 2 2
2sin θ 1 sin θ 2 cos θ 1 sin θ
2 2
2sin θ 1 sin θ 2

2
3sin θ 2 1
2
3
sin θ
3
2
sin θ 1
sinθ 1
That is,
sinθ 1
sinθ sin90 sin90 1
θ 90
or
sinθ 1
sinθ sin90
sin θ sin90
sin θ sin90
θ 90
θ 90
θ 360 90 270
Hence, and .
θ 90
270
Question: 13
Show that .
2 2
cos 45 θ cos 45 θ
1
tan 60 θ tan 30 θ

Solution
Given:
2 2
cos 45 θ cos 45 θ
1
tan 60 θ tan 30 θ
LHS
2 2
cos 45 θ cos 45 θ
tan 60 θ tan 30 θ
2 2
cos 45 θ cos 90 45 θ
tan 60 θ tan 90 30 θ
2 2
cos 45 θ sin 45 θ
tan 60 θ cot 60 θ
2 2
1
cos A sin A 1
tan 60 θ cot 60 θ
1 1
cot A
1
tanA
tan 60 θ
tan 60 θ
1
1
1
RHS
Hence proved.
Question: 14
An observer 1.5 metres tall is 20.5 metres away from
a tower 22 metres high. Determine the angle of
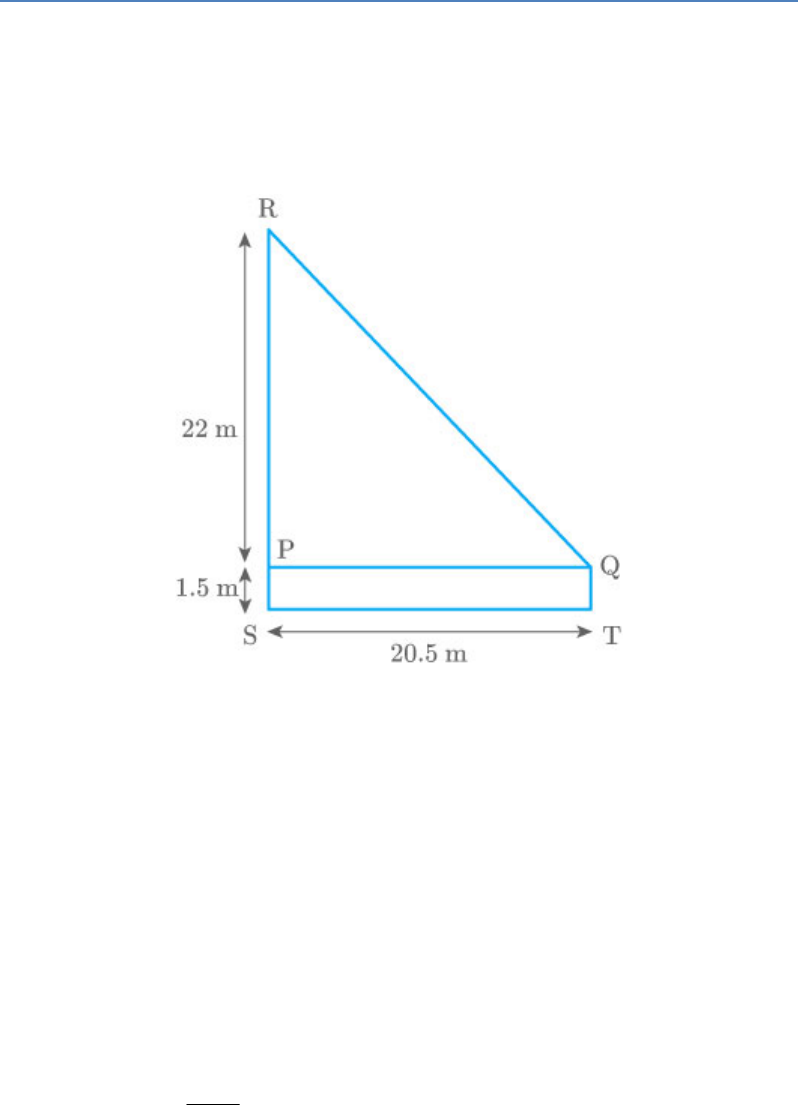
elevation of the top of the tower from the eye of the
observer.
Solution
Let RS be a tower of height 22 m and QT be an
observer of height 1.5 m standing at a distance of
20.5 m from the tower.
From the figure,
PR 22 1.5 20.5
PQ ST 20.5
PS QT 1.5
n triangle PQR,
PR
tan RQP
PQ

20.5
tan RQP
20.5
tan RQP 1
tan RQP tan45 tan45 1
RQP 45
Hence, the angle of elevation of the top of the tower
from the eye of the observer is .
45
Question: 15
Show that .
4 2 4 2
tan θ tan θ sec θ sec θ
Solution
Given:
4 2 4 2
tan θ tan θ sec θ sec θ
LHS
4 2 2 2
tan θ tan θ tan θ tan θ 1
2 2 2 2
sec θ 1 sec θ tan θ 1 sec θ
4 2
sec θ sec θ
RHS
LHS = RHS
Hence proved.
Exercise 8.4 (18)

Question: 1
If , then prove that .
cosecθ cot θ p
2
2
p 1
cosθ
p 1
Solution
Given:
cosecθ cot θ p
Now, solve the expression.
cosecθ cot θ p
1 cosθ
p
sinθ sinθ
1 cosθ
p
sinθ
Squaring on both sides.
2
2
2
1 cosθ
p
sin θ
2
2 2 2
2
1 cosθ
p sin θ 1 cos θ
1 cos θ
2
2
1 cosθ
p
1 cosθ 1 cosθ
2
1 cosθ
p ...... 1
1 cosθ
We have to prove that .
2
2
p 1
cosθ
p 1
Take RHS,

2
2
p 1
p 1
Put the value of from equation (1).
2
p
2
2
1 cosθ
1
1 cosθ
p 1
1 cosθ
p 1
1
1 cosθ
1 cosθ 1 cosθ
1 cosθ
1 cosθ 1 cosθ
1 cosθ
1 cosθ 1 cosθ
1 cosθ 1 cosθ
2cosθ
2
cosθ
LHS
LHS = RHS
Hence proved.
Question: 2
Prove that
2 2
sec θ cosec θ tanθ cot θ
Solution
Given:
2 2
sec θ cosec θ tanθ cot θ

LHS
2 2
2 2
1 1
sec θ cosec θ
cos θ sin θ
2 2
2 2
sin θ cos θ
sin θcos θ
2 2
2 2
1
sin θ cos θ 1
sin θcos θ
1
sinθcosθ
2 2
2 2
sin θ cos θ
sin θ cos θ 1
sinθcosθ
2 2
sin θ cos θ
sinθcosθ sinθcosθ
sinθ cosθ
cosθ sinθ
tanθ cot θ
RHS
Hence proved.
Question: 3
The angle of elevation of the top of a tower from
certain point is . If the observer moves 20 metres
30
towards the tower, the angle of elevation of the top
increases by . Find the height of the tower.
15
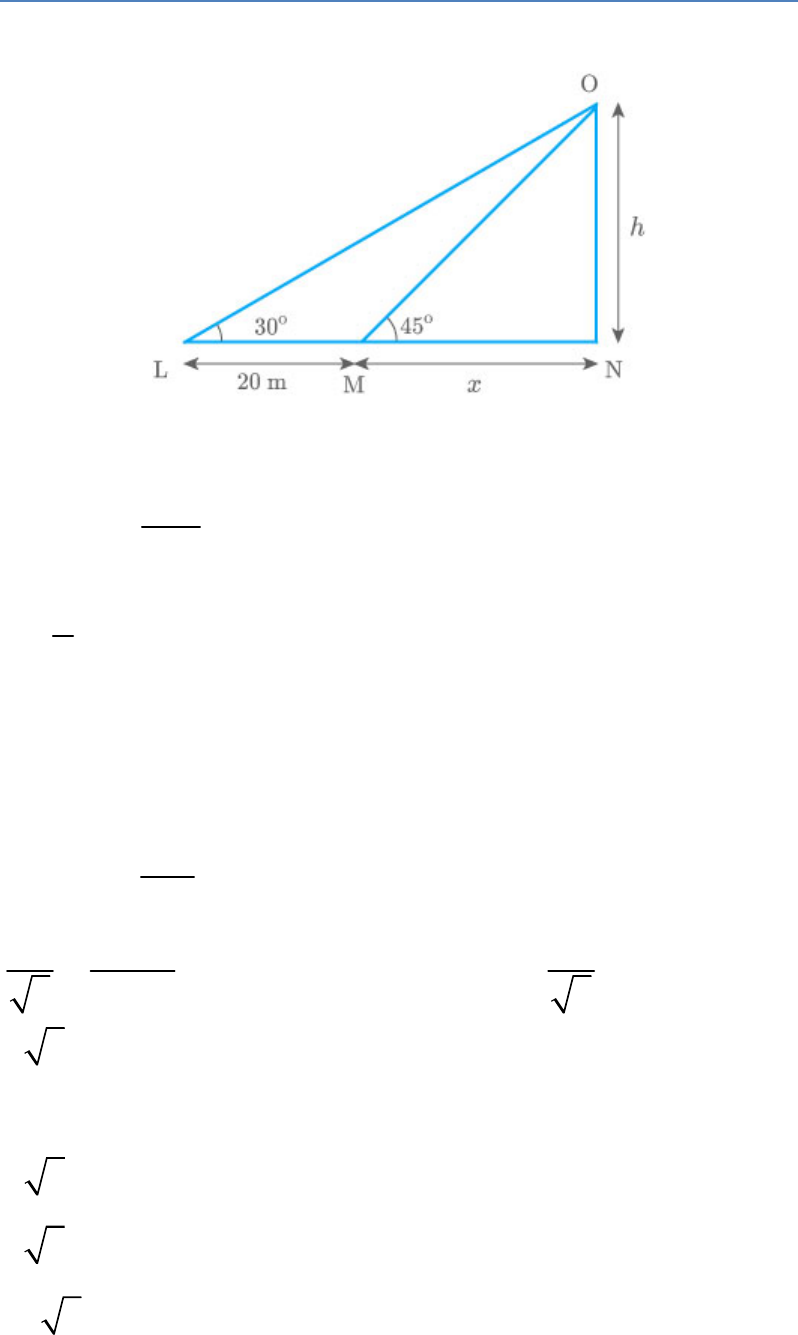
Solution
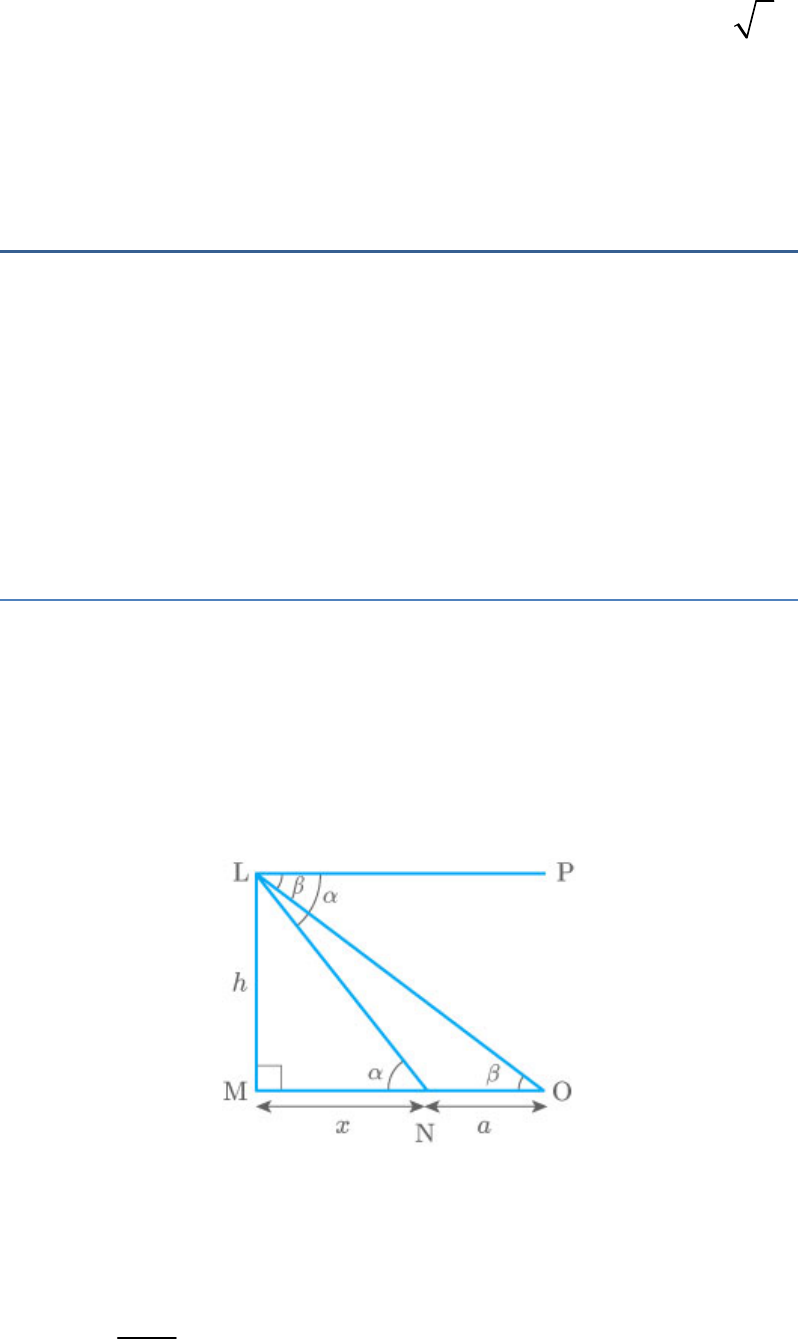
Let ON be a tower of height h.
In triangle OMN,
ON
tan45
MN
h
1 tan45 1
x
h x ...... 1
In triangle OLN,
ON
tan30
LN
1 h 1
tan30
20 x
3 3
h 3 20 x
Put the value of from equation (1).
x
h 3 20 h
h 3 h 20
h 3 1 20
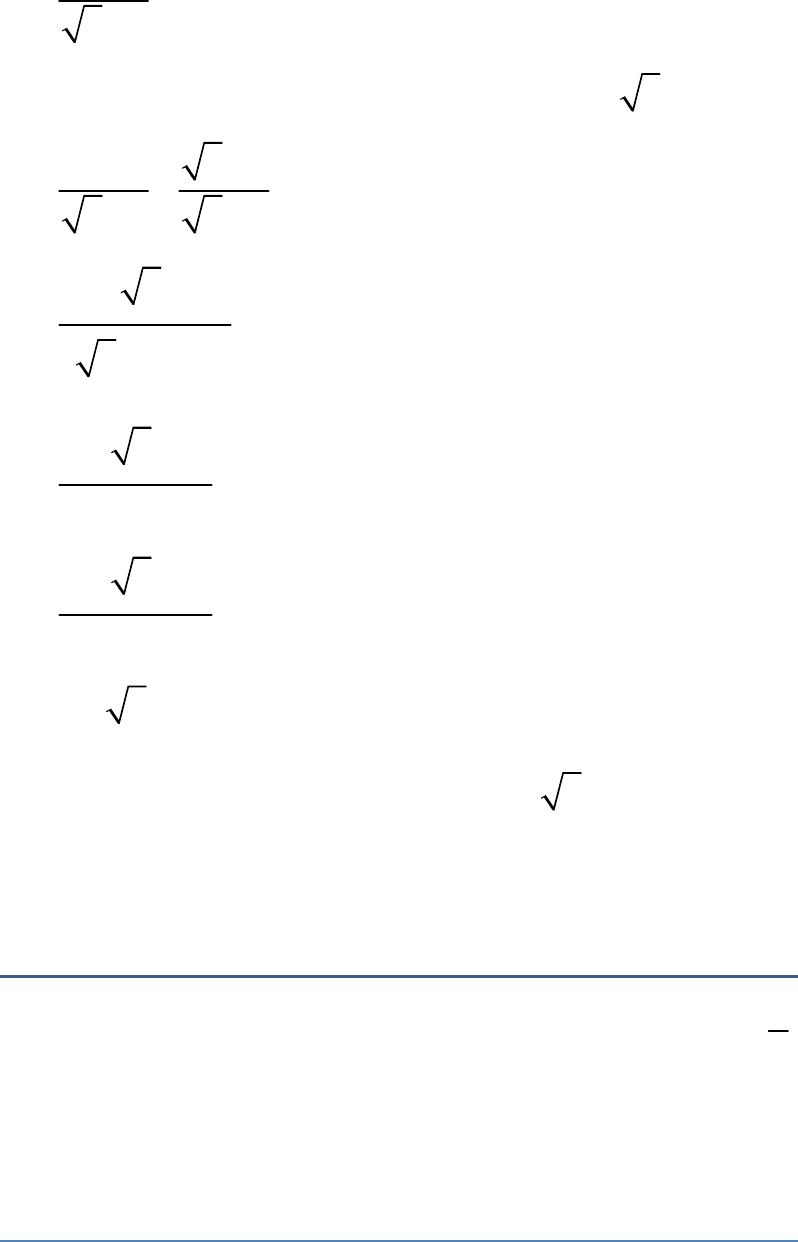
20
h
3 1
Multiply numerator and denominator by .
3 1
20 3 1
h
3 1 3 1
2
2
20 3 1
h
3 1
20 3 1
h
3 1
20 3 1
h
2
h 10 3 1
Hence the height of the tower is metres.
10 3 1
Question: 4
If , then prove that
2
1 sin θ 3sinθcosθ
1
tanθ 1or
2
.
Solution
Given:
2
1 sin θ 3sinθcosθ

2
1 sin θ 3sinθcosθ
2 2 2 2 2
sin θ cos θ sin θ 3sinθcosθ sin θ cos θ 1
2 2
2sin θ cos θ 3sinθcosθ 0
2 2
2sin θ 2sinθcosθ sinθcosθ cos θ 0
2sinθ sinθ cosθ cosθ sinθ cosθ 0
sinθ cosθ 2sinθ cosθ 0
That is,
or
sinθ cosθ 0
2sinθ cosθ 0
or
sinθ cosθ
2sinθ cosθ
or
sinθ
1
cosθ
sinθ 1
cosθ 2
or
tanθ 1
1
tanθ
2
sinθ
tanθ
cosθ
Hence proved.
Question: 5
Given that , then prove that
sinθ 2cosθ 1
.
2sinθ cosθ 2
Solution
Given:
sinθ 2cosθ 1 ...... 1
We have to prove:
2sinθ cosθ 2 ...... 2

Squaring and adding LHS of equations (1) and (2).
2 2
sinθ 2cosθ 2sinθ cosθ
2 2 2 2
sin θ 4cos θ 4sinθcosθ 4sin θ cos θ 4sinθcosθ
2 2
5sin θ 5cos θ
2 2
5 sin θ cos θ
2 2
5 sin θ cos θ 1
Thus,
2 2
sinθ 2cosθ 2sinθ cosθ 5
Put the value of from equation (1).
sinθ 2cosθ
2 2
1 2sinθ cosθ 5
2
2sinθ cosθ 5 1
2
2sinθ cosθ 4
2sinθ cosθ 4
2sinθ cosθ 2
Hence proved.
Question: 6
The angle of elevation of the top of a tower from two
points distant and from its foot are
s
t
complementary. Prove that the height of the tower is
.
st
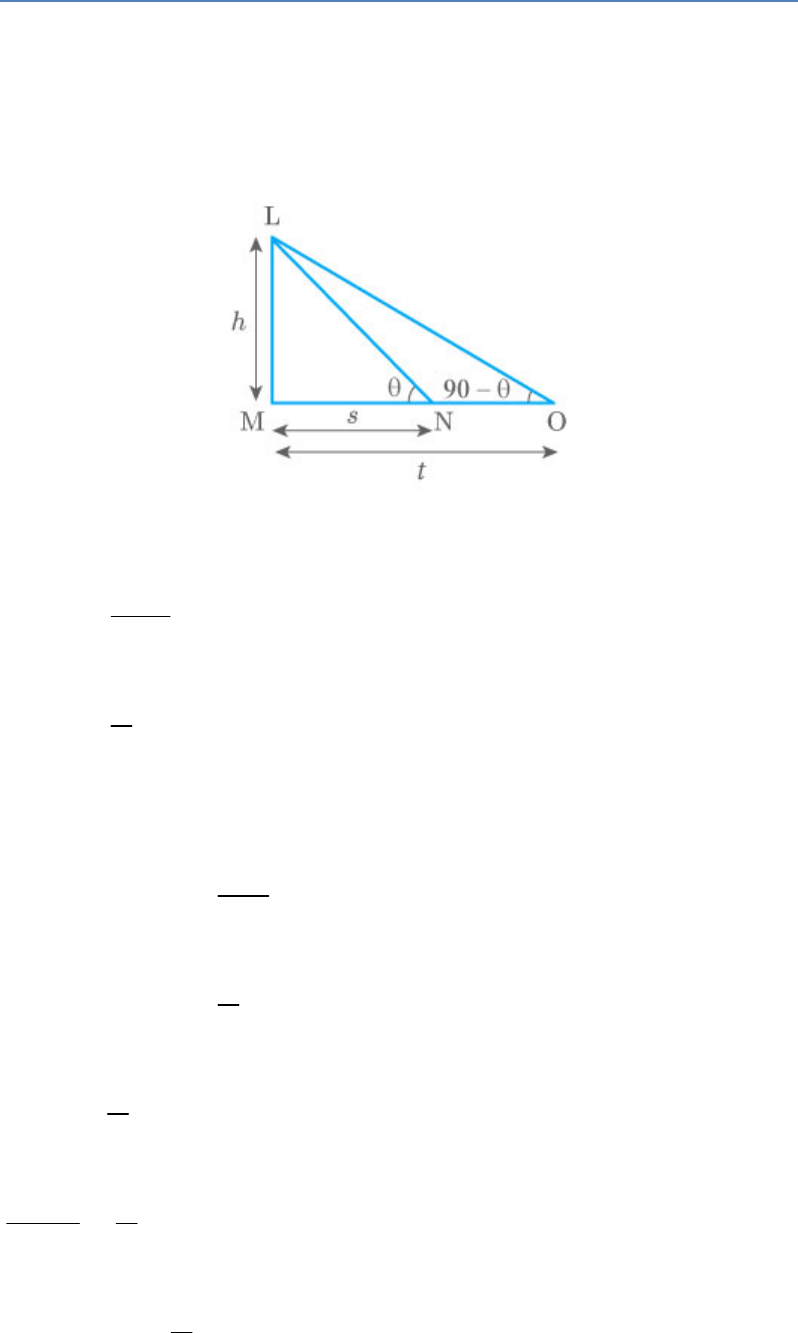
Solution
Let LM be a tower of height and the angle of
h
elevation of the top of the tower from two points
distant and from its foot are and .
s
t
θ
90 θ
In ,
LMN
LM
tanθ
MN
h
tanθ ...... 1
s
In ,
LMO
LM
tan 90 θ
t
h
tan 90 θ
t
h
cot θ tan 90 θ cot θ
t
1 h
tanθ t
Put from equation (1).
h
tanθ
s

1 h
tanθ t
1 h
h
t
s
s h
h t
2
h st
h st
Hence, the height of the tower is .
st
Question: 7
The shadow of a tower standing on a level plane is
found to be 50 m longer when Sun’s elevation is
30
than when it is . Find the height of the tower.
60
Solution
Let LM be a tower of height
h
In ,
LMN
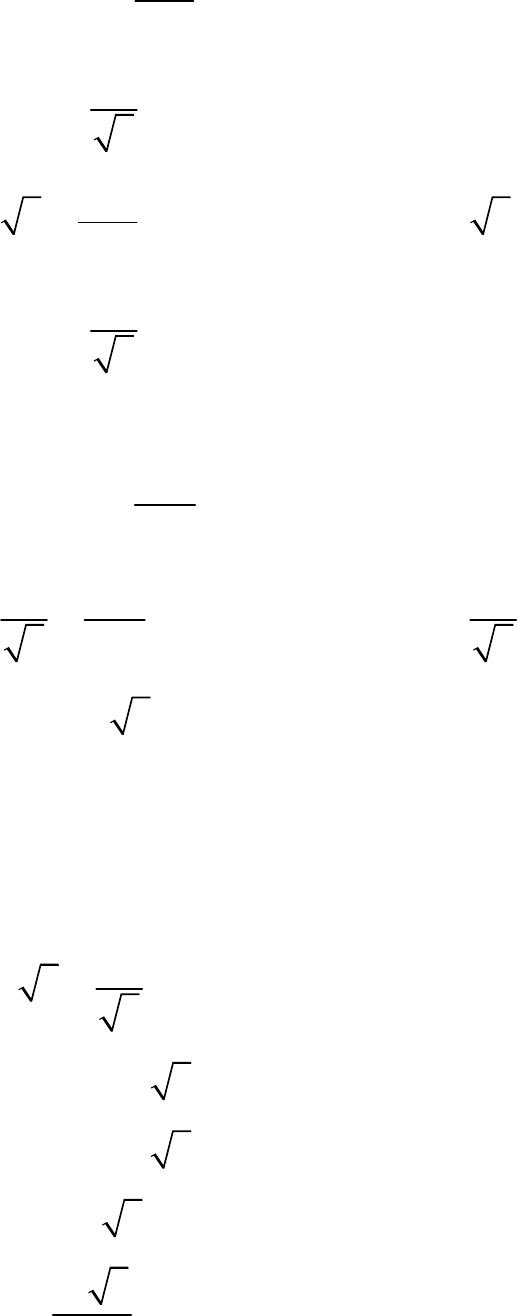
LM
tan60
MN
h
MN
3
h
3 tan60 3
MN
h
MN ...... 1
3
In ,
LMO
LM
tan30
MO
1 h 1
tan30
MO
3 3
MO h 3
From the figure,
MO MN NO
Put the values of MO, MN and NO.
h
h 3 50
3
3h h 50 3
3h h 50 3
2h 50 3
50 3
h
2

h 25 3
Hence, the height of the tower is m.
25 3
Question: 8
A vertical tower stands on a horizontal plane and is
surmounted by a vertical flag staff of height . At a
h
point on the plane, the angles of elevation of the
bottom and the top of the flag staff are and ,
respectively. Prove that the height of the tower is
.
htan
tan tan
Solution
Let MN be a tower of height and LM be a flag staff
x
of height .
h
The angles of elevation of the bottom and the top of
the flag staff are and , respectively.

In ,
MON
MN
tan
ON
x
tan
ON
x
ON ...... 1
tan
In ,
LON
LN
tan
ON
h x
tan
ON
h x
ON ...... 2
tan
From equations (1) and (2).
x h x
tan tan
xtan h x tan
xtan htan xtan
xtan xtan htan
x tan tan htan
htan
x
tan tan

Hence, the height of the tower is .
htan
tan tan
Question: 9
If , then prove that .
tanθ secθ l
2
l 1
secθ
2l
Solution
Given:
tanθ secθ l
tanθ secθ l
sinθ 1
l
cosθ cosθ
1 sinθ
l
cosθ
Squaring on both sides.
2
2
1 sinθ
l
cosθ
2
2
2
1 sinθ
l
cos θ
2
2 2 2
2
1 sinθ
l cos θ 1 sin θ
1 sin θ
2
1 sinθ 1 sinθ
l
1 sinθ 1 sinθ

2
1 sinθ
l
1 sinθ
We have to prove that .
2
l 1
secθ
2l
Take RHS,
2
l 1
2l
Put the value of and .
2
l
l
2
1 sinθ
1
1 sinθ
l 1
1 sinθ
2l
2
cosθ
1 sinθ 1 sinθ
1 sinθ
2 1 sinθ
cosθ
2 cosθ
1 sinθ 2 1 sinθ
2
cosθ
1 sin θ
2 2
2
cosθ
1 sin θ cos θ
cos θ
1
cosθ

1
cosθ
secθ
LHS
Thus, LHS = RHS.
Hence proved.
Question: 10
If and , then prove
sinθ cosθ p
secθ cosecθ q
that .
2
q p 1 2p
Solution
Given:
sinθ cosθ p
Squaring on both sides.
2
2
sinθ cosθ p
2 2 2
sin θ cos θ 2sinθcosθ p
2
1 2sinθcosθ p ...... 1
secθ cosecθ q
1 1
q
cosθ sinθ
sinθ cosθ
q ...... 2
sinθcosθ
We have to prove that .
2
q p 1 2p

Put the values of from equations (1) and (2)
2
p andq
in LHS.
LHS
2
sinθ cosθ
q p 1 1 2sinθcosθ 1
sinθcosθ
sinθ cosθ
2sinθcosθ
sinθcosθ
2 sinθ cosθ
2p sinθ cosθ p
RHS
LHS = RHS
Hence proved.
Question: 11
If , then prove that
asinθ bcosθ c
.
2 2 2
acosθ bsinθ a b c
Solution
Given:
asinθ bcosθ c ...... 1
To prove:
2 2 2
acosθ bsinθ a b c ...... 2
Squaring and adding LHS of equations (1) and (2).
2 2
asinθ bcosθ acosθ bsinθ
2 2 2 2
2 2
2 2
a sin θ b cos θ
2absinθcosθ a cos θ
b sin θ 2absinθcosθ
2 2 2 2 2 2
a sin θ cos θ b sin θ cos θ
2 2 2 2
a b sin θ cos θ 1
Thus,
2 2
2 2
asinθ bcosθ acosθ bsinθ a b
From equation (1), .
asinθ bcosθ c
2
2 2 2
c acosθ bsinθ a b
2
2 2 2
acosθ bsinθ a b c
2 2 2
acosθ bsinθ a b c
Hence proved.
Question: 12
Prove that .
1 secθ tanθ 1 sinθ
1 secθ tanθ cosθ
Solution
To prove:
1 secθ tanθ 1 sinθ
1 secθ tanθ cosθ
LHS

2 2
sec θ tan θ secθ tanθ
1 secθ tanθ
1 secθ tanθ 1 secθ tanθ
secθ tanθ secθ tanθ secθ tanθ
1 secθ tanθ
secθ tanθ 1 secθ tanθ
1 secθ tanθ
secθ tanθ
1 sinθ
cosθ cosθ
1 sinθ
cosθ
RHS
Hence proved.
Question: 13
The angle of elevation of the top of a tower 30 m
high from the foot of another tower in the same
plane is and the angle of elevation of the top of
60
the second tower from the foot of the first tower is
. Find the distance between the two towers and
30
also the height of the other tower.
Solution
Let LM and ON be two towers with angle of
elevations of their tops be and respectively.
30
60
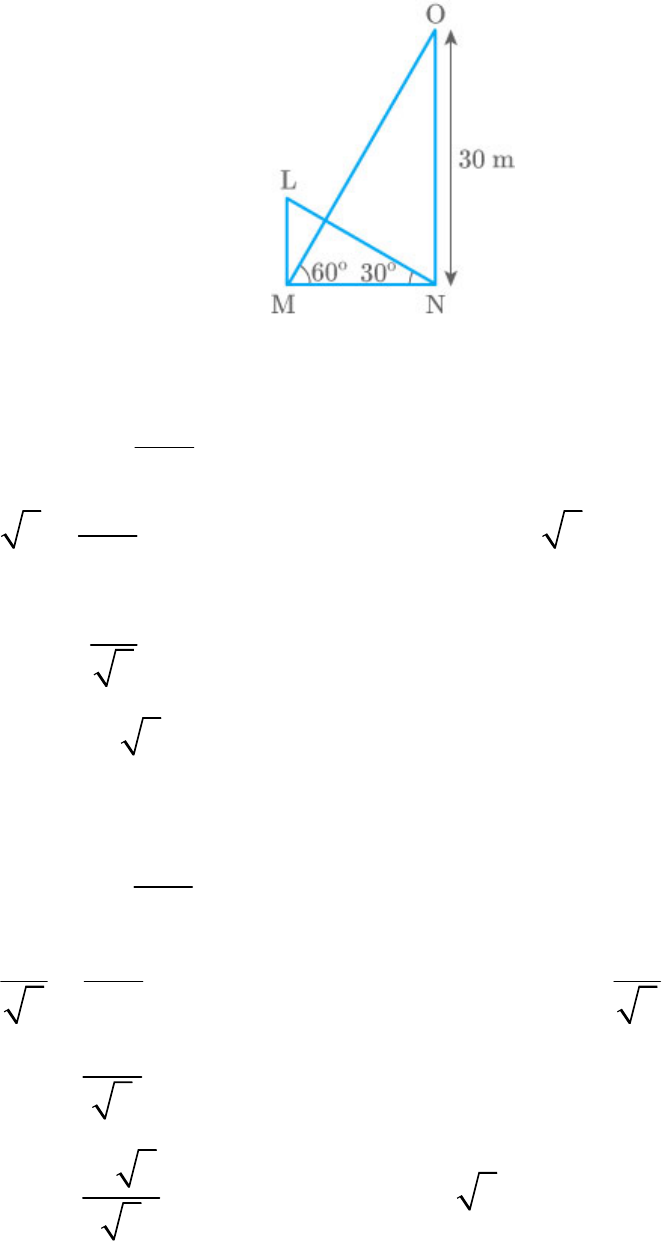
And .
ON 30m
In ,
OMN
ON
tan60
MN
30
3 tan60 3
MN
30
MN
3
MN 10 3
In ,
LMN
LM
tan30
MN
1 LM 1
tan30
MN
3 3
MN
LM
3
10 3
LM MN 10 3
3
LM 10
Hence, the distance between the two towers is
10 3
m and the height of the other tower is 10 m.
Question: 14
From the top of a tower m high, the angles of
h
depression of two objects, which are in line with the
foot of the tower are and . Find the
distance between the two objects.
Solution
Let LM be a tower of height .
h
N and O are two objects and the angles of depression
of the objects from the top of the tower are and
respectively.
Let and .
MN x
NO a
In ,
LMN
LM
tan
MN

h
tan
x
h
x ...... 1
tan
In ,
LMO
LM
tan
MO
h
tan
x a
h
x a ...... 2
tan
Subtract equation (1) from (2).
h h
x a x
tan tan
1 1
h a
tan tan
tan tan
h a
tan tan
tan tan
a h
tan tan
Hence, the distance between the two objects is
.
tan tan
h
tan tan

Question: 15
A ladder rests against a vertical wall at an inclination
to the horizontal. Its foot is pulled away from the
wall through a distance so that its upper end slides
p
a distance down the wall and then the ladder
q
makes an angle to the horizontal. Show that
.
p cos cos
q sin sin
Solution
Let LO be a ladder that rests against vertical wall LN.
at an inclination to the horizontal.
After pulling it away from the wall through a
distance so that its upper end slides a distance
p
q
down the wall, the ladder makes an angle to the
horizontal.
.
LM q and OP p
Let .
LO MP h
In ,
LNO
LN
sin
LO
LN hsin
NO
cos
LO
NO
cos
h
NO hcos
In ,
MNP
MN
sin
MP
MN
sin
h
MN hsin
NP
cos
MP
NP
cos
h
NP hcos
Now, calculate .
p
q
p OP
q LM

p NP NO
q LN MN
p hcos hcos
q hsin hsin
p cos cos
q sin sin
Hence proved.
Question: 16
The angle of elevation of the top of a vertical tower
from a point on the ground is . From another
60
point 10 m vertically above the first, its angle of
elevation is . Find the height of the tower.
45
Solution
Let LP be a tower of height m.
h
NO MP 10m
LM h 10
In ,
LPO
LP
tan60
PO
h
3 tan60 3
PO
… (1)
h
PO
3
In ,
LMN
LM
tan45
MN
h 10
1 tan45 1
MN
MN h 10
From the figure, .
MN PO
Thus,
PO h 10 ...... 2
Equating equations (1) and (2).
h
h 10
3
h h 3 10 3
h 3 1 10 3
10 3
h
3 1
Multiply numerator and denominator by .
3 1

10 3 3 1
h
3 1 3 1
30 10 3
h
3 1
30 10 3
h
2
h 15 5 3
Hence, the height of the tower is m.
15 5 3
Question: 17
A window of a house is metres above the ground.
h
From the window, the angles of elevation and
depression of the top and the bottom of another
house situated on the opposite side of the lane are
found to be and respectively. Prove that the
height of the other house is metres.
h 1 tan cot
Solution
Let the window is situated at point L and the angles
of elevation and depression of the top and the
bottom of another house PN be and
respectively.
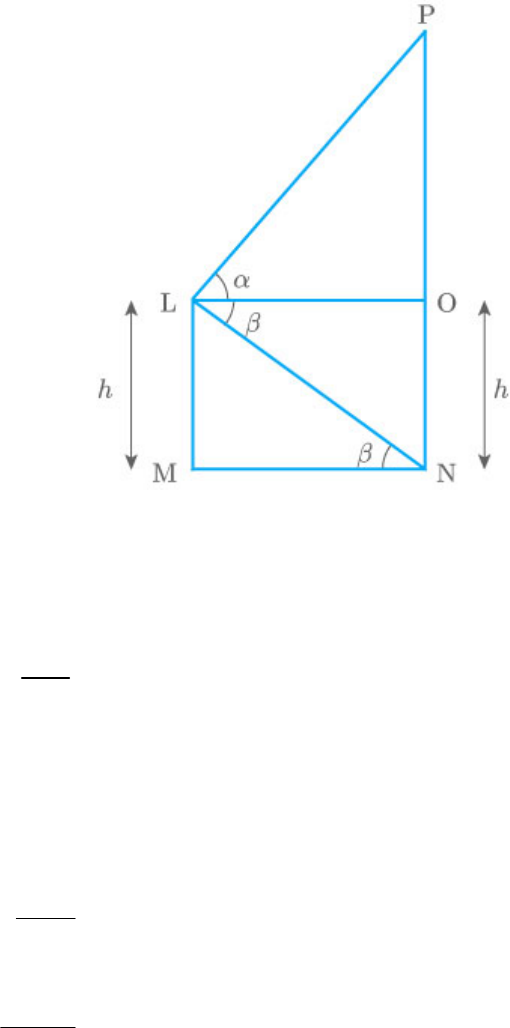
LM ON h
In ,
PLO
PO
tan
LO
PO LOtan ...... 1
In ,
LMN
LM
tan
MN
h
MN
tan
MN hcot ...... 2
From the figure, .
MN LO
Thus,
LO hcot
Put this value in equation (1).
PO LOtan

PO hcot tan ...... 3
From the figure,
PN PO ON
PN PO h
Put the value of PO from equation (3).
PN PO h
PN hcot tan h
PN h 1 tan cot
Thus, the height of the other house is
metres.
h 1 tan cot
Question: 18
The lower window of a house is at a height of 2 m
above the ground and its upper window is 4 m
vertically above the lower window. At certain instant,
the angles of elevation of a balloon from these
windows are observed to be and respectively.
60
30
Find the height of the balloon above the ground.
Solution
Let Q be the lower window and R be the upper
window.
Let .
LM x m
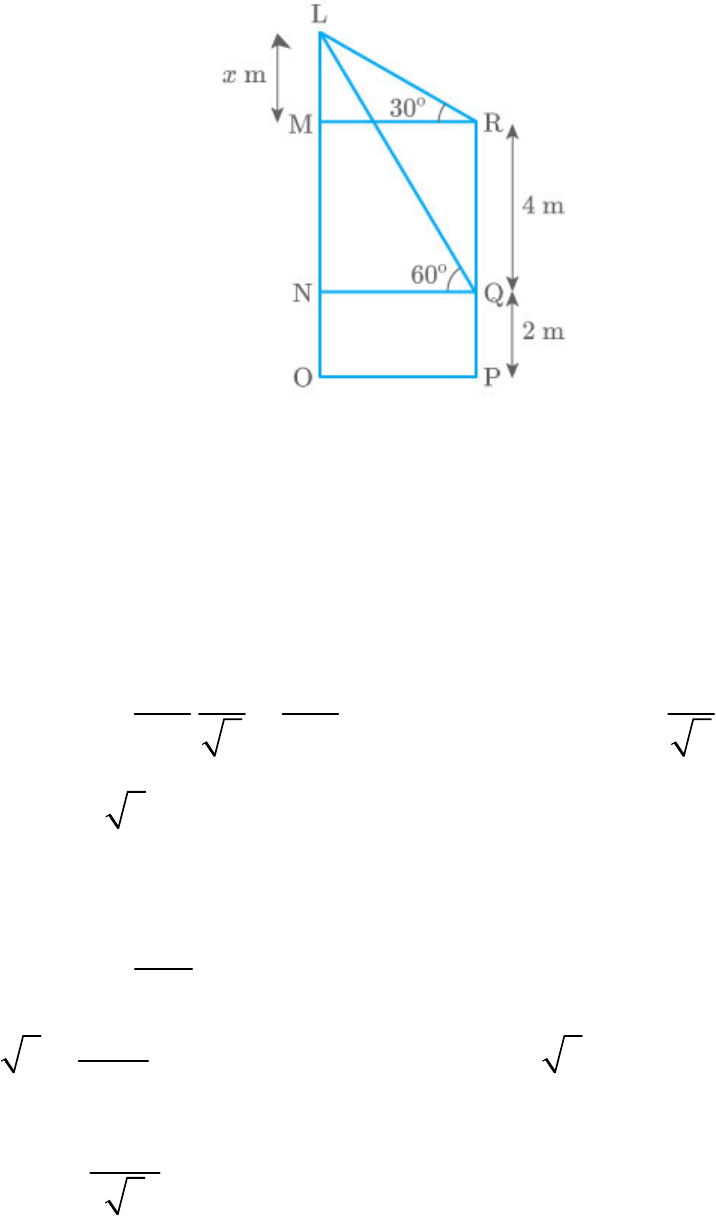
From the figure,
MN RQ 4m
NO QP 2m
In ,
LMR
LM
tan30
MR
1 x 1
tan30
MR
3 3
MR x 3 ...... 1
In ,
LNQ
LN
tan60
NQ
x 4
3 tan60 3
NQ
x 4
NQ ...... 2
3
From the figure, .
MR NQ
From equations (1) and (2).
x 4
x 3
3
3x x 4
2x 4
x 2
The height of the balloon above the ground
LM MN NO
x 4 2
2 4 2
8
Thus, the height of the balloon above the ground is 8
m.