Lesson: Triangles
Exercise 6.1 (12)
Choose the correct answer from the given four options:
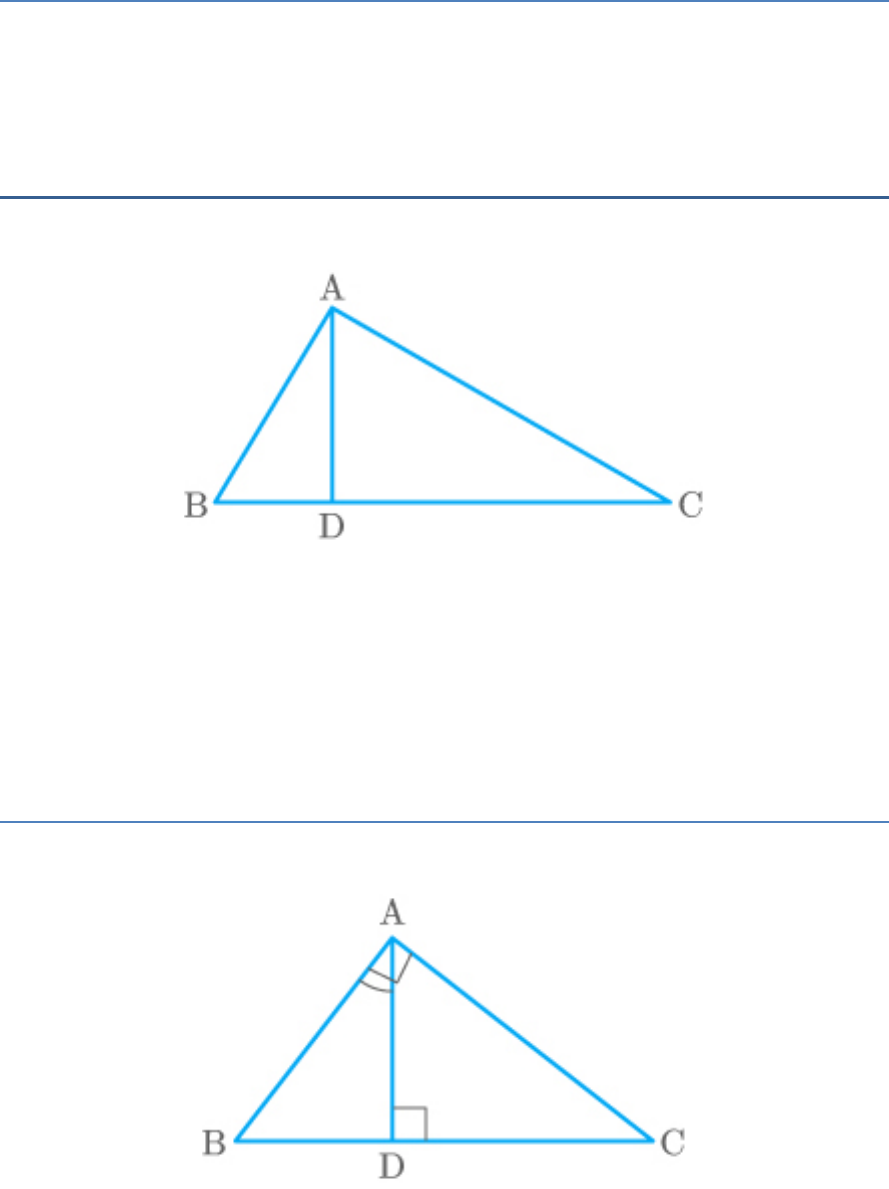
Question: 1
In the adjoining figure, and AD BC. Then,
BAC 90
a.
2
BD.CD BC
b.
2
AB.AC BC
c.
2
BD.CD AD
d.
2
AB.AC AD
Solution:
(c)
In and ,
ADC
ADB

BDA ADC 90
B DAC 90 C
[by AA similarity criteria]
ADB|| CDA
Since, the triangles are similar the ratio of their
corresponding sides will be equal.
AD AB DB
CD CA DA
That is,
AD DB
CD DA
2
AD BD.DC
Hence, proved.
Question: 2
The lengths of the diagonals of a rhombus are 16 cm and 12
cm. Then, the length of the side of the rhombus is
a.
9 cm
b.
10 cm
c.
8 cm
d.
20 cm
Solution:
(b)
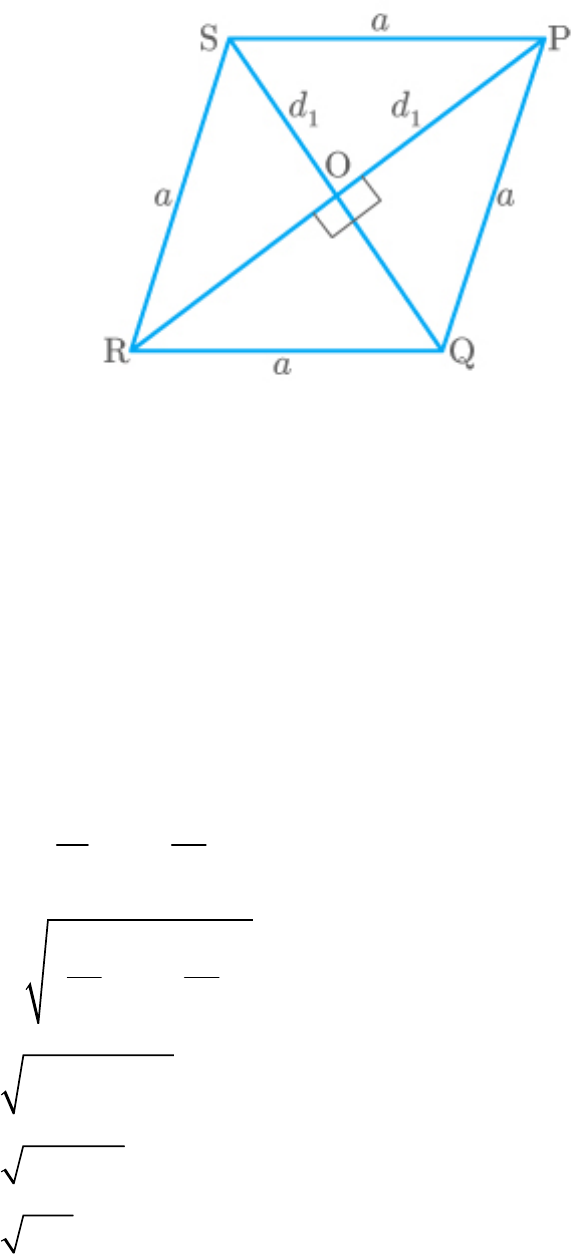
Let, be the side of the rhombus.
a
The diagonals of the rhombus are and .
1
d 12 cm
2
d 16 cm
Diagonals of rhombus intersect each other at . Therefore,
90
is a right-angled triangle.
OPQ
Applying Pythagoras theorem,
2 2 2
PQ OQ OP
2 2
2
1 2
d d
a
2 2
2 2
12 16
a
2 2
2 2
6 8
36 64
100
10 cm
Hence, the side of the rhombus is .
10 cm

Question: 3
If and is not similar to , then
ABC|| EDF
ABC
DEF
which of the following is not true?
a.
BC.EF AC.FD
b.
AB.EF AC.DE
c.
BC.DE AB.EF
d.
BC.DE AB.FD
Solution:
(c)
Given: Similar triangles have similar
ABC|| EDF
corresponding sides.
So,
ABC|| EDF
AB AC BC
ED EF DF
By the equalities,
AB AC
ED EF
AB.EF AC.DE
AC BC
EF DF
AC.FD BC.EF
AB BC
ED DF
BC.DE AB.FD
BC.DE AB.EF
Hence, option C is incorrect.
Question: 4
If in two triangles ABC and PQR, , then
AB BC CA
QR PR PQ
a.
PQR|| CAB
b.
PQR|| ABC
c.
CBA|| PQR
d.
BCA|| PQR
Solution:
(a)
Compare the corresponding vertex of the two triangles.
Vertex A corresponds to vertex Q, vertex P corresponds to
vertex C and vertex R corresponds to vertex B.
Therefore, .
PQR|| CAB
Hence, option A is correct.
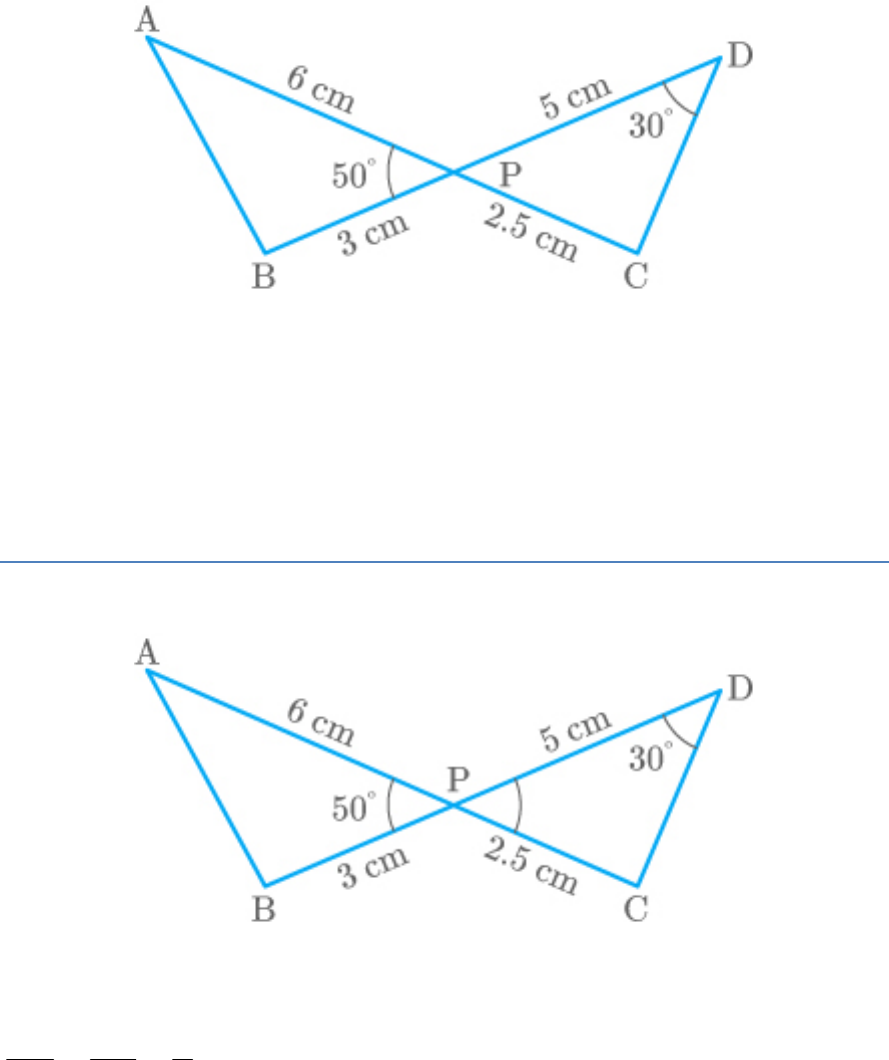
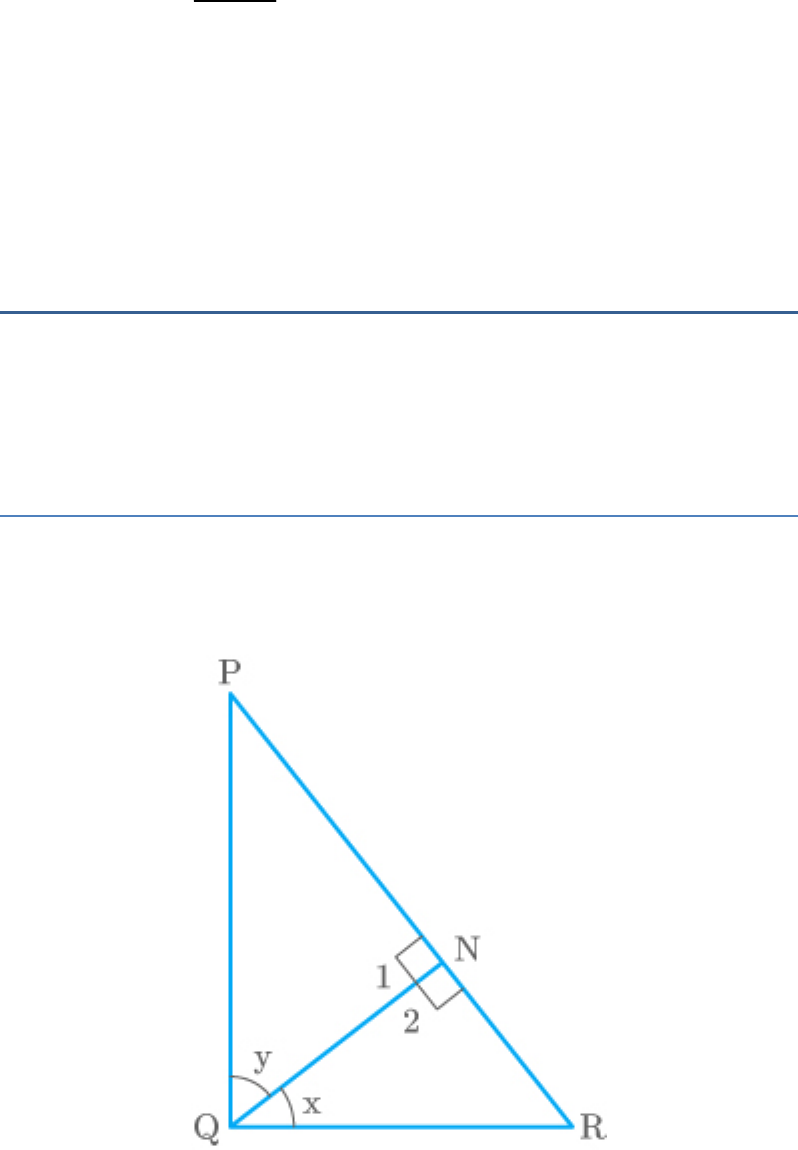
Question: 5
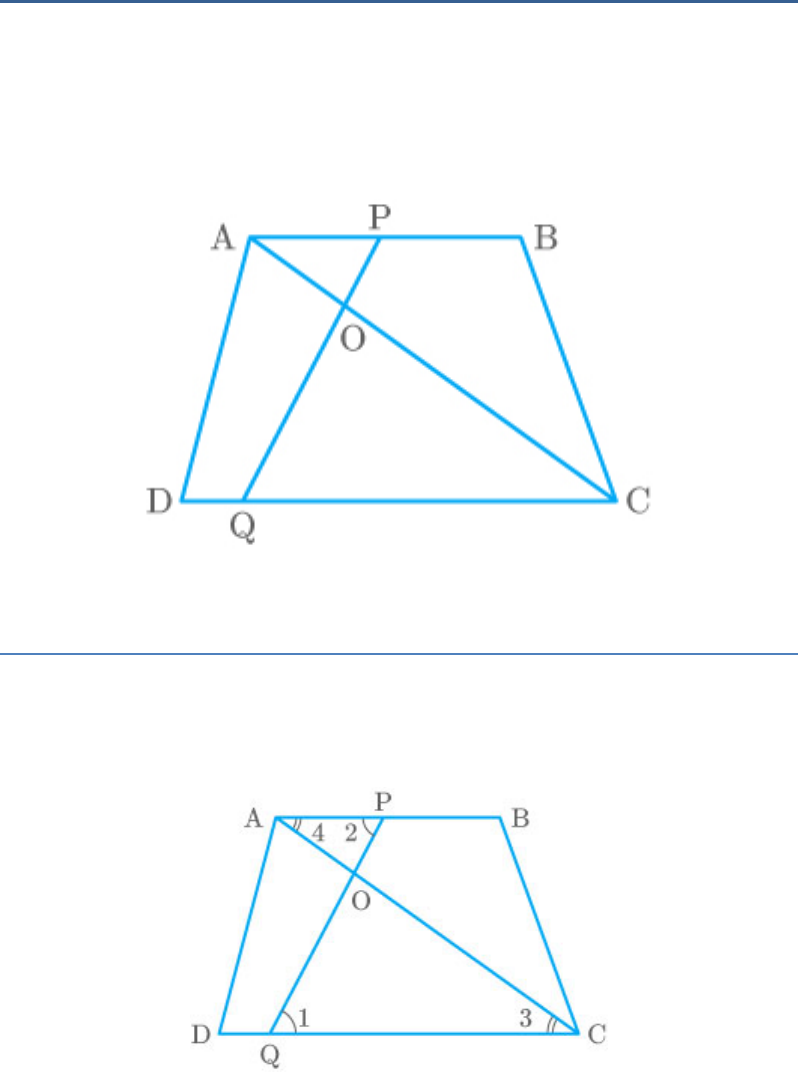
In the adjoining figure, two line segments AC and BD
intersect each other at the point P such that PA = 6 cm, PB =
3 cm, PC = 2.5 cm, PD = 5 cm, = and =
APB
50
CDP
. Then, is equal
30
PBA
a.
50
b.
30
c.
60
d.
100
Solution:
(d)
From and ,
APB
PDC
PA PB 6
PD PC 5
Also, [vertically opposite
APB DPC 50
angles]
[By SAS similarity criterion]
APB|| DPC
Since, angles corresponding to similar triangles are equal,
PBA PCD

PDC 30
Sum of angles of a triangle is
180
In
PDC,
PCD DPC PDC 180
PCD 50 30 180
PCD 180 80
PCD 100
So,
PCD PBA 100
Hence, option D is correct.
Question: 6
If in two triangles DEF and PQR, and
D Q
R E
then which of the following is not true?
a.
EF DF
PR PQ
b.
DE EF
PQ RP
c.
DE DF
QR PQ
d.
EF DE
RP QR
Solution:
(b)

In and ,
DEF
PQR
=
D Q
R E
[AA similarity rule]
DEF|| PQR
So,
DE DF EF
QR PQ RP
Which implies , and .
EF DF
RP PQ
DE DF
QR PQ
DE DF
QR PQ
Thus, option B is incorrect.
Question: 7
In triangles ABC and DEF, , and AB = 3
B E
F C
DE. Then, the two triangles are
a. congruent but not similar
b. similar but not congruent
c. neither congruent nor similar
d. congruent as well as similar
Solution:

(b)
Given: AB = 3DE and
B Eand C F
[AA similarity criterion]
ABC|| EDF
But AB = 3DE, which implies that the sides of both the
triangles are not equal.
Hence, they are not congruent.
Thus, both are similar but not congruent.
Question: 8
It is given that ,with . Then,
ABC|| PQR
BC 1
QR 3
is equal to
ar PRQ
ar BCA
a. 9
b. 3
c.
1
3
d.
1
9
Solution:

(a)
Given:
BC 1
QR 3
Ratio of areas of similar triangle,
2
2
ar PRQ
QR
ar BCA BC
That is,
2
2
ar PRQ
QR
ar BCA BC
2
2
3
1
9
1
Hence, option A is correct.
Question: 9
It is given that , , AB = 5
ABC|| DFE
A 30
C 50
cm, AC = 8 cm and DF= 7.5 cm. Then, the following is true:
a.
DE 12 cm,
F 50
b.
DE 12 cm,
F 100
c.
EF 12 cm,
D 100
d.
EF 12 cm,
D 30
Solution:
(b)
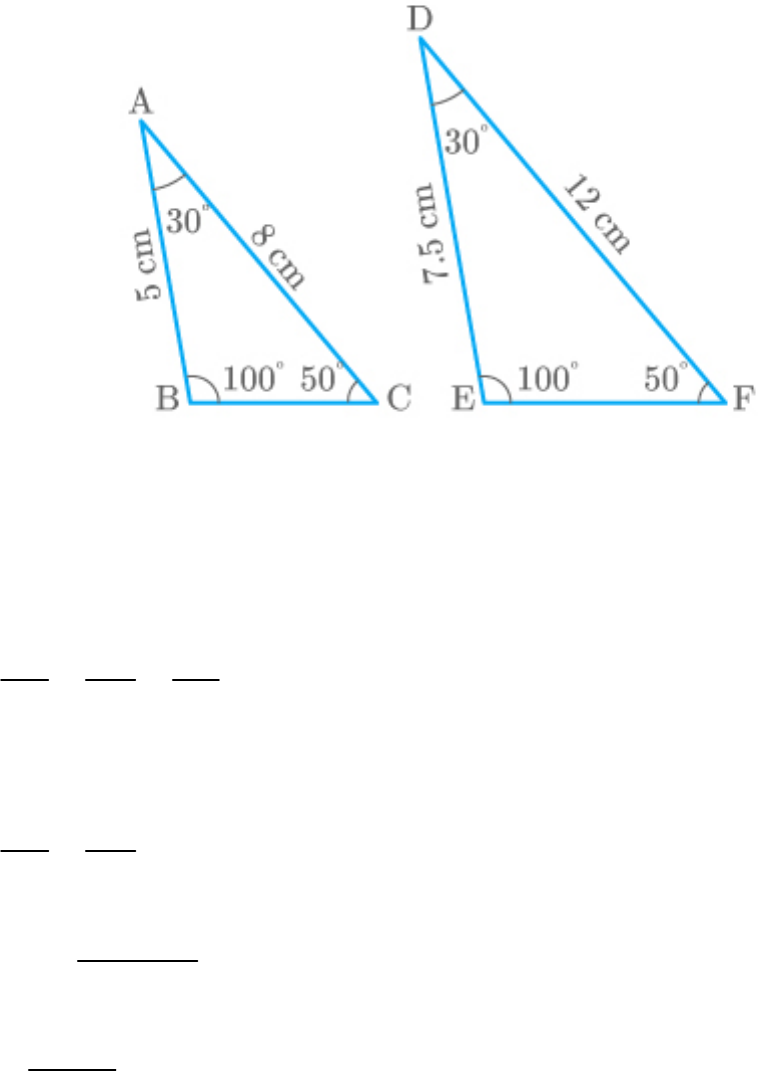
Given: , AB = 5 cm, AC = 8 cm and
A 30
C 50
DF= 7.5 cm
Since, ,
ABC|| DEF
AB AC BC
DF DE FE
AB = 5 cm, AC = 8 cm and DF = 7.5 cm.
AB AC
DF DE
AC DF
DE
AB
8 7.5
5
12 cm
A D 30
C E 50
F 180 50 30
100
Thus,
B F 100
Hence, option B is correct.
Question: 10
If in triangles ABC and DEF, , then they will be
AB BC
DE FD
similar, when
a.
B E
b.
A D
c.
B D
d.
A F
Solution:
(c)
In and ,
ABC
EFD
AB BC
DE FD
AB and BC formed an angle B.
DE and FD formed an angle D.
B D
Both the triangles will be similar by SAS similarity rule.

Hence, option C is correct.
Question: 11
If , , AB = 18 cm and BC = 15
ABC QRP
ar ABC
9
ar PQR 4
cm, then PR is equal to
a. 10 cm
b. 12 cm
c. cm
20
3
d. 8 cm
Solution:
(a)
Given: AB = 18 cm, BC = 15 cm and
ar ABC
9
ar PQR 4
Since, ,
ABC|| QRP
2 2
2 2
ar ABC
BC AB
ar PQR RP QR
2 2
2 2
9 15 18
4 RP QR
2
2
9 15
4 RP

2
15 4
RP
9
15 15 4
9
100
10 cm
Hence, PR is equals to .
10 cm
Question: 12
If S is a point on side PQ of a such that
PQR
PS = QS = RS, then
a.
2
PR.QR RS
b.
2 2 2
QS RS QR
c.
2 2 2
PR QR PQ
d.
2 2 2
PS RS PR
Solution:
(c)
In ,
PQR
PS = QS = RS

In , PS = RS,
PSR
Since, angle opposite to equal sides are equal.
P 1
Similarly, In , QS = RS,
SQR
Q 2
Now, in ,
PQR
P Q R 180
1 2 1 2 180
1 2 90
PRQ 90
Thus, is a right-angled triangle.
PQR
By applying Pythagoras theorem,
2 2 2
PQ PR RQ
Thus, option C is correct.
Exercise 6.2 (12)
Question: 1
Is the triangle with sides 25 cm, 5 cm and 24 cm a right
triangle? Give reasons for your answer.
Solution:
A triangle is a right-angled triangle if it follows Pythagoras
theorem.

Let, AB = 24 cm, BC = 5 cm and CA = 25 cm be the sides of
the triangle.
By applying Pythagoras theorem,
2 2 2
AC AB BC
2 2 2
25 5 24
625 25 576
625 601
Since, Pythagoras theorem is not followed, the given triangle
is not a right-angled triangle.
Question: 2
It is given that . Is it true to say that
DEF|| RPQ
D R
and ? Why?
F P
Solution:
Since, , all the corresponding angles of both
DEF|| RPQ
triangles are equal.
D R
E P
F Q
Hence, is true but
D R
F P
Question: 3
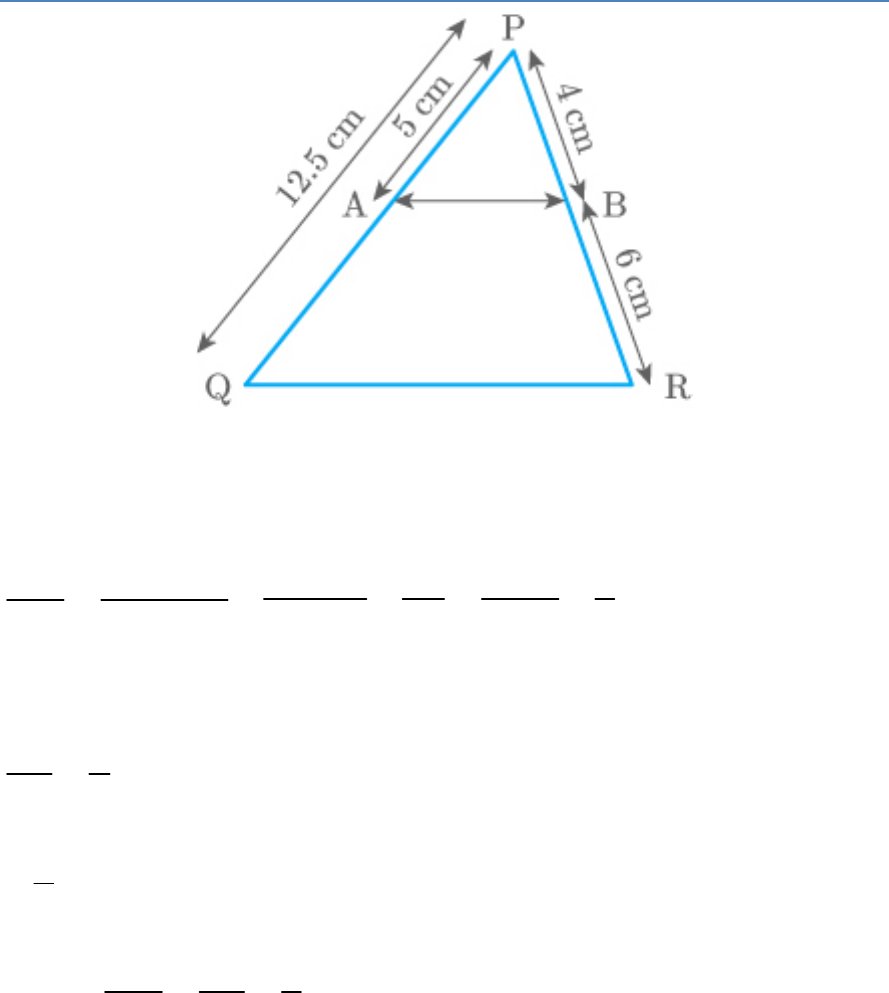
A and B are respectively the points on the sides PQ and PR
of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR =
6 cm and PB = 4 cm. Is ?
AB||QR
Give reasons for your answer.
Solution:
According to the converse of basic proportionality theorem,
AB || QR if AB divides PQ and PR in the same ratio.
PA PA
AQ PQ AP
5
12.5 5
5
7.5
5 10
75
2
3
PB 4
BR 6
2
3
Since, ,
PA PB 2
AQ BR 3
AB||QR
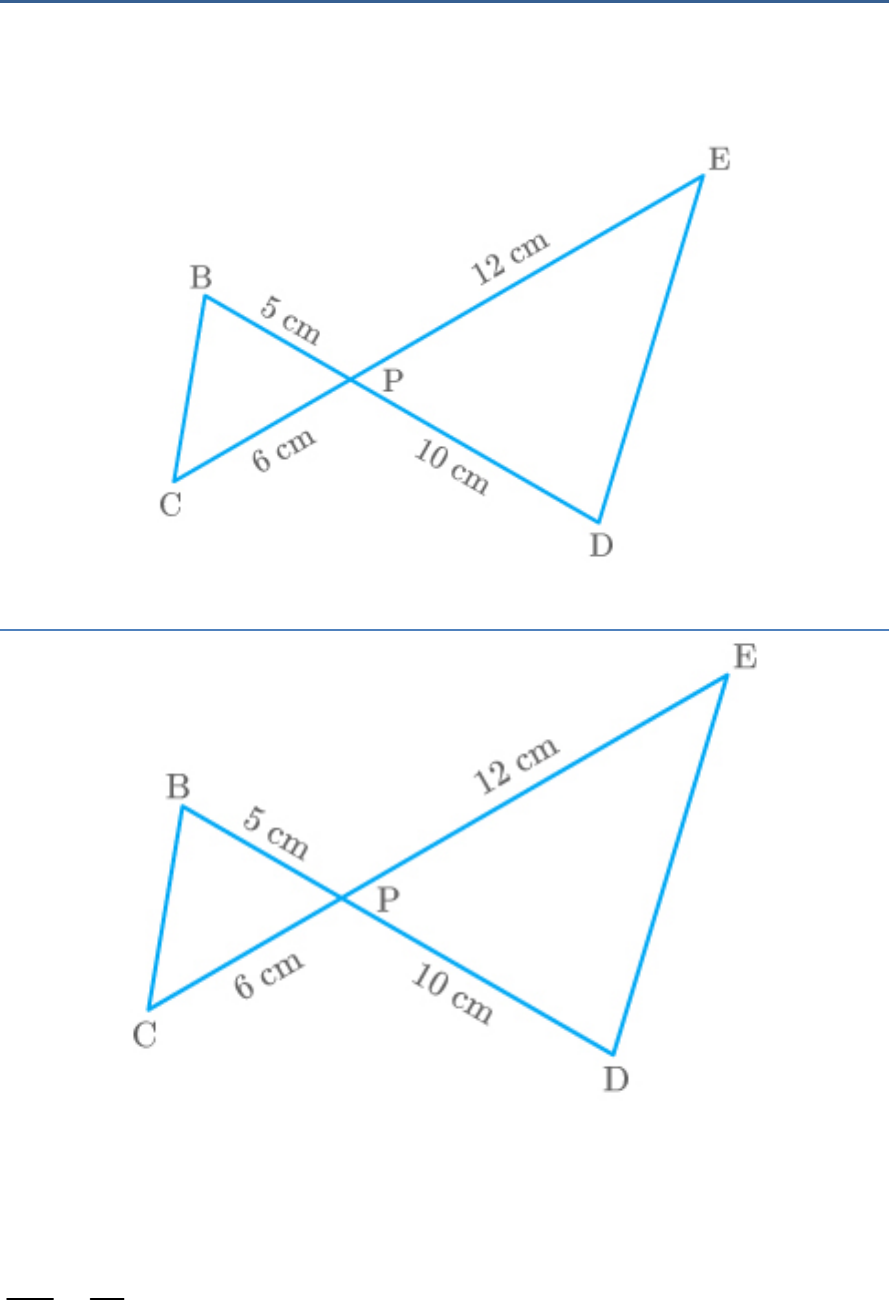
Question: 4
In the adjoining figure, BD and CE intersect each other at
the point P. Is ? Why?
PBC|| PDE
Solution:
In , [Vertically opposite
PBC and PDE
BPC DPE
angles]
BP 5
PD 10

1
2
PC 6
PE 12
1
2
So,
BP PC
PD PE
Thus, [By SAS similarity rule]
PBC|| PDE
Hence, the given statement is correct.
Question: 5
In triangles PQR and MST, , ,
P 55
Q 25
M 100
and . Is ? Why?
S 25
PQR|| TSM
Solution:
In , and
PQR
P 55
= 25 Q

+ + = 180 P R Q
55 + + 25 = 180 R
= 180 55 25 R
= 100 R
Similarly, in ,
TSM
M 100
S 25
T S M 180
T 180 100 25
T 55
Since,
P S
Q T
is not similar to .
PQR
TSM
Question: 6
Is the following statement true? Why?
“Two quadrilaterals are similar, if their corresponding angles
are equal”.
Solution:
False.
Two quadrilaterals will be similar if their angles as well as
ratio of their corresponding sides will be equal.
Question: 7
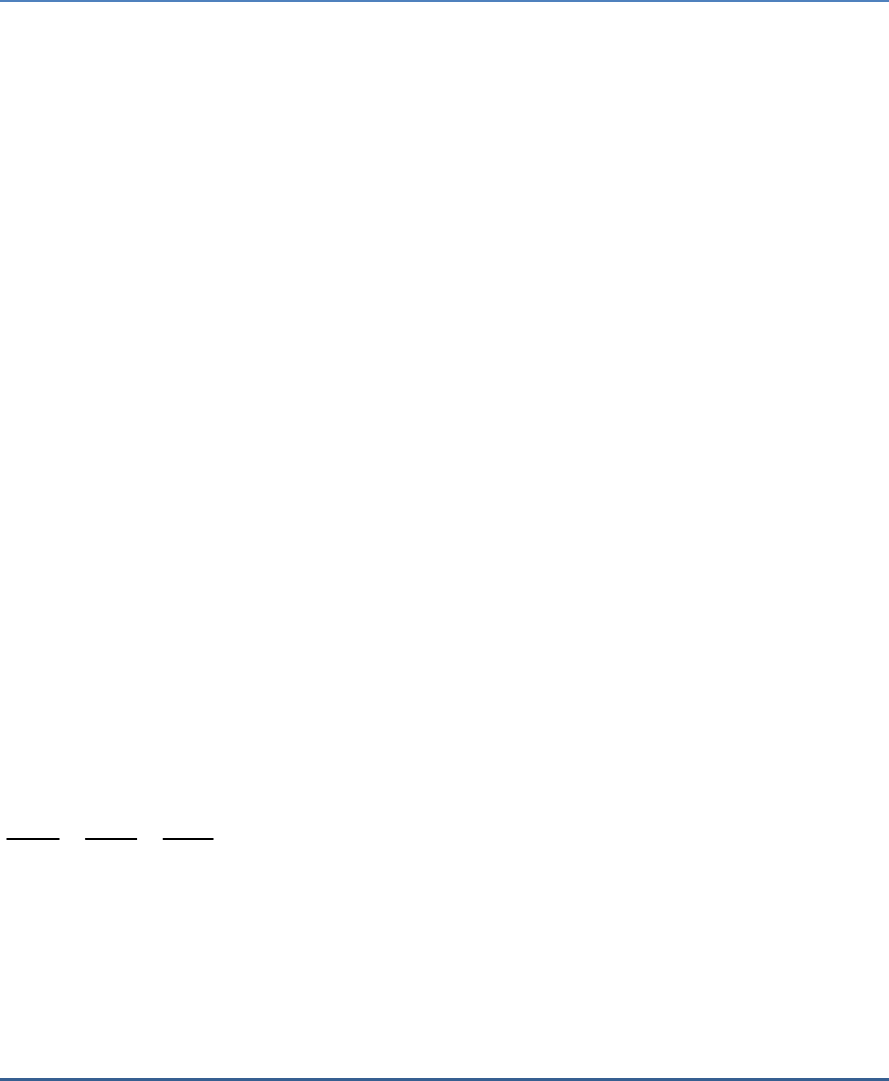
Two sides and the perimeter of one triangle are respectively
three times the corresponding sides and the perimeter of the
other triangle. Are the two triangles similar? Why?
Solution:
Let the two triangles be and .
ABC
PQR
In ,
ABC
Let the sides be AB, BC and CA.
Then the perimeter of ,
ABC
1
p AB BC CA
Similarly, in ,
PQR
Let the sides be PQ, QR and RP.
And the perimeter will be given by
2
p PQ QR RP
PQ 3 AB
QR 3 BC
2 1
p 3 p
PQ QR RP 3 AB BC CA
3 AB 3 BC RP 3 AB+3 BC+3 CA
RP 3 CA
AB BC CA
= = 3
PQ QR RP
Hence, [By SSS similarity criterion]
ABC|| PQR
Question: 8
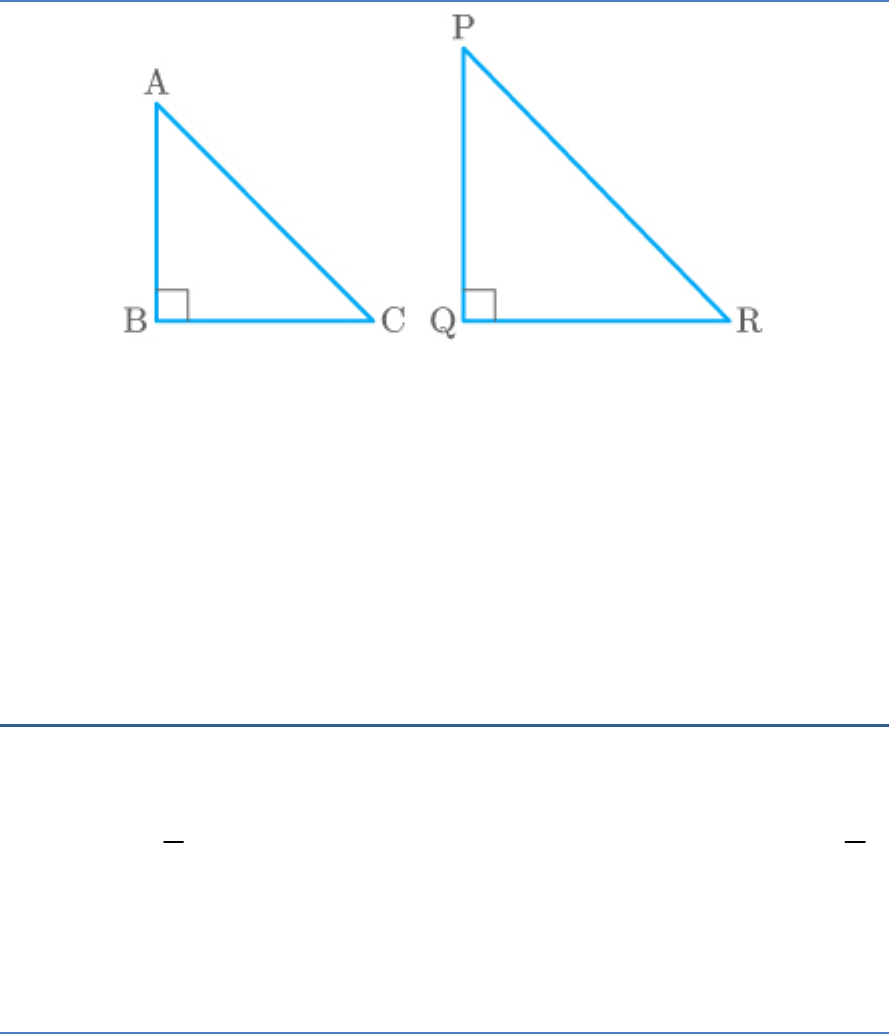
If in two right triangles, one of the acute angles of one
triangle is equal to an acute angle of the other triangle, can
you say that the two triangles will be similar? Why?
Solution:
and are right angled triangles.
ABC
PQR
B Q 90
C R
Thus, and the given statement is true.
ABC|| PQR
Question: 9
The ratio of the corresponding altitudes of two similar
triangles is . Is it correct to say that ratio of their areas is
3
5
6
5
? Why?
Solution:
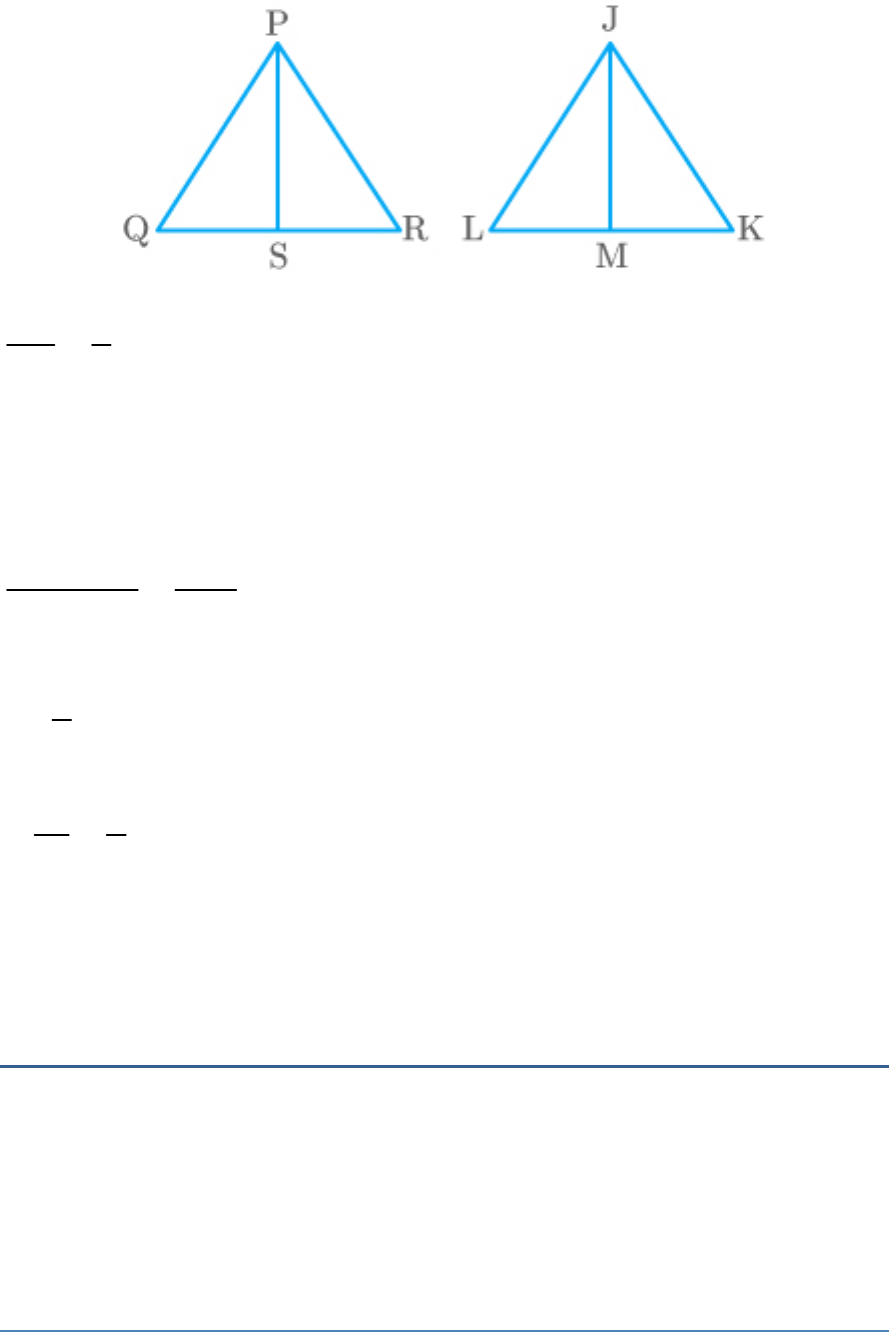
PS 3
JM 5
Ratio of areas of the two similar triangles PQR and
JKL can be given by,
2
2
ar PQR
PS
ar JKL JM
2
3
5
9 6
25 5
Hence, the above statement is not correct.
Question: 10
D is a point on side QR of such that
PQR
PD QR. Will it be correct to say that ?
PQD RPD:
Why?
Solution:
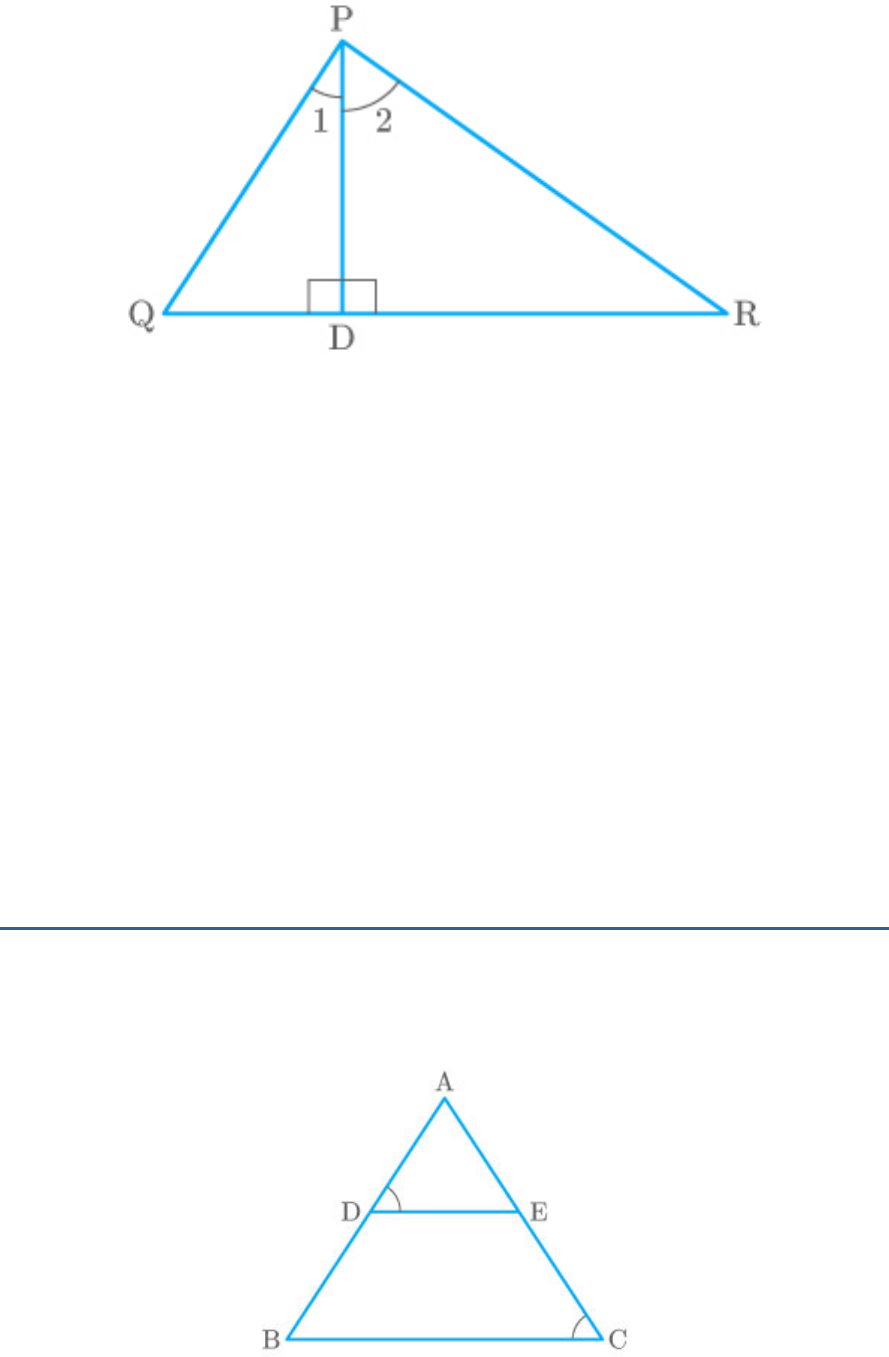
In and ,
PQD
PDR
[ ]
PDR PDQ 90
PD QR
[PD does not bisect ]
1 2
P
[PQ QR]
Q R
Ratio of sides are also not equal.
Hence, is not similar to and the above
PQD
PDR
statement is false.
Question: 11
In the adjoining figure, if , then is it true that
D C
? Why?
ADE|| ACB

Solution:
In and ,
ADE
ABC
D C
A A
Hence, [By AA similarity criterion]
ADE ABC:
Hence, the above statement is true.
Question: 12
Is it true to say that if in two triangles, an angle of one
triangle is equal to an angle of another triangle and two sides
of one triangle are proportional to the two sides of the other
triangle, then the triangles are similar? Give reasons for your
answer.
Solution:
The ratio of two sides of the triangles are proportional to
each other but the angle corresponding to those sides is not
included.
Hence, the given statement is false.
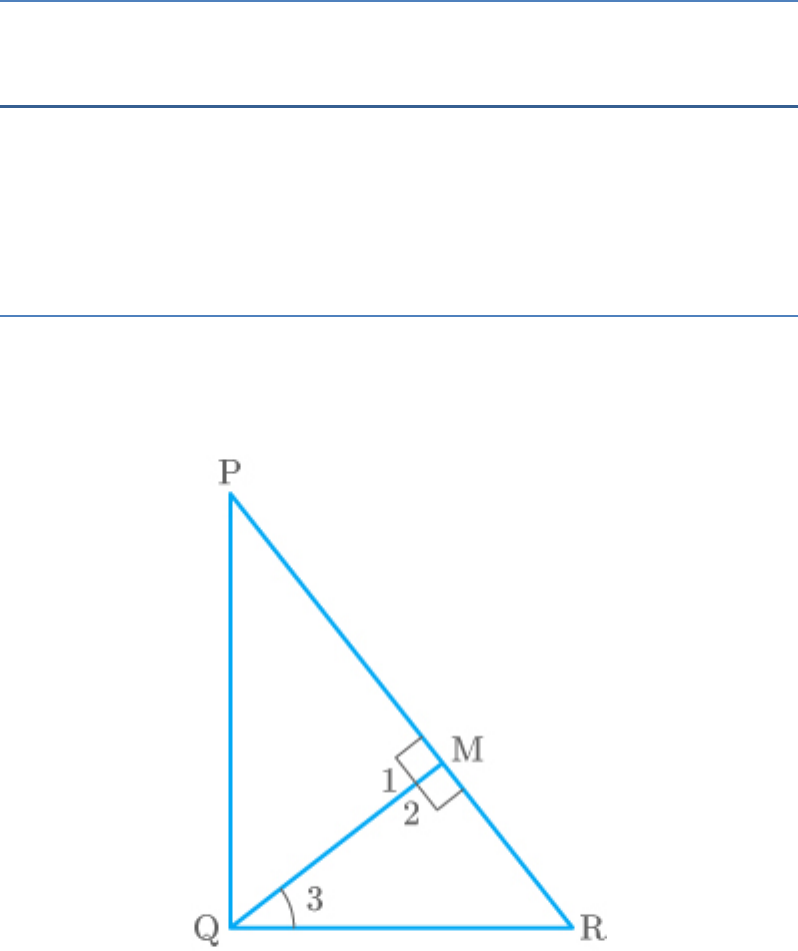
Exercise 6.3 (15)
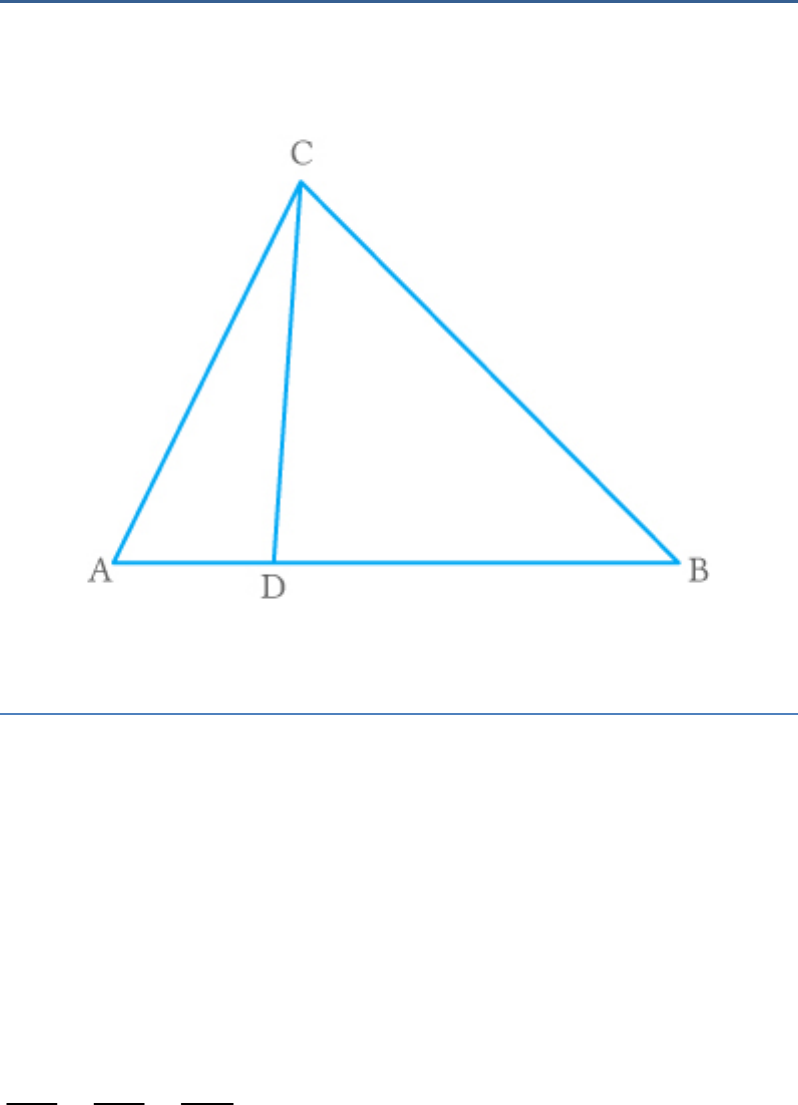
Question: 1
In a PQR, and M is a point on side
2 2 2
PR – PQ QR
PR such that QM PR. Prove that .
2
QM PM MR
Solution
Given: A PQR such that .
2 2 2
PR – PQ QR
And M is a point on side PR such that QM PR.
To Prove:
2
QM PM MR
Proof:
In ,
PQR
2 2 2
PR – PQ QR
2 2 2
PR PQ QR
By the converse of Pythagoras theorem,

PQR 90
In triangles QMP and QMR,
QM PR
Thus,
1 2 90
We know that the sum of all the interior angles in a
triangle is .
180
Thus,
2 3 R 180
90 3 R 180
3 90 R ......(1)
Similarly,
P 90 R ......(2)
From equations (1) and (2),
3 P
Thus,
QMP|| QMR
PM QM
QM MR
2
QM PM MR
Hence proved.
Question: 2
Find the value of for which DE||AB in the given
x
figure.
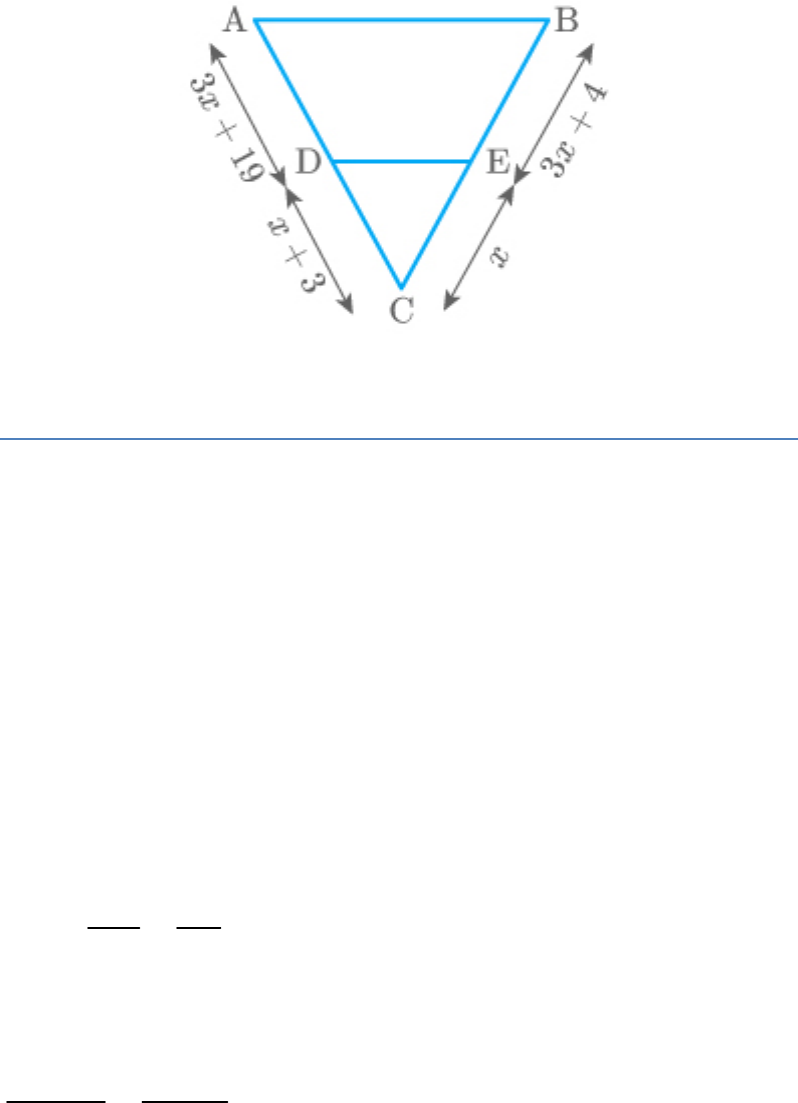
Solution
Given: A triangle ABC in which DE||AB.
From the figure,
AD 3x 19
DC x 3
BE 3x 4
EC x
In , DE||AB.
ABC
Thus,
AD BE
DC EC
Put the values of and .
AD,DC,BE
EC
3x 19 3x 4
x 3 x
x 3x 19 x 3 3x 4
2 2
3x 19x 3x 4x 9x 12
2 2
3x – 3x 19x–13x 12
6x 12
x 2
Thus, the value of is 2.
x
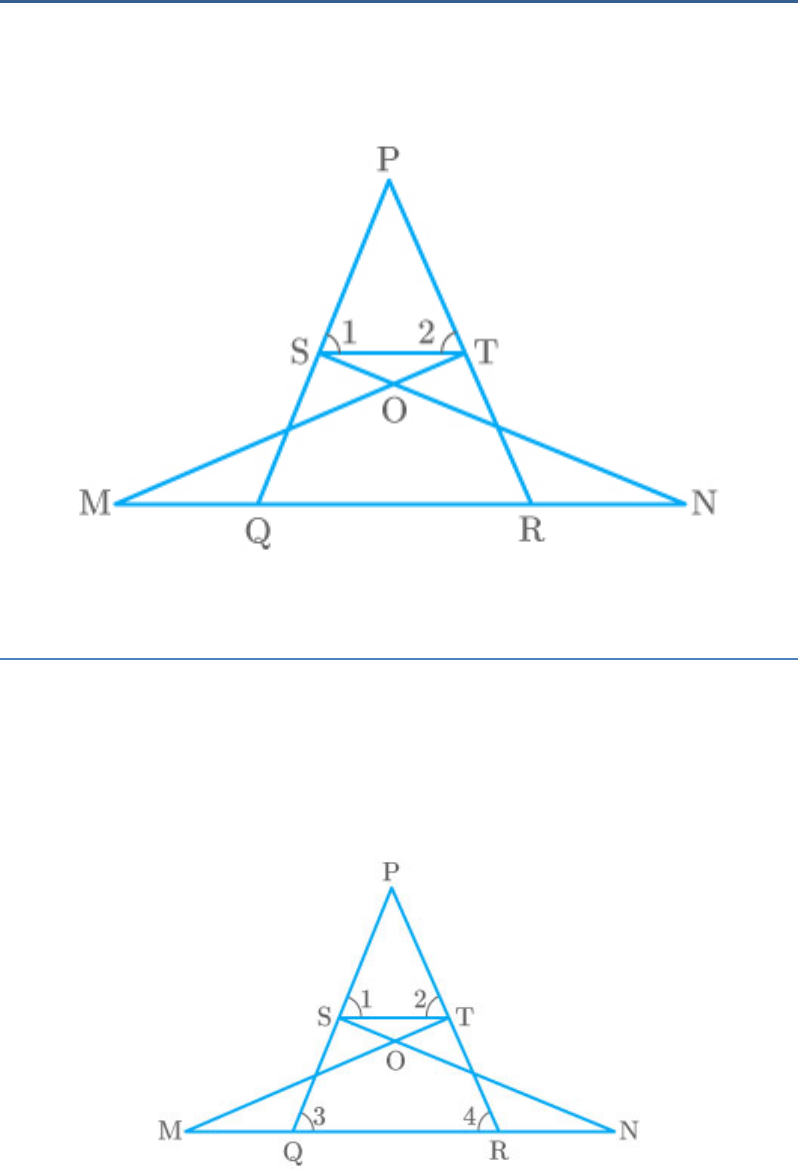
Question: 3
In the adjoining figure, if and
1 2
, then prove that .
NSQ MTR
PTS|| PRQ
Solution
Given: A in which points S and T are on PQ
PQR
and PR respectively such that
1 2
Also,
NSQ MTR
To Prove:
PTS|| PRQ

Proof:
NSQ MTR
Thus, … (1)
SQ TR By CPCT
1 2
We know that the sides opposite to equal angles in a
triangle are equal.
Thus, … (2)
PT PS
From equations (1) and (2),
PT PS
TR SQ
Thus, by the converse of BPT,
ST||QR
In triangles PTS and PRQ,
ST||QR
1 3
Corresponding angles
2 4
Corresponding angles
Thus,
PTS|| PRQ
Hence proved.
Question: 4
Diagonals of a trapezium PQRS intersect each other at
the point O, PQ RS and . Find the ratio of
:
PQ 3RS
the areas of triangles POQ and ROS.
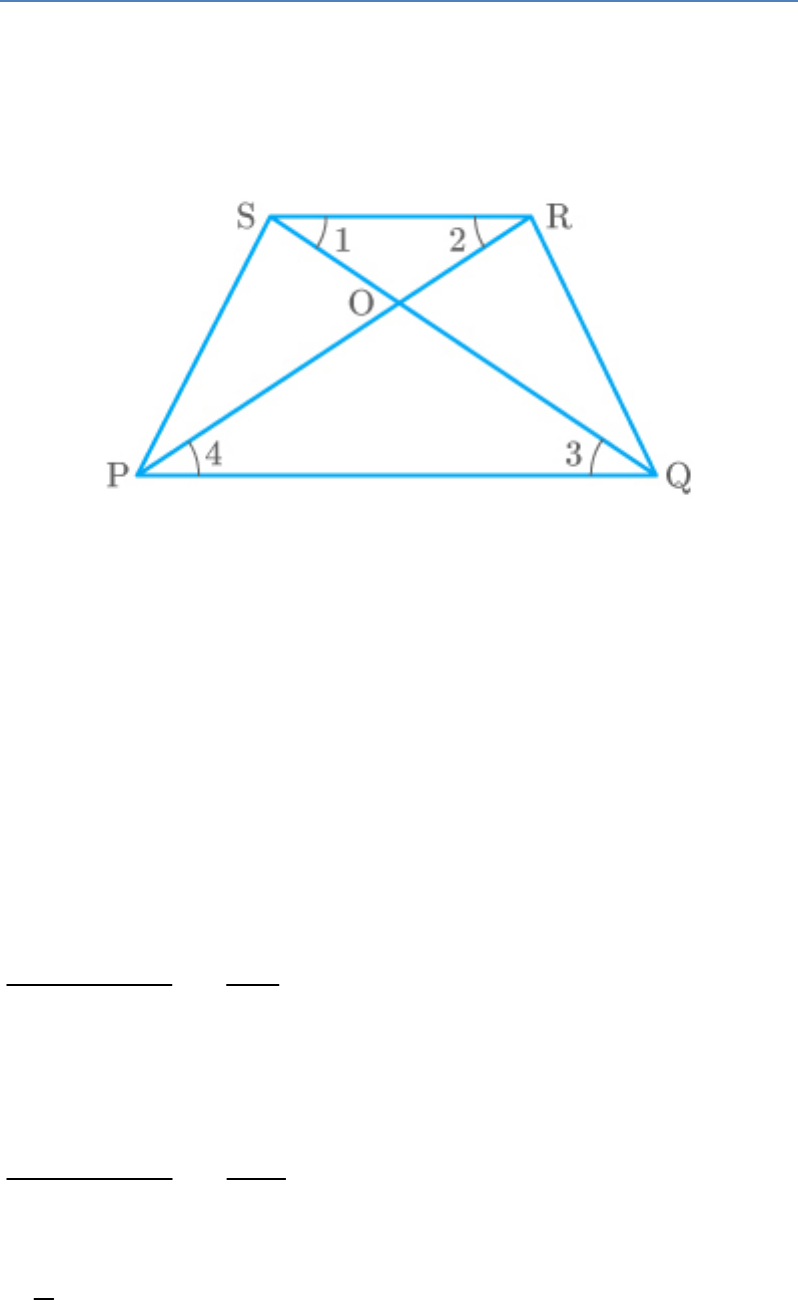
Solution
Given: A trapezium PQRS in which diagonals
intersect at the point O.
Also, PQ||RS and .
PQ 3RS
In triangles POQ and ROS,
PQ||RS
1 3
Aletrnate interior angles
2 4
Aletrnate interior angles
Thus,
POQ|| ROS
By AA similarity criterion
By area theorem,
2
ar POQ
PQ
ar ROS RS
Given that
PQ 3RS
2
ar POQ
3RS
ar ROS RS
9
1
Thus, the ratio of the areas of triangles POQ and ROS
is .
9 :1
Question: 5
In the adjoining figure, if AB||DC and AC and PQ
intersect each other at the point O, prove that
.
OA.CQ OC.AP
Solution
Given: A quadrilateral ABCD such that AB DC and
:
AC and PQ intersect each other at the point O.
Fig. Exm_6.3_5 (Sol)
To prove:
OA.CQ OC.AP
Proof: In triangles OPA and OQC,
1 2
Aletrnate interior angles
3 4
Aletrnate interior angles
Thus,
OPA|| OQC By AA similarity criterion
OQ OC CQ
OP OA AP
OA.CQ OC.AP
Hence proved.
Question: 6
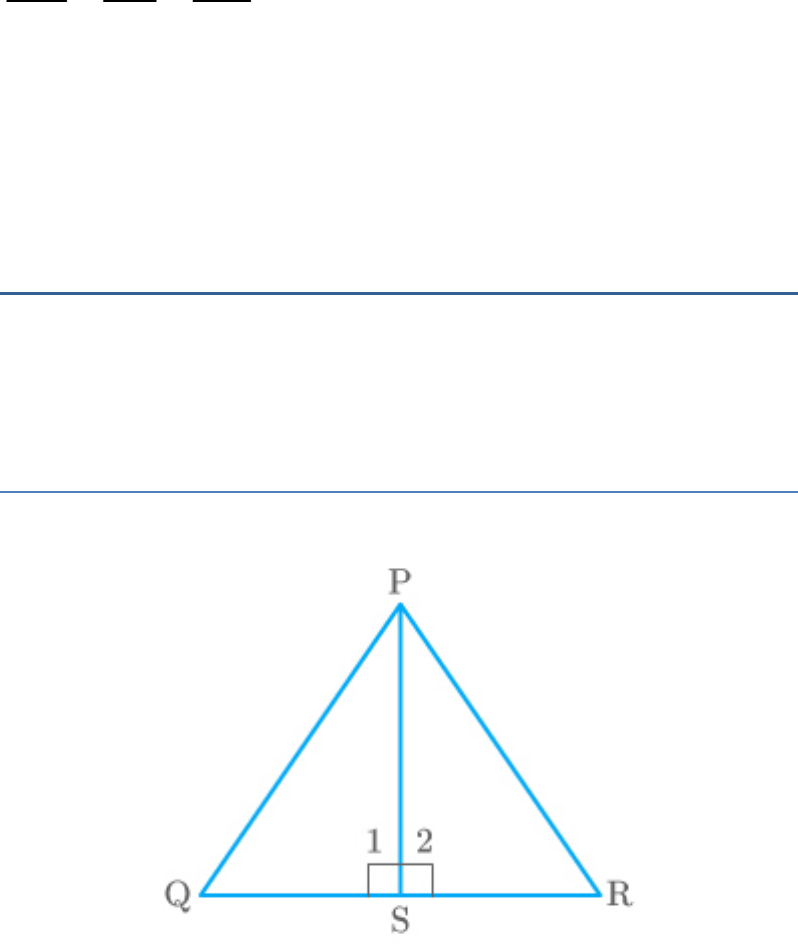
Find the altitude of an equilateral triangle of side 8
cm.
Solution
Let PQR be an equilateral triangle of side 8 cm.

PS is an altitude.
PS QR
Thus,
1 2 90
In triangles PSQ and PSR,
PQ PR Equilateral triangle property
1 2 90
PS PS Common
Thus,
PSQ PSR By RHS congruence criterion
QS SR
CPTC
Thus,
QR PQ 8
QS SR 4 cm
2 2 2
By Pythagoras theorem in ,
PQS
2 2 2
PS QS PQ
2 2
2
PS 4 8
2
PS 64 16
2
PS 48
PS 4 3
Thus, the altitude of the equilateral triangle is
4 3 cm
.
Question: 7
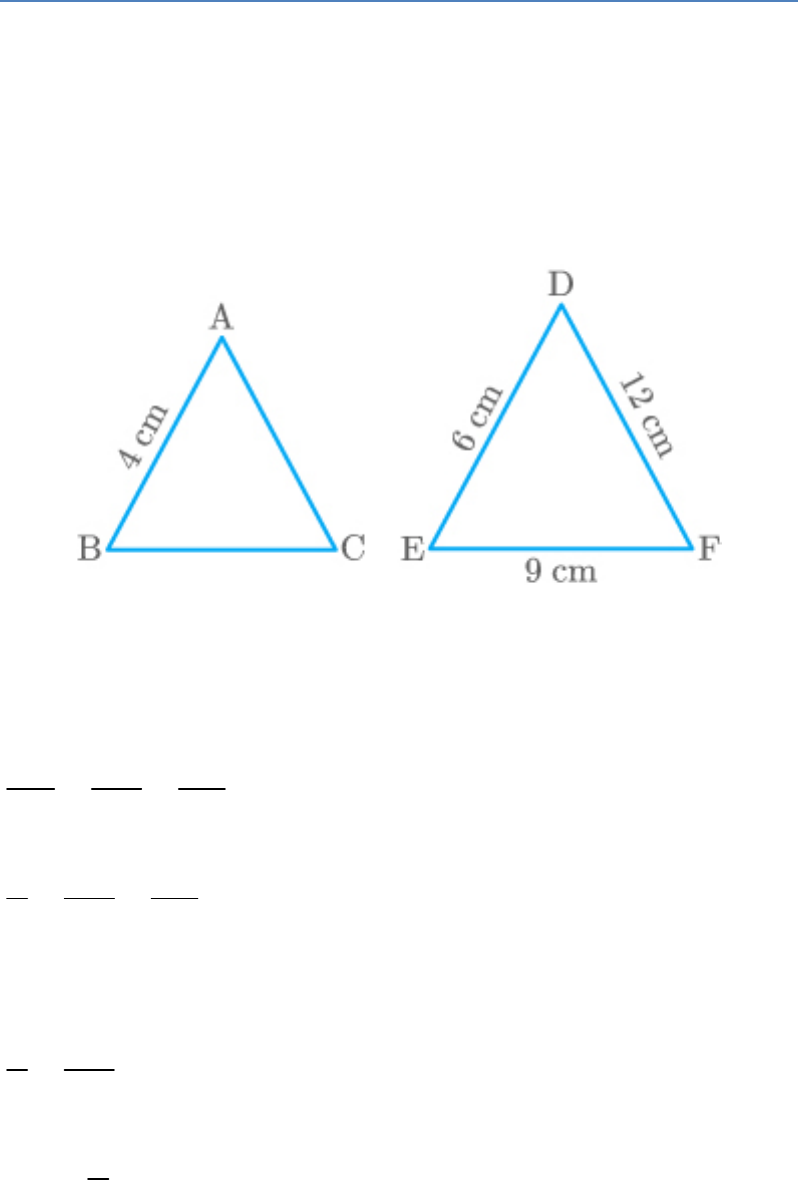
If , AB = 4 cm, DE = 6 cm, EF = 9 cm
ABC|| DEF
and FD = 12 cm, find the perimeter of ABC.
Solution
Given: Two triangles ABC and DEF such that
.
ABC|| DEF
Also, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12
cm
Given:
ABC|| DEF
Thus,
AB AC BC
DE DF EF
4 AC BC
6 12 9
Take first and second part.
4 AC
6 12
4
AC 12 8
6
Take first and third part.
4 BC
6 9
4
BC 9 6
6
The perimeter of ABC AB BC AC
4 6 8
18
Thus, the perimeter of ABC is 18 cm.
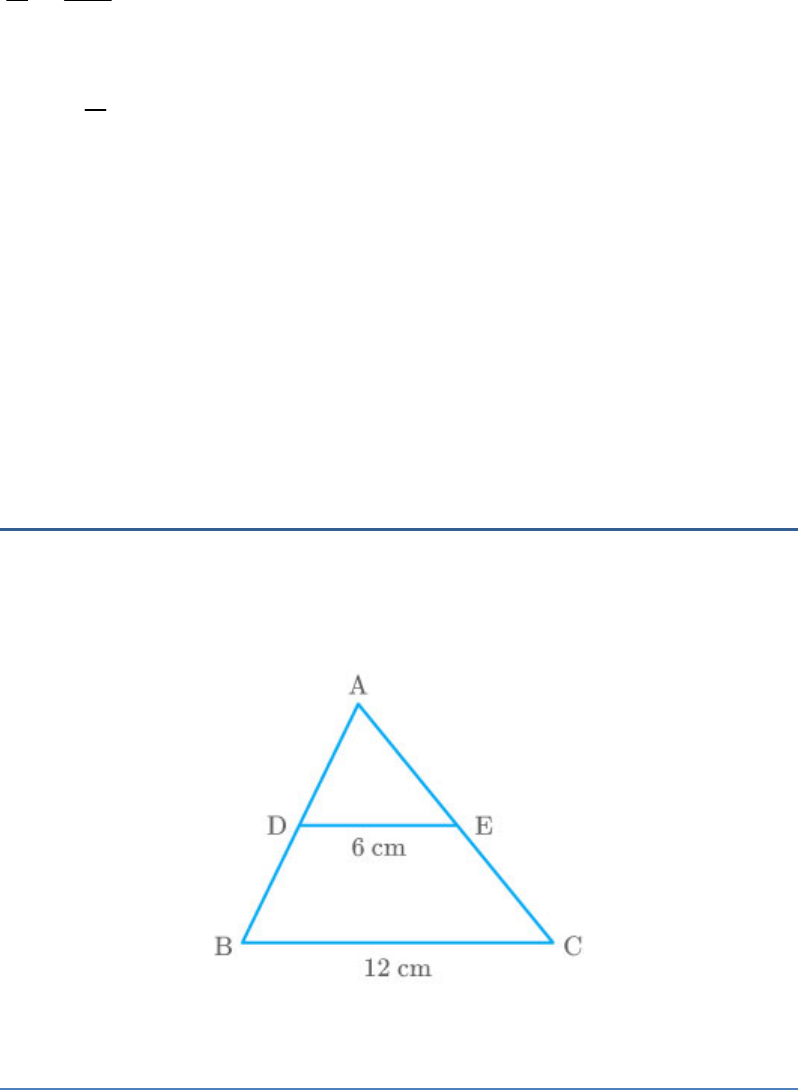
Question: 8
In the adjoining figure, if DE||BC, find the ratio of
and .
ar ADE
ar DECB
Solution
Given: A triangle ABC such that DE||BC.
Also, DE = 6 cm and BC = 12 cm.

In triangles ADE and ABC,
DE BC:
1 2
Corresponding angles
3 4
Corresponding angles
Thus,
ADE|| ABC
AA similarity criterion
We know that in two similar triangles, the ratio of the
areas is equal to the squares of the ratio of their
corresponding sides.
Thus,
2
ar ABC
BC
ar ADE DE
2
ar DECB ar ADE
BC
ar ADE DE
2
ar DECB
12
1
ar ADE 6
:

2
ar DECB
2 1
ar ADE
:
ar DECB
3
ar ADE 1
:
ar ADE
1
ar DECB 3:
Thus, the ratio of and is .
ar ADE
ar DECB
1:3
Question: 9
ABCD is a trapezium in which AB||DC and P and Q
are points on AD and BC, respectively such that
PQ||DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm,
find AD.
Solution
Given: A trapezium ABCD in which AB||DC and P
and Q are points on AD and BC such that PQ||DC.
Also, PD = 18 cm, BQ = 35 cm and QC = 15 cm.

In trapezium ABCD,
AB|| CD
PQ||CD
Thus,
AB||CD||PQ ......(1)
In , from the equation (1).
BCD
OQ CD:
Thus,
BO BQ
OD QC
By BPT
......(2)
Similarly, in ,
DAB
PO AB:
BO AP
OD PD
By BPT
......(3)
From equations (2) and (3).
AP BQ
PD QC
AP 35
18 15
35
AP 18
15
AP 42
AD AP PD
AD 42 18
AD 60
Thus,
AD 60 cm
Question: 10
Corresponding sides of two similar triangles are in the
ratio of . If the area of the smaller triangle is
2 :3
, find the area of the larger triangle.
2
48 cm
Solution
Let LMN and PQR be two similar triangles with sides
in the ratio of .
2 :3
Let the area of smaller be .
LMN
2
48 cm
Given that
LMN PQR:
By Area theorem,
2
ar LMN
LM
ar PQR PQ
2
48 2
ar PQR 3
48 4
ar PQR 9
48 9
ar PQR
4
ar PQR 108
Thus, the area of the larger triangle is
PQR
2
108 cm
Question: 11
In a triangle PQR, N is a point on PR such that QN
PR. If , prove that .
2
PN.NR QN
PQR 90
Solution
Given: A triangle PQR with a point N on PR such that
QN PR and
2
PN.NR QN
To prove:
PQR 90
Proof:
In triangles QNP and QNR,

QN PR
1 2 90
2
PN.NR QN
Thus,
QN NP
NR QN
Thus,
QNP QNR:
By SAS similarity criterion
P RQN x ......(1)
1 2 90
PQN R y ......(2)
In ,
PQR
P PQR R 180
Angle sum property
From equations (1) and (2),
x x y y 180
2x 2y 180
x y 90
Thus,
PQR 90
Hence proved.
Question: 12
Areas of two similar triangles are 36 and 100 .
2
cm
2
cm
If the length of a side of the larger triangle is 20 cm,
find the length of the corresponding side of the smaller
triangle.
Solution
Let LMN and PQR be two similar triangles with areas
36 and 100 respectively.
2
cm
2
cm
2
ar LMN 36 cm
2
ar PQR 100 cm
PQ 20 cm
Given that,
LMN PQR:
2
ar LMN
LM
ar PQR PQ
2
36 LM
100 20
LM 6
20 10
6 20
LM
10
LM 12
Thus, the length of the corresponding side of the
smaller triangle is 12 cm.
Question: 13
In the adjoining figure, if , AC = 8 cm
ACB CDA
and AD = 3 cm, find BD.
Solution
In triangles ACD and ACB,
ACB CDA
A A Common
ACD ACB:
AA similarity criterion
Thus,
AC DC AD
AB BC AC

8 DC 3
AB BC 8
Take first and third part.
8 3
AB 8
8 8
AB
3
64
AB
3
BD AB AD
64
3
3
55
3
18.33
Thus,
BD 18.33 cm
Question: 14
A 15 metres high tower casts a shadow 24 metres long
at a certain time and at the same time, a telephone pole
casts a shadow 16 metres long. Find the height of the
telephone pole.
Solution
Let AB be a tower of height 15 m and CB be its
shadow.
Let PQ be a pole of height m and RQ be its shadow.
x

AB = 15 m
CB = 24 m
PQ x m
RQ = 16 m
In triangles ABC and PQR,
B Q 90
C R
Angular elevation of sun
Thus,
ABC PQR:
AB AC CB
PQ PR RQ
Take first and third part.
AB CB
PQ RQ
15 24
x 16
15 16
x
24
x 10
Hence, the height of the telephone pole.is 10 m.
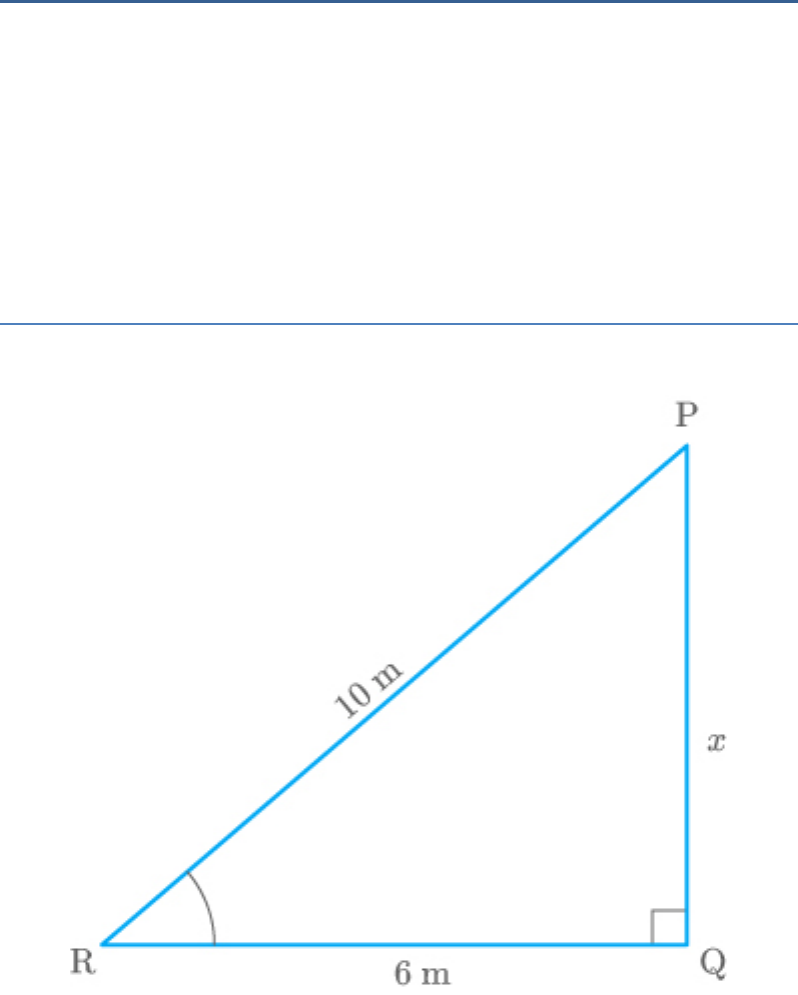
Question: 15
Foot of a 10 m long ladder leaning against a vertical
wall is 6 m away from the base of the wall. Find the
height of the point on the wall where the top of the
ladder reaches.
Solution
Let RP be a ladder leaning against vertical wall PQ.
RP = 10 m
QR = 6 m
Let
PQ x m
By Pythagoras theorem,
2 2 2
RP PQ QR
2 2 2
10 x 6
2
x 100 36
2
x 64
x 8
Thus, the height of the point on the wall where the top
of the ladder reaches is 8 m.
Exercise 6.4 (18)
Question: 1
In the adjoining figure, if , AB = 6 cm, BP =
A C
15 cm, AP = 12 cm and CP = 4 cm, then find the
lengths of PD and CD.
Solution
Given: , AB = 6 cm, BP = 15 cm, AP = 12
A C
cm and CP = 4 cm
In triangles ABP and CDP,
A C
1 2
Vertically opposite angles
Thus,
ABP CDP AA similarity criterion:
Thus,
AB AP BP
CD CP PD
6 12 15
CD 4 PD
Take first and second part.
6 12
CD 4

6 4
CD
12
CD 2
Take second and third part.
12 15
4 PD
4 15
PD
12
PD 5
Thus, PD = 5 cm and CD = 2 cm
Question: 2
It is given that such that AB = 5 cm,
ABC EDF:
AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the
lengths of the remaining sides of the triangles.
Solution
Given:
ABC EDF:
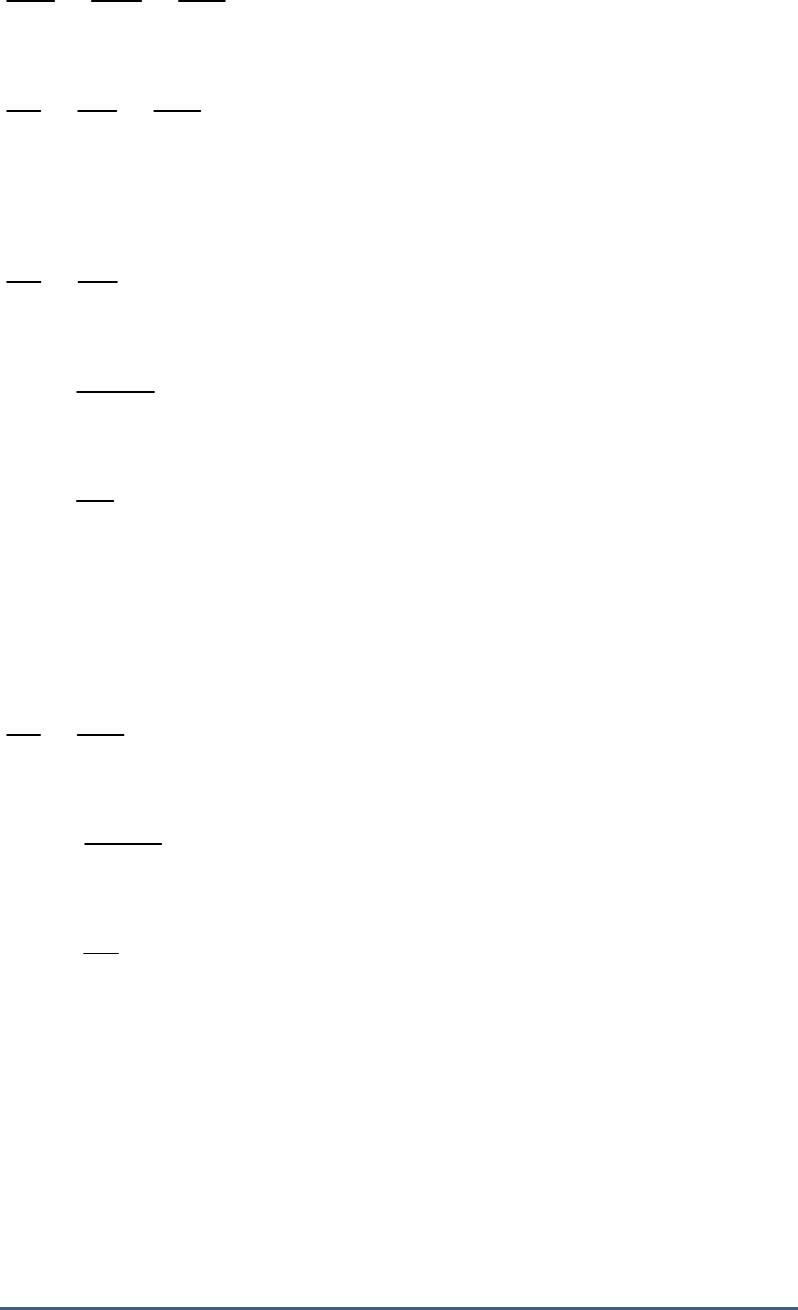
AB AC BC
ED EF DF
5 7 BC
12 EF 15
Take first and second part.
5 7
12 EF
12 7
EF
5
84
EF
5
EF 16.8
Take first and third part.
5 BC
12 15
15 5
BC
12
25
BC
4
BC 6.25
Hence, the lengths of the remaining sides EF and BC
are 16.8 cm and 6.25 cm respectively.
Question: 3
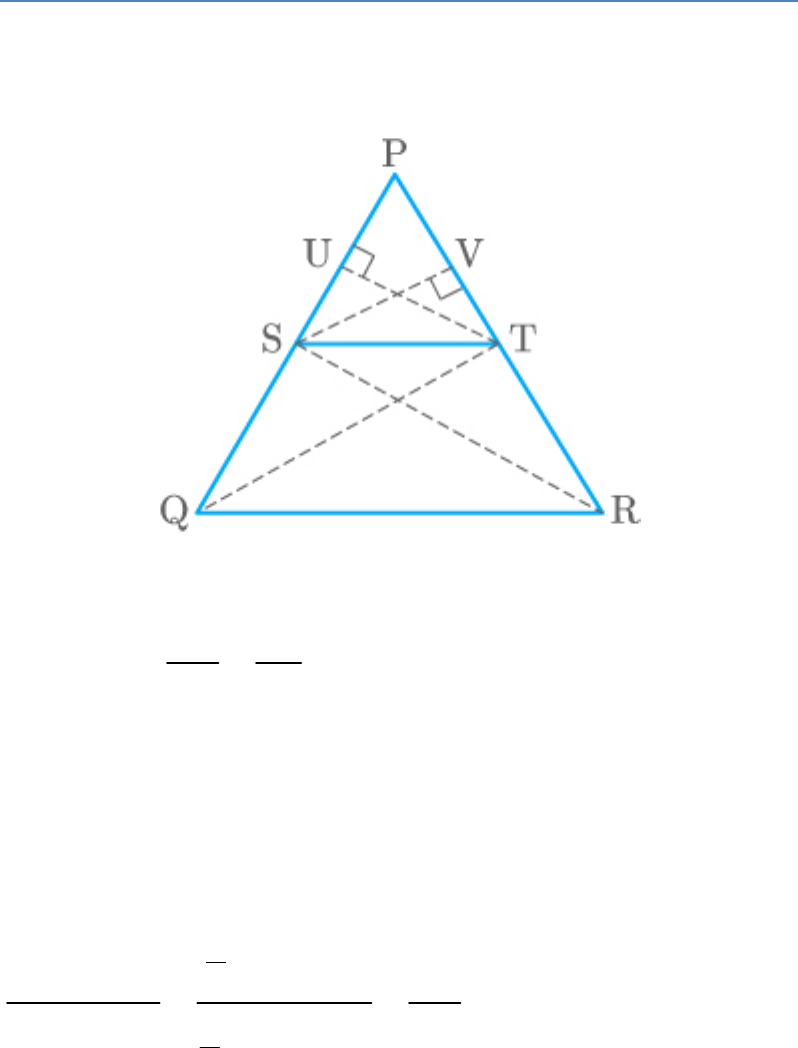
Prove that if a line is drawn parallel to one side of a
triangle to intersect the other two sides, then the two
sides are divided in the same ratio.
Solution
Let PQR be a triangle and the line ST is drawn parallel
to the side QR that intersects the other two sides.
To prove:
PS PT
SQ TR
Construction: Draw TU PQ and SV PR. Join SR
and QT.
Proof:
1
PS TU
ar PST
PS
2
......(1)
1
ar SQT SQ
SQ TU
2

1
PT SV
ar PTS
PT
2
......(2)
1
ar TRS TR
TR SV
2
From the figure, SQT and TRS are situated on
same base between same parallel lines.
Thus,
ar SQT ar TRS ......(3)
From equations (2) and (3).
ar PTS
PT
......(3)
ar SQT TR
From equations (1) and (4).
PS PT
SQ TR
Hence proved.
Question: 4
In the adjoining figure, if PQRS is a parallelogram and
AB PS, then prove that OC SR.
:
:
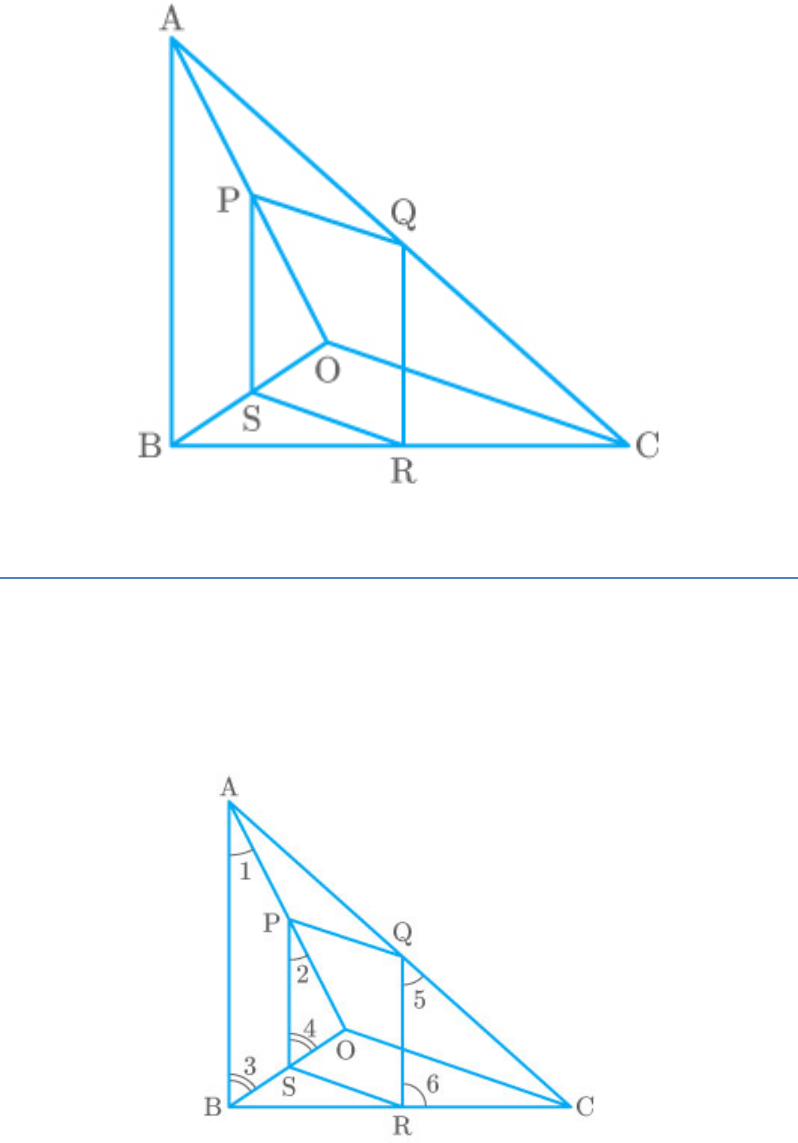
Solution
Given: A parallelogram PQRS inside and AB
ABC
:
PS.
To Prove: OC SR
:
Proof:
In triangles OAB and OPS,
AB PS:
1 2
Corresponding angles

3 4
Corresponding angles
Thus,
OAB OPS:
By AA similarity criterion
OP OS PS
......(1)
OA OB AB
… (2)
PS||QR
Parallelogram property
So,
QR AB ......(3):
In triangles CQR and CAB,
QR AB:
CAB 5
Corresponding angles
CBA 5
Corresponding angles
Thus,
CQR CAB:
By AA similarity criterion
CQ CR QR
CA CB AB
From equation (2),
PS QR:
Thus,
PS CR CQ
......(4)
AB CB CA
From equations (1) and (4).
CR OS
CB OB
Thus, the ratios of two sides of BOC are equal.
By the converse of BPT,
OC SR:
Hence proved.
Question: 5
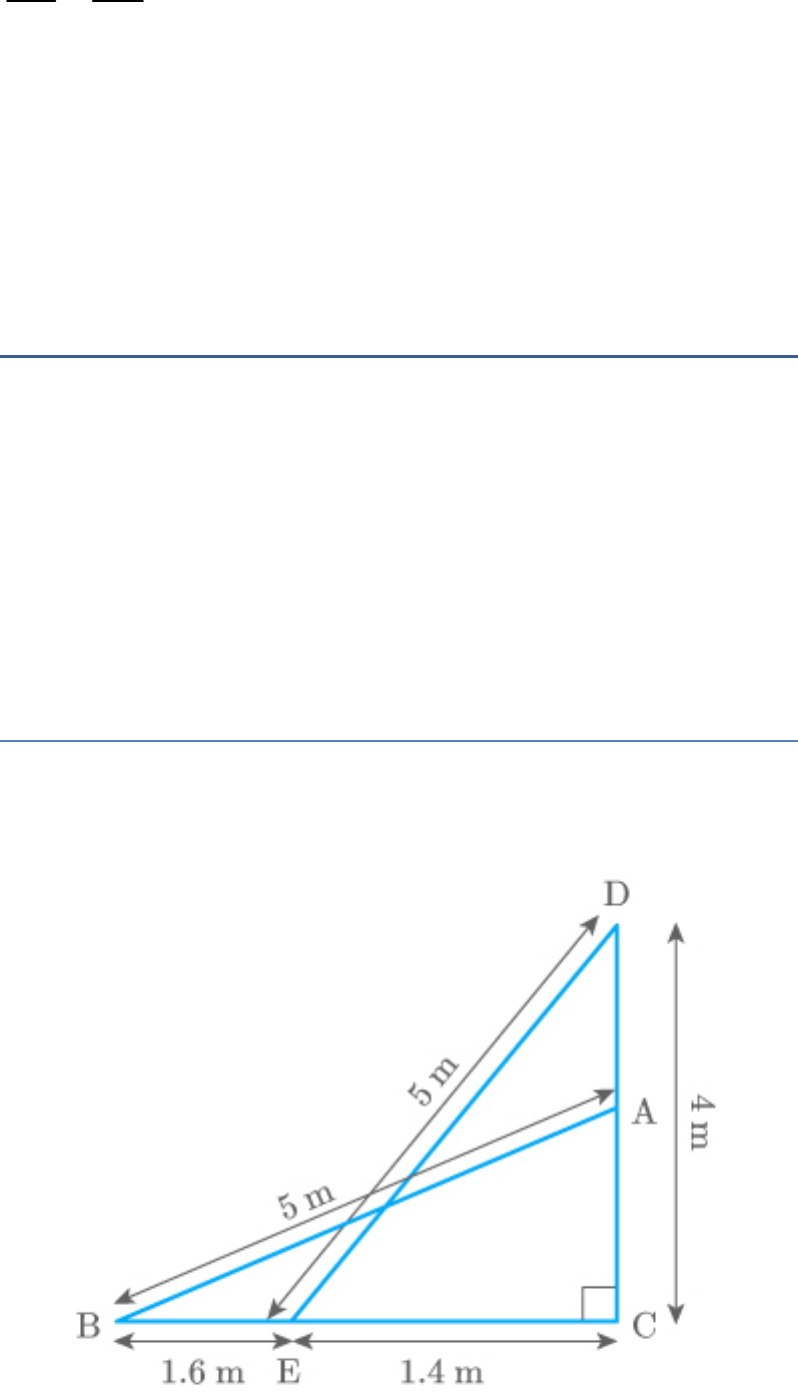
A 5 m long ladder is placed leaning towards a vertical
wall such that it reaches the wall at a point 4 m high. If
the foot of the ladder is moved 1.6 m towards the wall,
then find the distance by which the top of the ladder
would slide upwards on the wall.
Solution
Let AB be a ladder leaning towards vertical wall DC.
The ladder is moved 1.6 m towards the wall.
AB DE 5m
AC = 4 m
BE = 1.6 m
In triangle ABC, by the Pythagoras theorem,
2 2 2
AB AC BC
2 2 2
5 4 BC
2
BC 25 16
2
BC 9
BC 3
Now,
EC BC BE
EC 3 1.6
EC 1.4
In triangle DEC, by the Pythagoras theorem,
2 2 2
DE DC EC
2 2 2
5 DC 1.4
2
DC 25 1.96
2
DC 23.04
DC 4.8
Now,
DA DC AC
DA 4.8 4
DA 0.8
Thus, the distance by which the top of the ladder
would slide upwards on the wall is 0.8 m.
Question: 6
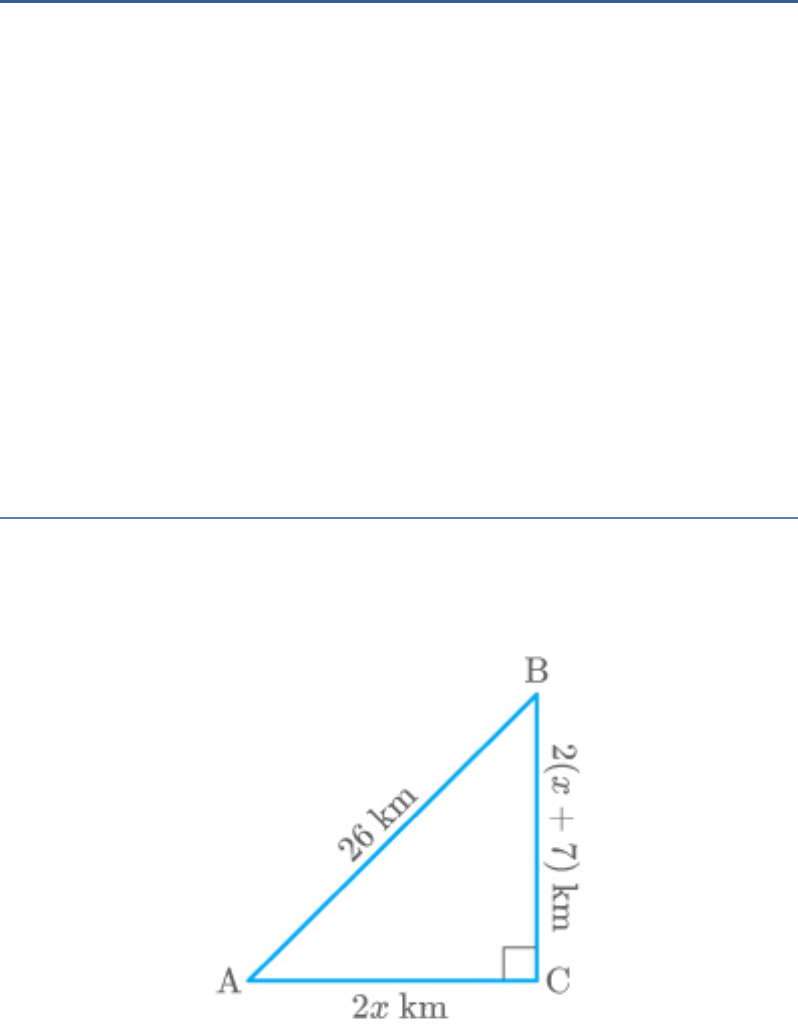
For going to a city B from city A, there is a route via
city C such that AC CB, km and
AC 2x
km. It is proposed to construct a 26 km
CB 2 x 7
highway which directly connects the two cities A and
B. Find how much distance will be saved in reaching
city B from city A after the construction of the
highway.
Solution
Given: Two cities A and B and a route between them
via city C.
AC CB
AC 2x

CB 2 x 7
AB 26
By Pythagoras theorem,
2 2 2
AC BC AB
2
2
2
2x 2 x 7 26
2
2
2
2x 2 x 7 26
2 2
4 x x 49 14x[ ] 676
2
676
2x 14x 49
4
2
2x 14x 49– 169 0
2
2x 14x– 120 0
2
x 7x– 60 0
Split the middle term to find factors.
2
x 12x – 5x– 60 0
x x 12 – 5 x 12 0
x 12 x – 5 0
That is,
or
x 12 0
x– 5 0
or
x 12
x 5
Distance cannot be negative,
Thus,
x 5

The saved distance after the
AC BC – AB
construction of the highway
2x 2x 14 – 26
4x–12
Put the value of in the above expression.
x
The saved distance 4 5 12
20 12
8
Thus, the distance that will be saved in reaching city B
from city A after the construction of the highway is 8
km.
Question: 7
A flag pole 18 m high casts a shadow 9.6 m long. Find
the distance of the top of the pole from the far end of
the shadow.
Solution
Let AB be a flag pole and CB be its shadow.
AB = 18 m
CB = 9.6 m
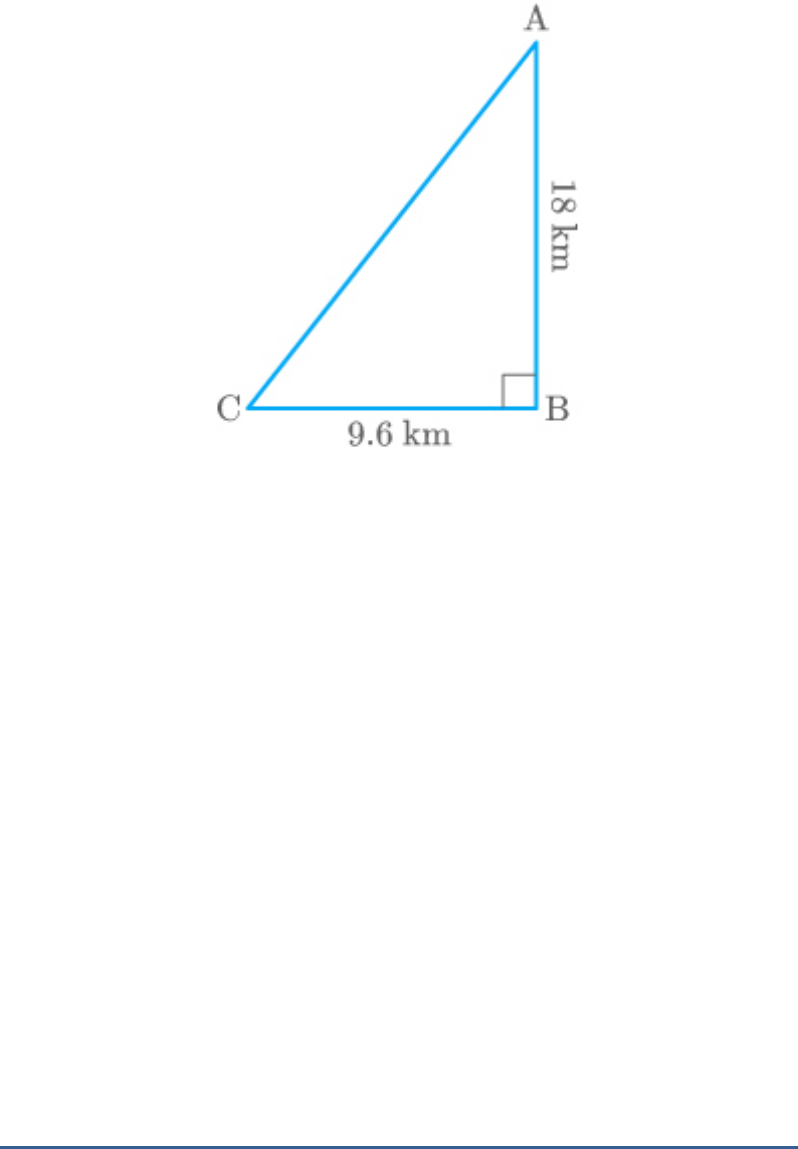
By Pythagoras theorem,
2 2 2
AC AB BC
2 2 2
AC 18 9.6
2
AC 324 92.16
2
41AC 6.16
AC 20.4
Hence, the distance of the top of the pole from the far
end of the shadow.is 20.4 m.
Question: 8
A street light bulb is fixed on a pole 6 m above the
level of the street. If a woman of height 1.5 m casts a
shadow of 3 m, find how far she is away from the base
of the pole.
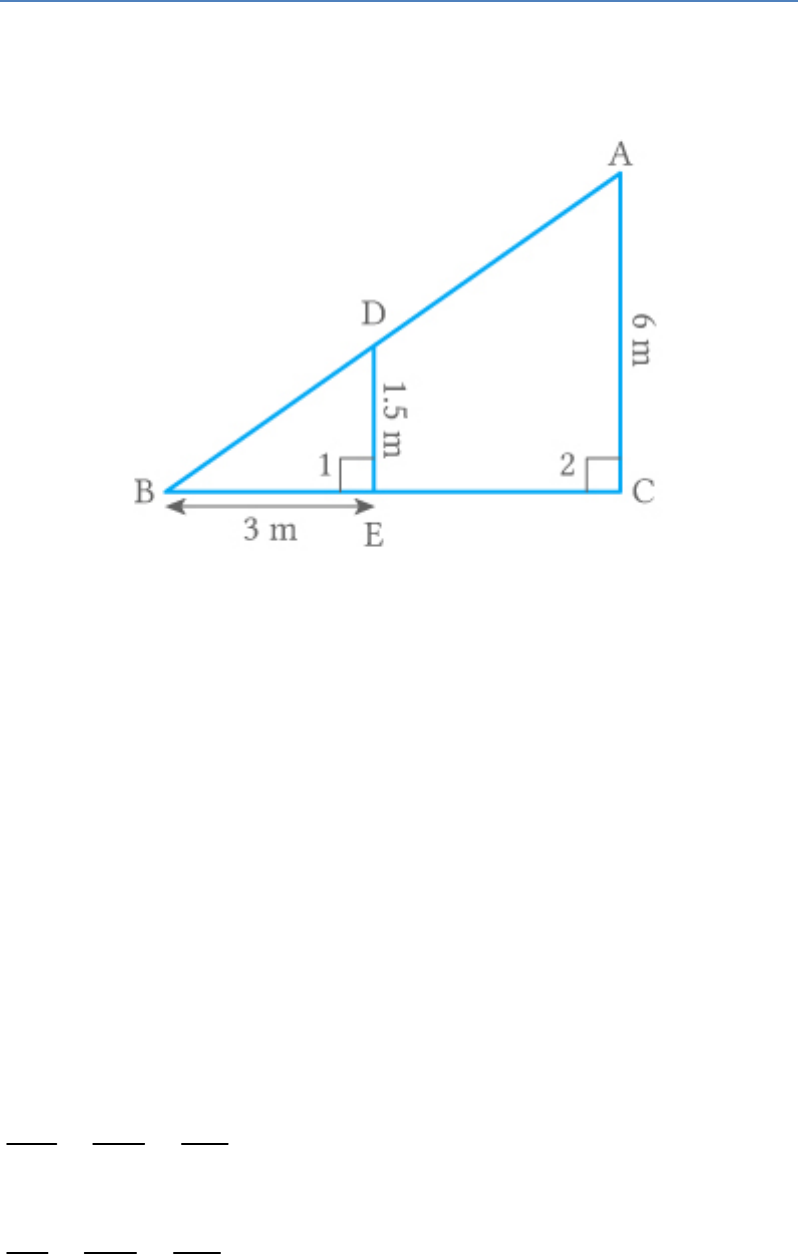
Solution
Let the bulb is fixed at point A on the pole AC. DE be
the woman and BE be her shadow.
AC = 6 m
DE = 1.5 m
BE = 3 m
In triangles ABC and DBE.
1 2 90
B B
Common
Thus,
ABC DBE:
By AA similarity criterion
AC AB BC
DE AD BE
6 AB BC
1.5 AD 3
Take first and third part.
6 BC
1.5 3
6 3
BC
1.5
BC 12
Now,
EC BC BE
EC 12 3
EC 9
Thus, the woman is 9 m away from the base of the
pole.
Question: 9
In the given figure, ABC is a triangle right angled at B
and . If AD = 4 cm, and CD = 5 cm, find BD
BD AC
and AB.
Solution
According to the question,

In ,
ABC
ABC 90
Also,
BD AC
So,
2
BD AD CD
Now, put the values of AD and CD in the above
equation.
2
BD 4 5
2
BD 20
BD 20
BD 2 5 cm
Now, in ,
BDA
It is given that
BD AC
So,
BDA 90
Now, by Pythagoras theorem,
2 2 2
AB AD BD
Put the values of AD and BD in the above equation.
2 2 2
AB AD BD
2
2
2
AB 4 2 5
2
AB 16 20
2
AB 36
2 2
AB 6
AB 6 cm
Thus, the lengths of BD and AB are
2 5 cm and 6 cm
respectively.
Question: 10
In the given figure, PQR is a right triangle right angled
at Q and . If PQ = 6 cm and PS = 4 cm, find
QS PR
QS, RS and QR.
Solution
According to the question,
In ,
PQR
PQR 90
Also,
QS PR
So,
2
QS PS RS ......(1)
Now, in , apply the Pythagoras theorem.
PSQ
2 2 2
PQ QS PS
Put the values of PS and PQ in the above equation.
2 2 2
6 QS 4
2
QS 36 16

2
QS 20
QS 2 5 cm
Now, substitute the value of QS and PS in equation
.
1
2
2 5 4 RS
20
RS
4
RS 5 cm
Now, in ,
QSR
QSR 90
QS PR
Apply, Pythagoras theorem.
2 2 2
QR QS RS
Now, substitute the value of QS and RS in the above
equation.
2
2
2
QR 2 5 5
2
QR 20 25
2
QR 45
QR 45
Thus, the lengths of QS, RS and QR are
respectively.
2 5 cm, 5 cm and 3 5 cm
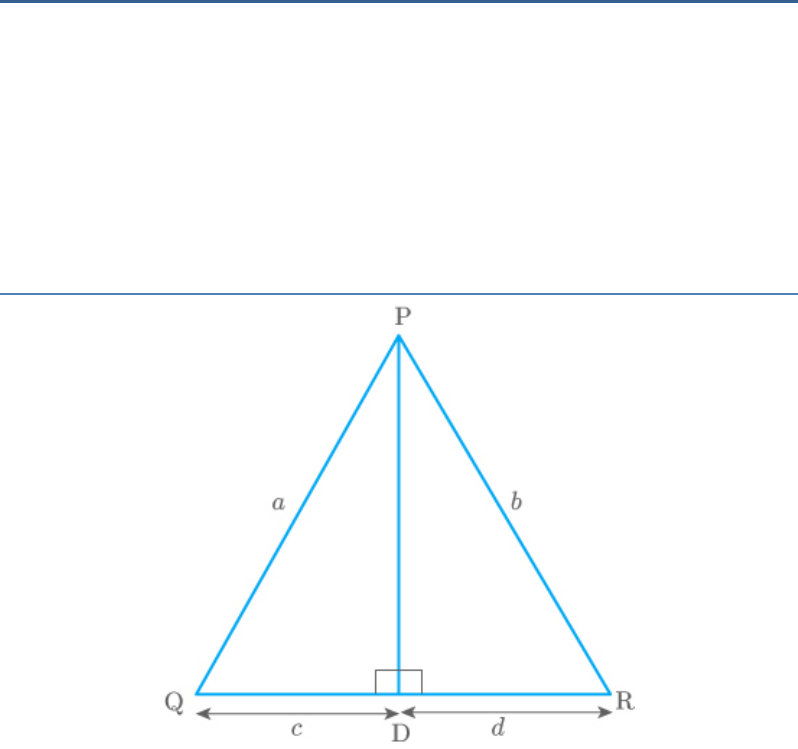
Question: 11
In , such that D lies on QR. If PQ
PQR
PD QR
a
, PR , QD and DR , prove that
b
c
d
.
a b a b c d c d
Solution
According to the question,
Given: In ,
PQR
PD QR
So,
PDQ PDR 90
It is also given that, PQ , PR , QD and DR
a
b
c
d
To prove:
a b a b c d c d
Proof: In , right angled at D,
PDQ
Apply, Pythagoras theorem.
2 2 2
PD QD PQ

Substitute the values of QD and PQ in the above
equation.
2 2 2
PD c a
2 2 2
PD a c ......(1)
Now, in , right angled at D,
PDR
Apply, Pythagoras theorem.
2 2 2
PD DR PR
Substitute the values of DR and PR in the above
equation.
2 2 2
PD d b
2 2 2
PD b d ......(2)
Now, from equations and .
1
2
2 2 2 2
a c b d
2 2 2 2
a b c d
a b a b c d c d
Hence proved.
Question: 12
In a quadrilateral ABCD, . Prove that
A D 90
[Hint: Produce AB and DC to
2 2 2 2
AC BD AD BC
meet at E.]
Solution
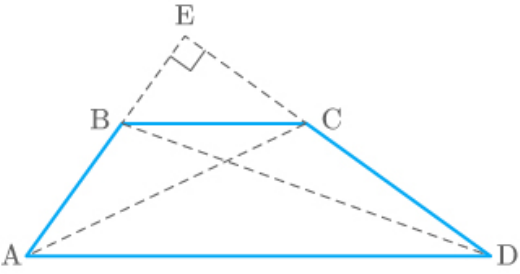
Given: ABCD is a quadrilateral having
A D 90
To prove:
2 2 2 2
AC BD AD BC
Proof: First, produce the sides AB and DC to meet
each other at point E.
Now, in , it is given that,
EAD
EAD EDA 90
So, (By interior angles property of triangle)
E 90
Now, apply Pythagoras theorem in and .
EAD
EBC
So,
2 2 2
AD AE DE ......(1)
And,
2 2 2
BC BE CE ......(2)
Add equations .
1 and 2
2 2 2 2 2 2
AD BC AE DE BE CE ......(3)
Similarly, apply Pythagoras theorem in
.
ECAand EBD
So,
2 2 2
AC AE CE ......(4)
And,
2 2 2
BD BE DE ......(5)
Add equations .
4 and 5
2 2 2 2 2 2
AC BD AE CE BE DE ......(6)
Now, from equations and .
3
6
2 2 2 2
AC BD AD BC
Hence proved.
Question: 13
In the given figure, and line segments AB, CD
l m:
and EF are concurrent at point P. Prove that
AE AC CE
BF BD FD
Solution
Given: Two lines parallel to each other.
l and m
Also, line segments AB, CD and EF all meet at point
P.
To prove:
AE AC CE
BF BD FD
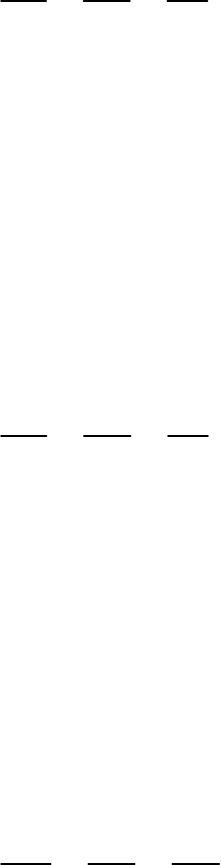
Proof: In ,
AEP and BFP
l m:
… (Alternate interior angles)
PAE PBF
Also, … (Alternate interior angles)
AEP BFP
So, … (By similarity criterion)
AEP|| BFP
Thus,
AE AP EP
......(1)
BF BP PF
Now, in and ,
CEP
DFP
l|| m
… (Alternate interior angles)
PCE PDF
Also, … (Alternate interior angles)
CEP DFP
So, … (By similarity criterion)
CEP|| DFP
Thus,
CE CP EP
......(2)
DF DP PF
Now, in ,
ACP and BPD
l|| m
… (Alternate interior angles)
PAC PBD
Also, … (Alternate interior angles)
ACP PDB
So, … (By similarity criterion)
ACP BPD:
Thus,
AC AP CP
......(3)
BD BP DP
Now, from equations and ,
1 ,
2
3
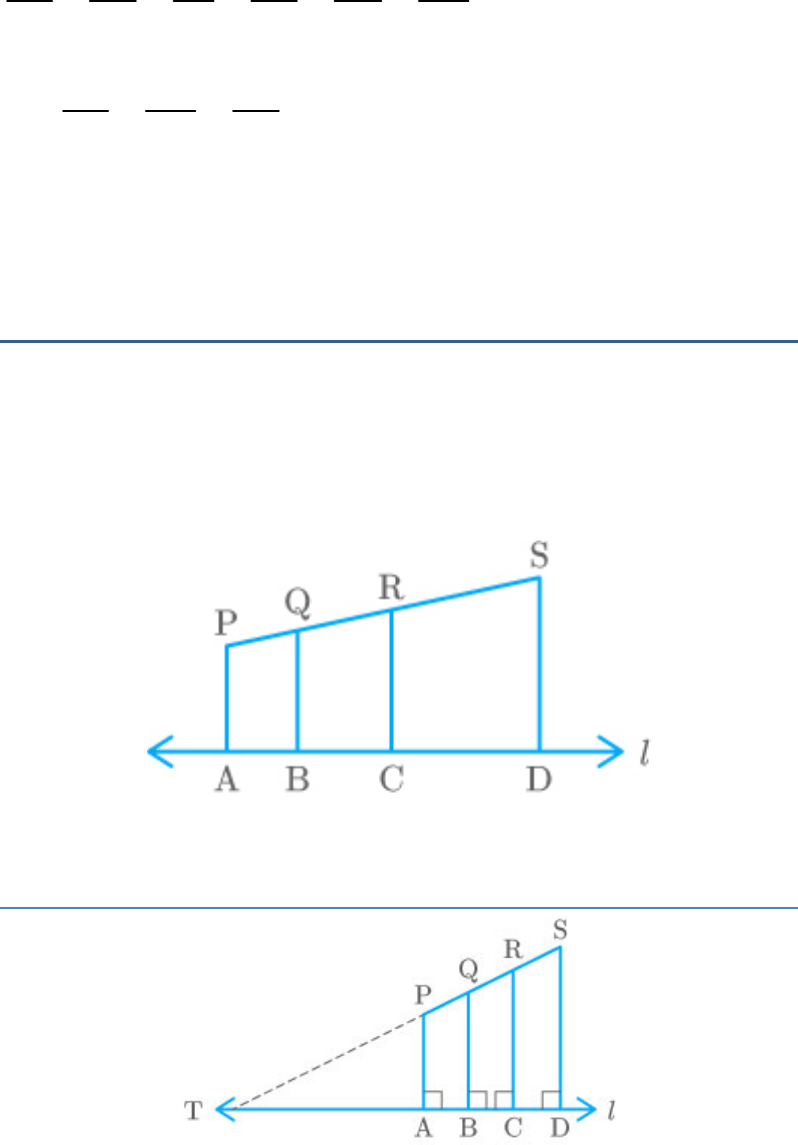
AE AP EP CE CP AC
BF BP PF DF DP BD
So,
AE AC CE
BF BD FD
Hence proved.
Question: 14
In the given figure, PA, QB, RC and SD are all
perpendiculars to a line , AB = 6 cm, BC = 9 cm, CD
l
= 12 cm and SP = 36 cm. Find PQ, QR and RS.
Solution
According to the question,
PA l, QB l,RC l and SD l
Produce the line and SP, so that they meet at point T.
l
Now, in ,
TDS

PA QB RC SD: : :
So,
PQ :QR:RS AB:BC : CD
It is given that, AB = 6 cm, BC = 9 cm and CD = 12
cm
So,
PQ :QR:RS 6 : 9 :12
Let us assume, PQ , QR and RS
6x
9x
12x
Now, as SP
36
So,
PQ QR RS 36
Now, substitute the values of PQ, QR and RS in the
above equation.
6x 9x 12x 36
27x 36
36
x
27
4
x
3
Now, find PQ, QR and RS.
PQ
6x
4
6
3
8 cm
QR
9x
4
9
3
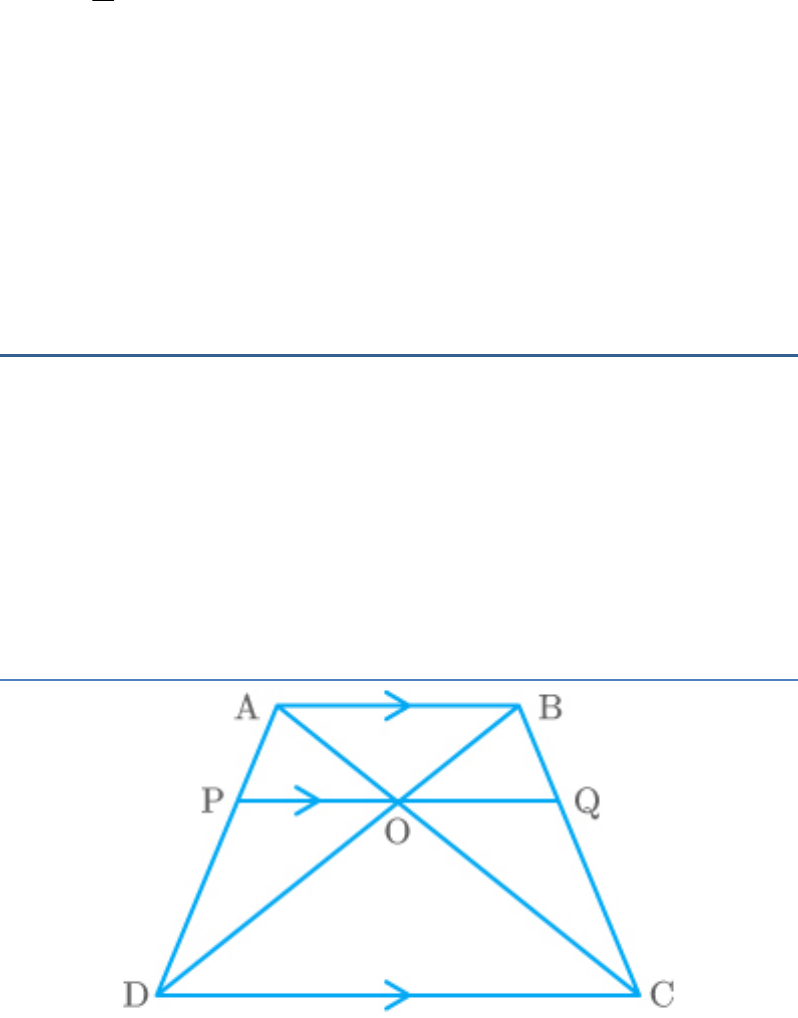
12 cm
RS
12x
4
12
3
16 cm
Hence, the lengths of PQ, QR and RS are 8 cm, 12 cm
and 16 cm respectively.
Question: 15
O is the point of intersection of the diagonals AC and
BD of a trapezium ABCD with . Through O,
AB DC:
a line segment PQ is drawn parallel to AB meeting
AD in P and BC in Q. Prove that .
PO QO
Solution
Given: A trapezium ABCD with .
AB DC:
Also,
PQ AB:
To prove:
PO QO
Proof: In ,
ADB
PO AB:

So,
AP BO
......(1)
PD OD
Now, in , (As, )
BDC
OQ CD:
AB DC:
So,
BO BQ
......(2)
OD QC
From equations and ,
1
2
AP BQ
PD QC
Add 1 on both sides of the above equation.
AP BQ
1 1
PD QC
Now, solve the above equation.
AP PD BQ QC
PD QC
AD BC
PD QC
The above equation can also be written as,
PD QC
......(3)
AD BC
Now, in ,
DOP and DBA
It is given that,
AB PO:
Therefore, (corresponding angles)
DPO DAB
And, (corresponding angles)
DOP DBA
So, (By similarity criterion)
DOP DBA:

PO DP
......(4)
AB DA
Now, in
COQ and CAB
AB OQ:
Therefore, (corresponding angles)
COQ CAB
And, (corresponding angles)
CQO CBA
So, (By similarity criterion)
COQ CAB:
OQ QC
......(5)
AB BC
Now, from equations ,
3 , 4 and 5
PD QC PO OQ
AD BC AB AB
So,
PO OQ
AB AB
Thus,
PO QO
Hence proved.
Question: 16
In the given figure, line segment DF intersect the side
AC of a triangle ABC at the point E such that E is the
mid–point of CA and . Prove that
AEF AFE
[Hint: Take point G on AB such that
BD BF
CD CE
]
CG||DF
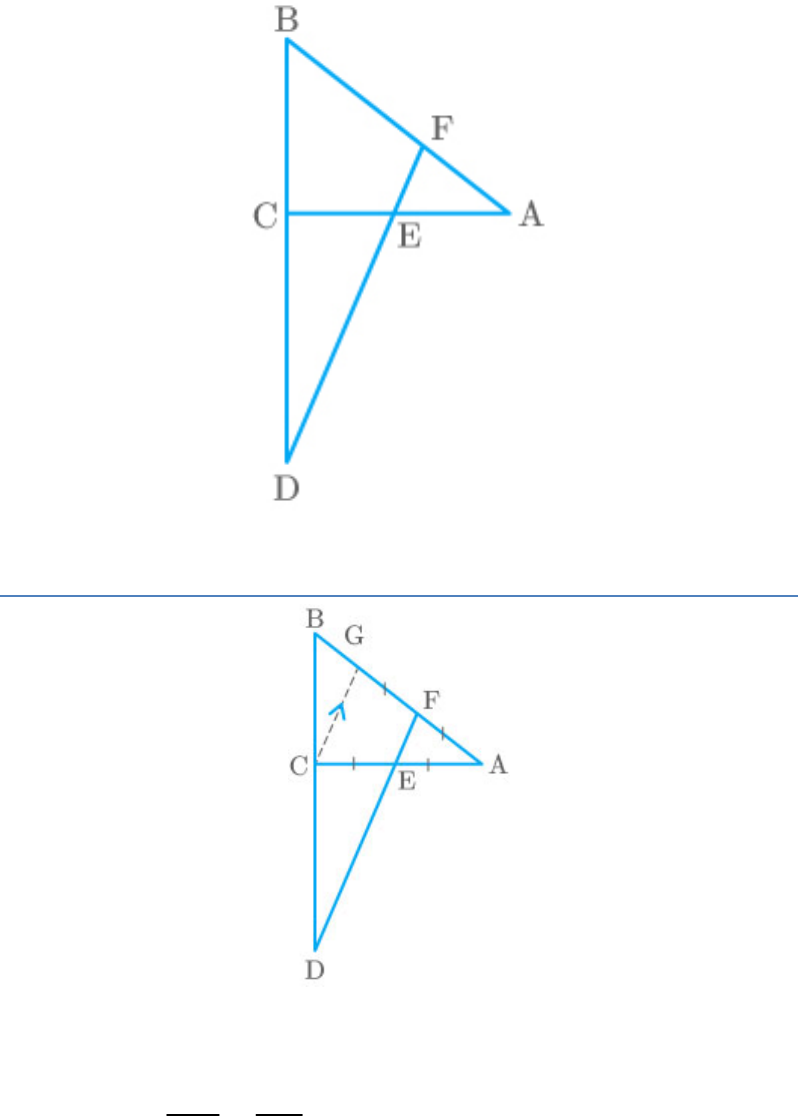
Solution
Given: In , AE = CE = AF
ABC
To prove:
BD BF
CD CE
Proof: Draw a line CG parallel to EF.
In ,
ACG
CG EF:
And, E is the mid–point of CA.
So, F will be the mid–point of GA.

Therefore, AF = FG
But it is given that, AE = CE = AF
So, FG = FA = EA = EC
......(1)
Now, in ,
BCG and BDF
CG EF:
So,
BC BG
CD GF
Add 1 on both sides of the above equation.
BC BG
1 1
CD GF
Now, solve the above equation.
BC+CD BG+GF
CD GF
BD BF
CD GF
Now, from equation ,
1
FG = CE
So,
BD BF
CD CE
Hence proved.
Question: 17
Prove that the area of the semicircle drawn on the
hypotenuse of a right angled triangle is equal to the
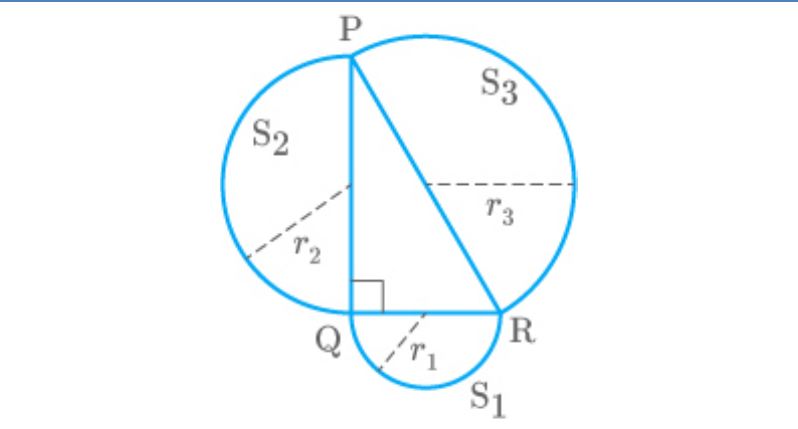
sum of the areas of the semicircles drawn on the other
two sides of the triangle.
Solution
Given: is right angled at B.
PQR
The semicircles are drawn on sides QR,
1 2 3
S , S and S
PQ and PR of .
PQR
To prove: Area of semicircles Area of
1 2
S S
semi–circle
3
S
Proof: Firstly, let us assume the radii of hemispheres
be .
1 2 3
S , S and S
1 2 3
r ,r and r
In
PQR, Q 90
Now, apply Pythagoras theorem.
2 2 2
PQ QR PR
Now,
2
2 2
2 1 3
2r 2r 2r

2 2 2
1 2 3
4 r r 4r
2 2 2
1 2 3
r r r
Now, multiply on both the sides of the above
1
π
2
equation.
2 2 2
1 2 3
1 1
π r r πr
2 2
2 2 2
1 2 3
1 1 1
πr πr πr
2 2 2
So, area of semicircles Area of semi–circle
1 2
S S
3
S
Hence proved.
Question: 18
Prove that the area of the equilateral triangle drawn on
the hypotenuse of a right angled triangle is equal to the
sum of the areas of the equilateral triangles drawn on
the other two sides of the triangle.
Solution

Given: A right angled
PQR
Let PQ , QR , PR and
a
b
c
Q 90
Also, equilateral triangles are drawn with sides PQ,
QR and PR
To prove: Area of equilateral triangle with side
c
Sum of the areas of equilateral triangles with sides
a and b
Proof: In
PQR, Q 90
Now, apply Pythagoras theorem.
So,
2 2 2
PQ QR PR
Substitute the values of PQ, QR and PR in the above
equation.
2 2 2
a b c
Multiply on both sides of the above equation.
3
4
2 2 2
3 3 3
a b c
4 4 4
Or,
2 2 2
3 3 3
c a b
4 4 4
So, area of equilateral triangle with side Sum of
c
the areas of equilateral triangles with sides
a and b
Hence proved.