
Lesson: Pair of linear equations in two variables.
Exercise 3.1 (13)
Question: 1
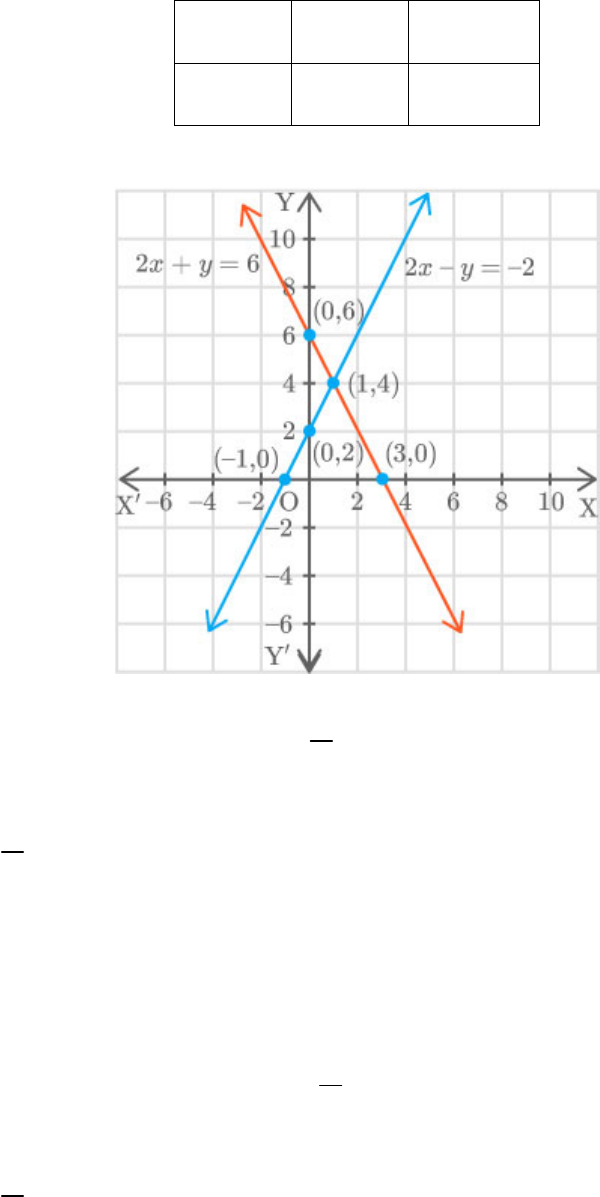
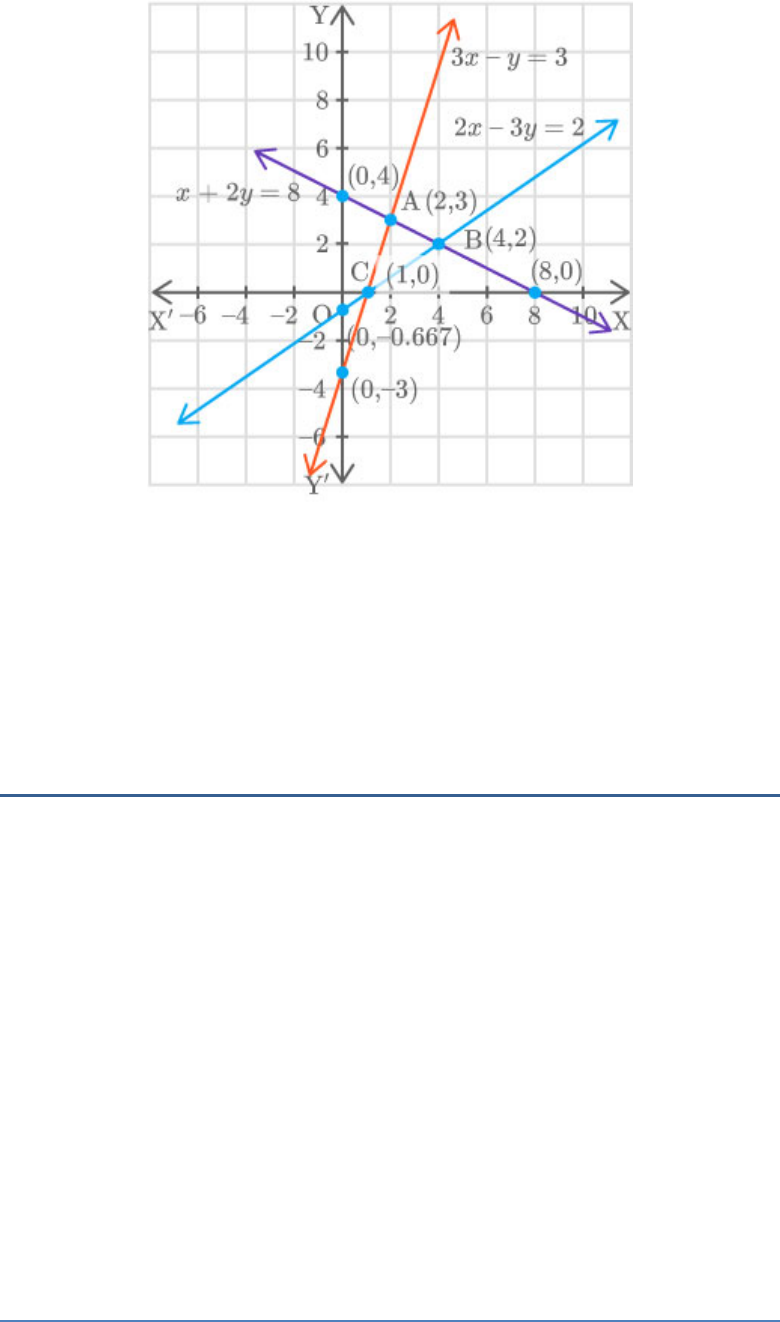
Graphically, the pair of equations
6 3 10 0
x y
2 9 0
x y
Represents two lines which are
a. intersecting at exactly one point
b. intersecting at exactly two points
c. coincident
d. parallel
Solution:
(d)
Given equations are: and
6 3 10 0
x y
2 9 0
x y
Compare with and
1 1 1
0
a x b y c
2 2 2
0
a x b y c
,
, and .
1
2
6 3
2 1
a
a
1
2
3 3
1 1
b
b
1
2
10
9
c
c
Now, observe that

1 1 1
2 2 2
a b c
a b c
If holds then these are parallel lines.
1 1 1
2 2 2
a b c
a b c
Thus, the lines are parallel.
Question: 2
The pair of equations and
2 5 0
x y
have
3 6 1 0
x y
a. a unique solution
b. exactly two solutions
c. infinitely many solutions
d. no solution
Solution:
(d)
Given equations are
and
2 5 0x y
3 6 1 0x y
Compare with and
1 1 1
0
a x b y c
2 2 2
0
a x b y c
,
, and .
1
2
1 1
3 3
a
a
1
2
2 1
6 3
b
b
1
2
5
1
c
c
Now, observe that

1 1 1
2 2 2
a b c
a b c
If holds then the lines have no solution.
1 1 1
2 2 2
a b c
a b c
Thus, the lines have no solution.
Question: 3
If a pair of linear equations is consistent, then the
lines will be
a. parallel
b. always coincident
c. intersecting or coincident
d. always intersecting
Solution:
(c)
We have a given condition that when a pair of
linear equations is consistent, then the lines are
intersecting or coincident.
Thus, the lines are intersecting or coincident.
Question: 4
The pair of equations and has
0
y
7
y

a. one solution
b. two solutions
c. infinitely many solutions
d. no solution
Solution:
(d)
Given: and
0
y
7
y
The pair of linear equations and both
0
y
7
y
lines are parallel to -axis.
x
Also, parallel lines never intersect.
Thus, there is no solution of these lines.
Question: 5
The pair of equations and graphically
x a
y b
represent lines which are
a. parallel
b. intersecting at
,
b a
c. coincident
d. intersecting at
,
a b
Solution:
(d)

Given: and
x a
y b
The line is parallel to –axis and the line
x a
y
is parallel to –axis.
y b
x
Thus, the lines and are perpendicular to
x a
y b
each other and intersect each other at .
,
a b
Question: 6
For what value of , do the equations
k
3 8 0
x y
and represent coincident lines?
6 16
x ky
a.
1
2
b.
1
2
c.
2
d.
2
Solution:
(c)
Given equations are: and
3 8 0
x y
6 16
x ky
We can rewrite them as,
and
3 8 0
x y
6 16 0
x ky
Compare with and
1 1 1
0
a x b y c
2 2 2
0
a x b y c
,
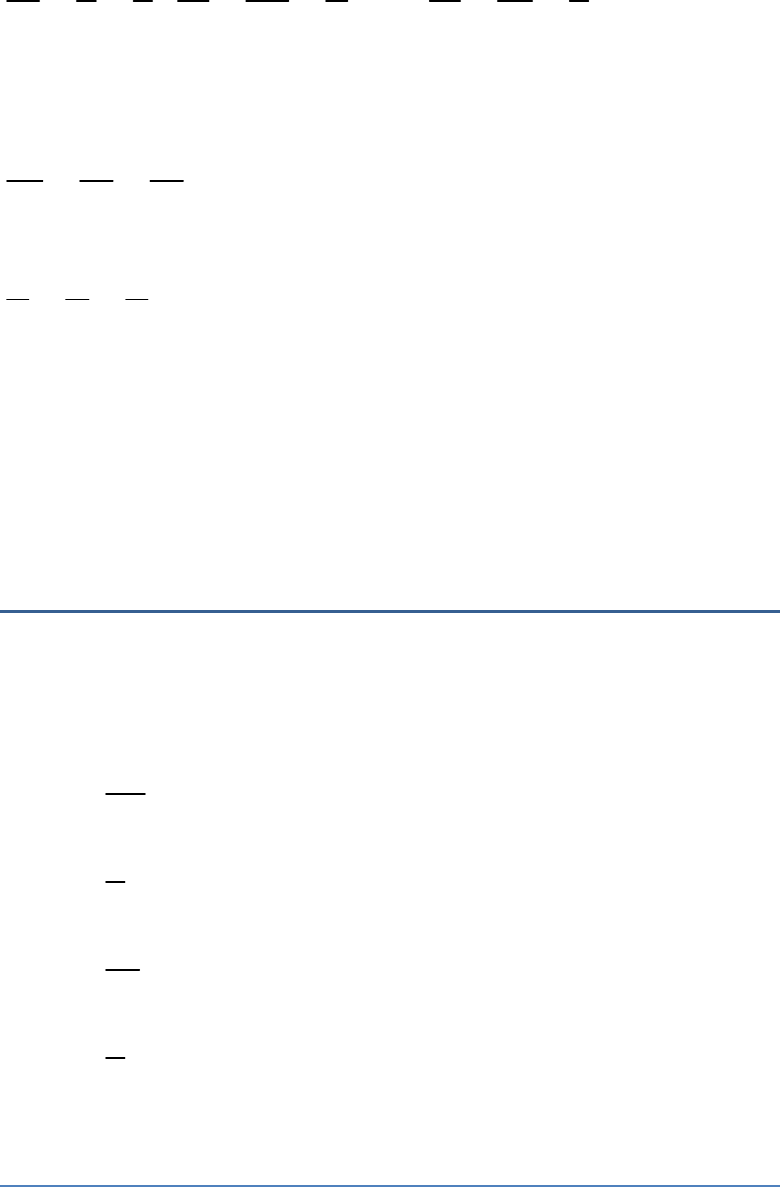
, and .
1
2
3 1
6 2
a
a
1
2
1 1
b
b k k
1
2
8 1
16 2
c
c
For coincident lines,
1 1 1
2 2 2
a b c
a b c
1 1 1
2 2k
2k
Thus, the value of is .
k
2
Question: 7
If the lines given by and
3 2 2
x ky
2 5 1 0
x y
are parallel, then the value of is
k
a.
5
4
b.
2
5
c.
15
4
d.
3
2
Solution:
(c)
Given equations are: and
3 2 2
x ky
2 5 1 0
x y
We can rewrite them as,
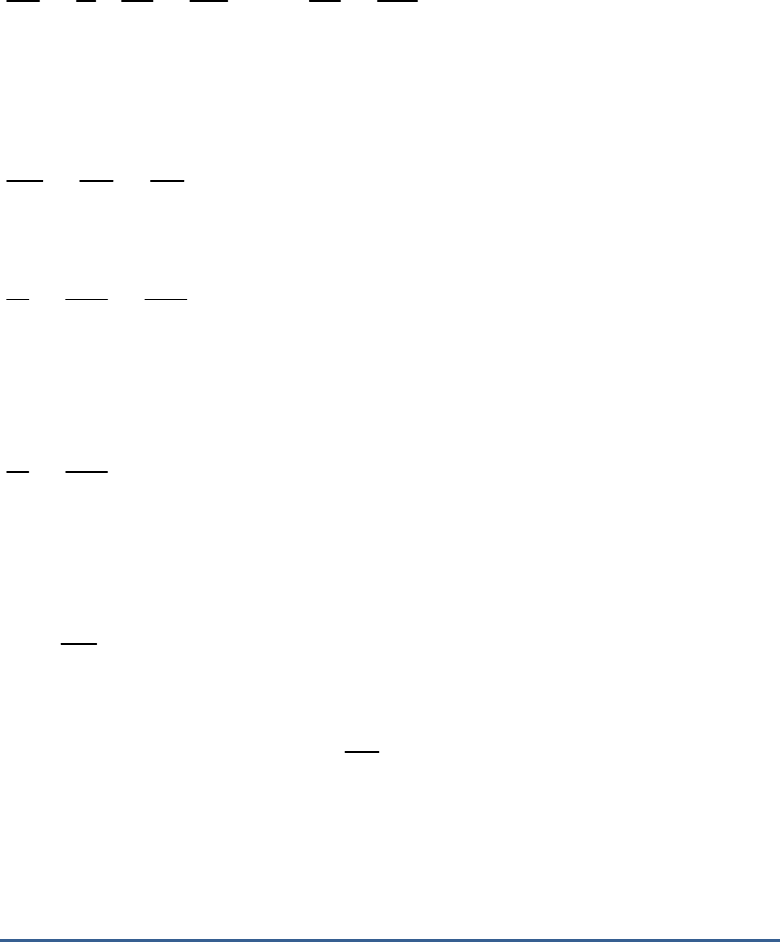
and
3 2 2 0
x ky
2 5 1 0
x y
Compare with and
1 1 1
0
a x b y c
2 2 2
0
a x b y c
,
, and .
1
2
3
2
a
a
1
2
2
5
b k
b
1
2
2
1
c
c
For parallel lines,
1 1 1
2 2 2
a b c
a b c
3 2 2
2 5 1
k
Solve the first two ratios,
3 2
2 5
k
15 4k
15
4
k
Thus, the value of is .
k
15
4
Question: 8
The value of for which the pair of equations
c
and will have infinitely many
2
cx y
6 2 3
x y
solutions is
a.
3

b.
3
c.
12
d. no value
Solution:
(d)
Given equations are: and
2
cx y
6 2 3
x y
We can rewrite them as,
and
2 0
cx y
6 2 3 0
x y
Compare with and
1 1 1
0
a x b y c
2 2 2
0
a x b y c
,
, and
1
2
6
a c
a
1
2
1 1
2 2
b
b
1
2
2 2
3 3
c
c
For infinite many solutions,
1 1 1
2 2 2
a b c
a b c
By the above values,
1 1
2 2
b c
b c
Thus, no value of exists for which the equations
c
have infinite solutions.
Question: 9
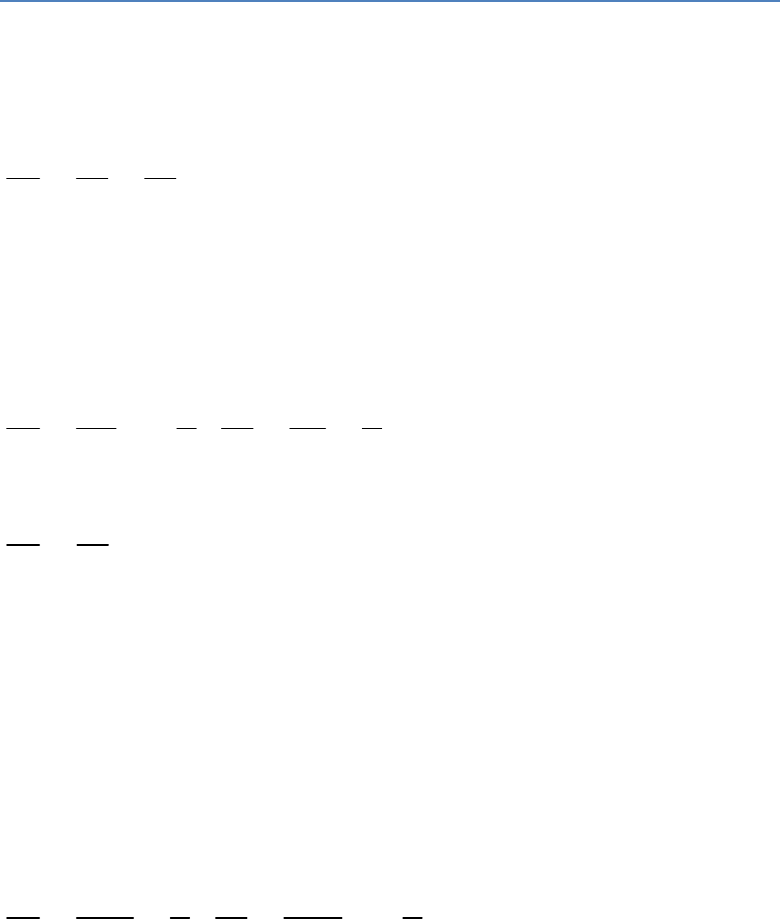
One equation of a pair of dependent linear
equations is . The second equation can
5 7 2
x y
be
a.
10 14 4 0
x y
b.
10 14 4 0
x y
c.
10 14 4 0
x y
d.
10 14 4
x y
Solution:
(d)
For dependent linear equations,
1 1 1
2 2 2
a b c
a b c
Given linear equation is .
5 7 2 0
x y
For case (A),
10 14 4 0
x y
,
1
2
5 1
10 2
a
a
1
2
7 1
14 2
b
b
1 1
2 2
a b
a b
Thus, and are not
10 14 4 0
x y
5 7 2 0
x y
dependent.
For case (B),
10 14 4 0
x y
,
1
2
5 1
10 2
a
a
1
2
7 1
14 2
b
b

1 1
2 2
a b
a b
Thus, and are not
10 14 4 0
x y
5 7 2 0
x y
dependent.
For case (C),
10 14 4 0
x y
, and
1
2
5 1
10 2
a
a
1
2
7 1
14 2
b
b
1
2
2 1
4 2
c
c
1 1 1
2 2 2
a b c
a b c
Thus, and are not
10 14 4 0
x y
5 7 2 0
x y
dependent.
For case (D),
10 14 4 0
x y
, and
1
2
5 1
10 2
a
a
1
2
7 1
14 2
b
b
1
2
2 1
4 2
c
c
1 1 1
2 2 2
a b c
a b c
Thus, and are
10 14 4 0
x y
5 7 2 0
x y
dependent.
Question: 10
A pair of linear equations which has a unique
solution is
2, 3
x y

a.
1
2 3 5
x y
x y
b.
2 5 11
4 10 22
x y
x y
c.
2 1
3 2 0
x y
x y
d.
4 14 0
5 13 0
x y
x y
Solution:
(d)
For case (A),
Given equations are:
… (1)
1
x y
… (2)
2 3 5
x y
Put in LHS of equation (1),
2, 3
x y
2 3x y
2 3
1
RHS
Put in LHS of equation (2),
2, 3
x y
2 3 2 2 3 3x y
4 9
13
13 5
LHS RHS
Thus, satisfies only one of the
2,x
3y
equation.
Hence, case (A) is false.
For case (B),
Given equations are:
… (1)
2 5 11
x y
… (2)
4 10 22
x y
Put in LHS of equation (1),
2,x
3y
2 5 2 2 5 3x y
4 15
11
RHS
Put in LHS of equation (2),
2,x
3y
4 10 4 2 10 3x y
8 30
22
RHS
Thus, satisfies both the equations.
2,x
3y
But these pair of equations are coincident.
So, there are infinite many solutions.
Hence, case (B) is false.
For case (C),
Given equations are:
… (1)
2 1
x y
… (2)
3 2 0
x y
Put in LHS of equation (1),
2,x
3y
2 2 2 3x y
4 3
7
7 11
LHS RHS
Put in LHS of equation (2),
2,x
3y
3 2 3 2 2 3x y
6 6
0
RHS
Thus, satisfies only one of the
2,x
3y
equation.
Hence, case (C) is false.
For case (D),
Given equations are:
… (1)
4 14 0
x y
… (2)
5 13 0
x y

Put in LHS of equation (1),
2,x
3y
4 14 2 4 3 14x y
2 12 14
0
RHS
Put in LHS of equation (2),
2,x
3y
5 13 5 2 3 13x y
10 3 13
0
RHS
Thus, satisfies both the equation.
2,x
3y
Hence, case (D) is true.
Question: 11
If is the solution for the equations,
,x a
y b
and , then the values of and
2
x y
4
x y
a
b
respectively, are
a.
and3 5
b.
and5 3
c.
and3 1
d.
and1 3
Solution:
(c)

If is the solution of the equations
,x a
y b
and .
2
x y
4
x y
… (1)
2
a b
… (2)
4
a b
Add equations (1) and (2),
2 4a b a b
2 6a
3a
Put the value of in equation (2),
a
4a b
3 4b
4 3b
1b
Thus, and .
3a
1b
Question: 12
Aruna has only Re 1 and Rs 2 coins with her. If the
total number of coins she has is 50, and the amount
of money with her is Rs 75, then the number of Re 1
and Rs 2 coins, respectively, are
a.
and35 15
b.
and35 20
c.
and15 35
d.
and25 25

Solution:
(d)
Let be the number of coins of Re 1 and be the
a
b
number of coins Rs. 2.
Total number of coins
50
… (1)
50
a b
Total amount of money with her
Rs75
1 2 75a b
… (2)
2 75a b
Subtract equation (1) from equation (2),
2 75 50a b a b
2 25a b a b
25b
Put the value of in equation (1),
b
50a b
25 50a
50 25a
Thus, and .
25a
25b
Question: 13
The father’s age is six times his son’s age. Four
years hence, the age of the father will be four times

his son’s age. The present ages, in years, of the son
and the father, respectively, are
a.
and4 24
b.
and5 30
c.
and6 36
d.
and3 24
Solution:
(d)
Let the father’s age
years
a
Let the son’s age
years
b
As the father’s age is six times his son’s age,
… (1)
6
a b
After years,
4
The father’s age years
4
a
The son’s age years
4
b
Four years hence, the age of the father will be four
times his son’s age,
4 4 4a b
… (2)
4 12a b
From equation (1) and (2),
6 4 12b b
2 12b
6b

Put the value of in equation (1),
b
6 6a
36
Thus, the father’s age is 36 years and the son’s age
is 6 years.
Exercise 3.2 (6)
Question: 1
Do the following pair of linear equations have no
solution? Justify your answer.
(i)
2 4 3x y
12 6 6y x
(ii)
2x y
2y x
(iii)
3 3 0x y
2
2 2
3
x y
Solution:
(i) The given equations can be written as
2 4 3 0x y
12 6 6 0y x

Compare with and
1 1 1
0
a x b y c
,
2 2 2
0
a x b y c
and
1
2,a
1
4b
1
3c
2
6,a
2
12,b
2
6c
1
2
2 1
,
6 3
a
a
1
2
4 1
,
12 3
b
b
1
2
3 1
6 2
c
c
1 1 1
2 2 2
a b c
a b c
Thus, the pair of linear equations has no
solution.
(ii) The given equations can be written as
2 0x y
2 0x y
Compare with and
1 1 1
0
a x b y c
,
2 2 2
0
a x b y c
and
1
1,a
1
2,b
1
0c
2
2,a
2
1,b
2
0c
1
2
1
,
2
a
a
1
2
2
1
b
b
1 1
2 2
a b
a b
Thus, the pair of linear equations has unique
solution.

(iii) The given equations can be written as
3 3 0x y
2
2 2 0
3
x y
Compare with and
1 1 1
0
a x b y c
,
2 2 2
0
a x b y c
and
1
3,a
1
1,b
1
3c
2
2,a
2
2
,
3
b
2
2c
1
2
3
,
2
a
a
1
2
3
,
2
a
a
1
2
3 3
2 2
c
c
1 1 1
2 2 2
a b c
a b c
Thus, the pair of linear equations has infinitely
many solutions.
Question: 2
Do the following equations represent a pair of
coincident lines? Justify your answer.
(i)
1
3 3
7
x y
7 3 7x y
(ii)
2 3 1x y
6 4 2y x

(iii)
2
0
2 5
x
y
5
4 8 0
16
x y
Solution:
(i) The given equations can be written as
1
3 3 0
7
x y
7 3 7 0x y
Compare with and
1 1 1
0
a x b y c
,
2 2 2
0
a x b y c
and
1
3,a
1
1
,
7
b
1
3c
2
7,a
2
3,b
2
7
1
2
3
,
7
a
a
1
2
1
1 1 1
7
3 7 3 21
b
b
1 1
2 2
a b
a b
Thus, the equations do not represent a pair of
coincident lines.
(ii) The given equations can be written as
2 3 1 0x y
4 6 2 0x y
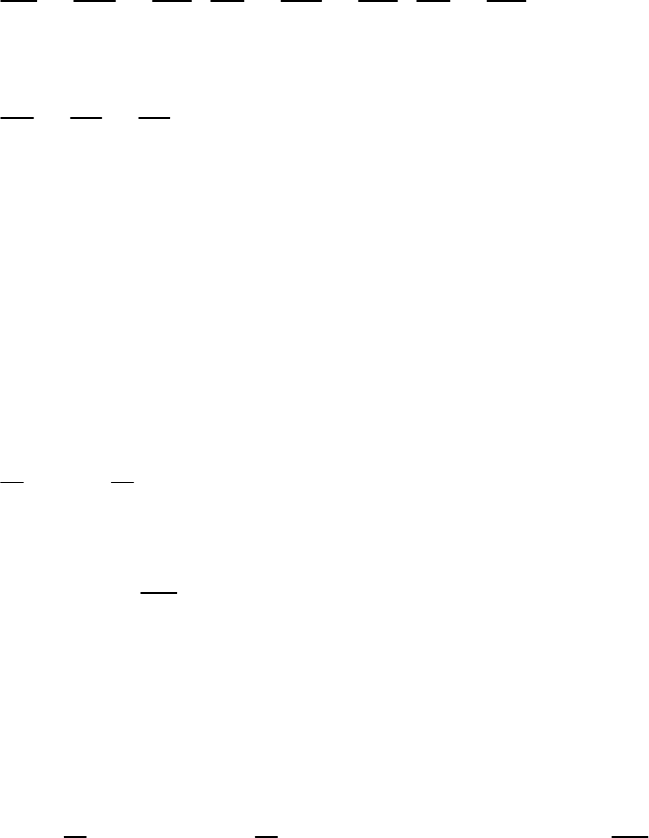
Compare with and
1 1 1
0
a x b y c
,
2 2 2
0
a x b y c
and
1
2,a
1
3,b
1
1c
2
4,a
2
6,b
2
2c
1
2
2 1
,
4 2
a
a
1
2
3 1
,
6 2
b
b
1
2
1
2
c
c
1 1 1
2 2 2
a b c
a b c
Thus, the equations represent a pair of
coincident lines.
(iii) The given equations can be written as
2
0
2 5
x
y
5
4 8 0
16
x y
Compare with and
1 1 1
0
a x b y c
.
2 2 2
0
a x b y c
and
1
1
,
2
a
1
1,b
1
2
5
c
2
4,a
2
8,b
2
5
16
c

1
2
1
1 1 1
2
,
4 2 4 8
a
a
1
2
1
,
8
b
b
1
2
2
2 16 32
5
5
5 5 25
16
c
c
1 1 1
2 2 2
a b c
a b c
Thus, the equations do not represent a pair of
coincident lines.
Question: 3
Are the following pair of linear equations
consistent? Justify your answer.
(i)
3 4 12x y
4 3 12y x
(ii)
3 1
5 2
x y
1 1
3
5 6
x y
(iii)
2ax by a
4 2 2 0;ax by a
, 0a b
(iv)
3 11x y
2 2 6 22x y
Solution:
(i) The given equations can be written as
3 4 12 0x y
3 4 12 0x y
Compare with and
1 1 1
0
a x b y c
.
2 2 2
0
a x b y c
and
1
3,a
1
4,b
1
12c
2
3,a
2
4,b
2
12c
1
2
3
1,
3
a
a
1
2
4
1,
4
b
b
1
2
12
1
12
c
c
1 1 1
2 2 2
a b c
a b c
Thus, the pair of linear equations is
inconsistent.
(ii) The given equations can be written as
3 1
0
5 2
x y
1 1
3 0
5 6
x y
Compare with and
1 1 1
0
a x b y c
.
2 2 2
0
a x b y c
and
1
3
,
5
a
1
1,b
1
1
2
c
2
1
,
5
a
2
3,b
2
1
6
c

1
2
3
3 5 3
5
,
1
5 1 1
5
a
a
1
2
1 1
3 3
b
b
1 1
2 2
a b
a b
Thus, the pair of linear equations is consistent.
(iii) The given equations can be written as
2 0ax by a
4 2 2 0ax by a
Compare with and
1 1 1
0
a x b y c
.
2 2 2
0
a x b y c
and
1
2 ,a a
1
,b b
1
c a
2
4 ,a a
2
2 ,b b
2
2c a
1
2
2 1
,
4 2
a a
a a
1
2
1
,
2 2
b b
b b
1
2
1
2 2
c a
c a
1 1 1
2 2 2
a b c
a b c
Thus, the pair of linear equations is consistent.
(iv) The given equations can be written as
3 11 0x y
4 12 22 0x y

Compare with and
1 1 1
0
a x b y c
.
2 2 2
0
a x b y c
and
1
1,a
1
3,b
1
11c
2
4,a
2
12,b
2
22c
1
2
1
,
4
a
a
1
2
3 1
,
12 4
b
b
1
2
11 1
22 2
c
c
1 1 1
2 2 2
a b c
a b c
Thus, the pair of linear equations is
inconsistent.
Question: 4
For the pair of equations
3 7x y
2 6 14x y
to have infinitely many solutions, the value of
should be . Is the statement true? Give reasons.
1
Solution:
The given equations can be written as
3 7 0x y
2 6 14 0x y
Compare with and
1 1 1
0
a x b y c
2 2 2
0
a x b y c
.

and
1
,a
1
3,b
1
7c
2
2,a
2
6,b
2
14c
1
2
,
2
a
a
1
2
3 1
,
6 2
b
b
1
2
7 1
14 2
c
c
Now, the given pair of linear equations will have
infinitely many solutions if
1 1 1
2 2 2
a b c
a b c
So,
1 1
2 2 2
and
1
1
But
1 1
Thus, the given statement is not true.
Question: 5
For all real values of , the pair of equations
c
2 8x y
5 10x y c
has a unique solution. Justify whether it is true or
false.
Solution:
The given equations can be written as
2 8 0x y
5 10 0x y c

Compare with and
1 1 1
0
a x b y c
2 2 2
0
a x b y c
.
and
1
1,a
1
2,b
1
8c
2
5,a
2
10,b
2
c c
1
2
1
,
5
a
a
1
2
2 1
10 5
b
b
1 1
2 2
a b
a b
The equations do not have a unique solution.
Thus, the given statement is false.
Question: 6
The line represented by is parallel to the –
7
x
x
axis. Justify whether the statement is true or not.
Solution:
Given:
7
x
Any line which is parallel to -axis is of the form
x
, where is a real number.
y a
a
So, is a straight line that is parallel to -axis.
7
x
y
Thus, the statement if false.
Exercise 3.3 (22)

Question: 1
For which value(s) of , do the pair of linear
equations
and have
2
x y
1x y
(i) no solution?
(ii) infinitely many solutions?
(iii) a unique solution?
Solution:
Given pair of linear equations:
and
2
x y
1x y
We can rewrite them as,
and
2
0x y
1 0x y
Compare with and
1 1 1
0
a x b y c
2 2 2
0
a x b y c
.
Here, and .
1
,a
1
1,b
2
1
c
2
1,a
2
,b
2
1c
1
2
,
1
a
a
1
2
1
,
b
b
2 2
1
2
1 1
c
c
(i) The given pair of linear equations has no
solution if
and
1 1 1
2 2 2
a b c
a b c
1 1
2 2
a b
a b
1 1
2 2
a c
a c

Substitute the value of and ,
1
,a
2
,a
1
,b
2
,b
1
c
2
c
and
1
1
2
1 1
and
2
1
2
and
2
1
2
0
and
2
1
1 0
and
1,
1
0
1
Hence, the given pair of linear equations will
have no solution when .
1
(ii) The given pair of linear equations will have
infinitely many solutions if
1 1 1
2 2 2
a b c
a b c
2
1
1 1
and
1
1
2
1 1
and
2
1
2
0
and
1,
1
1 0
and
1,
1
0,
1
1

Hence, the given pair of linear equations will
have infinitely many solutions when .
1
(iii) The given pair of linear equations will have a
unique solution if
1 1
2 2
a b
a b
1
1
2
1
1,
1
Hence, the given pair of linear equations will
have a unique solution for all real values of
except .
1, 1
Question: 2
For which value(s) of will the pair of equations
k
3 3kx y k
12x ky k
have no solution?
Solution:
Given:
3 3kx y k
12x ky k
We can rewrite as,
3 3 0kx y k
12 0x ky k
Here, and
1
,a k
1
3,b
1
3c k
2
12,a
2
,b k
2
c k
Now, the given pair of linear equations has no
solution if
1 1 1
2 2 2
a b c
a b c
3
3
12
k
k
k k
3
3
12
k
k
k k
and
3
12
k
k
3
3
k
k k
and
2
36k
3 3k
and
6k
6k
6k
Hence, the given pair of linear equations has no
solution when .
6
k

Question: 3
For which values of and , will the following pair
a
b
of linear equations have infinitely many solutions?
2 1
x y
2
a b x a b y a b
Solution:
The given pair of linear equations can be written as
2 1 0
x y
2 0
a b x a b y a b
The given pair of linear equations have infinitely
many solutions if
1 1 1
2 2 2
a b c
a b c
1 2 1
2a b a b a b
1 2 1
2a b a b a b
So,
1 2
a b a b
2a b a b
2 2a b a b

3 ......(1)a b
2 1
2a b a b
2 2 4a b a b
4 ......(2)a b
From (1) and (2),
3 4b b
4 4b
1b
Substitute the value of in (1),
b
3a b
3 1
3
Thus, the pair of linear equations have infinitely
many solutions if .
3,a
1b
Question: 4
Find the value(s) of in (i) to (iv) and and in
p
p
q
(v) for the following pair of equations:
(i) and ,
3 5 0x y
6 2 0x y p
if the lines represented by these equations are
parallel.
(ii) and ,
1x py
1px y

if the pair of equations has no solution.
(iii) and ,
3 5 7x y
2 3 1px y
if the lines represented by these equations are
intersecting at a unique point.
(iv) and ,
2 3 5 0x y
6 8 0px y
if the pair of equations has a unique solution.
(v) and ,
2 3 7x y
2 28px py qy
if the pair of equations have infinitely many
solutions.
Solution:
(i) The given pair of linear equations is
and
3 5 0x y
6 2 0x y p
Here, and
1
3,a
1
1,b
1
5c
2
6,a
2
2,b
2
c p
Now, the lines represented by the given pair of
linear equations will be parallel if
1 1 1
2 2 2
a b c
a b c
3 1 5
6 2 p
1 1 5
2 2 p

1 5
2 p
10p
Hence, the lines represented by the given pair
of linear equations will be parallel for all real
values of except 10.
p
(ii) The given pair of linear equations is
and
1x py
1px y
We can rewrite them as,
and
1 0x py
1 0px y
Here, and
1
1,a
1
,b p
1
1c
2
,a p
2
1,b
2
1c
Now, the lines represented by the given pair of
linear equations will have no solution if
1 1 1
2 2 2
a b c
a b c
1 1
1 1
p
p
1 1
1 1
p
p
1
1
p
p
2
1p
1p
If ,
1
p
1
2
1,
a
a
1
2
1,
b
b
1
2
1
c
c
1 1 1
2 2 2
a b c
a b c
If ,
1
p
1
2
1,
a
a
1
2
1,
b
b
1
2
1
c
c
1 1 1
2 2 2
a b c
a b c
Hence, the lines represented by the given pair
of linear equations will have no solution for all
real values of except 1.
p
(iii) The given pair of linear equations is
and
3 5 7x y
2 3 1px y
We can rewrite them as,
and
3 5 7 0x y
2 3 1 0px y
Here, and
1
3,a
1
5,b
1
7c
2
2 ,a p
2
3,b
2
1c
Now, the lines represented by the given pair of
linear equations will intersect at a unique
point if
1 1
2 2
a b
a b
3 5
2 3p
10 9p
9
10
p
Hence, the lines represented by the given pair
of linear equations will intersect at a unique
point for all real values of except .
p
9
10
(iv) The given pair of linear equations is
and
2 3 5 0x y
6 8 0px y
Here, and
1
2,a
1
3,b
1
5c
2
,a p
2
6,b
2
8c
Now, the lines represented by the given pair of
linear equations will have a unique solution if
1 1
2 2
a b
a b
2 3
6p
3 12p
4p
Hence, the lines represented by the given pair
of linear equations will have a unique solution
for all real values of except .
p
4
(v) The given pair of linear equations is
and
2 3 7x y
2 28px py qy
We can rewrite them as,
and
2 3 7 0x y
2 28 0px p q y
Here, and
1
2,a
1
3,b
1
7c
2
2 ,a p
2
,b p q
2
28c
Now, the lines represented by the given pair of
linear equations, will have infinitely many
solutions if
1 1 1
2 2 2
a b c
a b c
2 3 7
2 28p p q
1 3 1
4p p q
and
1 1
4p
3 1
4p q
and
4p
12p q
and
4p
4 12q

and
4p
4p
and
12 4q
8q
Hence, the lines represented by the given pair
of linear equations will have infinitely many
solutions for all real values of and except
p
q
and .
4
8
Question: 5
Two straight paths are represented by the
equations and . Check
3 2
x y
2 6 5
x y
whether the paths cross each other or not.
Solution:
Given equations:
and
3 2
x y
2 6 5
x y
We can rewrite them as,
and
3 2 0
x y
2 6 5 0
x y
Here, and
1
1,a
1
3,b
1
2c
2
2,a
2
6,b
2
5c
1
2
1
,
2
a
a
1
2
3
,
6
b
b
1
2
2
5
c
c
1
2
1
,
2
a
a
1
2
1
,
2
b
b
1
2
2
5
c
c

1 1 1
2 2 2
a b c
a b c
Thus, the paths do not cross each other.
Question: 6
Write a pair of linear equations which has the
unique solution . How many such pairs
1,x
3y
can you write?
Solution:
Given: Required pair of equations
1,x
3y
2x y
2 1x y
There is infinite many such pair are possible.
Question: 7
If and , find the values of
2 23x y
4 19x y
and .
5 2y x
2
y
x
Solution:
Given equations:
2 23 ......(1)x y
4 19 ......(2)x y
Add equations (1) and (2),
2 4 23 19x y x y
6 42x
7x
Put the value of in equation (1),
x
2 23x y
2 7 23y
14 23y
23 14y
9y
Now, calculate the value of and .
5 2y x
2
y
x
5 2 5 9 2 7y x
45 14
31
9
2 2
7
y
x
9 14
7
5
7
Thus, and .
5 2 31
y x
5
2
7
y
x

Question: 8
Find the values of and in the following
x
y
rectangle.
Solution:
The opposite sides of a rectangle are equal.
3 7 ......(1)x y
3 13 ......(2)x y
Multiply equation (2) by 3,
3 9 39 ......(3)x y
Subtract equation (1) from equation (3),
3 9 3 39 7x y x y
3 9 3 39 7x y x y
8 32y
4y
Put the value of in equation (1),
y
3 7x y

3 4 7x
3 7 4x
3 3x
1x
Thus, .
1,x
4y
Question: 9
Solve the following pairs of equations:
(i)
3.3x y
1,
3 2
0.6
x y
3 2 0x y
(ii)
4
3 4
x y
5
4
6 8
x y
(iii)
6
4 15x
y
8
6 14,x
y
0y
(iv)
1 1
1
2x y
1 1
8,
2x y
, 0x y
(v)
43 67 24x y
67 43 24x y

(vi)
x y
a b
a b
2 2
2,
x y
a b
, 0a b
(vii)
2 3
2
xy
x y
3
,
2 10
xy
x y
0,2 0x y x y
Solution:
(i) Given equations:
.3 ......( )3 1x y
0 6
1
3 2
.
x y
3 2 0 6 ......(2).x y
Multiply equation (1) by 2,
2 2 6 6 ..... (3). .x y
Add equation (2) and (3),
2 2 3 2 6.6 0.6x y x y
5 6x
6
5
x
.1 2x
Put the value of in equation (1),
x
3.3x y
1.2 3.3y
3.3 1.2y
2.1y
Thus, .
1.2,x
2.1y
(ii) Given equations:
4 ......(1)
3 4
x y
5
4 ......(2)
6 8
x y
Multiply equation (1) by 12,
12 12
48
3 4
x y
4 3 48 ......(3)x y
Multiply equation (2) by 24,
5 24
24
96
6 8
x
y
20 3 96 .......(4)x y
Add equation (3) and (4),
4 3 20 3 48 96x y x y
24 144x
6x
Put the value of in equation (3),
x
4 3 48x y
4 6 3 48y
24 3 48y
3 48 24y
3 24y
8y
Thus, .
6,x
8y
(iii) Given equations:
6
4 15x
y
8
6 14x
y
Let .
1
a
y
4 6 15 ......(1)x a
6 8 14 ......(2)x a
Multiply equation (1) by 4,
16 24 60 ......(3)x a
Multiply equation (2) by 3,
18 24 42 ......(4)x a
Add equation (3) and (4),
16 24 18 24 60 42x a x a
34 102x
3x

Put the value of in equation (1),
x
4 6 15x a
4 3 6 15a
12 6 15a
6 15 12a
6 3a
3
6
a
1
2
a
Since, .
1
a
y
So,
1 1
2y
2y
Thus, .
3,x
2y
(iv) Given equations:
1 1
1
2x y
1 1
8
2x y
Put .
1 1
,
a b
x y
1 ......(1)
2
a
b
8 ......(2)
2
b
a
Multiply the equation (1) by ,
1
2
1
......(3)
4 2 2
a b
Add equation (2) and (3),
1
8
2 4 2 2
b a b
a
16 1
4 2
a
a
5 15
4 2
a
15 4
2 5
a
6a
Put the value of in equation (2),
a
8
2
b
a
6 8
2
b
8 6
2
b
2
2
b
4b
So,
6,a
4b
1
6,
x
1
4
y
1
,
6
x
1
4
y
Thus, .
1
,
6
x
1
4
y
(v) Given equations:
43 67 24 ......(1)x y
67 43 24 ......(2)x y
Add equation (1) and (2),
110 110 0x y
0 ......(3)x y
Subtract equation (1) and (2),
24 24 48x y
2 ......(4)x y
Add (3) and (4),
0 2x y x y
2x y x y
2 2y
1y
Put the value of in equation (3),
y
0x y
1 0x
1x
Thus, .
1,x
1y
(vi) Given equations:
......(1)
x y
a b
a b
2 2
2 ......(2)
x y
a b
Multiply the equation (1) by ,
1
a
2
......(3)
x y a b
a ab a
Subtract equation (2) from (3),
2 2 2
2
x y x y a b
a ab a b a
2 2 2
2
x y x y a b
a ab a b a
2
2
y y a b
ab b a
2
1 1 2a b a
y
ab b a
2
b a b a
y
ab a
2
b a
ab
y
a b a
2
y b
Put the value of in equation (2),
y
2 2
2
x y
a b
2
2 2
2
x b
a b
2
1 2
x
a
2
2 1
x
a
2
1
x
a
2
x a
Thus, .
2
,x a
2
y b
(vii) Given equations:
2 3
......(1)
2
xy
x y
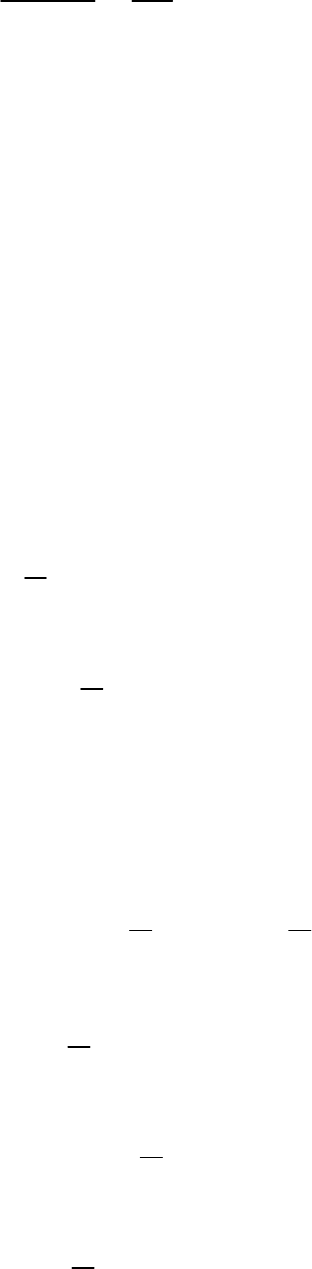
3
......(2)
2 10
xy
x y
3 3 4 ......(3)x y xy
10 3 2xy x y
6 3 10 ......(4)x y xy
Subtract equation (4) from (3),
3 3 6 3 4 10x y x y xy xy
3 3 6 3 4 10x y x y xy xy
9 6x xy
9
6
y
3
2
y
Put the value of in equation (3),
y
3 3 4x y xy
3 3
3 3 4
2 2
x x
9
3 6
2
x x
9
3 6
2
x x
9
9
2
x

1
2
x
Thus, .
1
,
2
x
3
2
y
Put in both equations,
0
x
.
0
y
So, is a solution if .
0,x
0y
0,x
0y
Question: 10
Find the solution of the pair of equations
and , hence, find , if
1 0
10 5
x y
15
8 6
x y
.
5
y x
Solution:
Given equations:
1 0 ......(1)
10 5
x y
15 ......(2)
8 6
x y
Multiply equation (1) by 10,
10 10
10
10 5
x y
2 10 ......(3)x y
Multiply equation (2) by 24,

24 24
15 24
8 6
x y
3 4 360 ......(4)x y
Multiply equation (3) by 3,
3 6 30 ......(5)x y
Subtract equation (4) from (5),
3 6 3 4 30 360x y x y
3 6 3 4 30 360x y x y
2 330y
165y
Put the value of in equation (5),
y
3 6 30x y
3 6 165 30x
3 990 30x
3 30 990x
3 1020x
340x
Thus, .
340,x
165y
Now,
5
y x
165 340 5
165 5 340
340 170

170
340
1
2
Thus, .
1
2
Question: 11
By the graphical method, find whether the
following pair of equations are consistent or not. If
consistent, solve them.
(i)
3 4 0x y
6 2 4 0x y
(ii)
2 6x y
3 6 0x y
(iii)
3x y
3 3 9x y
Solution:
(i) Given equations:
3 4 0x y
6 2 4 0x y
Equation 1:
3 4 0 ......(1)x y
Equation 2:

6 2 4 0 ......(2)x y
To represent these equations graphically, you
must have at least two solutions for each
equation.
For equation 1:
The points are and .
0, 4
2,2
3 4
y x
x
0
1
2
y
4
1
2
For equation 2:
The points are and .
0,2
2, 4
6 2 4 0x y
2 6 4y x
3 2y x
x
0
1
2
y
2
1
4
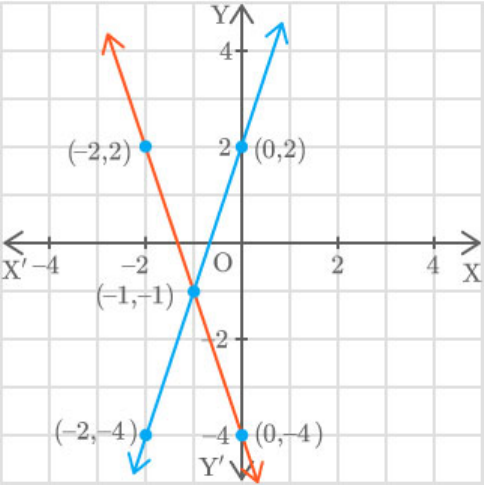
These lines intersect at point . So, these
1, 1
lines are consistent.
(ii) Given equations:
2 6x y
3 6 0x y
Equation 1:
2 6 ......(1)x y
Equation 2:
3 6 0 ......(2)x y
To represent these equations graphically, you
must have at least two solutions for each
equation.
For equation 1:
The points are and .
0, 3
6,0
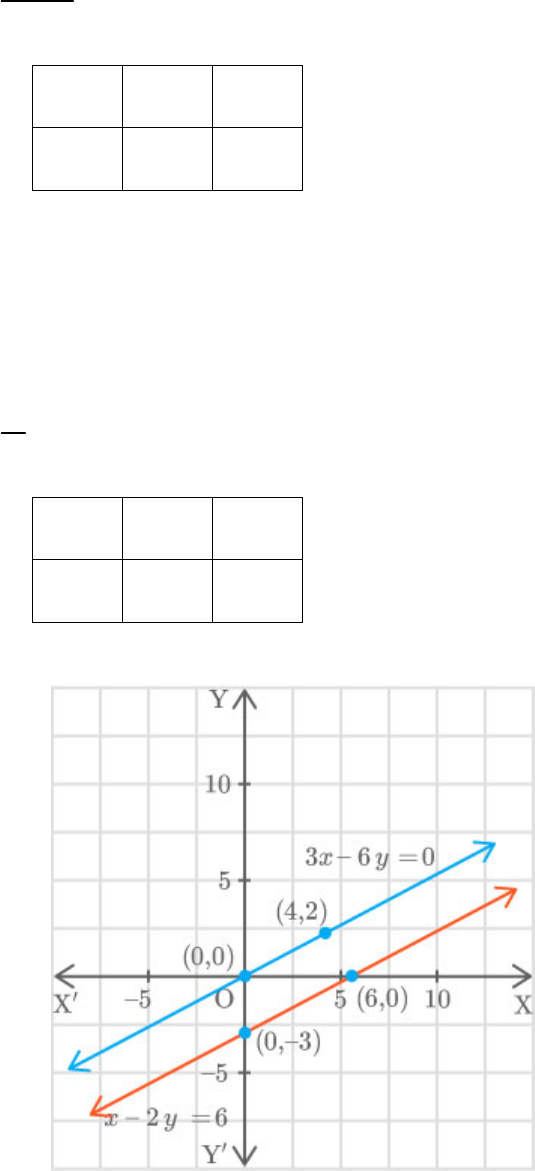
6
2
x
y
x
0
6
y
3
0
For equation 2:
The points are and .
0,0
4,2
2
x
y
x
0
4
y
0
2
These lines are parallel. So, these lines are
inconsistent.

(iii) Given equations:
3x y
3 3 9x y
Equation 1:
3 ......(1)x y
Equation 2:
3 3 9 ...... 2x y
… (2)
To represent these equations graphically, you
must have at least two solutions for each
equation.
For equation 1:
The points are and .
0,3
3,0
3
y x
x
0
3
y
3
0
For equation 2:
The points are and .
0,3
3,0
3
y x
x
0
3

y
3
0
These lines are coinciding each other. So, these
lines are consistent.
Question: 12
Draw the graph for a pair of equations,
2 4
x y
and . Write the vertices of the triangle
2 4
x y
formed by these lines and the -axis. Also, find the
y
area of this triangle.
Solution:
Equation 1:
2 4 ...... 1x y
Equation 2:

2 4 ...... 2x y
To represent these equations graphically, you must
have at least two solutions for each equation.
For equation 1:
The points are .
and0,4 2,0
4 2
y x
x
0
2
y
4
0
For equation 2:
The points are and .
0, 4
2,0
2 4
y x
x
0
2
y
4
0
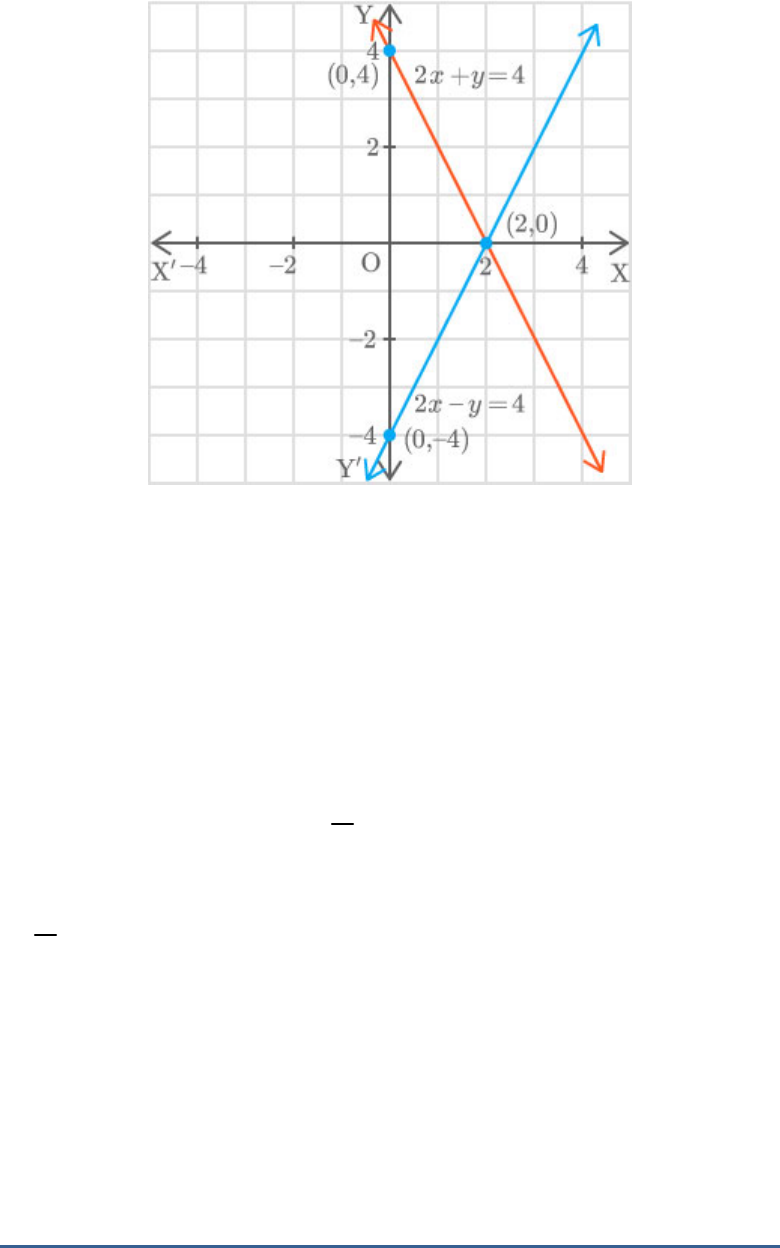
The coordinates of the triangle are and
0,4 , 2,0
.
0, 4
Base
8
Height
2
Area of the triangle base height
1
2
1
8 2
2
8
Thus, the area of the triangle is square unit.
8
Question: 13
Write an equation of a line which passes through
the point representing the solution of the pair of

linear equations, and . How
2
x y
2 1
x y
many such lines can we find?
Solution:
Given equations:
2 ...... 1x y
2 1 ...... 2x y
Add equations (1) and (2),
2 2 1x y x y
3 3x
1x
Put the value of in equation (1),
x
2x y
1 2y
2 1y
1y
Thus, .
1,x
1y
The line representing the equation passes
2 3
x y
through .
1,1
There are infinite such lines that can be possibly
drawn.
Question: 14

If is a factor of , then find
1
x
3 2
2 2 1
x ax bx
the values of and given that .
a
b
2 3 4
a b
Solution:
Let
3 2
2 2 1
p x x ax bx
is a factor of .
1
x
p x
1 0
p
3 2
2 1 1 2 1 1 0a b
2 2 1 0a b
2 1 ...... 1a b
2 3 4 ...... 2a b
Multiply equation (1) by 2,
2 4 2 ...... 3a b
Subtract equation (2) from equation (3),
2 4 2 3 2 4a b a b
2 4 2 3 2 4a b a b
2b
2b
Put the value of in equation (1),
b
2 1a b
2 2 1a
4 1a

1 4a
5a
Thus, .
5,a
2b
Question: 15
The angles of a triangle are and . The
,
x y
40
difference between the two angles and is .
x
y
30
Find and .
x
y
Solution:
The angles of a triangle are and .
,
x y
40
By the angle sum property,
40 180x y
180 40x y
140 ...... 1x y
30 ...... 2x y
Add equation (1) and (2),
140 30x y x y
2 170x
85x
Put the value of in equation (2),
x
30x y
85 30y

30 85y
55y
55y
Thus, .
85 ,x
55y
Question: 16
Two years ago, Salim was thrice as old as his
daughter and six years later, he will be four years
older than twice her age. How old are they now?
Solution:
Let Salim’s age
years
x
Let his daughter’s age
years
y
years ago,
2
2 3 2x y
2 3 6x y
3 6 2x y
3 4 ...... 1x y
years later,
6
6 2 6 4x y
6 2 12 4x y
6 2 16x y
2 16 6x y

2 10 ...... 2x y
Subtract equation (1) from equation (2),
2 3 10 4x y x y
2 3 10 4x y x y
14y
Put the value of in equation (1),
y
3 14 4x
42 4x
4 42x
38x
Thus, the age of Salim is years and his
38
daughter's age is years.
14
Question: 17
The age of the father is twice the sum of the ages of
his two children. After years, his age will be
20
equal to the sum of the ages of his children. Find
the age of the father.
Solution:
Let the age of father be years and the sum of the
x
ages of his two children be years.
y
2x y

...... 1
2
x
y
After years,
20
20 40x y
20 40
2
x
x
2 40 80x x
2 80 40x x
Hence, the age of the father is years.
40
Question: 18
Two numbers are in the ratio . If is subtracted
5: 6
8
from each of the numbers, the ratio becomes .
4:5
Find the numbers.
Solution:
Let and be two numbers such that
x
y
5
6
x
y
6 5 0 ...... 1x y
is subtracted from both the numbers, the ratio is
8
.
4:5
8 4
8 5
x
y

5 8 4 8x y
5 40 4 32x y
5 4 32 40x y
5 4 8 ...... 2x y
Multiply equation (1) by and equation (2) by ,
4
5
24 20 0 ...... 3x y
25 20 40 ...... 4x y
Subtract equation (3) from (4),
25 20 24 20 40 0x y x y
25 20 24 20 40 0x y x y
40x
Put the value of in equation (1),
x
6 5 0x y
6 40 5 0y
240 5 0y
5 240y
240
5
y
48y
Thus, the numbers are and .
40
48
Question: 19

There are some students in two examination halls,
A and B. To make the number of students equal in
each hall, students are sent from A to B. But if
10
students are sent from B to A, the number of
20
students in A becomes double the number of
students in B. Find the number of students in the
two halls.
Solution:
Let the number of students in hall A
x
Let the number of students in hall B
y
students are sent from A to B,
10
10 10x y
20 ...... 1x y
students are sent from B to A,
20
2 20 20y x
2 40 20y x
2 60y x
60
...... 2
2
x
y
Substitute (2) in (1),
20x y
60
20
2
x
x

2 60 40x x
2 100x x
100x
Put the value of in equation (1),
x
20x y
100 20y
100 20y
80y
Thus, the number of students in hall A is and in
100
hall B is .
80
Question: 20
A shopkeeper gives books on rent for reading. She
takes a fixed charge for the first two days, and an
additional charge for each day thereafter. Latika
paid Rs for a book kept for six days, while Anand
22
paid Rs for a book kept for four days. Find the
16
fixed charges and the charge for each extra day.
Solution:
Let fixed charge
Rs.
x
Let charge for per day
Rs.
y
So, Latika kept a book for days.
6

She pays fixed charge for 2 days and additional
charge for days.
4
4 22 ...... 1x y
She pays fixed charge for 2 days and additional
charge for days.
2
2 16 ...... 2x y
Subtract equation (2) from equation (1),
4 2 22 16x y x y
4 2 22 16x y x y
2 6y
3y
Put the value of in equation (1),
y
4 22x y
4 3 22x
12 22x
22 12x
10x
Thus, fixed charge for first two days is Rs. and
10
charge per day is Rs. .
3
Question: 21

In a competitive examination, one mark is awarded
for every correct answer while mark is deducted
1
2
for every wrong answer. Jayanti answered
120
questions and got marks. How many questions
90
did she answer correctly?
Solution:
Let the number of correct answers be and the
x
number of wrong answers be .
y
120x y
120 ...... 1x y
1
90 ...... 2
2
x y
Substitute equation (1) in equation (2)
1
90
2
x y
1
120 90
2
y y
3
120 90
2
y
3
90 120
2
y
3
30
2
y

2
30
3
y
20y
Put the value of in equation (2),
y
120x y
120 20
100
Thus, the number of correct answer is .
100
Question: 22
The angles of a cyclic quadrilateral ABCD are
A 6 10 ,x
B 5 ,x
C ,x y
D 3 10y
Find and , and hence the values of the four
x
y
angles.
Solution:
Given:
A 6 10 ,x
B 5 ,x
C ,x y
D 3 10y
The sum of opposite angles of a cyclic quadrilateral
is .
180
A C 180
6 10 180x x y
7 180 10x y
7 170 ...... 1x y
B D 180
5 3 10 180x y
5 3 180 10x y
5 3 190 ...... 2x y
Multiply equation (1) by 3,
21 3 510 ...... 3x y
Subtract equation (2) from equation (3),
21 3 5 3 510 190x y x y
21 3 5 3 510 190x y x y
16 320x
20x
Put the value of in equation (2),
x
5 3 190x y
5 20 3 190y
3 190 100y
3 90y
30y
The four angles are:
A 6 10x

6 20 10
120 10
130
B 5x
5 20
100
C x y
20 30
50
D 3 10y
3 30 10
90 10
80
Thus, .
A 130 ,
B 100 ,
C 50 ,
D 80
Exercise 3.4 (13)
Question: 1
Graphically, solve the following pair of equations:
2 6
x y
2 2 0
x y

Find the ratio of the areas of the two triangles
formed by the lines representing these equations
with the -axis and the lines with the -axis.
x
y
Solution:
The given equations are:
2 6
x y
2 2 0
x y
We can rewrite them as
6 2 ...... 1y x
2 2 ...... 2y x
To represent these equations, you must have at
least two solutions for each equation.
For equation 1:
The points are .
and0,6 3,0
6 2
y x
x
0
3
y
6
0
For equation 2:
The points are and .
0,2
1,0
2 2
y x
x
0
1
y
2
0
Area of triangle ABC base height
1
2
1
4 1
2
2
The area of triangle ABC is square unit.
2
Area of triangle APQ base height
1
2
1
4 4
2
8
The area of triangle APQ is square unit.
8
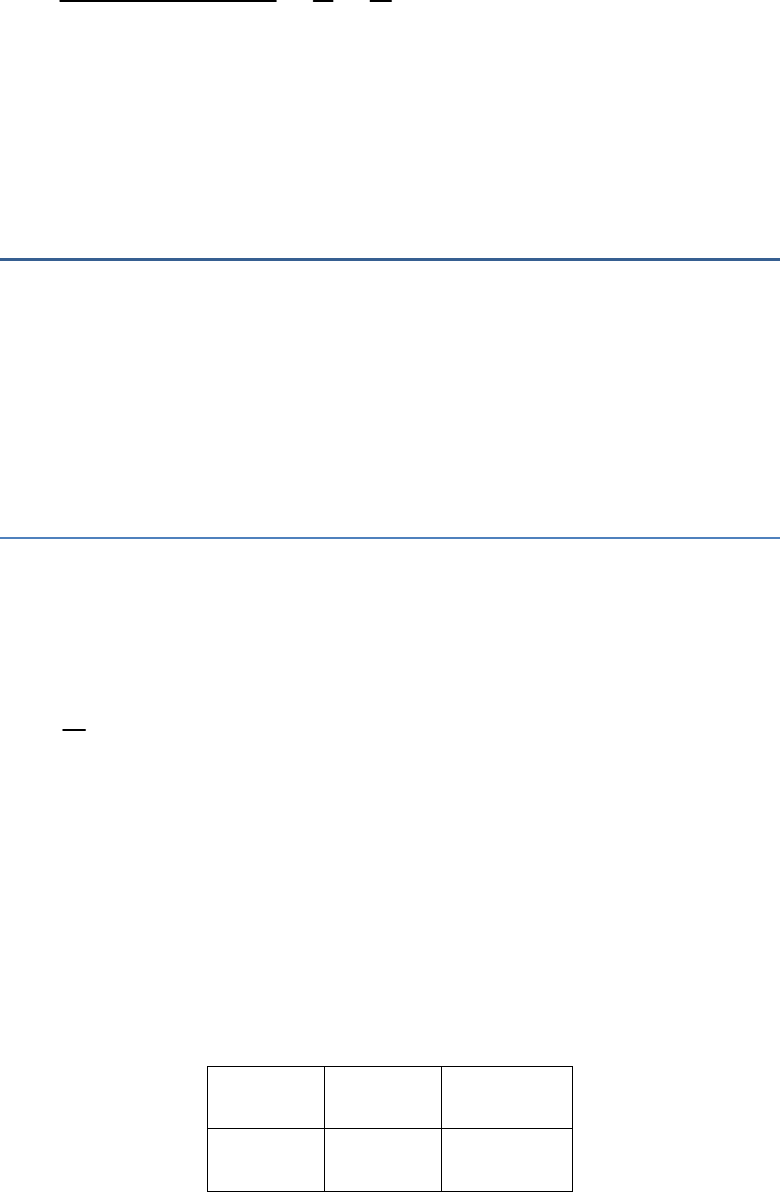
So, .
Area of APQ
Area of ABC
8 4
2 1
Thus, the ratio of the areas of two triangles is .
4:1
Question: 2
Determine, graphically, the vertices of the triangle
formed by the lines
y x
3
y x
8
x y
Solution:
The given equations are:
...... 1y x
...... 2
3
x
y
8 ...... 3x y
For equation 1:
The points are and .
2,2
4,4
y x
x
2
4
y
2
4
For equation 2:
The points are and .
3,1
6,2
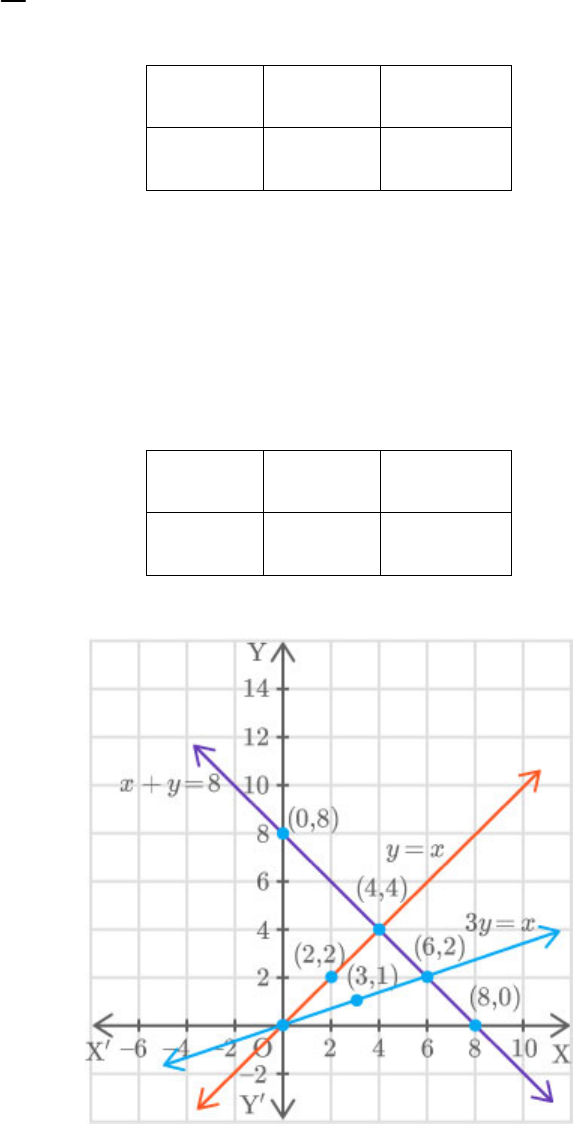
3
x
y
x
3
6
y
1
2
For equation 3:
The points are and .
0,8
8,0
8
y x
x
0
8
y
8
0
The vertices of the triangle are and
0,0 ,
4,4
.
6,2

Question: 3
Draw the graphs for the equations, and
3, 5x x
. Also, find the area of the
2 4 0x y
quadrilateral formed by the lines and the –axis.
x
Solution:
The given linear equations are:
and
3, 5x x
2 4 0x y
The graph of is a straight line parallel to -
3
x
y
axis and is at a distance of right to -axis.
units3
y
The graph of is a straight line parallel to -
5
x
y
axis and is at a distance of right to -axis.
units5
y
,
2 4
y x
The points are and .
2,0
0, 4
x
2
0
y
0
4
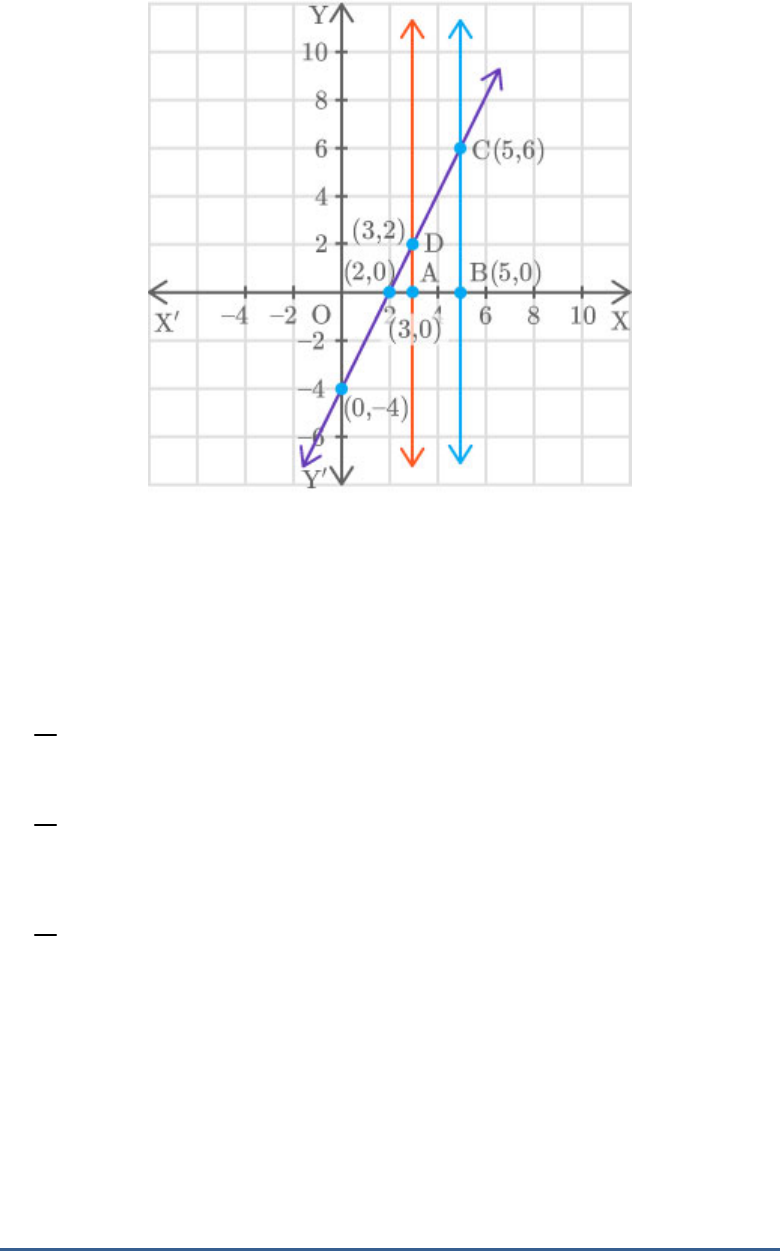
and .
2 ,AB units
2AD units
6BC units
Now, calculate the area of the quadrilateral.
Required area area of trapezium ABCD
1
2
sum of parallel sides height
1
2
AD BC AB
1
2 6 2
2
.8 sq units
Thus, the area of the trapezium is sq. units.
8
Question: 4
The cost of pens and pencil boxes is Rs .
4
4
100
Three times the cost of a pen is Rs more than the
15
cost of a pencil box. Form the pair of linear

equations for the above situation. Find the cost of a
pen and a pencil box.
Solution:
Let be the cost of one pen and be the
Rs.
x
Rs.
y
cost of one pencil box.
According to the questions,
… (1)
4 4 100
x y
3 15x y
… (2)
3 15x y
Multiply the equation (2) by 4.
… (3)
12 4 60
x y
Add equation (1) and (3),
4 4 12 4 100 60x y x y
16 160x
10x
Put the value of in equation (1),
x
4 4 100x y
4 10 4 100y
40 4 100y
4 100 40y
4 60y
15y

Thus, the cost of one pen is Rs. 10 and the cost of
one pencil box is Rs. 15.
Question: 5
Determine algebraically, the vertices of the triangle
formed by the lines
3 3
x y
2 3 2
x y
2 8
x y
Solution:
The given equations are:
3 3
x y
2 3 2
x y
2 8
x y
We can rewrite them as
3 3 ...... 1y x
2 3
...... 2
2
y
x
8 2 ...... 3x y
To represent these equations, you must have at
least two solutions for each equation.
For equation 1:
The points are .
and0, 3 1,0
3 3
y x
x
0
1
y
3
0
For equation 2:
The points are .
and4,2 1,0
2 3
2
y
x
x
4
1
y
2
0
For equation 3:
The points are and .
0,4
8,0
8 2
x y
x
0
8
y
4
0
The graph is:
Thus, the vertices of a triangle are and
2,3 , 4,2
.
1,0
Question: 4
Ankita travels km to her home partly by
14
rickshaw and partly by bus. She takes half an hour
if she travels km by rickshaw and the remaining
2
distance by bus. On the other hand, if she travels
4
km by rickshaw and the remaining distance by bus,
she takes minutes longer. Find the speed of the
9
rickshaw and of the bus.
Solution:
Let be the speed of bus and be the
km h/
x
km h/
y
speed of rickshaw.
Case 1:
Distance covered by rickshaw
km2
Distance covered by bus
14 km 2 km
12 km
Time taken by bus time taken by rickshaw
1
2
hours.
12 2 1
...... 1
2x y
Case 2:
Distance covered by rickshaw
km4
Distance covered by bus
14 km 4 km
10 km
Time taken by bus time taken by rickshaw
30 min 9 min
39 min
.
39
hour
60
10 4 39
...... 2
60x y
Multiply the equation (1) by ,
2
24 4 2
...... 3
2x y
Subtract equation (3) from equation (2),
10 4 24 4 39
1
60x y x y
10 24 39
1
60x x
Take LCM on both sides,
10 24 39 60
60x
14 21
60x
60
14
21
x
40 km / hx
Put the value of in equation (1),
x
12 2 1
2x y
12 2 1
40 2y
2 1 12
2 40y
2 1 3
2 10y
2 5 3
10y

2 2
10y
10 km / hy
Thus,
Speed of the bus
km h40 /
Speed of the rickshaw
km h10 /
Question: 7
A person, rowing at the rate of km/h in still water,
5
takes thrice as much time in going km upstream
40
than in going km downstream. Find the speed of
40
the stream.
Solution:
Let be the speed of the stream.
x
Speed of the boat in still water
km h5 /
The speed of the boat upstream
km h5 /
x
The speed of the boat downstream
km h5 /
x
Now, according to the condition,
40 km 40 km
3
5 km / h 5 km / hx x
1 3
5 5x x

5 15 3x x
3 15 5x x
4 10x
10
4
x
.
5
2 5 km / h
2
x
Thus, the speed of the stream is .
km h2.5 /
Question: 8
A motor boat can travel km upstream and km
30
28
downstream in hours. It can travel km
7
21
upstream and return in hours. Find the speed of
5
the boat in still water and the speed of the stream.
Solution:
Let be the speed of the boat in still water and
x
y
be the speed of the stream.
30 28
7 ...... 1
x y x y
21 21
5
x y x y
1 1 5
21x y x y

Multiply both sides by ,
28
28 28 5
28
21x y x y
28 28 20
...... 2
3x y x y
Subtract equation (2) from (1),
30 28 28 28 20
7
3x y x y x y x y
30 28 21 20
3x y x y
2 1
3x y
6 ...... 3x y
1 1 5
6 21x y
1 5 1
21 6x y
1 10 7
42x y
1 3 1
42 14x y
14 ...... 4x y
Add equation (3) and (4),
6 14x y x y

2 20x
10x
Put the value of in equation (3),
x
6x y
10 6y
6 10y
4y
4y
Thus,
Speed of boat in still water
km h10 /
Speed of stream
km h4 /
Question: 9
A two-digit number is obtained by either
multiplying the sum of the digits by and then
8
subtracting or by multiplying the difference of
5
the digits by and then adding . Find the
16
3
number.
Solution:
Let the unit digit of the number be and the ten’s
x
digit of the number be .
y
The number
10
y x
Sum of the digits
x y
10 8 5y x x y
10 8 8 5y x x y
10 8 8 5y y x x
2 7 5y x
7 2 5 ...... 1x y
Difference of the digits
y x
x y
10 16 3y x y x
10 16 16 3y x y x
10 16 16 3y y x x
17 6 3 ...... 2x y
Multiply equation (1) by 3,
21 6 15 ...... 3x y
Subtract equation (2) from (3),
21 6 17 6 15 3x y x y
21 6 17 6 15 3x y x y
4 12x
3x
Put the value of in equation (1),
x
7 2 5x y
7 3 2 5y
21 2 5y
2 5 21y

2 16y
8y
Thus, the unit digit of the number is and the ten’s
3
digit number is .
8
The number is .
83
Question: 10
A railway half ticket costs half the full fare, but the
reservation charges are the same on a half ticket as
on a full ticket. One reserved first class ticket from
the station A to B costs Rs . Also, one reserved
2530
first class ticket and one reserved first class half
ticket from A to B costs Rs . Find the full first
3810
class fare from station A to B, and also the
reservation charges for a ticket.
Solution:
Let be the cost of full ticket from station to .
x
A
B
Let be the cost of reservation.
y
A reserved first class ticket costs Rs.
2530
2530 ...... 1x y
Now, one full and one half first class reserved ticket
costs is Rs. .
3810
3
2 3810 ...... 2
2
x y
Multiply the equation (1) by 2,
2 2 5060 ...... 3x y
Subtract the equation (2) from (3),
3
2 2 2 5060 3810
2
x y x y
3
2 2 2 5060 3810
2
x y x y
1
1250
2
x
2500x
Put the value of in equation (1),
x
2530x y
2500 2530y
2530 2500y
30y
Thus, the first-class ticket from to is Rs.
A
B
2500
and the reservation cost is Rs. .
30
Question: 11
A shopkeeper sells a saree at profit and a
8%
sweater at discount, thereby, getting a sum Rs.
10%
. If she had sold the saree at profit and the
1008
10%
sweater at discount, she would have got Rs.
8%
. Find the cost price of the saree and the list
1028
price (price before discount) of the sweater.
Solution:
Let be the CP of the saree and be the CP of the
x
y
sweater.
Case 1:
Saree is sold at profit.
8%
8
SP of saree
100
x
x
100 8
100
x x
108
100
x
Sweater is sold at discount.
10%
10
SP of sweater
100
y
y
100 10
100
y y
90
100
y
The saree and sweater fetch Rs. .
1008
108 90
1008
100 100
x y

108 90
1008
100
x y
108 90 100800x y
6 5 5600x y
5600 5
...... 1
6
y
x
Saree is sold at profit.
10%
10
SP of saree
100
x
x
100 10
100
x x
110
100
x
Sweater is sold at discount.
8%
8
SP of sweater
100
y
y
100 8
100
y y
92
100
y
The saree and sweater fetch Rs. .
1028
110 92
1028
100 100
x y
110 92
1028
100
x y
110 92 102800 ...... 2x y
… (2)
Put the value of in equation (2),
x
110 92 102800x y
5600 5
110 92 102800
6
y
y
110 5600 110 5
92 102800
6 6
y
y
616000 550
92 102800
6 6
y
y
550 616000
92 102800
6 6
y
y
Take LCM on both sides,
550 552 616800 616000
6 6
y y
2 800
6 6
y
2 800y
400y
Put the value of in equation (1),
y
5600 5
6
y
x
5600 5 400
6

5600 2000
6
3600
600
6
Thus, the CP of saree is Rs. and the CP of
600
sweater is Rs. .
400
Question: 12
Susan invested a certain amount of money in two
schemes A and B, which offer interest at the rate of
8% per annum and per annum, respectively. She
9%
received Rs as annual interest. However, had
1860
she interchanged the amount of investments in the
two schemes, she would have received Rs more
20
as the annual interest. How much money did she
invest in each scheme?
Solution:
Let be the amount invested in scheme A and be
x
y
the amount invested in scheme B.
Case 1:
8% of 9% of 1860x y
1 8 9 1
1860
100 100
x y

8 9
1860
100 100
x y
8 9 186000 ...... 1x y
Case 2:
9% of 8% of 1860 20x y
1 9 8 1
1880
100 100
x y
9 8
1880
100 100
x y
9 8 188000 ...... 2x y
Add equation (1) and (2),
8 9 9 8 186000 188000x y x y
17 17 374000x y
22000 ...... 3x y
Subtract equation (1) from equation (2),
9 8 8 9 188000 186000x y x y
9 8 8 9 2000x y x y
2000 ...... 4x y
Add equation (3) and (4),
22000 2000x y x y
2 24000x
12000x
Put the value of in equation (3),
x

22000x y
12000 22000y
22000 12000y
10000y
Thus, the amount invested in scheme A is Rs. 12000
and in scheme B is Rs. 10000.
Question: 13
Vijay had some bananas, and he divided them into
two lots A and B. He sold the first lot at the rate of
Rs for bananas and the second lot at the rate of
2
3
Re per banana, and got a total of Rs . If he had
1
400
sold the first lot at the rate of Re per banana, and
1
the second lot at the rate of Rs for bananas, his
4
5
total collection would have been Rs . Find the
460
total number of bananas he had.
Solution:
Let be the number of bananas in lot A and be
x
y
the number of bananas in lot B.
Case 1:
In lot A, the cost of bananas
3
Rs 2.
In lot A, the cost of bananas
x
Rs Rs
2 2
3
.
3
.
x
x

In lot B, the cost of bananas
1
Re 1.
In lot B, the cost of bananas
y
Rs.
y
Total cost of lot A and lot B
Rs 0. 40
2
400
3
x
y
2 3 1200 ...... 1x y
Case 2:
In lot A, the cost of bananas .
1
Re 1.
In lot A, the cost of bananas
x
Rs.
x
In lot B, the cost of bananas .
5
Rs 4.
In lot B, the cost of bananas
y
Rs Rs
4 4
5
.
5
.
y
y
Total cost of lot A and lot B
Rs 0. 46
4
460
5
y
x
5 4 2300 ...... 2x y
Multiply equation (1) by 5 and multiply equation (2)
by 2.
10 15 6000 ...... 3x y
10 8 4600 ...... 4x y
Subtract equation (4) from equation (3),
10 15 10 8 6000 4600x y x y
10 15 10 8 6000 4600x y x y
7 1400y
200y
Put the value of in equation (1),
y
2 3 1200x y
2 3 200 1200x
2 600 1200x
2 1200 600x
2 600x
300x
The number of bananas in lot A
300
The number of bananas in lot B
200
Total number of bananas
300 200 500
Thus, the total number of bananas is .
500