
Lesson: Surface Areas And Volumes
Exercise 12.1 (20)
Question: 1
A cylindrical pencil sharpened at one edge is the
combination of
a. a cone and a cylinder
b. frustum of a cone and a cylinder
c. a hemisphere and a cylinder
d. two cylinders.
Solution:
(a)
The part with the pointed end is a cone, and the
rest of the part is a cylinder.
Hence, the correct option is (A).
Question: 2
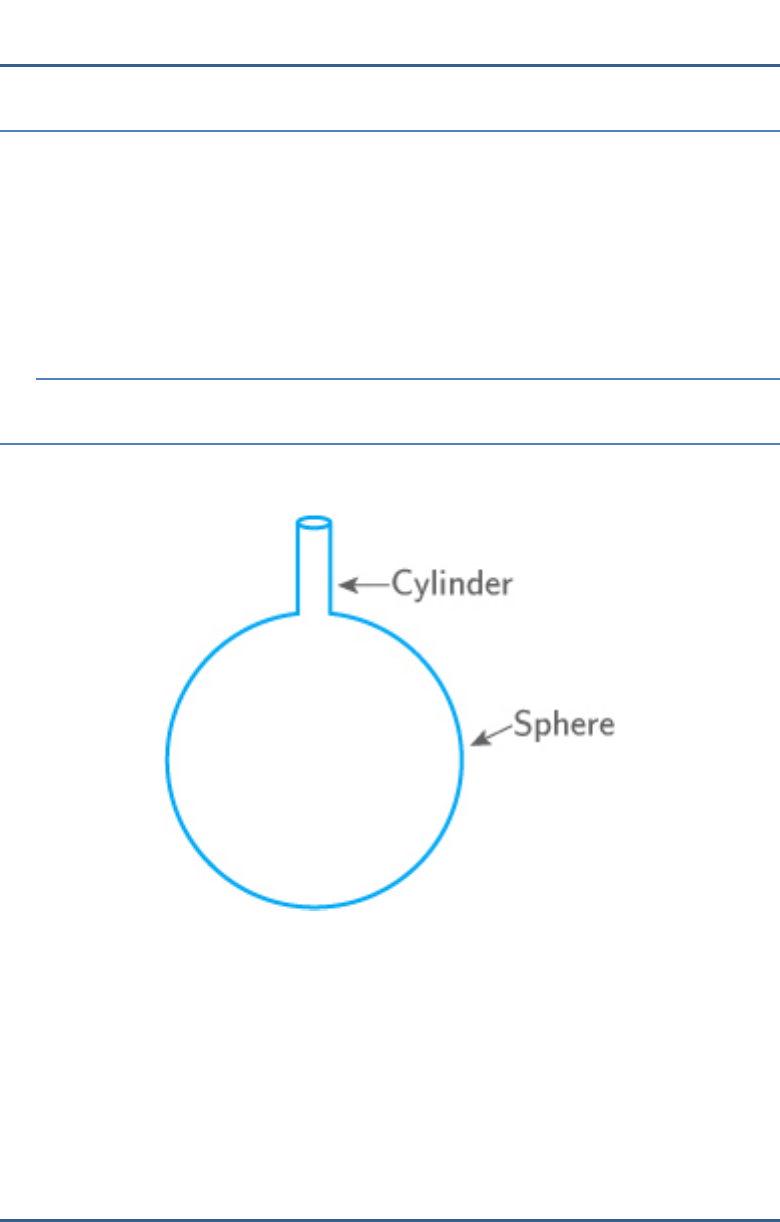
A surahi is the combination of
a. a sphere and a cylinder
b. a hemisphere and a cylinder
c. two hemispheres
d. a cylinder and a cone
Solution:
(a)
A surahi is formed by combining a sphere and a
cylinder.
Hence, the correct option is (A).
Question: 3
A plumbline (sahul) is the combination of (see given
figure)
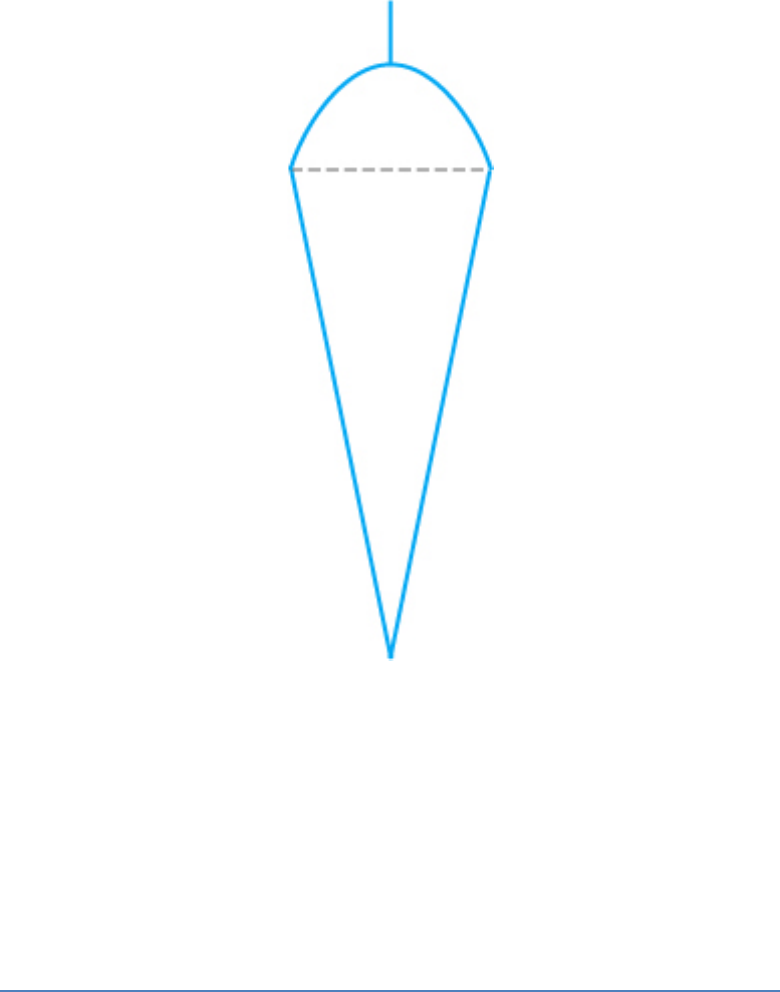
a. a cone and a cylinder
b. a hemisphere and a cone
c. frustum of a cone and a cylinder
d. sphere and cylinder
Solution:
(b)
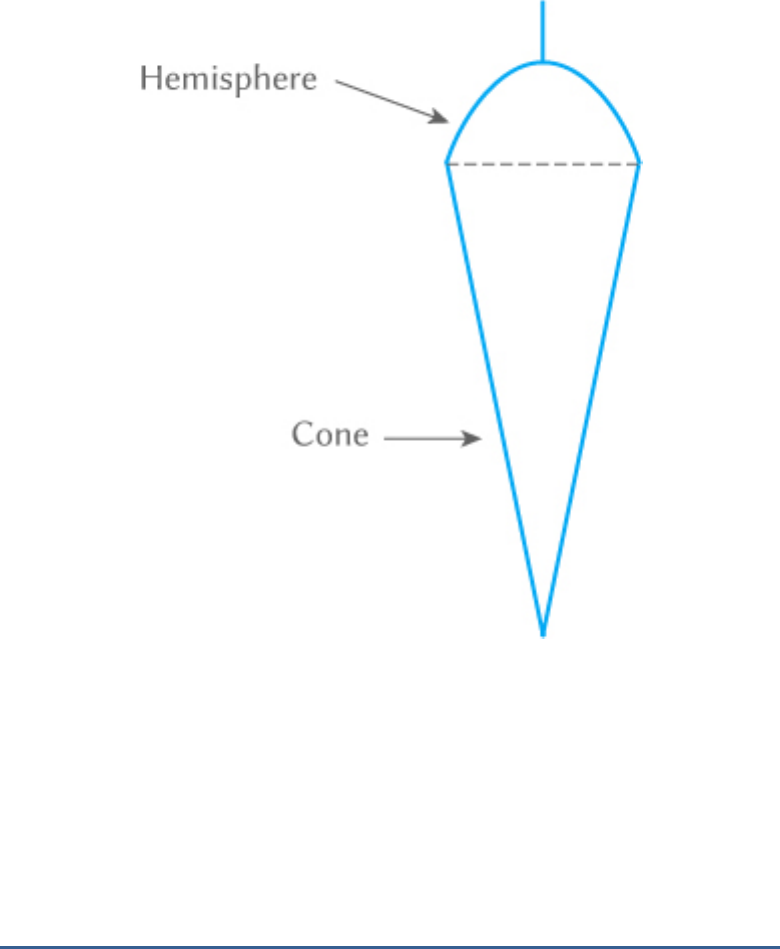
A plumbline is a formed by combining a hemisphere
and a cone.
Hence, the correct option is (B).
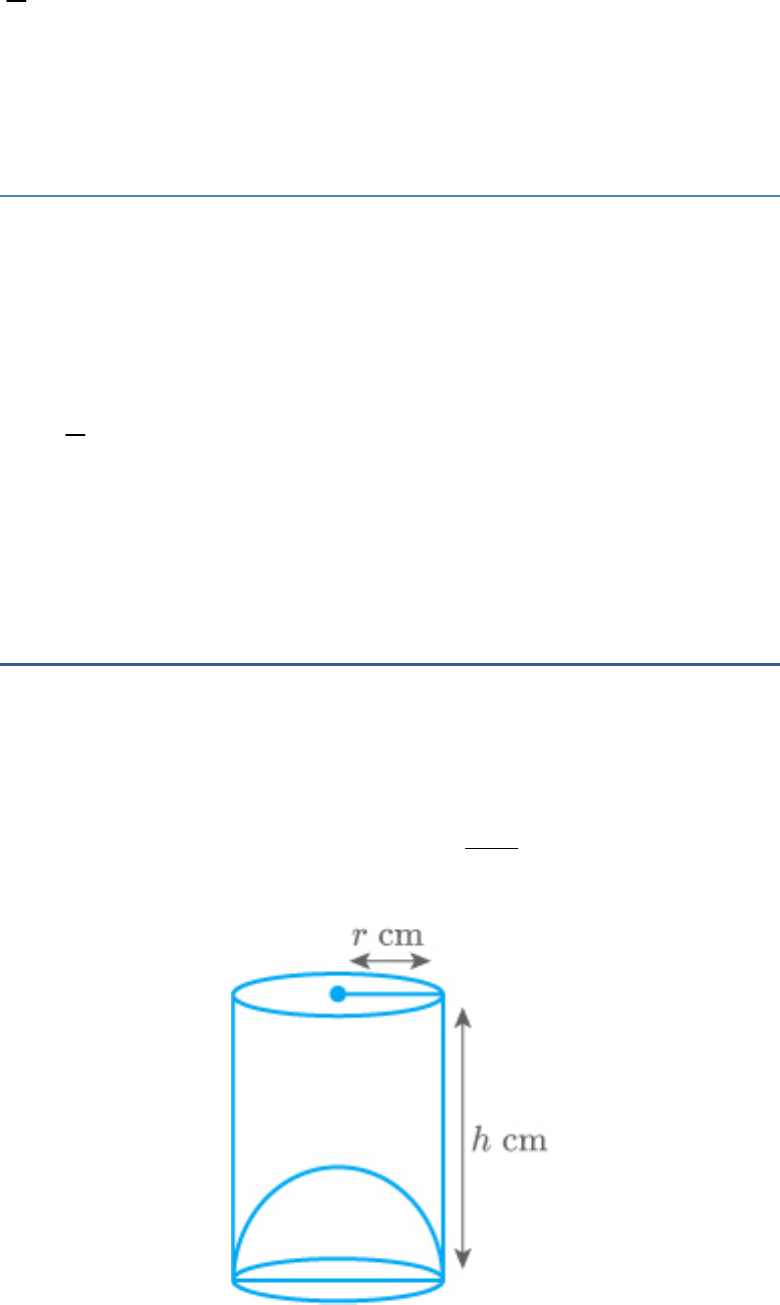
Question: 4
The shape of a glass (tumbler) (see given figure) is
usually in the form of
a. a cone
b. frustum of a cone
c. a cylinder
d. a sphere
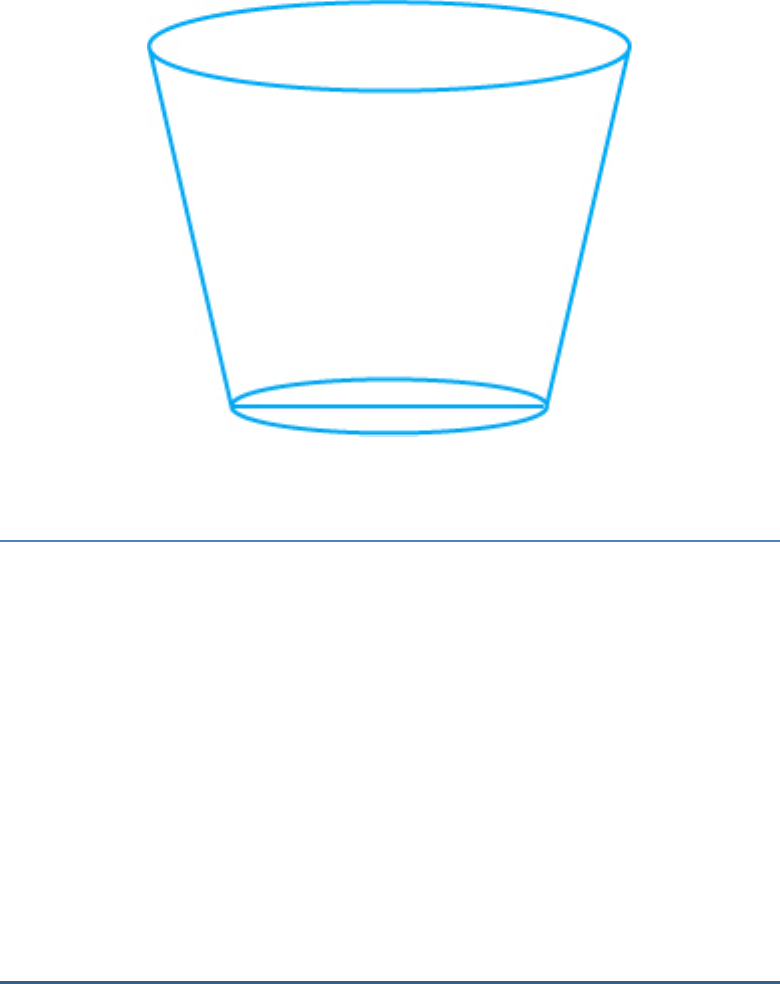
Solution:
(b)
The shape of a glass is frustum of a cone.
This is because, the radius of the upper circular part
is larger than the lower circular part.
Hence, the correct option is (B).
Question: 5
The shape of a gilli, in the gilli-danda game (see
given figure), is a combination of
a. two cylinders
b. a cone and a cylinder
c. two cones and a cylinder
d. two cylinders and a cone
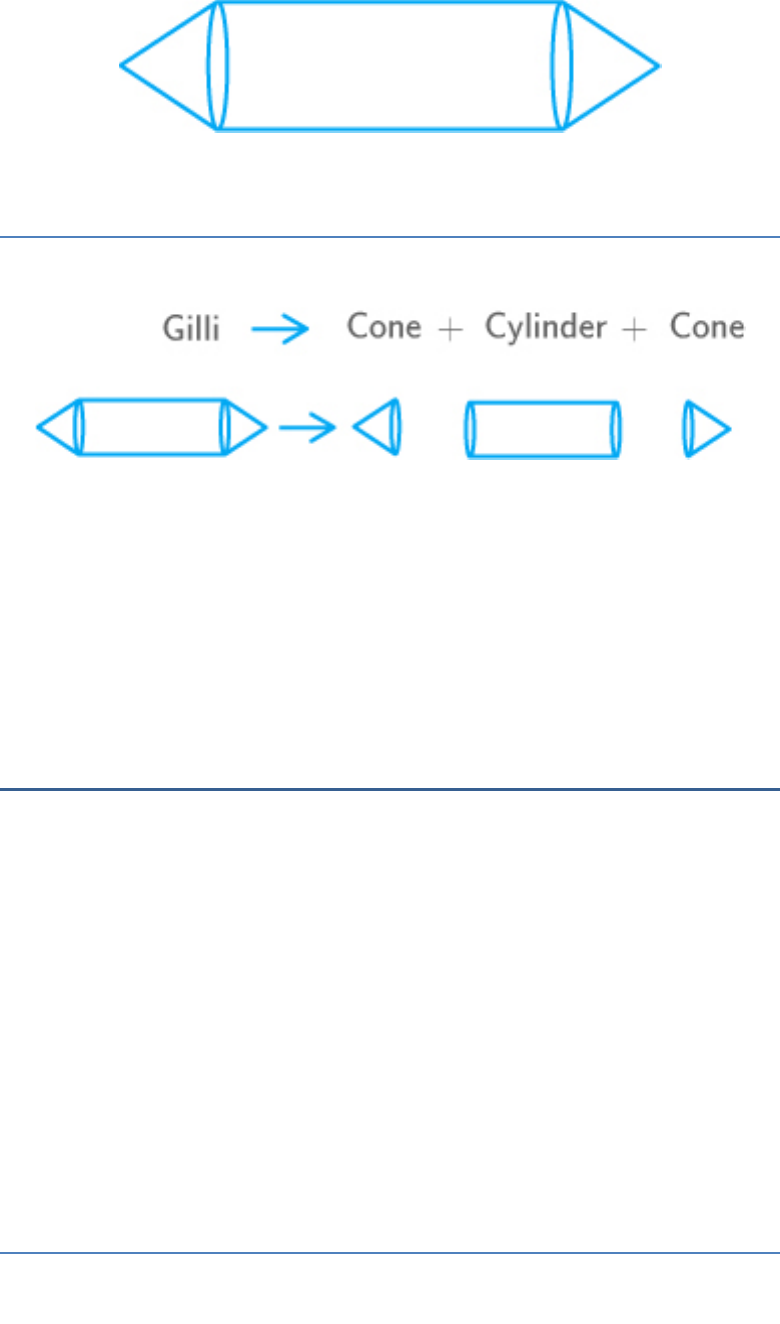
Solution:
(c)
The shape of gilli, is formed by combining two
cones and a cylinder.
Hence, the correct option is (C).
Question: 6
A shuttle cock used for playing badminton has the
shape of the combination of
a. a cylinder and a sphere
b. a cylinder and a hemisphere
c. a sphere and a cone
d. frustum of a cone and a hemisphere
Solution:
(d)

A shuttle cock is formed by combining a frustum of
a cone and a hemisphere.
Hence, the correct option is (D).
Question: 7
A cone is cut through a plane parallel to its base
and then the cone that is formed on one side of that
plane is removed. The new part that is left over on
the other side of the plane is called
a. a frustum of a cone
b. cone
c. cylinder
d. sphere
Solution:
(a)

The part that is left after removing the conical part
has the shape of a frustum of a cone.
Hence, the correct option is (A).
Question: 8
A hollow cube of internal edge 22 cm is filled with
spherical marbles of diameter 0.5 cm and it is
assumed that space of the cube remains unfilled.
1
8
Then the number of marbles that the cube can
accommodate is
a. 142296
b. 142396
c. 142496
d. 142596
Solution:
(a)
Let the radius of the spherical marble be .
r

Given: Diameter of the spherical marble
0.5cm
So, radius
0.5
r
2
5
10 2
1
cm
4
Length of the cube
l 22cm
Fig. Exm_12.1_8 (ii)

Let the number of marbles that can fill the cube be
.
x
Volume of part of the
x marbles
volume of the cube
1
1
8
3 3
4 7
x πr l
3 8
3
3
7 3
x l
8 4πr
7 22 22 22 3 7 4 4 4
x
8 4 22
x 7 22 11 3 7 4
x 142296
Hence, the number of marbles, that the cube can
accommodate are 142296 marbles.
Question: 9
A metallic spherical shell of internal and external
diameters 4 cm and 8 cm, respectively is melted and
recast into the form a cone of base diameter 8 cm.
The height of the cone is
a. 12 cm
b. 14 cm
c. 15 cm
d. 18 cm
Solution:
(b)
When we recast a shape into another shape, there
is no change in its volume.
Internal diameter of shell
4 cm
So, internal radius
1
r
4
2
2cm
External diameter of shell
8cm
So, external radius
2
r
8
2
4 cm
Diameter of the base of the cone
8cm
Radius
8
r
2
4 cm
Now, find the height of the cone.
Volume remains the same during recasting so,
Volume of Volume of the
cone spherical shell
2 3 3
2 1
1 4 4
πr h πr πr
3 3 3
2 3 3
2 1
1 4
πr h π r r
3 3
2 3 3
2 1
r h 4 r r
2 3 3
4 h 4 4 2
4 h 64 8
56
h
4
h 14 cm
Hence, height of the cone is 14 cm.
Question: 10
A solid piece of iron in the form of a cuboid of
dimensions , is moulded to
49cm 33cm 24cm
form a solid sphere. The radius of the sphere is
a. 21 cm
b. 23 cm
c. 25 cm
d. 19 cm
Solution:
(a)
Length of the cuboid
l
49cm
Breadth of the cuboid
b
33cm
Height of the cuboid
h
24cm
Now, find the radius of the solid sphere.
r
Volume remains the same during moulding from
one shape to another so,
Volume of cuboid Volume of sphere
3
4
l b h πr
3
3
4 22
49 33 24 r
3 7
3
49 33 24 7 3
r
4 22
3
r 49 3 3 7 3
3
r 7 7 3 3 7 3
3
3
r 21

r 21cm
Hence, radius of the sphere is 21 cm.
Question: 11
A mason constructs a wall of dimensions
with the bricks each of
270cm 300cm 350cm
size and it is assumed
22.5cm 11.25cm 8.75cm
that space is covered by the mortar. Then the
1
8
number of bricks used to construct the wall is
a. 11100
b. 11200
c. 11000
d. 11300
Solution:
(b)
The space covered by the mortar in making the wall
1
8

So,
The space covered by the bricks
volu
1
me of wa1
8
ll
volume of l
7
8
wal
Length of brick
1
l 22.5cm
Breadth of brick
1
b 11.25cm
Height of brick
1
h 8.75cm
Now, Length of wall
l 270cm
Breadth of wall
b 300cm
Height of wall
h 350cm
Let the total number of bricks used be .
x
Now, according to the question,
7
Volume of x bricks olume of wallV
8
1 1 1
7
x l b h l b h
8
7 270 300 350
x
8 22.5 11.25 8.75
7 270 300 350 10 100 100
x
8 225 1125 875
x 11200
Hence, the number of bricks used are 11200.
Question: 12
Twelve solid spheres of the same size are made by
melting a solid metallic cylinder of base diameter 2
cm and height 16 cm. The diameter of each sphere
is
a. 4 cm
b. 3 cm
c. 2 cm
d. 6 cm
Solution:
(c)
When we recast a shape into another shape, there
is no change in its volume.
Now, diameter of base of the cylinder
2cm
Radius of base of the cylinder
2
r
2
1cm
Height of the cylinder
16cm
Now, find the radius of the sphere.
Volume of Volume of
12spheres cylinder
3 2
4
12 πR πr h
3
3 2
16 R r h
2
3
r h
R
16

2
3
1 16
R
16
3
R 1
R 1cm
So, diameter of sphere
2R
2 1
2cm
Hence, the diameter of each sphere is 2 cm.
Question: 13
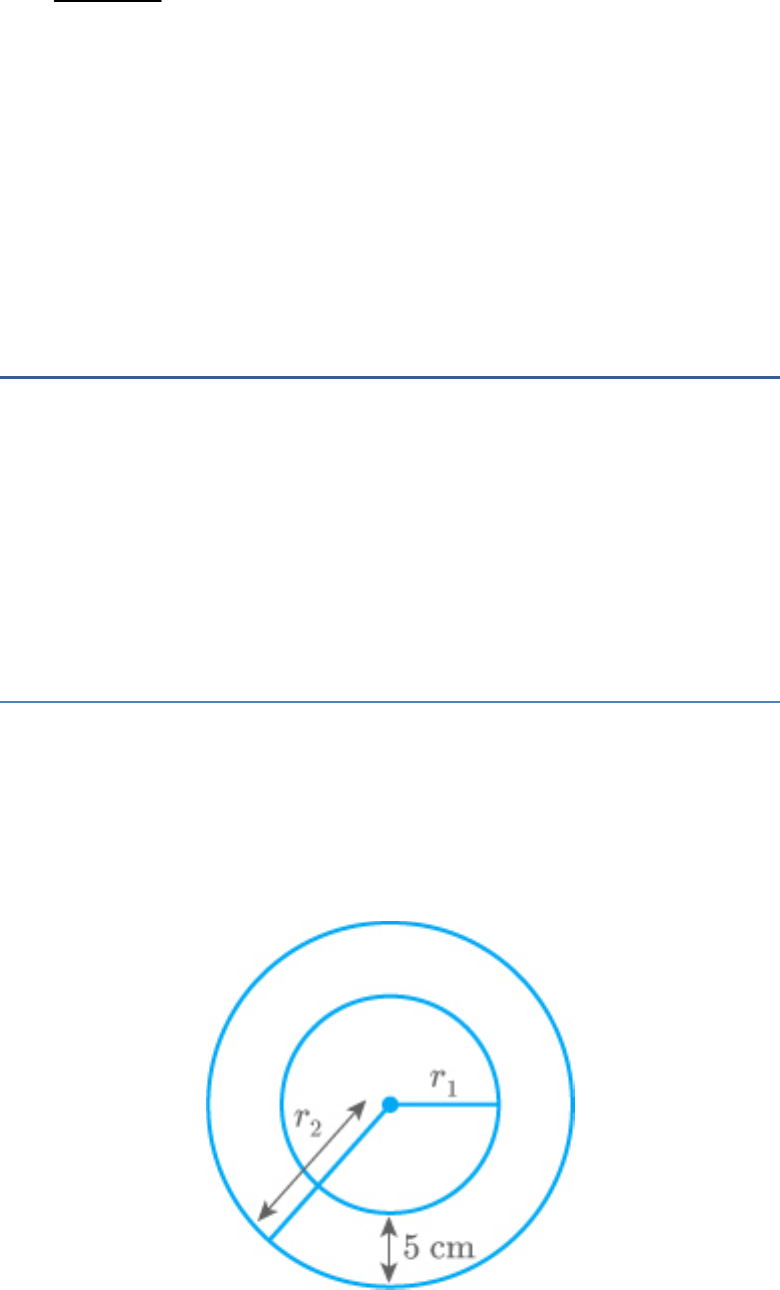
The radii of the top and bottom of a bucket of slant
height 45 cm are 28 cm and 7 cm, respectively. The
curved surface area of the bucket is
a. 4950
2
cm
b. 4951
2
cm
c. 4952
2
cm
d. 4953
2
cm
Solution:
(a)

Radius of bottom
1
r 7cm
Radius of top
2
r 28cm
Slant height
l 45cm
1 2
Curved surface
πl r r
area of bucket
22
45 7 28
7
22
45 35
7
2
4950cm
Hence, curved surface area of the bucket is
.
2
4950cm
Question: 14
A medicine-capsule is in the shape of a cylinder of
diameter 0.5 cm with two hemispheres stuck to
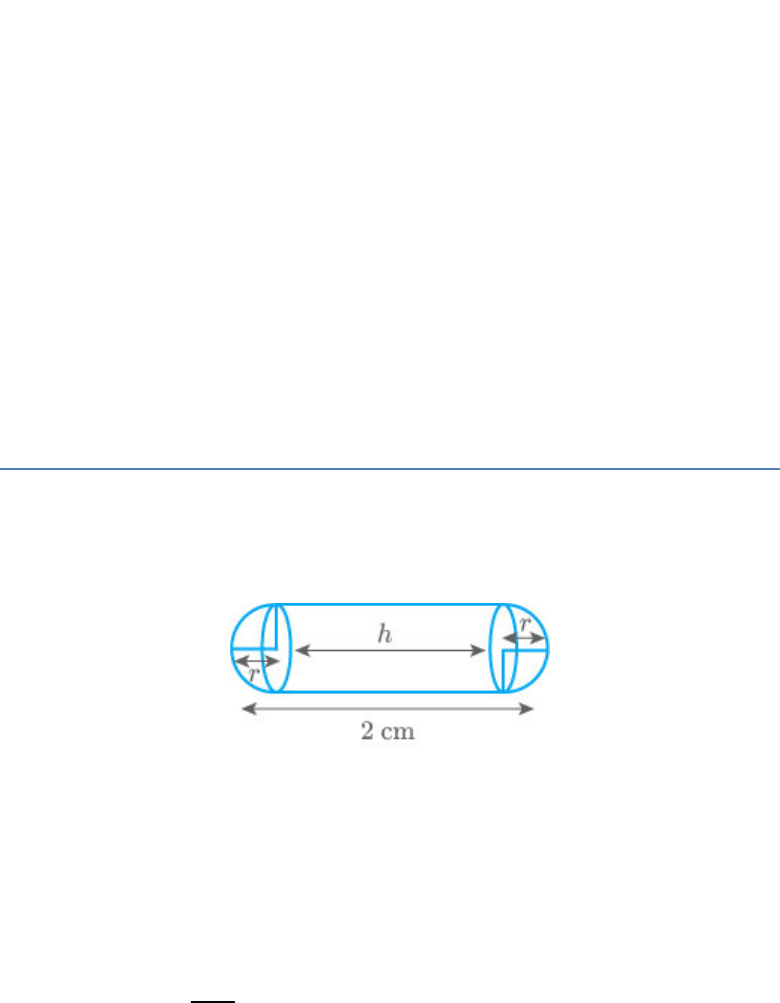
each of its ends. The length of entire capsule is 2
cm. The capacity of the capsule is
a. 0.36
3
cm
b. 0.35
3
cm
c. 0.34
3
cm
d. 0.33
3
cm
Solution:
(a)
Capsule Cylinder 2Hemsphere
Diameter of the cylinder is same as the diameter of
the two hemispheres.
Diameter
0.5cm
Radius
0.5
r
2
0.25cm
Now, find the height of the cylinder.
Total length of thecapsule r r h
2 0.25 0.25 h
h 2 0.5
h 1.5cm

Volume of Volume of
2
cylind
Volumeof
er Hemispc hapsule ere
2 3
2
πr h 2 πr
3
2
4
πr h r
3
22 4
0.25 0.25 1.5 0.25
7 3
22 25 25 15 4 25
7 100 100 10 3 100
22 1 1 3 1
7 4 4 2 3
22 1 1 9 2
7 4 4 6
22 1 1 11
7 4 4 6
121
336
2
0.36cm
Hence, the capacity of the capsule is .
2
0.36cm
Question: 15

If two solid hemispheres of same base radius are
r
joined together along their bases, then curved
surface area of this new solid is
a.
2
4πr
b.
2
6πr
c.
2
3πr
d.
2
8πr
Solution:
(a)
On joining the base of two hemispheres, having
equal radii, we get a new solid, which has the shape
of a sphere.
Curved surface area of sphere
2
4πr
Question: 16
A right circular cylinder of radius cm and height
r
cm just encloses a sphere of diameter
h
h 2r
a. cm
r
b. cm
2r
c. cm
h
d. cm
2h
Solution:
(b)
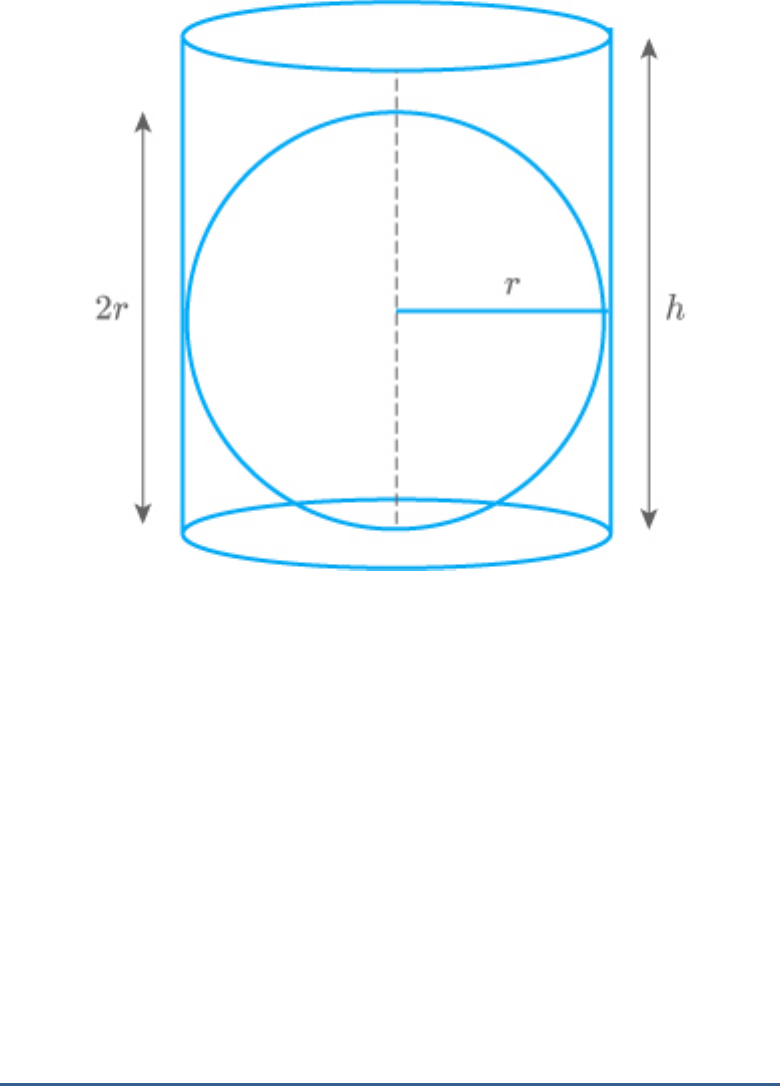
The cylinder encloses the sphere.
So, the diameter of cylinder is equal to the diameter
of the sphere.
Now, radius of cylinder
r
Diameter of cylinder
2r
Hence, diameter of circle is cm.
2r
Question: 17
During conversion of a solid from one shape to
another, the volume of the new shape will
a. increase
b. decrease
c. remain unaltered

d. be doubled
Solution:
(c)
When a solid is converted from one shape to
another, the volume of new solid formed will
remain unaltered.
Question: 18
The diameters of the two circular ends of the
bucket are 44 cm and 24 cm. The height of the
bucket is 35 cm. The capacity of the bucket is
a. 32.7 litres
b. 33.7 litres
c. 34.7 litres
d. 31.7 litres
Solution:
(a)
Bucket has the shape of frustum of a cone.

Diameter of the base of bucket = 24 cm
So, radius
1
24
r
2
12cm
Diameter of the top of bucket = 44 cm
So, radius
2
44
r
2
22cm
Height of the bucket
35cm
2 2
1 2 1 2
1
Volumeof thebucket πh r r rr
3
2 2
1 22
35 12 22 12 22
3 7
22 5
144 484 264
3
22 5
892
3
98120
3
32706.66

32.7litres
Hence, volume of the bucket is 32.7 litres.
Question: 19
In a right circular cone, the cross-section made by a
plane parallel to the base is a
a. circle
b. frustum of a cone
c. sphere
d. hemisphere
Solution:
(a)
If a cross-section of the plane is cut parallel to the
base in a right circular cone, we get a circle.
Question: 20
Volumes of two spheres are in the ratio . The
64:27
ratio of their surface areas is
a.
3:4
b.
4:3
c.
9:16
d.
16:9
Solution:
(d)
Let the volumes of two spheres be .
1 2
V and V
According to the question,
1
2
V 64
V 27
3
1
3
2
4
πr
64
3
4
27
πr
3
3
1
3
2
r 64
r 27
3
3
1
3
3
2
4
r
r
3
1
2
r 4
r 3
Now, find the ratio of the total surface areas of the
two spheres.
2
1 1
2
2 2
TSA 4πr
TSA 4πr
2
1
2
2
r
r
2
4
3
16
9
Hence, the ratio of the total surface areas of the
two spheres is .
16:9
Exercise 12.2 (8)
Write ‘True’ or ‘False’ and justify your answer in
the following:
Question: 1
Two identical solid hemispheres of equal base
radius cm are stuck together along their bases.
r
The total surface area of the combination is .
2
6πr
Solution:
The given statement is false.
On joining the base of two hemispheres, having
equal radii, we get a new solid, which has the shape
of a sphere.
Total surface area of sphere
2
4πr
Hence, the given statement is false.
Question: 2

A solid cylinder of radius and height is placed
r
h
over other cylinder of same height and radius. The
total surface area of the shape so formed is
.
2
4πrh 4πr
Solution:
The given statement is false.
If a solid cylinder of radius and height is placed
r
h
over other cylinder of same height and radius, then
the shape formed will also be a cylinder.
Height of new cylinder
2h
Radius of new cylinder
r
Total surfacearea
of new formed cylinder
2πr r 2h
2
2πr 4πrh
2
4πrh 2πr
Hence, the given statement is false.
Question: 3
A solid cone of radius and height is placed over
r
h
a solid cylinder having same base radius and height
as that of a cone. The total surface area of the
combined solid is .
2 2
πr r h 3r 2h
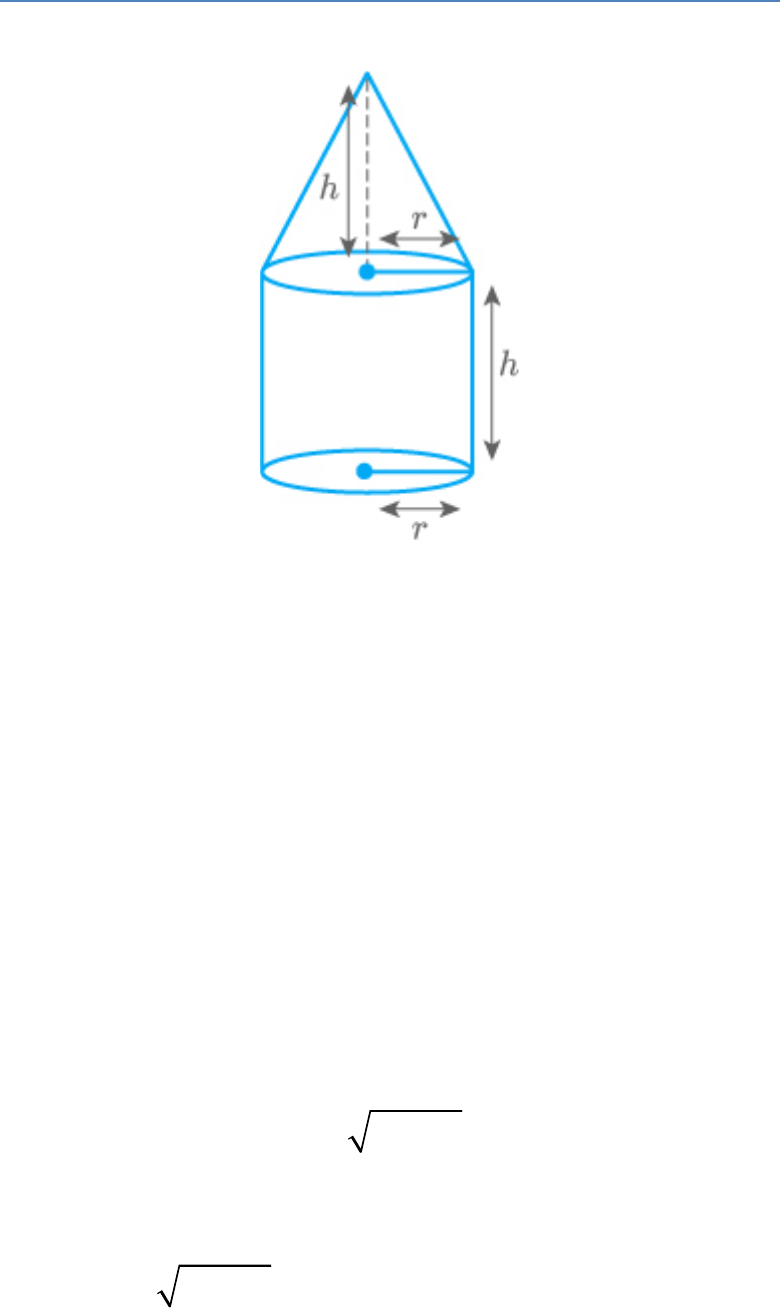
Solution:
The given statement is false.
Radius of the cone and cylinder
r
Height of the cone and cylinder
h
Curved
Curved surface
surface area
The total surface
area of cone
of cylinder
area of the
combined solid
Area of base
of cylinder
2
TSA πrl 2πrh πr
πr l 2h r ...... 1
Now, slant height
2 2
l r h
Put the equation of slant height in equation .
1
2 2
TSA πr r h 2h r
Hence, the given statement is false.

Question: 4
A solid ball is exactly fitted inside the cubical box of
side . The volume of the ball is .
a
3
4
πa
3
Solution:
The given statement is false.
If a solid ball is exactly fitted inside the box having
the shape of a cube, then the diameter of the ball
will be equal to the side of cube.
Side of the cube
a
So, diameter of the ball
a
Now, radius of ball
a
2
Volume of a sphere
3
4
πr
3
3
4 a
π
3 2
3
πa
6
Hence, the given statement is incorrect.
Question: 5
The volume of the frustum of a cone is
, where is vertical height of the
2 2
1 2 1 2
1
πh r r rr
3
h
frustum and are the radii of the ends.
1 2
r ,r
Solution:
The given statement is false.
Volume of the frustum of a cone is given by the
formula,
2 2
1 2 1 2
1
V πh r r rr
3
Hence, the given statement is incorrect.
Question: 6
The capacity of a cylindrical vessel with a
hemispherical portion raised upward at the bottom
as shown in the given figure is .
2
πr
3h 2r
3

Solution:
The given statement is true.
Radius of the cylinder and the hemispherical
portion is .
r cm
Height of the cylinder
h cm
Now, find the capacity of vessel.
Capacity of Volume of Volume of
the vessel cylinder hemisphere
2 3
2
πr h πr
3
2
2
πr h r
3
2
πr
3h 2r
3
Hence, the given statement is correct.
Question: 7
The curved surface area of a frustum of a cone is
, where , are the
1 2
πl r r
2
2
1 2
l h r r
1 2
r andr
radii of the two ends of the frustum and is the
h
vertical height.
Solution:
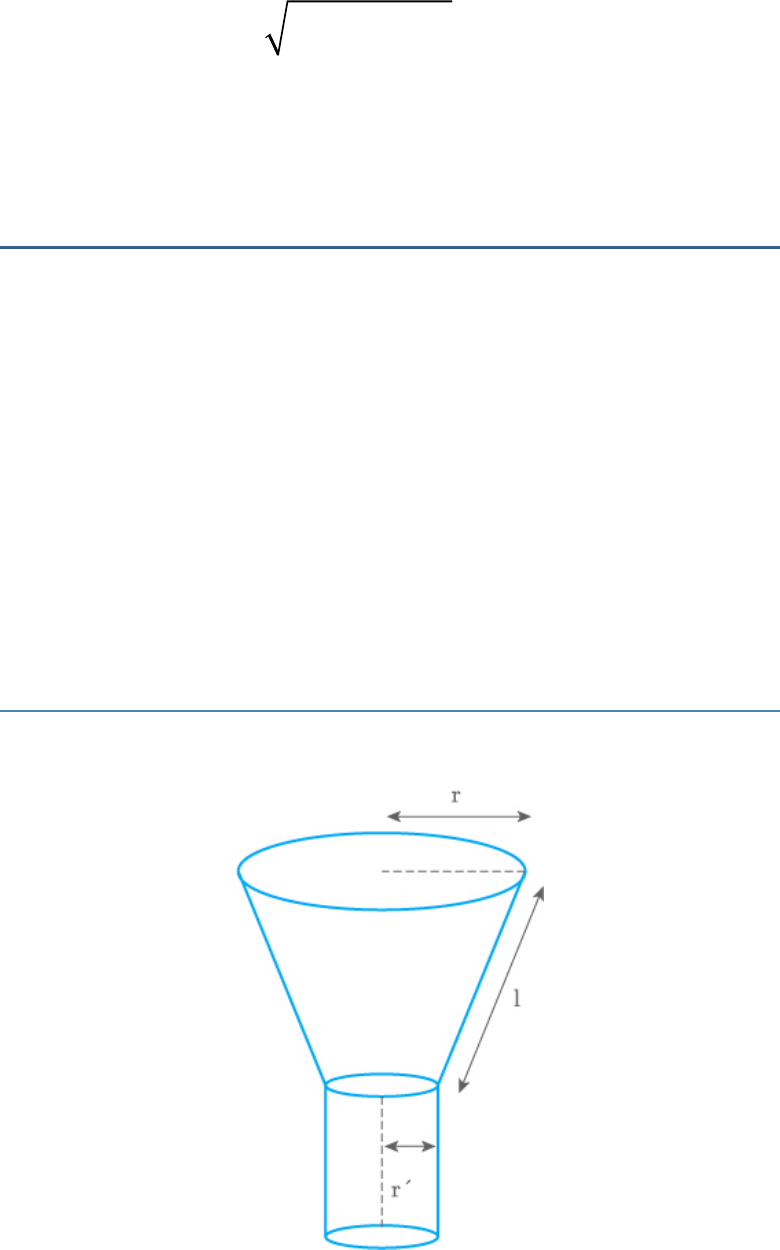
The given statement is false.
1 2
Curved surfacearea πl r r
Slant height
2
1 2
l h r r
Hence, the statement is incorrect.
Question: 8
An open metallic bucket is in the shape of a frustum
of a cone, mounted on a hollow cylindrical base
made of the same metallic sheet. The surface area
of the metallic sheet used is equal to
curved surface area of frustum of a cone + area of
circular base + curved surface area of cylinder
Solution:
The given statement is true.

The total surface area of the metallic sheet used for
making the vessel will be equal to the curved
surface area of frustum of a cone and the total
surface area of cylinder excluding the area of its
top.
So,
Curved surface Curved surface
area of frustum area of cylinder
Total surface
area of vessel
Area of thebase
of cylinder
Hence, the statement is correct.
Exercise 12.3 (14)
Question: 1
Three metallic solid cubes whose edges are 3 cm, 4
cm and 5 cm are melted and formed into a single
cube. Find the edge of the cube so formed.
Solution:
According to the question,
Length of the side of first cube
3cm
3
1
Volume of fir Vst cube 3

3
27cm
Length of the side of second cube
4 cm
3
2
Volume of seco Vnd cube 4
3
64 cm
Length of the side of third cube
5cm
3
3
Volume of thi Vrd cube 5
3
125cm
Let the side of the new cube be .
a
1 2 3
Volume of the new cu e V Vb V V
3
a 27 64 125
3
a 216
3 3
a 6
a 6
Hence, the side of the new cube is 6 cm.
Question: 2
How many shots each having diameter 3 cm can be
made from a cuboidal lead solid of dimensions
?
9cm 11cm 12cm
Solution:
Length of the cuboidal lead
l 12cm

Breadth of the cuboidal lead
b 11cm
Height of the cuboidal lead
h 9cm
Diameter of the shots
3cm
So, radius of shots
3
2
1.5cm
The spherical shots are made from the cuboidal
lead.
Let the number of shots made be .
x
Volume of x shots Volume of cuboidal lead
3
4
x πr l b h
3
3
4 22
x 1.5 12 11 9
3 7
12 11 9 3 7
x
4 22 1.5 1.5 1.5
3 9 3 7 10 10 10
x
2 15 15 15
x 3 7 2 2
x 84
Hence, the total number of lead shots which can be
made are 84.
Question: 3
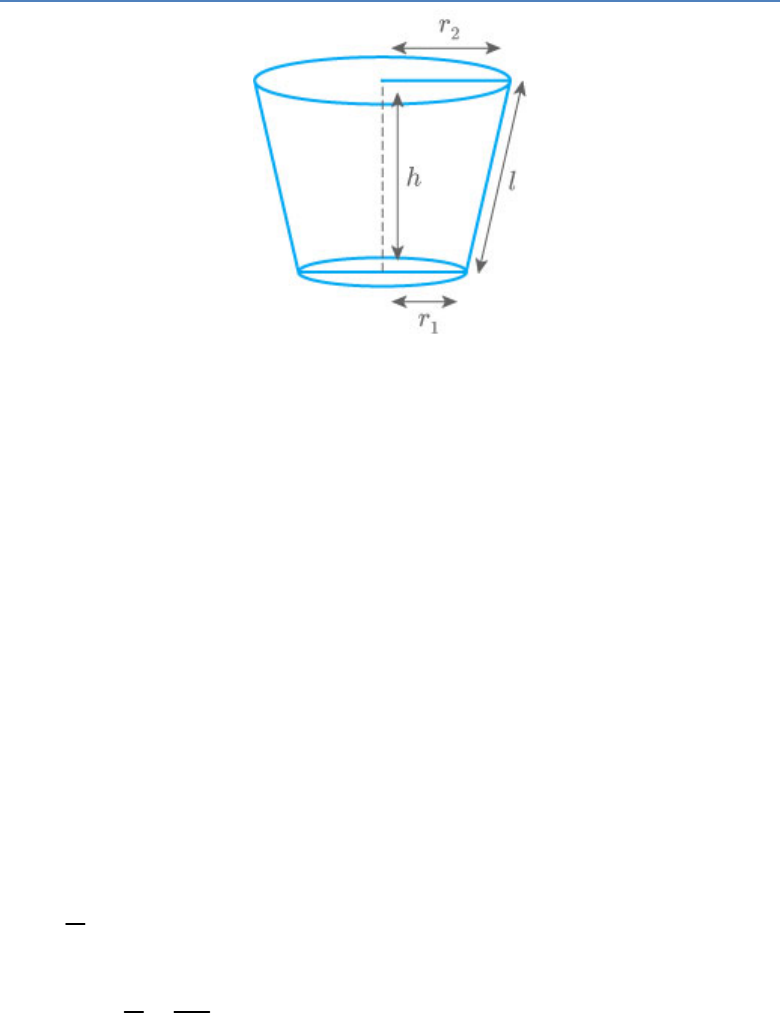
A bucket is in the form of a frustum of a cone and
holds 28.490 litres of water. The radii of the top and
bottom are 28 cm and 21 cm, respectively. Find the
height of the bucket.
Solution:
Let the radius of bottom and top of the bucket be
1
r
.and respectively and let the height of the bucket
2
r
be .
h
Now, according to the question,
1
r 21cm
2
r 28cm
Volume of the bucket = 28490
3
cm
Now, find the volume of the frustum of a cone.
2 2
1 2 1 2
1
V πh r r rr
3
2 2
1 22
28490 h 21 28 21 28
3 7
1 22
28490 h 441 784 588
3 7
1 22
28490 h 1813
3 7
28490 3 7
h
1813 22
h 15
Hence, the height of the bucket is 15 cm.
Question: 4
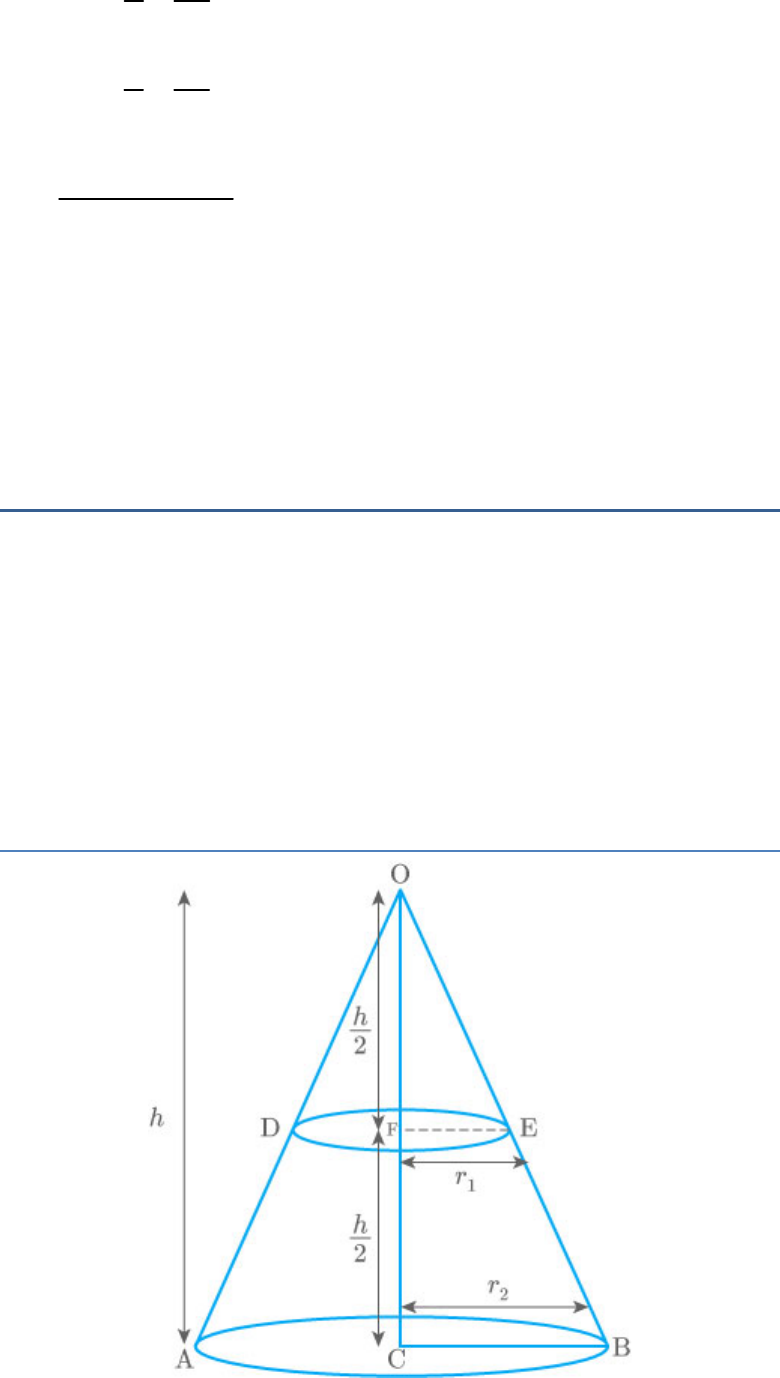
A cone of radius 8 cm and height 12 cm is divided
into two parts by a plane through the mid-point of
its axis parallel to its base. Find the ratio of the
volumes of two parts.
Solution:

Let the original cone be OAB.
Radius of AOB = 8 cm
2
r
Height of AOB = 12 cm
h
Now, from the figure,
New cone formed is DEO.
Let the radius of DEO be .
1
r
Height of DEO
1
h
h
2
12
2
6cm
New frustum formed is DABE.
Radius of its top is cm
1
r 4
Radius of its bottom cm
2
r 8
Height = 6 cm
2
h
Now, (By similarity criterion)
ΔOAB||ΔODE
So,
1 1
2 2
r h
r h
1
h
r
2
8 h
1
r 1
8 2
1
2r 8

1
r 4 cm
Now, find the required ratio.
2 2
2 1 2 1 2
2
1 1
1
πh r r rr
Volumeof frustum
3
1
Volumeof cone
πr h
3
2 2
2
6 4 8 4 8
4 6
16 64 32
16
112
16
7
1
Hence, the required ratio is .
7:1
Question: 5
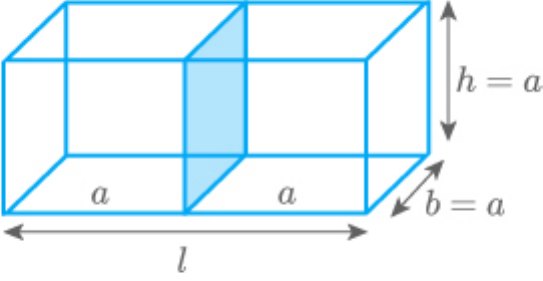
Two identical cubes each of volume 64 are
3
cm
joined together end to end. What is the surface area
of the resulting cuboid?
Solution:
Let the edge of two identical cubes be .
a
Volume of the cube
3
64 cm
So,
3
a 64
3
3
a 4
a 4
Now, according to the question,
Length of the cuboid
2a
Breadth of cuboid
a
Height of cuboid
a
Now, find the surface area of the cuboid.
Surface area 2 lb lh bh
2 2a a 2a a a a
2 2 2
2 2a 2a a
2
2a 2 2 1
2
2a 5
2
2 4 5
2
160cm
Hence, the surface area of cuboid formed is 160
2
cm
.
Question: 6
From a solid cube of side 7 cm, a conical cavity of
height 7 cm and radius 3 cm is hollowed out. Find
the volume of the remaining solid.
Solution:
Let the side of the cube be .
a
a 7cm
Height of the conical cavity
h 7cm
Radius of the conical cavity
r 3cm
Now, find the volume of the remaining solid.
Volume of Volume of Volume of
–
remaining solid cube conical cavity
3 2
1
a πr h
3
3 2
1 22
7 3 7
3 7
343 66

2
277cm
Hence, volume of the remaining solid is 277 .
3
cm
Question: 7
Two cones with same base radius 8 cm and height
15 cm are joined together along their bases. Find
the surface area of the shape so formed.
Solution:
Radius of the two cones
r 8cm
Height of the two cones
h 15cm
2 2
Slant heig l h rht
2 2
15 8
225 64
289
17cm
On joining two identical cones base to base, the
total surface area of new shape formed, will be
equal to the sum of curved surface areas of both the
cones.
Total surface area Curved surface
2
of new shape area of cone
TSA 2 πrl
22
2 8 17
7
5984
7
3
854.857cm
Hence, surface area of the new solid is 854.857 .
3
cm
Question: 8
Two solid cones A and B are placed in a cylindrical
tube as shown in the given figure. The ratio of their
capacities is . Find the heights and capacities of
2:1
cones. Also, find the volume of the remaining
portion of the cylinder.
Solution:
Let the heights of two cones be
1 2
h andh
respectively.
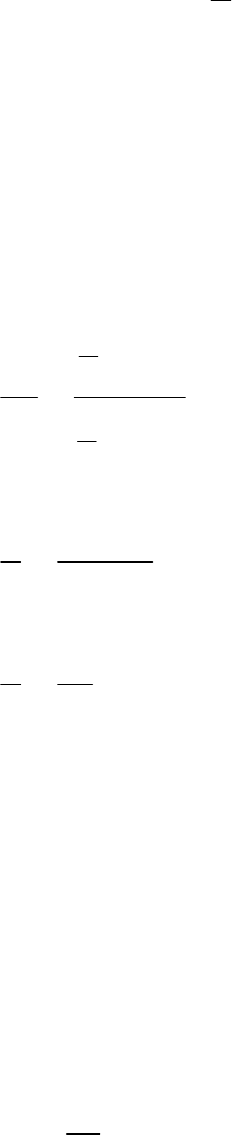
Now, both the cones have same diameter, which is
equal to 6 cm.
So, radii
1
6
r
2
3cm
According to the question,
The ratio of the capacities of two cones is .
2:1
So,
1
2
1
1
2
2
2 2
1
πr h
V
3
1
V
πr h
3
2
1
2
2
3 h
2
1
3 h
1
2
2 h
1 h
1 2
h 2h
Now, the length of the cylinder is 21 cm.
So,
1 2
h h 21 ...... 1
Now,
2 2
2h h 21
2
3h 21
2
21
h
3
2
h 7cm

Put the value of in equation .
2
h
1
1 2
h h 21
1
h 7 21
1
h 21 7
1
h 14 cm
Now, find the volume of both the cones separately.
1
2
1 1
Volume of first
1
V πc
3
e ron h
2
1 22
3 14
3 7
22 3 2
3
132cm
2
2 2 2
Volume of second
1
V πc
3
e ron h
2
1 22
3 7
3 7
22 3
3
66cm
2
Volume of cylinder πr h
2
22
3 21
7
3
22 3
3
594 cm
Now, find the capacity of the remaining portion of
the tube.
Volume of Volume of Sum of volume
remaining portion cylinder of two cones
594 132 66
594 198
3
396cm
Hence, the volume of remaining portion is 396 .
3
cm
Question: 9
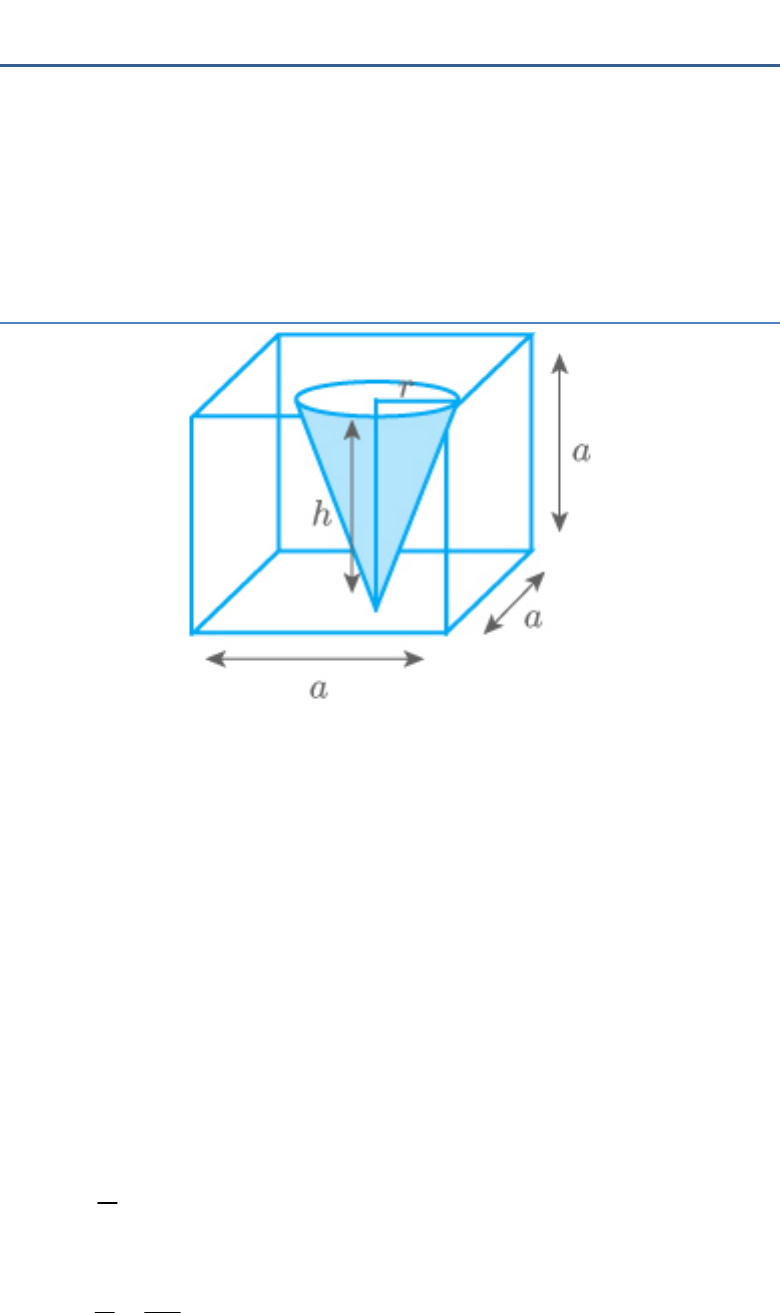
An ice cream cone full of ice cream having radius 5
cm and height 10 cm as shown in the given figure.
Calculate the volume of ice cream, provided that its
part is left unfilled with ice cream.
1
6
Solution:
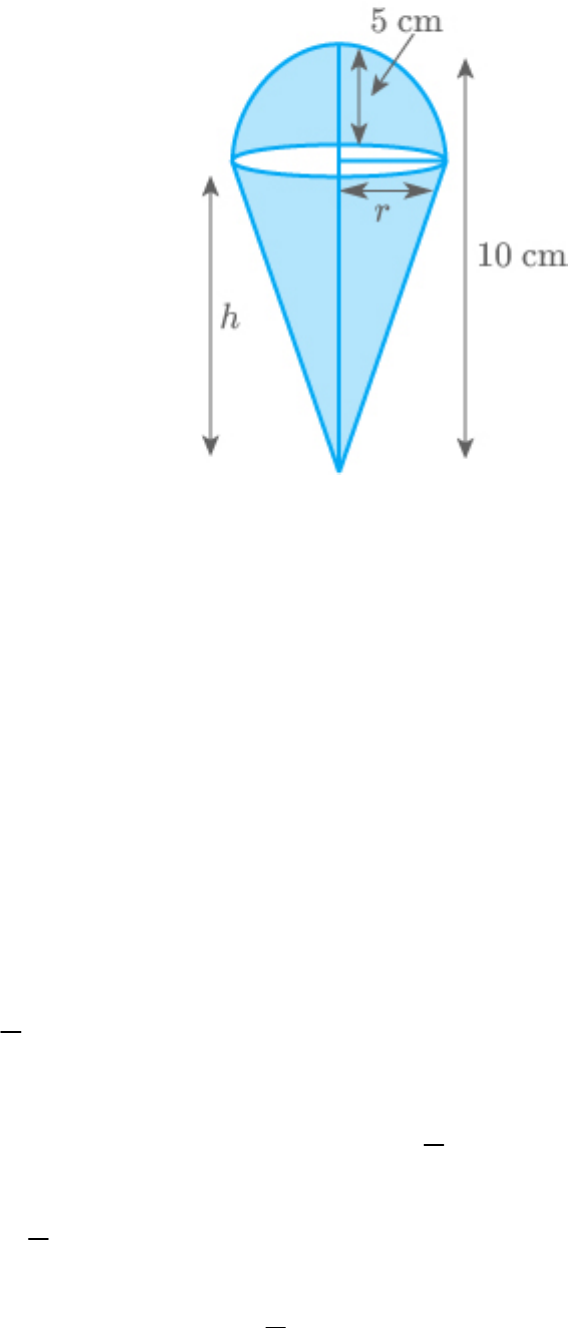
An ice-cream cone is a combination of a cone and a
hemisphere.
Radii of both the hemisphere and the cone are same
and is equal to 5 cm.
Total height of the ice-cream is 10 cm.
Height of cone
10 5
5cm
According to the question,
part is left unfilled with ice cream.
1
6
Volume of ice-cr
1
1
6
eam
5
Volumeof cone Volumeof hemisphere
6
2
1
Volume of cone πr h
3

2
1 22
5 5
3 7
1 22
125
3 7
3
130.952cm
3
2
Volume of hemisphere πr
3
3
2 22
5
3 7
2 22
125
3 7
3
261.904 cm
Volume of ice-cream
5
130.952 261.904
6
5
392.856
6
3
327.38cm
Hence, the volume of ice-cream is 327.4 .
3
cm
Question: 10
Marbles of diameter 1.4 cm are dropped into a
cylindrical beaker of diameter 7 cm containing
some water. Find the number of marbles that
should be dropped into the beaker so that the water
level rises by 5.6 cm.
Solution:
Let the number of marbles dropped in the beaker be
.
x
Now, diameter of the cylinder is 7 cm.
So, radius
7
r
2
3.5cm
Height of water raised
h 5.6cm
2
Volume of water raised πr h
2
22 7
5.6
7 2
14
11 7
5
3
215.6cm
3
Volume of spherical marbles
4
πR
3
3
4 22 1.4
3 7 2
3
4 22 14
3 7 2 10
4 22 14 14 14
3 7 2 10 2 10 2 10
22 14 14
3 10 10 10
3
1.437cm
So,
Volume of water raised Volume of x marbles
215.6 x 1.437
215.6
x
1.437
x 150
Hence, the total number of marbles dropped is 150.
Question: 11
How many spherical lead shots each of diameter 4.2
cm can be obtained from a solid rectangular lead
piece with dimensions 66 cm, 42 cm and 21 cm.
Solution:

Length of the cuboid
l 66cm
Breadth of the cuboid
b 42cm
Height of the cuboid
h 21cm
Let the number of spherical lead shots obtained be
.
x
Diameter of the sphere
4.2cm
So, radius of the sphere
4.2
r
2
2.1cm
Now, according to the question,
Volumeof cuboid Volumeof x spherical shot
3
4
l b h x πr
3
3
4 22
66 42 21 x 2.1
3 7
66 42 21 3 7
x
4 22 2.1 2.1 2.1

66 42 21 3 7 10 10 10
x
4 22 21 21 21
x 3 5 10 10
x 1500
Hence, the number of shots obtained are 1500.
Question: 12
How many spherical lead shots of diameter 4 cm
can be made out of a solid cube of lead whose edge
measures 44 cm.
Solution:
Let the number of spherical shots casted be .
x
Length of the solid cube
a 44 cm
Diameter of lead shots
4 cm
So, radius
4
r
2
2cm
Now, according to the question,
Volume of cube Volume of x spheres
3 3
4
a x πr
3
3 3
4 22
44 x 2
3 7

44 44 44 3 7
x
4 22 2 2 2
x 11 11 3 7
x 2541
Hence, the total number of spherical lead shots are
2541.
Question: 13
A wall 24 m long, 0.4 m thick and 6 m high is
constructed with the bricks each of dimensions
. If the mortar occupies of
25cm 16cm 10cm
th
1
10
the volume of the wall, then find the number of
bricks used in constructing the wall.
Solution:
The space covered by the mortar in making the wall
1
10
So, the space covered by the bricks
1
1
10
volume of
9
10
wall
Length of brick
1
l 25cm 0.25m

Breadth of brick
1
b 16cm 0.16m
Height of brick
1
h 10cm 0.10m
Now, length of wall
l 24m
Breadth of wall
b 0.4m
Height of wall
h 6m
Let the total number of bricks used be .
x
Now, according to the question,
9
Volume of xbricks Volume of wall
10
1 1 1
9
x l b h l b h
10
9
x 0.25 0.16 0.10 24 0.4 6
10
9
x 0.004 57.6
10
9
x 0.004 57.6
10
9 57.6
x
10 0.004
9 576 10
x
4
x 12960
Hence, the number of bricks used are 12960.

Question: 14
Find the number of metallic circular disc with 1.5
cm base diameter and of height 0.2 cm to be melted
to form a right circular cylinder of height 10 cm and
diameter 4.5 cm.
Solution:
Let the number of discs to be melted be .
x
Diameter of disc
1.5cm
So, radius
1.5
R
2
15
20
3
cm
4
Height of disc
H 0.2cm
Now, diameter of cylinder
4.5cm
So, radius
4.5
r
2
45
20
9
cm
4
Height of disc
h 10cm
Now, according to the question,

Volume of x discs Volume of cylinder
2 2
x πR H πr h
2
2
πr h
x
πR H
2
2
r h
x
R H
2
2
9
10
4
x
3
0.2
4
9 9 10 10
x
3 3 2
x 9 5 10
x 450
Hence, the number of metallic circular discs to be
melted are 450.
Exercise 12.4 (20)
Question: 1
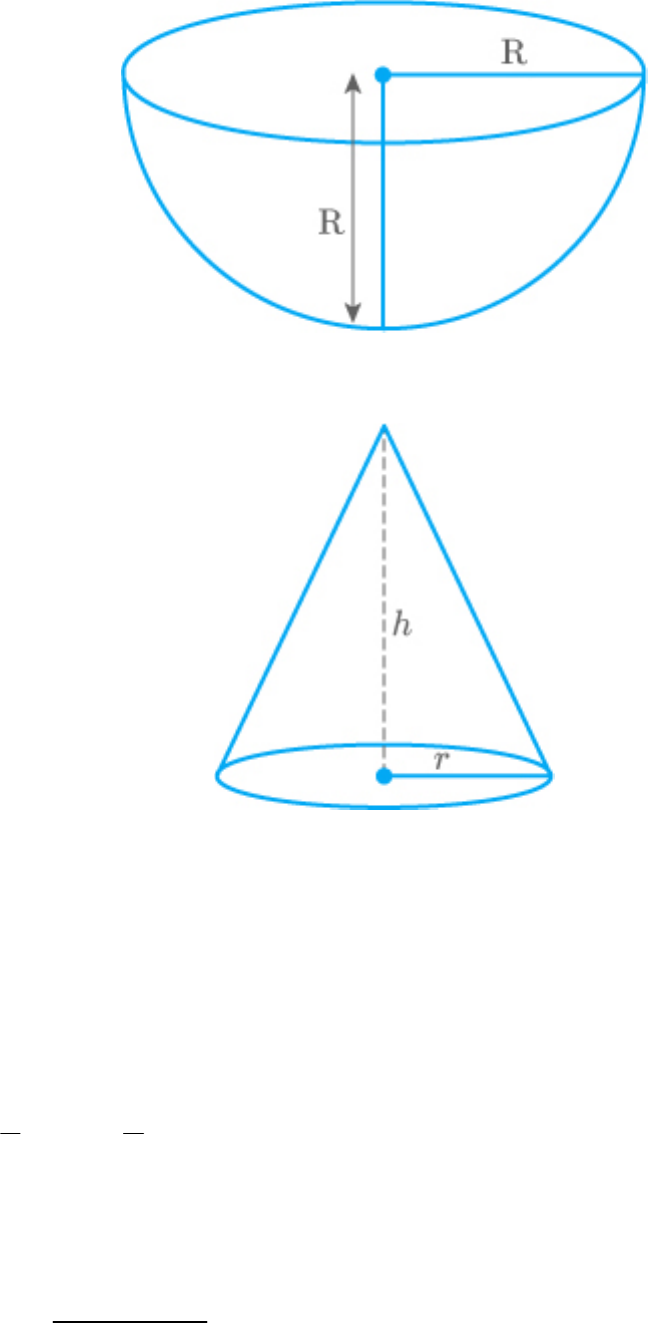
A solid metallic hemisphere of radius 8 cm is melted
and recasted into a right circular cone of base
radius 6 cm. Determine the height of the cone.
Solution:
Let the height of the cone be .
h
Radius of hemisphere
R 8cm
Radius of cone
r 6cm
Now, find the height of cone.
Volume of Volume
hemisphere of cone
2 3
1 2
πr h πR
3 3
2 3
6 h 2 8
2 8 8 8
h
6 6
2 2 8 8
h
3 3
h 28.44 cm
Hence, the height of the recasted right circular cone
is 28.44 cm.
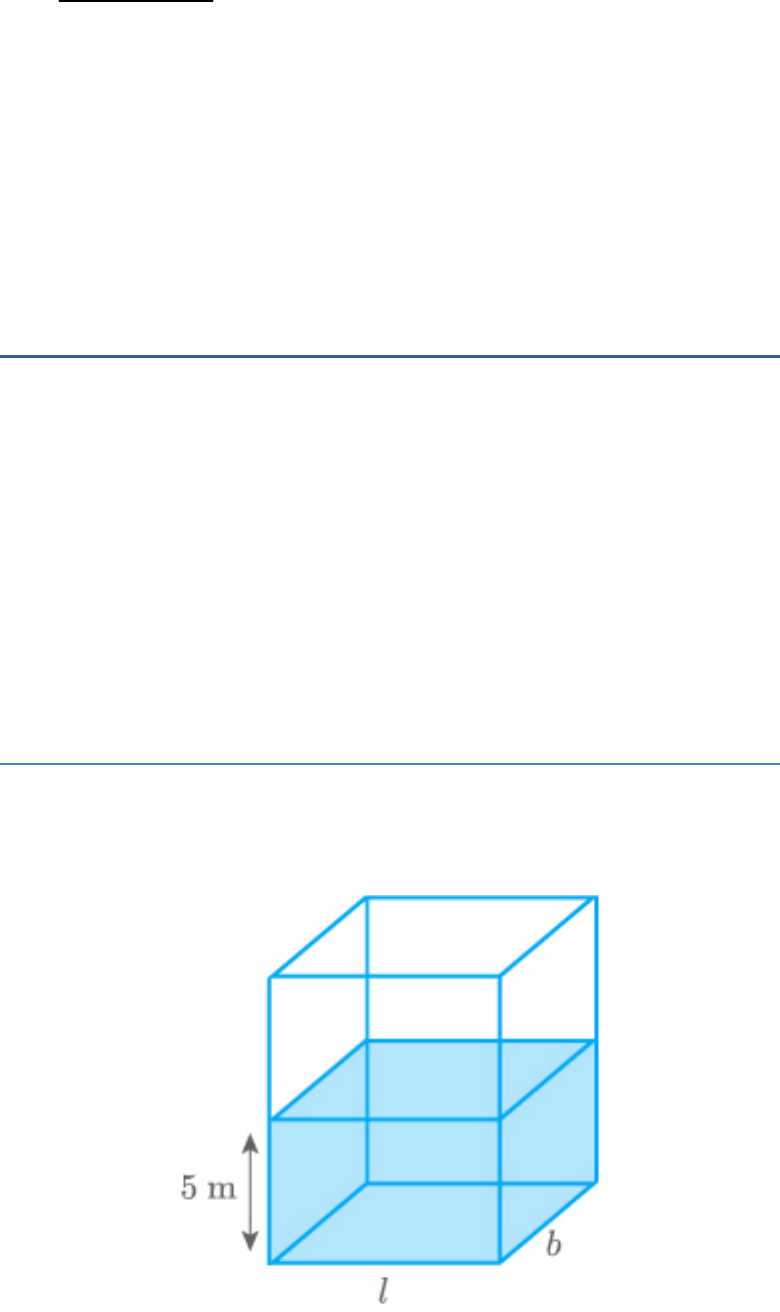
Question: 2
A rectangular water tank of base
11m 6m
contains water up to a height of 5 m. If the water in
the tank is transferred to a cylindrical tank of
radius 3.5 m, find the height of the water level in
the tank.
Solution:
Let the height of the water level in cylindrical tank
be .
h
Length of rectangular water tank
l 11m
Breadth of rectangular water tank
b 6m
Height of water level in rectangular tank
H 5m
Radius of cylindrical tank
r 3.5m
Now, according to the question, water from the
rectangular tank is transferred to the cylindrical
tank.
Volume of water Volume of water
in cylindrical tank in rectangular tank
2
lr h bπ H
2
22
3.5 h 11 6 5
7
330 7
h
22 3.5 3.5

330 7 10 10
h
22 35 35
6 10
h
7
h 8.571m
Hence, the height of the water level in the tank is
8.58 m approx.
Question: 3
How many cubic centimetres of iron is required to
construct an open box whose external dimensions
are and provided the thickness
36cm,
25cm
16.5cm
of the iron is 1.5 cm. If one cubic cm of iron weighs
7.5 g, find the weight of the box.
Solution:
Given: External dimensions of the box are as
follows.
Length
1
l 36cm
Breadth
1
b 25cm
Height
1
h 16.5cm
Now, calculate the internal dimensions of the box.
Length
2
l 36 1.5 1.5
33cm
Breadth
2
b 25 1.5 1.5
22cm
Height
2
h 16.5 1.5
15cm
Now, according to the question,
1 1 1 2 2 2
Volume of iron
in the open
l bh
box
l b h
36 25 16.5 33 22 15
14850 10890
3
3960cm
Weight of one cubic cm of iron = 7.5 g
So, weight of , iron
3
3960cm
7.5 3960
29700

29700
1000
29.7Kg
Hence, the open box weighs 29.7 kg.
Question: 4
The barrel of a fountain pen, cylindrical in shape, is
7 cm long and 5 mm in diameter. A full barrel of ink
in the pen is used up on writing 3300 words on an
average. How many words can be written in a bottle
of ink containing one fifth of a litre?
Solution:
Let the barrel of ink be filled times.
x
Height of the cylindrical barrel
h 7cm
Diameter of the cylindrical barrel
5mm
So, radius
5
r
2 10
1
cm
4
Now, according to the question,
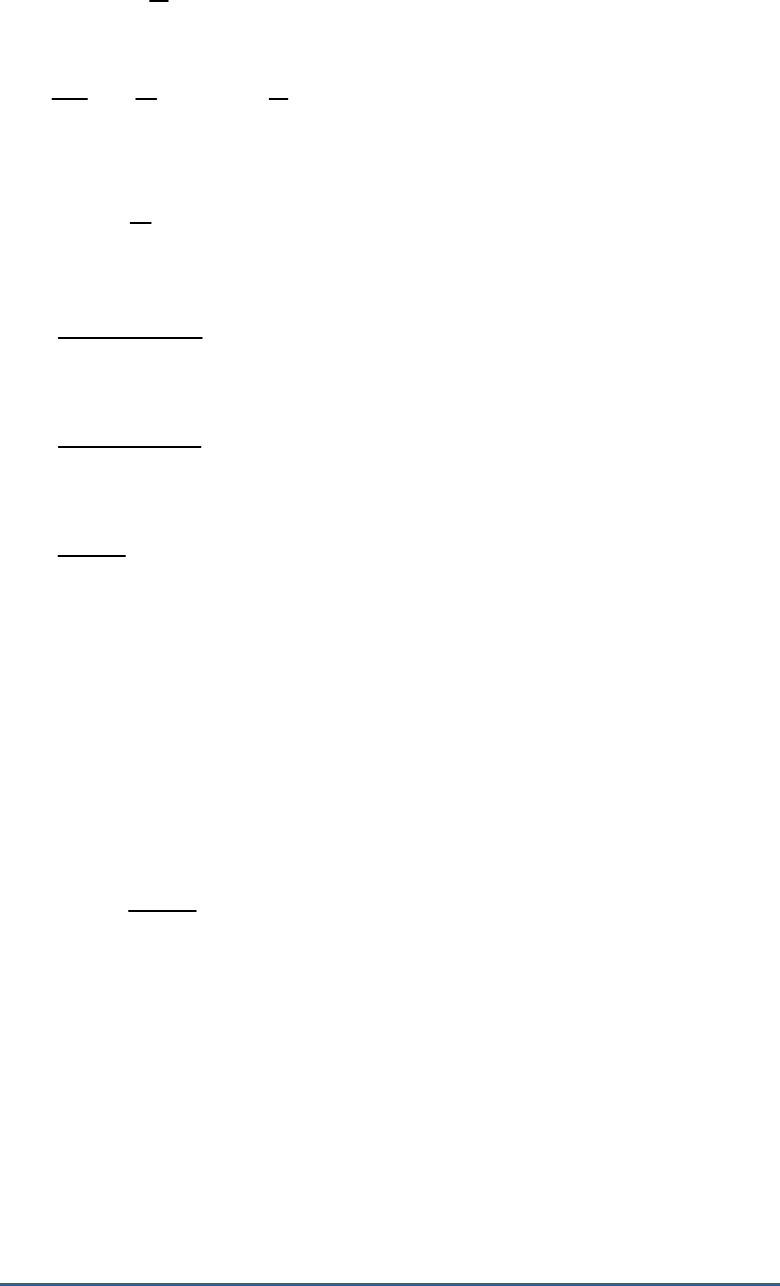
x Volumeof barrel Volumeof ink used
2
1
x πr h onelitre
5
2
3
22 1 1
x 7 1000cm
7 4 5
2
1
x 22 200
4
200 4 4
x
22
100 4 4
x
11
1600
x
11
A full barrel of ink in the pen can write 3300 words.
So, find the number of words can be written by
x
number of barrels.
number of barrels can write words
x
3300 x
1600
3300
11
480000
Hence, the number of words that can be written are
480000.
Question: 5

Water flows at the rate of 10 m/minute through a
cylindrical pipe 5 mm in diameter. How long would
it take to fill a conical vessel whose diameter at the
base is 40 cm and depth 24 cm?
Solution:
Water flows through a cylindrical pipe into the
conical vessel.
Diameter of the pipe = 5 mm
So, radius of pipe
5
r mm
2
5
m
2000
Rate of flow of water
v 10m / min
10
m/sec
60
1
= m/sec
6
Now, volume of flowing water V A v t
Here, is the area of the base and let time be .
A
t
Now, diameter of conical vessel = 40 cm
So, radius
40
R cm
2
40
m
200
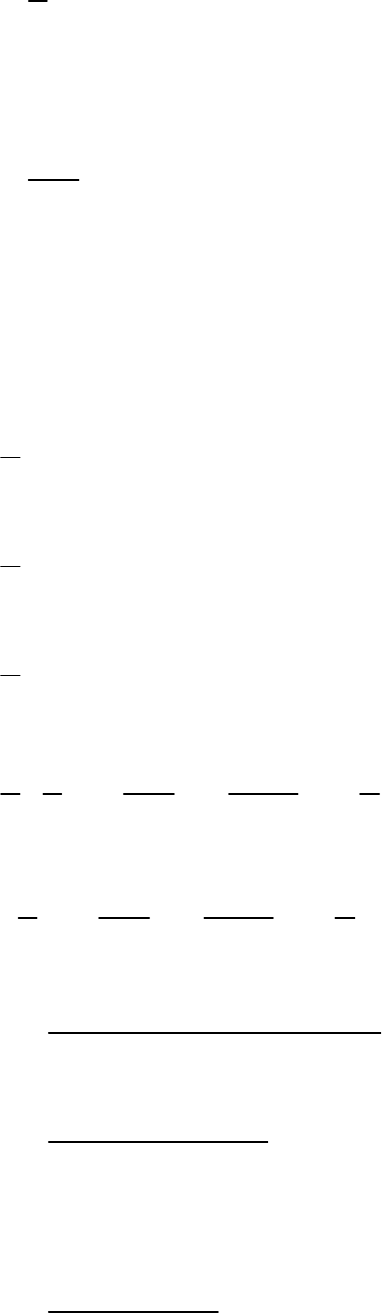
1
m
5
Height of conical vessel
h 24 cm
24
m
100
According to the question,
Volume of water Volume of
in conical vessel flowing water
2
1
πR h A v t
3
2 2
1
πR h πr v t
3
2 2
1
R h r v t
3
2 2
1 1 24 5 1
t
3 5 100 2000 6
2 2
1 8 5 1
t
5 100 2000 6
1 1 8 2000 2000 6
t
5 5 100 5 5
8 2000 20 6
t
5 5 5 5
t 8 16 4 6
8 16 4 6
t minutes
60

8 16 4
t minutes
10
512
t minutes
10
t 51.2minutes
Now,
t 51minutes 0.2minutes
t 51minutes 0.2 60seconds
t 51minutes 12seconds
Hence, it will take 51 minutes and 12 seconds to fill
the conical vessel.
Question: 6
A heap of rice is in the form of a cone of diameter 9
m and height 3.5 m. Find the volume of the rice.
How much canvas cloth is required to just cover the
heap?
Solution:
According to the question,
Heap of rice has the shape of a cone.
Diameter of cone = 9 m
So, radius
9
r m
2
Height of the cone
h 3.5m
Now, find the volume of cone.
2
1
Volumeof cone πr h
3
2
1 22 9
3.5
3 7 2
1 22 9 9 35
3 7 2 2 10
3 9
11
2 2
3
74.25m
Now, find the quantity of canvas required to cover
the heap of rice.
It is equal to the curved surface area of the conical
heap of rice.
2 2
Slant height l r h
2
2
9
3.5
2
2 2
4.5 3.5
20.25 12.25
32.5
5.7m
Curved surfacearea CSA πrl
22 9
5.7
7 2

11
9 5.7
7
2
80.61m
Hence, the area of canvas cloth required to cover
the heap is .
2
80.61m
Question: 7
A factory manufactures 120000 pencils daily. The
pencils are cylindrical in shape each of length 25 cm
and circumference of base as 1.5 cm. Determine the
cost of colouring the curved surfaces of the pencils
manufactured in one day at Rs 0.05 per .
2
dm
Solution:
According to the question,
The pencils manufactured are cylindrical in shape.
Height of the cylinder = 25 cm
Circumference of the base = 1.5 cm
2πr
Now, find the curved surface area of one pencil.
Curved surface CSR ar a he 2πr
2πr h
1.5 25
2
37.5cm

Curved surface area
of 12000
120000 37.5
0pencils
4500000
4500000
100
2
45000dm
Cost of colouring 1 curved surfaces of the
2
dm
pencils = Rs 0.05
So, cost of colouring, 45000 curved surfaces of
2
dm
the pencils
45000 0.05
450 5
2250
Hence, cost of colouring the pencils per day is Rs
2250.
Question: 8
Water is flowing at the rate of 15 km/h through a
pipe of diameter 14 cm into a cuboidal pond which
is 50 m long and 44 m wide. In what time will the
level of water in pond rise by 21 cm?
Solution:
Water flows through a cylindrical pipe into the
cuboidal pond.

Diameter of the pipe = 14 cm
So, radius of pipe
14
r
2
7cm
0.07m
Rate of flow of water
v 15km / hour
15000m / hour
Volume of flowin Vg water A v t
Here, is the area of the base and let time be .
A
t
Now, length of cuboidal pond
l 50m
Breadth of cuboidal pond
b 44m
Height of cuboidal pond
h 21m
According to the question,
Volume of water in pond Volume of flowing water
l b h A v t
2
l b h πr v t
2
22
50 44 21 0.07 15000 t
7
50 44 0.21 7
t
22 0.07 0.07 15000
50 44 21 7 100 100
t
22 7 7 15000 100
50 44 21
t
22 7 15 10
5 2 3
t
15
t 2hours
Hence, the level of water in pond will rise in 2
hours.
Question: 9
A solid iron cuboidal block of dimensions
is recast into a hollow cylindrical
4.4m 2.6m 1m
pipe of internal radius 30 cm and thickness 5 cm.
Find the length of the pipe.
Solution:
Length of the cuboidal block
l 4.4m
Breadth of the cuboidal block
b 2.6m
Height of the cuboidal block
h 1m
Now, let the height of pipe be .
H

Internal radius of the pipe
1
r 30cm
0.3m
Thickness of the pipe
t 5cm
0.05m
So, external radius
2
r 0.3 0.05
0.35m
Now, find the height of the cylindrical pipe.
According to the question,
Volume of cuboid Volume of cylindrical pipe
2 2
2 1
l b h πH r r
2 2
22
4.4 2.6 1 H 0.35 0.30
7
2 2
4.4 2.6 7
H
22 0.35 0.30
44 26 7
H
22 0.1225 0.09 10 10
2 26 7
H
0.0325 10 10
2 26 7 10000
H
325 10 10
2 26 7 100
H
325
H 112m

Hence, the length of the hollow cylindrical pipe is
112 m.
Question: 10
500 persons are taking a dip into a cuboidal pond
which is 80 m long and 50 m broad. What is the rise
of water level in the pond, if the average
displacement of the water by a person is ?
3
0.04m
Solution:
The pond is cuboidal in shape.
So, length of the pond
l 80m
Breadth of the pond
b 50m
Now, let the rise of water level be .
h
According to the question,
Average displacement of the water by one person
3
0.04m
Total number of persons taking a dip into the pond
= 500
Now, total volume of water displaced
500 0.04
500 4
100
3
20m

Volume of Total volume of
the pond water displaced
l b h 20
80 50 h 20
20
h
50 80
0.005
0.005 100
0.5cm
Hence, the water level rises by 0.5 cm.
Question: 11
16 glass spheres each of radius 2 cm are packed into
a cuboidal box of internal dimensions
and then the box is filled with
16cm 8cm 8cm
water. Find the volume of water filled in the box.
Solution:
Radius of one sphere = 2 cm
r
Length of cuboidal box
l 16cm
Breadth of cuboidal box
b 8cm
Height of cuboidal box
h 8cm
Now, according to the question,

Volume of Volume Volume of
water filled of cuboid 16 spheres
3
4
l b h 16 πr
3
3
4 22
16 8 8 16 2
3 7
4 22
16 8 8 16 8
3 7
11
16 8 8 1
21
21 11
1024
21
10
1024
21
3
487.6cm
Hence, the volume of water filled in the box is
.
3
487.6cm
Question: 12
A milk container of height 16 cm is made of metal
sheet in the form of a frustum of a cone with radii
of its lower and upper ends as 8 cm and 20 cm
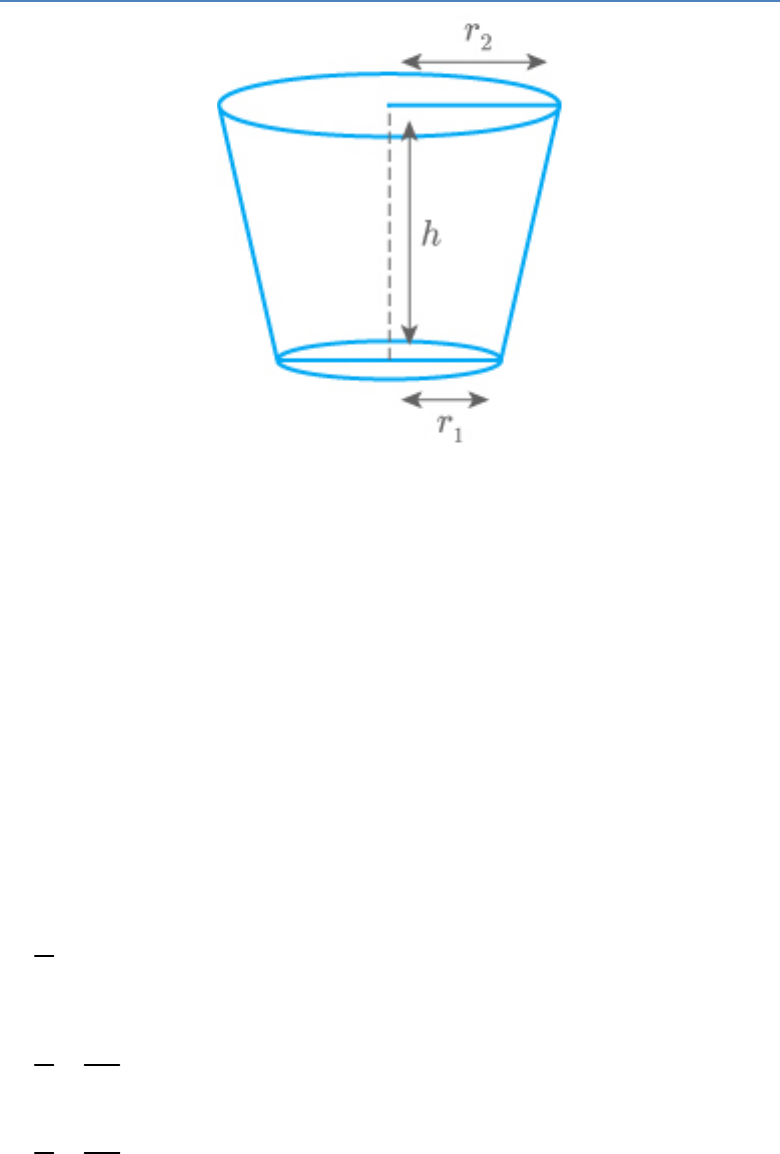
respectively. Find the cost of milk at the rate of Rs.
22 per litre which the container can hold.
Solution:
It is given that the milk container has the shape of a
frustum of a cone.
So, height of frustum
h 16cm
Lower radius of frustum
1
r 8cm
Upper radius of frustum
2
r 20cm
Volume of milk Volume of
in a container frustum
2 2
1 2 1 2
1
πh r r rr
3
2 2
1 22
16 8 20 8 20
3 7
1 22
16 64 400 160
3 7

1 22
16 624
3 7
22
16 208
7
3
10459.4 cm
10.459litre
Cost of 1 litre of milk = Rs. 22
So, cost of milk
10.459litres
22 10.459
230.098
Hence, the cost of milk which the container can
hold is Rs. 230.098.
Question: 13
A cylindrical bucket of height 32 cm and base radius
18 cm is filled with sand. This bucket is emptied on
the ground and a conical heap of sand is formed. If
the height of the conical heap is 24 cm, find the
radius and slant height of the heap.
Solution:
According to the question,
A cylindrical bucket is emptied, and the heap of
sand forms a cone.
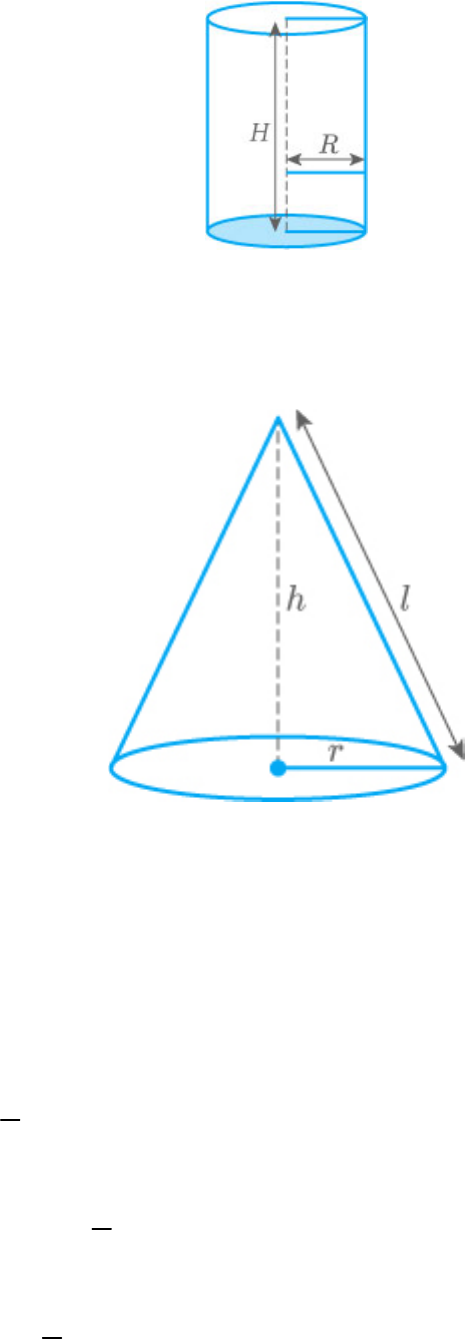
Height of the cylinder
H 32cm
Radius of cylinder
R 18cm
Let the radius and slant height of the cone be
respectively.
r andl
Height of cone
h 24 cm
Volume of cylinder Volume of cone
2 2
1
h hπ πr
3
r
2 2
1
π 18 32 πr 24
3
2 2
1
18 32 r 24
3

2
18 18 32 3
r
24
2
18 18 32
r
8
2
r 18 18 4
2
r 18 18 2 2
2
2
r 18 2
r 18 2
r 36cm
Now, find the value of slant height.
2 2
Slant heig l r hht
2 2
l 36 24
1296 576
1872
43.266cm
Hence, the radius and slant height of the conical
heap are 36 cm and 43.266 cm respectively.
Question: 14
A rocket is in the form of a right circular cylinder
closed at the lower end and surmounted by a cone
with the same radius as that of the cylinder. The
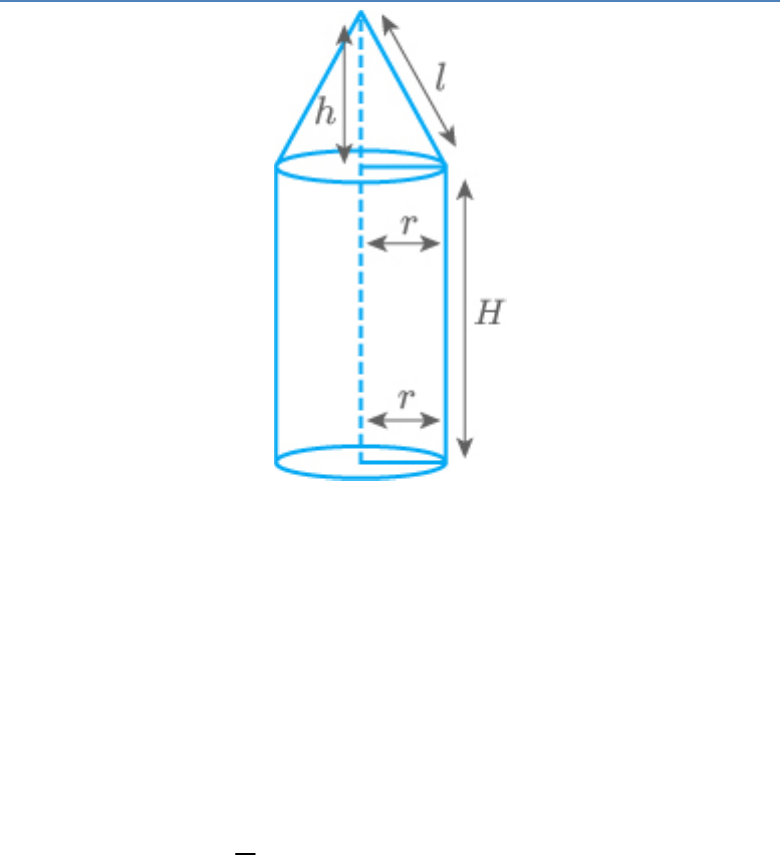
diameter and height of the cylinder are 6 cm and 12
cm, respectively. If the slant height of the conical
portion is 5 cm, find the total surface area and
volume of the rocket [Use = 3.14].
π
Solution:
The shape of the rocket is the combination of a
cylinder and a cone.
Let the height of the cone be .
h
Diameter of cone and cylinder is same and is equal
to 6 cm.
So, radius
6
r
2
3cm
Height of the cylinder
H 12cm
Now, slant height of cone
l 5cm

2 2
Slant height l r h
2 2
5 3 h
2
2 2
5 3 h
2
25 9 h
2
h 25 9
2
h 16
h 4
Now, find the volume of rocket.
Volume Volume of Volume
of rocket cylinder of cone
2 2
1
πr H πr h
3
2
1
πr H h
3
2
1
3.14 3 12 4
3
2
4
3.14 3 12
3
2
36 4
3.14 3
3
2
40
3.14 3
3
3.14 3 40

3
376.8cm
Now, find the total surface area of the rocket.
Curved Surface
Area of cone
Total Surface
Area of the
Area of the
Curved Surface
base of
rocket TSA
Area of cylinder
cylinder
2
πrl 2πrH πr
πr l 2H r
3.14 3 5 2 12 3
3.14 3 5 24 3
3.14 3 32
3.14 96
2
301.44 cm
Hence, the volume and surface area of rocket are
and respectively.
3
376.8cm
2
301.44 cm
Question: 15
A building is in the form of a cylinder surmounted
by a hemispherical vaulted dome and contains
of air. If the internal diameter of dome is
3
19
41 m
21

equal to its total height above the floor, find the
height of the building?
Solution:
According to the question,
Building is formed by the combination of a cylinder
and a hemisphere.
Volume of air in the building =
3
19
41 m
21
So, Volume of building = Volume of air
Let the radii of both the cylinder and hemisphere be
.
r
Also, let the heights of the cylinder and the building
be respectively.
h andH
Now, diameter of the dome
2r
It is given that internal diameter of dome is equal to
total height of building.
So,
H 2r
Height of Height of Height of
–
cylinder building hemisphere
h H r
2r r
r
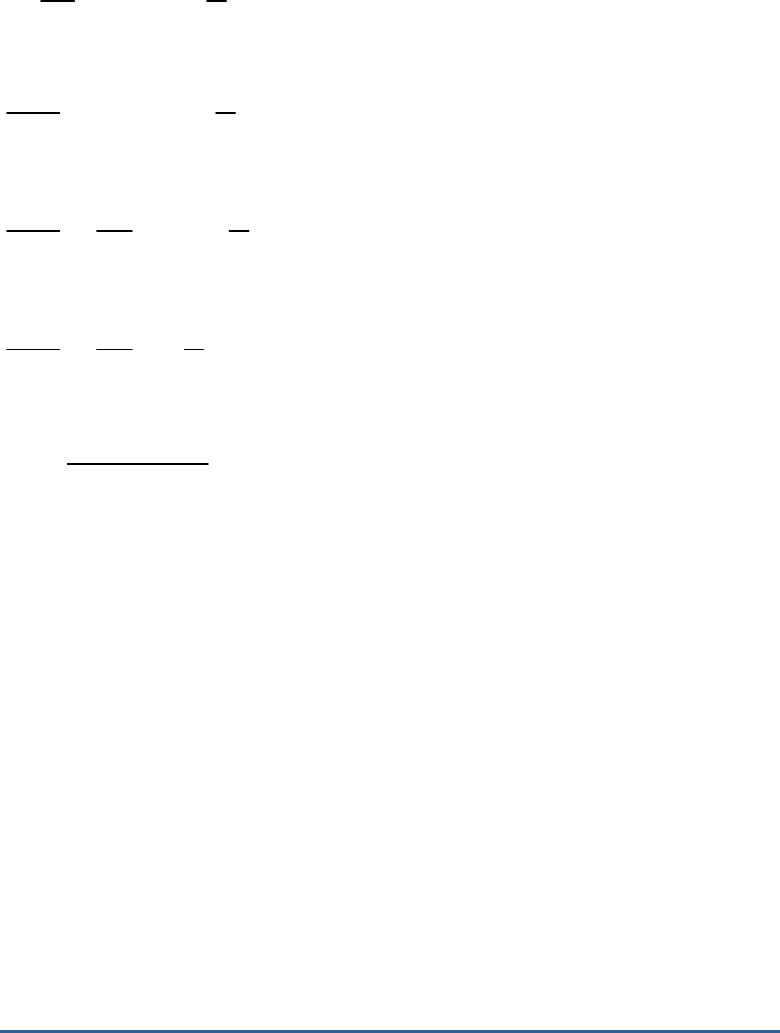
Volume of Volume of Volume of
building cylinder hemisphere
2 3
19 2
41 πr h πr
21 3
2
880 2
πr h r
21 3
2
880 22 2
r r r h r
21 7 3
3
880 22 5
r
21 7 3
3
880 7 3
r
21 22 5
3
r 8
r 2
Now, height of the building
H 2r
2 2
4m
Hence, height of the building is 4 m.
Question: 16
A hemispherical bowl of internal radius 9 cm is full
of liquid. The liquid is to be filled into cylindrical
shaped bottles each of radius 1.5 cm and height 4
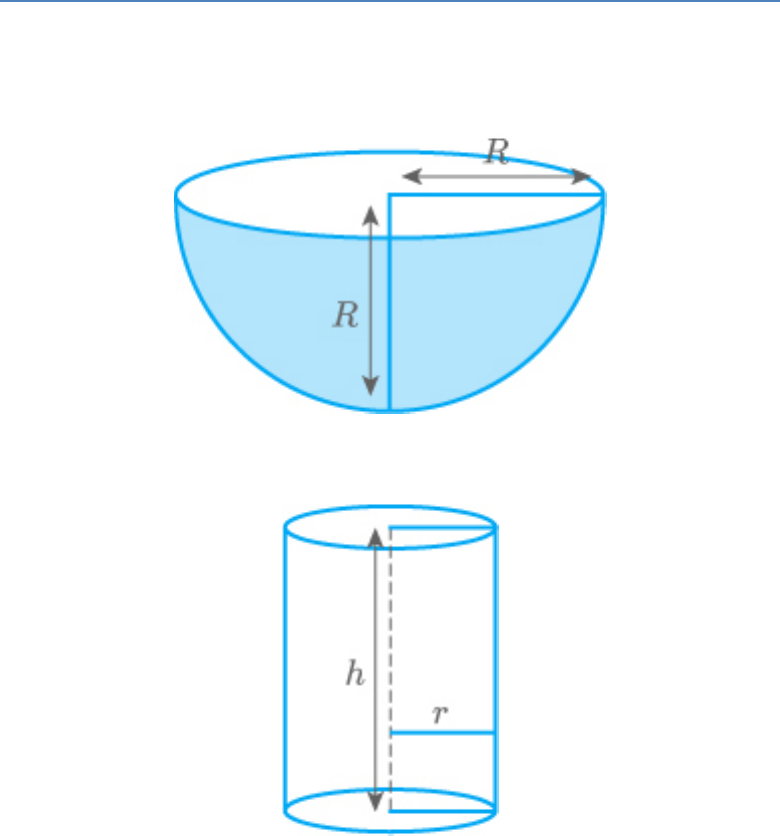
cm. How many bottles are needed to empty the
bowl?
Solution:
Let the number of bottles required to empty the
bowl be .
x
Radius of the bowl
R 9cm
Now, radius of cylindrical bottle
r 1.5cm
Height of the bottle
h 4 cm
Now, according to the question,
Volume of Volume of x
bowl number of bottles

3 2
2
πR x πr h
3
3
2
2
π R
3
x
πr h
3
2
2R
x
3r h
3
2
2 9
x
3 1.5 4
3 9 9
x
1.5 1.5 2
3 9 9 10 10
x
15 15 2
x 54
Hence, the total number of bottles required are 54.
Question: 17
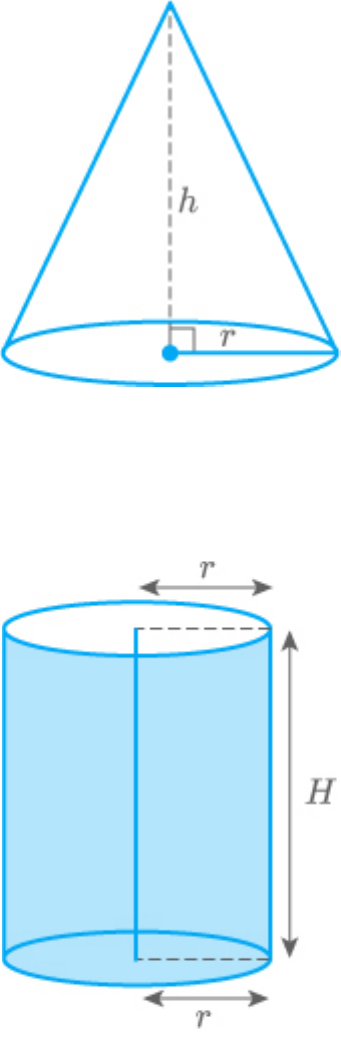
A solid right circular cone of height 120 cm and
radius 60 cm is placed in a right circular cylinder
full of water of height 180 cm such that it touches
the bottom. Find the volume of water left in the
cylinder, if the radius of the cylinder is equal to the
radius of the cone.
Solution:
Height of the cone
h 120cm
Radius of the cone
r 60cm
Now, radius of cylinder is same as that of cone.
So, radius of cylinder
r 60cm
Height of cylinder
H 180cm
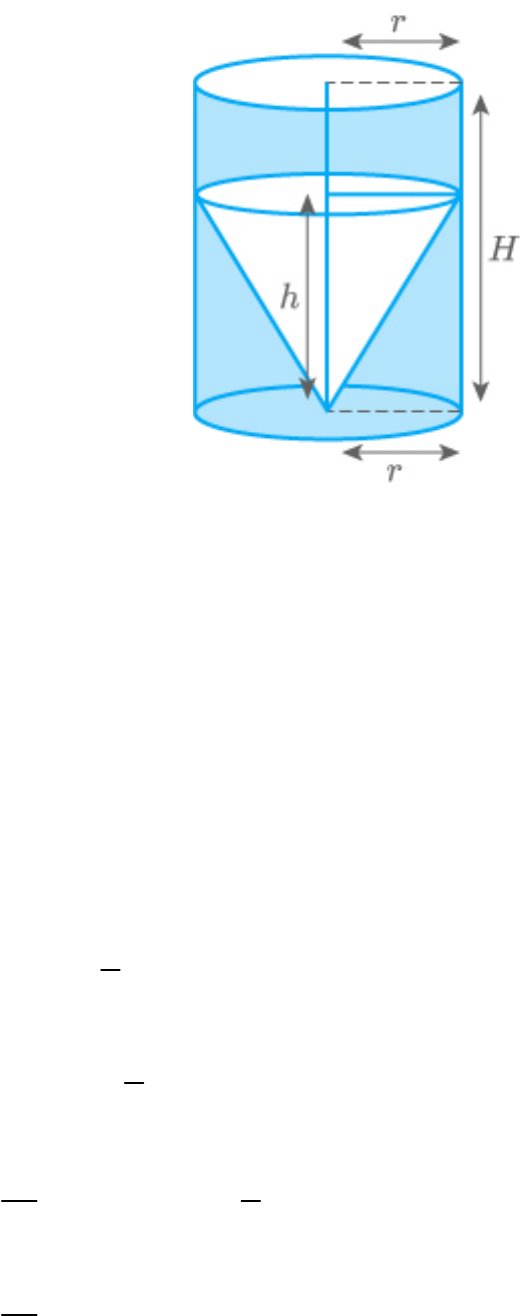
According to the question,
Cone is placed inside the cylinder having water up
to the brim. So, volume of water displaced by the
cylinder will be equal to the volume of cone.
Now, find the volume of water left in the cylinder.
Volume of Volume of Volume
–
water left cylinder of cone
2 2
1
πr H πr h
3
2
1
πr H h
3
2
22 1
60 180 120
7 3
22
60 60 180 40
7

22
60 60 140
7
22 60 60 20
3
1584000cm
3
6
1584000
m
10
3
1.584m
Hence, volume of water left in the cylinder is
.
3
1.584m
Question: 18
Water flows through a cylindrical pipe, whose inner
radius is 1 cm, at the rate of 80 cm/sec in an empty
cylindrical tank, the radius of whose base is 40 cm.
What is the rise of water level in tank in half an
hour?
Solution:
Water flows through a cylindrical pipe into the
cylindrical tank.
Inner radius of pipe
r 1cm
Rate of flow of water
v 80cm / sec
Now, area of the base of cylinder
2
A πr

Time
1
t hour
2
1
60 60
2
1800seconds
Now, let the height of the cylindrical tank be .
h
Radius of the bases
R 40cm
According to the question,
Volume of Volume of
water in tank flowing water
2
πR h A v t
2 2
πR h πr v t
2 2
R h r v t
2 2
40 h 1 80 1800
80 1800
h
40 40
2 180
h
4
h 90cm
Hence, in half an hour, the water level rises by 90
cm in the tank.
Question: 19

The rain water from a roof of dimensions
drains into a cylindrical vessel having
22m 20m
diameter of base 2 m and height 3.5 m. If the rain
water collected from the roof just fill the cylindrical
vessel, then find the rainfall in cm.
Solution:
The roof has the shape of a cuboid.
Let the height of cuboid be , which is equal to
h cm
the rainfall.
Length of cuboid
l 22m
2200cm
Breadth of cuboid
b 20m
2000cm
Now, water drains into a cylindrical vessel.
Diameter of cylinder = 2 m
So, its radius
2
r
2
1m
100cm
Height of cylinder
H 3.5m
350cm
Volume of cuboid Volume of cylinder
2
l b h πr H

2
22
2200 2000 h 100 350
7
22 100 100 350
h
7 2200 2000
22 35
h
7 22 2
5
h
2
h 2.5cm
Hence, the measurement of rainfall is 2.5 cm.
Question: 20
A pen stand made of wood is in the shape of a
cuboid with four conical depressions and a cubical
depression to hold the pens and pins, respectively.
The dimension of the cuboid are 10 cm, 5 cm and 4
cm. The radius of each of the conical depressions is
0.5 cm and the depth is 2.1 cm. The edge of the
cubical depression is 3 cm. Find the volume of the
wood in the entire stand.
Solution:
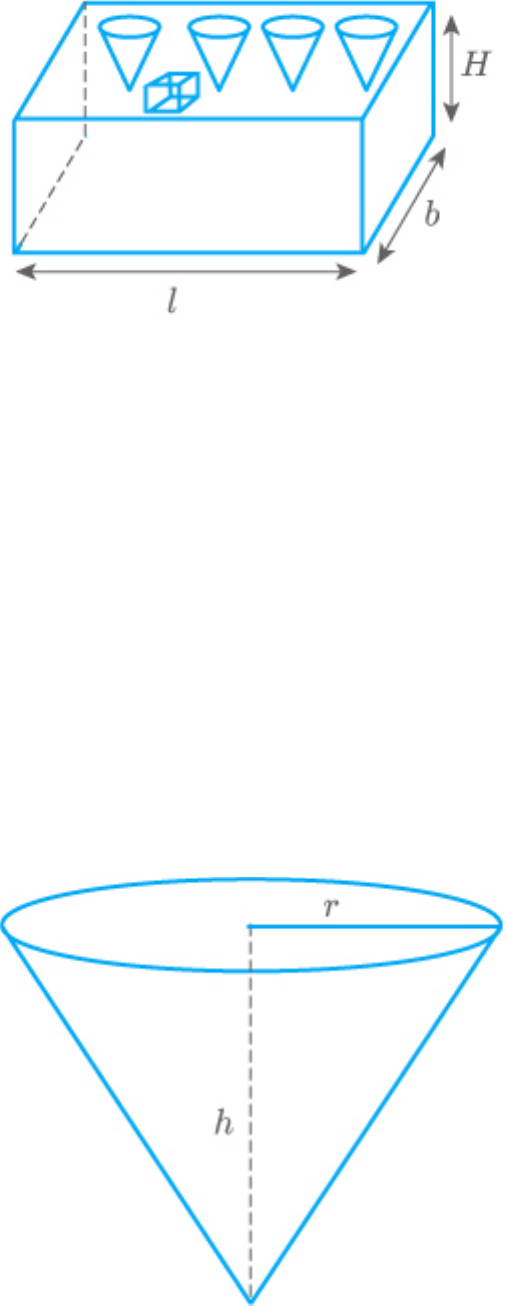
The pen stand has the shape of a cuboid with four
conical depressions and a cubical depression.
Length of the cuboid
l 10cm
Breadth of the cuboid
b 5cm
Height of the cuboid
h 4 cm
1
Volume of cub V lo d bi h
10 5 4
3
200cm
Height of conical depression
h 2.1cm
Radius of conical depression
r 0.5cm
2
2
Volume of conical depres
1
sio hn V πr
3
2
1 22
0.5 2.1
3 7
1 22 5 5 21
3 7 10 10 10
11
2 10
3
11
cm
20
Edge of cubical depression
a 3cm
3
3
Volume of cubical depressio Vn a
3
3
3
27cm

Now, according to the question,
Volume Volume of 4
–
of cuboid conical depression
Volume
of wood
Volume of cubical
–
depression
1 2 3
V 4 V V
11
200 4 27
20
11
200 27
5
1000 11 135
5
854
5
3
170.8cm
Hence, the volume of the wood in the entire stand
is .
3
170.8cm