
Lesson: Circles
Exercise 9.1 (10) (Multiple Choice Questions and
Answers)
Choose the correct answer from the given four
options:
Question: 1
If radii of two concentric circles are 4 cm and 5 cm,
then the length of each chord of one circle which is
tangent to the other circle is
a. 3 cm
b. 6 cm
c. 9 cm
d. 1 cm
Solution
(b)
Let C1, C2 be concentric circles with centre O. PQ be
the chord of circle C2 that touches C1 at R.
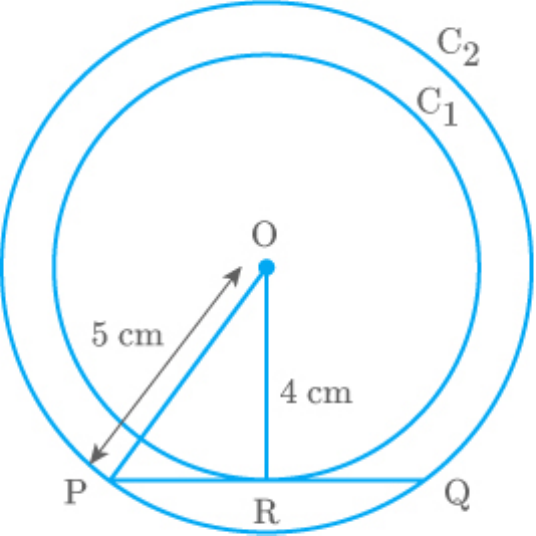
OR is radius and PQ is tangent at R.
Thus,
OR PQ
From the figure,
and
R 90 ,
OP 5cm
OR 4cm
In , by Pythagoras theorem,
OPR
2 2 2
OP OR PR
2 2
2
5 4 PR
2
PR 25 16
2
PR 9
PR 3
The chord is bisected by the perpendicular from the
origin.
Thus,
PQ 2 PR
2 3
6
Hence, length of the chord is 6 cm.
Question: 2
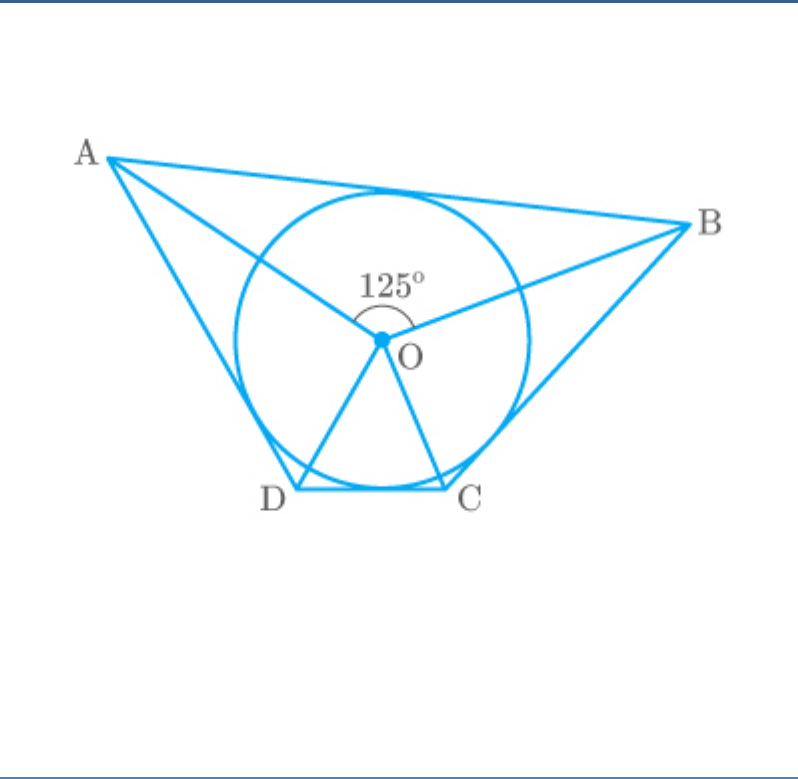
In the adjoining figure, if , then
AOB 125
COD
is equal to:
a.
62.5
b.
45
c.
35
d.
55
Solution
(d)
We know that supplementary angles are subtended
at the centre of a circle by a quadrilateral
circumscribing that circle.
Thus,
AOB COD 180
125 COD 180
COD 180 125
COD 55
Hence, is .
COD
55
Question: 3
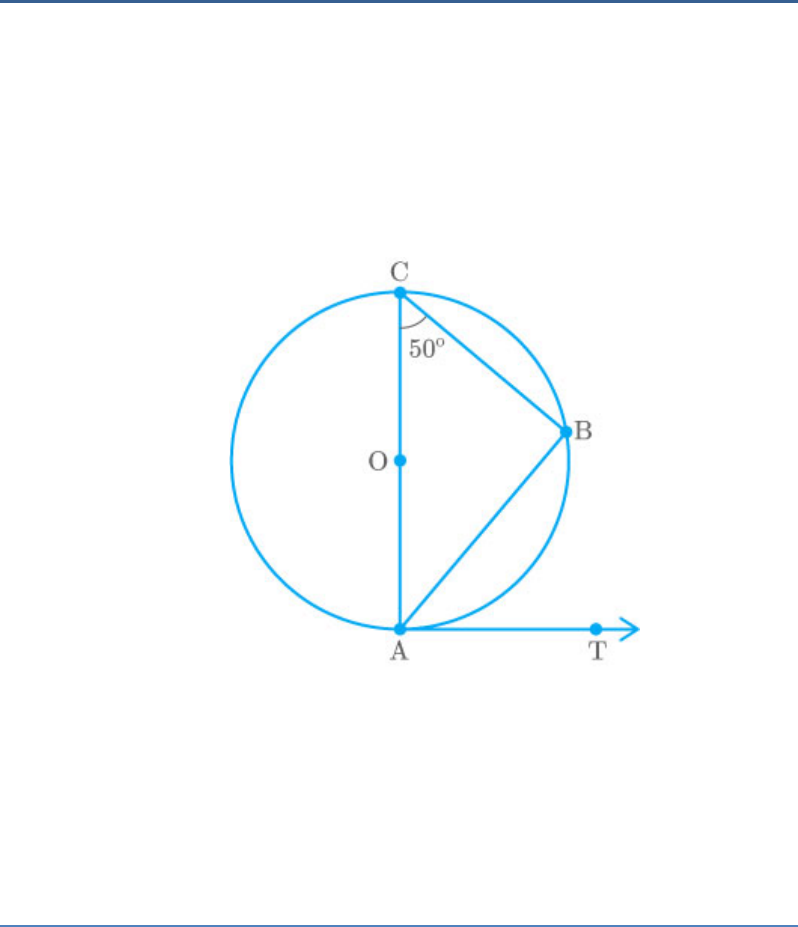
In the adjoining figure, AB is a chord of the circle
and AOC is its diameter such that . If AT
ACB 50
is the tangent to the circle at the point A, then
is equal to
BAT
a.
65
b.
60
c.
50
d.
40
Solution
(c)
From the given figure,

B 90 Anglein semicircle
BAC 180 C B Anglesumproperty
BAC 180 50 90
BAC 40
AT is a tangent at the point A and OA is a radius,
Thus, and
AT OA
OAT 90
OAB BAT 90
40 BAT 90
BAT 90 40
BAT 50
Hence, is .
BAT
50
Question: 4
From a point, P which is at a distance of 13 cm from
the centre O of a circle of radius 5 cm, the pair of
tangents PQ and PR to the circle are drawn. Then
the area of the quadrilateral PQOR is
a.
2
60cm
b.
2
65cm
c.
2
30cm
d.
2
32.5cm
Solution
(a)
According to the question,

PQ is a tangent at point Q and QO is a radius.
Thus,
PQO 90
In , by the Pythagoras theorem,
OPQ
2 2 2
PQ OP OQ
2 2
2
PQ 13 5
2
PQ 169 25
2
PQ 144
PQ 12
By SSS criterion of congrOPQ OPR uence
Thus,
area of OPQ area of OPR
Area of the quadrilateral PQOR
2 area of OPR
Area of the
quadrilateral PQO
1
2 base alti
2
R
tude
RP OR
12 5
60
Hence, the area of the quadrilateral PQOR is .
2
60cm

Question: 5
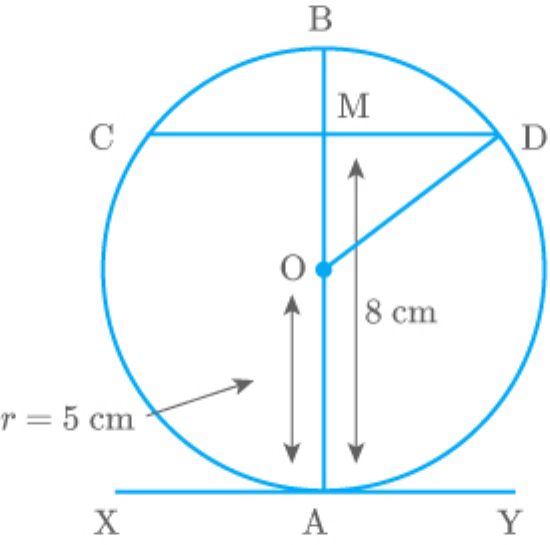
At one end A of a diameter AB of a circle of radius 5
cm, tangent XAY is drawn to the circle. The length of
the chord CD parallel to XY and at a distance 8 cm
from A is
a.
4 cm
b.
5cm
c.
6cm
d.
8cm
Solution
(d)
AO is a radius and XAY is a tangent to the circle at
point A.
Thus,
OAY 90
From the figure,
AO 5cm
There is a chord CD at a perpendicular distance of 8
cm from A. CD intersects AB at M and .
CMD||XAY
Join OD.
OD 5cm Radiusof circle
OM 8 5
3cm
OMD OAY 90
In , by Pythagoras theorem,
OMD
2 2 2
MD OD MO
2 2
2
MD 5 3
2
MD 25 9
2
MD 16
MD 4
The chord CD is bisected by the perpendicular from
centre O of circle.
Thus,
CD 2 MD
2 4
8
So,
CD 2MD 2 4 8 cm
Hence, the length of chord CD is 8 cm.
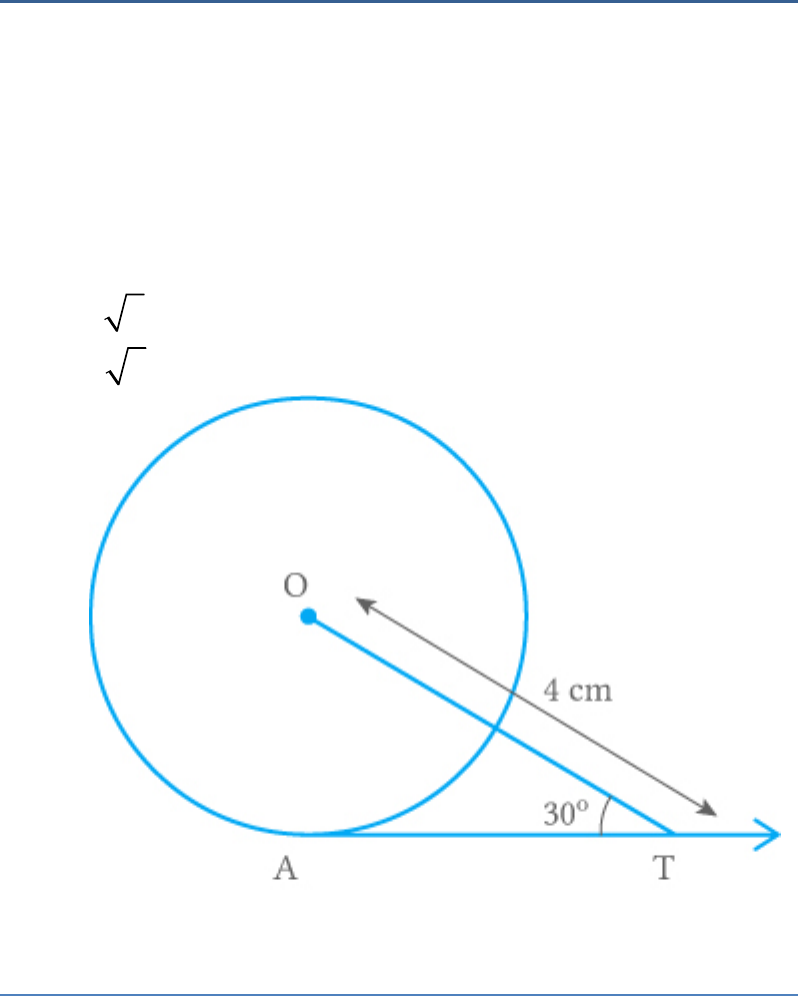
Question: 6
In the adjoining figure, AT is a tangent to the circle
with centre O such that OT 4 cm and .
OTA 30
Then AT is equal to
a.
4 cm
b.
2cm
c.
2 3 cm
d.
4 3 cm
Solution
(c)
Join OA.
From the figure,
AT is a tangent at the point A and OA is a radius.
Thus,
OAT 90
and
OT 4 cm
OTA 30
Now, in ,
OTA
Base
cos30
Hypotenuse
AT
cos30
4
3 AT 3
cos30
2 4 2
AT 2 3
Hence, the length of AT is .
2 3 cm
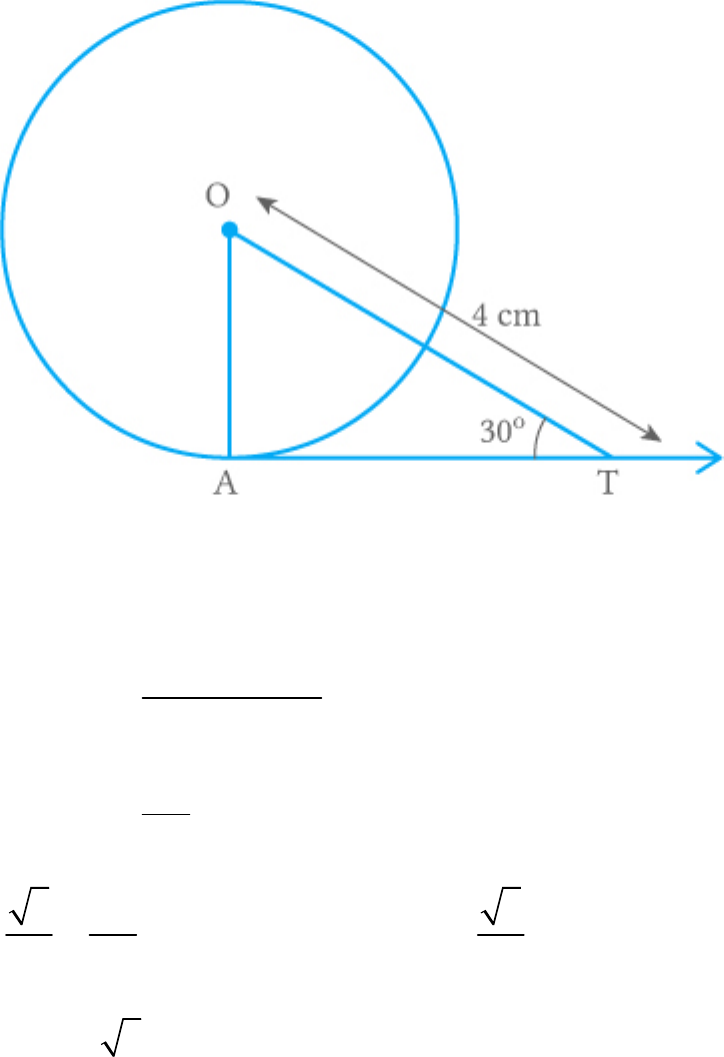
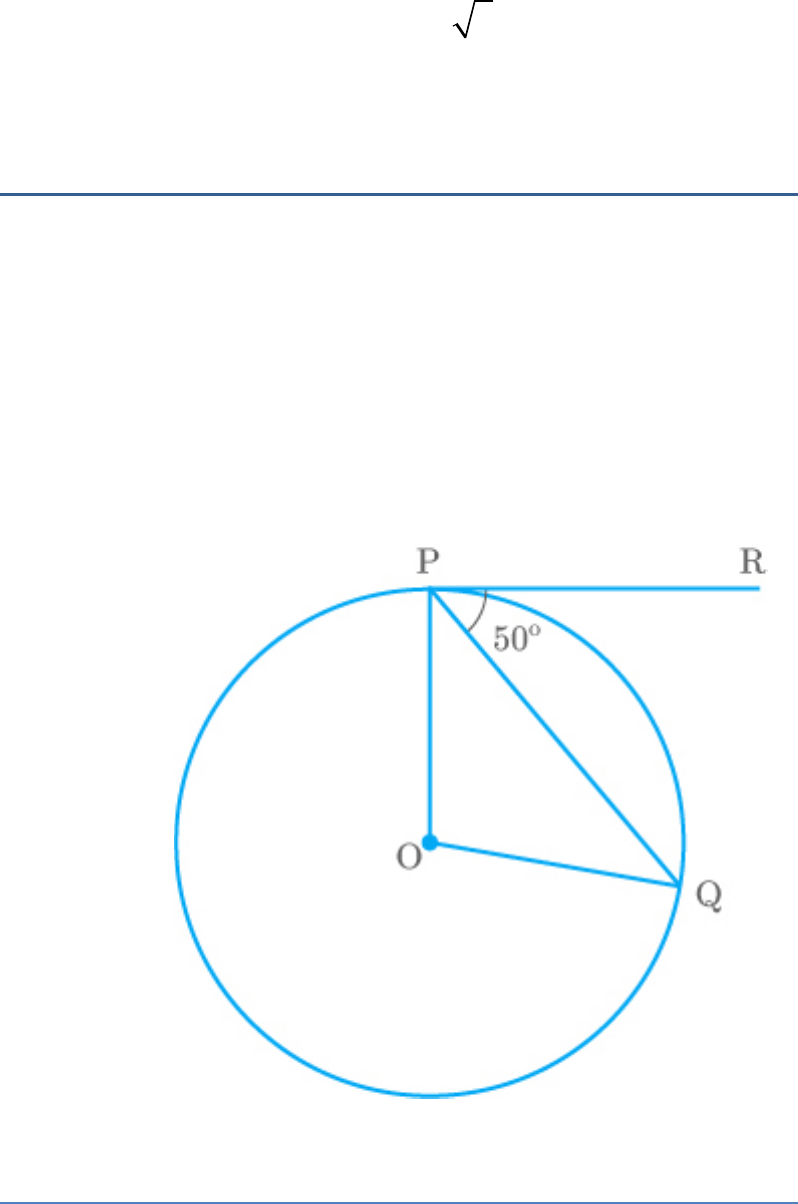
Question: 7
In the adjoining figure, if O is the centre of a circle,
PQ is a chord and the tangent PR at P makes an
angle of with PQ, then is equal to
50
POQ
a.
100
b.
80
c.
90
d.
75
Solution
(a)
From the figure,
PR is a tangent to the circle at point P.

OP is a radius of the circle.
Thus,
OPR 90
OPQ 50 90
OPQ 90 50
OPQ 40
In ,
OPQ
OP OQ Radii of samecircle
Thus,
Angles opposite to equal Q OPQ 40 sides
We know that, the sum of the interior angles in a
triangle is .
180
Thus, in ,
OPQ
POQ P Q 180
POQ 180 P Q
POQ 180 40 40
POQ 100
Hence,
POQ 100
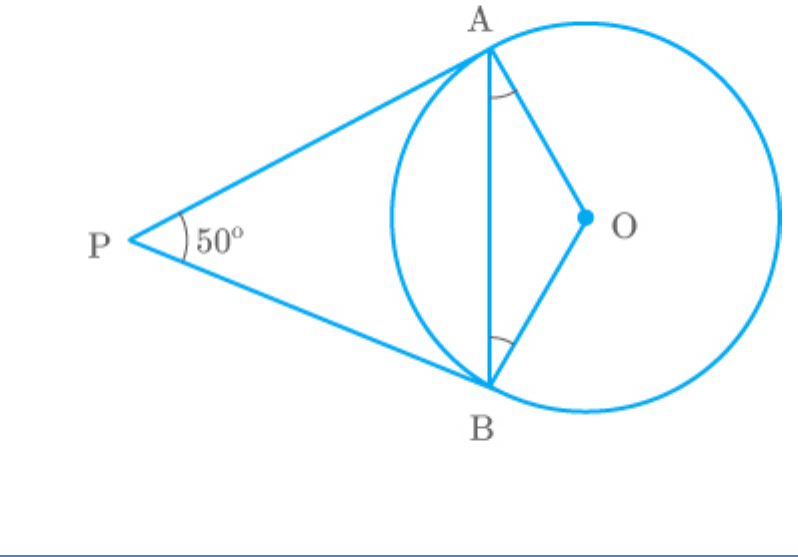
Question: 8
In the adjoining figure, if PA and PB are tangents to
the circle with centre O such that , then
APB 50
is equal to
OAB
a.
25
b.
30
c.
40
d.
50
Solution
(a)
In ,
OAB
OA OB Radii of samecircle
Angles opposite to equal OAB OBA sides
PA is a tangent to the circle at point A and OA is a
radius.
Thus,
OAP 90
Similarly,
OBP 90
We know that in a quadrilateral, the sum of all the
interior angles is .
360
Thus, in quadrilateral PAOB,

P A O B 360
50 90 O 90 360
O 360 90 90 50
O 130
We know that, the sum of all the interior angles of a
triangle is .
180
Thus, in ,
OAB
O OAB OBA 180
130 OAB OAB 180 OAB OBA
2 OAB 180 130
2 OAB 50
50
OAB
2
OAB 25
Hence, is .
OAB
25
Question: 9
If two tangents inclined at an angle are drawn to
60
a circle of radius 3 cm, then length of each tangent is
equal to
a.
3
3 cm
2
b.
6cm
c.
3cm
d.
3 3 cm
Solution
(d)
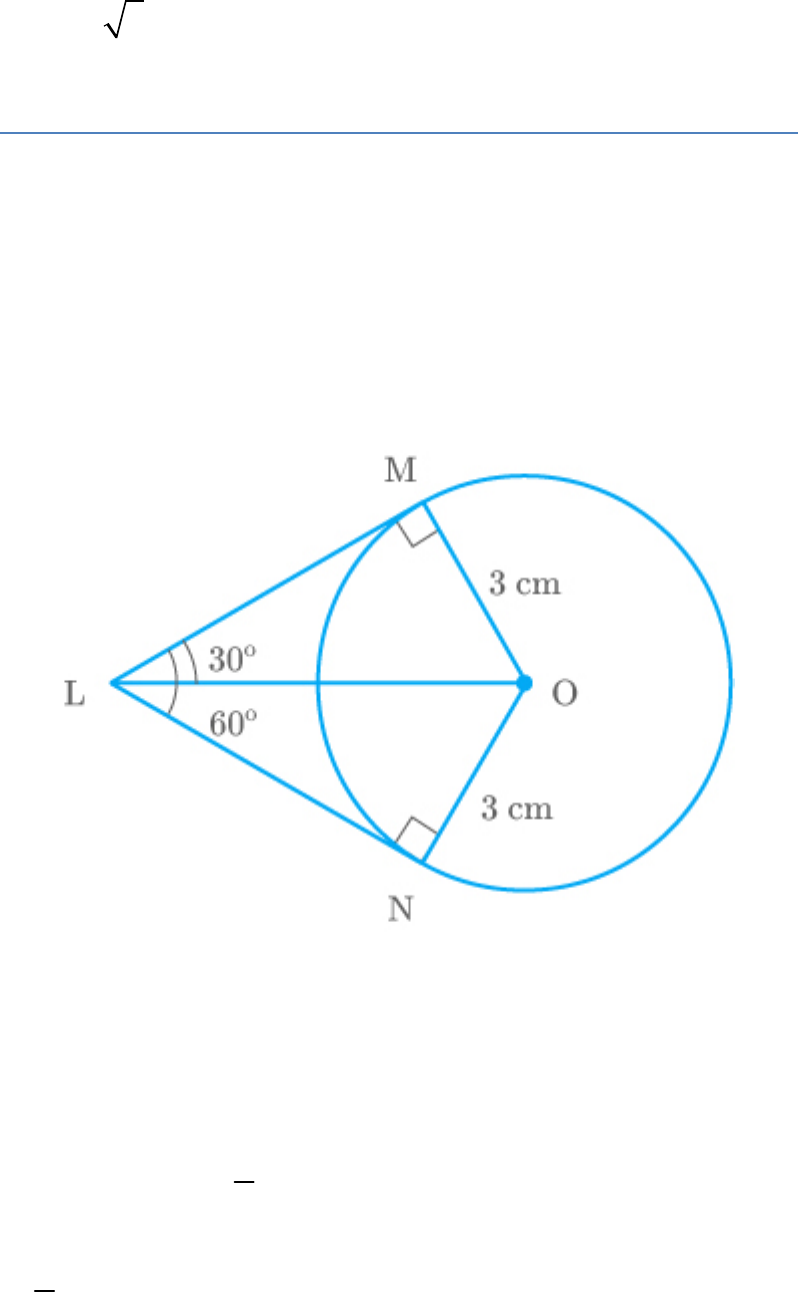
In the figure given below,
LM and LN are tangents at points M and N of the
circle respectively and OM is the radius of the circle.
OM 3cm
Thus,
LMO 90
The line from the centre of the circle bisects the
angle formed by the two tangents.
Thus,
1
OLM NLM
2
1
60
2
30

In ,
LMO
OM
tan30
LM
1 3
LM
3
LM 3 3
Similarly,
LN 3 3
Hence, the length of each tangent is .
3 3 cm
Question: 10
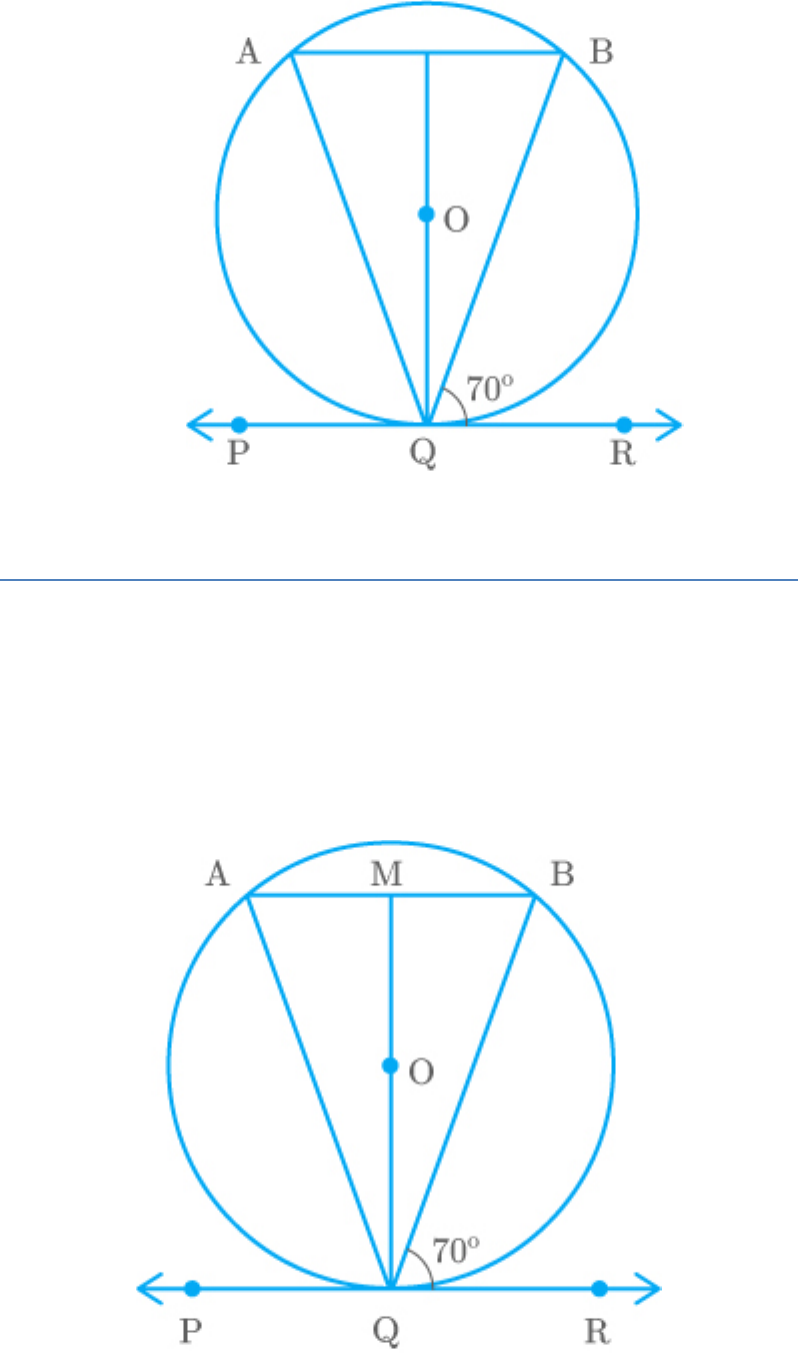
In the adjoining figure, if PQR is the tangent to a
circle at Q whose centre is O, AB is a chord parallel
to PR and , then is equal to
BQR 70
AQB
a.
20
b.
40
c.
35
d.
45
Solution
(b)
Given:
AB PQRA
Alternate interior aB BQR 70 ngles
Alternate interior aOQR AMQ ngles
PQR is a tangent at point Q and OQ is a radius of
the circle.
Thus,
OQR 90
OQB BQR 90
OQB 70 90
OQB 90 70
OQB 20
QM is a perpendicular to the chord AB that bisects
AB.
Thus, and
AMO 90
MA MB
QMA QMB Each 90
MQ MQ Common side
Thus,
By SAS criterion of congrQMA QMB uence
A B
A 70 B 70
We know that the sum of the interior angles in a
triangle is .
180
Thus,
A AMQ AQM 180
70 90 AQM 180
AQM 180 70 90
AQM 20

AQB AQM OQB
AQB 20 20
AQB 40
Hence, is equal to .
AQB
40
Exercise 9.2 (10)
Write ‘True’ or ‘False’ and justify your answer in
each of the following:
Question: 1
If a chord AB subtends an angle of at the centre
60
of a circle, then angle between the tangents at A and
B is also .
60
Solution
False.
In the figure,
AP and PB are two tangents to a circle and AB is a
chord.
It is clear that PBOA is a cyclic.
Thus,
AOB APB 180 Supplimentary angles
60 APB 180
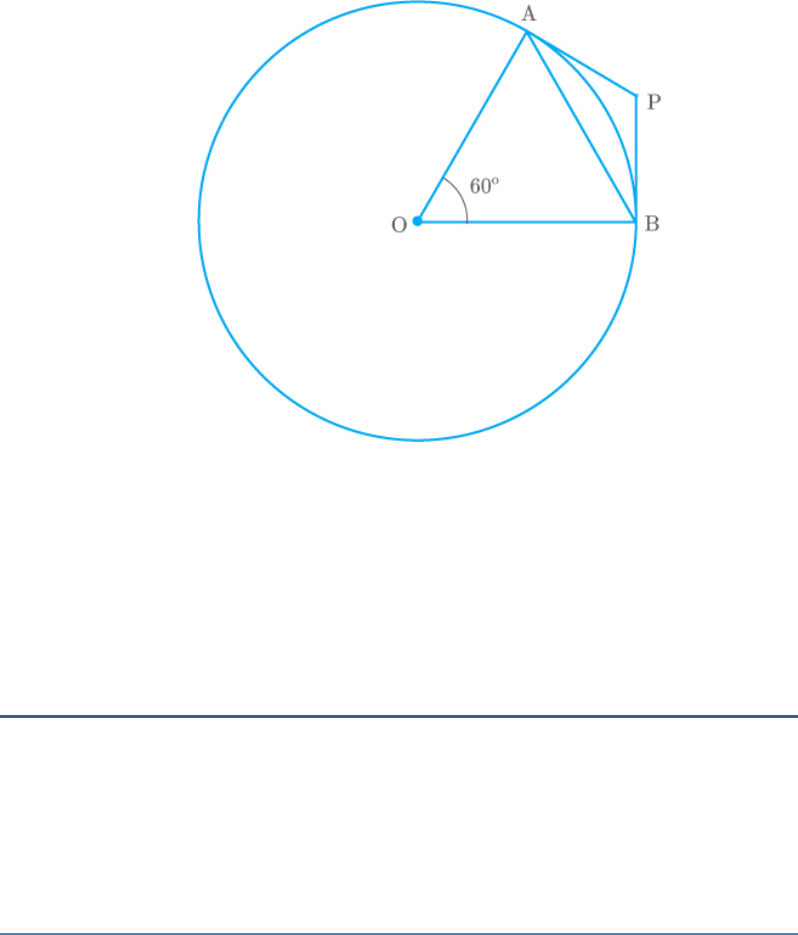
APB 180 60
APB 120
Hence, the angle between the tangents at A and B is
not .
60
Question: 2
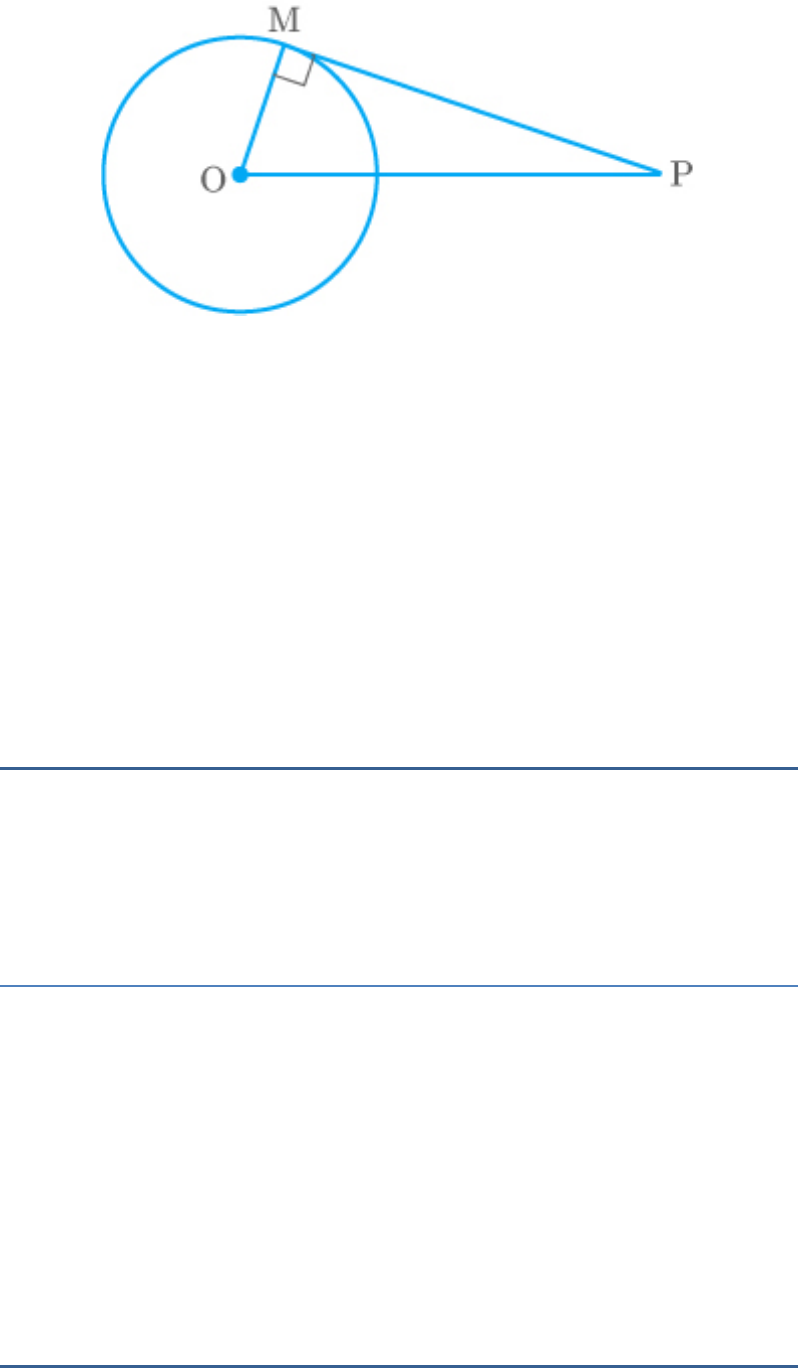
The length of tangent from an external point on a
circle is always greater than the radius of the circle.
Solution
False.
From the figure,
LM is a tangent and OM is a radius.
Thus,
OML 90

Let
OL 5cm and OM 4 cm
In , by Pythagoras theorem,
OML
2 2 2
OL OM ML
2 2
2
5 4 ML
2
ML 25 16
2
ML 9
ML 3
It is clear that .
ML OM
Hence, tangent is less than the radius.
Question: 3
The length of tangent from an external point P on a
circle with centre O is always less than OP.
Solution
True.
From the figure,
PM is a tangent and OM is a radius.
Thus,
OMP 90
Fig. Exm_9.2_3
Since, in a right-angled triangle, hypotenuse is the
longest side.
Thus,
In , .
OMP
OP PM
Question: 4
The angle between two tangents to a circle may be
.
0
Solution
False.
The angle between two tangents to a circle cannot be
because in this condition, two tangents will
0
become one.
Question: 5
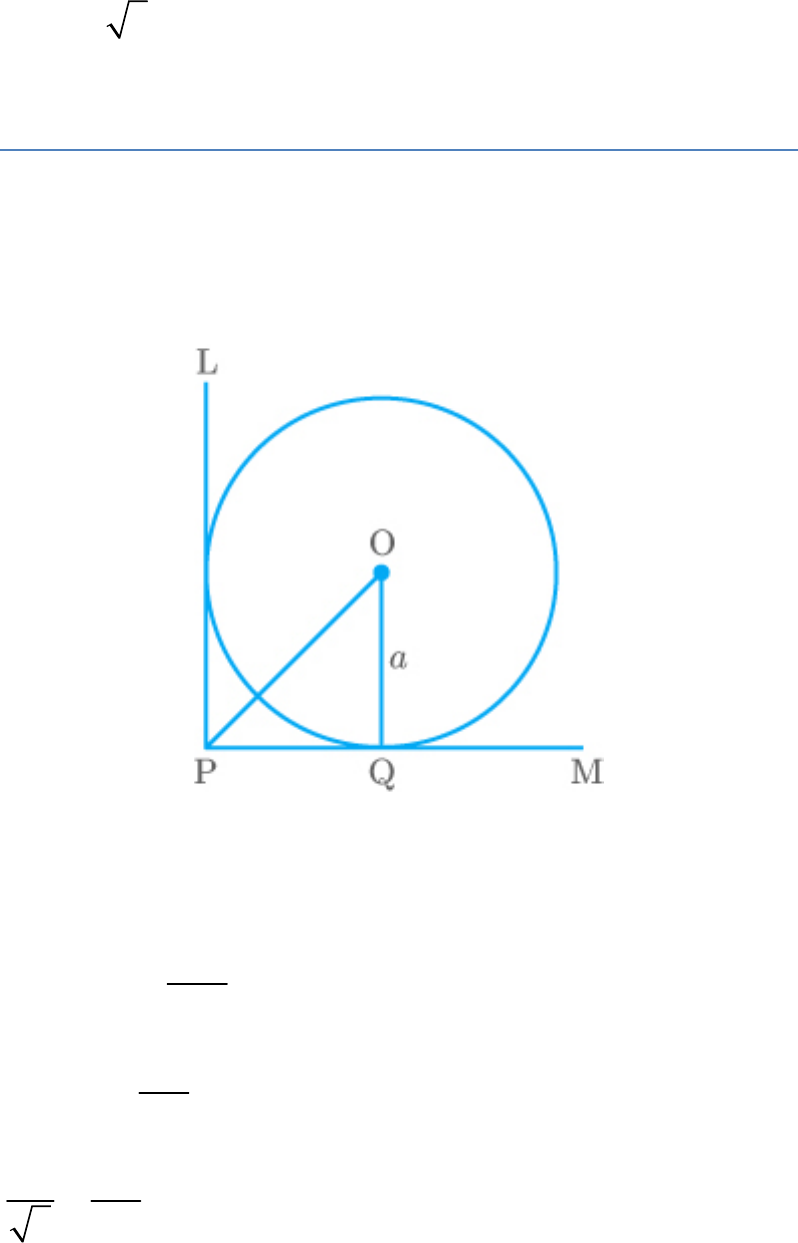
If angle between two tangents drawn from a point P
to a circle of radius and centre O is , then
a
90
.
OP a 2
Solution
True.
From the figure,
PL and PM are tangents and OQ is a radius.
In ,
OPQ
OPQ 45
OQ
sin OPQ
OP
a
sin 45
OP
1 a
OP
2
OP a 2
Question: 6
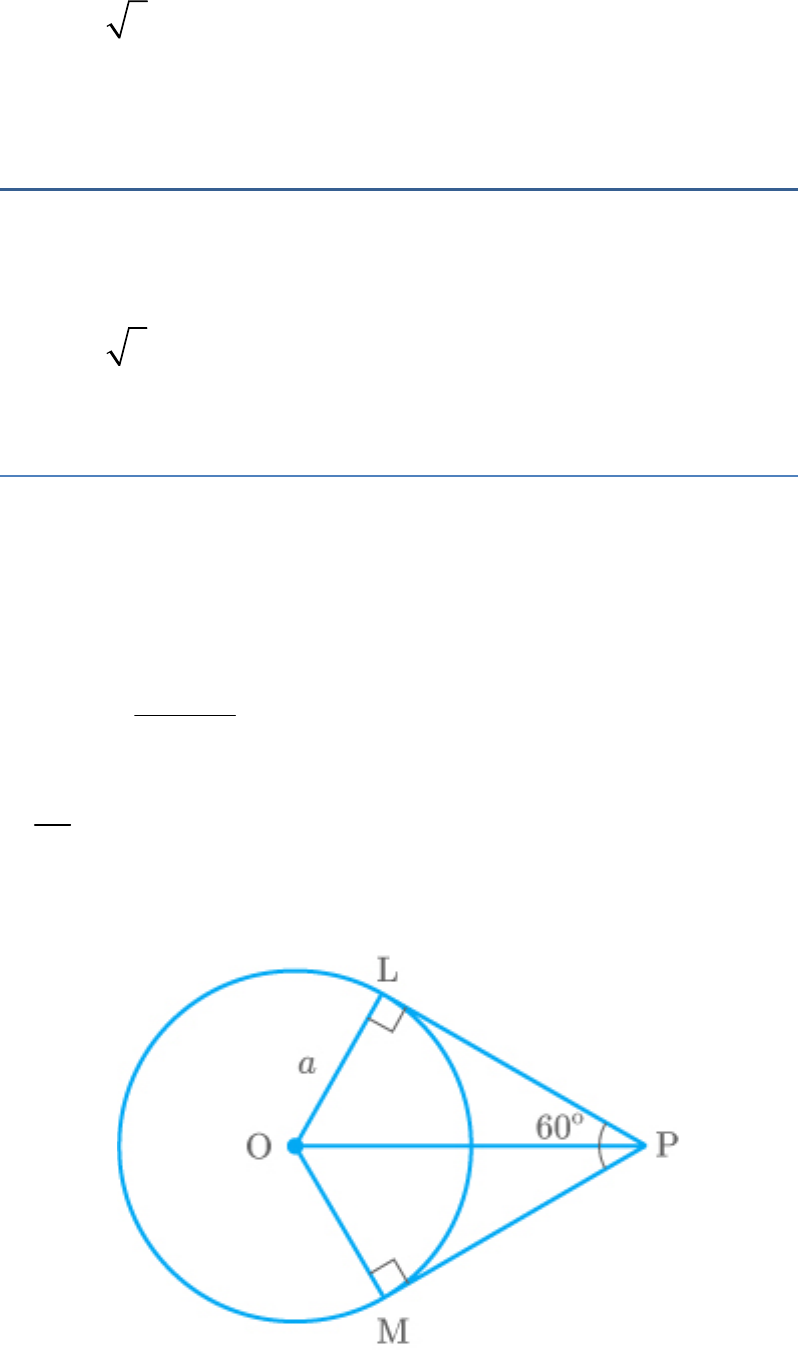
If angle between two tangents drawn from a point P
to a circle of radius and centre O is , then
a
60
.
OP a 3
Solution
False.
From the figure,
PL and PM are tangents and OL and OM are radius.
LPM
OPL
2
60
2
30
In ,
OLP

OL
sin OPL
OP
a
sin 30
OP
1 a
2 OP
OP 2a
Question: 7
The tangent to the circumcircle of an isosceles
triangle ABC at A, in which , is parallel to
AB AC
BC.
Solution
True.
From the figure,
In ,
ABC
AB AC Given
Isosceles triC B angle
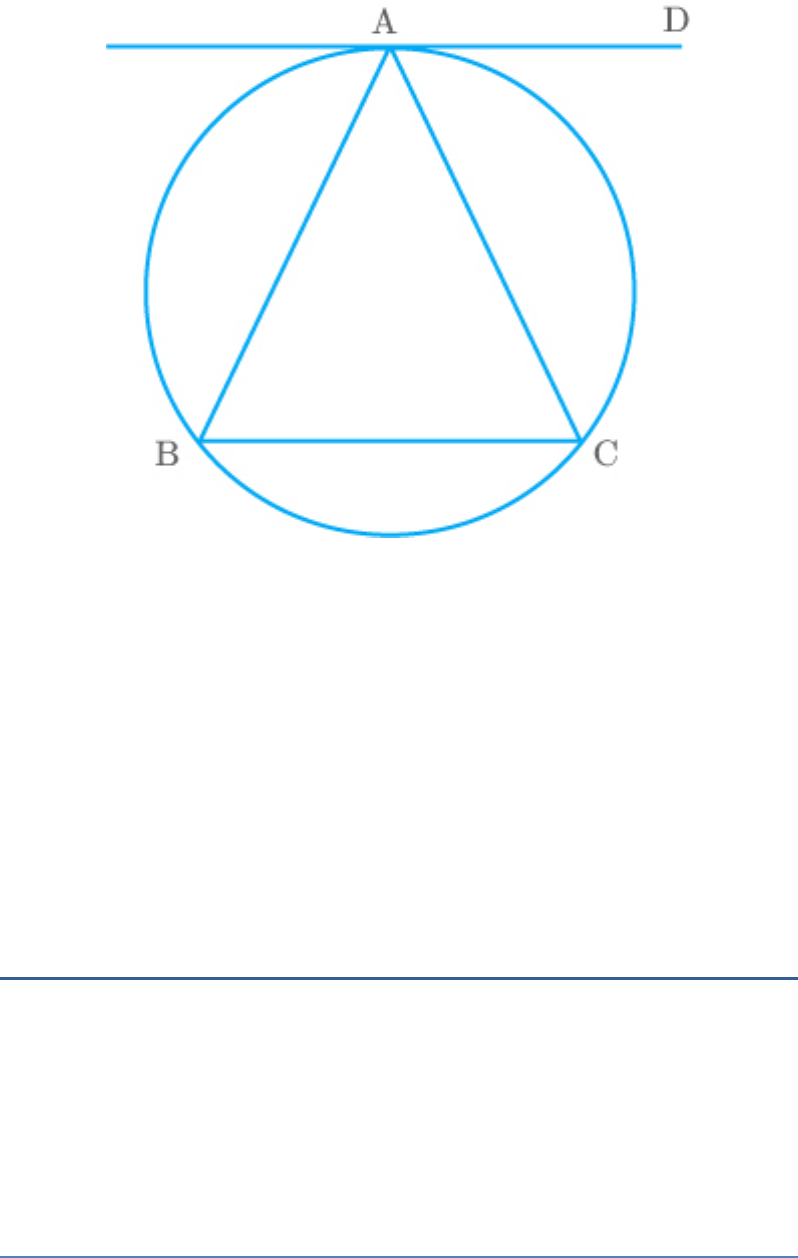
Anglesin alternate
CAD B
segment
CAD C
These angles are alternate interior angles.
Thus,
AD||BC
Question: 8
If a number of circles touch a given line segment PQ
at a point A, then their centres lie on the
perpendicular bisector of PQ.
Solution
True.
From the figure,
PQ is a line segment.
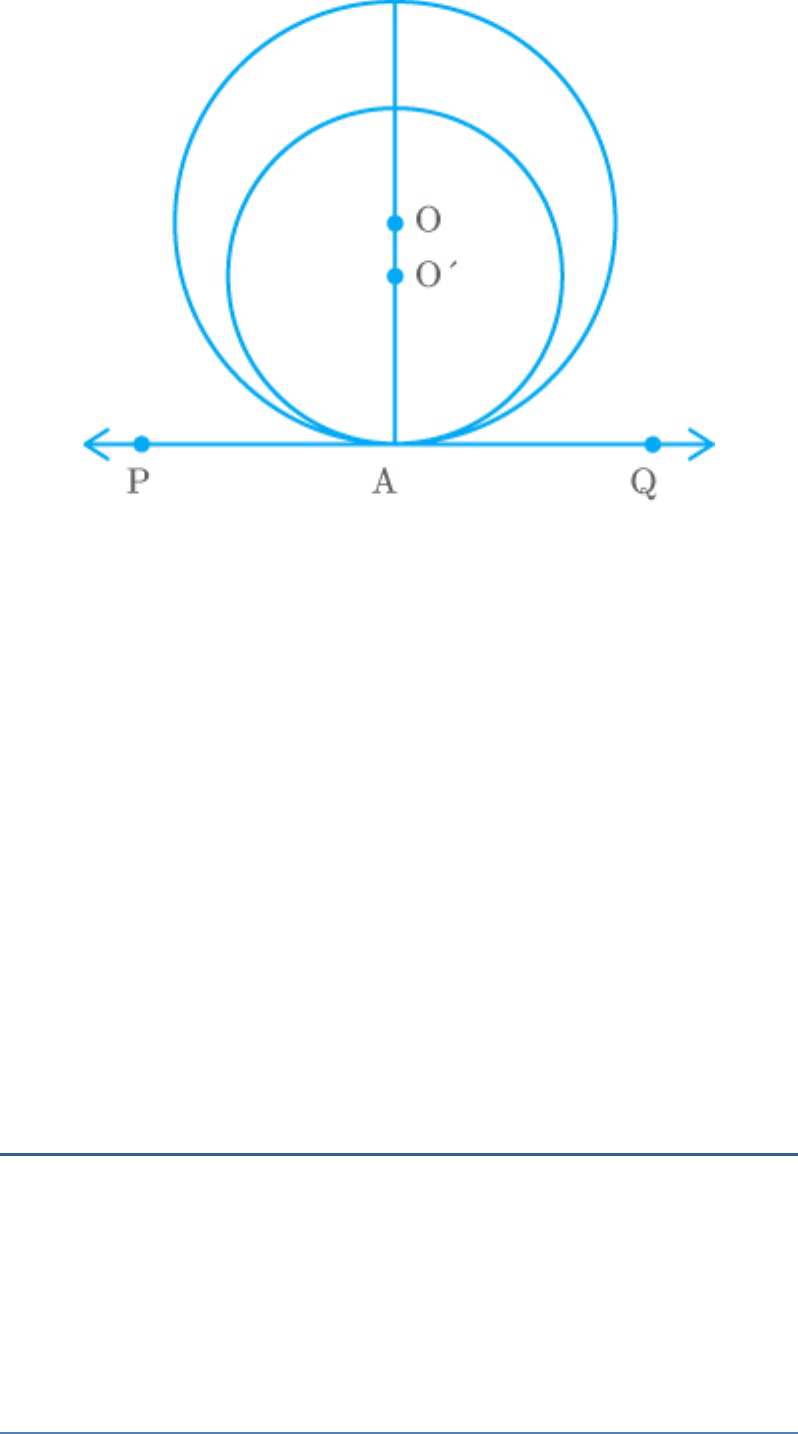
There are two circles with centres that
O andO
touches PQ on A.
PQ is a tangent and radius of the two
OA andO A
circles.
Thus,
OAQ O AQ 90
It is possible only when and lie on the same line.
O
O
Hence, the centres of all circles lie on the
perpendicular bisector of PQ.
Question: 9
If a number of circles pass through the end points P
and Q of a line segment PQ, then their centres lie on
the perpendicular bisector of PQ.
Solution
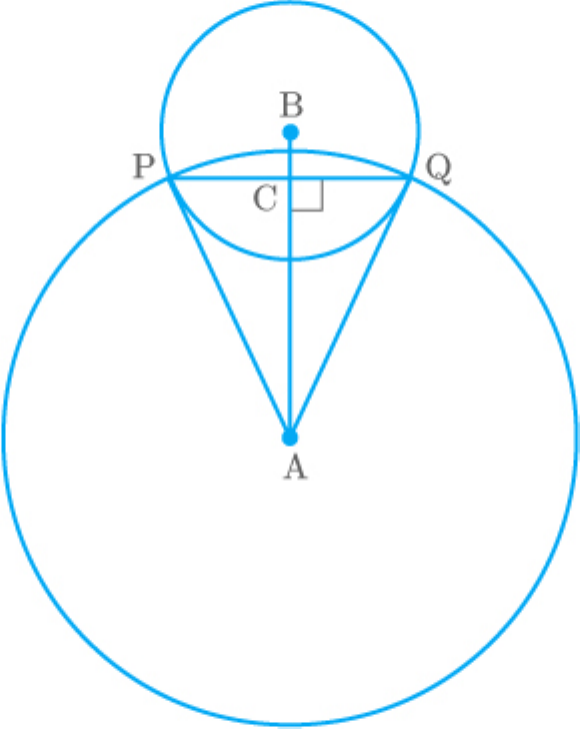
True.
From the figure,
A and B are the centres of the two circles that passes
through the end points P and Q of the line segment
PQ.
In and ,
ACP
ACQ
AP AQ
AC AC
ACP ACQ 90
Thus,
ACP ACQ
Thus, .
CP CQ
Hence, the centres of the circles lie on the
perpendicular bisector of PQ.
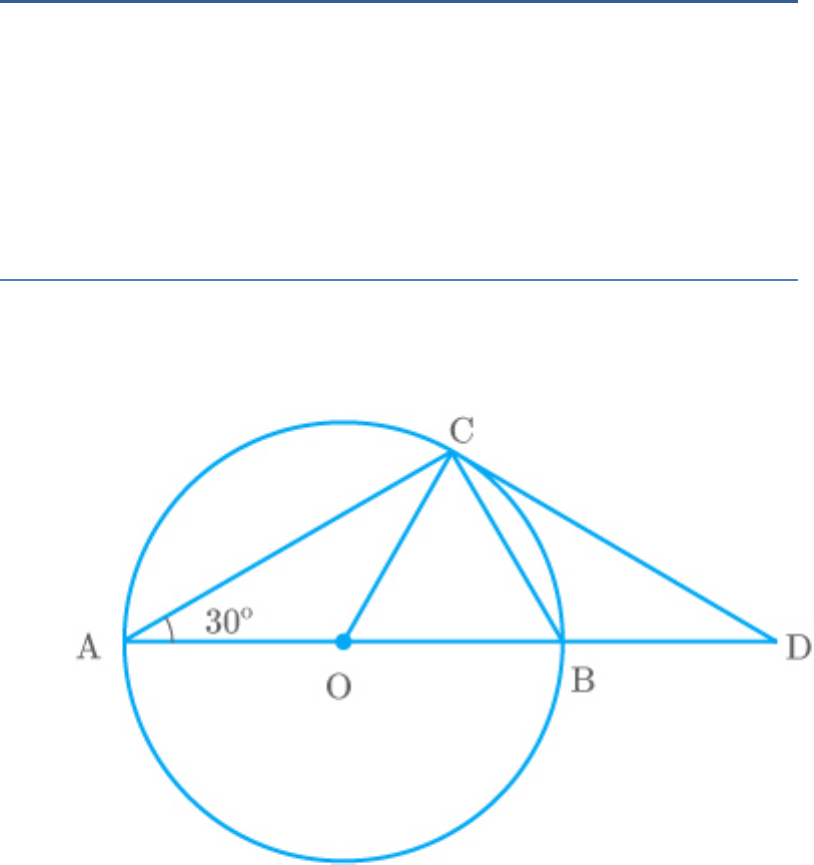
Question: 10
AB is a diameter of a circle and AC is its chord such
that . If the tangent at C intersects AB
BAC 30
extended at D, then .
BC BD
Solution
True.
From the figure,
We know that the angle made by a segment on the
centre of a circle is two times of the angle made by
any part of the circle.
Thus,
BOC 2 BAC

2 30
60
In ,
CDO
CDO 180 60 90 Anglesumproperty
30
CBD CAB ACB Exterior Angleproperty
120
BAC BDC 30
Thus,
BC BD
Exercise 9.3 (10)
Question: 1
Out of the two concentric circles, the radius of the
outer circle is 5 cm and the chord AC of length 8 cm
is a tangent to the inner circle. Find the radius of the
inner circle.
Solution
From the figure,
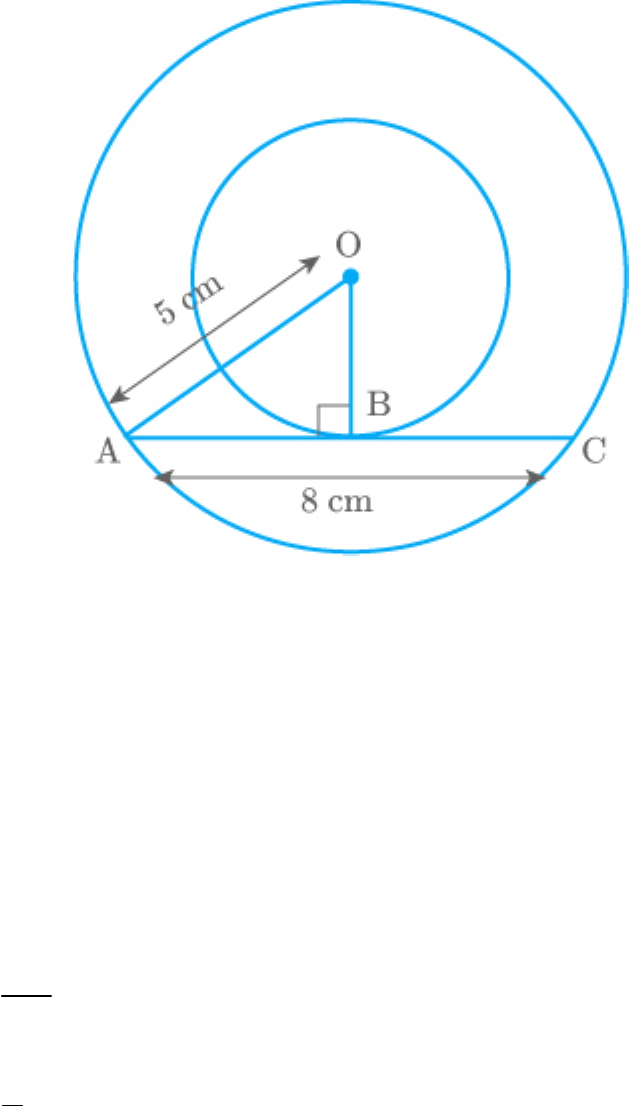
and
OA 5cm
AC 8cm
AC is a tangent at the point B and OB is a radius.
Thus, and .
OBA 90
OB AC
We know that the perpendicular from the centre
bisects the chord.
Thus,
AC 2AB
AC
AB
2
8
AB
2
AB 4
In ,
AOB
2 2 2
OA AB OB
2 2
2
5 4 OB
2
OB 25 16
2
OB 9
OB 3
Hence, the radius of the inner circle is 3 cm.
Question: 2
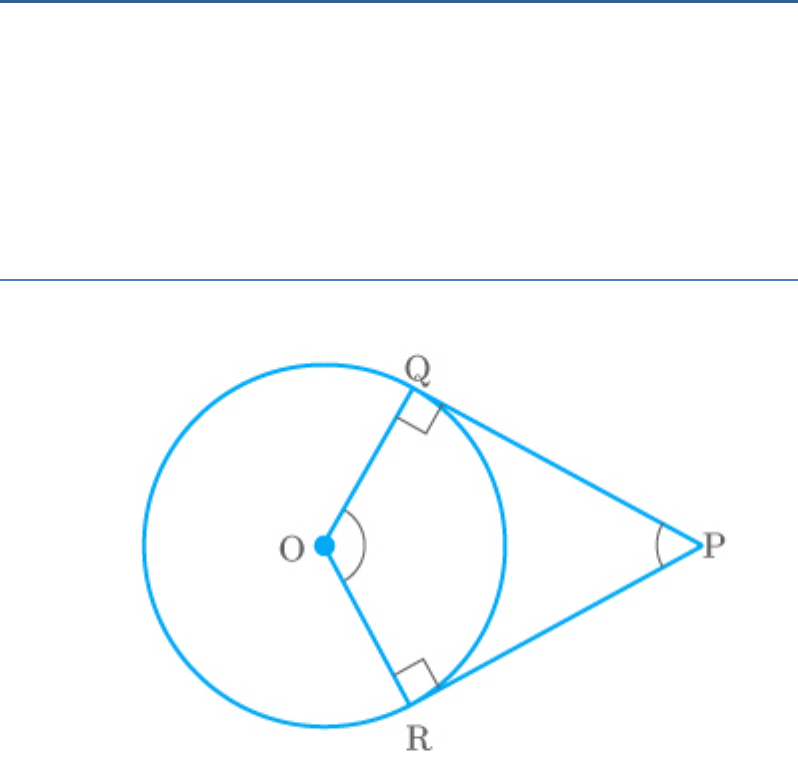
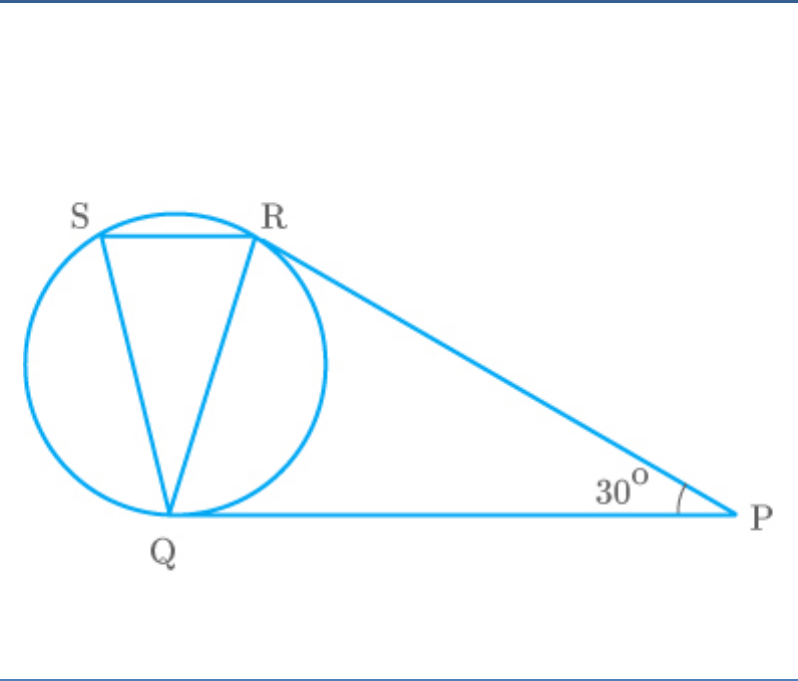
Two tangents PQ and PR are drawn from an external
point to a circle with centre O. Prove that QORP is a
cyclic quadrilateral.
Solution
From the figure,
PQ and PR are tangents to the circle and OQ and OR
are radius.
Thus,
OQP ORP 90
In quadrilateral QORP, by the angle sum property,
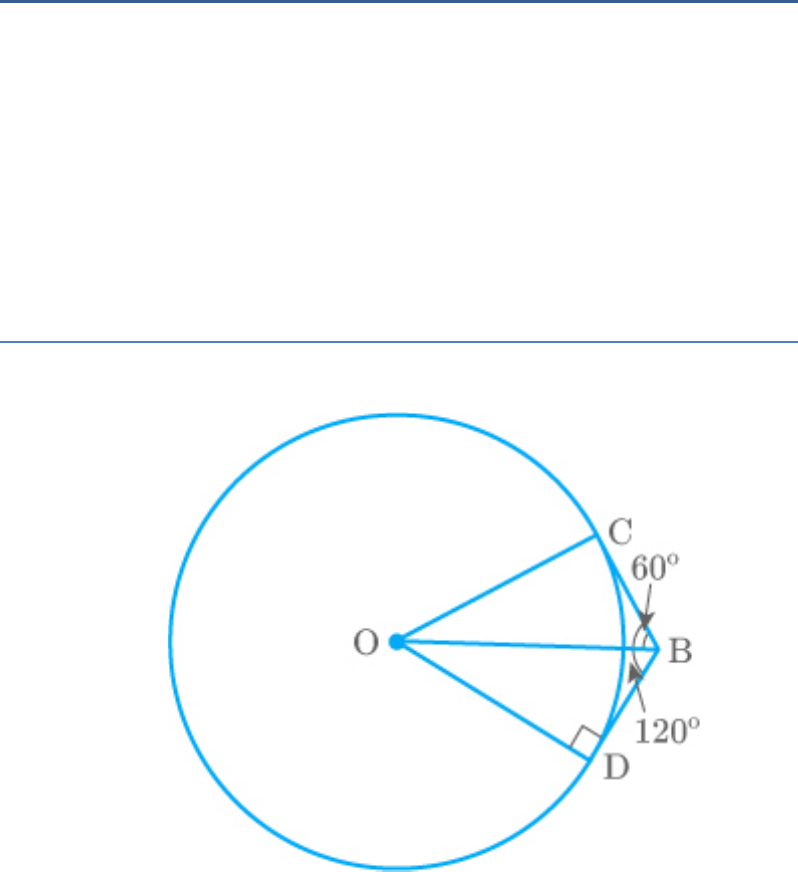
OQP ORP QOR QPR 360
90 90 QOR QPR 360
QOR QPR 360 90 90
QOR QPR 180
Hence, quadrilateral QORP is cyclic.
Question: 3
If from an external point B of a circle with centre O,
two tangents BC and BD are drawn such that
, prove that i.e.
DBC 120
BC BD BO
.
BO 2 BC
Solution
From the figure,
DBC 120
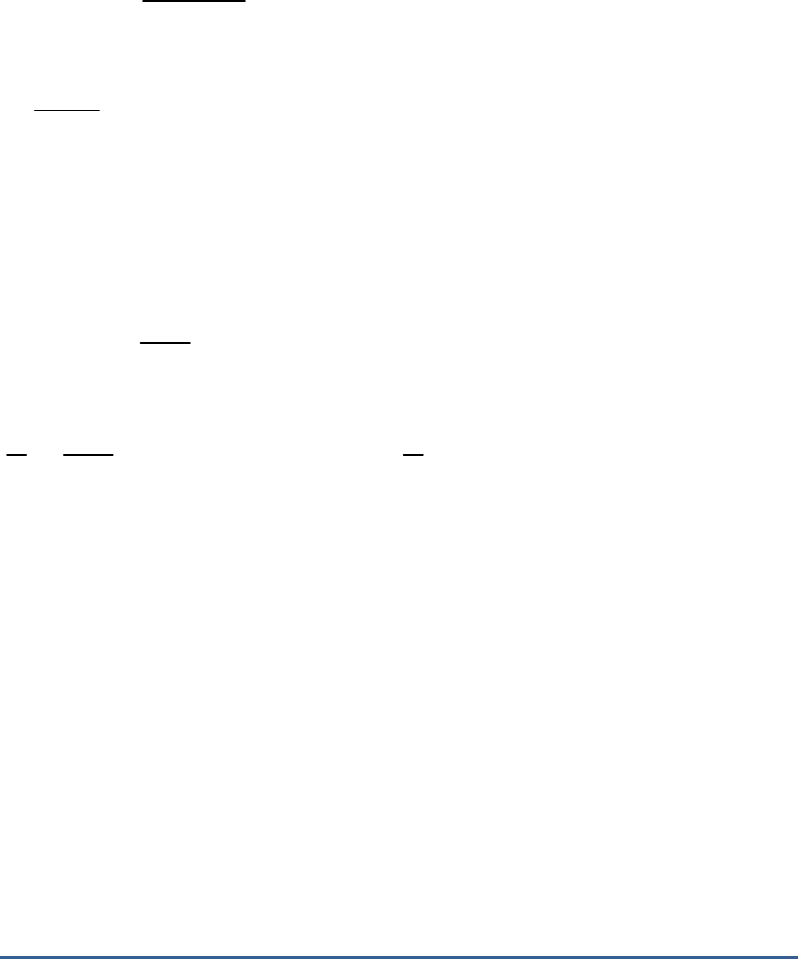
BC and BD are two tangents to the circle and OC
and OD are radius of the circle.
ODB 90
We know that the tangents are inclined equally to
the line joining the centre of the circle to the external
point.
Thus,
CBD
OBD
2
120
2
60
In ,
ODB
BD
cos60
BO
1 BD 1
cos60
2 BO 2
BO 2BD
BO BD BD
The tangents are from same external point.
Thus,
BC BD
Hence,
BO BC BD
Question: 4
Prove that the centre of a circle touching two
intersecting lines lies on the angle bisector of the
lines.
Solution
From the figure,
AB and are the tangents to the circle
A B
intersecting at L. and are radius.
O N
O M
Let LP does not pass through .
O
In and ,
O ML
O NL
O ML O NL 90
O L O L Common
O M O N Radius
Thus,
O ML O NL
Thus,
MLO O LN
This condition is possible when lies on LP.
O
Thus, LP passes through the centre that lies on
O
the angle bisector of the tangents.
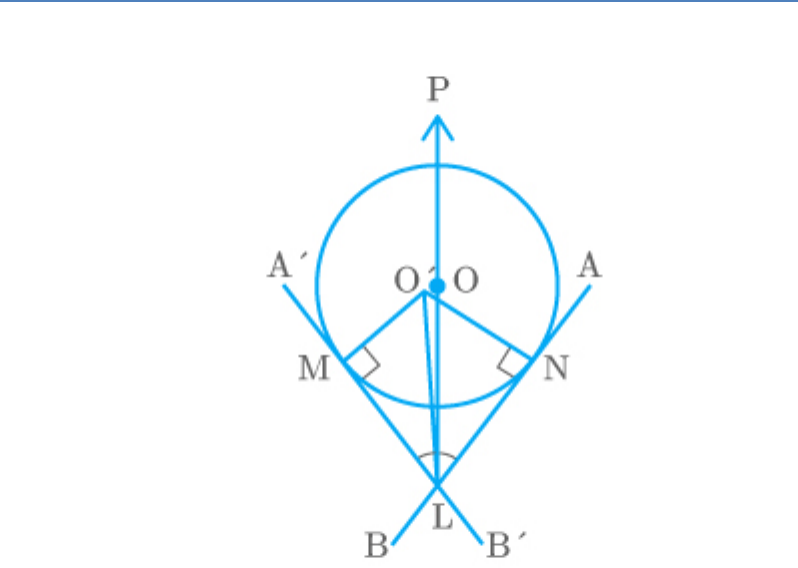
Question: 5
In the adjoining figure, AB and CD are common
tangents to two circles of unequal radii. Prove that
AB CD.
Solution
From the figure,
AB and CD are common tangents to the two circles.
Extend AB and CD that meet at E.

Now, EA and EC are two tangents from the same
point.
Thus,
EA EC ...... 1
Similarly, EB and ED are two tangents from the same
point.
Thus,
EB ED ...... 2
Subtract equation (2) from (1).
EA EB EC ED ...... 3
From the figure,
and
EA EB AB
EC ED CD
Put the above result in equation (3).
Hence,
AB CD
Question: 6
In Question 5 above, if radii of the two circles are
equal, prove that AB CD.
Solution
From the figure,
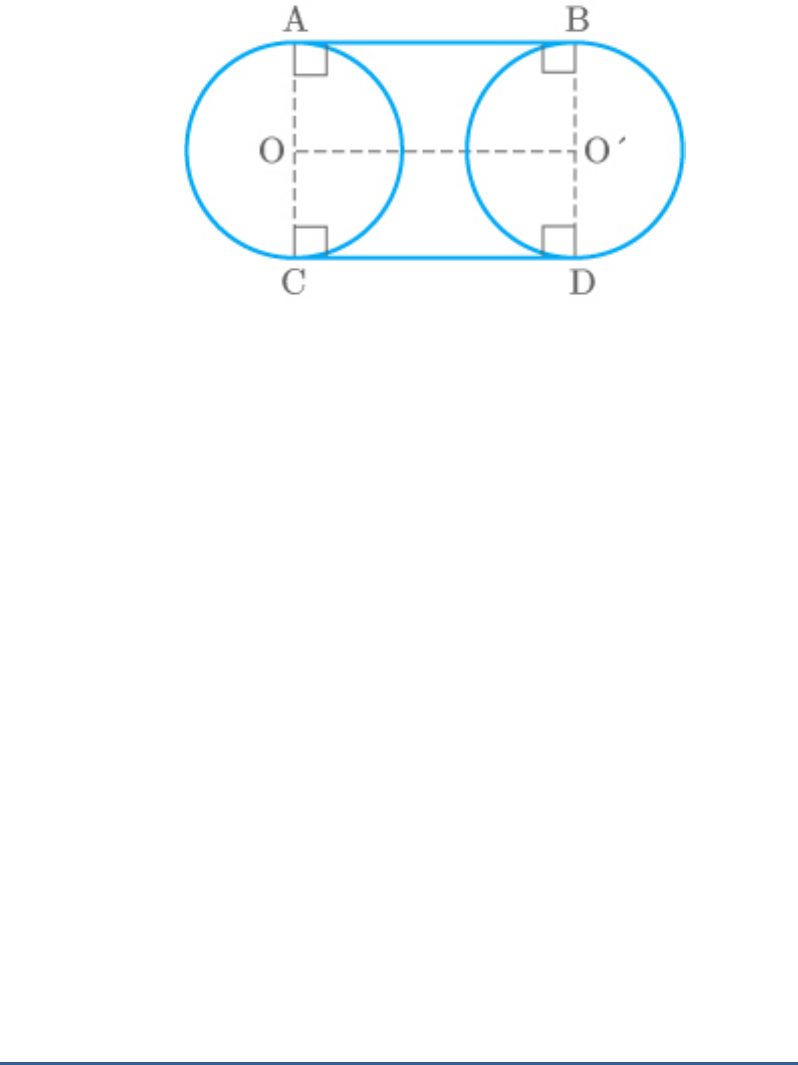
AB and CD are common tangents to the two circles.
A B 90
Thus,
OA O BA
OA O B Equal radii of two circles
Thus, quadrilateral is a parallelogram.
AOO B
Similarly, quadrilateral is a parallelogram.
COO D
AB OO Oppositesidesof parallelogram
CD OO Oppositesidesof parallelogram
Thus,
AB CD
Hence proved.
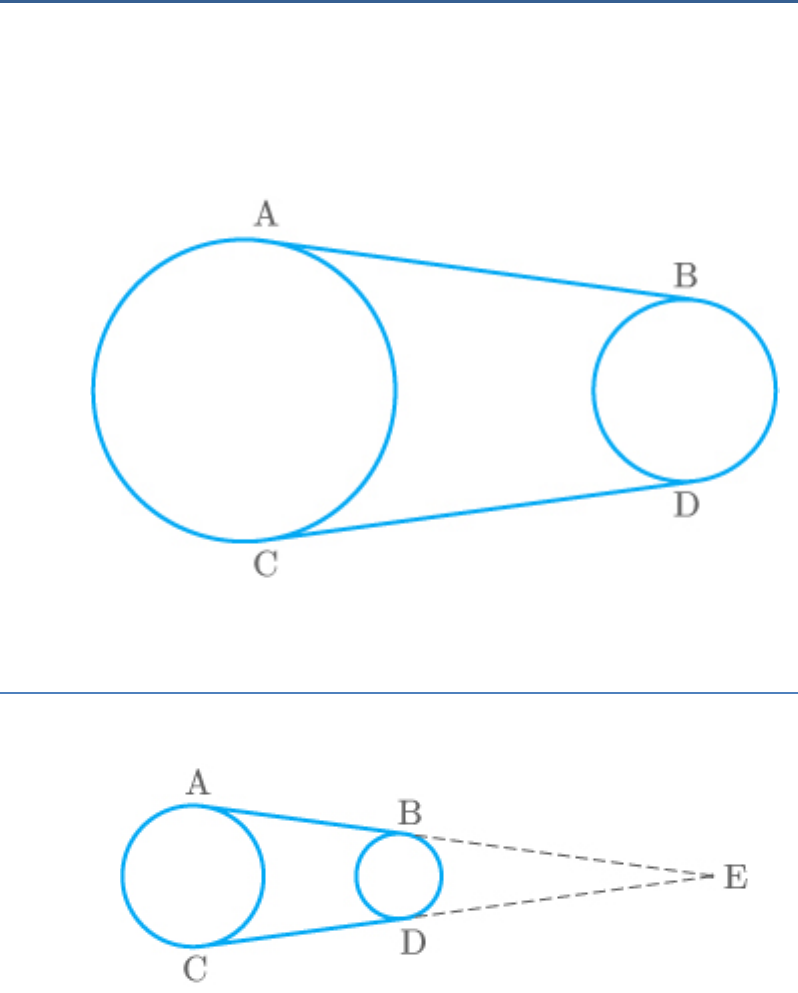
Question: 7
In the adjoining figure, common tangents AB and
CD to two circles intersect at E. Prove that AB CD.
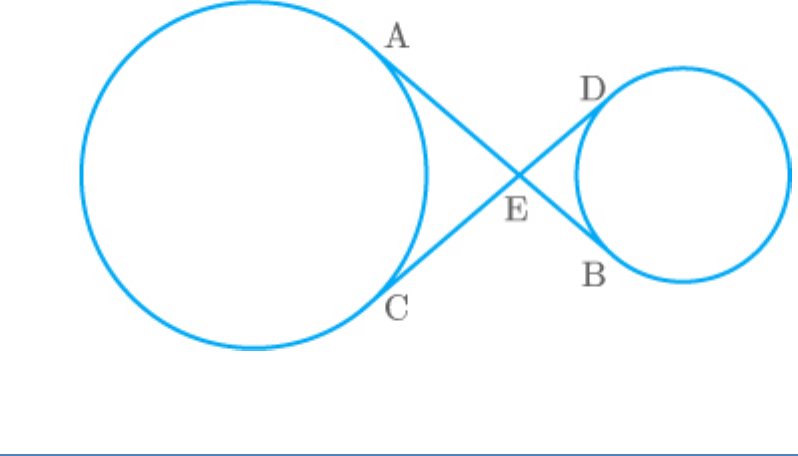
Solution
From the given figure,
AB and CD are common tangents to two circles that
intersect at E.
EA and EC are two tangents from the same points.
Thus,
EA EC ...... 1
Similarly, EB and ED are two tangents from the same
points.
Thus,
EB ED ...... 2
Add equations (1) and (2).
EA EB EC ED ...... 3
From the given figure,
and
EA EB AB
EC ED CD
Put the above result in equation (3).
AB CD
Hence proved.
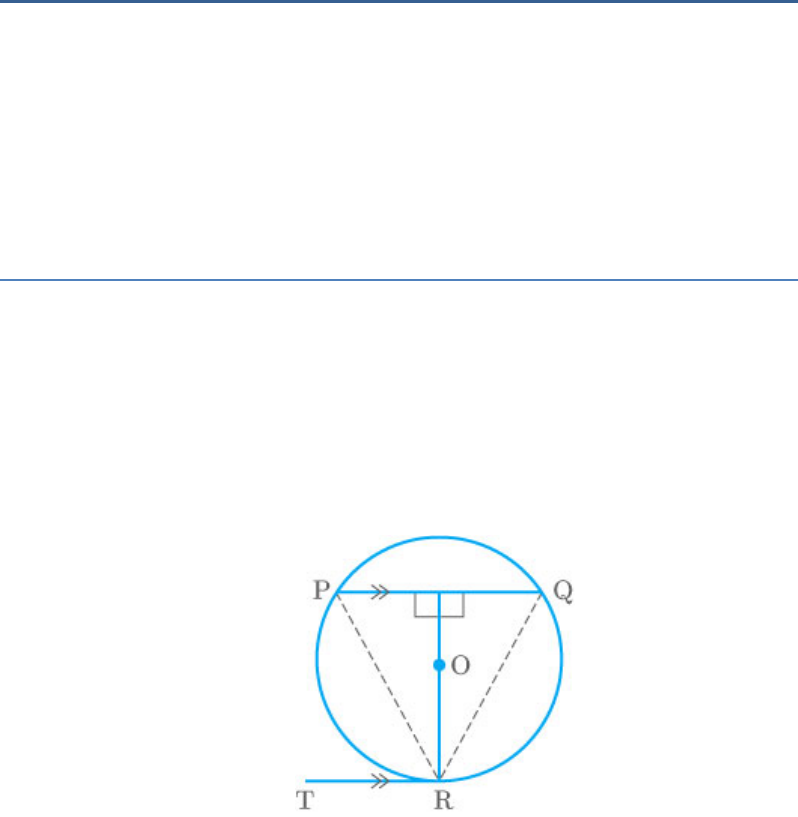
Question: 8
A chord PQ of a circle is parallel to the tangent
drawn at a point R of the circle. Prove that R bisects
the arc PRQ.
Solution
From the figure,
PQ is a chord of the circle and TR is a tangent at the
point R.
Join PR and QR.
Now,
TRP Q Anglesin alternatesegment
TRP P PQ TR A
Thus,
P Q
RQ RP Converseof isosceles property
A
A
RQ RP
Hence, R bisects the arc PRQ.
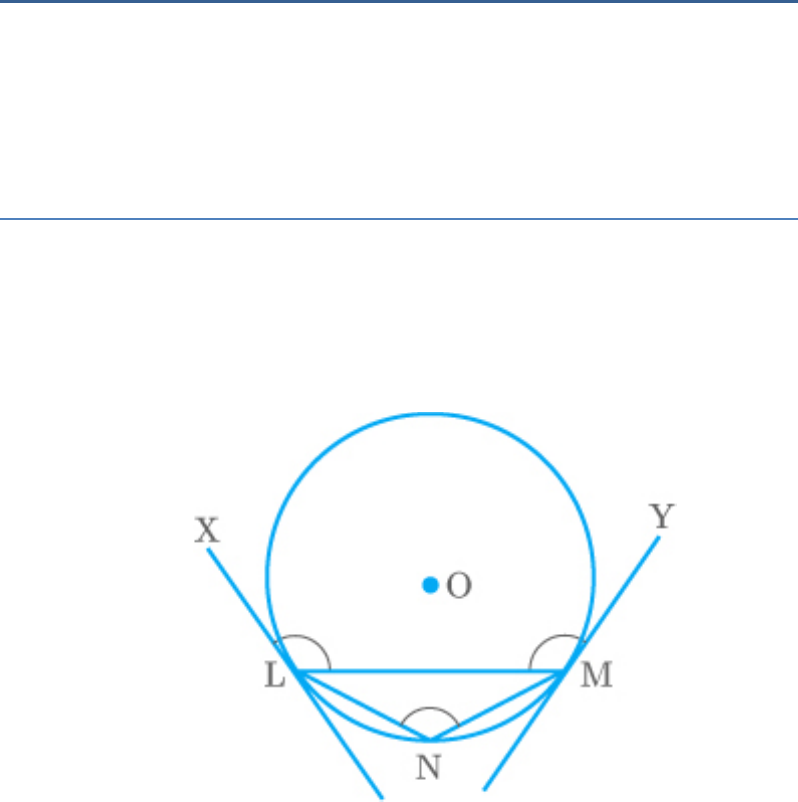
Question: 9
Prove that the tangents drawn at the ends of a chord
of a circle make equal angles with the chord.
Solution
From the figure,
LM is a chord and XL and YM are two tangents at
points L and M.
Locate a point N on arc LM and join LN and MN.
YML N Anglesin alternatesegment
XLM N
From the above results,
YML XLM
Hence, the tangents drawn at the ends of a chord of
a circle make equal angles with the chord.
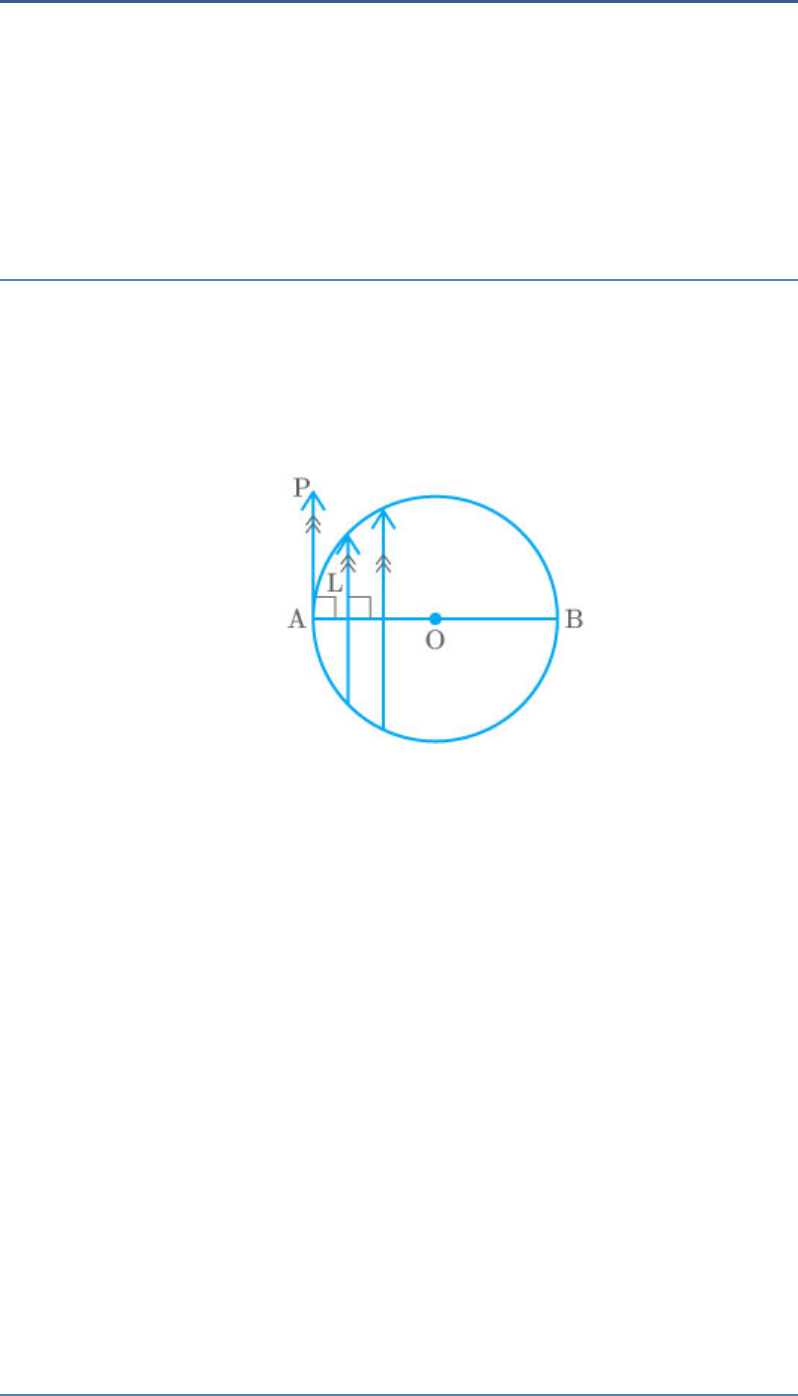
Question: 10
Prove that a diameter AB of a circle bisects all those
chords which are parallel to the tangent at the point
A.
Solution
From the figure,
AB is a diameter of a circle and AP is a tangent at
point A.
L is a chord parallel to AP.
PAB 90 radius tangent
PAB 1 AP L
Thus,
AB L
We know that the perpendicular from the centre of
the circle to the chord bisects the chord.
Hence, AB bisects all those chords which are parallel
to AP.
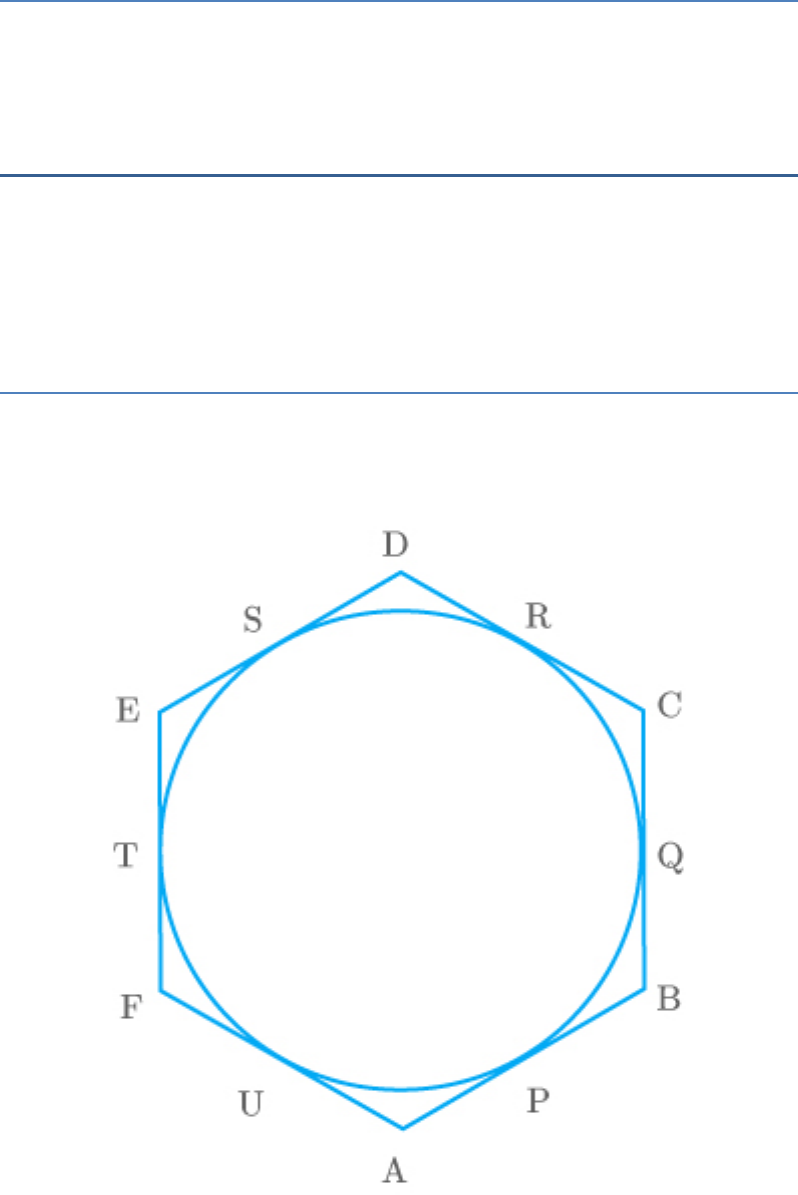
Exercise 9.4 (14)
Question: 1
If a hexagon ABCDEF circumscribe a circle, prove
that .
AB CD EF BC DE FA
Solution
From the figure, ABCDEF is a hexagon
circumscribing a circle.
We know that the tangents from the same external
points are equal.

Thus,
AP AU
BP BQ
CR CQ
DR DS
ET ES
FT FU
Add all the above results.
AP BP CR DR ET FT AU BQ CQ DS ES FU
AB CD EF BC DE FA
Hence Proved.
Question: 2
Let s denote the semi-perimeter of a triangle ABC in
which , , . If a circle touches the
BC a
CA b
AB c
sides BC, CA, AB at D, E, F, respectively, prove that
.
BD s– b
Solution
From the figure,
ABC is a triangle and a circle touches the sides BC,
CA, AB at D, E, F, respectively.
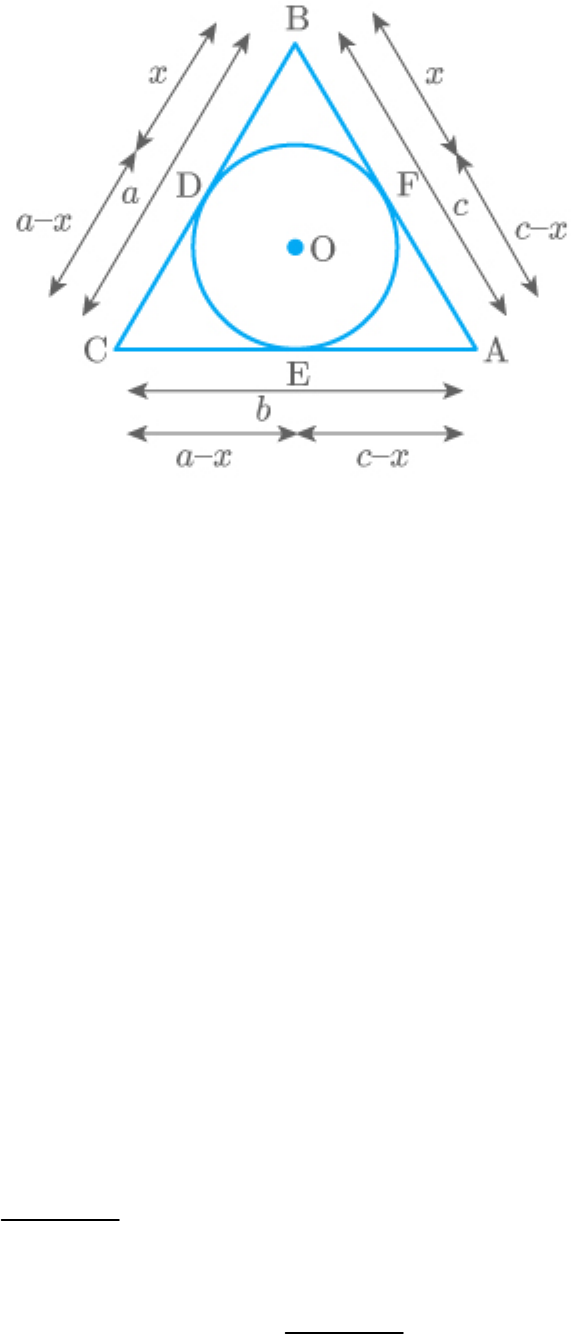
We know that the tangents from the same external
points are equal.
Thus,
BD BF x
AF AE c x
CD CE a x
AC AE CE
b c x a x
b 2x a c
Add on both sides.
b
2b 2x a b c
a b c
b x
2
a b c
b x s s
2
x s b
BD s b BD x
Hence,
BD s– b
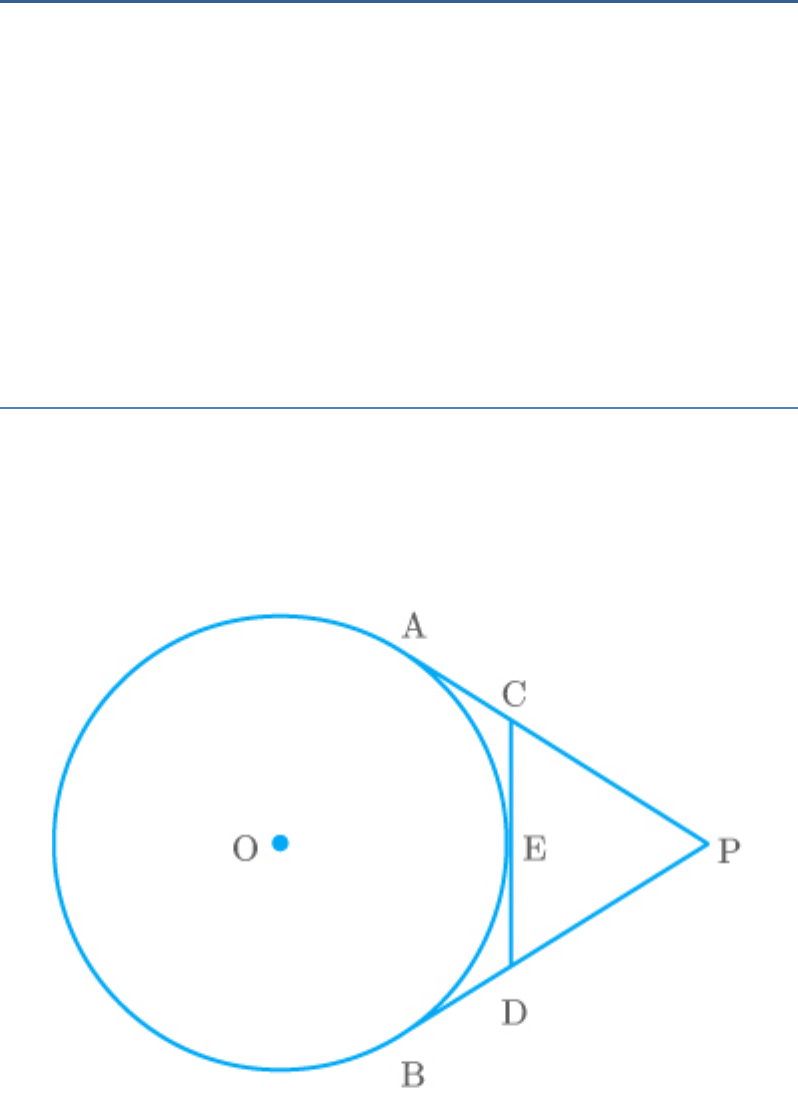
Question: 3
From an external point P, two tangents, PA and PB
are drawn to a circle with centre O. At one point E on
the circle tangent is drawn which intersects PA and
PB at C and D, respectively. If , find the
PA 10cm
the perimeter of the triangle PCD.
Solution
From the figure,
PA and PB are two tangents drawn to a circle from
external point P and .
PA 10cm

Perimeter of the
PC CD PD
triangle PCD
PC CE ED PD CD CE ED
We know that the tangents from same external
points are equal.
Thus, and .
CE CA
DE DB
So,
Perimeter of the
PC CA DB PD
triangle PCD
PA PB PA PC CA andPB DB PD
PA PA PA PB
2PA
2 10
20
Hence, the perimeter of the triangle PCD is 20 cm.
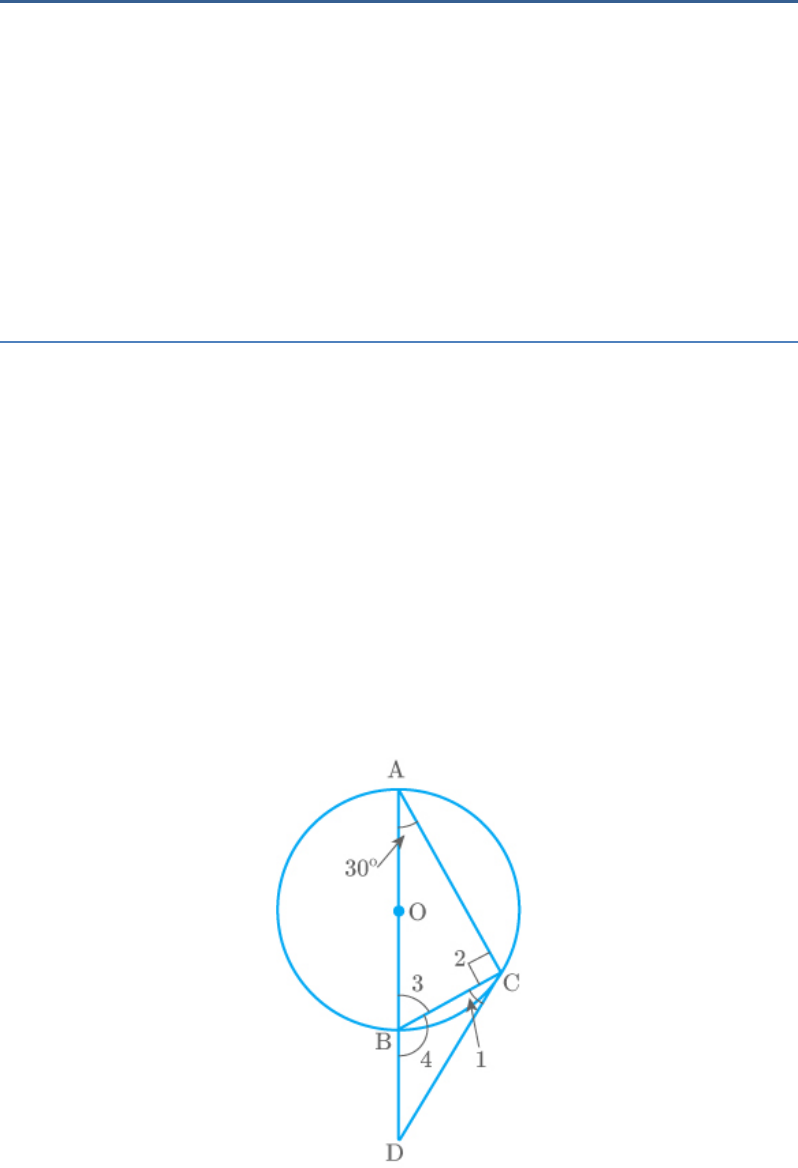
Question: 4
If AB is a chord of a circle with centre O, AOC is a
diameter and AT is the tangent at A as shown in
figure. Prove that .
BAT ACB
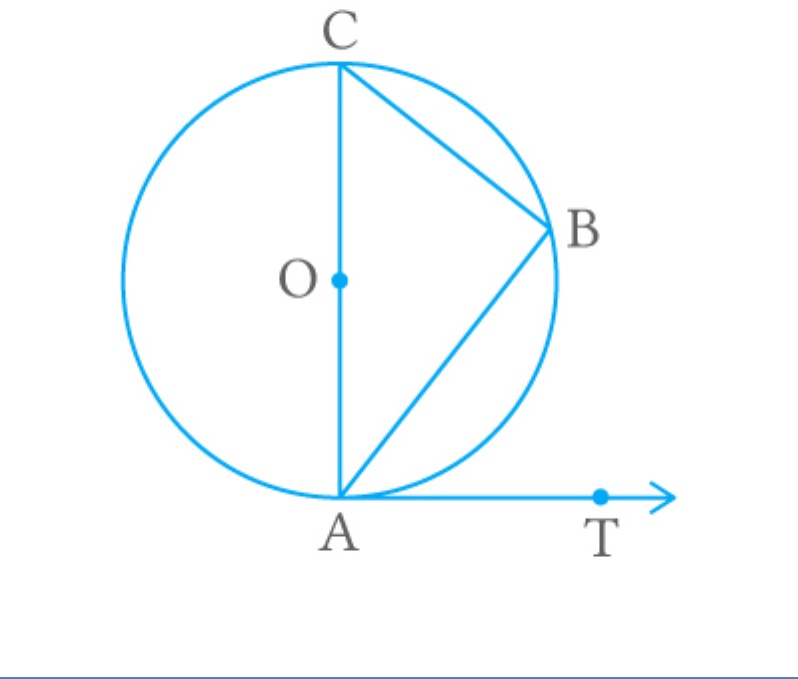
Solution
From the figure,
AB is a chord of the circle and AT is the tangent at
the point A.
B 90 Anglein semicircle
In triangle ABC, by the angle sum property,
B CAB ACB 180
90 CAB ACB 180
CAB ACB 180 90
CAB ACB 90 ...... 1
Now,
CAT 90 radius tangent
CAB BAT 90 ...... 2
From equations (1) and (2).
CAB ACB CAB BAT
ACB BAT
BAT ACB
Hence proved.
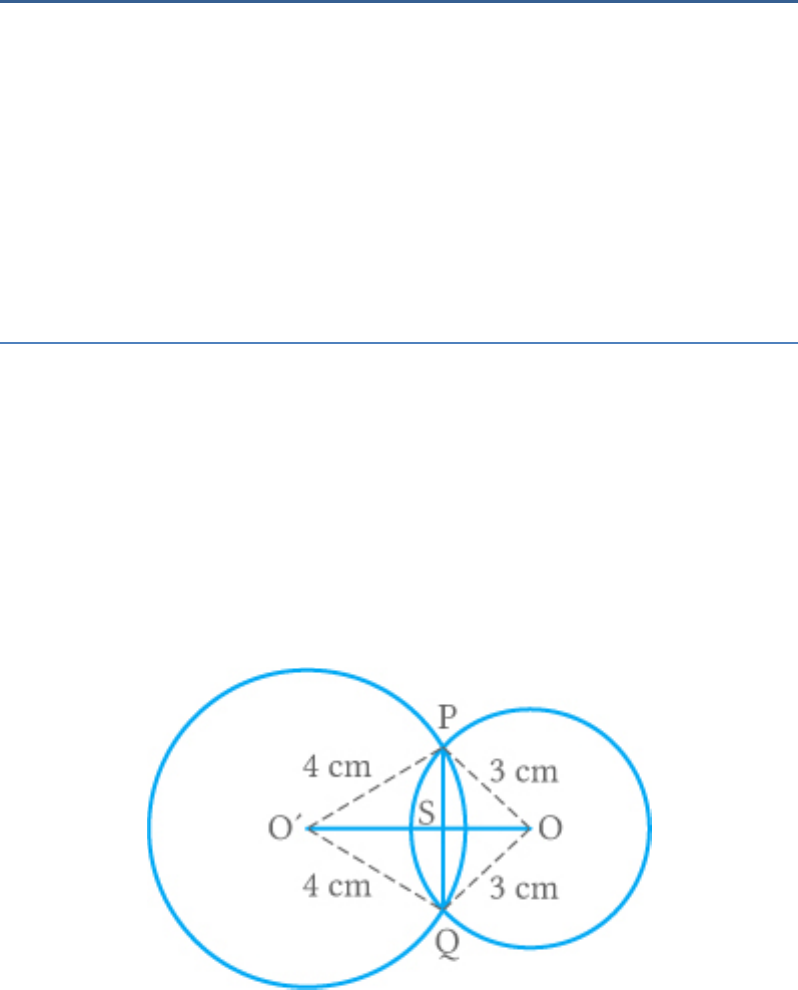
Question: 5
Two circles with centres O and of radii 3 cm and 4
O
cm, respectively intersect at two points P and Q such
that OP and are tangents to the two circles. Find
O P
the length of the common chord PQ.
Solution
From the figure,
OP OQ 3cm
O P O Q 4 cm
Thus, quadrilateral is a kite.
OPO Q
and are tangents.
OP
O P
PQ OO Diagonalsof akite
PSO 90
O PO 90 Radius tangent
In triangle ,by the Pythagoras theorem,
O PO
2 2 2
OO O P OP
2 2 2
OO 4 3
2
OO 16 9
2
OO 25
OO 25
OO 5
We know that in a triangle,
a b c
s
2
Here, and
a 3,
b 4
c 5
Thus,
3 4 5
s
2
12
2
6
Area of
triangleO PO
s s a s b s c
6 6 3 6 4 6 5
6 3 2 1
36
6

1
Area of O PO OO PS
2
1
6 5 PS
2
2
PS 6
5
12
PS
5
Similarly,
12
QS
5
Now,
PQ PS QS
12 12
5 5
24
5
Hence, PQ is cm.
24
5
Question: 6
In a right triangle, ABC in which , a circle is
B 90
drawn with AB as diameter intersecting the
hypotenuse AC and P. Prove that the tangent to the
circle at P bisects BC.
Solution
From the figure,
B 90
In triangle ABC, by the angle sum property,
A B C 180
A 90 C 180
A C 180 90
...A C 90 ... 2
5 90 Anglein semicircle
Now in triangle APB, by the angle sum property,
A 1 5 180
A 1 90 180
A 1 180 90
A 1 90 ...... 2
From equations (1) and (2).
A C A 1
..C 1 .... 3
1 3 Anglesin alternatesegment
...... 4
3 4 Oppositeangles
...... 5
From equations (3), (4) and (5).
C 4
Now, by the converse of isosceles triangle property,
MP MC
We know that tangents from the same points are
equal.
Thus,
MP MB
Thus,
MB MC
Hence, the tangent to the circle at P bisects BC.
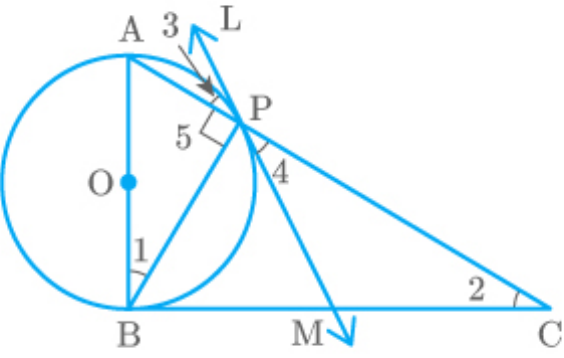
Question: 7
In the adjoining figure, tangents PQ and PR are
drawn to a circle such that . A chord RS
RPQ 30
is drawn parallel to the tangent PQ. Find .
RQS
Solution
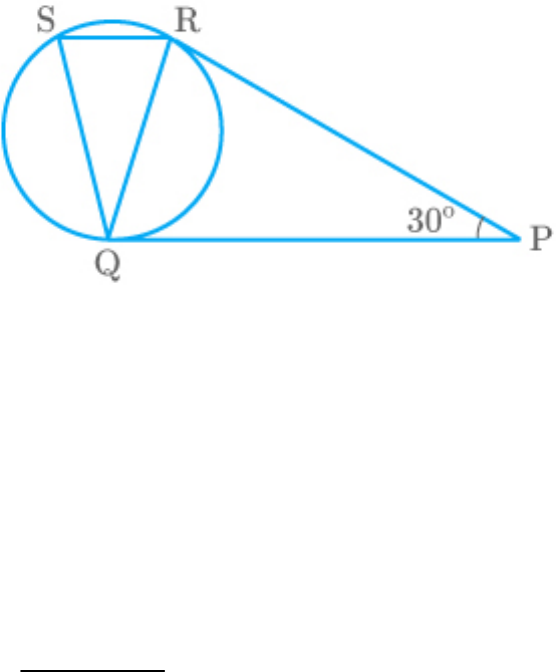
From the figure,
and
RPQ 30
RS QPA
In ,
PQR
PQ PR Tangentsfrom samepoint
PRQ RQP Isosceles triangleproperty
Now by the angle sum property,
PRQ RQP RPQ 180
PRQ PRQ RPQ 180
2 PRQ 30 180
180 30
PRQ
2
PRQ 75
Thus,
PRQ RQP 75
RQP QRS 75 Alternateinterior angles
PRQ RSQ 75 Anglesin alternatesegment
In triangle RSQ, by the angle sum property,
RQS 75 75 180
RQS 180 75 75
RQS 30
Hence, is .
RQS
30
Question: 8
AB is a diameter and AC is a chord of a circle with
centre O such that . The tangent at C
BAC 30
intersects extended AB at a point D. Prove that
.
BC BD
Solution
From the figure,
BAC 30
1 BAC 30 Anglesin alternatesegment
2 90 Anglein semicircle
4 2 BAC Exterior angleproperty
4 90 30
4 120

In triangle BDC, by the angle sum property,
1 4 BDC 180
30 120 BDC 180
BDC 180 30 120
BDC 30
1 BDC 30
Now, by the converse of isosceles triangle property,
.
BD BC
Question: 9
Prove that the tangent drawn at the mid-point of an
arc of a circle is parallel to the chord joining the end
points of the arc.
Solution
From the figure,
SR is a tangent and Q is the midpoint of arc TP.
We know that angles in alternate segment are equal.
Thus,
..1 4 .... 1
..2 3 .... 2
Since, Q is the midpoint of arc TP.
Arc TQ Arc QP
Thus, QT QP
In triangle QPT,
QT QP
2 4 Isoscelestriangleproperty
...... 3
From equations (1), (2) and (3).
1 2
We know that and are alternate interior
1
2
angles.
Thus,
PT||SR
Hence proved.
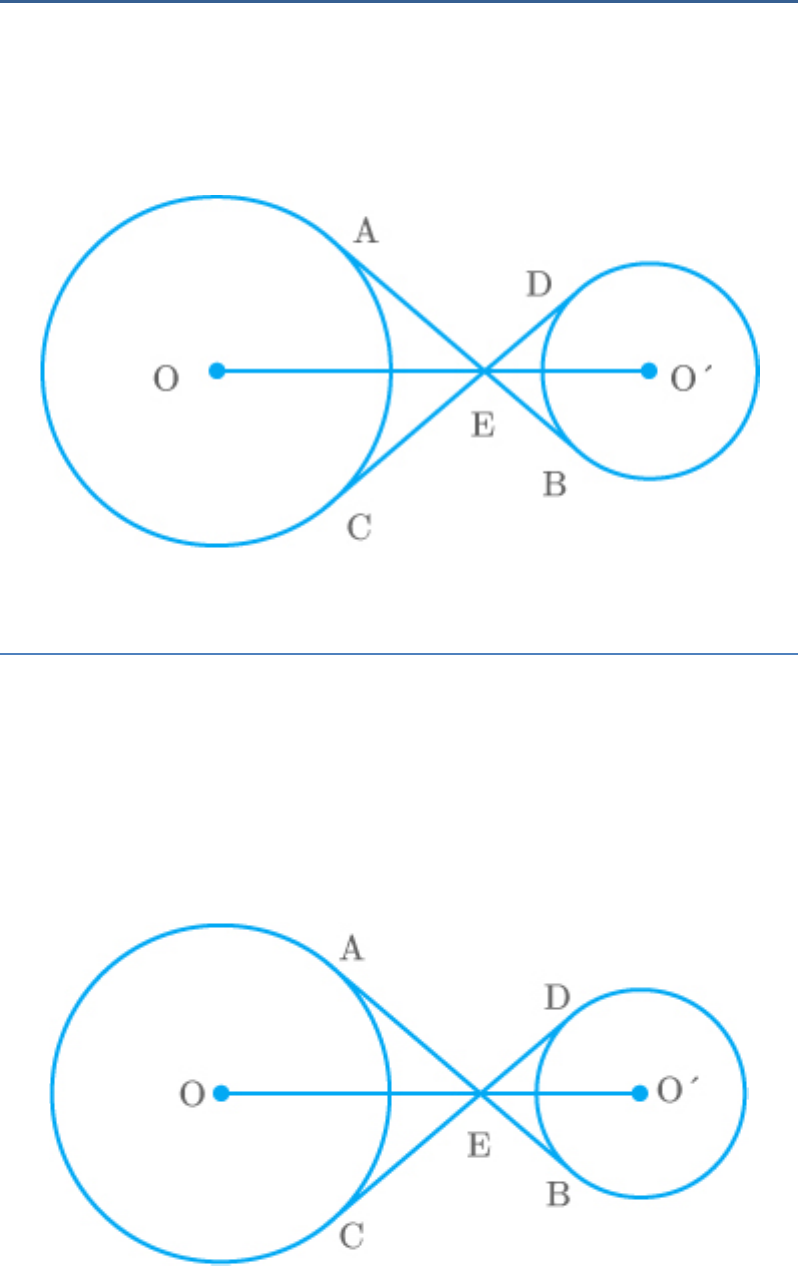
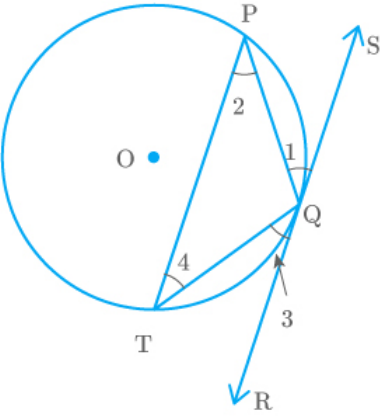
Question: 10
In the adjoining figure, the common tangent, AB and
CD to two circles with centres O and intersect at
O
E. Prove that the points O, E, are collinear.
O
Solution
From the figure,
AB and CD are two tangents common to the two
circles.
AED CEB Vertically oppositeangles

We know that the tangents are equally inclined to
the line that joins the centre to the external point.
Thus,
AEO OEC
DEO O EB
We know that the sum of angles around a point is
.
360
Thus,
AED CEB OEC AEO O EB DEO 360
AED AED AEO AEO DEO DEO 360
2 AED AEO DEO 360
AED AEO DEO 180
OEO 180
Hence, the points O, E and are collinear.
O
Question: 11
In the adjoining figure, O is the centre of a circle of
radius 5 cm, T is a point such that and
OT 13cm
OT intersects the circle at E. If AB is the tangent to
the circle at E, find the length of AB.
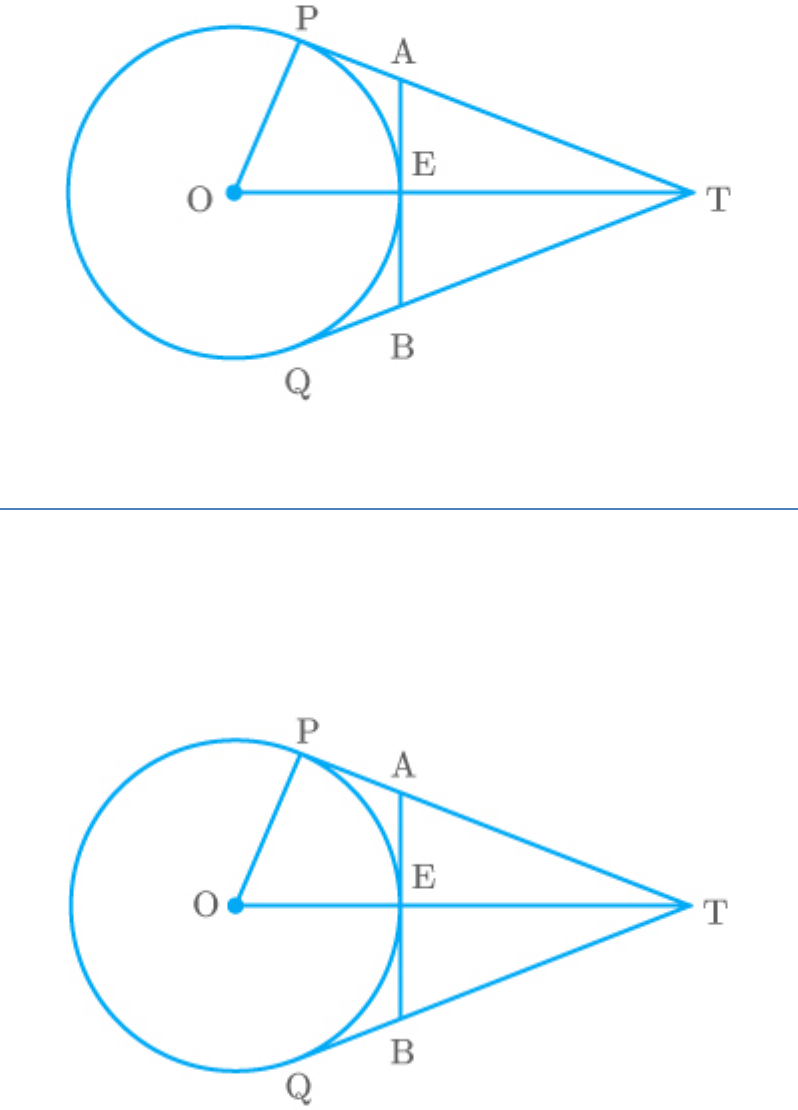
Solution
From the figure,
, AB is a tangent at the point E of the
OT 13cm
circle of radius
r 5cm
AEO OPA 90 Radius tangent
In triangle OPT, by Pythagoras theorem,
2 2 2
PT OT OP
2 2 2
PT 13 5

2
PT 169 25
2
PT 144
PT 144
PT 12
Now,
OP OE 5cm
ET OT OE
13 5
8
AET 180 AEO
180 90
90
We know that tangents from same external point are
equal.
Let
AP AE x
In , by Pythagoras theorem,
AET
2 2 2
AT AE ET
2 2
2
12 x x 8
2 2
144 x 2 12x x 64
24x 144 64
80
x
24
10
x
3
Similarly,
10
BE
3
AB AE BE
10 10
3 3
20
3
Hence,
20
AB cm
3
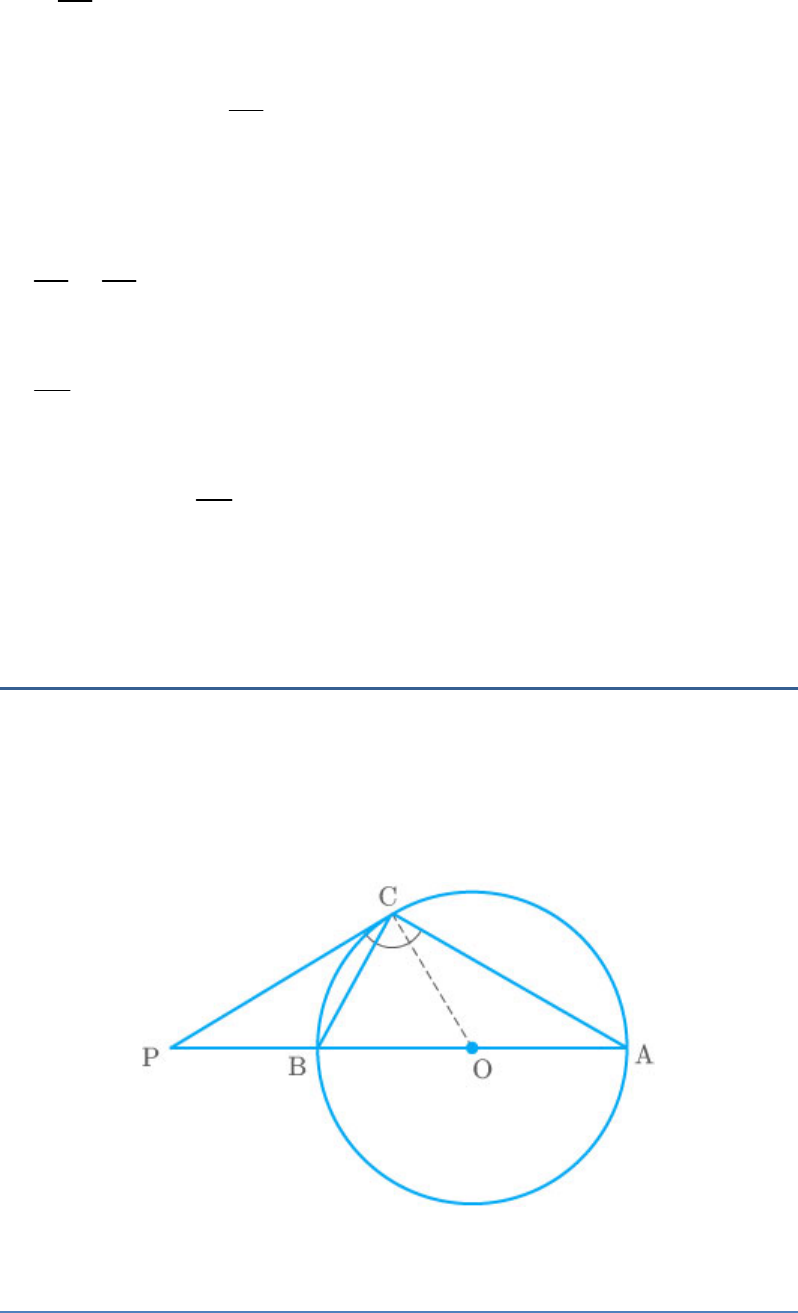
Question: 12
The tangent at a point C of a circle and a diameter
AB when extended intersect at P. If ,
PCA 110
find CBA.
Solution
According to the question,

PCA 110
Thus,
PCB BCA 110
PCB 110 BCA
PCB 110 90 BCA 90
PCB 20
CAB PCB 20 Anglesin alternatesegment
In triangle BCA, by the angle sum property,
BCA CAB CBA 180
90 20 CBA 180
CBA 180 90 20
CBA 70
Hence, is
CBA
70
Question: 13
If an isosceles triangle ABC, in which
, is inscribed in a circle of radius 9
AB AC 6cm
cm, find the area of the triangle.
Solution
From the figure,
AB AC 6cm
OB OC OA 9cm
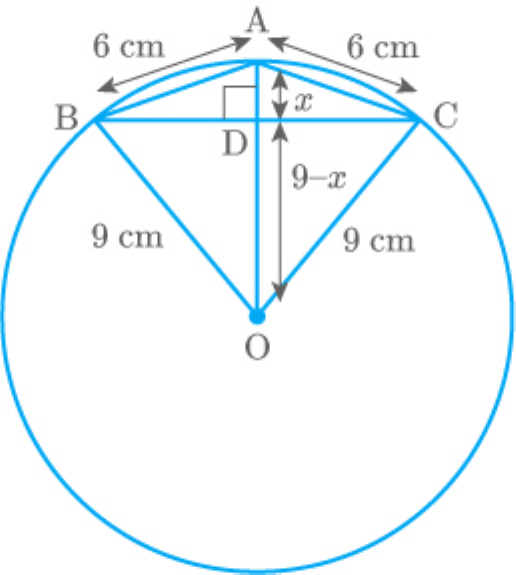
Thus, quadrilateral ABOC is a kite.
We know that the diagonals of a kite are
perpendicular to each other.
Thus,
AO BC
Let
AD x
In triangle ABD, by Pythagoras theorem,
2 2 2
AB AD BD
2 2 2
BD AB AD
2 2 2
BD 6 x
2
2
BD 36 x ...... 1
In triangle BDO, by the Pythagoras theorem,
2 2 2
BD 9 9 x
2
2
BD 81 81 x 2 9x
2
2
BD 81 81 x 18x
2
2
BD x 18x ...... 2
From (1) and (2).
2 2
36 x x 18x
36
x
18
x 2
Put the value of in equation (1).
x
2
2
BD 36 x
2 2
BD 36 2
2
BD 36 4
2
BD 32
BD 4 2
Similarly,
CD 4 2
BC BD CD
4 2 4 2
8 2
Area of ABC
1
BC AD
2
1
BC AD
2
1
8 2 2
2
8 2
Hence, the area of the triangle is .
2
8 2 cm
Question: 14
A is a point at a distance 13 cm from the centre O of
a circle of radius 5 cm. AP and AQ are the tangents
to the circle at P and Q. If a tangent BC is drawn at a
point R lying on the minor arc PQ to intersect AP at
B and AQ at C, find the perimeter of the .
ABC
Solution
From the figure,
OP 5cm
OA 13cm
BC is a tangent to the circle at point R.
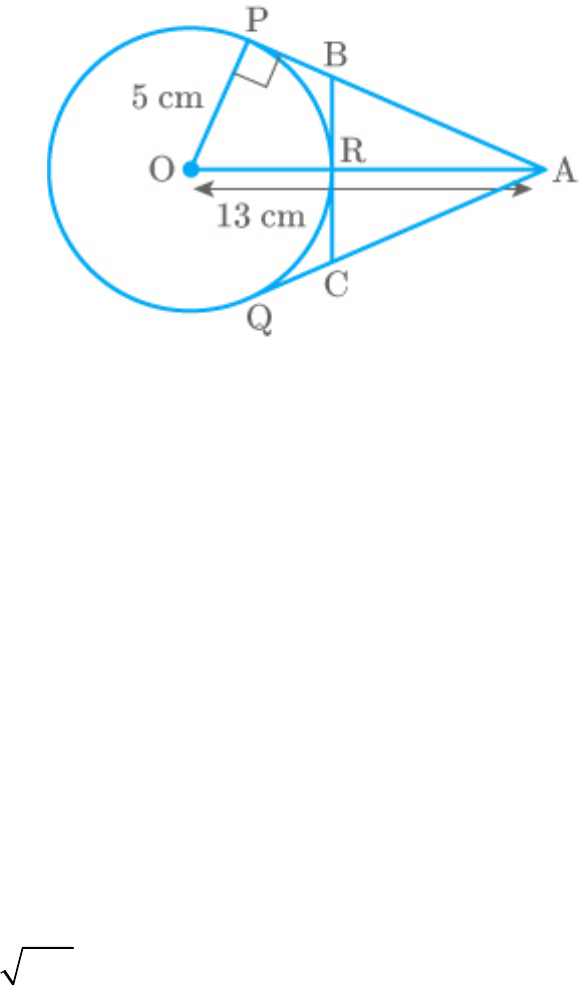
BP is a tangent and OP is a radius.
Thus,
BPO 90
In triangle OPA, by the Pythagoras theorem,
2 2 2
OA OP AP
2 2 2
AP OA OP
2 2 2
AP 13 5
2
AP 169 25
2
AP 144
AP 144
AP 12
Perimeter of trian ABgl Be AB CC CA
AB BR CR CA
We know that tangents from same external point are
equal.
Thus, and
BR BP
CR CQ
So,
Perimeter of triang AB BP Cle AB QC CA
AP AQ
AP AP
2AP
2 12
24
Hence, the perimeter of the is .
ABC
24 cm