
Lesson: Algebraic Expressions and Identities
Exercise 9.1
Question 1
Identify the terms, their coefficients for each of the following expressions:
(i) 5xyz
2
–
3zy (ii) 1 + x + x2 (iii) 4x
2
y
2
– 4x2y2z2
+ z2
(iv) 3 – pq + qr – rp (v)
xy
xy
22
(vi) 0.3a – 0.6ab + 0.5b
Answer:
Term Coefficient
(i) 5xyz
2
5
– 3zy – 3
(ii) 1 1
x 1
x
2
1
(iii) 4x
2
y
2
4
– 4 x
2
y
2
z
2
– 4
z
2
1
(iv) 3 3
– pq –1
qr 1
– rp –1
(v)
2
x
1
2
2
y
1
2
–xy –1
(vi) 0.3a 0.3
– 0.6ab – 0.6
0.5b 0.5
Solution:
(i) 5xyz
2
– 3zy. There are two terms, i.e., 5xyz
2
and – 3zy
Coefficient of 5xyz
2
= 5; Coefficient of – 3zy = – 3

(ii) 1 + x + x2; There are three terms, i.e., 1, x and x
2
Coefficient of 1 = 1; Coefficient of x = 1; Coefficient of x
2
= 1
(iii) 4x
2
y
2
– 4x
2
y
2
z
2
+ z
2
There are three terms, i.e., 4x
2
y
2
, – 4x
2
y
2
z
2
and z
2
Coefficient of 4x
2
y
2
= 4; Coefficient of – 4x
2
y
2
z
2
= – 4; Coefficient of z
2
= 1
(iv) 3 – pq + qr – rp.
There are four terms, i.e., 3, – pq, qr and – rp Coefficient of
3 = 3; Coefficient of – pq = – 1; Coefficient of qr =1; Coefficient of – rp = – 1
(v)
xy
xy
22
.
There are three terms, i.e.,
xy
,
22
and – xy
Coefficient of
x1
22
; Coefficient of
y1
22
; Coefficient of – xy = – 1
(vi) 0.3a – 0.6ab + 0.5b. There are three terms 0.3a, – 0.6ab and 0.5b
Coefficient of 0.3a = 0.3
Coefficient of – 0.6ab = – 0.6
Coefficient of 0.5b = 0.5
Question 2
Classify the following polynomials as monomials, binomials, trinomials.
Which polynomials do not fit in any of these three categories?
x + y, 1000, x + x
2
+ x
3
+ x
4
, 7 + y + 5x, 2y – 3y
2
, 2y – 3y
2
+ 4y
3
,
5x – 4y + 3xy, 4z – 15z
2
, ab + bc + cd + da, pqr, p
2
q + pq
2
, 2p + 2q
Answer:
Monomials: 1000, pqr Binomials: x + y, 2y – 3y
2
, 4z –15z
2
, p
2
q +pq
2
, 2p + 2q
Trinomials:7 + y + 5x, 2y – 3y
2
+ 4y
3
, 5x – 4y + 3xy
Polynomials, which do not fit in these categories, are:
x + x
2 +
x3
+
x4, ab +bc+ cd + da)

Solution:
Monomial: 1000, pqr
Binomial: x + y, 2y – 3y
2
, 4z – 15z
2
, p
2
q + pq
2
, 2p + 2q
Trinomial: 7 + y + 5x, 2y – 3y
2
+ 4y
3
, 5x – 4y + 3xy
Polynomials: x + x
2
+ x
3
+ x
4
,
ab + bc + cd + da do not fit in any of these categories.
Question 3
Add the following:
(i) ab – bc, bc – ca, ca – ab
(ii) a – b + ab, b – c + bc, c – a + ac
(iii) 2p
2
q
2
– 3pq + 4, 5 + 7pq – 3p
2
q
2
(iv) l
2
+ m
2
, m
2
+ n
2
+ l
2
, 2lm + 2mn + 2nl, n
2
Answer:
(i) 0
(ii) ab + bc + ac
(iii) – p
2
q
2 +
4pq + 9
(iv) 2(l
2
+ m
2
+ n
2
+ lm + mn + nl)
Solution:
(i) ab –bc
+bc –ca
–ab +ca
________________________
0 + 0 + 0
0
(ii) a –b +ab
+b – c + bc
–a + c + ac
––––––––––––––––––––––––––
0 + 0 + ab + 0 +bc + ac
= ab + bc + ac

(iii) 2p
2
q
2
–3pq +4
–3p
2
q
2
+7pq +5
–––––––––––––––––––––––––––––
–p
2
q
2
+4pq +9
= – p
2
q
2
+ 4pq + 9
(iv) l
2
+ m2
+ m
2
+ n
2
+ +
2
l
+ n2
+ 2lm+ 2mn + 2nl
–––––––––––––––––––––––––––––––––––––––
2l
2
+ 2m
2
+ 2n
2
+ 2lm + 2mn + 2nl
= 2l
2
+ 2m
2
+ 2n
2
+ 2lm + 2mn + 2nl = 2
(l
2
+ m
2
+ n
2
+ lm + mn + nl)
Question 4
(a) Subtract : 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
(b) Subtract : 3xy + 5yz – 7zx from 5xy – 2yz + 10xyz
(c) Subtract : 4p
2
q – 3pq + 5pq
2
– 8p + 7q – 10 from 18 – 3p – 11q + 5pq –
2pq
2
+ 5p
2
q.
Answer:
(a) 8a – 2ab + 2b – 15
(b) 2xy – 7yz + 5zx + 10xyz
(c) p
2
q – 7pq
2
+ 8pq – 18q + 5p + 28
Solution:
(a) 12a – 9ab + 5b – 3
4a – 7ab + 3b + 12
(-) (+) (-) (-)
––––––––––––––
8a – 2ab + 2b – 15
= 8a – 2ab + 2b – 15
(b) 5xy – 2yz – 2zx + 10xyz
3xy + 5yz – 7zx
(-) (–) (+)
––––––––––––––
2xy – 7yz + 5zx + 10xyz
= 2xy – 7yz + 5zx + 10xyz
(c) 5p
2
q – 2pq
2
+ 5pq – 3p – 11q + 18
4p
2
q + 5pq
2
– 3pq – 8p + 7q – 10
(-) (-) (+) (+) (-) (+)
–––––––––––––––––––––––––––––––––
p
2
q –7pq
2
+ 8pq + 5p – 18q + 28
= p
2
q – 7pq
2
+ 8pq + 5p – 18q + 28
Exercise 9.2
Question 1
Find the product of the following pairs of monomials
(i) 4, 7p (ii) – 4p, 7p (iii) – 4p, 7pq
(iv) 4p
3
, – 3p (v) 4p, 0
Answer:
(i) 28p (ii) – 28p
2
(iii) – 28p
2
q (iv) – 12p
4
(v) 0
Solution:
(i) 4 × 7p = (4 × 7) × p = 28p
(ii) 4p × 7p = (– 4 × 7) × (p × p) = – 28p
2
(iii) 4p × 7pq = (– 4 × 7) × (p × pq) = – 28p
2
q
(iv) 4p
3
× (– 3p) = [(4) × (– 3)] × (p
3
× p) = – 12p
4
(v) 4p × 0 = (4 × 0) × p = 0
Question 2
Find the areas of rectangles with the following pairs of monomials as their lengths
and breadths respectively.
(p, q); (10m, 5n); (20x
2
, 5y
2
); (4x, 3x
2
); (3mn, 4np)
Answer:
pq; 50 mn; 100 x
2
y
2
; 12x
3
; 12mn
2
p
Solution:
Area of rectangle = l × b sq. unit
(i) If l = p, b = q
Area of rectangle = p × q = pq sq. unit.
(ii) If l = 10m, b = 5n
Area of rectangle = 10m × 5n = 50mn sq. unit.
(iii) If l = 20x
2
, b = 5y
2
Area of rectangle = 20x
2
× 5y
2
= 100x
2
y
2
sq. unit.
(iv)If l = 4x, b = 3x
2
Area of rectangle = 4x × 3x
2
= 12x
3
sq. unit
(v) If l = 3mn, b = 4np
Area of rectangle = 3mn × 4np = 12mn
2
p sq. unit.
Question 3
Complete the table of products:

Answer:
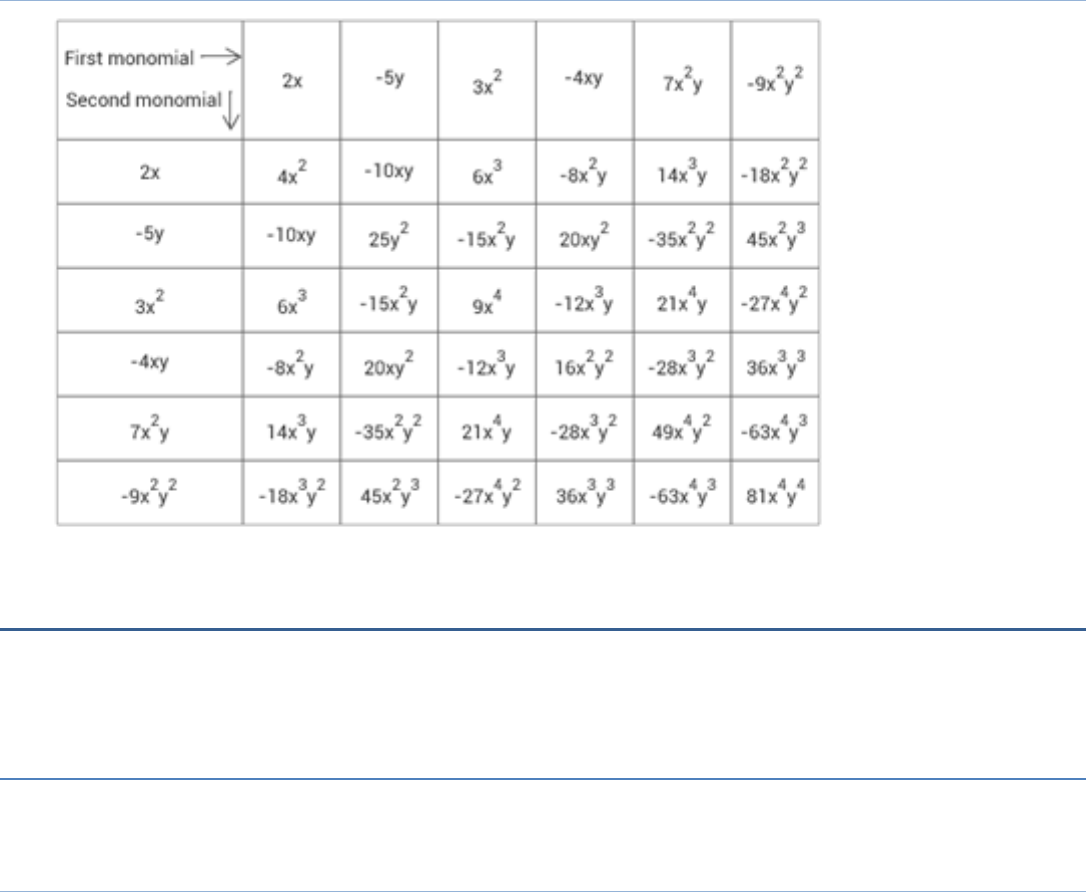
Solution:
Question 4
Obtain the volume of rectangular boxes with following length, breadth and height
respectively:
(i) 5a, 3a
2
, 7a
4
(ii) 2p, 4q, 8r (iii) xy, 2x
2
y, 2xy
2
(iv) a, 2b, 3c
Answer:
(i) 105a
7
(ii) 64pqr (iii) 4x
4
y
4
(iv) 6abc
Solution:
We know that, volume of a cuboid = l × b × h
(i) Here, l = 5a, b = 3a2 and h = 7a4
Volume of the rectangular box:
l × b × h = 5a × 3a
2
× 7a
4
= ( 5 × 3 × 7) × (a × a
2
× a
4
) = 105 a
7
cubic
unit
(ii) Here, l = 2p, b = 4q and h = 8r
Volume of the rectangular box = l × b × h = 2p × 4q × 8r
= (2 × 4 × 8) × (p × q × r) = 64pqr cubic unit
(iii) Here, l = xy, b = 2x2y and h = 2xy2
Volume of the rectangular box = l × b × h = xy × 2x
2
y × 2xy
2
= (1 × 2 × 2) × (xy × x
2
y × xy
2
) = 4x
4
y
4
cubic unit
(iv) Here, l = a, b = 2b and h = 3c
Volume of the rectangular box = l × b × h = a × 2b × 3c
= (1 × 2 × 3) × (a × b × c) = 6abc cubic unit
Question 5
Obtain the product of:
(i) xy, yz, zx
(ii) a, – a
2
, a
3
(iii) 2, 4y, 8y2, 16y
3
(iv) a, 2b, 3c, 6abc
(v) m, – mn, mnp
Answer:
(i) x
2
y
2
z
2
(ii) a
6
(iii) 1024y
6
(iv) 36a
2
b
2
c
2
(v) m
3
n
2
p
Solution:
(i) xy × yz × zx = x
2
y
2
z
2
(ii) a × (– a
2
) × (a
3
) = – a
6
(iii) 2 × 4y × 8y
2
× 16y
3
= (2 × 4 × 8 × 16) × (y × y
2
× y
3
) = 1024y
6
(iv) a × 2b × 3c × 6abc = (2 × 3 × 6) × (a × b × c × abc) = 36a
2
b
2
c
2
(v) m × (– mn) × (mnp) = – m
3
n
2
p
Exercise 9.3
Question 1
Carry out the multiplication of the expressions in each of the following pairs:
(i) 4p, q + r (ii) ab, a – b (iii) a + b, 7a
2
b
2
(iv) a
2
– 9, 4a (v) pq + qr + rp, 0
Answer:
(i) 4pq + 4pr (ii) a
2
b – ab
2
(iii) 7a
3
b
2
+ 7a
2
b
3
(iv) 4a
3 –
36a (v) 0
Solution:
(i) 4p(q + r) = 4pq + 4pr (ii) ab × (a – b) = a
2
b – ab
2
(iii) (a + b) × (7a
2
b
2
) = 7a
3
b
2
+ 7a
2
b
3
(iv) (a
2
– 9) × 4a = 4a
3
– 36a
(v) (pq + qr + rp) × 0 = 0
Question 2
Complete the table:
First expression Second expression Product
(i) a b + c + d ......
(ii) x + y – 5 5xy ......
(iii) p 6p
2
– 7p + 5 ......
(iv) 4p
4
q
2
p
2
– q
2
......
(v) a + b+ c abc ......
Answer:
(i) ab + ac + ad
(ii) 5x
2
y + 5xy2
–
25xy
(iii) 6p
3 –
7p2
+
5p
(iv) 4p
6
q
2
– 4p
4
q
4
(v) a
2
bc + ab
2
c + abc
2
Solution:
(i) ab + ac + ad (ii) 5x
2
y + 5xy
2
– 25xy (iii) 6p
3
– 7p
2
+ 5p
(iv) 4p
6
q
2
– 4p
4
q
4
(v) a
2
bc + ab
2
c + abc
2
Question 3
Find the product.
(i) (a
2
) × (2a
22
) × (4a
26
) (ii)
22
29
xy x y
3 10
(iii)
33
10 6
– pq p q
35
(iv) x × x
2
× x
3
× x
4

Answer:
(i) 8a
50
(ii)
33
3
5
xy
(iii) 4p
4
q
4
(iv) x
10
Solution:
(i) a
2
× 2a
22
× 4a
26
= 2 × 4 × a
2+22+26
= 8a
50
(ii)
2 2 2 2
2 9 2 9
xy x y xy x y
3 10 3 10
= –
3
5
x
3
y
3
(iii)
33
10 6 10 6
– pq p q
3 5 3 5
× pq
3
×
p
3
q = – 4p
4
q
4
(iv) x × x
2
× x
3
× x
4
= x
1+2+3+4
= x
10
Question 4
(a) Simplify 3x (4x – 5) + 3 and find its values for (i) x = 3, (ii) x = 1/2
(b) Simplify a(a
2
+ a + 1) + 5 and find its value for (i) a = 0, (ii) a = 1, (iii) a = –1
Answer:
(a) 12x
2
– 15x + 3; (i) 66 (ii)
3
2
(b) a
3 +
a
2
+ a + 5; (i) 5 (ii) 8 (iii) 4
Solution:
(a) 3x(4x – 5) + 3 = (3x × 4x) – (3x × 5) + 3 = 12x
2
– 15x + 3
(i) The value of 12x
2
– 15x + 3 when x = 3
= 12(3)
2
– 15(3) + 3 = 12 × 9 – 45 + 3 = 108 – 45 + 3 = 66
(ii) The value of 12x
2
– 15x + 3 when x =
1
2
,
12x
2
– 15x + 3 = 12
2
1
2
– 15
1
2
+ 3
= 12 ×
1
4
– 15 ×
1
2
+ 3 = 3 –
15
2
+ 3 = 6 –
15
2
=
12 15 3
22
(b) a (a
2
+ a + 1) + 5 = (a × a
2
) + (a × a) + (a × 1) + 5 = a
3
+ a
2
+ a + 5
(i) The value of a
3
+ a
2
+ a + 5 when a = 0
a
3
+ a
2
+ a + 5 = (0)
3
+ (0)
2
+ 0 + 5 = 0 + 0 + 0 + 5 = 5
(ii) The value of a
3
+ a
2
+ a + 5 when a = 1,

a
3
+ a
2
+ a + 5 = (1)
3
+(1)
2
+ 1 + 5 = 8
(iii) The value of a
3
+ a
2
+ a + 5 when a = – 1,
a
3
+ a
2
+ a + 5 = (– 1)
3
+ (– 1)
2
– 1 + 5 = – 1 + 1 – 1 + 5 = 4
Question 5
(a) Add: p (p – q), q (q – r) and r (r – p)
(b) Add: 2x(z – x – y) and 2y(z – y – x)
(c) Subtract: 3l(l – 4m + 5n) from 4 l (10n – 3m + 2 l)
(d) Subtract: 3a (a + b + c) – 2b (a – b + c) from 4c (–a + b + c).
Answer:
(a) p
2
+ q
2
+ r
2
– pq – qr – pr
(b) – 2x
2
– 2y
2
– 4xy + 2yz + 2zx
(c) 5l
2
+ 25ln
(d) – 3a
2
– 2b
2
+ 4c
2
– ab + 6bc – 7ac
Solution:
(a) p(p – q) + q(q – r) + r(r – p) = p
2
– pq + q
2
– qr + r
2
– pr
= p
2
+ q
2
+ r
2
– pq – qr – pr
(b) 2x(z – x – y) + 2y(z – y – x) = 2xz – 2x
2
– 2xy + 2yz – 2y
2
– 2xy
= – 2x
2
– 2y
2
– 4xy + 2yz + 2xz
(c) 3 l (l – 4m + 5n) = 3 l
2
– 12m l + 15 l n
and 4 l (10n – 3m + 2 l) = 40 l n – 12m l + 8 l
2
Now on subtracting, (40 l n – 12m l + 8 l
2
) – (3 l
2
– 12m l + 15 l n)
= 40 l n – 12m l + 8 l
2
– 3 l
2
+ 12m l – 15 l n
= (40 l n – 15 l n) + (– 12m l + 12m l) + (8 l
2
– 3 l
2
)
= 25 l n + 0 + 5 l
2
= 25 l n + 5 l
2
(d) 3a (a + b + c) – 2b (a – b + c) = 3a
2
+ 3ab + 3ac – 2ab + b
2
– 2bc
and 4c (– a + b + c) = – 4ac + 4bc + 4c
2
Now on subtracting,(– 4ac + 4bc + 4c
2
) – (3a
2
+ 2b
2
+ ab – 2bc + 3ac)
= – 4ac + 4bc + 4c
2
– 3a
2
– 2b
2
– ab + 2bc – 3ac
= (– 4ac – 3ac) + (4bc + 2bc) – ab – 3a
2
– 2b
2
+ 4c
2
= – 7ac + 6bc – ab – 3a
2
– 2b
2
+ 4c
2
= – 3a
2
– 2b
2
+ 4c
2
– ab + 6bc – 7ac
Exercise 9.4
Question 1
Multiply the binomials:
(i) (2x + 5) and (4x – 3) (ii) (y – 8) × (3y – 4)
(iii) (2.5 l – 0.5m) and (2.5 l + 0.5m) (vi) (a + 3b) and (x + 5)
(v) (2pq + 3q
2
) and 3pq – 2q
2
(vi)
22
3
a 3b
4
and
22
2
4 a b
3
Answer:
(i) 8x
2
+ 14x – 15
(ii) 3y
2
– 28y + 32
(iii) 6.25l
2
– 0.25m
2
(iv) ax + 5a + 3bx + 15b
(v) 6p
2
q
2
+ 5pq
3
– 6q
4
(vi) 3a
4
+10a
2
b
2
– 8b
4
Solution:
(i) (2x + 5) × (4x – 3) = 8x
2
– 6x + 20x – 15 = 8x
2
+ 14x – 15
(ii) (y – 8) × (3y – 4) = 3y
2
– 4y – 24y + 32 = 3y
2
– 28y + 32
(iii) (2.5 l– 0.5m)×(2.5l+0.5m) = 6.25l
2
+ 1.25l m – 1.25l m – 0.25m
2
= 6.25 l
2
– 0.25m
2
(iv) (a + 3b) × (x + 5) = ax + 5a + 3bx + 15b = ax + 3bx + 5a + 15b
(v) (2pq + 3q
2
) × (3pq – 2q
2
) = 6p
2
q
2
– 4pq
3
+ 9pq
3
– 6q
4
= 6p
2
q
2
+ 5pq
3
– 6q
4
(vi)
2 2 2 2 2 2 2 2 2
3 2 3 3 8
a 3b 4 a b a 4a a b 3b
4 3 4 4 3
2 2 2
8
4a 3b b
3
= 3a
4
– 2a
2
b
2
+ 12a
2
b
2
– 8b
4
= 3a
4
+ 10a
2
b
2
– 8b
4
Question 2
Find the product:
(i) (5 – 2x) (3 + x) (ii) (x + 7y) (7x – y)
(iii) (a
2
+ b) (a + b
2
) (iv) (p
2
– q
2
) (2p + q)
Answer:
(i) 15 – x – 2x
2
(ii) 7x
2
+ 48xy – 7y
2
(iii) a
3
+ a
2
b
2
+ ab + b
3
(iv) 2p
3
+ p
2
q – 2pq
2
– q
3
Solution:
(i) (5 – 2x) × (3 + x) = 15 + 5x – 6x – 2x
2
= 15 – x – 2x
2
(ii) (x + 7y) × (7x – y) = 7x
2
– xy + 49xy – 7y
2
= 7x
2
– 7y
2
+ 48xy
(iii) (a
2
+ b) × (a + b
2
) = a
3
+ a
2
b
2
+ ab + b
3
= a
3
+ b
3
+ a
2
b
2
+ ab
(iv) (p
2
– q
2
) × (2p + q) = 2p
3
+ p
2
q – 2pq
2
– q
3
= 2p
3
– q
3
+ p
2
q – 2pq
2
Question 3
Simplify:
(i) (x
2
– 5)(x + 5) + 25
(ii) (a
2
+ 5) (b
3
+ 3) + 5
(iii) (t + s
2
) (t
2
– s)
(iv) (a + b)(c – d) + (a – b)(c + d) + 2(ac + bd)
(v) (x + y) (2x + y) + (x + 2y) (x – y)
(vi) (x + y) (x
2
– xy + y
2
)
(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y
(viii) (a + b + c)(a + b – c)
Answer:
(i) x
3
+ 5x
2
– 5x
(ii) a
2
b
3
+ 3a
2
+ 5b
3
+ 20

(iii) t
3
– st + s
2
t
2
– s
3
(iv) 4ac
(v) 3x
2 +
4xy – y
2
(vi) x
3
+ y
3
(vii) 2.25x
2
– 16y
2
(viii) a
2
+ b
2
– c
2
+ 2ab
Solution:
(i) (x
2
– 5)(x + 5) + 25 = x
3
+ 5x
2
– 5x – 25 + 25 = x
3
+ 5x
2
– 5x
(ii) (a
2
+ 5)(b
3
+ 3) + 5 = a
2
b
3
+ 3a
2
+ 5b
3
+ 15 + 5 = a
2
b
3
+ 3a
2
+ 5b
3
+ 20
(iii) (t + s
2
)(t
2
– s) = t
3
– st + s
2
t
2
– s
3
= t
3
– s
3
+ s
2
t
2
– st
(iv) (a + b)(c – d) + (a – b)(c + d) + 2 (ac + bd)
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd = 4ac
(v) (x + y) × (2x + y) + (x + 2y) × (x – y)
= 2x
2
+ xy + 2xy + y
2
+ x
2
– xy + 2xy – 2y
2
= 3x
2
– y
2
+ 4xy
(vi) (x + y)(x
2
– xy + y
2
) = x
3
– x
2
y + xy
2
+ x
2
y – xy
2
+ y
3
= x
3
+ y
3
(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y
= 2.25x
2
+ 6xy + 4.5x – 6xy – 16y
2
– 12y – 4.5x + 12y = 2.25x
2
– 16y
2
(viii) (a + b + c)(a + b – c) = a
2
+ ab – ac + ab + b
2
– bc + ac + bc – c
2
= a
2
+ b
2
– c
2
+ 2ab.
Exercise 9.5
Question 1
Use a suitable identity to get each of the following products:
(i) (x + 3) (x + 3)
(ii) (2y + 5) (2y + 5)
(iii) (2a – 7) (2a – 7)

(iv)
11
3a – 3a –
22
(v) (1.1m – 0.4) (1.1.m + 0.4)
(vi) (a
2
+ b
2
) (– a
2
+ b
2
)
(vii) (6x – 7) (6x + 7)
(viii) (– a + c) (– a + c)
(ix)
x 3y x 3y
.
2 4 2 4
(x) (7a – 9b) (7a – 9b)
Answer:
(i) x
2
+ 6x + 9
(ii) 4 y
2
+ 20y + 25
(iii) 4 a
2
– 28a + 49
(iv) 9a
2
– 3a +
1
4
(v) 1.21m
2
–0.16
(vi) b
4
– a
4
(vii) 36x
2
– 49
(viii) a
2
– 2ac + c
2
(ix)
22
39
4 4 16
x xy y
(x) 49a
2 –
126ab + 81b2
Solution:
(i) (x + a)(x + b) = x
2
+ (a + b)x + ab
(x + 3)(x + 3) = x
2
+ (3 + 3)x + 3 × 3 = x
2
+ 6x + 9.
(ii) (a + b)
2
= a
2
+ 2ab + b
2
(2y + 5)(2y + 5) = (2y + 5)
2
= (2y)
2
+ 2 × 2y × 5 + (5)
2
= 4y
2
+
20y + 25.

(iii) (2a – 7)(2a – 7) = (2a – 7)
2
[ (a – b)
2
= a
2
– 2ab + b
2
]
= (2a)
2
– 2 × 2a × 7 + (7)
2
= 4a
2
– 28a + 49.
(iv)
2
1 1 1
3a 3a 3a
2 2 2
= (3a)
2
– 2 × 3a ×
1
2
+
2
1
2
= 9a
2
–
3a +
1
4
(v) (a + b) (a – b) = a
2
– b
2
(1.1m – 0.4)(1.1.m + 0.4) = (1.1m)
2
– (0.4)
2
= 1.21m
2
– 0.16
(vi) (a
2
+ b
2
)(– a
2
+ b
2
) = (b
2
+ a
2
)(b
2
– a
2
) = (b
2
)
2
– (a
2
)
2
= b
2
– a
2
(vii) (6x – 7)(6x + 7) = (6x)
2
– (7)
2
= 36x
2
– 49.
(viii) (c – a)(c – a) = (c – a)
2
= c
2
– 2ca + a
2
.
(ix)
22
22
x 3y x 3y x x 3y 3y x 3xy 9y
2
2 4 2 4 2 2 4 4 4 4 16
(x) (7a – 9b) (7a – 9b) = (7a – 9b)
2
= (7a)
2
– 2 × 7a × 9b + (9b)
2
= 49a
2
– 126ab + 81b
2
Question 2
Use the identity (x + a)(x + b) = x
2
+ (a + b)x + ab to find the following products :
(i) (x + 3) (x + 7) (ii) (4x + 5)(4x + 1) (iii) (4x – 5)(4x – 1)
(iv) (4x + 5)(4x – 1) (v) (2x + 5y)(2x + 3y) (vi) (2a
2
+ 9)(2a
2
+ 5)
(vii) (xyz – 4)(xyz – 2)
Answer:
(i) x
2
+ 10x + 21
(ii) 16x
2
+ 24 + 5
(iii) 16x
2
– 24x + 5
(iv) 16x
2
+ 16x – 5

(v) 4x
2
+ 16xy + 15y
2
(vi) 4a
4
+ 28a
2
+ 45
(vii) x
2
y
2
z
2
– 6xyz + 8
Solution:
(i) (x + 3) (x + 7) = x
2
+ (3 + 7)x + 3 × 7 = x
2
+ 10x + 21.
(ii) (4x + 5)(4x + 1) = (4x)
2
+ (5 + 1)4x + 5 × 1 = 16x
2
+ 24x + 5
(iii) (4x – 5)(4x – 1) = (4x)
2
+ (( – 5) + ( – 1)) 4x + (– 5 × – 1) = 16x
2
– 24x + 5
(iv) (4x + 5)(4x – 1) = (4x)
2
(5 + ( – 1)) 4x + [5 × ( – 1)] = 16x
2
+ 16x – 5
(v) (2x + 5y)(2x + 3y) = (2x)
2
+ (5y + 3y)2x + 5y × 3y = 4x
2
+ 16xy + 15y
2
(vi) (2a
2
+ 9)(2a
2
+ 5) = (2a
2
)
2
+ (9 + 5)2a
2
+ 9 × 5 = 4a
4
+ 28a
2
+ 45
(vii) (xyz – 4)(xyz – 2) = (xyz)
2
+ [( – 4) + ( – 2)] xyz + ( – 4) × ( – 2)]
= x
2
y
2
z
2
– 6xyz + 8.
Question 3
Find the following squares by using the identities:
(i) (b – 7)
2
(ii) (xy + 3z)
2
(iii) (6x
2
– 5y)
2
(iv)
2
23
mn
32
(v) (0.4p – 0.5q)
2
(vi) (2xy + 5y)
2
Answer:
(i) b
2
– 14b + 49
(ii) x
2
y
2 +
6xyz + 9z
2
(iii) 36x
4
– 60x
2
y + 25y
2
(iv)
2
4
9
m
+ 2mn +
2
9
4
n
(v) 0.16p
2
– 0.4pq + 0.25q
2
(vi) 4x
2
y
2
+ 20xy
2
+ 25y
2

Solution:
(i) (b – 7)
2
= b
2
– 2 × b × 7 + 7
2
[ (a – b)
2
= a
2
– 2ab + b
2
] = b
2
– 14b + 49.
(ii) (xy + 3z)
2
= (xy)
2
+ 2 × xy × 3z + (3z)
2
[ (a + b)
2
= a
2
+ 2ab + b
2
]
= x
2
y
2
+ 6xyz +9z
2
.
(iii) (6x
2
– 5y)
2
= (6x
2
)
2
– 2 × 6x
2
× 5y + (5y)
2
= 36x
2
– 60x
2
y + 25y
2
.
(iv)
2 2 2
2 3 2 2 3 3
m n m 2 m n n
3 2 3 3 2 2
=
2
4
m
9
+ 2mn +
9
4
n
2
(v) (0.4p – 0.5q)
2
= (0.4p)
2
– 2 × 0.4p × 0.5q + (0.5q)
2
=0.16p
2
–0.4pq+ 0.25 q
2
(vi) (2xy + 5y)
2
= (2xy)
2
+ 2 × 2xy × 5y + (5y)
2
= 4x
2
y
2
+ 20xy
2
+ 25y
2
.
Question 4
Simplify:
(i) (a
2
– b
2
)
2
(ii) (2x + 5)
2
– (2x – 5)
2
(iii) (7m – 8n)
2
+ (7m + 8n)
2
(iv) (4m + 5n)
2
+ (5m + 4n)
2
(v) (2.5p – 1.5q)
2
– (1.5p – 2.5q)
2
(vi) (ab + bc)
2
– 2ab
2
c
(vii) (m
2
– n
2
m)
2
+ 2m
2
n
2
Answer:
(i) a
4
– 2a
2
b
2
+ b
4
(ii) 40x
(iii) 98m
2
+ 128n
2
(iv) 41m
2
+ 80mn + 41n
2
(v) 4p
2
– 4q
2
(vi) a
2
b
2 +
b
2
c
2
(vii) m
4 +
n
4
m
2

Solution:
(i) (a
2
– b
2
)
2
= (a
2
)
2
– 2 × a
2
× b
2
+ (b
2
)
2
= a
4
– 2a
2
b
2
+ b
4
.
(ii) (2x + 5)
2
– (2x – 5)
2
= [(2x + 5) + (2x – 5)][(2x + 5) – (2x – 5)]
= (2x + 5 + 2x – 5) (10) = 4x × 10 = 40x.
(iii) (7m – 8n)
2
+ (7m + 8n)
2
= (7m)
2
– 2 × 7m × 8n + (8n)
2
+ (7m)
2
+ 2 × 7m × 8n + (8n)
2
= 98m
2
+ 128n
2
(iv) (4m + 5n)
2
+ (5m + 4n)
2
= (4m)
2
+ 2 × 4m × 5n + (5n)
2
+ (5m)
2
+ 2 × 5m × 4n + (4n)
2
= 41m
2
+ 80mn + 41n
2
(v) (2.5p – 1.5q)
2
– (1.5p – 2.5q)
2
= [(2.5p)
2
– 2 × 2.5p × 1.5q + (1.5q)
2
] – [(1.5p)
2
– 2 × 1.5p × 2.5q +
(2.5q)
2
]
= 6.25p
2
– 7.5pq + 2.25q
2
– 2.25p
2
+ 7.5pq – 6.25q
2
= 4p
2
– 4q
2
(vi) (ab + bc)
2
– 2ab
2
c = (ab)
2
+ 2 × ab × bc + (bc)
2
– 2ab
2
c
= a
2
b
2
+2ab
2
c + b
2
c
2
– 2ab
2
c = a
2
b
2
+ b
2
c
2
(vii) (m
2
– n
2
m)
2
+ 2m
3
n
2
= (m
2
)
2
– 2 × m
2
× n
2
m + (n
2
m)
2
+ 2m
3
n
2
= m
4
– 2m
3
n
2
+ n
4
m
2
+ 2m
3
n
2
= m
4
+ n
4
m
2
.
Question 5
Show that:
(i) (3x + 7)
2
– 84x = (3x – 7)
2
(ii) (9p – 5q)
2
+ 180pq = (9p + 5q)
2
(iii)
2
4 3 16 9
m n 2mn m n
3 4 9 16
(iv) (4pq + 3q)
2
– (4pq – 3q)
2
= 48pq
2
(v) (a – b)(a + b) + (b – c)(b + c) + (c – a)(c + a) = 0
Answer:
(i) (3x + 7)
2
– 84x = (3x – 7)
2
LHS = (3x)
2
+ 2 × 3x × 7 + (7)
2
– 84x = 9x
2
+ 42x + 49 – 84x

= 9x
2
– 42x + 49 = (3x – 7)
2
(ii) (9p – 5q)
2
+ 180pq = (9p + 5q)
2
LHS = (9p)
2
– 2 × 9p × 5q + (5q)
2
+ 180pq = (9p)
2
+ 2 × 9p × 5q +
(5q)
2
= (9p + 5q)
2
= RHS
(iii) LHS =
22
4 4 3 3
m 2 m n n 2mn
3 3 4 4
=
2
16 9
m 2mn n 2mn
9 16
16 9
m n RHS
9 16
(iv) (4pq + 3q)
2
– (4pq – 3q)
2
= 48pq
2
LHS = [(4pq + 3q) + (4pq – 3q) [(4pq + 3q) – (4pq – 3q)]]
= 8pq × 6q = 48pq
2
= RHS
(v) (a – b)(a + b) + (b – c)(b + c) + (c – a)(c + a) = 0
LHS = a
2
– b
2
+ b
2
– c
2
+ c
2
– a
2
= 0 = RHS
Solution:
(i) (3x + 7)
2
– 84x = (3x – 7)
2
LHS = (3x)
2
+ 2 × 3x × 7 + (7)
2
– 84x = 9x
2
+ 42x + 49 – 84x
= 9x
2
– 42x + 49 = (3x – 7)
2
(ii) (9p – 5q)
2
+ 180pq = (9p + 5q)
2
LHS = (9p)
2
– 2 × 9p × 5q + (5q)
2
+ 180pq = (9p)
2
+ 2 × 9p × 5q +
(5q)
2
= (9p + 5q)
2
= RHS
(iii) LHS =
22
4 4 3 3
m 2 m n n 2mn
3 3 4 4
=
2
16 9
m 2mn n 2mn
9 16
16 9
m n RHS
9 16
(iv) (4pq + 3q)
2
– (4pq – 3q)
2
= 48pq
2
LHS = [(4pq + 3q) + (4pq – 3q) [(4pq + 3q) – (4pq – 3q)]]
= 8pq × 6q = 48pq
2
= RHS
(v) (a – b)(a + b) + (b – c)(b + c) + (c – a)(c + a) = 0
LHS = a
2
– b
2
+ b
2
– c
2
+ c
2
– a
2
= 0 = RHS
Question 6
Using identities, evaluate:
(i) (71)
2
(ii) (99)
2
(iii) (102)
2
(iv) (998)
2
(v) (5.2)
2
(vi) 297 × 303 (vii) 78 × 82 (viii) (8.9)
2
(ix) 10.5 × 9.5
Answer:
(i) 5041 (ii) 9801 (iii) 10404 (iv) 996004 (v) 27.04
(vi) 89991 (vii) 6396 (viii) 79.21 (ix) 9.975
Solution:
(i) (70 + 1)
2
= (70)
2
+ 2 × 70 × 1 + (1)
2
= 4900 + 140 + 1 = 5041
(ii) (99)
2
= (100 – 1)
2
= (100)
2
– 2 × 100 × 1 + (1)
2
= 10000 – 200 + 1 = 9801.
(iii) (102)
2
= (100 + 2)
2
= (100)
2
+ 2 × 100×2 + (2)
2
= 10000 + 400 + 4 = 10404.
(iv) (998)
2
= (1000 – 2)
2
= (1000)
2
– 2 × 1000 × 2 + (2)
2
= 1000000 – 4000 +
4 = 996004.
(v) (5.2)
2
= (5 + 0.2)
2
= (5)
2
+ 2 × 5 × 0.2 + (0.2)
2
= 25 + 2.0 + 0.04 = 27.04
(vi) 297 × 303 = (300 – 3)(300 + 3) = (300)
2
– (3)
2
= 90000 – 9 = 89991.
(vii) 78 × 82 = (80 – 2)(80 + 2) = (80)
2
– (2)
2
= 6400 – 4 = 6396.
(viii) (8.9)
2
= (9 – 0.1)
2
= (9)
2
– 2 × 9 × 0.1 + (0.1)
2
= 81 – 1.8 + 0.01 = 79.21
(ix) 10.5 × 9.5 = (10 + 0.5)(10 – 0.5) = (10)
2
– (0.5)
2
= 100 – 0.25 = 99.75
Question 7
Using a
2
– b
2
= (a + b) (a – b), find
(i) (51)
2
– (49)
2
(ii) (1.02)
2
– (0.98)
2

(iii) (153)
2
– (147)
2
(iv) (12.1)
2
– (7.9)
2
Answer:
(i) 200 (ii) 0.08 (iii) 1800 (iv) 84
Solution:
(i) (51 + 49) (51 – 49) = 100 × 2 = 200
(ii) (1.02)
2
– (0.98)
2
= (1.02 + 0.98)(1.02 – 0.98) = 2.00 × 0.04 = 0.08
(iii) (153)
2
– (147)
2
= (153 + 147)(153 – 147) = 300 × 6 = 1800.
(iv) (12.1)
2
– (7.9)
2
= (12.1 + 7.9)(12.1 – 7.9) = 20.0 × 4.2 = 84.0 = 84.
Question 8
Using (x + a)(x + b) = x
2
+ (a + b)x + ab, find :
(i) 103 × 104 (ii) 5.1 × 5.2 (iii) 103 × 98 (iv) 9.7 × 9.8
Answer:
(i) 10712 (ii) 26.52 (iii) 10094 (iv) 95.06
Solution:
(i) (100 + 3) (100 + 4) = (100)
2
+ (3 + 4) × 100 + 3 × 4
= 10000 + 700 + 12 = 10712.
(ii) (5 + 0.1) (5 + 0.2) = 5
2
+ (0.1 + 0.2) × 5 + (0.1 × 0.2)
= 25 + 0.3 × 5 + 0.02 = 25 + 1.5 + 0.02 = 26.52.
(iii) (100 + 3) (100 – 2) = (100)
2
+ [3 + ( – 2)] × 100 + 3 × ( – 2)
= 10000 + 100 – 6 = 10094.
(iv) 9.7 × 9.8 = (10 – 0.3) (10 – 0.2)
= (10)
2
+ [( – 0.3) + ( – 0.2)] × 10 + ( – 0.3) × ( – 0.2)
= 100 – 5 + 0.06 = 95.06