Lesson: Data Handling
Exercise 5.1
Question 1
For which of these would you use a histogram to show the data?
(a) The number of letters for different areas in a postman’s bag.
(b) The height of competitors in an athletics meet.
(c) The number of cassettes produced by 5 companies.
(d) The number of passenger-boarding trains from 7: 00 a.m. to 7: 00 p.m. at a station.
Answer:
(b), (d). In all these cases data can be divided into class intervals
Solution:
Give reasons for each.
(a) Different areas X, Y, Z... have a certain number of letters.
These areas cannot be divided into class intervals.
Thus, it is better to represent the data by a bar graph than by a histogram.
(b) Height of competitors lie between certain ranges, hence, can be divided into
class intervals.
Therefore, we use a histogram to represent the data.
(c) There are names of five companies. So, there is no class-interval.
Thus, we can’t show the data by a histogram.
(d) Class-intervals like 7 a.m. – 9 a.m., 9 a.m. – 11 a.m. etc. are necessary to show
the number of passenger-boarding trains during these time intervals.
Thus, a histogram is a suitable representation of data.
Question 2
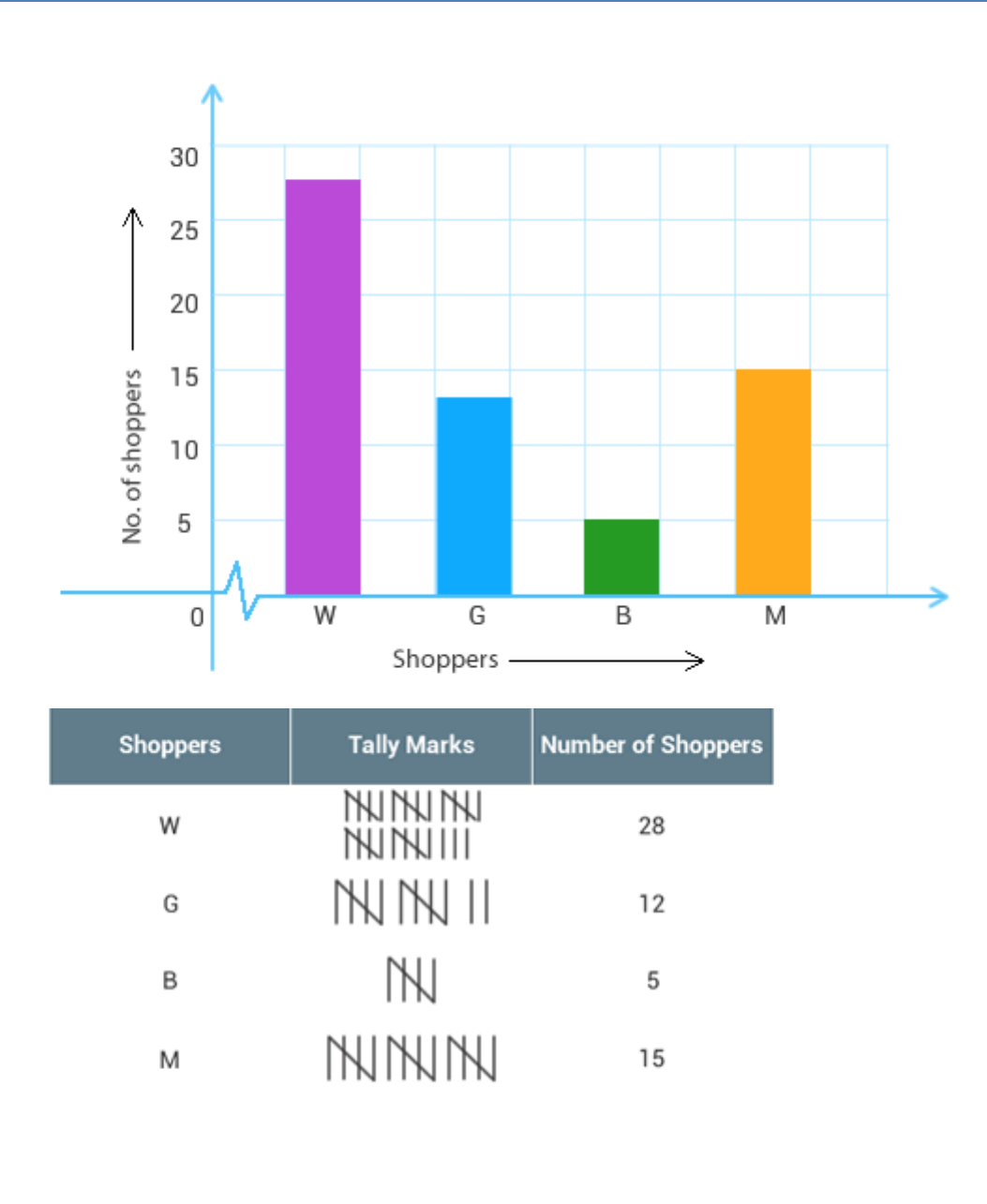
The shoppers who come to a departmental store are marked as: man (M), woman (W),
boy (B)
or girl (G).
The following list is of the shoppers who came during the first hour in the morning:
W WW G B W W M G G M M W WWW G B M W B G G M W W M M W WW
M W B WGM WWWW G W M M W W M W G W M G W M M B G G W
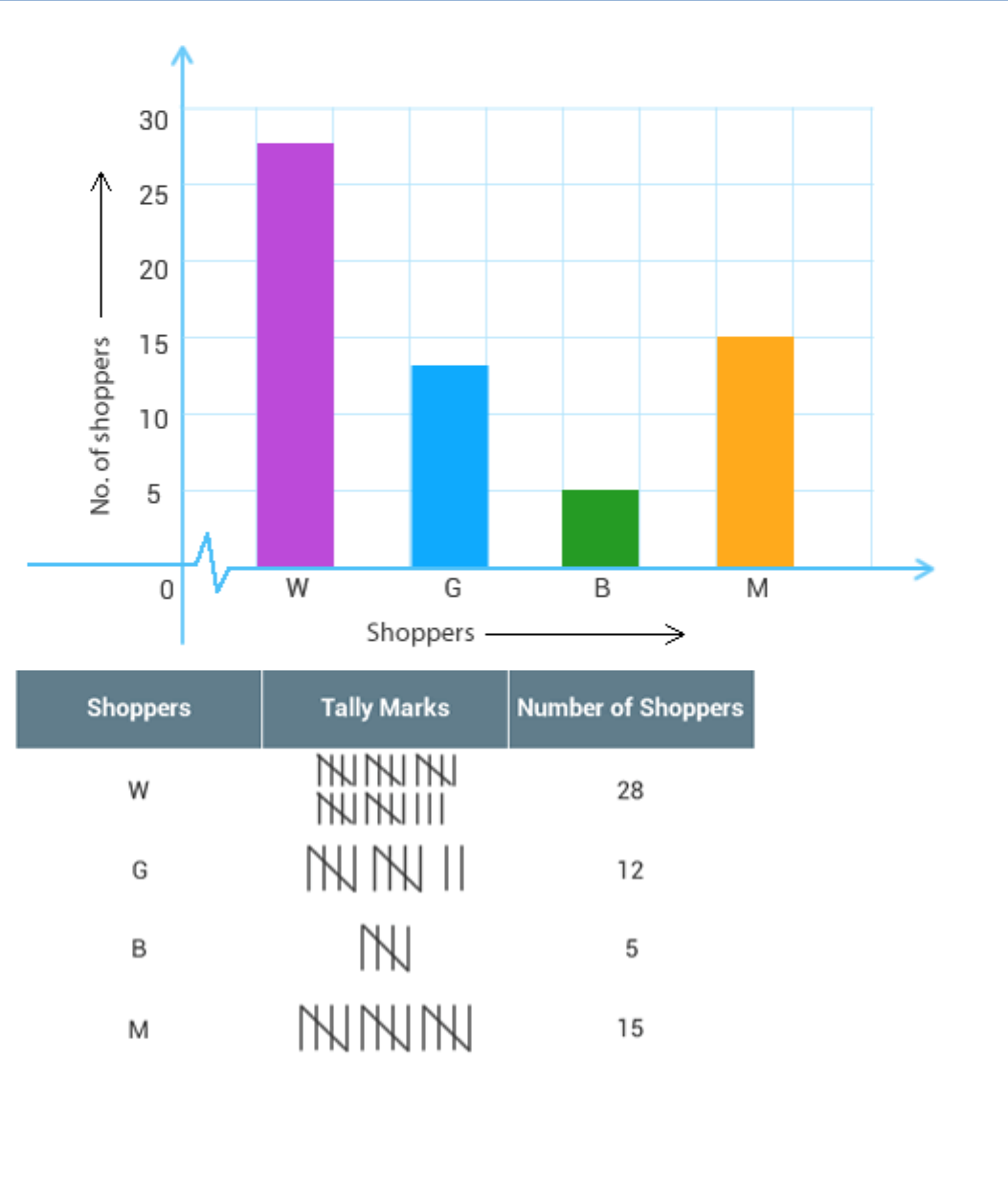
Make a frequency distribution table using tally marks. Draw a bar graph to illustrate it.
Answer:
Solution:
The required bar graph is shown below:

Question 3
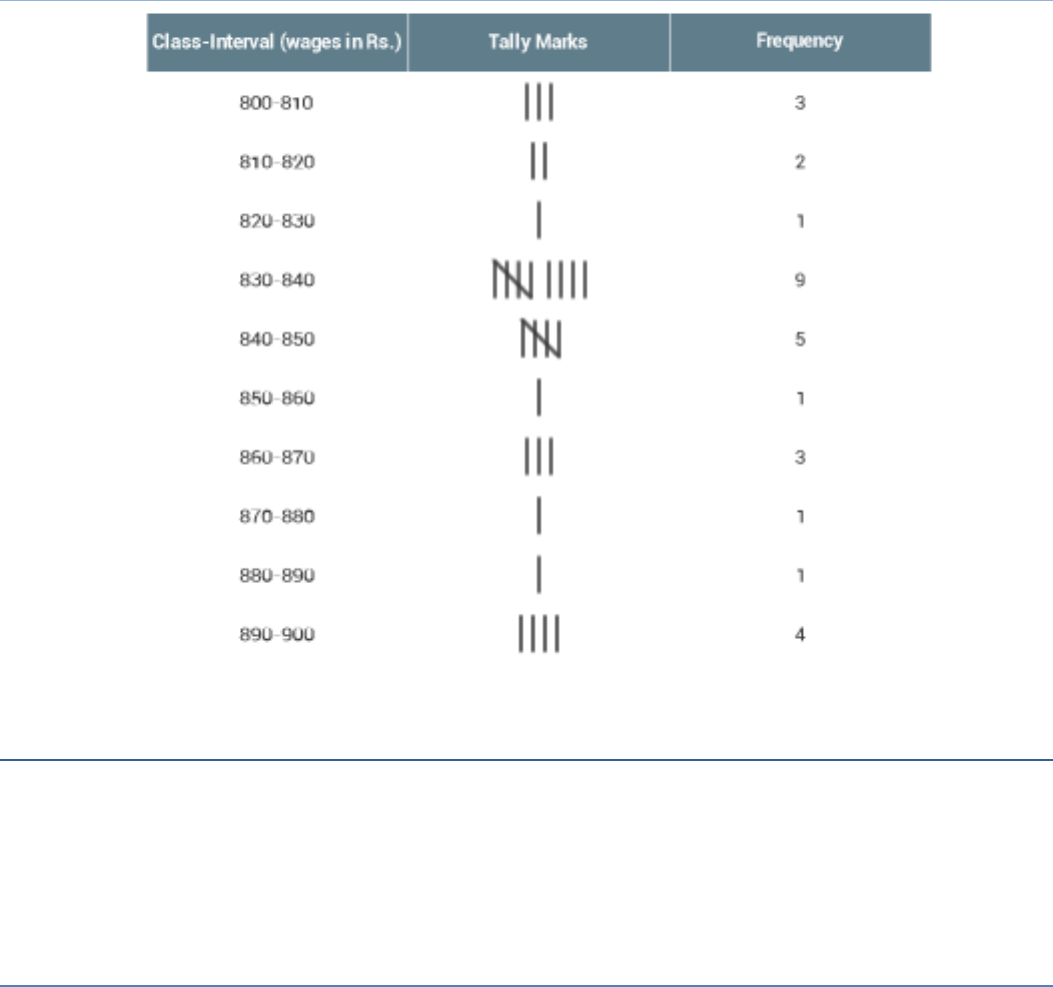
The weekly wages (in Rs.) of 30 workers in a factory are:
830, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860, 832, 833, 855, 845,
804, 808, 812, 840, 885, 835, 835, 836, 878, 840, 868, 890, 806, 840.
Using tally marks make a frequency table with intervals as 800 – 810, 810 – 820 and
so on.
Answer:
Solution:
Question 4
Draw a histogram for the frequency table made for the data in Q.3, and answer
the following questions:
(i) Which group has the maximum number of workers?
(ii) How many workers earn Rs. 850 and more?
(iii) How many workers earn less than Rs. 850?
Answer:
(i) 830-840 (ii) 10 (iii) 20
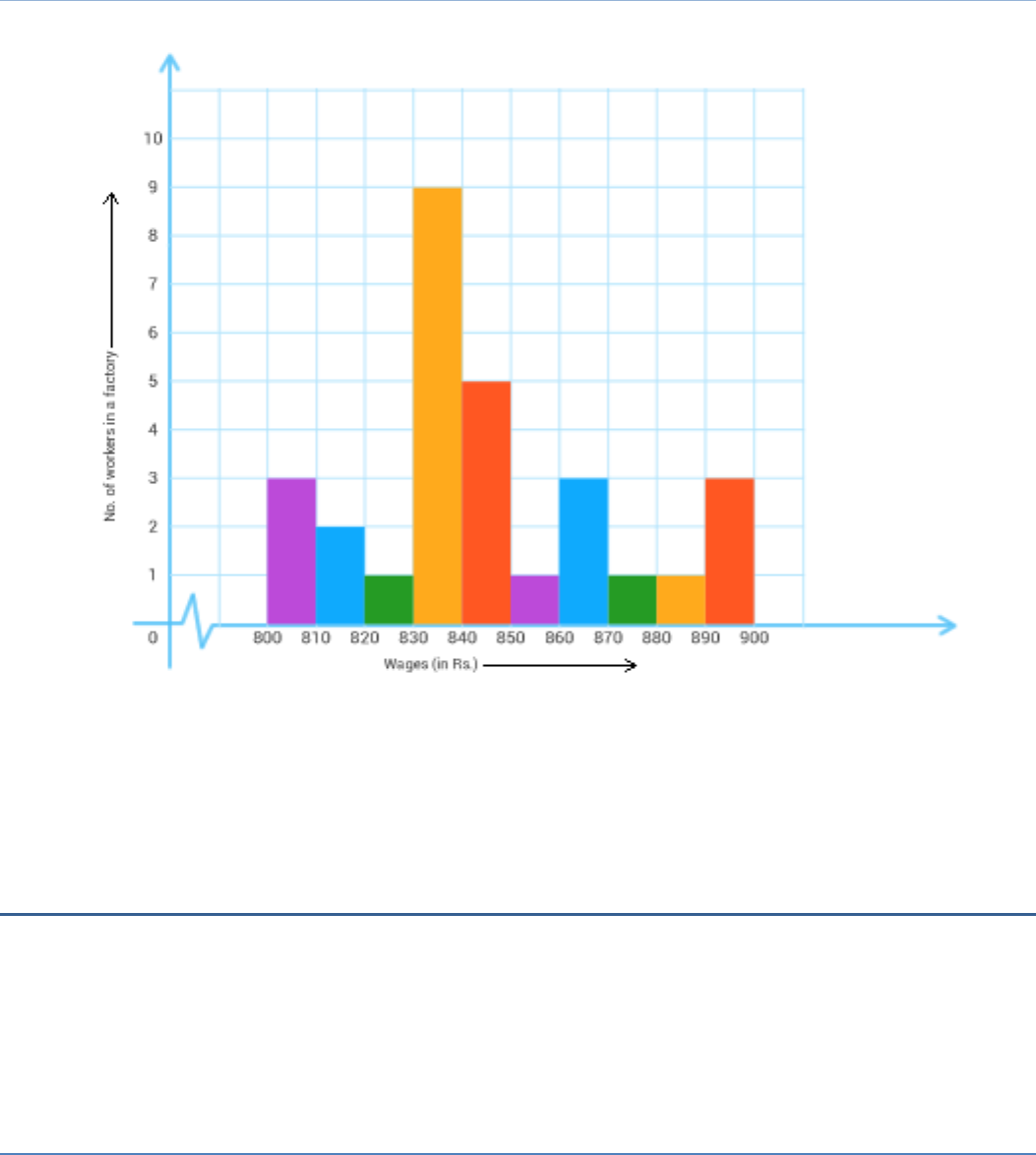
Solution:
The required histogram is given below:
(i) Group 830 – 840 has maximum number of workers.
(ii) No. of workers whose earning is Rs. 850 and more = 1 + 3 + 1 + 1 + 4 = 10.
(iii) No.of workers whose earning is less than 850 = 3 + 2 + 1 + 9 + 5 = 20.
Question 5
The number of hours for which students of a particular class watched television
during holidays is shown through the given graph.
Answer the following:
(i) For how many hours did the maximum number of students watch TV?
(ii) How many students watched TV for less than 4 hours?
(iii) How many students spent more than 5 hours, watching TV?
Answer:
(i) 4-5 hours (ii) 34 (iii) 14
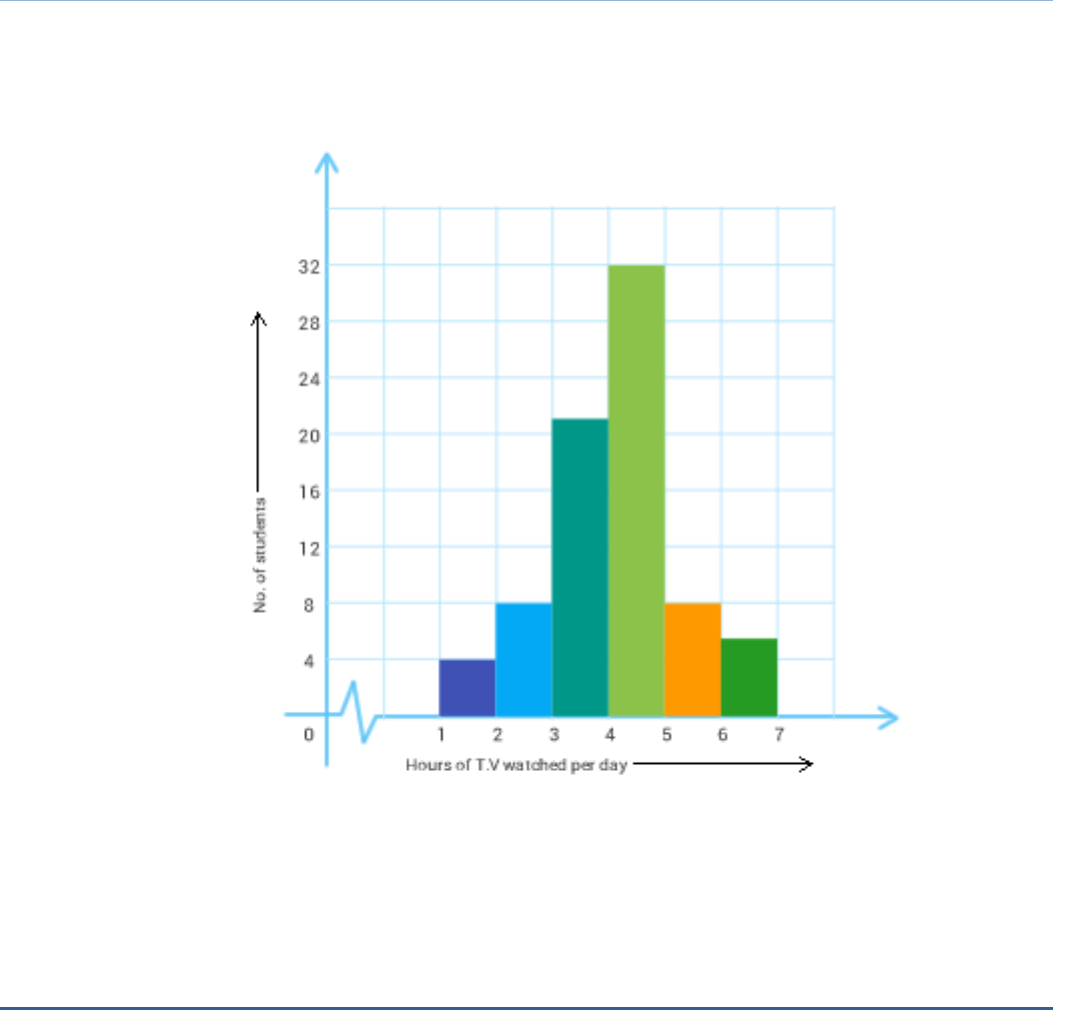
Solution:
(i) Maximum number of students watched TV for (4 – 5) hours.
(ii) No. of students watched TV for less than 4 hours = 4 + 8 + 22 = 34.
(iii) No. of students who spent more than 5 hours, watching TV = 8 + 6 = 14.
Excercise 5.2
Question 1
A survey was made to find the type of music that a certain group of young people
liked in a city.
Adjoining pie chart shows the finding of this survey.
From this pie chart answer the following:
(i) If 20 people liked classical music, how many young people were surveyed?
(ii) Which type of music is liked by the maximum number of people?
(iii) If a cassette company were to make 1000 CDs, how many of each type
would they make?
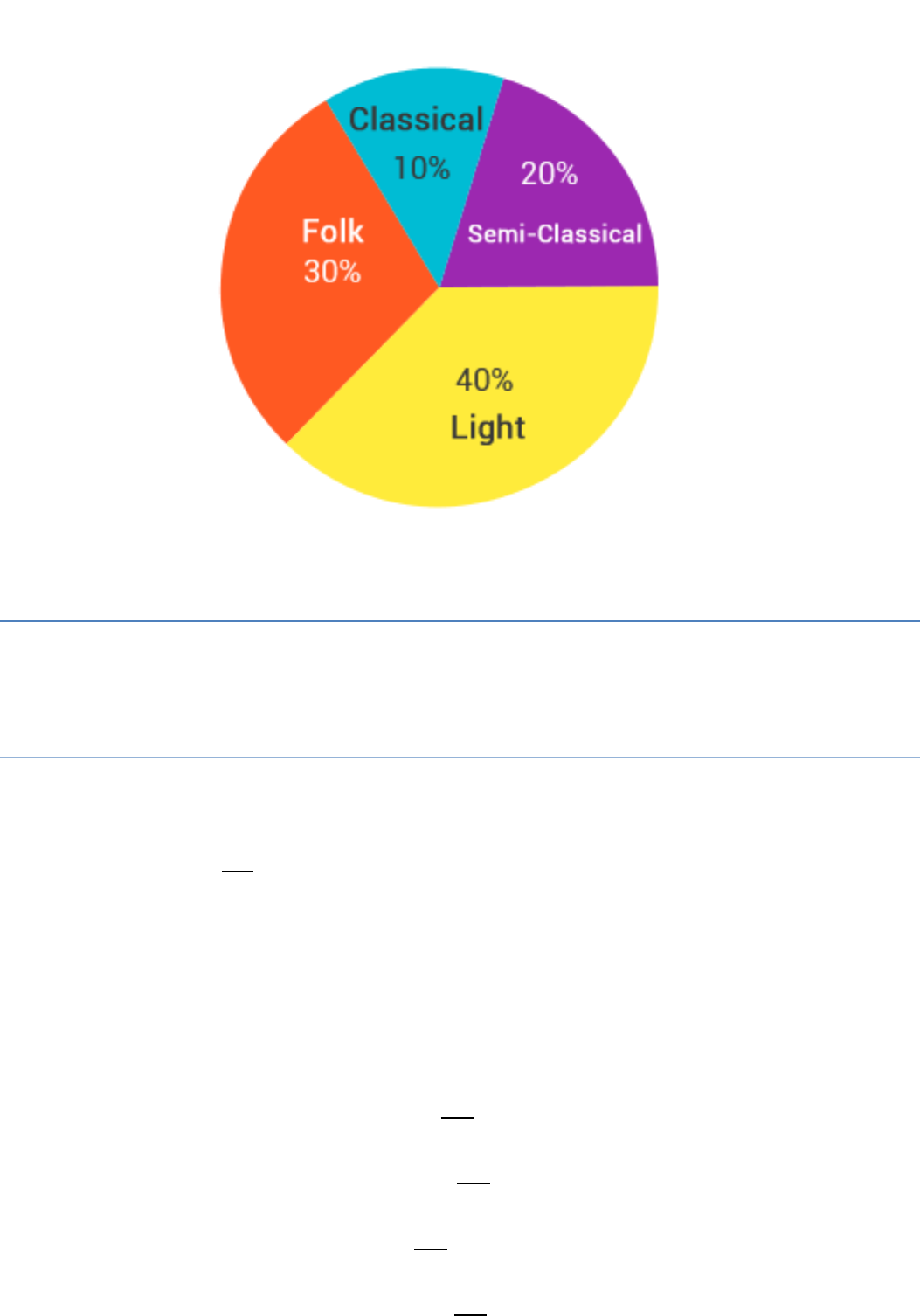
Answer:
(i) 200
(ii) Light music
(iii) Classical - 100, Semi classical - 200, Light - 400, Folk – 300
Solution:
(i) Let no. of young people be x. No. of people who liked classical music = 20.
Percentage of people who liked classical music = 10%
10% of x = 20
10
20
100
x
200x
The no. of young people who were surveyed = 200.
(ii) Light music
(iii) No. of semi classical CDs = 20% of 1000 =
20
100
× 1000 = 200
No. of classical music CDs = 10 % of 1000 =
10
100
× 1000 = 100
No. of folk music CDs = 30% of 1000 =
30
100
× 1000 = 300
No. of light music CDs = 40 % of 1000 =
40
100
× 1000 = 400.
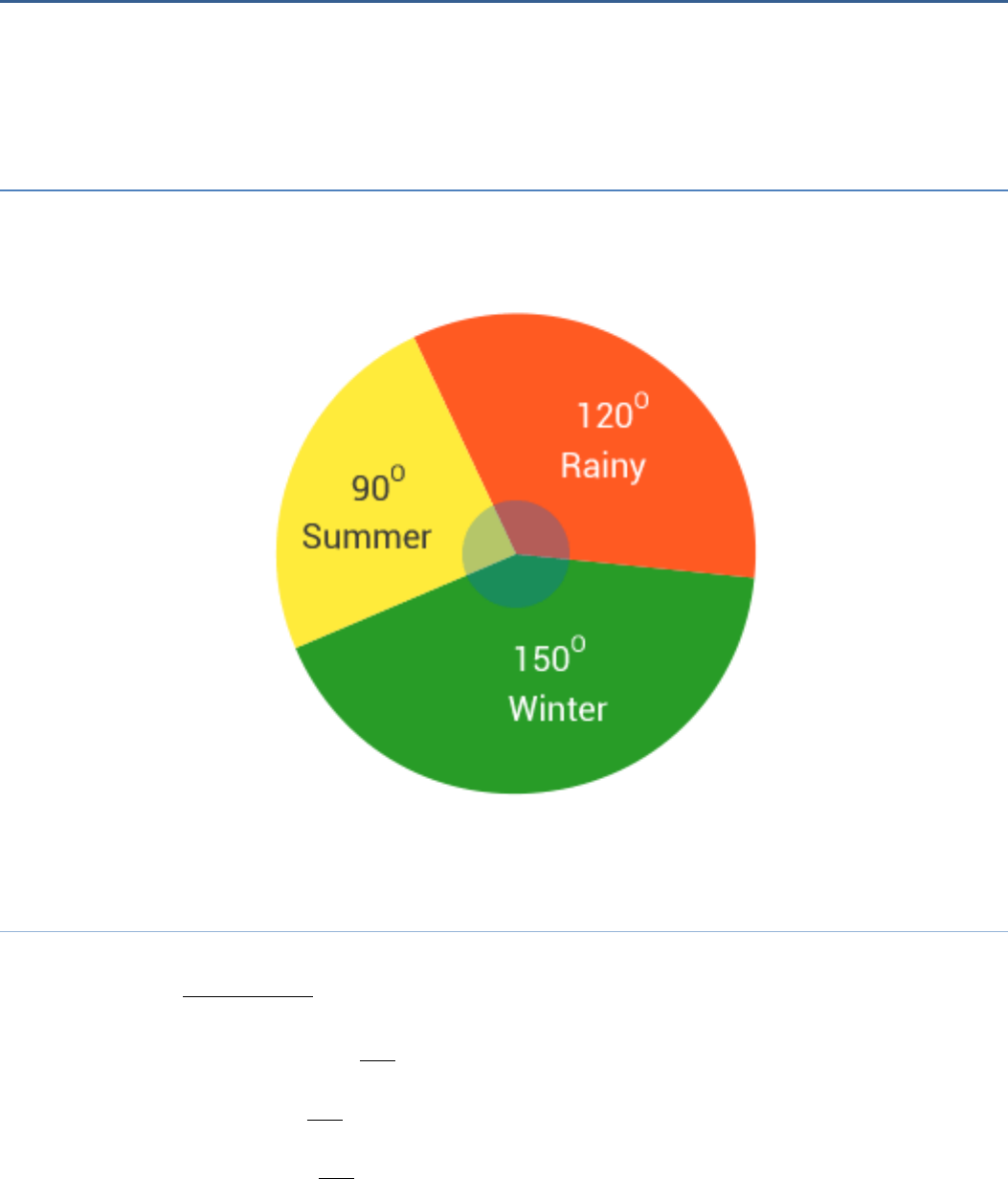
Question 2
A group of 360 people were asked to vote for their favourite season from the three
seasons rainy, winter and summer.
(i) Which season got the most votes?
(ii) Find the central angle of each sector.
(iii) Draw a pie chart to show this information.
Answer:
(i)Winter (ii) Winter - 150°, Rainy - 120°, Summer - 90° (iii)
Solution:
(i) Winter.
(ii)Central angle =
Value of item
Total value
× 360°
Central angle for summer season =
90
360
× 360° = 90°
Central angle for rainy season =
120
360
× 360° = 120° and
Central angle for winter season =
150
360
× 360° =150°
(iii)The required pie chart is shown:
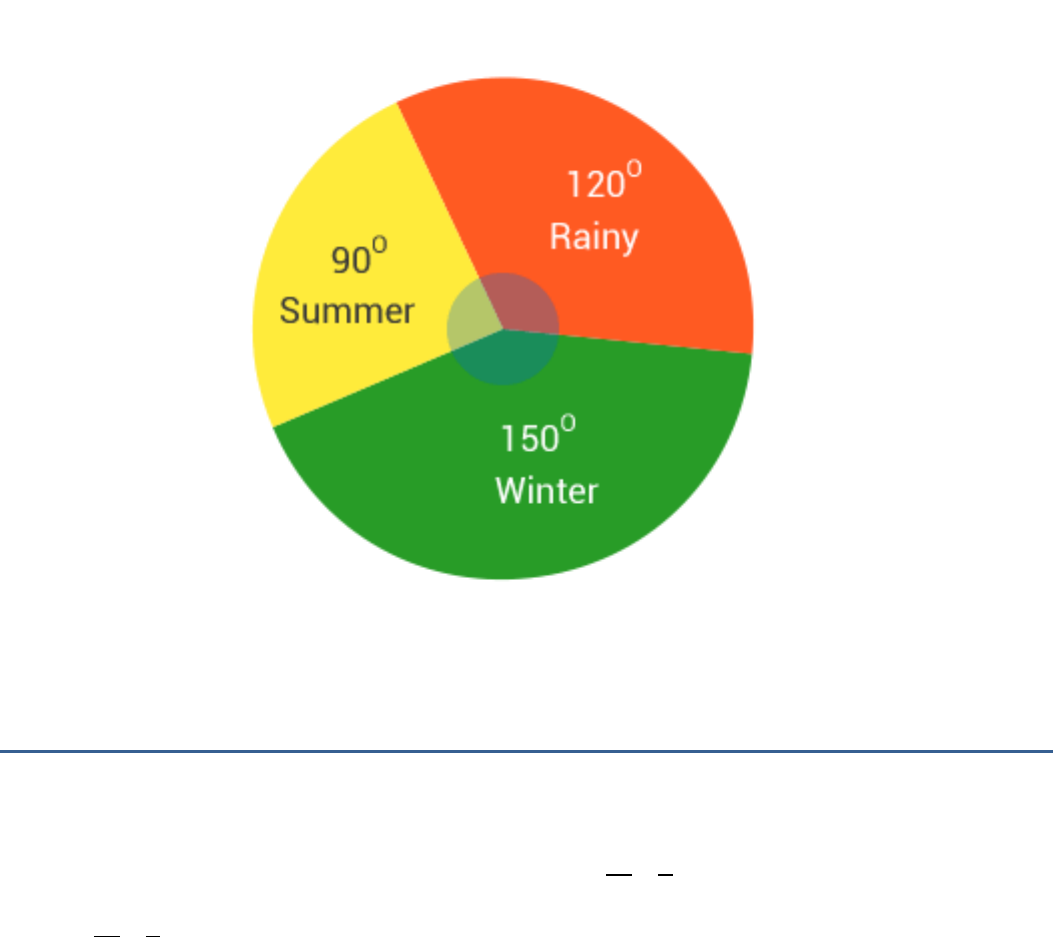
Question 3
Draw a pie chart showing the following information.
The table shows the colours preferred by a group of people.
Hint: Find the proportion of each sector. For example, Blue is
18 1
36 2
Green is
91
36 4
and so on.
Use this to find the corresponding angles
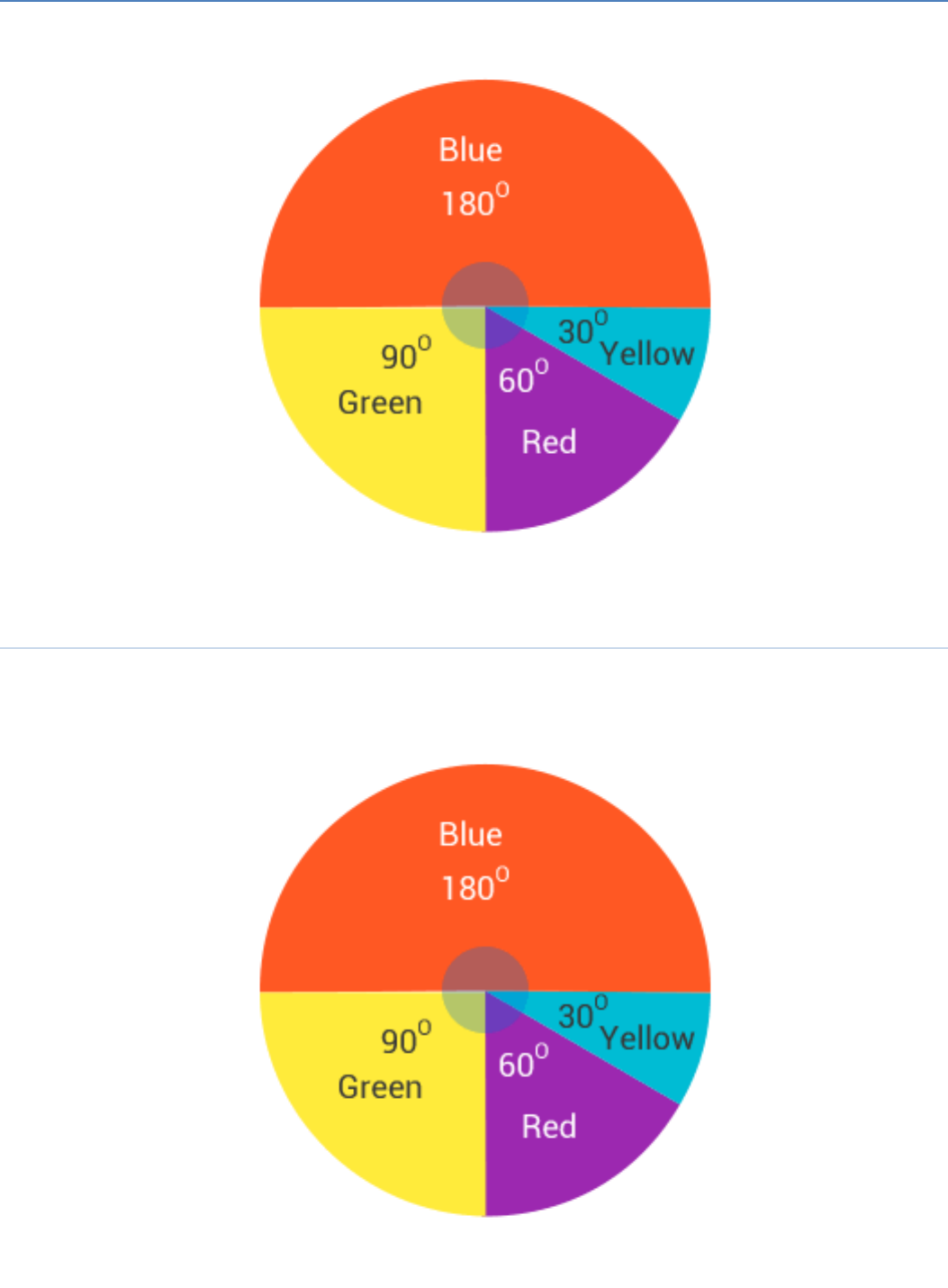
Answer:
Solution:
Now, we make the pie chart as shown below using protractor, compasses and ruler.
Question 4
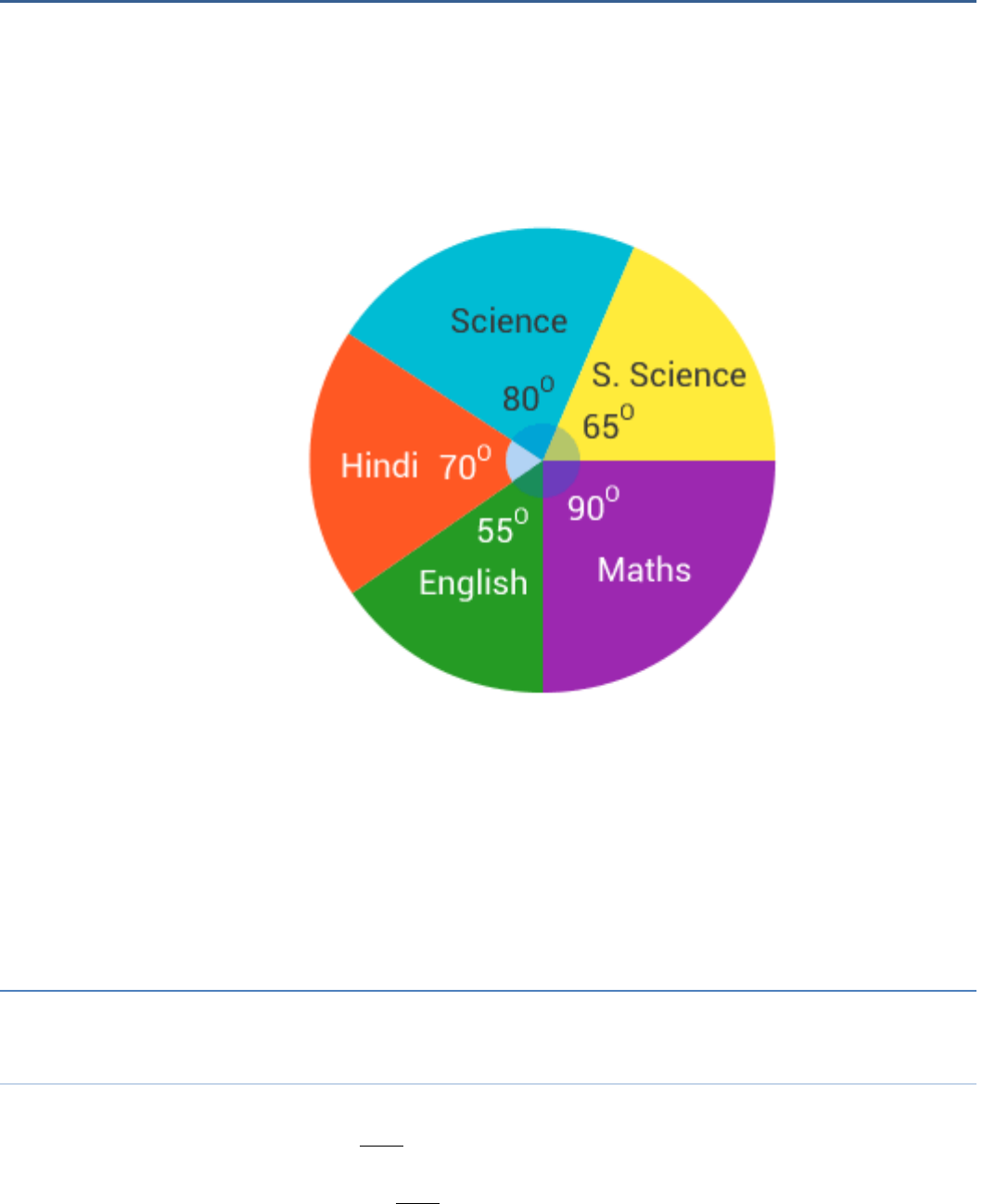
The given pie chart gives the marks scored in an examination by a student in
Hindi, English, Mathematics, Social Science and Science.
If the total marks obtained by the students were 540, answer the following questions:
(i) In which subject did the student score 105 marks?
(ii) How many more marks were obtained by the student in Mathematics than in Hindi?
(iii) Examine whether the sum of the marks obtained in Social Science and
Mathematics is more than that in Science and Hindi.
Answer:
(i) Hindi (ii) 30 marks (iii) Yes
Solution:
(i)
For 540 marks, the central angle = 360°
For 1 mark, the central angle =
360
540
For 105 marks, the central angle =
360
540
× 105 = 70°
Thus, it is obvious, from the pie chart that the student scored 105 marks in
Hindi, as central angle for Hindi is 70°.

(ii) For 360°, marks obtained = 540
For 1°, marks obtained =
540
360
For 90°, marks obtained =
540
360
× 90 = 135
i.e., Marks obtained in Mathematics = 135
and Marks obtained in Hindi = 105 [From part (i)]
Difference in marks = 135 – 105 = 30.
(iii) Marks obtained in Social Science
=
Total marks
Total central angle
× Central angle of an item =
540
360
× 65 = 97.5
And Marks obtained in Science =
540
360
× 80 = 120.
Marks obtained in social Science and Mathematics = 97.5 + 135 = 232.5
Marks obtained in Science and Hindi = 120 + 105 = 225
So, sum of the marks obtained in Social Science and Mathematics is more than
in Science and Hindi.
Question 5
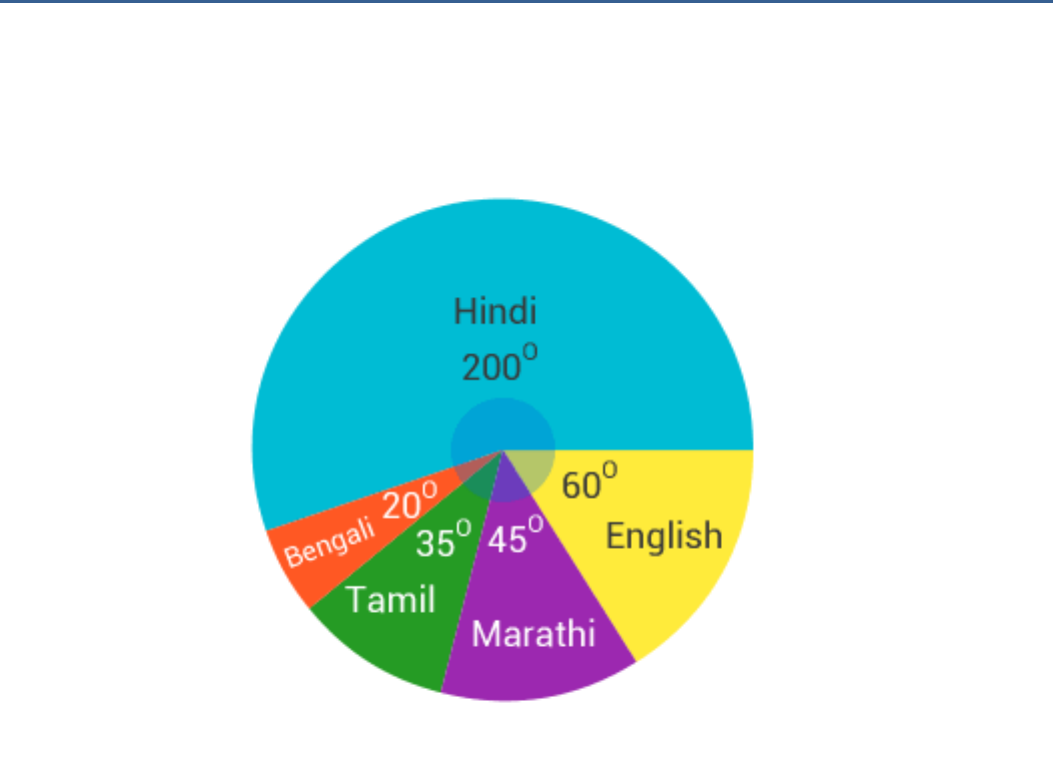
The number of students in a hostel, speaking different languages is given below;
Display the data in a pie chart.
Answer:
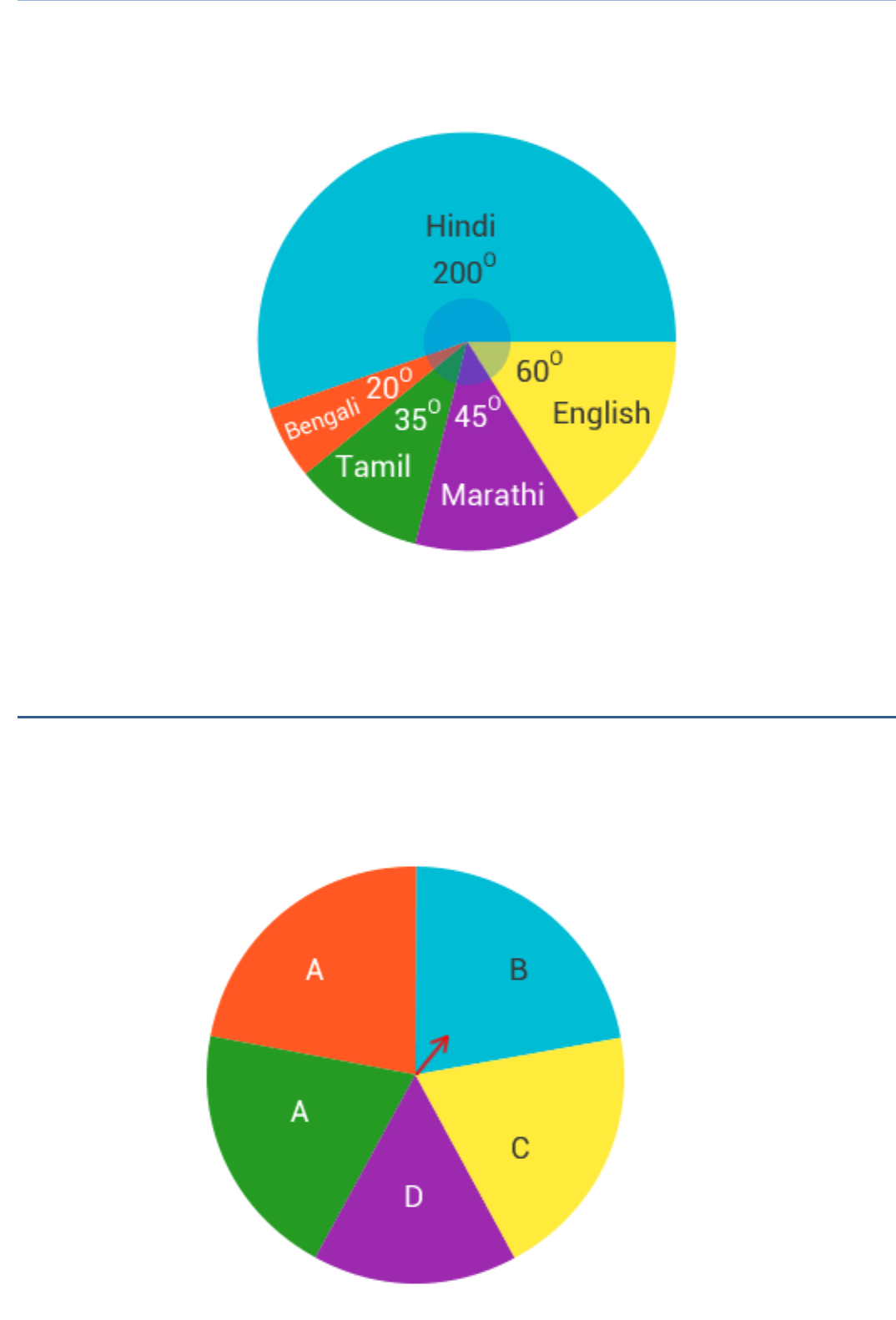
Solution:
The required pie chart is shown below:
Exercise 5.3
Question 1
List the outcomes you can see in these experiments.
a) Spinning a wheel
b) Tossing two coins together
Answer:
(a) Outcomes
A, B, C, D (b) HH, HT, TT, TH (Here HT means Head on first coin
and Tail on the second coin and so on).
Solution:
a) Outcomes you can see in spinning a wheel are A, B, C, D
b) Outcomes you can see when tossing two coins together are (HH), (HT), (TT)
and (TH).
Question 2
When a die is thrown, list the outcomes of an event of getting
(i) (a) a prime number (b) not a prime number
(ii) (a) a number greater than 5 (b) a number not greater than 5.
Answer:
Outcomes of an event of getting
(i)
(a) 2, 3, 5
(b) 1, 4, 6
(ii)
(a) 6
(b) 1, 2, 3, 4, 5
Solution:
(i) (a) A prime number 2, 3, 5
(b) Not a prime number 1, 4, 6
(ii) (a) A number greater than 5 is 6.
(b) A number not greater than 5 are 1, 2, 3, 4 and 5.
Question 3

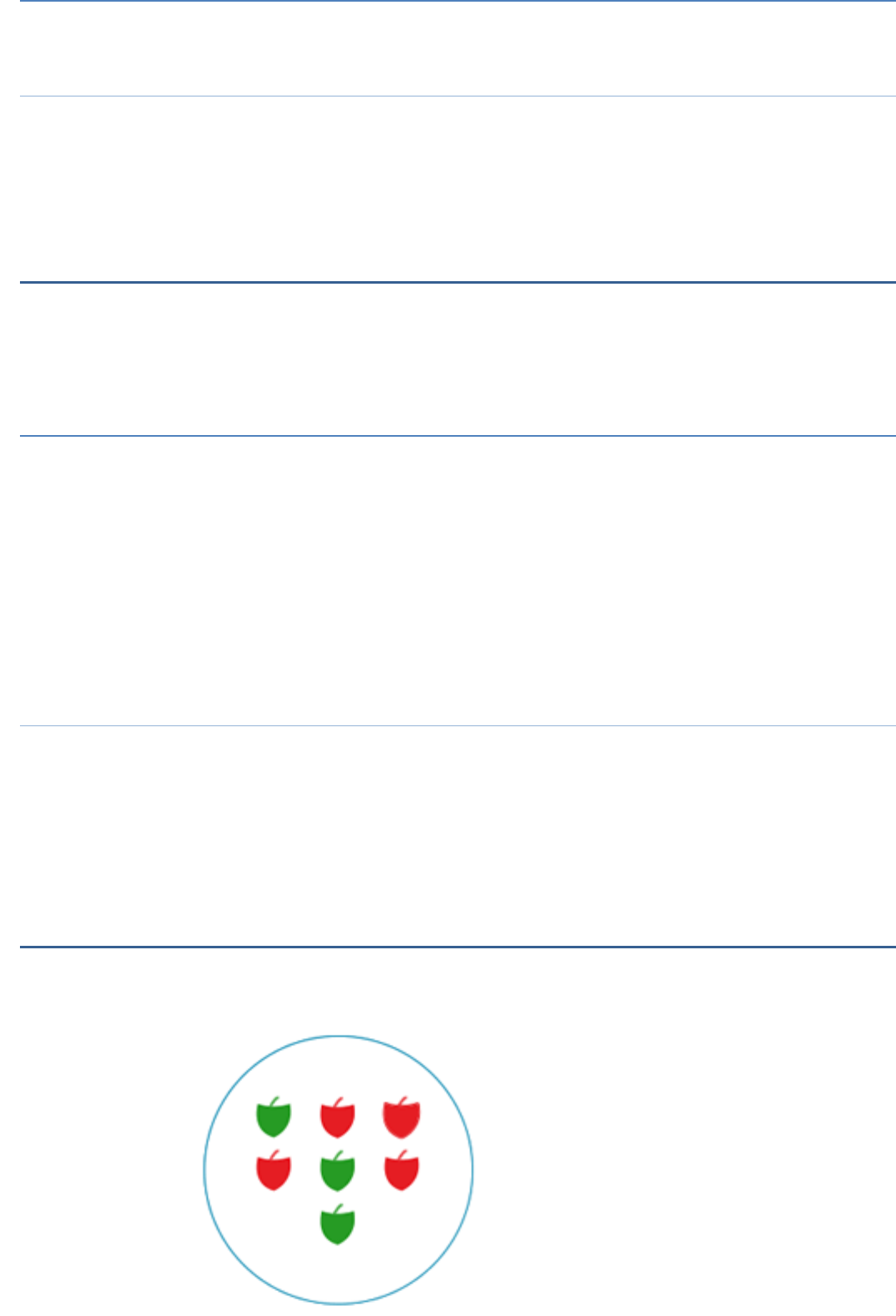
Find the
(a) Probability of the pointer stopping on D in above question (a)?
(b) Probability of getting an ace from a well shuffled
deck of 52 playing cards?
(c) Probability of getting a red apple.
(See figure)
Answer:
1 1 4
(a) (b) (c)
5 13 7
Solution:
(a) Number of possible outcomes for pointer stopping on D = 1.
Total number of outcomes of the experiment = 5.
P (the pointer stopping on D) =
1
5
(b) Total no. of aces = 4
Total no. of outcomes = 52
P (an ace) =
41
52 13
(c) No. of red apples = 4
Total no. of outcomes (apples) = 7
P (getting a red apple) =
4
7
Question 4
Numbers of 1 to 10 are written on ten separate slips (one number on one slip), kept
in a box and mixed well. One slip is chosen from the box without looking into it.
What is the probability of
(i) Getting a number 6? (ii) Getting a number less than 6?
(iii) Getting a number greater than 6? (iv) Getting a 1-digit number?
Answer:
1 1 2 9
(i) (ii) (iii) (iv)
10 2 5 10
Solution:
(i) No. of slip with number 6 written on it = 1
Total no. of outcomes (Slips) = 10
P (getting a Number 6) =
1
10

(ii) Nos. less than 6 are 1, 2, 3, 4, 5, therefore the no. of numbers less than 6 = 5
Total no. of slips (outcomes) = 10
P (getting a no. less than 6) =
51
10 2
(iii) Nos. greater than 6 are 7, 8, 9, 10, therefore the no. of numbers less than 6 = 4
P (getting a no. greater than 6) =
42
10 5
(iv) One digit numbers, are 1, 2, 3, 4, 5, 6, 7, 8 and 9 therefore the no. of one
digit numbers = 9.
Total no. of outcomes = 10
P (1 digit no.) =
9
10
Question 5
If you have a spinning wheel, with 3 green sectors, 1 blue sector and 1 red sector,
What is the probability of getting a green sector?
What is the probability of getting a non-blue sector?
Answer:
Probability of getting a green sector =
3
5
; probability of getting a non-blue sector
=
4
5
Solution:
Total no. of outcomes (sectors) of the experiment = 3 + 1 + 1 = 5
No. of green sectors = 3; No. of non-blue sectors = 3 green + 1 red = 4
P (getting a green sector) =
3
5
and P (getting a non-blue sector) =
4
5
.
Question 6
Find the probability of the following events, when a die is thrown,
(i) (a) a prime number (b) Not a prime number
(ii) (a) a number greater than 5 (b) A number not greater than 5.
Answer:
Probability of getting a prime number =
1
2
; probability of getting which is not
prime =
1
2

Probability of getting a number greater than 5 =
1
6
Probability of getting a number not greater than 5 =
5
6
Solution:
(i) (a) P (a prime number) =
31
62
(b) P (not a prime number) =
31
62
(ii) (a) P (a number greater than 5) =
1
6
(b) P (a number not greater than 5) =
5
6