Lesson: Practical Geometry

Exercise 4.1

Question 1

Construct the following quadrilaterals:

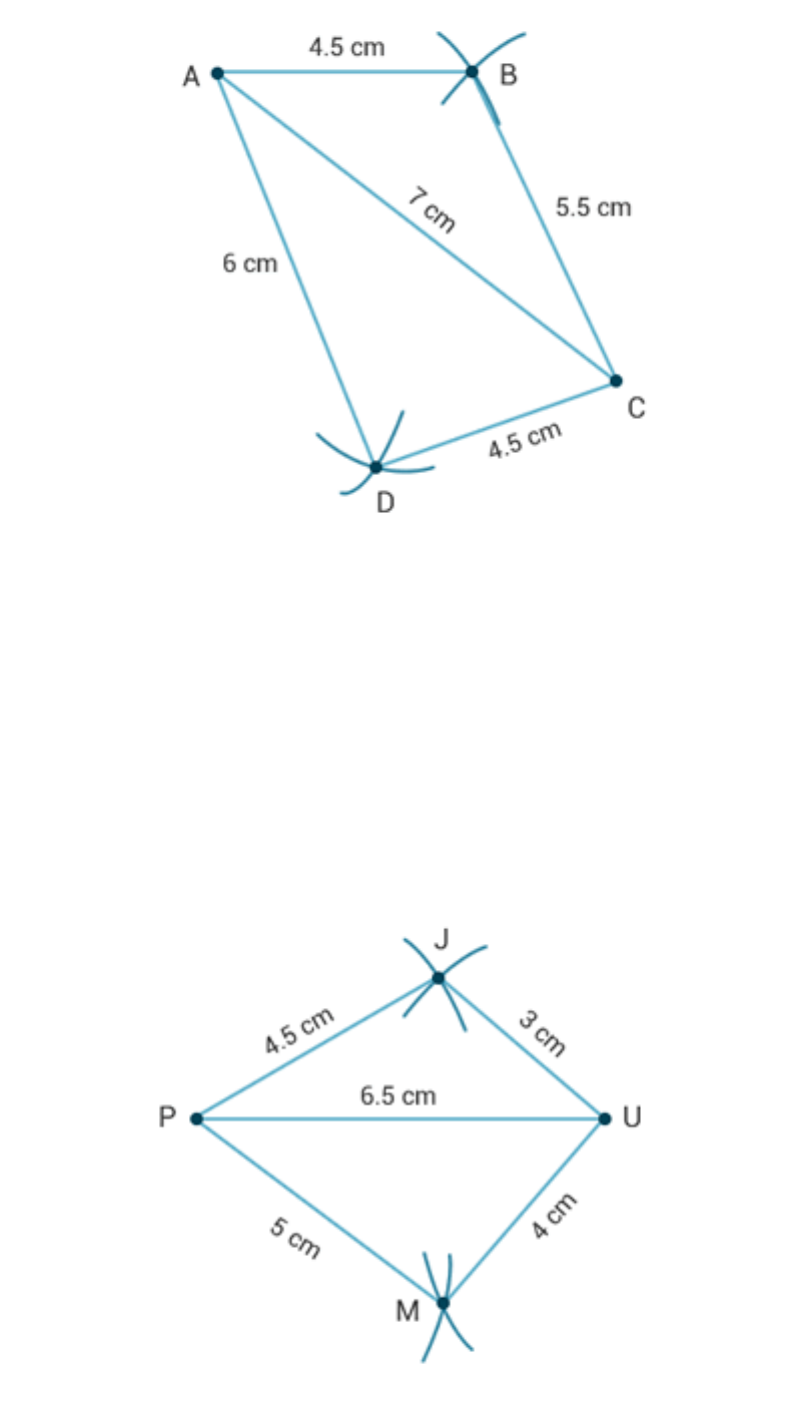
(i) Quadrilateral ABCD:

AB = 4.5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm, AC = 7 cm.

(ii) Quadrilateral JUMP

JU = 3.5 cm, UM = 4 cm, MP = 5 cm, PJ = 4.5 cm, PU = 6.5 cm.

(iii) Parallelogram MORE

OR = 6 cm, RE = 4.5 cm, EO = 7.5 cm.

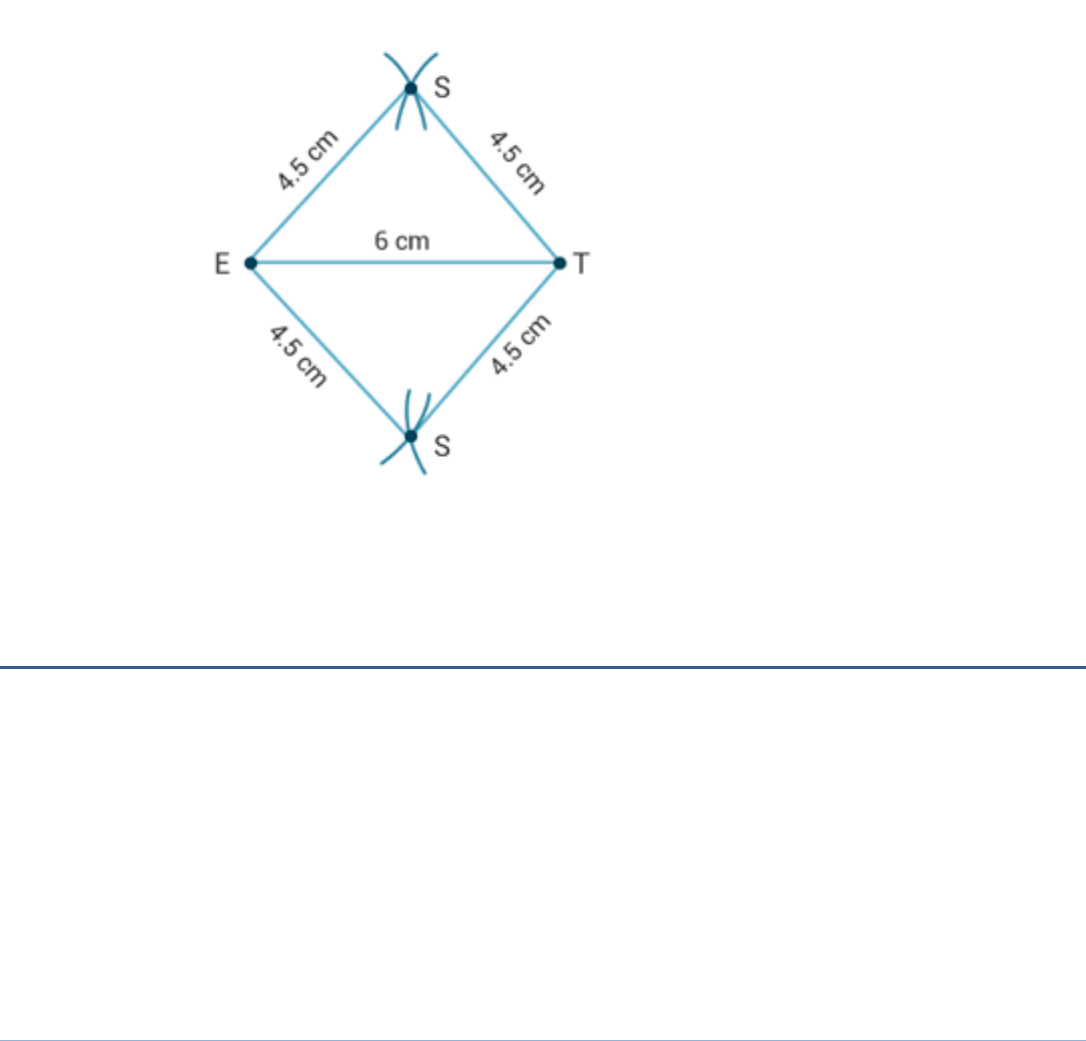
(iv) Rhombus BEST:

BE = 4.5 cm, ET = 6 cm.

Solution:

(i) Steps of construction:

1. Draw a line segment AC = 7 cm.

2. Draw an arc of radius AB = 4.5 cm taking A as centre.

3. Draw another arc of radius 5.5 cm taking C as centre on the same side of

AC in which the earlier arc was drawn.

4. Let these two arcs intersect at B.

5. Join AB and CB to obtain ABC.

6. Similarly, draw ADC on the other side of AC taking = 6 cm and DC = 4

cm.

7. ABCD is the required quadrilateral.

(ii) Steps of construction:

1. Draw a line segment PU = 6.5 cm.

2. Taking P as centre draw an arc of radius 4.5 cm.

3. Taking U as centre draw another arc of radius 3.5 cm on the same side of

PU in which the earlier arc was drawn.

4. Let these two arcs intersect at J.

5. Join PJ and UJ.

6. Similarly, obtain the point M on the opposite side of diagonal PU, where

PM= 5 cm and MU = 4 cm.

7. JUMP is the required quadrilateral.

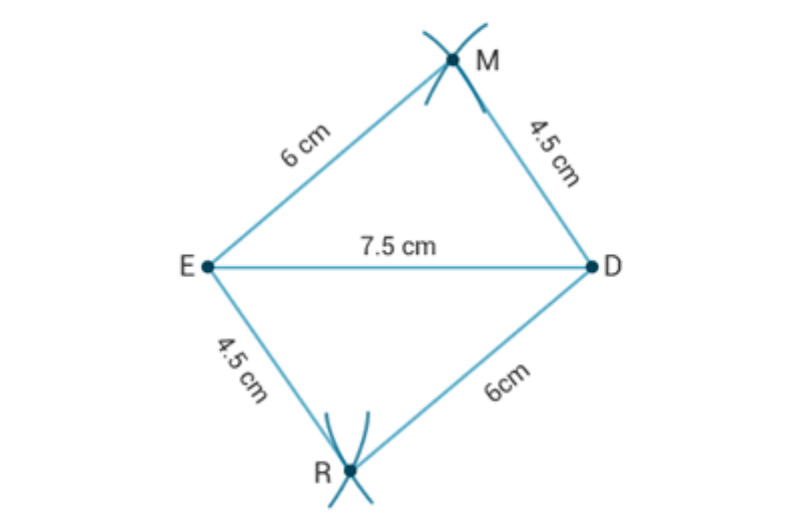
(iii) Steps of construction:

1. Draw a line segment EO = 7.5 cm.

2. Taking E as centre draw an arc of radius 6 cm.

3. Taking O as centre draw another arc of radius 4.5 cm

on the same side of EO in which the earlier arc was drawn.

4. Let the point of intersection of these two arcs be M.

5. Join EM and MO.

6. We get the EMO.

7. Similarly, obtain EOR with arc lengths ER = 4.5 cm and OR = 6 cm

on the other side of EO.

8. MORE is the required parallelogram.

(iv) Steps of construction:

1. Draw ET = 6 cm.

2. Draw two arcs of radius 4.5 cm taking E and T as centre on the same side

of ET.

3. Let these two arcs meet at B. Join EB and TB.

4. Similarly, on the opposite side of ET draw triangle EST by taking

ES = TS = 4.5 cm.

5. BEST is the required rhombus.

Exercise 4.2

Question 1

Construct the following quadrilaterals:

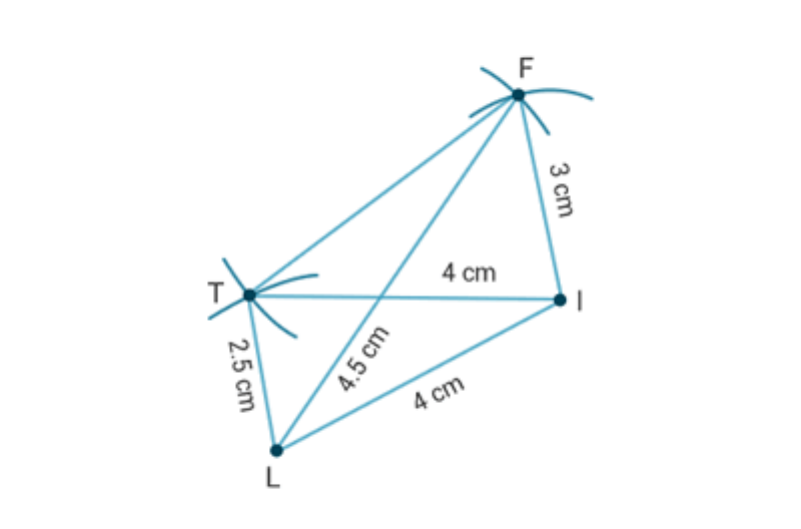
(i) Quadrilateral LIFT

LI = 4 cm, IF = 3 cm, TL = 2.5 cm, LF = 4.5 cm, IT = 4 cm,

(ii) Quadrilateral GOLD

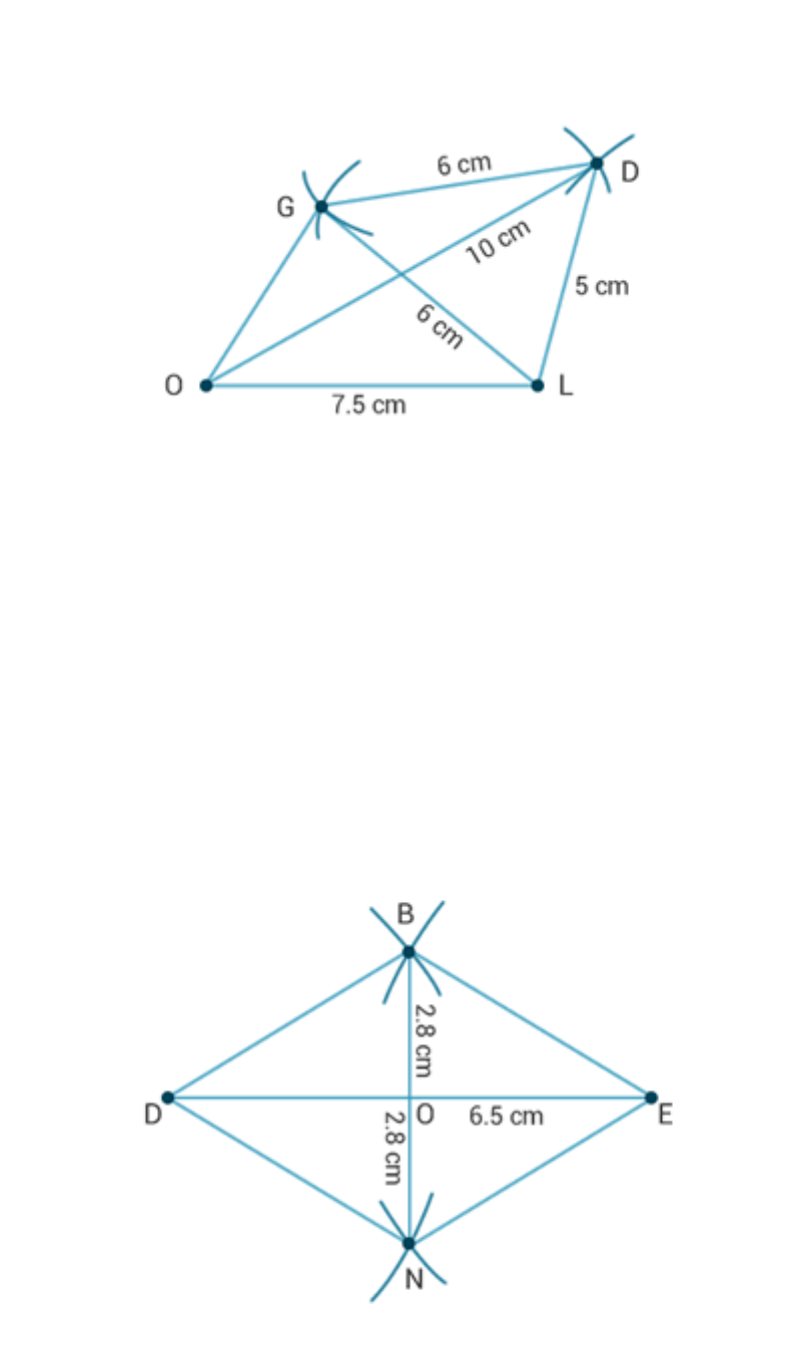
OL = 7.5 cm, GL = 6 cm, GD = 6 cm, LD = 5 cm, OD = 10 cm

(iii) Rhombus BEND

BN = 5.6 cm, DE = 6.5 cm

Solution:

(i) Steps of construction:

1. Draw a line segment LI = 4 cm.

2. With L and I as centers and radii of 2.5 cm and 4 cm

respectively draw two arcs intersecting at T.

3. Join TL and TI.

4. Again with L and I as centers and radii of 4.5 cm and

3cm respectively draw two arcs intersecting at F.

5. Join FL, TF and FI.

6. LIFT is the required quadrilateral.

(ii) Steps of construction:

1. Draw a line segment OL = 7.5 cm.

2. With O and L as centers and radii 10 cm and 5 cm

respectively draw two arcs intersecting at D.

3. Join OD and LD.

4. Again with L and D as centers and radii 6 cm, draw

two arcs intersecting each other at G.

5. Join GD, GO and LG.

6. GOLD is the required quadrilateral.

(iii) Steps of construction:

1. Draw a line segment DE = 6.5 cm.

2. Draw perpendicular bisector XY of DE which

Intersects DE at O.

3. Taking O as centre draw two arcs of radii 2.8 cm on

opposite sides of DE, which intersects XY at B and N

as shown in figure.

4. Join BD, BE, EN and DN.

5. BEND is the required rhombus.

Exercise 4.3

Question 1

Construct the following quadrilaterals:

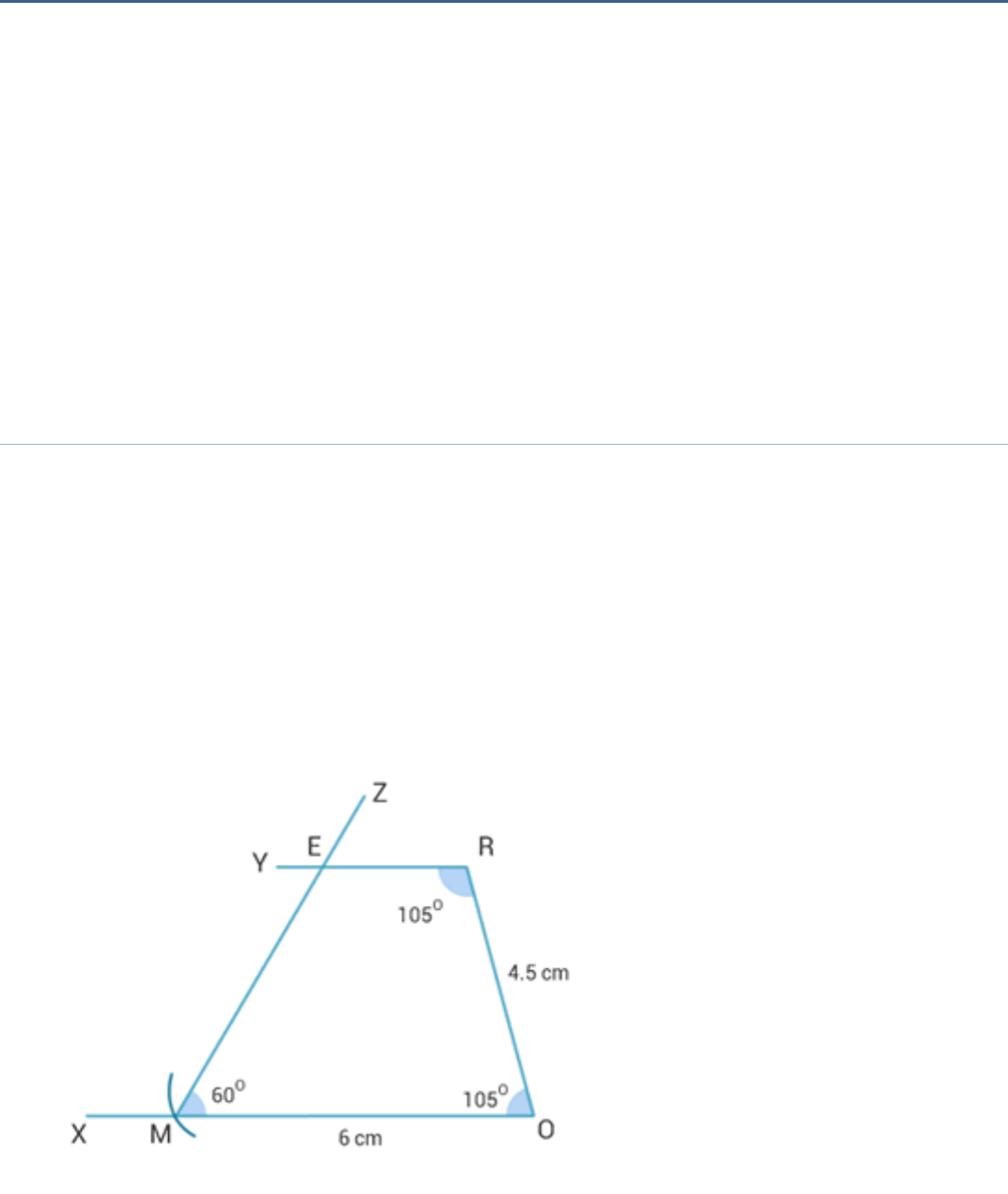
(i) Quadrilateral MORE

MO = 6 cm, OR = 4.5 cm,  M = 60

,  O = 105°,  R = 105°,

(ii) Quadrilateral PLAN

PL = 4 cm, LA = 6.5 cm,P = 90°,  A = 110°,  N = 85°

(iii) Parallelogram HEAR

HE = 5 cm, EA = 6 cm,  R = 85°

(iv) Rectangle OKAY

OK = 7 cm, KA = 5 cm

Solution:

(i) Steps of construction:

1. Draw a line segment MO = 6 cm.

2. At O, draw an  XOR = 105° .

3. From ray OX, cut OM = 6 cm.

4. At R, draw an  ORY = 105° .

5. At M, draw  OMZ = 60°, the rays RY and MZ

intersect each other at E.

6. MORE is the required quadrilateral.

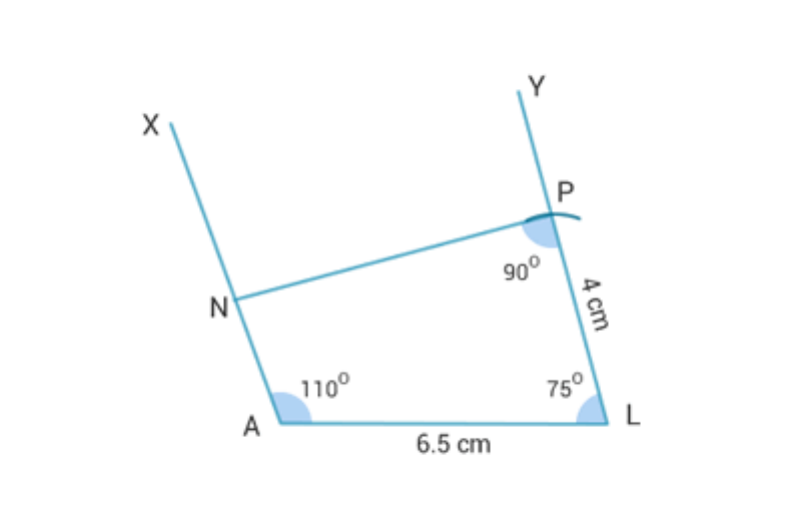
(ii) Steps of construction:

1. Draw a line segment AL = 6.5 cm.

2. At A, draw an  XAL = 110°.

3. At L, draw an angle YLA = 75°.

4. Taking L as centre draw an arc of radius 4 cm, which

will intersects LY at P.

5. At P draw angle LPN = 90°. Ray AX and arm PN of

angle LPN intersect at N.

6.  PNA = 85°, because remaining three angles add up

to 275°.

7. PLAN is the required quadrilateral.

(iii) Steps of construction:

1. Draw a line segment HE = 5 cm.

2. At E, draw  HEX= 85° and cut off EA = 6 cm from

EX.

3. Here H = 180° – 85° = 95°.

4. Now draw  EHY = 95° and cut off HR=6 cm from HY.

5. Join HR and RA.

6. HEAR is the required parallelogram.

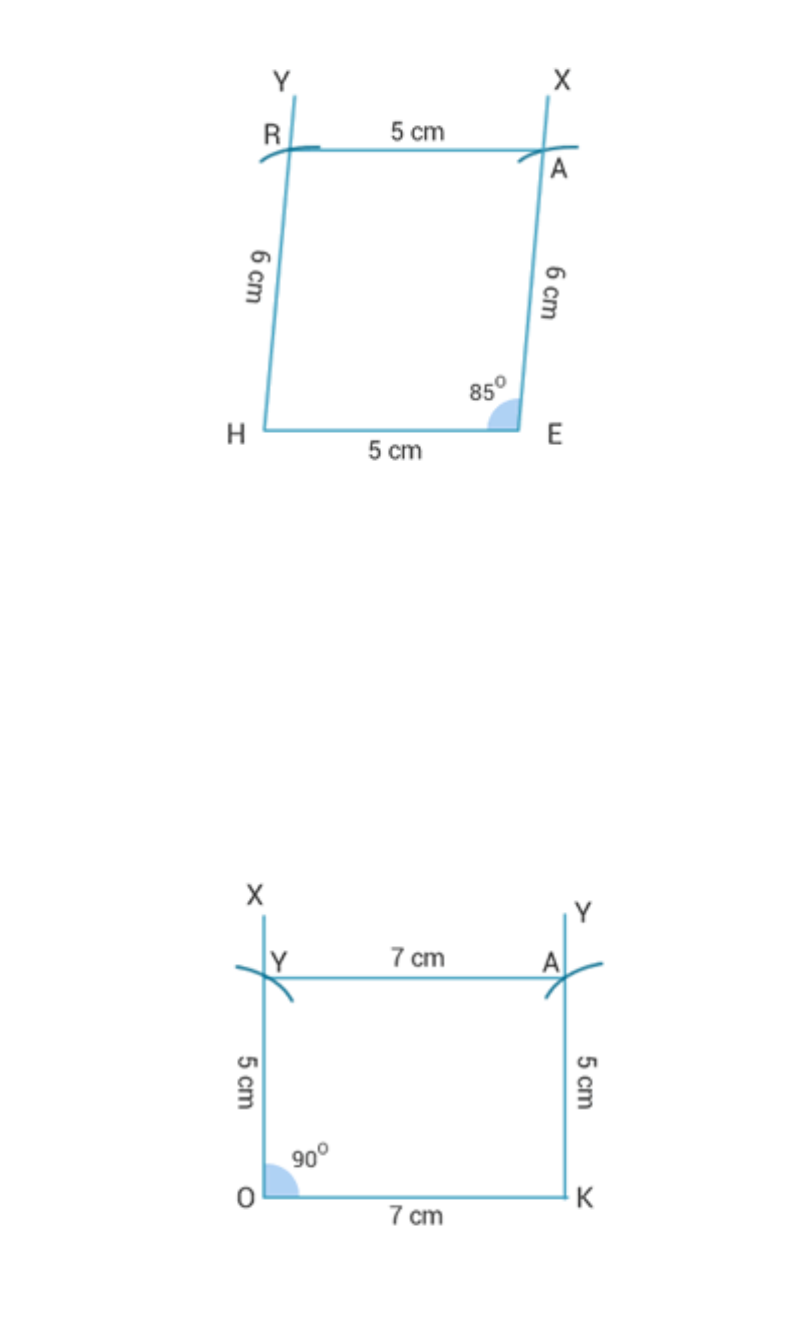
(iv) Steps of construction:

1. Draw a line segment OK = 7 cm.

2. AT O, draw an  XOK = 90°.

3. From ray OX, cut off OY = 5 cm.

4. Also at K, draw an  OKZ = 90°.

5. From ray KZ, cut off KA = 5 cm.

6. Join AY.

7. OKAY is the required rectangle.

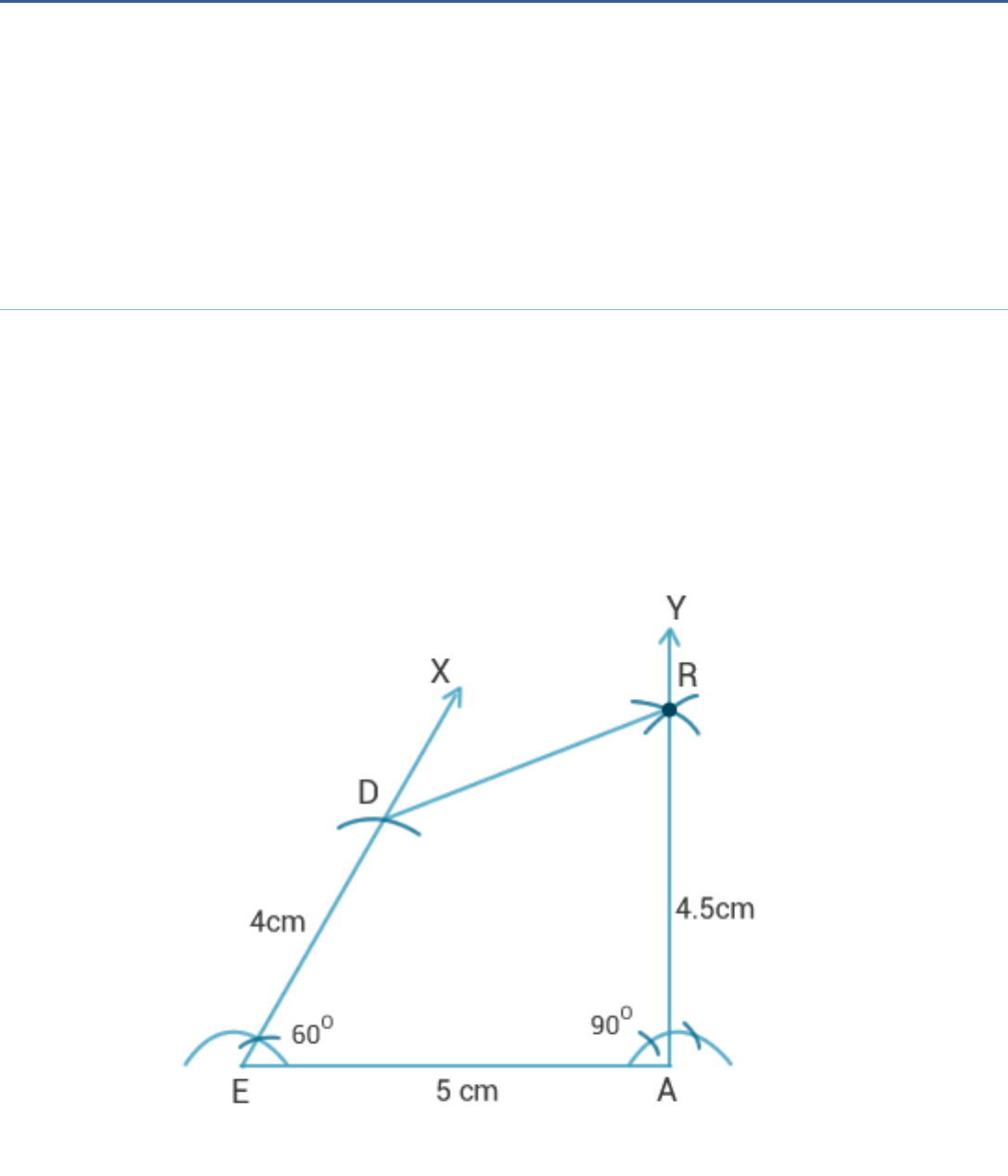
Exercise 4.4

Question 1

Construct the following quadrilaterals:

(i) Quadrilateral DEAR

DE = 4 cm, EA = 5 cm, AR = 4.5 cm, E = 60°°,  A = 90°

(ii) Quadrilateral TRUE

TR = 3.5 cm, RU = 3 cm, UE = 4 cm,  R = 75°,  U = 120°

Solution:

(i) Steps of construction:

1. Draw a line segment EA = 5 cm.

2. Draw an  XEA = 60° and  EAY = 90°.

3. Cut off ED = 4 cm from EX and AR = 4.5 cm

from AY.

4. Join DR.

5. DEAR is the required quadrilateral.

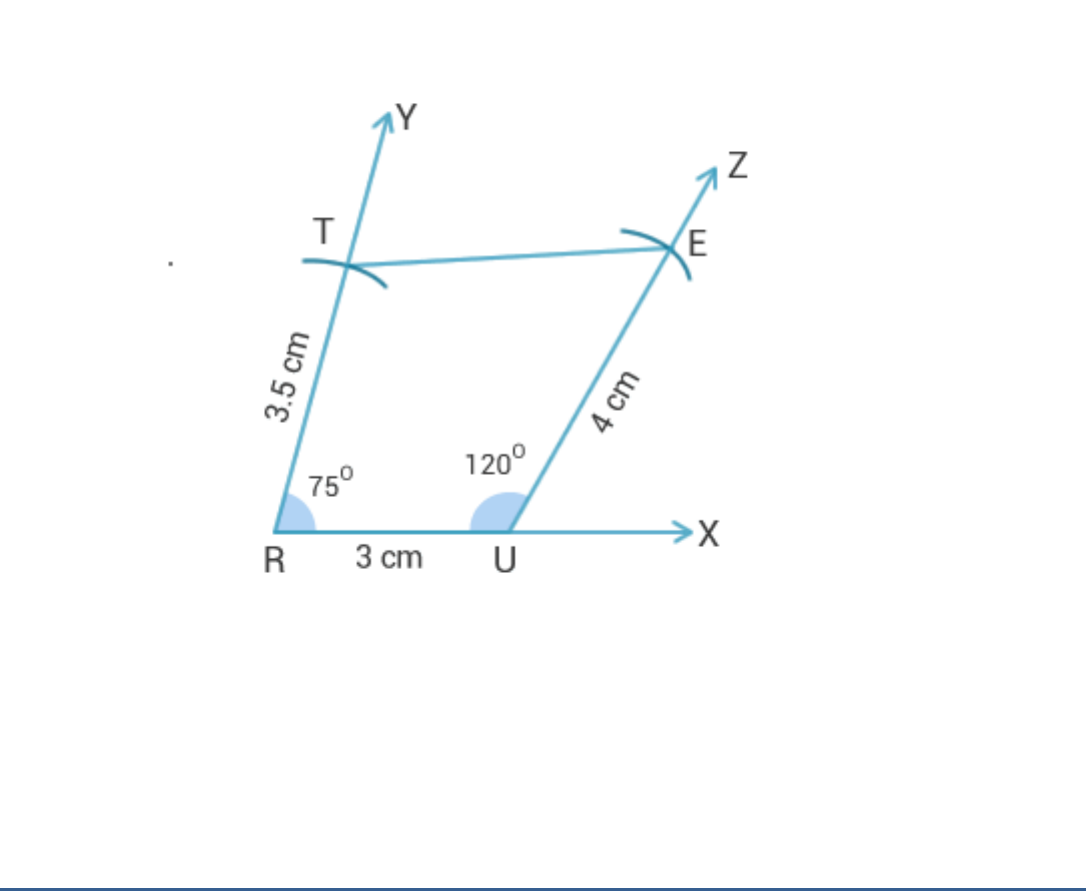
(ii) Steps of construction:

1. Draw  YRX = 75°.

2. With centre R and radius 3.5 cm draw and arc to

intersect RY in T.

3. With centre R and radius 3 cm draw an arc to intersect

RX in U. Note- In the figure make RU = 3 cm.

4. Draw  RUZ = 120°.

5. With centre U and radius 4 cm draw an arc to intersect

UZ in E.

6. Join TE.

7. TRUE is the required quadrilateral.

Exercise 4.5

Question 1

Draw the following:

The square READ with RE = 5.1 cm.

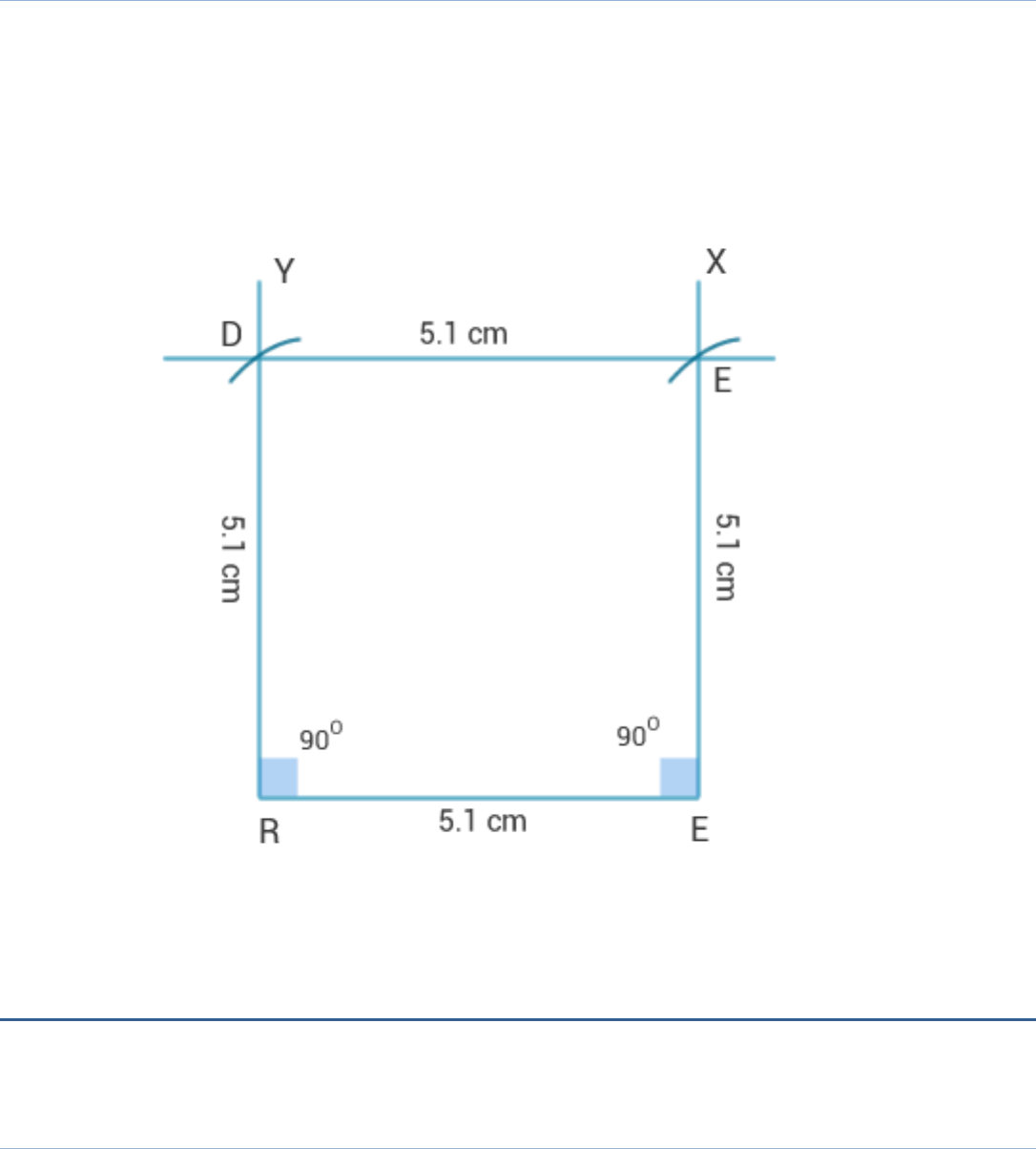
Solution:

Steps of construction:

1. Draw a line segment RE = 5.1 cm.

2. At R, draw angle ERY = 90° and at E, draw angle REX = 90°.

3. Taking E and R as centre draw two arcs of radius 5.1 cm, which

intersect RY and EX at D and A respectively.

4. Join AD.

5. READ is the required square.

Question 2

Draw the following:

A rhombus whose diagonals are 5.2 cm and 6.4 cm long.

Solution:

Steps of Construction:

1. Show the point Y in the figure.

2. Draw a line segment BD = 5.2 cm.

3. Draw perpendicular bisector XY of BD which intersects BD at O.

4. Now, taking O as centre draw two arcs of radius 3.2 cm on the

opposite sides of BD, which intersect BD at A and C.

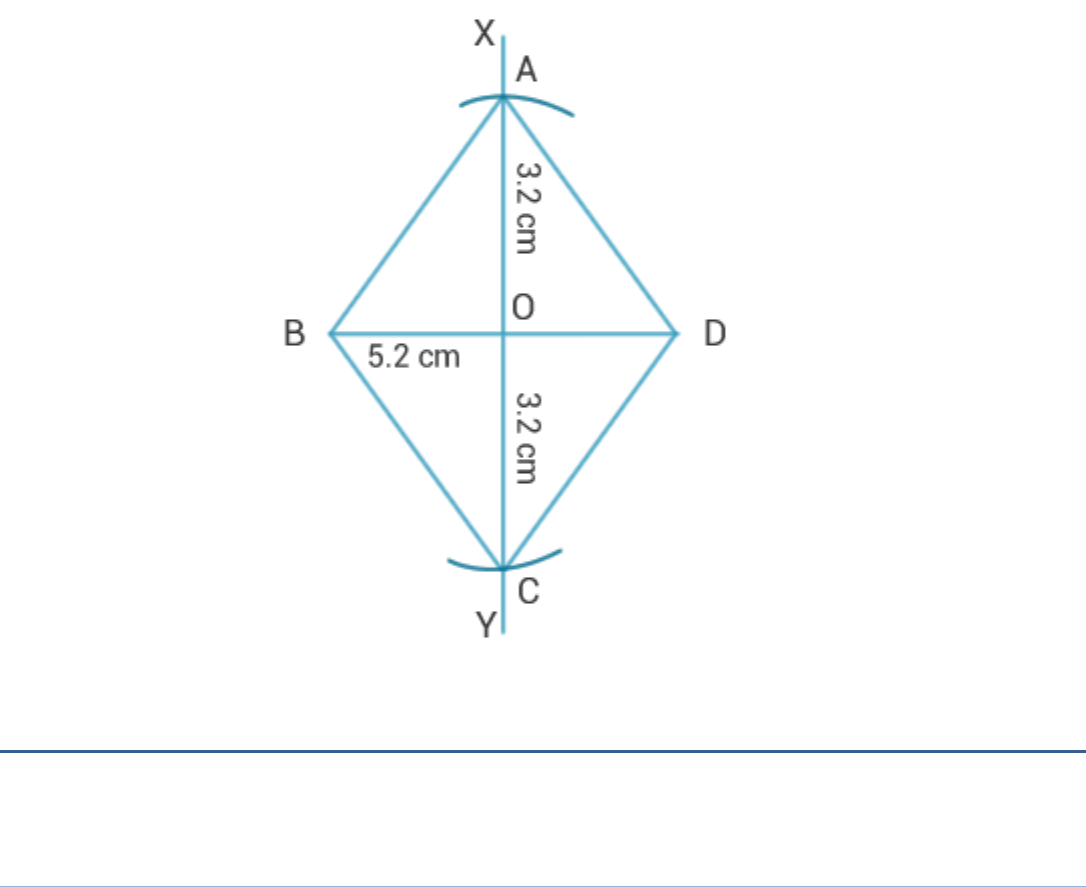
5. Join AB, AD, BC and CD.

6. ABCD is the required rhombus.

Question 3

Draw the following:

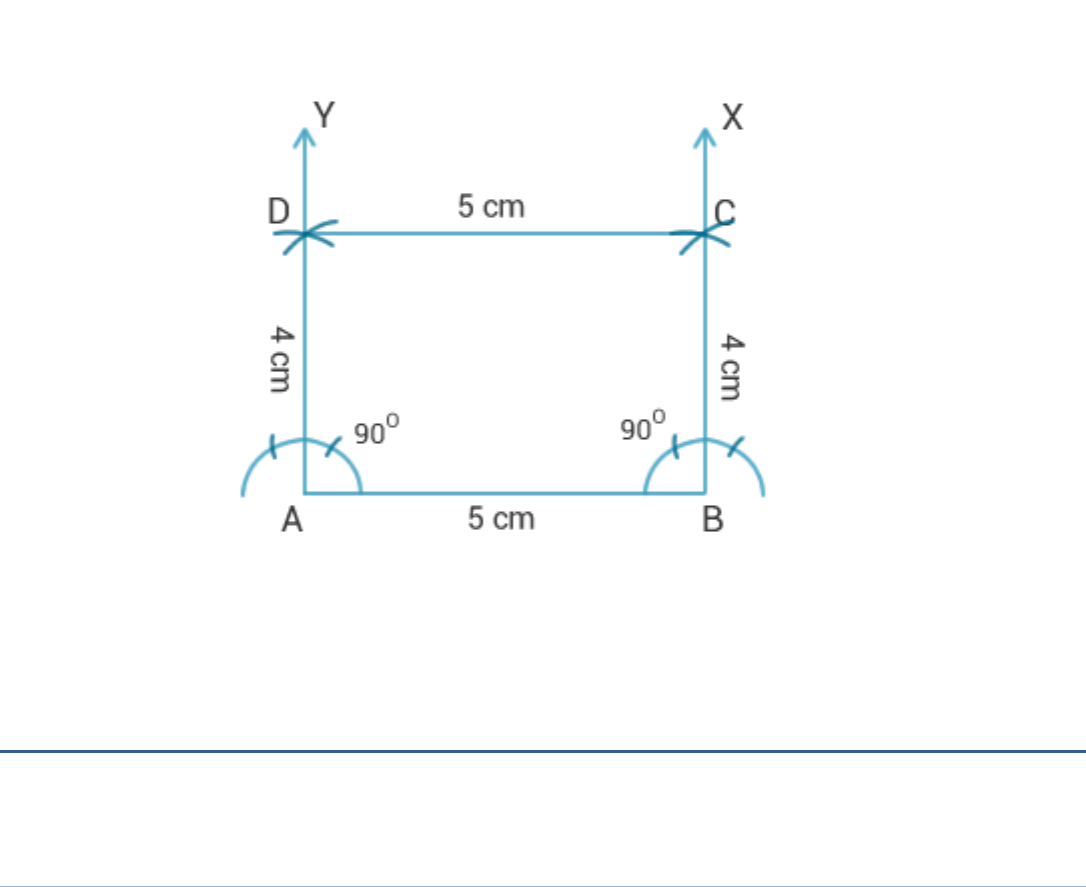
A rectangle with adjacent sides of lengths 5cm and 4cm.

Solution:

Steps of construction:

1. Draw a line segment AB = 5 cm.

2. Construct  BAY =  ABX = 90°.

3. Draw arcs of radius 4 cm.

4. Taking A and B as centre,

which intersect AY and BX at D and C respectively.

5. Join DC.

6. ABCD is the required rectangle.

Question 4

Draw the following:

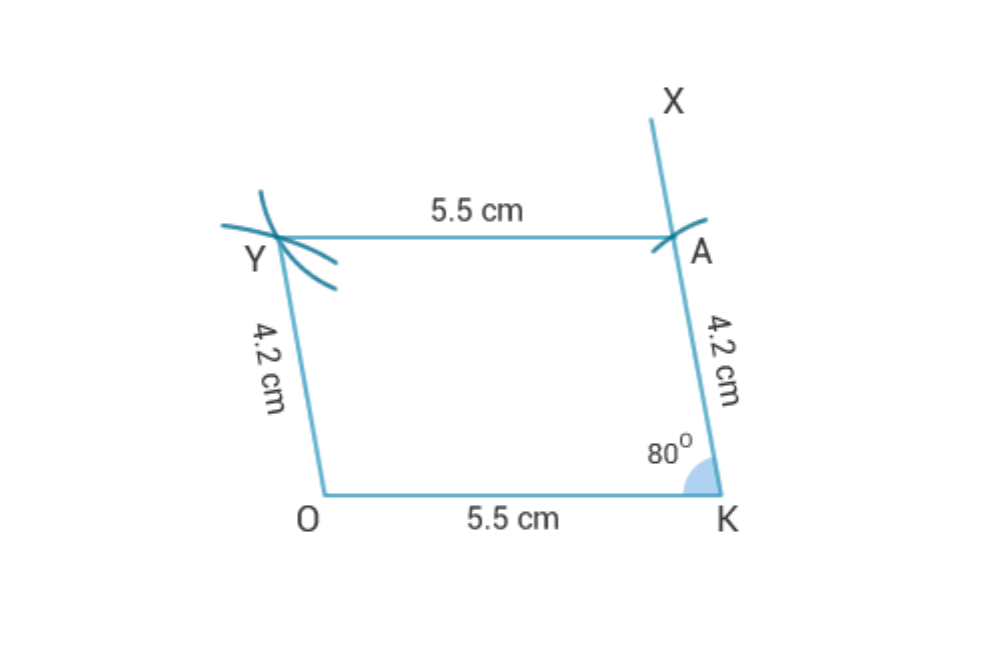
A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm. Is it unique?

Solution:

We know that, opposite sides of a parallelogram are equal and sum of

adjacent angles is 180°

i.e., OK = YA = 5.5 cm and

OY = KA = 4.2 cm.

Steps of Construction:

1. Draw OK = 5.5 cm.

2. Let  K = 80°, so construct  OKX = 80°.

3. Cut off KA = 4.2 cm in KX .

4. Draw arcs of 5.5 cm and 4.2 cm with centre as A and O respectively.

5. Join AY and OY.

6. OKAY is the required parallelogram.

Note: You may take one angle of any measurement.

Therefore, such a parallelogram is not unique.