
Lesson: Linear Equations in One Variable
Exercise – 2.1
Question 1
Solve:
27x
Answer:
x = 9
Solution:
We have,
27x
Adding 2 to both sides, we get
2 2 7 2x
9x
Question 2
Solve:
3 10y
Answer:
y = 7
Solution:
We have,
3 10y
10 3y
(Transposing 3 to RHS)
7y
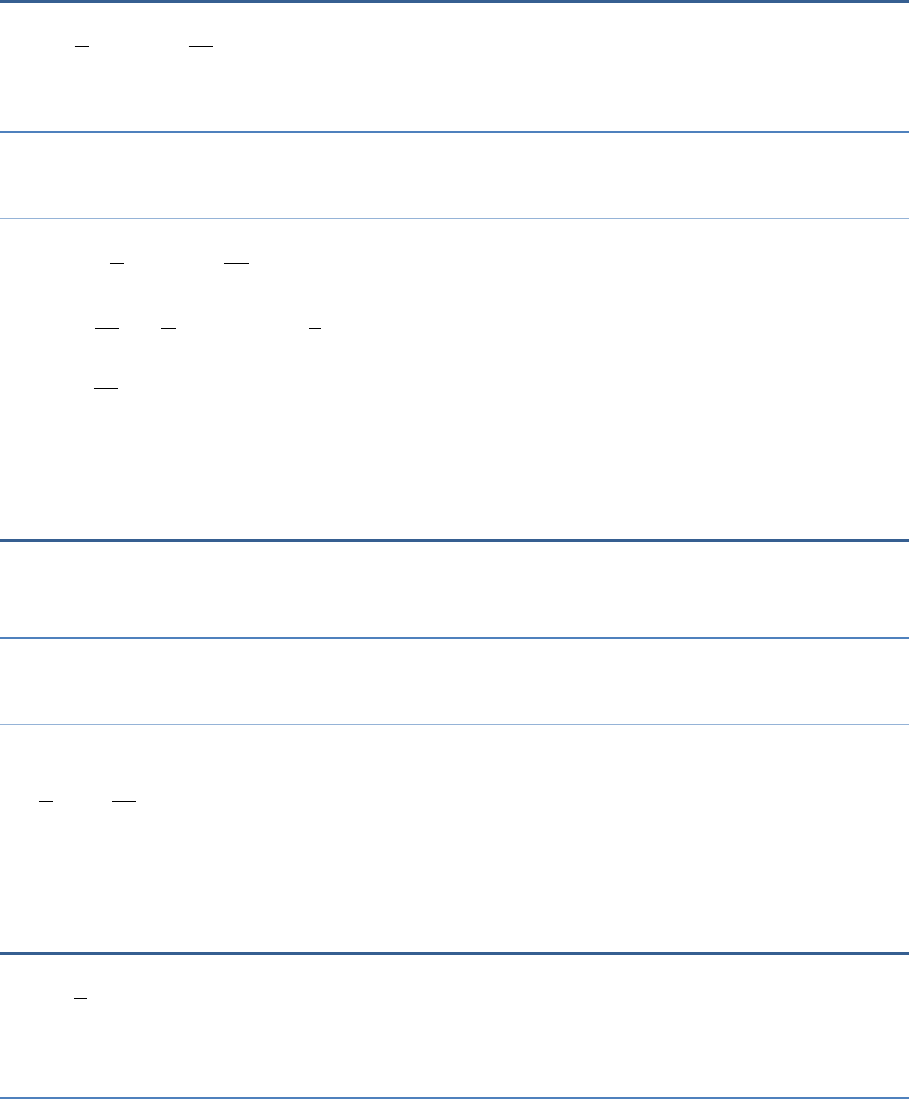
Question 3
Solve:
62z
Answer:
z = 4
Solution:
We have,
62z
62 z
(Transposing 2 to LHS)
4 z
4z
Question 4
Solve:
3 17
77
x
Answer:
x = 2
Solution:
We have,
3 17
77
x
17 3
77
x
(Transposing
3
7
to RHS)
14
7
x
2x
Question 5
Solve:
6 12x
Answer:
x = 2
Solution:
We have,
6 12x
6 12
66
x
(Dividing both sides by 6)
2x
Question 6
Solve:
10
5
t
Answer:
t = 50

Solution:
We have,
10
5
t
Multiplying both sides by 5,
5 10 5
5
t
50t
Question 7
Solve:
2
18
3
x
Answer:
x = 27
Solution:
We have,
2
18
3
x
Multiplying both sides by 3,we get
2
3 18 3
3
x
2 54x
2 54
22
x
(Dividing both sides by 2)
27x
Question 8
Solve:
1.6
1.5
y
Answer:
y = 2.4
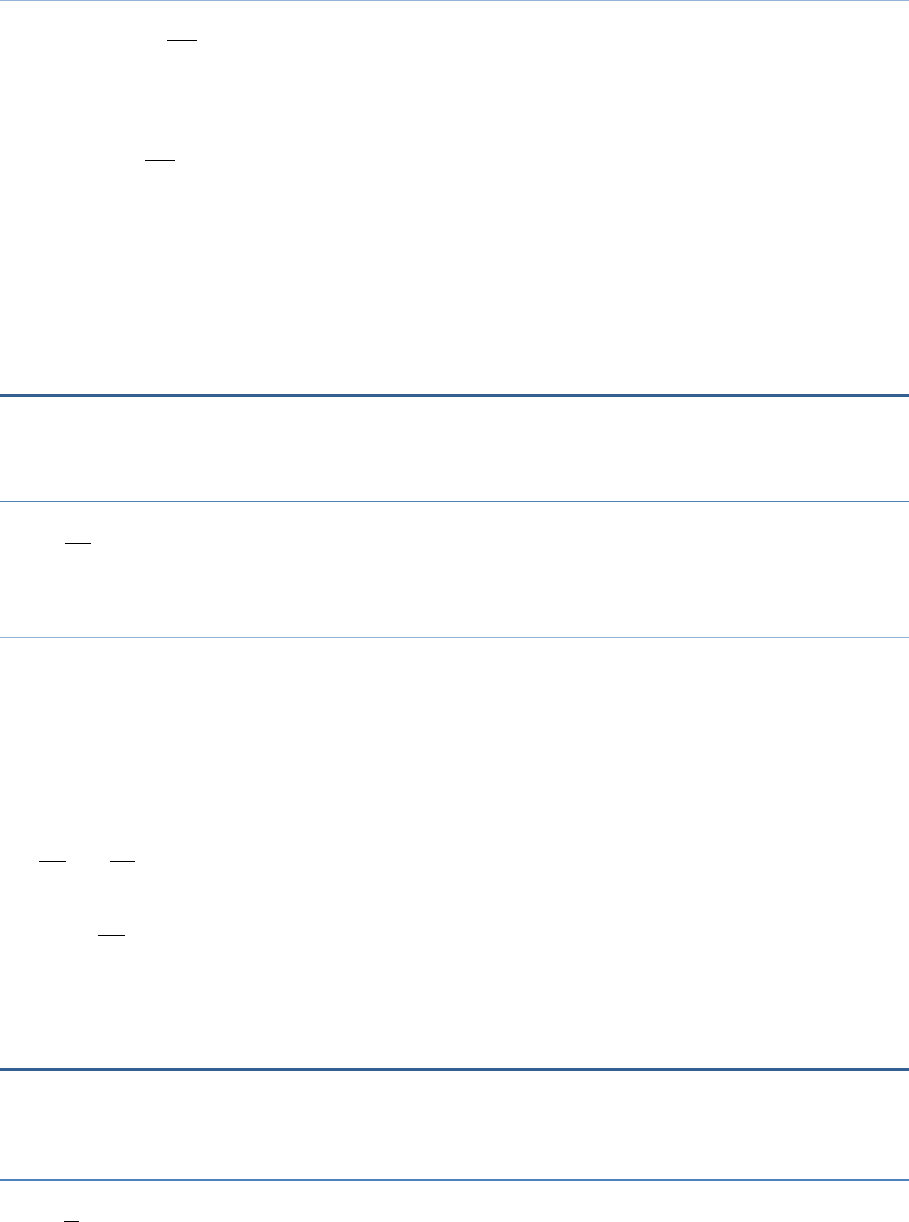
Solution:
We have,
1.6
1.5
y
Multiplying both sides by 1.5,we get
1.6 1.5 1.5
1.5
y
2.4 y
2.4y
Question 9
Solve:
7 9 16x
Answer:
25
7
x
Solution:
We have,
7 9 16x
Adding 9 to both sides,
7 9 9 16 9x
7 25x
7 25
77
x
(Dividing both sides by 7)
25
7
x
Question 10
Solve:
14 8 13y
Answer:
3
2
y

Solution:
We have,
14 8 13y
Adding 8 to both sides, we get
14 8 8 13 8y
14 21y
14 21
14 14
y
(Dividing both sides by 14)
3
2
y
Question 11
Solve:
17 6 9p
Answer:
4
3
p
Solution:
We have,
17 6 9p
6 9 17p
(Transposing
17
to RHS)
68p
8
6
p
(Dividing both sides by 6)
4
3
p
Question 12
Solve:
7
1
3 15
x
Answer:
8
5
x

Solution:
We have,
7
1
3 15
x
7
1
3 15
x
(Transposing 1 to RHS)
8
3 15
x
8
33
3 15
x
(Multiplying both sides by 3)
8
5
x
Exercise – 2.2
Question 1
If you subtract
1
2
from a number and multiply the result by
1
2
, you get
1
8
.
What is the number?
Answer:
3
4
Solution:
Let the number be
x
.
According to the question, we have
1 1 1
2 2 8
x
11
2
22
x
1
2
8
(Multiplying both sides by 2)
11
24
x
11
42
x
(Transposing
1
2
to RHS)

3
4
x
Question 2
The perimeter of a rectangular swimming pool is 154 m.
Its length is 2 m more than twice its breadth.
What is the length and the breadth of the pool?
Answer:
The breadth and length of the pool are 25 m and 52 m respectively
Solution:
Let the breadth of the swimming pool be x m, then its length =
2 2 mx
.
The perimeter of the swimming pool is
2 154 mlength breadth
Therefore,
154 2[(2 2) ]xx
154 2 2 2
154 2 3 2
154 6 4
xx
x
x
154 – 4
6 4 – 4x
(Subtracting 4 from both sides)
150 6x
150 6
66
x
(Dividing both sides by 6)
25 x
The length
(2 2) mx
=
(2 25 2) m
= (50 + 2) m = 52 m
Hence, the breadth and the length of the swimming pool are 25 mand 52 m respectively.
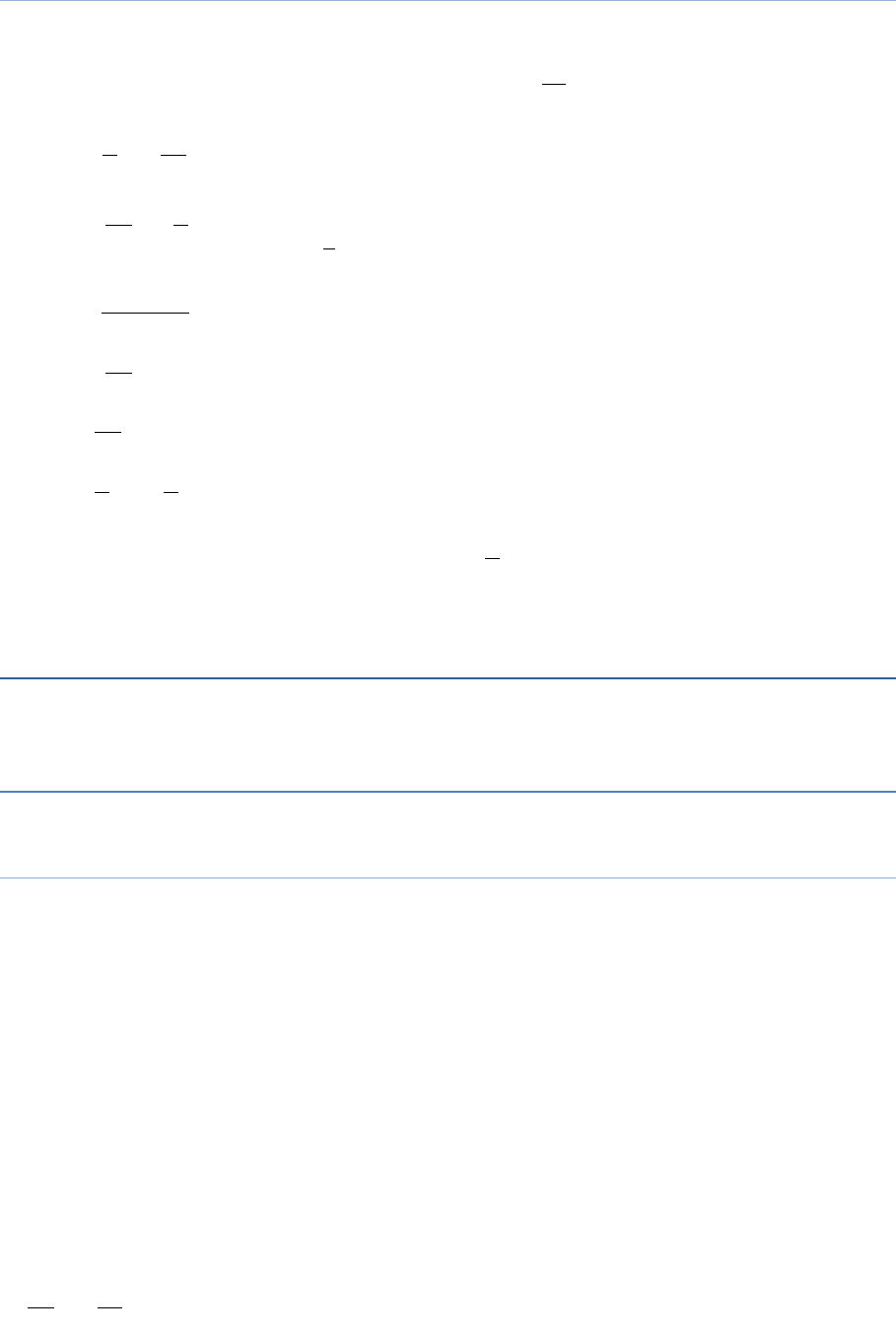
Question 3
The base of an isosceles triangle is
4
3
cm.
The perimeter of the triangle is
2
4
15
cm.
What is the length of either of the remaining equal sides?
Answer:
2
1 cm
5
Solution:
Let the length of each of the equal sides be
cmx
Perimeter of the triangle
x cm x cm base
2
4
15
cm
4 62
2
3 15
x
62 4
2
15 3
x
(Transposing
4
3
to R H S)
62 20
2
15
x
42
2
15
x
42
30
x
(Dividing both sides by 2)
7
5
x
2
1
5
Therefore, the length of each of the equal sides is
2
1 cm
5
.
Question 4
Sum of two numbers is 95.
If one exceeds the other by 15, find the numbers.
Answer:
The first number = 40 and the second number = 55
Solution:
Let one of the numbers be ‘
a
’
Therefore, the second number will be
a
+ 15
According to the question,
a
+
a
+ 15 = 95
⇒ 2
a
+ 15 = 95
⇒2
a
+ 15 – 15 = 95 – 15(subtracting 15 from both sides)
⇒ 2
a
= 95 – 15
⇒ 2
a
= 80
⇒
2 80
22
a
(dividing both sides by 2)

⇒
40a
So, the second number =
a
+ 15 = 55
Thus, the first number is 40 and the second number is 55.
Question 5
Two numbers are in the ratio 5:3.
If they differ by 18, what are the numbers?
Answer:
45 and 27
Solution:
Let one of the numbers be x, then the other number is x+18.
According the question,
18 5
3
x
x
By cross multiplication, we get
3x + 54 = 5x
54 = 5x –3x
54 = 2x
27 x
(Dividing both sides by 2)
18 27 18 45x
So, the numbers are 27 and 45.
Question 6
Three consecutive integers add up to 51.
What are these integers?
Answer:
16, 17 and18
Solution:
Let the three consecutive integers be
1,aa
, and
1a
.
The sum of these numbers =
( 1) ( ) ( 1) 51a a a
⇒
a
+
a
+
a
= 51
⇒
a
+
a
+
a
= 51
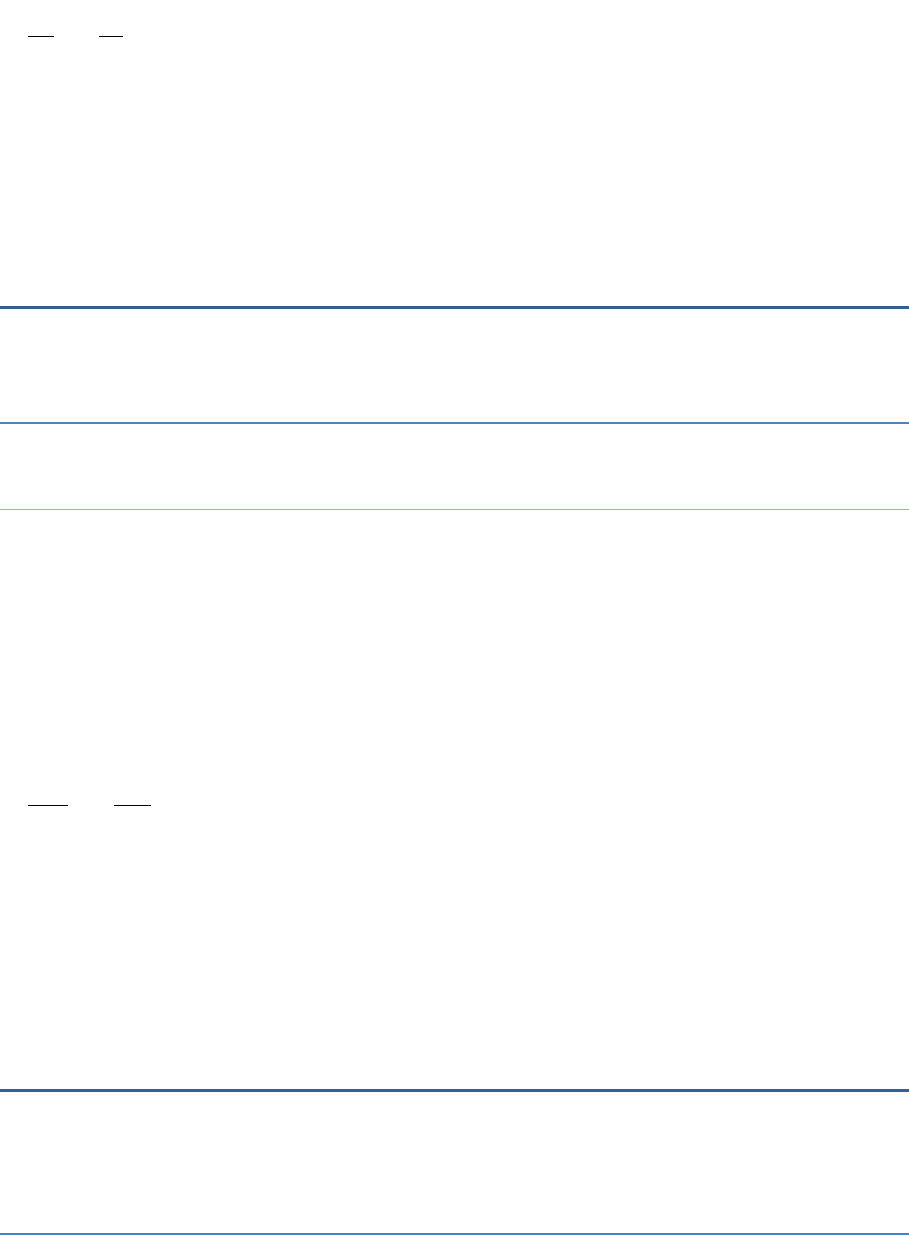
⇒ 3
a
= 51
⇒
3 51
33
a
(dividing both sides by 3)
⇒
17a
⇒
1 16a
⇒
1 18a
Hence, the consecutive integers are 16, 17, and 18.
Question 7
The sum of three consecutive multiples of 8 is 888.
Find the multiples.
Answer:
288, 296 and 304
Solution:
Let the three consecutive multiples of 8 be 8a, 8 (a + 1) and 8 (a + 2) respectively.
The sum of the numbers, as given, is 888
Therefore, 8
a
+ [8 (
a
+ 1)] + [8 (
a
+ 2)] = 888
⇒ 8
a
+ (8
a
+ 8) + (8
a
+ 16) = 888
⇒ 8
a
+ 8
a
+ 8 + 8
a
+ 16 = 888
⇒ 8
a
+ 8
a
+ 8
a
+ 8 + 16 = 888
⇒ 24
a
+ 24 = 888
⇒ 24
a
= 888 – 24(transposing 24 to RHS)
⇒ 24
a
= 864
⇒
24 864
24 24
a
(dividing both sides by 24)
⇒
36a
8 288a
(The first multiple of 8)
8( 1) 296a
(The second multiple of 8)
8( 2) 304a
(The third multiple of 8)
Thus, the three consecutive multiples of 8 are288, 296 and 304 respectively.
Question 8
Three consecutive integers are such that when they are taken in increasing order and
multiplied by 2, 3 and 4 respectively, they add up to 74.
Find these numbers.
Answer:
7, 8 and 9
Solution:
Let the first integer be
a
Therefore, second consecutive integer is (
a
+ 1) and the third consecutive integer is (
a
+ 2)
As per the question,
(First integer
2) + (second consecutive integer
3) + (third consecutive integer
4) = 74
( 2) [( 1) 3]aa
[( 2) 4] 74a
2 (3 3)aa
(4 8) 74a
2 3 3aa
4 8 74a
2 3 4a a a
3 8 74
9 11 74a
⇒
9 11 11 74 11a
(Subtracting 11 from both sides)
⇒
9 63a
⇒
9 63
99
a
(dividing both sides by 9)
⇒
7a
a + 1 = 8
a + 2 = 9
Thus, the three consecutive integers are 7, 8 and 9.
Question 9
The ages of Rahul and Haroon are in the ratio 5:7.
Four years later the sum of their ages will be 56 years.
What are their present ages?
Answer:
Rahul’s present age is 20 years; Haroon’s present age is 28 years
Solution:
Let the present age of Rahul be 5x years, then the present age of Haroon is 7x years.
After 4 years, the age of Rahul and Haroon will be 5x+4 years and 7x+ 4 years respectively.
According to the question,
(5 4) (7 4) 56xx
5 4 7 4 56xx
5 7 4 4 56xx
12 8 56x
12 56 8x
(Transposing 8 to RHS)
12 48x
4x
(Dividing both sides by 12)
Therefore, the present ages of Rahul and Haroon, in years, are
5 5 4 20x
and
7 7 4 28x
respectively.

Question 10
The number of boys and girls in a class are in the ratio 7:5.
The number of boys is 8 more than the number of girls.
What is the total class strength?
Answer:
48
Solution:
Let the number of boys be
7x
,
then the number of girls =
5x
As per the question,
7 8 5xx
8 5 7xx
(Transposing
7x
to RHS)
82x
82x
82
22
x
(Dividing both sides by 2)
4 x
4x
The strength of the class = Number of boys + Number of girls
Strength of the class
7 5 12x x x
12 4 48
Question 11
Baichung’s father is 26 years younger than Baichung’s grandfather and 29 years older than
Baichung.
The sum of the ages of all the three is 135 years.
What is the age of each one of them?
Answer:
Baichung’s = 17 years, Baichung’s father’s age = 46 years and Baichung’s grandfather’s age
= 72 years
Solution:
Let the age of Baichung’s father in years be m.
Then, the ages of Baichung’s grandfather and Baichung, in years, will be m + 26 and
m – 29 respectively.
According to the question,
Age of Baichung + Age of Baichung’s father + Age of Baichung’s grandfather = 135 years
⇒ (m – 29) + m + (m + 26) = 135
⇒m – 29 + m + m + 26 = 135
⇒m + m + m – 29 + 26 = 135
⇒ 3m – 3 = 135
⇒3m = 135 + 3(transposing – 3 to RHS)
⇒ 3m = 138
⇒
3m 138
33
(dividing both sides by 3)
m 46
The age of Baichung, in years, = m – 29 = 46 – 29 = 17
The age of Baichung’s grandfather, in years, = m + 26 = 46 + 26 = 72
Question 12
Fifteen years from now Ravi’s age will be four times his present age.
What is Ravi’s present age?
Answer:
Ravi’s present age is 5 years
Solution:
Let the present age of Ravi be m years.
According to question,
m + 15 = 4
m
⇒m + 15 = 4 m
⇒15 = 4m – m(transposing m to RHS)
⇒ 15 = 3m
⇒
15 3
33
m
(dividing both sides by 3)
⇒
5m
Thus, Ravi’s present age is 5 years.
Question 13
A rational number is such that when you multiply it by
5
2
and add
2
3
to the product, you get
7
12
. What is the number?
Answer:
1
2
Solution:
Let the number be x.
According to the given question,
5 2 7
2 3 12
x
Transposing
2
3
to R.H.S, we get
5 7 2
2 12 3
x
5
2
x
7 2 4
12
5 15
2 12
x
On multiplying both sides by
2
5
, we get
15 2 1
12 5 2
x
Hence, the rational number is
1
2
.
Question 14
Lakshmi is a cashier in a bank. She has currency notes of denominations Rs.100,
Rs.50 and Rs.10, respectively.
The ratio of the number of these notes is 2:3:5.
The total cash with Lakshmi is Rs.4, 00,000.
How many notes of each denomination does she have?
Answer:
The number of currency notes of Rs.100, Rs. 50 and Rs. 10 are 2000, 3000 and 5000
respectively.
Solution:
Let the number of currency notes of denomination of Rs.100 be 2
x
,
then the number of
currency notes of denomination of Rs.50 and Rs. 10 would be 3
x
and 5x respectively.
The value of currency notes of denomination of Rs.100 = Rs 2
x
100 = Rs 200
x
,
The value of currency notes of denomination of Rs.50 = Rs 3
x
50 = Rs 150
x
and
The value of currency notes of denomination of Rs.10 = Rs 5
x
10 = Rs 50
x
According to the question,
200 x + 150 x + 50 x = 4, 00,000.
400 400000x
1000x
2 2000x
3 3000x
5 5000x
Thus, the number of currency notes of Rs.100,Rs.50 and Rs.10 are 2000, 3000 and 5000
respectively.
Question 15
I have a total of Rs.300 in coins of denomination Rs.1, Rs.2 and Rs.5.
The number of Rs.2 coins is 3 times the number of Rs.5 coins.
The total number of coins is 160.
How many coins of each denomination are with me?
Answer:
The number of coins of Rs.1, Rs. 2 and Rs. 5 are 80, 60 and 20 respectively.
Solution:
Let the number of coins of Rs.5 be m.
Therefore, number of coins of Rs.2 = m
3 = 3m and the number of coins of Rs.1 =
= 160 – (m + 3m) = 160 – 4m
Total Amount= (Rs.1
Number of Rs.1 coins) + (Rs.2
Number of Rs.2 coins) + (Rs.5
Number of Rs.5 coins)
⇒ 300 = [1
(160 – 4m)] + (2
3m) + (5
m)
⇒ 300 = (160 – 4m) + 6m + 5m
⇒ 300 = 160 – 4m + 6m + 5m
⇒300 = 160 – 4m + 11m
⇒ 300 = 160 + 7m
⇒300 – 160 = 7m(transposing 160 to LHS)
⇒ 140 = 7 m
⇒
140 7
77
m
(dividing both sides by 7)
140
7
m
140
7
m
20m
Number of coins of Rs.1 = 160 – (4
20) = 160 – 80 = 80
Number of coins of Rs.2 = 3m = 3
20 = 60
Therefore, the number of coins of Rs1,Rs 2 and Rs 3 are 80, 60 and 20 respectively.

Question 16
The organisers of an essay competition decide that a winner in the competition gets
a prize of Rs.100 and a participant who does not win gets a prize of Rs.25.
The total prize money distributed is Rs.3, 000.
Find the number of winners, if the total number of participants is 63.
Answer:
19
Solution:
Let the number of winners be m
Number of losers = 63 – m
Total Prize money distributed to winners
= Number of winners
prize money distributed to each winner
= Rs m
100 = Rs100 m
Total prize money distributed to participants who are not winners
= Rs (63 – m)
25 = Rs ((63
25) – 25 m) = Rs (1575 – 25 m)
Total Prize money of winners + Total Prize money of losers = Total prize money
⇒100 m + 1575 – 25 m = 3000
⇒100 m – 25 m + 1575 = 3000
⇒100 m – 25 m = 3000 – 1575(transposing 1575 to RHS)
⇒75 m = 1425
⇒
75 1425
75 75
m
(dividing both sides by 75)
1425
19
75
m
Thus, number of winners is 19
Exercise – 2.3
Question 1
Solve the equation and check your result.
3 2 18xx
Answer:
x = 18
3 2 18xx
3 2 18xx
(Transposing
2x
to LHS)
18x
L.H.S
3 3 18 54x
R.H.S
2 18x
2 18 18
36 18 54
L.H.S = R.H.S
Question 2
Solve the equation and check your result.
5 3 3 5tt
Answer:
t =
1
Solution:
5 3 3 5tt
5 3 5 3tt
(Transposing
3t
to LHS and
3 to RHS)
22t
1t
(Dividing both sides by 2)
L.H.S
53t
5 ( 1) 3
5 3 8
R.H.S
3 5 3t
( 1) 5
3 5 8
L.H.S = R.H.S
Question 3
Solve the equation and check your result.
5 9 5 3xx
Answer:
x =
2
Solution:
5 9 5 3xx
5 3 5 9xx
(Transposing
3x
to LHS and 9 to RHS)
24x
2x
(Dividing both sides by 2)
L.H.S
5 9 5( 2) 9x
10 9 1
R.H.S
5 3 5 3( 2)x
5 6 1
L.H.S = R.H.S

Question 4
Solve the equation and check your result.
4 3 6 2zz
Answer:
3
2
z
Solution:
4 3 6 2zz
4 2 6 3zz
(Transposing
2z
to LHS and 3 to RHS)
23z
3
2
z
(Dividing both sides by 2)
L.H.S
3
4 3 4 3
2
z
6 3 9
R.H.S
3
6 2 6 2
2
z
6 3 9
L.H.S = R.H.S
Question 5
Solve the equation and check your result.
2 1 14xx
Answer:
x = 5
Solution:
2 1 14xx
2 14 1xx
(Transposing
x
to LHS and
1 to RHS)
3 15x
5x
(Dividing both sides by 3)
L.H.S
2 1 2(5) 1x
10 1 9
R.H.S
14 14 5 9x
L.H.S = R.H.S
Question 6
Solve the equation and check your result.
8 4 3 1 7xx
Answer:
x = 0
Solution:
8 4 3 1 7xx
8 4 3 3 7xx
8 4 3 4xx
8 3 4 4xx
(Transposing
3x
to LHS and 4 to RHS)
50x
0x
L.H.S
8 4 8(0) 4 4x
R.H.S
3 1 7x
3(0 1) 7
3 7 4
L.H.S = R.H.S
Question 7
Solve the equation and check your result.
4
10
5
xx
Answer:
x = 40
Solution:
4
10
5
xx
44
10
55
xx
4
8
5
xx
4
8
5
xx
(Transposing
4
5
x
to LHS)
54
8
5
xx
8
5
x
Multiplying both sides by 5, we get
40x
L.H.S
40x
R.H.S
4
10
5
x
4
(40 10)
5
4
(50) 40
5
L.H.S = R.H.S
Question 8
Solve the equation and check your result.
27
13
3 15
xx
Answer:
x = 10
Solution:
27
13
3 15
xx
27
31
3 15
xx
(Transposing
7
15
x
to LHS and 1 to RHS)
3
2
15
x
Multiplying both sides by 15,
we get,
3 30x
10x
(Dividing both sides by 3)
L.H.S
2
1
3
x
2(10)
1
3
20
1
3
23
3
R.H.S
7
3
15
x
7(10)
3
15
70
3
15
70 45
15
115 23
15 3
L.H.S = R.H.S

Question 9
Solve the equation and check your result.
5 26
2
33
yy
Answer:
7
3
y
Solution:
5 26
2
33
yy
26 5
2
33
yy
(Transposing –
y
to LHS and
5
3
to RHS)
21
3
3
y
37y
7
3
y
(Dividing both sides by 3)
L.H.S
5
2
3
y
75
2
33
14 5
33
19
3
R.H.S
26
3
y
26 7
33
19
3
L.H.S = R.H.S
Question 10
Solve the equation and check your result.
8
35
5
mm
Answer:
4
5
m
Solution:
8
35
5
mm
8
35
5
mm
(Transposing
5m
to LHS)

8
2
5
m
8
10
m
(Dividing both sides by 2)
4
5
m
L.H.S
4 12
33
55
m
R.H.S
8
5
5
m
48
5
55
20 8
5
12
5
L.H.S = R.H.S
Exercise – 2.4
Question 1
Amina thinks of a number and subtracts
5
2
from it.
She multiplies the result by 8.
The result now obtained is 3 times the same number she thought of.
What is the number?
Answer:
4
Solution:
Let the number thought by Amina be
a
According to the question,
5
83
2
The number The number
5
83
2
aa
5
83
2
aa
5
8 8 3
2
aa
40
83
2
aa
8 20 3aa

8 20 3 0aa
(Transposing
3a
to LHS)
8 3 20 0aa
8 3 20aa
(Transposing
20 to RHS)
5 20a
5 20
55
a
(Dividing both sides by 5)
20
4
5
a
Question 2
A positive number is 5 times another number.
If 21is added to both the numbers, then one of the new numbers becomes twice the other new
number.
What are the numbers?
Answer:
7 and 35
Solution:
Let the given positive number be
a
. Then
the other number will be 5
a
.
According to the question,
5
a
+ 21 = 2 (
a
+ 21)
⇒ 5
a
+ 21 = 2
a
+ 42
⇒ 5
a
+ 21 – 2
a
= 42(transposing 2
a
to LHS)
⇒ 5
a
– 2
a
= 42 – 21(transposing 21 to RHS)
⇒ 3
a
= 21
3 21
33
a
(dividing both sides by 3)
7a
Therefore, the other number is 5
a
= 5
7 = 35
Thus, the numbers are 7 and 35
Question 3
The sum of the digits of a two-digit number is 9.
When we interchange the digits, it is found that the resulting new number is greater
than the original number by 27.
What is the two-digit number?
Answer:
36

Solution:
Let the number at the ones place of the two digit number be a, then the digit at the
ten’s place = 9 –
a
Thus, the number = 10(9 –
a
) +
a
After interchange of digits, the new number =10
a
+ (9 –
a
)
As per the question, the new number – 27 = the original number
⇒ 10
a
+ (9 –
a
) – 27 = 10 (9 –
a
) +
a
⇒ 10
a
+ 9 –
a
– 27 = 90 – 10
a
+
a
⇒ 10
a
–
a
+ 9 – 27 = 90 – 9
a
⇒ 9
a
– 18 = 90 – 9
a
⇒9
a
= 90 – 9
a
+ 18(transposing
18 to RHS)
⇒9
a
+ 9
a
= 90 + 18(transposing – 9a to LHS)
⇒18
a
= 108
⇒
18 108
18 18
a
(dividing both sides by 18)
108
18
a
6a
9 –
a
= 9 – 6 = 3
Thus, the digit at the ten’s place = 3 and the digit at the ones place = 6
The number is 36.
Question 4
One of the two digits of a two digit number is three times the other digit.
If you interchange the digits of this two-digit number and add the resulting number
to the original number, you get 88.
What is the original number?
Answer:
26 or 62
Solution:
Let one of the digits, which is at ones place, of the two digit number be
a
Therefore, the other digit of the two digit number = 3
a
Therefore, the number = (10
3
a
) +
a
= 30
a
+
a
= 31
a
After interchange of the digits, the new number = 10
a
+ 3
a
= 13
a
As per the question,
31
a
+ 13
a
= 88
⇒ 44
a
= 88
44 88
44 44
a
(Dividing both sides by 44)
2a
31
a
= 31
2 = 62
13
a
= 13
2 = 26
Therefore, the two-digit number is either 26 or 62.
Question 5
Shobo’s mother’s present age is six times Shobo’s present age.
Shobo’s age five years from now will be one third of his mother’s present age.
What are their present ages?
Answer:
Shobo’s age: 5 years; Shobo’s mother’s age: 30 years
Solution:
Let the present age of Shobo be
a
years
Therefore, Shobo’s mother’s present age = 6
a
years
After five years, the age of Shobo = (
a
+ 5) years
As per the question,
1/3 of the present age of Shobo’s mother = Age of Shobo after 5 years.
6
5
3
a
a
25aa
25aa
(Transposing a to LHS)
5a
6 30a
Therefore, the present age of Shobo is 5 years and the present age of Shobo’s
mother is 30 years.
Question 6
There is a narrow rectangular plot, reserved for a school, in Mahuli village.
The length and breadth of the plot are in the ratio 11:4.
At the rate Rs.100 per metre it will cost the village panchayat Rs.75000 to fence
the plot.
What are the dimensions of the plot?
Answer:
Shob Length = 275 m; breadth = 100 m
Solution:
Let the length and breadth of the rectangular plot be
11 x
m and
4 x
m respectively.
The perimeter of the plot = 2 (length + breadth)
2 11 4 m 30 mx x x
It is given that the cost of fencing the plot, at the rate of Rs 100 per metre, is Rs 75000.
100 Perimeter = Rs 75000
100 30 75000x
3000 75000x
Dividing both sides by 3000, we get
25x

The length
11 m 11 25 m 275 mx
and the breadth
4 m 4 25 m 100 mx
Hence, the dimensions of the plot are, length = 275 m and breadth = 100 m.
Question 7
Hasan buys two kinds of cloth materials for school uniforms, shirt material that
costs him Rs. 50 per metre and trouser material that costs him Rs. 90 per metre.
For every 3 meters of the shirt material he buys 2 metres of the trouser material.
He sells the materials at 12% and 10% profit respectively.
His total sale is Rs.36, 600. How much trouser material did he buy?
Answer:
200 m
Solution:
Given:
The rate of the shirt material = Rs.50 per meter
The rate of the trouser material = Rs.90 per meter
The profit on the shirt material = 12%
The profit on the trouser material = 10%
The total sale price = Rs.36600.00
Since the profit on the cost price of the shirt material = 12%, therefore, the sale
price of the material = cost price + 12% of cost price
12
.50.000 .50.00
100
Rs Rs
.50.00 .6.00Rs Rs
.56.00Rs
Since, the profit on the cost price of the trouser material = 10%, therefore, sale
price of the trouser material = cost price of trouser material + 10% of cost price
10
.90.000 .90.00
100
Rs Rs
.90.00 .9.00Rs Rs
.99.00Rs
Let the shirt material and the trouser material being purchased by Hasan be
3mx
and
2mx
respectively.
Total sale price = Total sale price of the shirt material + Total sale price of
the trouser material
.36600Rs
3 .56 2 .99x Rs x Rs
.36600Rs
.168 .198Rs x Rs x
.36600 .366Rs Rs x
36600
366
x
366
366
x
(Dividing both sides by 366)
100x
2 200x
Thus, Hasan bought 200 m of trouser material.

Question 8
Half of a herd of deer is grazing in the field and three fourths of the remaining is
playing nearby.
The rest 9 are drinking water from the pond.
Find the number of deer in the herd.
Answer:
72
Solution:
Let the total number of deer be
x
Since, half of the herd is grazing in the field, the number of deer grazing =
2
x
Since,
3
4
th
of remaining are playing nearby,the number of deer playing
near b
33
2 4 8
xx
Number of deer drinking water = 9
(Given by the question)
Now, the total number of deer = the number of deer grazing + the number of
deer playing + the number of deer drinking water.
3
9
28
xx
x
43
9
8
xx
7
9
8
x
7
9
8
x
x
(Transposing
7
8
x
to LHS)
87
9
8
xx
9
8
x
72x
Hence, the total number of deer in the herd is 72.
Question 9
A grandfather is ten times older than his granddaughter.
He is also 54 years older than her.
Find their present ages.
Answer:
Granddaughter’s age = 6 years; Grandfather’s age = 60 years
Solution:
Let the age of the granddaughter be
x
years.
Therefore, the age of the grandfather =
10x
As per the question,
10 54xx
9 54x
9 54
99
x
(Dividing both sides by 9)
6x
Thus, the ages of the granddaughter and the grandfather are 6 years and 60 years
respectively.
Question 10
Aman’s age is three times his son’s age.
Ten years ago he was five times his son’s age.
Find their present ages.
Answer:
Aman’s age: 60 years; Aman’s son’s age: 20 years
Solution:
Let the age of Aman’s son be
x
years
Therefore, Aman’s age = 3x years
As per the question, the present age of Aman –10 years
(the present age of his son
10 years)
5
3 5 50 10xx
2 40x
2 40x
2 40
22
x
20x
3 60x
Hence the present age of Aman is 60 years and the present age of his son is 20 years.
Exercise – 2.5
Question 1
Solve the following linear equations.
11
2 5 3 4
xx
Answer:
27
10
x
Solution:
11
2 5 3 4
xx
L.C.M. of the denominators 2, 3, 4, and 5 is 60.
On multiplying both sides by 60, we get
1
60
25
x
1
60
34
x
⇒30x − 12 = 20x + 15 (opening the brackets)
⇒ 30x − 20x = 15 + 12(transposing
20x
to LHS and
12
to RHS)
⇒ 10x = 27
27
10
x
Question 2
Solve the following linear equation.
35
2 4 6
n n n
21
Answer:
n = 36
Solution:
35
21
2 4 6
n n n
L.C.M. of the denominators 2, 4, and 6, is 12.
On multiplying both sides by 12, get
6n − 9n + 10n = 252
7n = 252
252
7
n
36n
Question 3
Solve the following linear equations.
8 17 5
7
3 6 2
xx
x
Answer:
x =
5
Solution:
8 17 5
7
3 6 2
xx
x
L.C.M. of the denominators 2, 3, and 6 is 6.
Multiplying both sides by 6, we get
6x + 42 − 16x = 17 − 15x
6x − 16x + 15x = 17 – 42(transposing
15x
to LHS and 42 to RHS)
5x = −25
25
5
x
5x
Question 4
Solve the following linear equation.
53
35
xx
Answer:
x =
8
Solution:
53
35
xx
L.C.M. of the denominators 3 and 5 is 15.
On multiplying both sides by 15, we get
5(x − 5) = 3(x − 3)
5x − 25 = 3x – 9 (Opening the brackets)
5x − 3x = 25 − 9
2x = 16
16
2
x

8x
Question 5
Solve the following linear equation.
3 2 2 3
43
tt
2
3
t
Answer:
t = 2
Solution:
3 2 2 3
43
tt
2
3
t
L.C.M. of the denominators, 3 and 4, is 12.
Multiplying both sides by 12, we get
3(3t − 2) − 4(2t + 3) = 8 − 12t
9t − 6 − 8t − 12 = 8 − 12t (opening the brackets)
t − 18 = 8 − 12t
t + 12t = 8 + 18 (transposing
18 to RHS and
12t to LHS)
13t = 26
26
13
t
2t
Question 6
Solve the following linear equation.
1
2
m
m
2
1
3
m
Answer:
7
5
m
Solution:
1
2
m
m
2
1
3
m
L.C.M. of the denominators, 2 and 3, is 6.
Multiplying both sides by 6, we get
6m − 3(m − 1) = 6 − 2(m − 2)
6m − 3m + 3 = 6 − 2m + 4 (Opening the brackets)
3m + 3 = 10 − 2m
3m + 2m = 10– 3(transposing 3 to RHS and
2m to LHS)
5m = 7
7
5
m
Question 7
Solve the following linear equation.
3( 3) 5(2 1)tt
Answer:
2t
Solution:
3(t − 3) = 5(2t + 1)
3t − 9 = 10t + 5(opening the brackets)
−9 − 5 = 10t − 3t(transposing 3t to RHS and 5 to LHS)
−14 = 7t
14
7
t
2t
Question 8
Solve the following linear equation.
15( 4) 2( 9)yy
5( 6) 0y
Answer:
2
3
y
Solution:
15(y − 4) − 2(y − 9) + 5(y + 6) = 0
15y − 60 − 2y + 18 + 5y + 30 = 0(Opening the brackets)
18y − 12 = 0
18y = 12(transposing
12 to RHS)
12
18
y
2
3
y
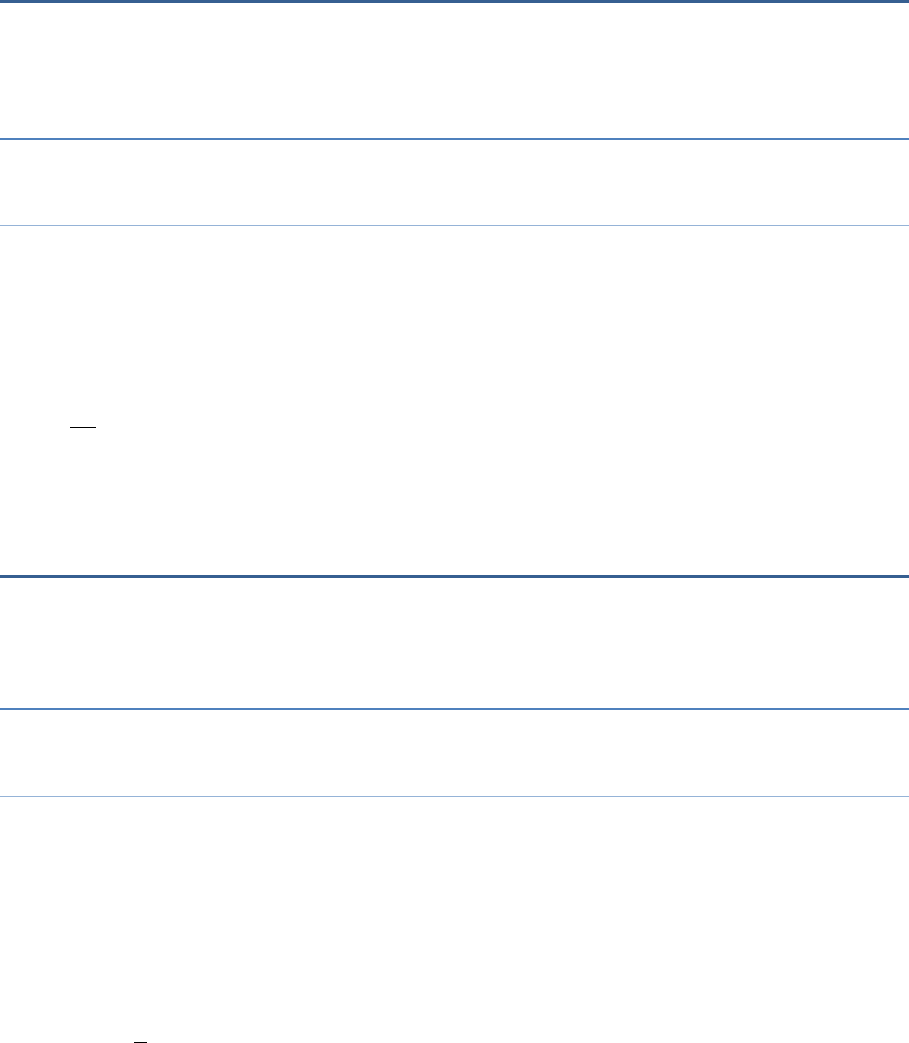
Question 9
Solve the following linear equation.
3(5 7) 2(9 11)zz
4 8 13 17z
Answer:
z = 2
Solution:
3(5z − 7) − 2(9z − 11) = 4(8z − 13)−17
15z − 21 − 18z + 22 = 32z − 52 – 17 (Opening the brackets)
−3z + 1 = 32z – 69 (transposing 32z to LHS and 1 to RHS)
−3z − 32z = −69 − 1
−35z = −70
70
35
z
2z
Question 10
Solve the following linear equation.
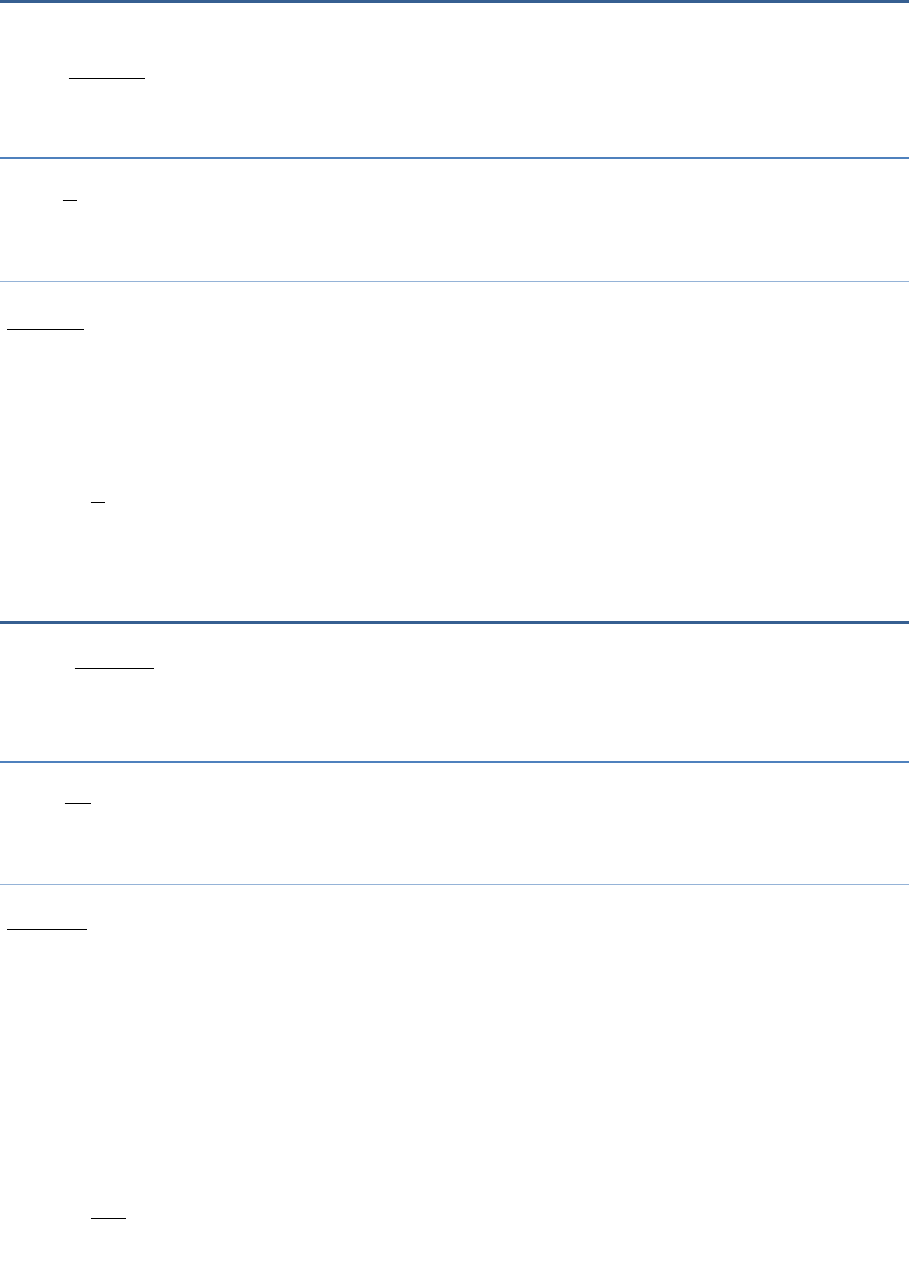
0.25(4 3)f
0.05 10 9f
Answer:
f = 0.6
Solution:
0.25(4 3)f
0.05 10 9f
Multiplying both sides by 20,
5(4f − 3) = 10f − 9
20f − 15 = 10f – 9(Opening the brackets)
20f − 10f = − 9 + 15(transposing 10f to LHS and
15 RHS)
10f = 6
3
5
f
0.6f
Exercise – 2.6
Question 1
Solve:
83
2
3
x
x
Answer:
3
2
x
Solution:
83
2
3
x
x
On multiplying both sides by3x, we obtain
8x − 3 = 6x (transposing
6x
to LHS and
3
to RHS)
8x − 6x = 3
2x = 3
3
2
x
Question 2
Solve:
9
15
76
x
x
Answer:
35
33
x
Solution:
9
15
76
x
x
On multiplying both sides by (7 − 6x), we obtain
9x = 15(7 − 6x)
9x = 105 − 90x
9x + 90x = 105(transposing
90x
to LHS)
99x = 105
105
99
x
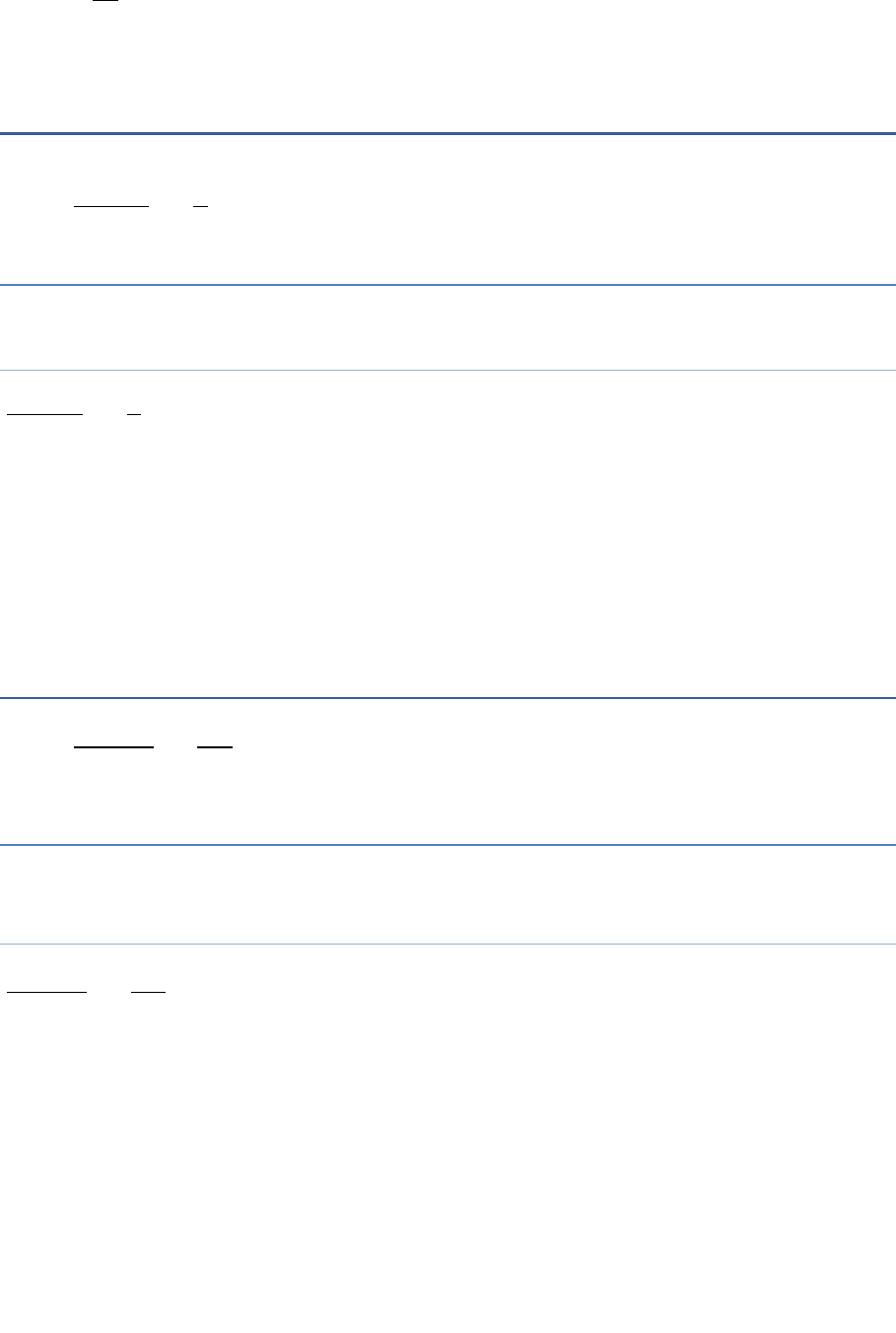
35
33
x
Question 3
Solve:
4
15 9
z
z
Answer:
z= 12
Solution:
4
15 9
z
z
On multiplying both sides by 9(z + 15), we obtain
9z = 4(z + 15)
⇒9z = 4z + 60
⇒9z − 4z = 60 (transposing
4z
to LHS)
⇒ 5z = 60
⇒z = 12
Question 4
Solve:
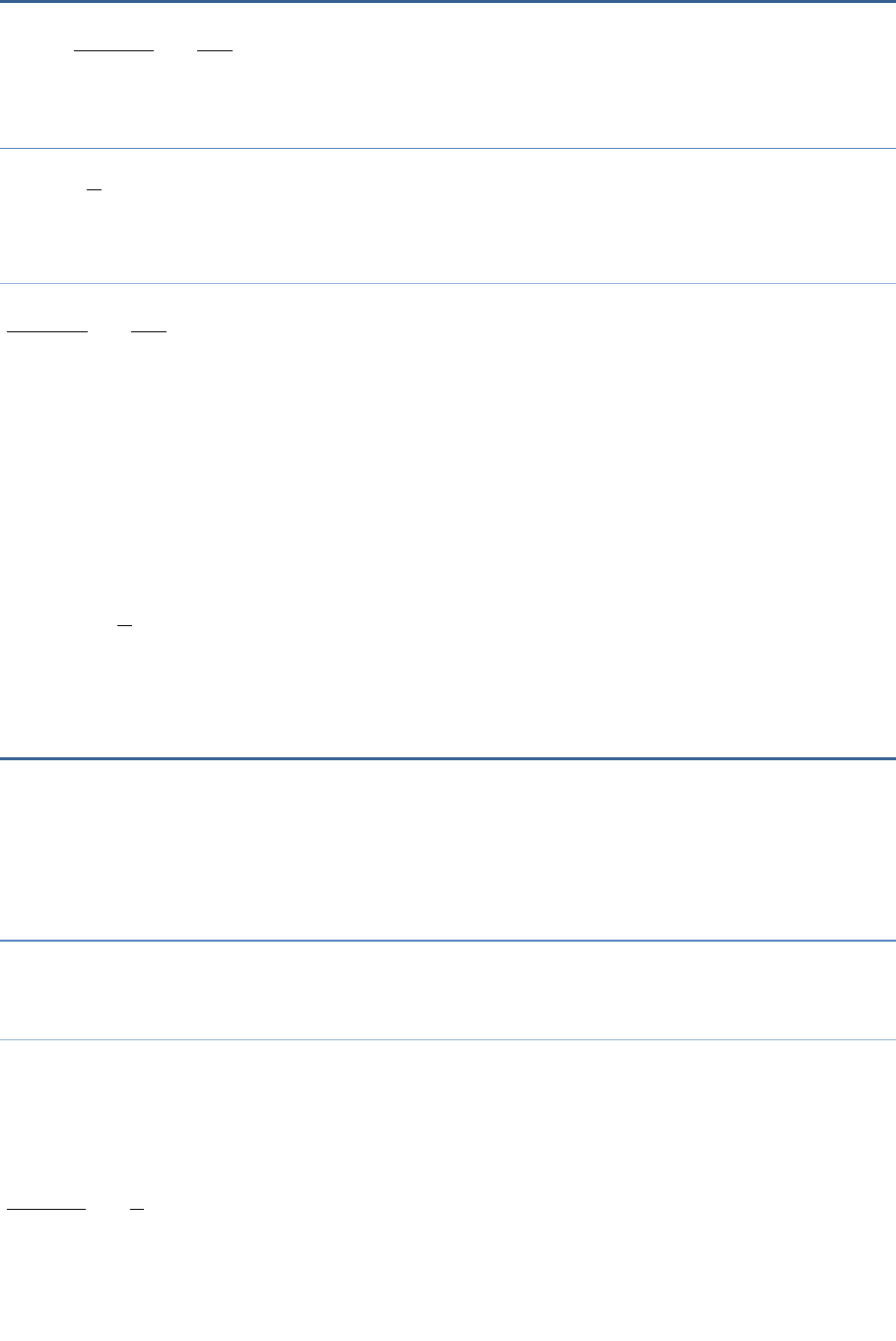
3 4 2
2 6 5
y
y
Answer:
y = −8
Solution:
3 4 2
2 6 5
y
y
On multiplying both sides by 5(2 − 6y), we obtain
5(3y + 4) = −2(2 − 6y)
⇒15y + 20 = − 4 + 12y
⇒ 15y − 12y = − 4 – 20 (transposing 12
y
to LHS and 20 to RHS)
⇒ 3y = −24
⇒ y =−8
Question 5
Solve:
7 4 4
23
y
y
Answer:
4
5
y
Solution:
7 4 4
23
y
y
On multiplying both sides by 3(y +2),we obtain
3(7y + 4) = −4(y + 2)
⇒ 21y + 12 = − 4y − 8
⇒ 21y + 4y = − 8 – 12(transposing
4y
to LHS and 12 to RHS)
⇒ 25y = −20
4
5
y
Question 6
The ages of Hari and Harry are in the ratio 5:7.
Four years from now the ratio of their ages will be 3:4.
Find their present ages.
Answer:
Hari’s age = 20 years; Harry’s age = 28 years
Solution:
Let the ages of Hari and Harry be 5x years and 7x years respectively.
Four years later, their ages will be (5x + 4) years and (7x + 4) years respectively.
According to the question,
5 4 3
7 4 4
x
x
By cross-multiplication,
4(5 4) 3(7 4)xx

20 16 21 12xx
16 12 21 20xx
4x
Hari’sage =5x years = (5 × 4) years = 20 years
Harry’s age = 7x years = (7 × 4) years = 28 years
Question 7
The denominator of a rational number is greater than its numerator by 8.
If the numerator is increased by 17 and the denominator is decreased by 1, the
Number obtained is
3
2
.
Find the rational number.
Answer:
13
21
Solution:
Let the numerator of the rational number be x.
Therefore, its denominator will be x + 8.
The rational number will be
8
x
x
.
According to the question,
17 3
8 1 2
x
x
17 3
72
x
x
By cross-multiplication,
⇒ 2(x +17) = 3(x + 7)
⇒ 2x + 34 = 3x + 21 (transposing
2x
to RHS and 21 to LHS)
⇒34 − 21 = 3x − 2x
⇒13 = x
Numerator of the rational number = x = 13
Denominator of the rational number = x + 8 = 13 + 8 = 21

Hence, the rational number is
13
21