
Lesson: Playing with Numbers
Exercise 16.1
Find the values of the letters in each of the following and give reasons for the
steps involved.
Question 1
3
25
2
A
B
Answer:
7, 6AB
Solution:
There are two letters A and B whose values we have to find.
The addition of A and 5 is giving a number whose ones digit is 2.
This is possible only when digit A is 7.
In that case, the addition of A (7) and 5 will give 12 and thus, 1 will be the carry-over
for the next step. In the next step,
1 3 2 6
Clearly, B is 6
So the puzzle can be solved as shown below.
37
25
62
Hence, A and B are 7 and 6 respectively
Question 2
4
98
3
A
CB

Answer:
5, 4, 1A B C
Solution:
There are three letters A, B and C whose values we have to find.
The addition of A and 8 is giving a number whose ones digit is 3.
This is possible only when digit A is 5.
In that case, the addition of A and 8 will give 13 and thus, 1 will be the carry-over
for the next step. In the next step,
1 4 9 14
So the puzzle can be solved as shown below.
45
98
1 4 3
Clearly, B and C are 4 and 1 respectively.
Hence, A, B, and C are 5, 4, and 1 respectively.
Question 3
1
9
A
A
A
Answer:
6A
Solution:
There is just one letter A whose value we have to find.
The multiplication of A with A itself gives a number whose ones digit is A again.
This happens only when
1, 5, 6.A or
If
1,A
then the multiplication will be
11 1 11
.
However, here, the tens digit is given as 9.
Therefore,
1A
is not possible.
Similarly, if
5,A
then the multiplication will be
15 5 75.
Thus,
5A
is also not possible.
If we take
6,A
then
16 6 96.
Therefore, A should be 6.
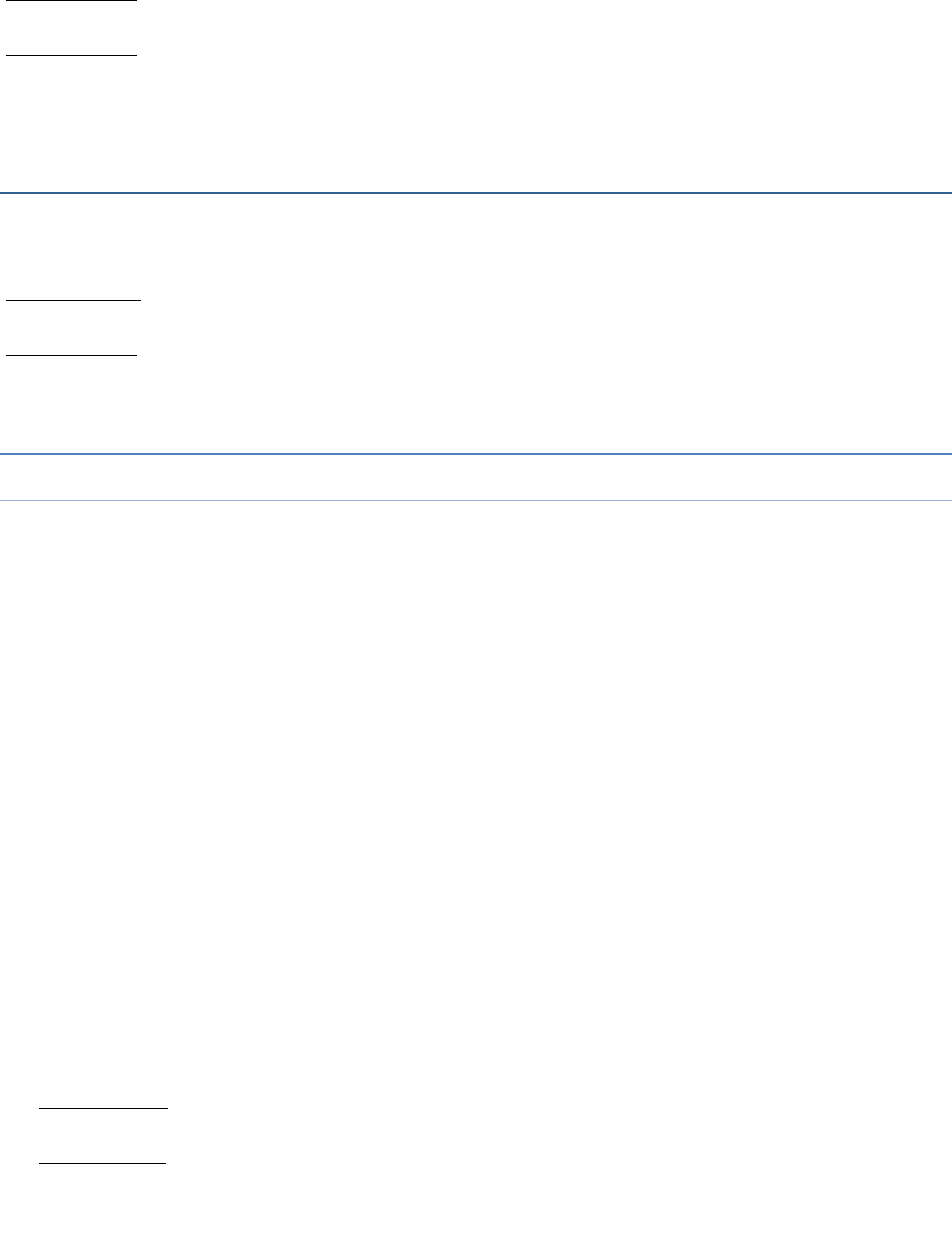
So the puzzle can be solved as shown below.
16
6
96
Hence, the value of A is 6
Question 4
37
6
AB
A
Answer:
2, 5AB
Solution:
There are two letters A and B whose values we have to find.
The addition of A and 3 is giving 6. There can be two cases.
(1) First step is not producing a carry-over
In that case, A comes to be 3 as
3 3 6.
Considering the first step in which the
addition of B and 7 is giving A (i.e., 3), B should be a number such that the unit
’s digit of this addition comes to be 3. It is possible only when
6B
. In this
case,
6 7 13.A
However, A is a single digit number. Hence, it is not
possible.
(2) First step is producing a carry-over
In that case, A comes to be 2 as
1 2 3 6.
considering the first step in
which the addition of B and 7 is giving A (i.e., 2), B should be a number such
that the unit’s digit of this addition comes to be 2. It is possible only when
5B
and
5 7 12.
So the puzzle can be solved as shown below.
25
37
62
Hence, the values of A and B are 2 and 5 respectively.

Question 5
3
AB
C A B
Answer:
5, 0, 1A B C
Solution:
There are three letters A,B and C whose values we have to find.
The multiplication of 3 and B gives a number whose ones digit is B again.
Hence, B must be 0 or 5.
Let B be 5.
Multiplication of first the step
3 5 15
1 will be a carry-over for the next step.
We have,
3 1 A
a two digit number CA (which is, in fact,
10CA
).
This is not possible for any value of A. Hence, B must be 0 only. If
0,B
then there
will be no carry-over for the next step.
We should obtain,
3 ,A CA
which is in fact
10CA
.
That is, the ones digit of
3 A
should be A.
This is possible when either
5 0.A or
However, A cannot be 0.
Therefore, A must be 5 only.
So the puzzle can be solved as shown below.
50
3
1 5 0
Hence, the values of A, B, and C are 5, 0, and 1 respectively.
Question 6
5
AB
C A B
Answer:
There are 3 sets of possible values of A, B, and C.
(i) 5, 0, and 2 respectively
(ii) 2, 5, and 1 respectively
(iii) 7, 5, and 3 respectively

Solution:
There are 3 sets of possible values of A, B, and C.
(i) 5, 0, and 2 respectively
(ii) 2, 5, and 1 respectively
(iii) 7, 5, and 3 respectively
There are three letters A, B and C whose values we have to find.
The multiplication of B and 5 is giving a number whose ones digit is B again.
This is possible when
5 0B or B
only.
In case of
5,B
the product,
5 5 5 25B
2 will be the carry-over for
the next step.
We have,
5 2 A CA
(which is, in fact,
10CA
). This is possible
for
2 7A or
The multiplication is as follows.
25
5
1 2 5
75
5
3 7 5
If
0,B
5 BB
0 5 0
There will not be any carry-over in this step.
In the next step,
5 A CA
(this is, in fact,
10CA
)
It can happen only when
5 0A or A
However, A cannot be 0 as AB is a two-digit number.
Hence, A can be 5 only.
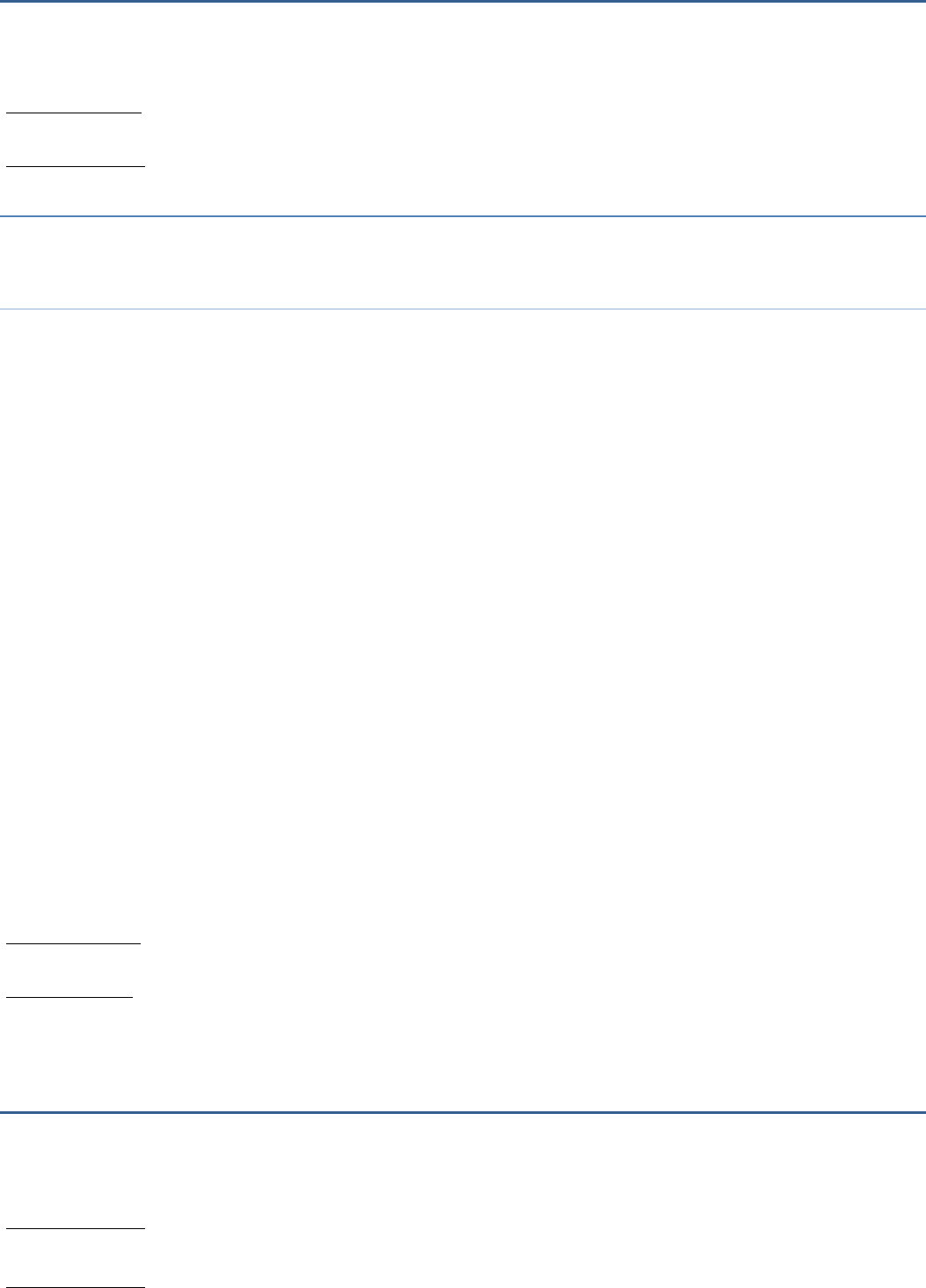
So the puzzle can be solved as shown below.
50
5
2 5 0
Hence, there are 3 possible values of A, B, and C.
(i) 5, 0, and 2 respectively
(ii) 2, 5, and 1 respectively
(iii) 7, 5, and 3 respectively
Question 7
6
AB
B B B
Answer:
7, 4AB
Solution:
There are two letters A and B whose values we have to find.
The multiplication of 6 and B gives a number whose ones digit is B again.
It is possible only when
0, 2, 4, 6, 8B or
If
0,B
then the product will be 0. Therefore, this value of B is not possible.
If
2,B
then
6 12B
and 1 will be a carry-over for the next step.
6 1 A BB
(which is
10BB
)
22
6 21A
and hence, any integer value of A is not possible.
If
6,B
then
6 36B
and 3 will be a carry-over for the next step.
6 3 A BB
(which is
10BB
)
66
6 63A
and hence, any integer value of A is not possible.
If
8,B
then
6 48B
and 4 will be a carry-over for the next step.
6 4 A BB
(which is
10BB
)
88
6 84A
and hence,
14A
. However, A is a single digit number.
Therefore, this value of A is not possible.
If
4,B
then
6 24B
and 2 will be a carry-over for the next step.
6 2 A BB
(which is
10BB
)
44
6 42A
and hence,
7A
So the puzzle can be solved as shown below.
74
6
4 4 4
Hence, the values of A and B are 7 and 4 respectively.
Question 8
1
1
0
A
B
B

Answer:
7, 9AB
Solution:
There are two letters A, and B whose values we have to find.
The addition of 1 and B is giving a number whose ones digit is 0.
This is possible only when digit B is 9.
In that case, the addition of 1 and B will give 10 and thus, 1 will be the carry-over
for the next step.
In the next step,
1 1 AB
Clearly,
7 1 7 1 9 A is as B
So the puzzle can be solved as shown below.
71
19
90
Hence, the values of A and B are 7 and 9 respectively.
Question 9
2
1
18
AB
AB
B
Answer:
4, 7AB
Solution:
There are two letters A and B whose values we have to find.
The addition of B and 1 is giving a number whose ones digit is 8.
This is possible only when digit B is 7.
In that case, the addition of B and 1 will give 8. In the next step,
AB
is giving
a number with one’s digit 1.
Clearly, A is 4.
4 7 11
and 1 will be a carry-over for the next step.
In the next step,
1 2 AB
1 2 4 7
So the puzzle can be solved as shown below.
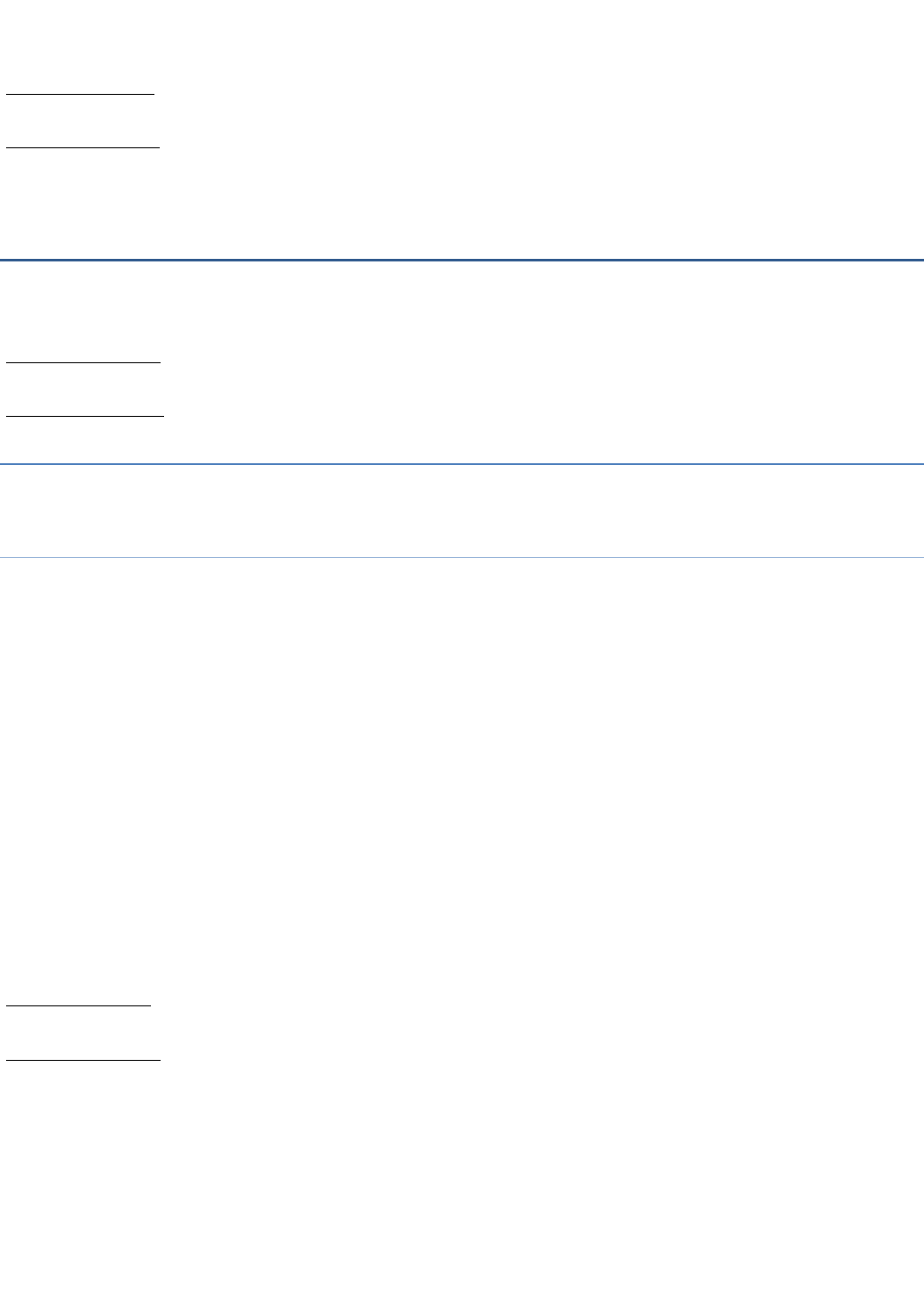
2 4 7
4 7 1
7 1 8
Hence, the values of A and B are 4 and 7 respectively.
Question 10
12
6
09
A
AB
A
Answer:
8, 1AB
Solution:
There are two letters A and B whose values we have to find.
The addition of A and B is giving 9, i.e., a number whose ones digit is 9.
The sum can be 9 only as the sum of two single digit numbers cannot be 19.
Therefore, there will not be any carry-over in this step.
In the next step,
2 A
giving a number with one’s digit 0
It is possible only when
8A
2 8 10
and 1 will be the carry-over for the next step.
1 1 6 A
Clearly, A is 8.
We know that the addition of A and B is giving 9.
As A is 8,therefore, B is 1.
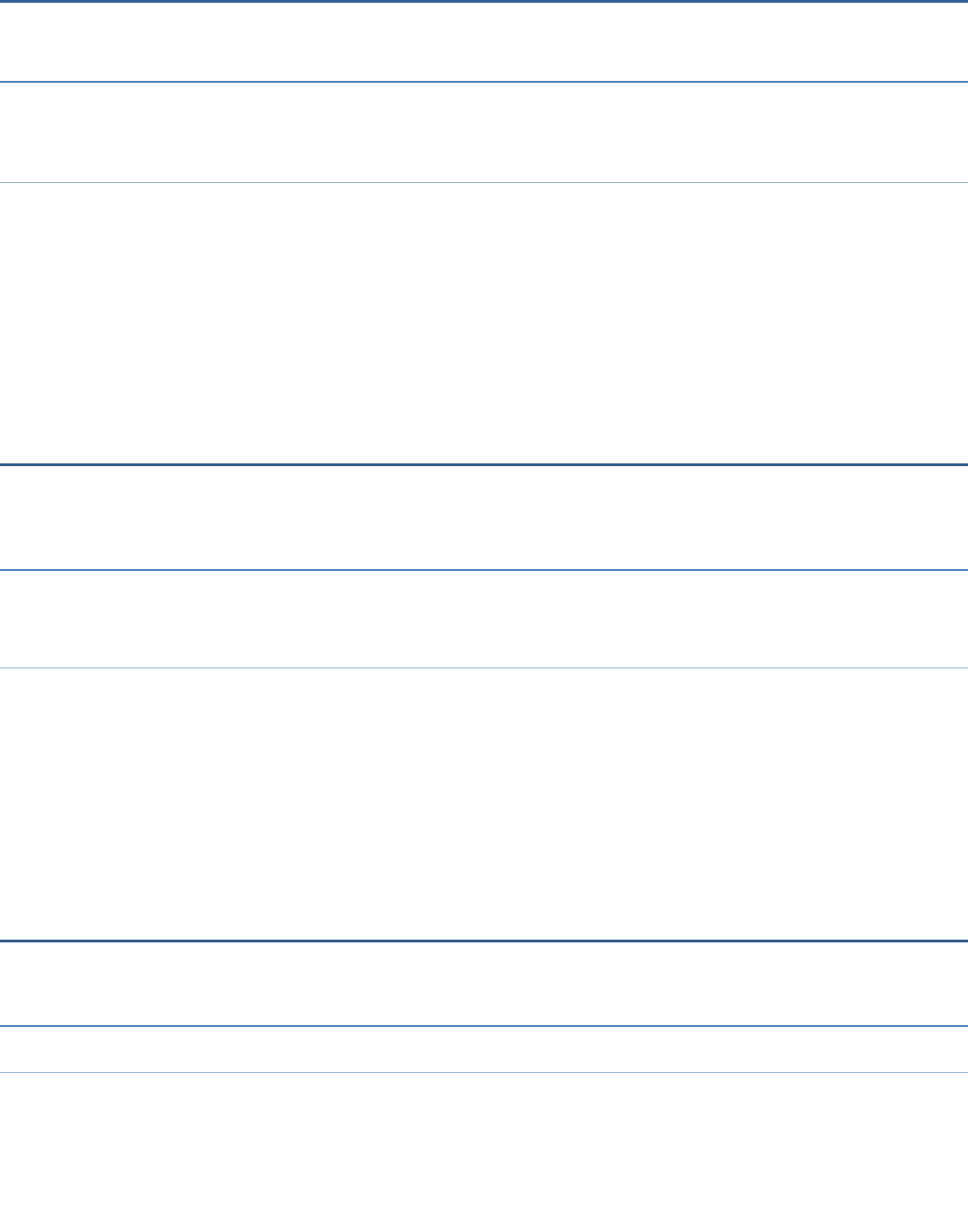
So the puzzle can be solved as shown below.
1 2 8
6 8 1
8 0 9
So, the values of A and B are 8 and 1 respectively.
Exercise16.2
Question 1
If 21y5 is a multiple of 9, where y is a digit, what is the value of y?
Answer:
1y
Solution:
If a number is a multiple of 9, then the sum of its digits will be divisible by 9.
Sum of the digits of
21 5 2 1 5 8 y y y
Hence,
8 y
should be a multiple of 9.
This is possible when
8 y
is any one of these numbers 0, 9, 18, 27, and so on …
However, since y is a single digit number, this sum can be 9 only.
So, y should be 1 only.
Question 2
If 31z5 is a multiple of 9, where z is a digit, what is the value of z?
You will find that there are two possible values of z. Why is this so?
Answer:
0 9z or
Solution:
If a number is a multiple of 9, then the sum of its digits will be divisible by 9.
Sum of the digits of
31 5 3 1 5 9 z z z
Hence,
9 z
should be a multiple of 9.
This is possible when
9 z
is any one of these numbers 0, 9, 18, 27, and so on …
However, since z is a single digit number, this sum can be either 9 or 18. So, z should
be either 0 or 9.
Question 3
If 24xis a multiple of 3, where x is a digit, what is the value of x?
Answer:
Solution:
Since 24x is a multiple of 3, the sum of its digits is a multiple of 3.
Sum of the digits of
24 2 4 6 x x x
Hence,
6 x
is a multiple of 3.
This is possible when
6 x
is any one of these numbers 0, 3, 6, 9, and so on …
Since x is a single digit number, the sum of the digits can be 6 or 9 or 12 or 15 and
Thus, the value of x comes to 0 or 3 or 6 or 9 respectively.
Question 4
If 31z5 is a multiple of 3, where z is a digit, what might be the values of z?
Answer:
0, 3, 6 9z or
Solution:
Since 31z5 is a multiple of 3, the sum of its digits will be a multiple of 3.
That is,
3 1 5 9 zz
is a multiple of 3.
This is possible when
9 z
is any one of 0, 3, 6, 9, 12, 15, 18, and so on …
Since z is a single digit number, the value of
9 z
can only be 9 or 12 or 15 or 18
and thus, the value of x comes to 0 or 3 or 6 or 9 respectively.
So, z can have its value as any one of the four different values 0, 3, 6, or 9.