Exercise 15.1
Question 1
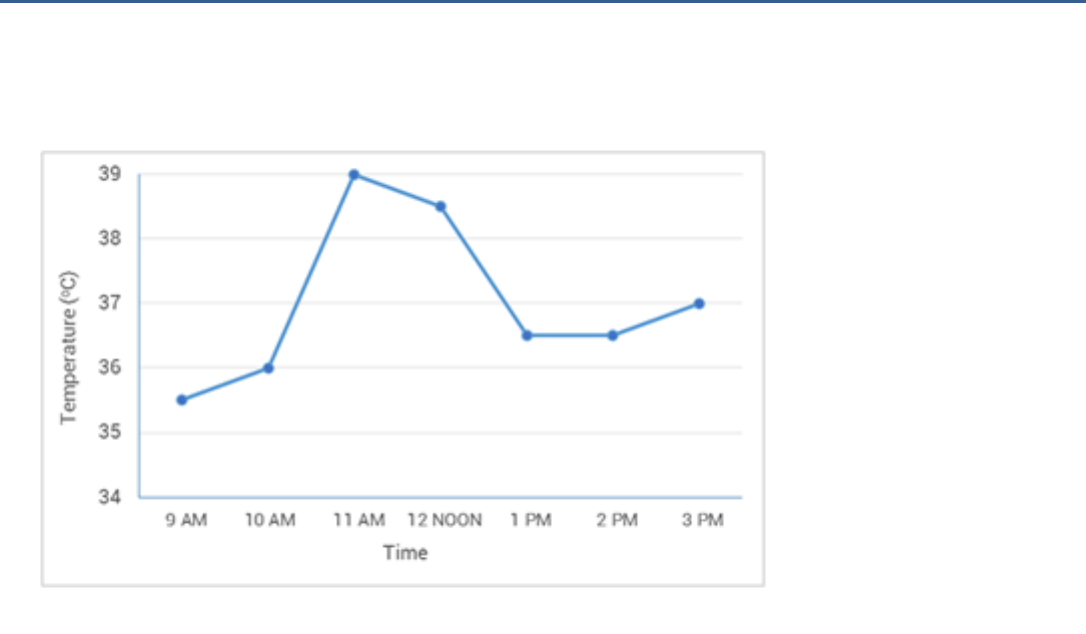
The following graph shows the temperature of a patient in a hospital,
recorded every hour.
(a) What was the patient’s temperature at 1 p.m?
(b) When was the patient’s temperature 38.5° C?
(c) The patient’s temperature was the same two times
during the period given.
What were these two times?
(d) What was the temperature at 1.30 p.m.?
How did you arrive at your answer?
(e) During which periods did the patient’s temperature
show an upward trend?
Answer:
(a) 36.5° C (b) 12 noon (c) 1 p.m., 2 p.m. (d) 36.5° C;
The point between 1 p.m. and 2 p.m. on the x-axis is equidistant from the
two points showing 1 p.m. and 2 p.m., so it will represent 1.30 p.m.
Similarly, the point on the y-axis, between 36° C and 37° C will
represent 36.5° C.
(e) 9 a.m. to 10 a.m., 10 a.m. to 11 a.m., 2 p.m. to 3 p.m.
Solution:
(a) The temperature at 1 p.m. is 36.5
o
C
(b) 12 noon
(c) 1 p.m. and 2 p.m.
(d) The temperature at 1.30 p.m. is 36.5
o
C.
The point between 1 p.m. and 2 p.m. on the x-axis is equidistant
from the two points showing 1 p.m. and 2 p.m., so it will
represent 1.30 p.m. Similarly the point on the y-axis, between
36
o
C and 37
o
C will represent 36.5
o
C.
(e) From 9 a.m. to 10 a.m., 10a.m. to 11 a.m. and 2 p.m. to 3 p.m., the
temperature of the patient shows an upward trend.
Question 2
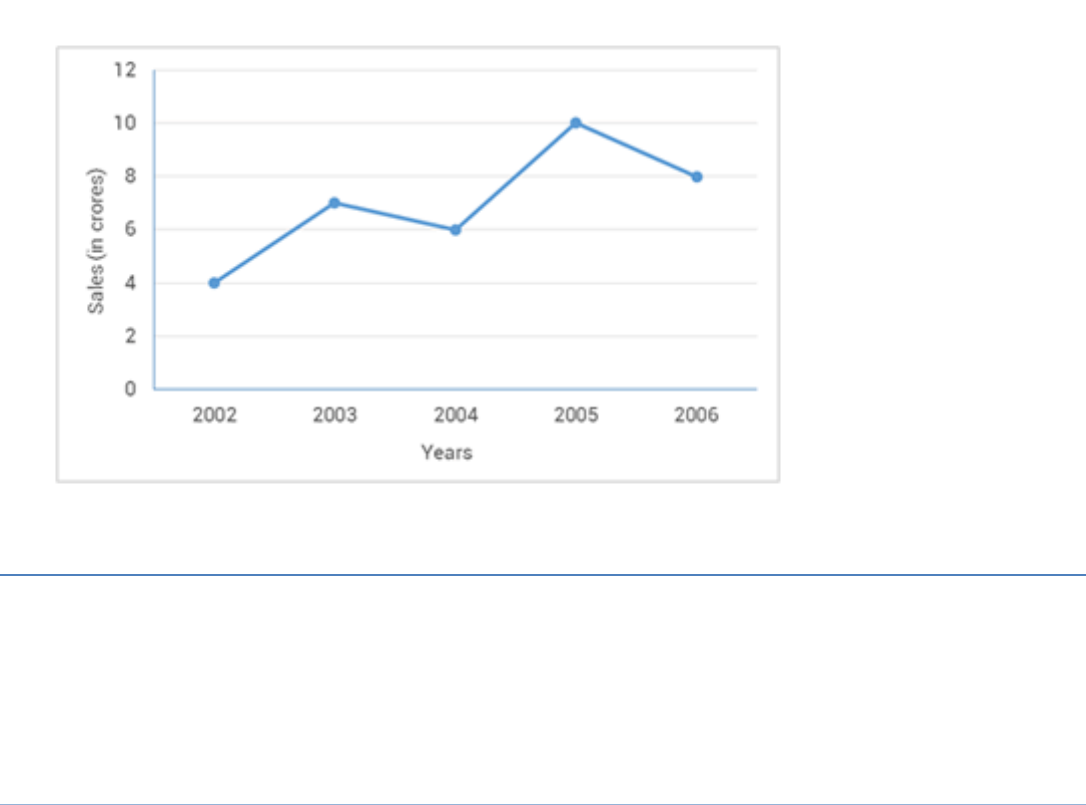
The following line graph shows the yearly sales figures for a
manufacturing company.
(a) What were the sales in?
(i) 2002 (ii) 2006?
(b) What were the sales in?
(i) 2003 (ii) 2005
(c) Compute the difference between the sales in 2002 and 2006.
(d) In which year was there the greatest difference between the sales
as compared to its previous year?
Answer:
(a) (i) Rs. 4 crore (ii) Rs. 8 crore
(b) (i) Rs.7 crore (ii) Rs.10 crore (approx.)
(c) Rs. 4 crore
(d) 2005
Solution:
(a) From the line graph,
(i) Sales in 2002 is Rs. 4 crore.
(ii) Sales in 2006 is Rs. 8 crore.
(b) From the line graph,
(i) Sales in 2003 is Rs. 7 crore.
(ii) Sales in 2005 is Rs. 10 crore.
(c) From line graph,
Sales in 2002 = Rs. 4 crore; Sales in 2006 = Rs. 8 crore.
Difference between the sales in 2002 and 2006 = Rs. (8– 4) crore
= Rs. 4 crore
(d) Difference of sales between 2003 and 2004 = (7 – 6) crore = 1 crore
Difference of sales between 2004 and 2005 = (10 – 6) crore = 4 crore
The year in which the difference was greatest as compared to that of
the previous year is 2005
Question 3
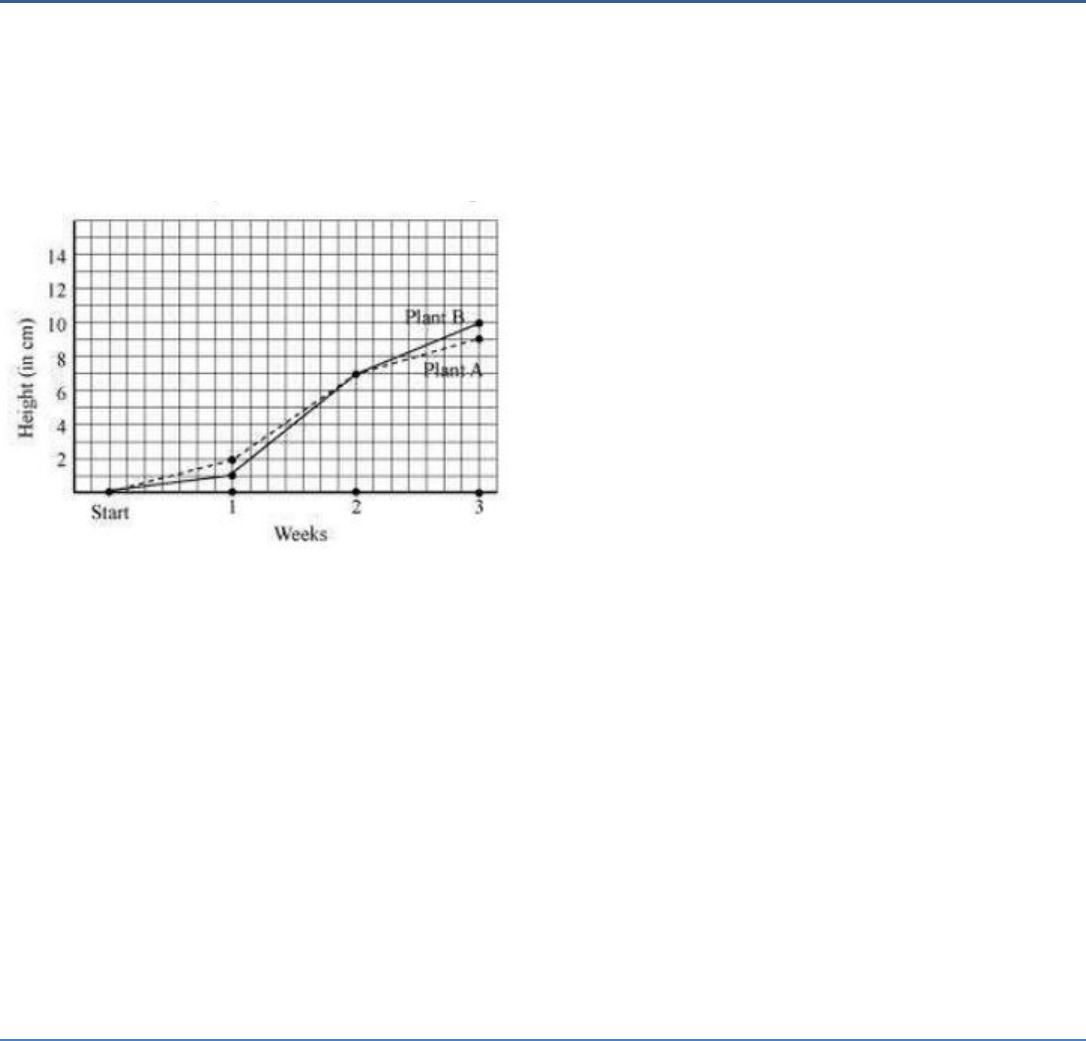
For an experiment in Botany, two different plants, plant A and plant B
were grown under similar laboratory conditions.
Their heights were measured at the end of each week for 3 weeks.
The results are shown by the following graph.
(a) How high was Plant A after (i) 2 weeks (ii) 3 weeks?
(b) How high was Plant B after (i) 2 weeks (ii) 3 weeks?
(c) How much did Plant A grow during the 3
rd
week?
(d) How much did Plant B grow from end of the 2nd week
to the end of the 3rd week?
(e) During which week did plant A grow most?
(f) During which week did plant B grow least?
(g) Were the two plants of the same height during any week shown here?
Specify.
Answer:
(a) (i) 7 cm (ii) 9 cm (b) (i) 7 cm (ii) 10 cm (c) 2 cm
(d) 3 cm (e) Second week (f) First week

(g) At the end of the 2nd week
Solution:
(a) (i) Height of the plant A after 2 weeks = 7 cm.
(ii) Height of the plant A after 3 weeks = 9 cm.
(b) (i) Height of the plant B after 2 weeks = 7 cm.
(ii) Height of the plant B after 3 weeks = 10 cm.
(c) During the 3rd week, the plant A grew = (9 – 7) cm = 2 cm.
(d) Growth of the plant B from the end of the 2
nd
week to the end
of the 3
rd
week = (10 – 7) cm = 3 cm.
(e) During the 2
nd
week, the plant A grew most i.e., (7 – 2) cm = 5cm.
(f) During the 1
st
week, the plant B grew least.
(g) At the end of the 2
nd
week, both the plants A & B were of same
height i.e., 7 cm.
Question 4
The following graph shows the temperature forecast and the actual
temperature for each day of a week.
(a) On which days was the forecast temperature the same as the actual
temperature?
(b) What was the maximum forecast temperature during the week?
(c) What was the minimum actual temperature during the week?
(d) On which day did the actual temperature differ the most from the
forecast temperature?
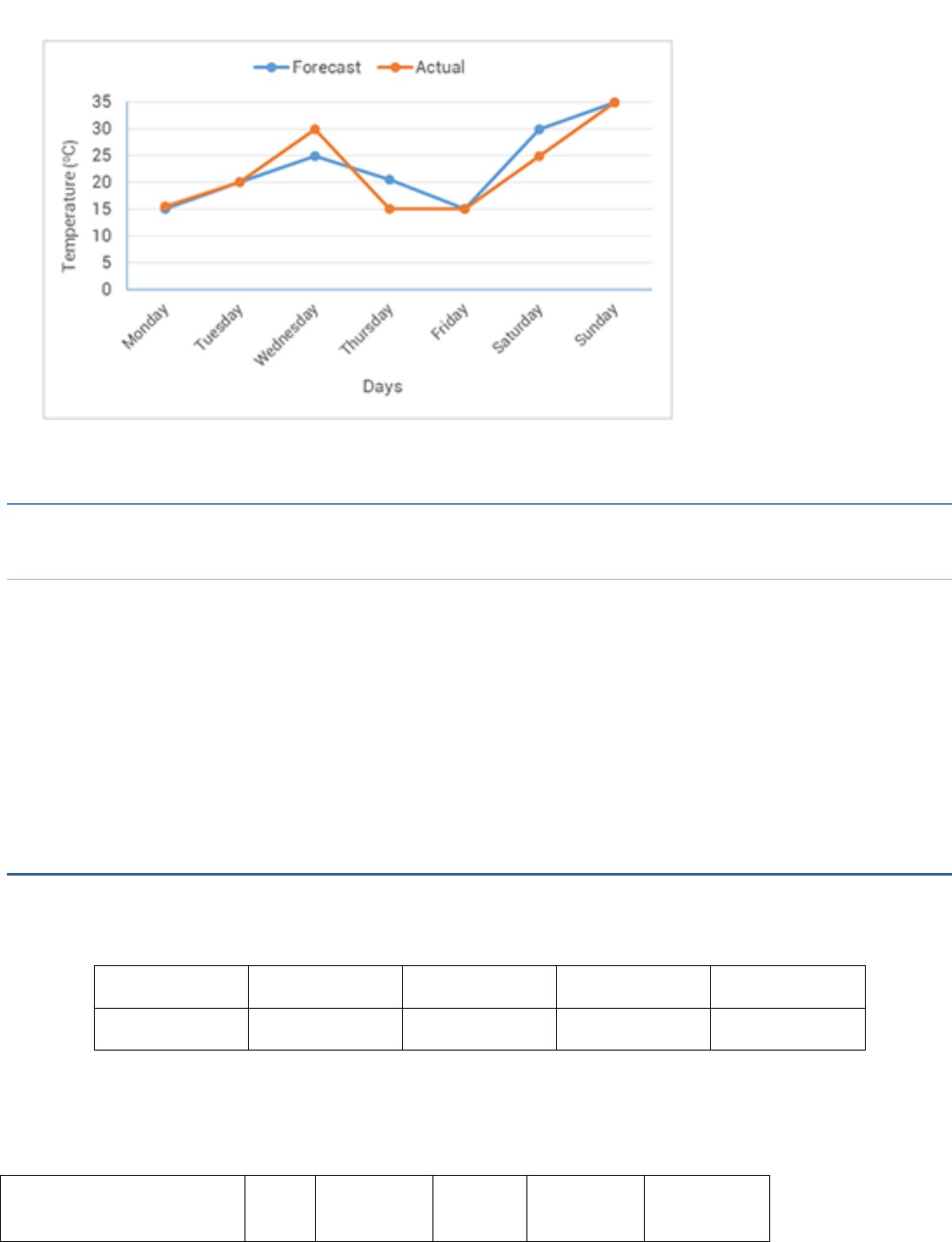
Answer:
(a) Tue, Fri, Sun (b) 35° C (c) 15° C (d) Thurs
Solution:
(a) Tuesday, Friday and Sunday.
(b) On Sunday, the maximum forecast temperature was 35
o
C.
(c) On Thursday and Friday, the minimum actual temperature was 15
o
C
(d) On Thursday, the actual temperature differ the most from the forecast
temperature i.e., 22.5
o
C – 15oC = 7.5oC.
Question 5
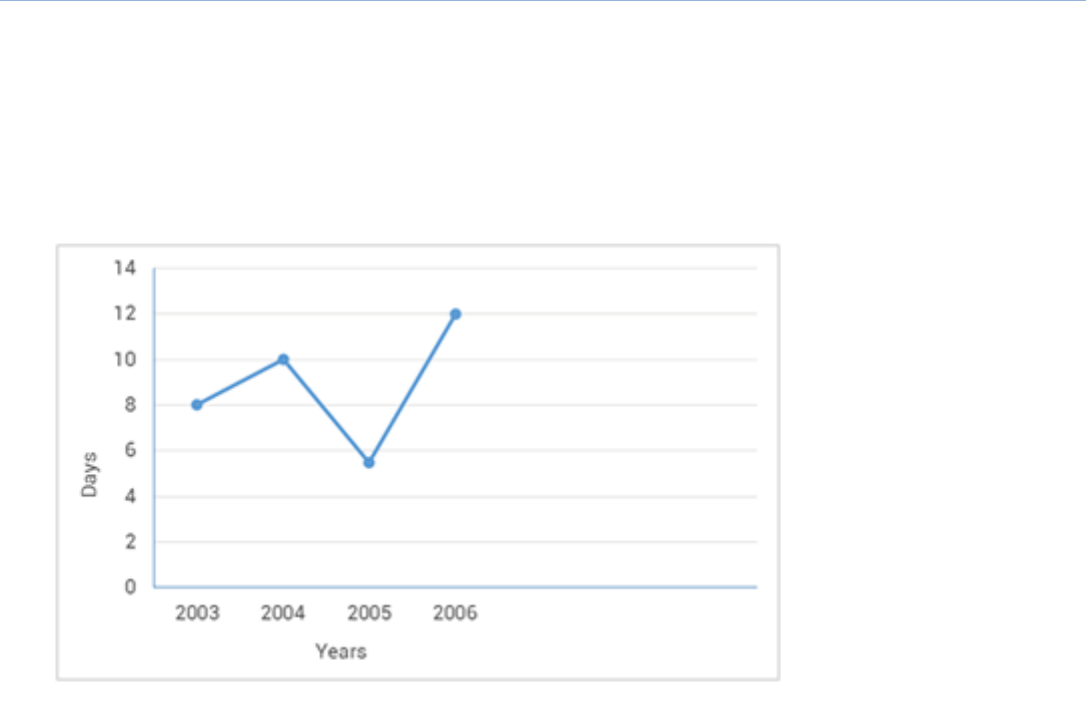
Use the tables below to draw linear graphs:
The number of days a hill side city received snow in different years.
Year
2003
2004
2005
2006
Days
8
10
5
12
Population (in thousands) of men and women in a village in different
years.
Years
2
003
2004
2005
2006
2007
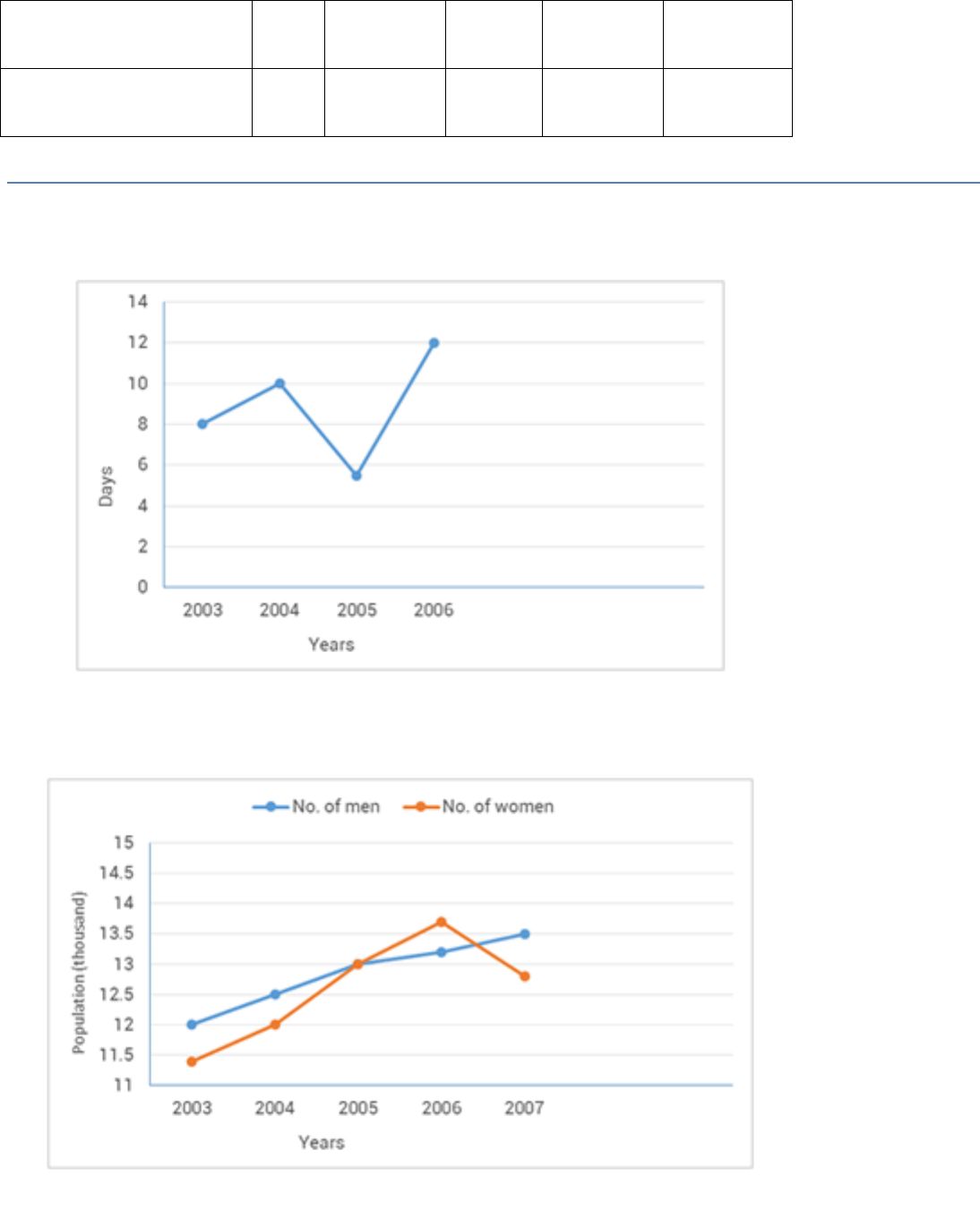
Number of Men
1
2
12.5
13
13.2
13.5
Number of Women
1
1.3
11.9
13
13.6
12.8
Answer:
(a)
(b)
Solution:
(a) By taking the years on the x-axis and the number of days on the
y-axis and taking the scale as 1 unit = 2 days on the y-axis and 2 unit = 1
year on the x-axis, the linear graph of the given information can be drawn
as follows.
(b) By taking the years on the x-axis and population on the y-axis and the scale as1
unit = 0.5 thousand on the y-axis and 2 unit = 1 year on the x-axis, the linear
graph of the given information can be drawn as follows.
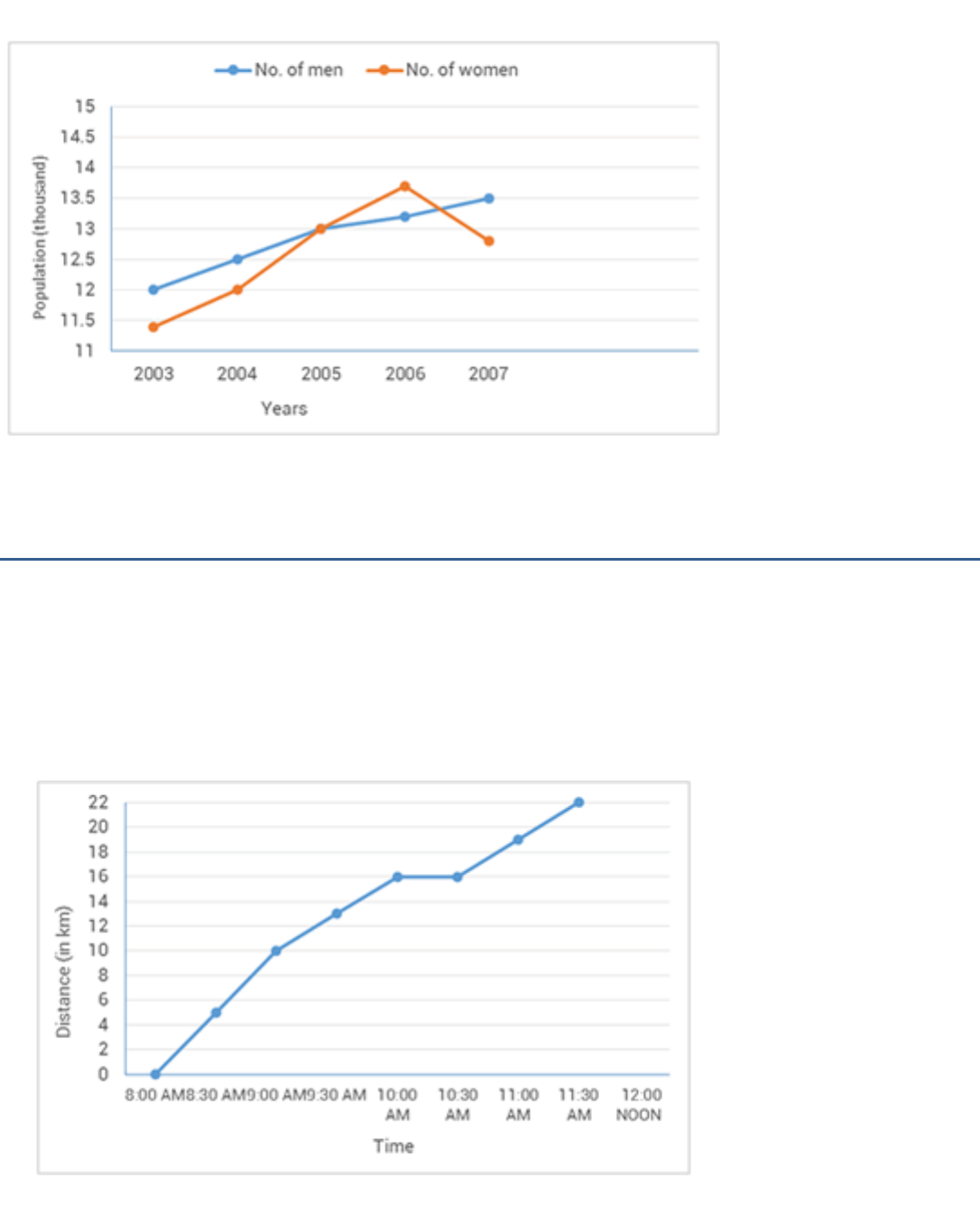
Question 6
A courier-person cycles from a town to a neighboring suburban area to deliver a
parcel to a merchant.
His distance from the town at different times is shown by the
following graph:

(a) What is the scale taken for the time axis?
(b) How much time did the person take for the travel?
(c) How far is the place of the merchant from the town?
(d) Did the person stop on his way? Explain.
(e) During which period did he ride fastest?
Answer:
(a) 4 units = 1 hour (b)
1
3 hours
2
(c) 22 km
(d) Yes; this is indicated by the horizontal part of the graph
(10 a.m. - 10.30 a.m.)
(e) Between 8 a.m. and 9 a.m.
Solution:
(a) The scale taken for the time axis is 4 units = 1 hour.
(b) 3
1
2
hours.
(c) 22 km
(d) Yes, this is indicated by the horizontal part of the graph i.e., 10 a.m.
to10.30a.m.
During this period, the distance covered remained to be16 km
(e) Between 8 a.m. to 9 a.m.
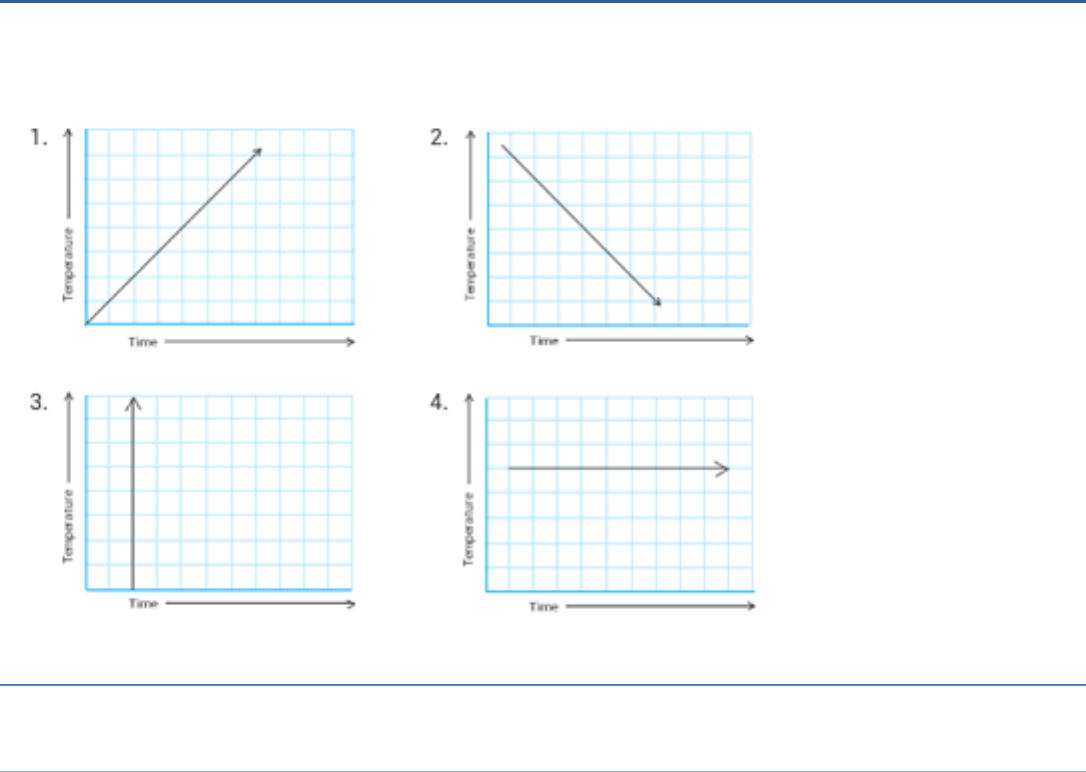
Question 7
Can there be a time- temperature graph as follows?
Justify your answer.
Answer:
(iii) is not possible
Solution:
(i) Yes, it may be a time- temperature graph because with change in
time, temperature may increase,
For example, day time in summer season.
(ii) Yes, it may be possible that with change in time, temperature may
fall uniformly.
For example, during night in winter season.
(iii) No, it cannot be a time-temperature graph.
Here, temperature is changing without any change of time,
which is impossible.
(iv) Yes, it may be possible for a short span of time that the temperature remains to
be constant.
Exercise 15.2
Question 1
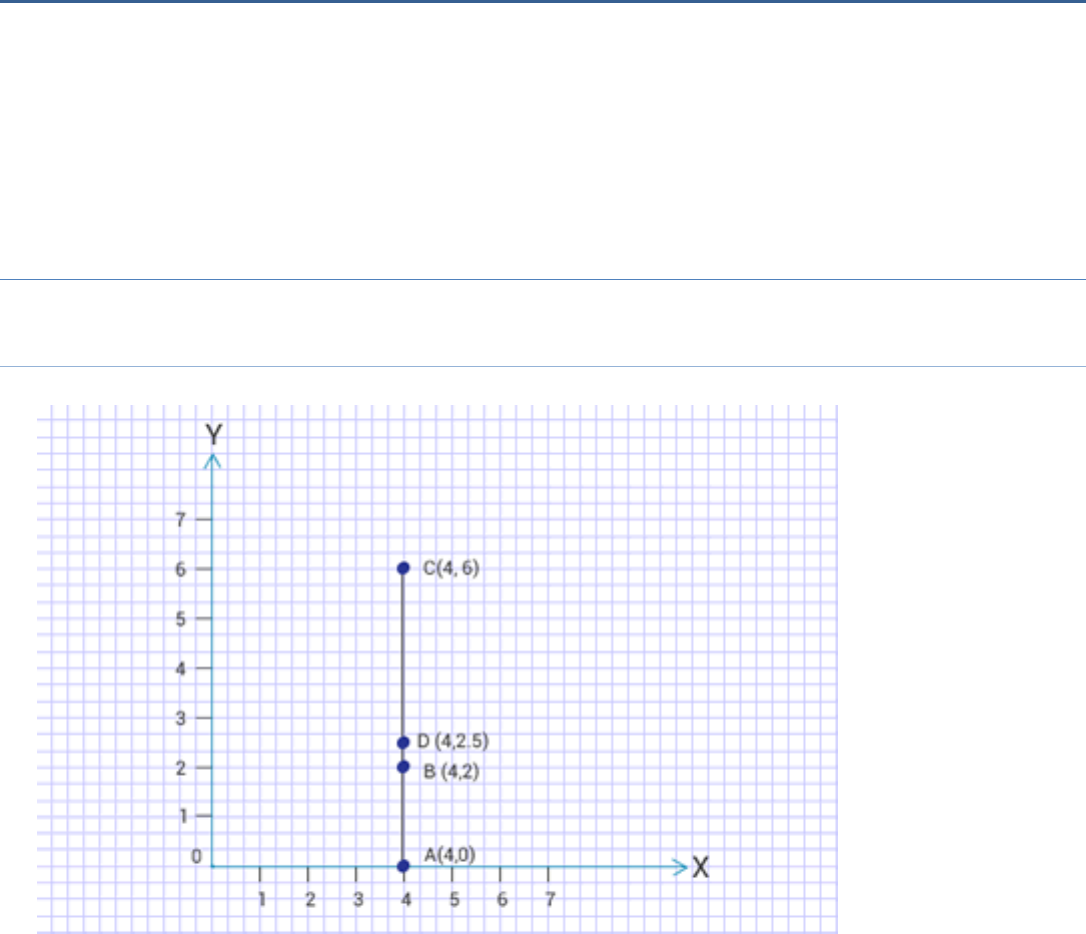
Plot the following points on a graph sheet.
Verify if they lie on a line:
(i) A (4, 0), B(4, 2), C(4, 6), D(4, 2.5)
(ii) P (1, 1), Q(2, 2), R(3, 3), S(4, 4)
(iii) K (2, 3), L(5, 3), M(5, 5), N(2, 5)
Answer:
Points in (a) and (b) lie on a line; Points in (c) do not lie on a line
Solution:
(i) Yes, all the points lie on a line
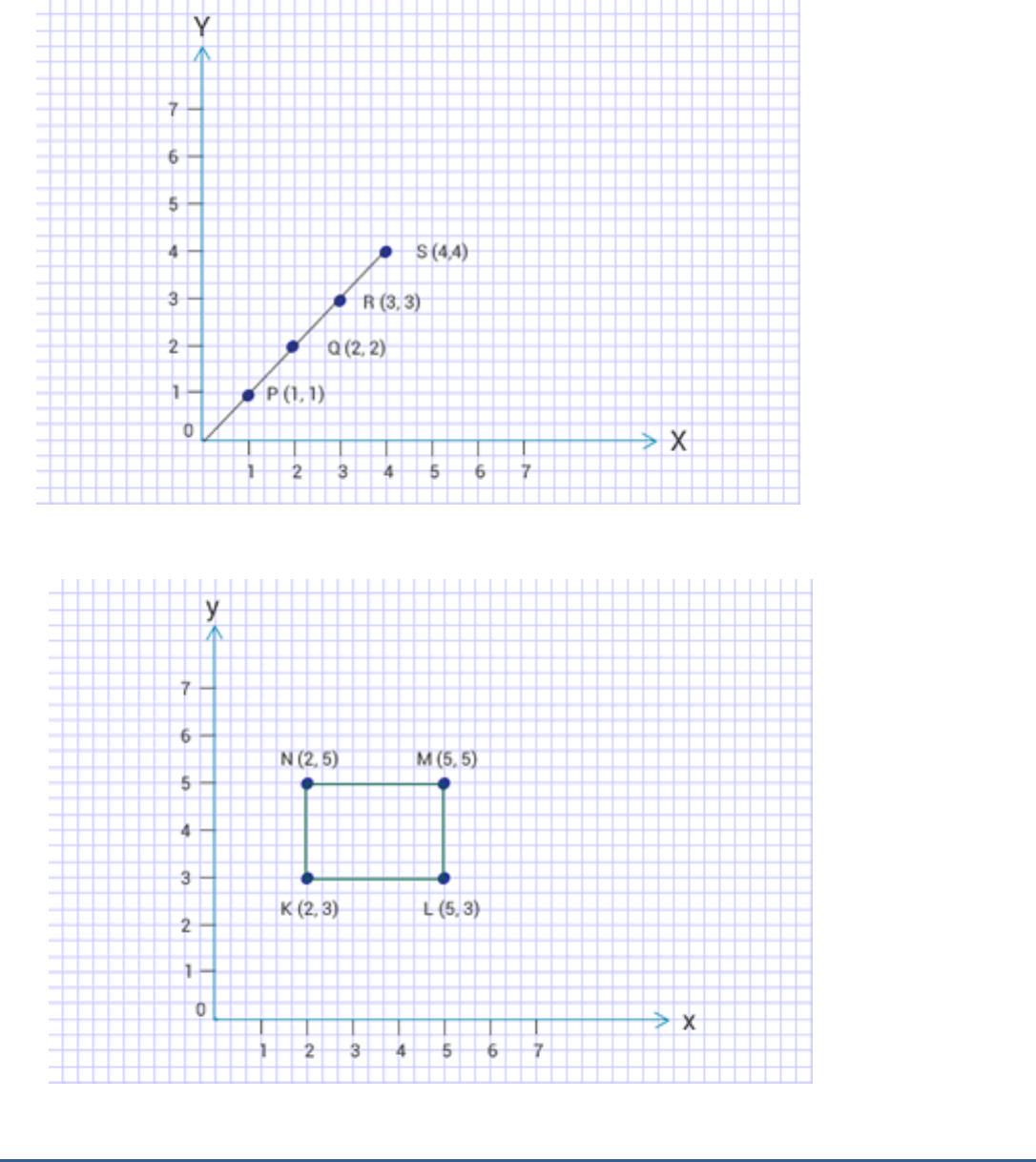
(ii) Yes, all the points lie on a line.
(iii) No, all the points do not lie on a line.
Question 2
Draw the line passing through (2, 3) and (3, 2).
Find the coordinates of the points at which this meets the
x-axis and y-axis.
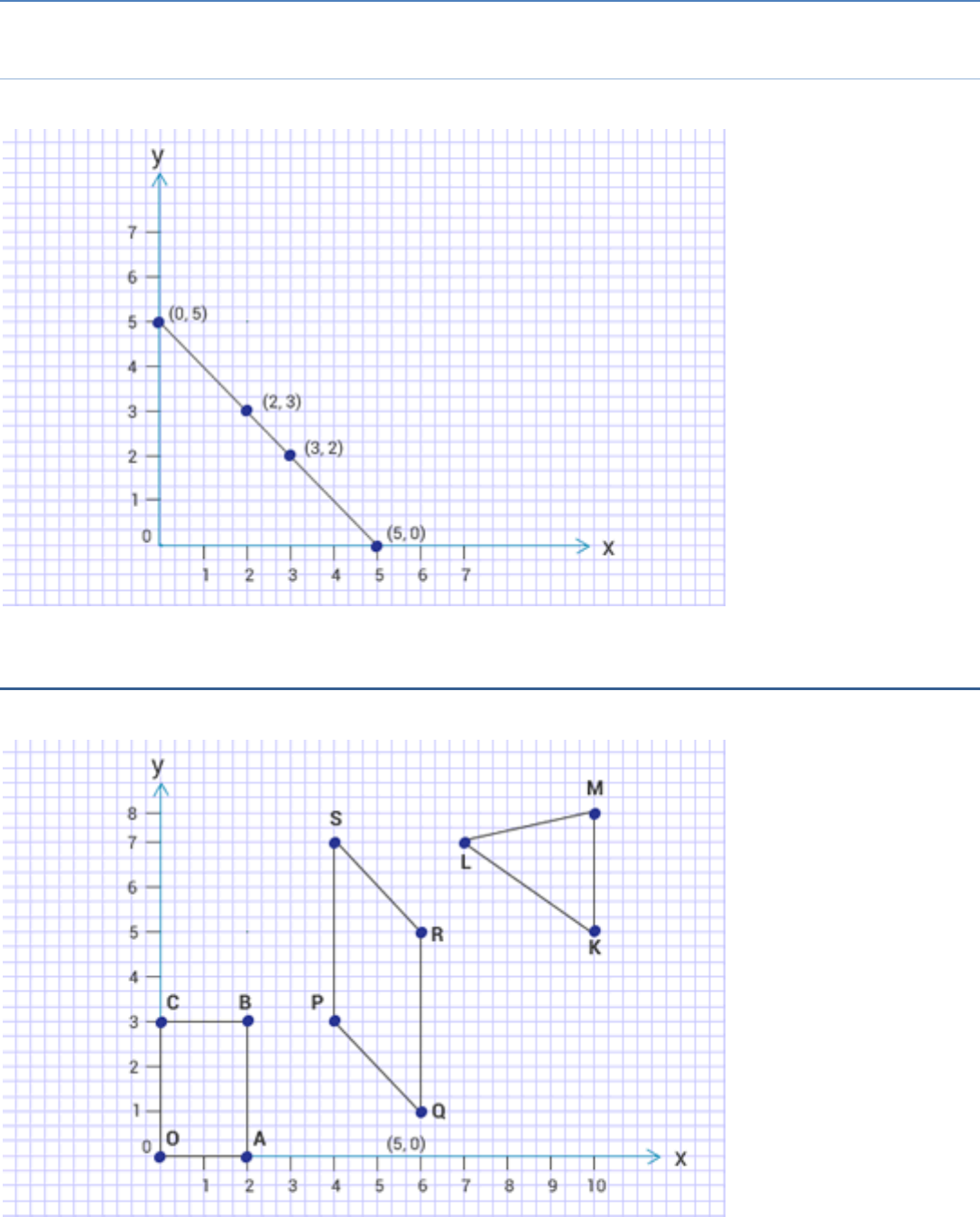
Answer:
The line will cut x-axis at (5, 0) and y-axis at (0, 5)
Solution:
The coordinates of the point P and Q are P (5, 0) and Q (0, 5)
Question 3
Write the coordinates of the vertices of each of these adjoining figures.
Answer:
O (0, 0), A (2, 0), B (2, 3), C (0, 3), P (4, 3), Q (6, 1), R (6, 5), S (4, 7),
K (10, 5), L (7, 7), M (10, 8)
Solution:
(i) Coordinates of the vertices of the rectangle are:
O (0, 0), A (2, 0), B (2, 3), C (0, 3).
(ii) Coordinates of the vertices of the parallelogram are:
P (4, 3), Q (6, 1), R (6, 5), S (4, 7).
(iii) Coordinates of the vertices of the triangle are:
L (7, 7), K (10, 5), M (10, 8).
Question 4
Sate whether True of False.
Correct those statements which are false.
(i) A point whose x coordinate is zero and y-coordinate is non-zero
will lie on the y axis.
(ii) A point whose y co-ordinate is zero and x-coordinate is 5 will lie on y-axis.
The coordinates of the origin are (0, 0)
Answer:
(i) True (ii) False (iii) True
Solution:
(i) True
(ii) False.
(iii) A point whose y co-ordinate is zero and x-coordinate is 5 will lie on the x-axis.
True.

Exercise 15.3
Question 1
Draw the graph for the following tables of values,
with suitable scales on the axes.
(a) Cost of apples
(b) Distance travelled by a car
(i) How much distance did the car cover during the period 7.30 a.m.
to 8 a.m.?
(ii) What was the time when the car had covered a distance of 100 km
since its start?
(iii) Interest on deposits for a year.
(i) Does the graph pass through the origin?
(ii) Use the graph to find the interest on Rs 2500 for a year.
(iii) To get an interest of Rs. 280 per year, how much money should be
deposited?
Deposit ( in Rs.) 1000 2000 3000 4000 5000
Simple Interest (in Rs.) 80 160 240 320 400
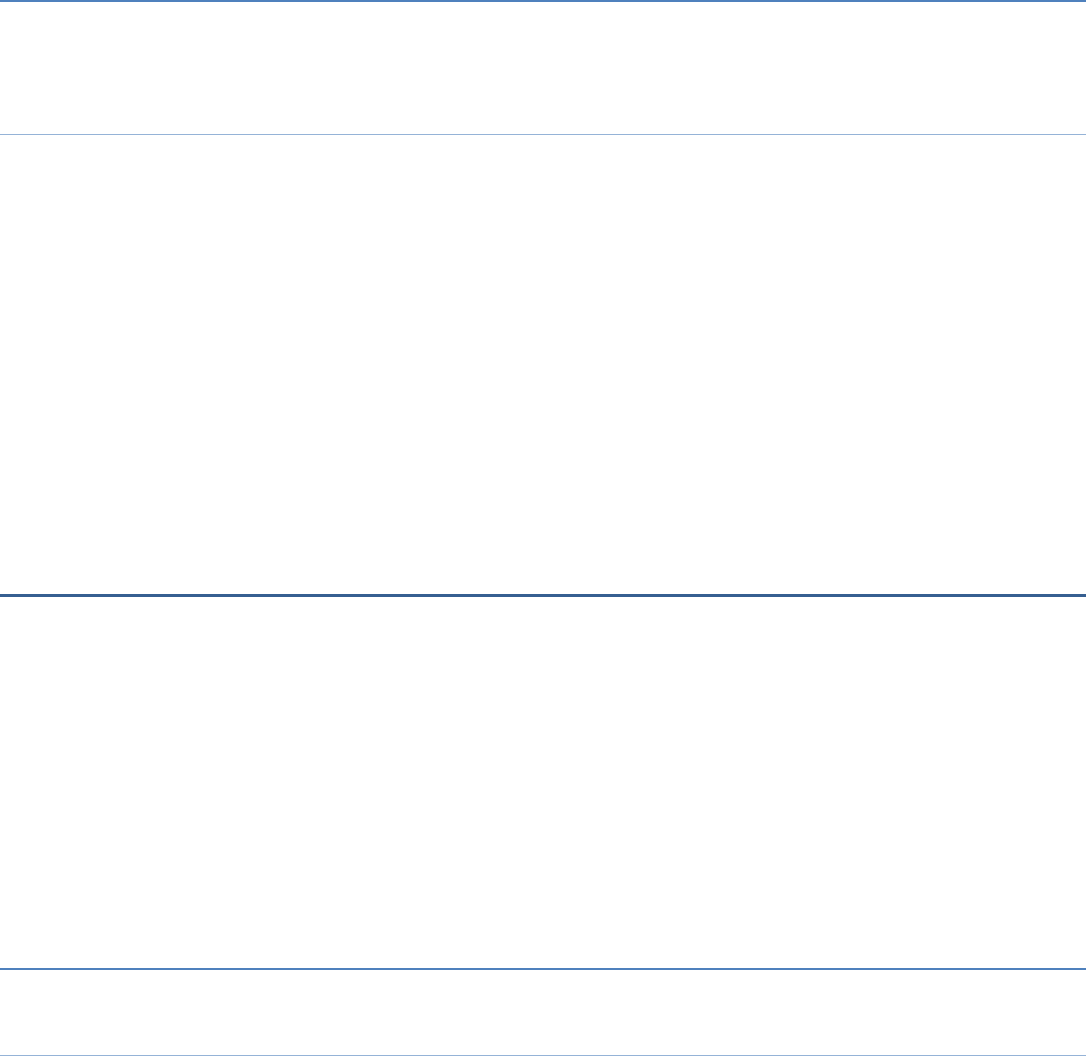
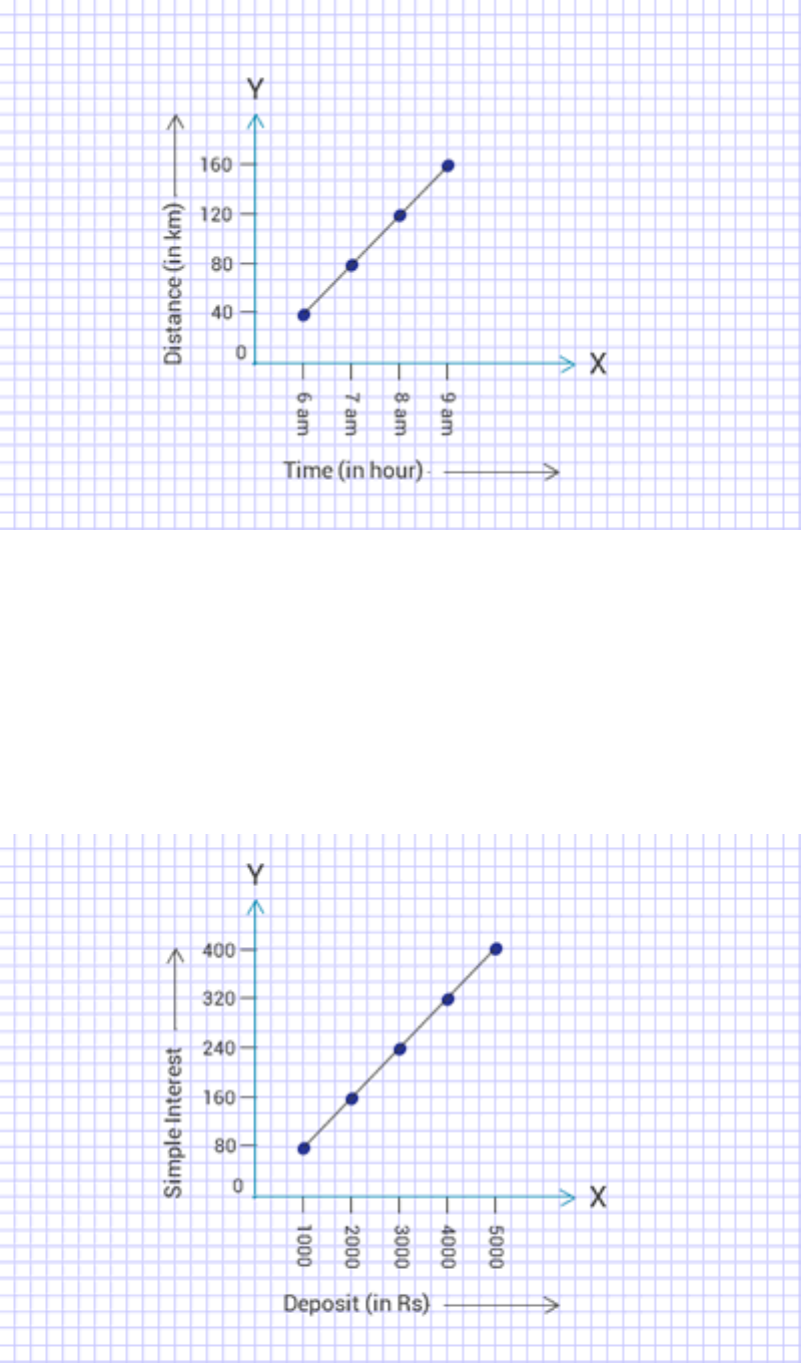
Number of apples 1 2 3 4 5
Cost (in Rs) 5 10 15 20 25
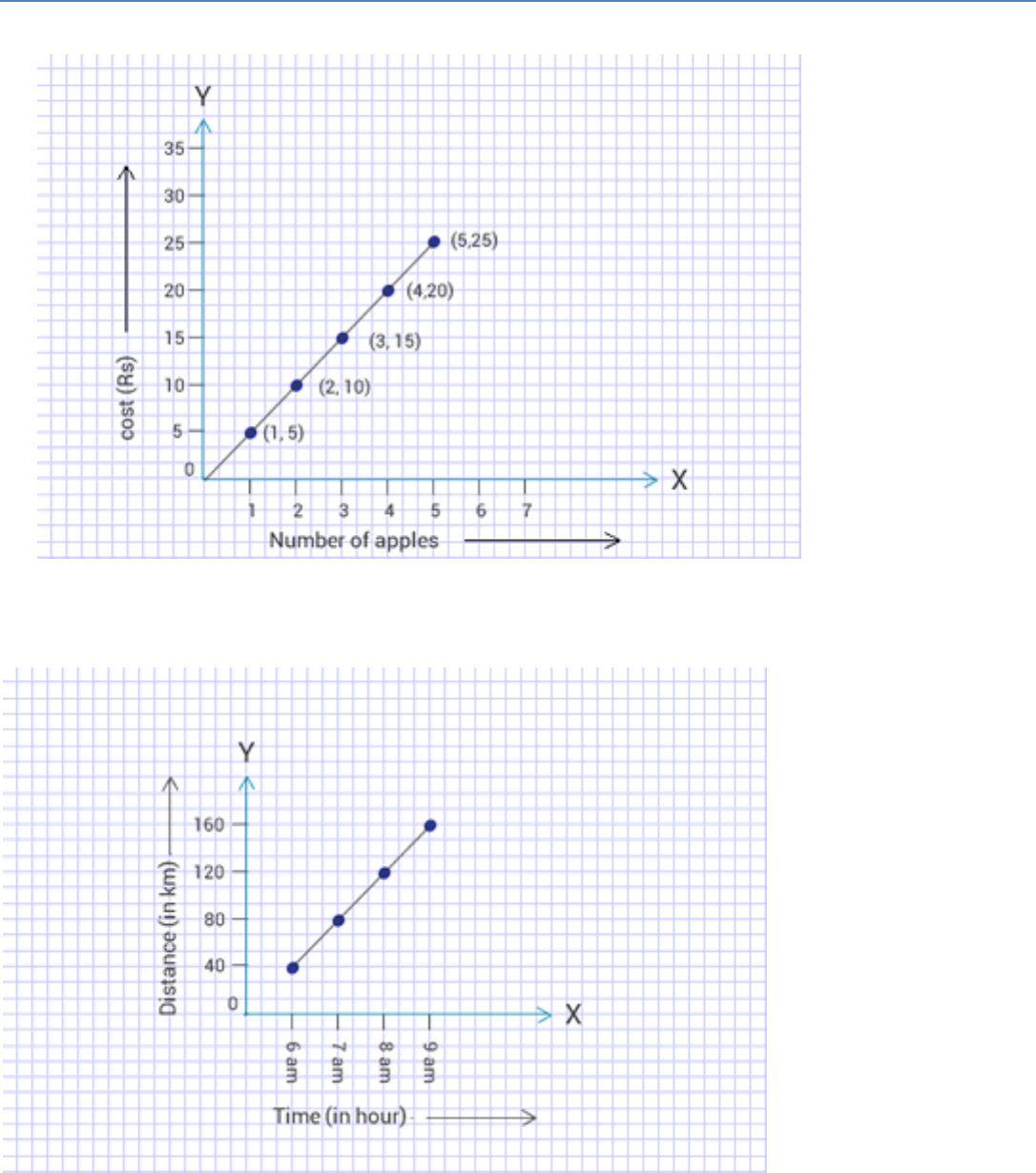
Time (in hours) 6 a.m. 7 a.m. 8 a.m. 9 a.m.
Distance (in km) 40 80 120 160
Answer:
(a)
(b) (i) 20 km (ii) 7.30 a.m.
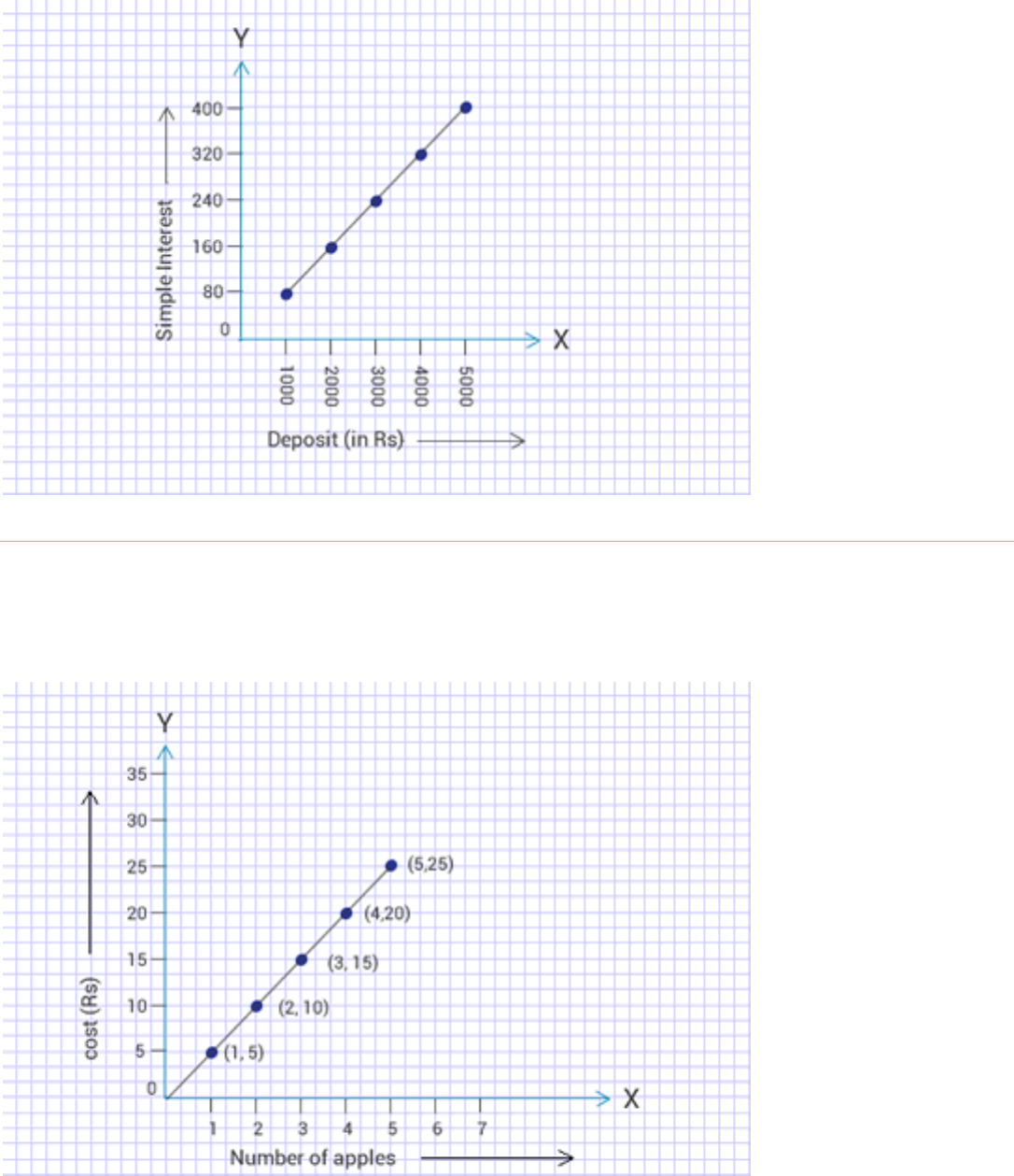
(c) (i) Yes (ii) Rs. 200 (iii) Rs. 3500
Solution:
(a)
x-axis 1 unit = No. of apples
y-axis 1 unit = Rs. 5
(b)
On x axis there should be a kink (a break) near the origin.
(i) Distance traveled by the car during the period 7.30 a.m. to 8 a.m.
= (120 – 100) km = 20 km
(ii) At 7.30 a.m. the car had covered a distance of 100 km.
(c) (i) Yes
(ii) Interest on Rs 2500 for 1 year = Rs 200
On Rs 3500, an interest of Rs 280 is obtained.
Question 2
Draw a graph for the following:
“Is it a linear graph?”
(i)
(ii)
Is it a linear graph?
Answer:
(i) Yes (ii) No
Solution:
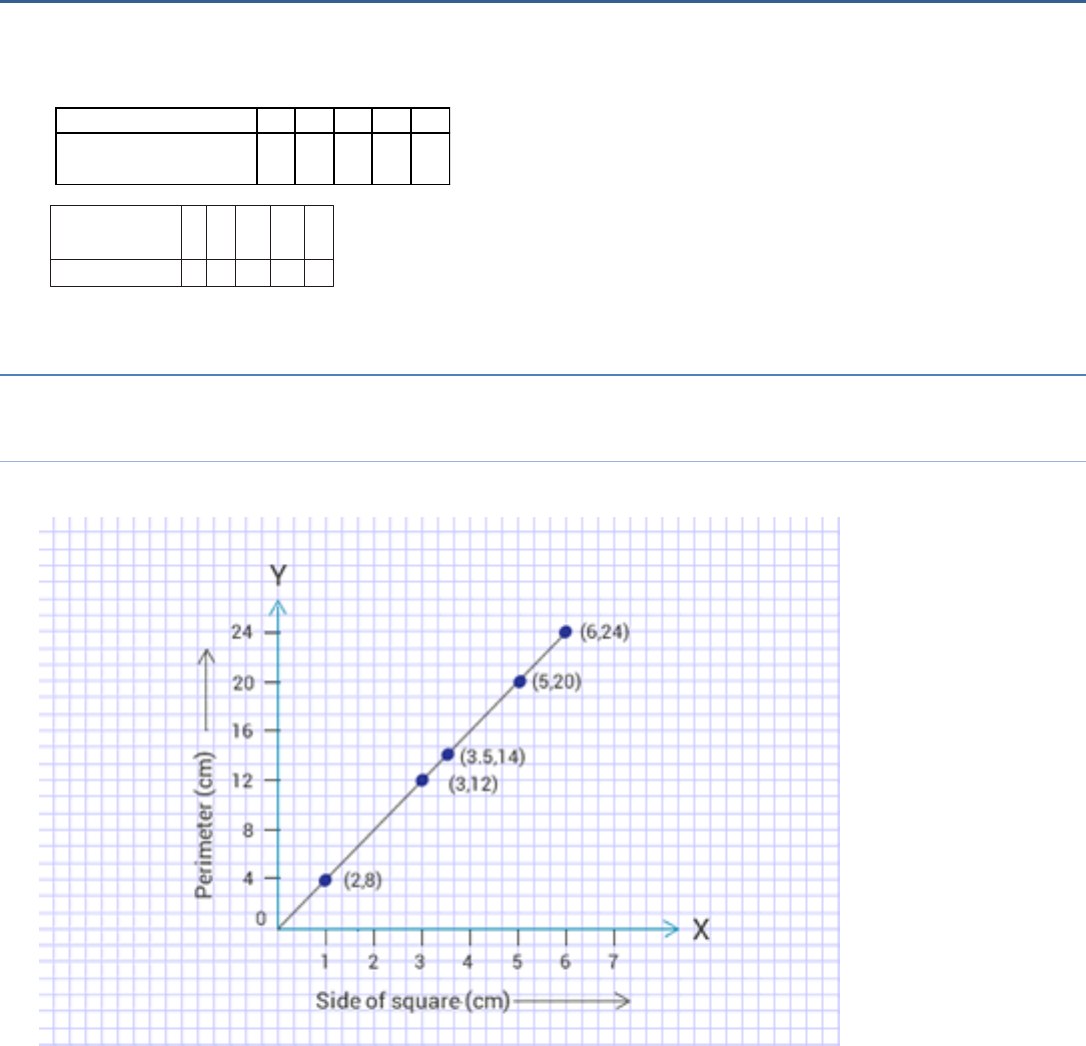
(i) Yes, it is a linear graph.
Side of square (in cm) 2 3 3.5 5 6
Perimeter (in cm) Is it a
linear graph
8 12 14 20 24
Side of square 2 3 4 5 6
(in cm)
Area (in cm ) 4 9 16 25 36
2
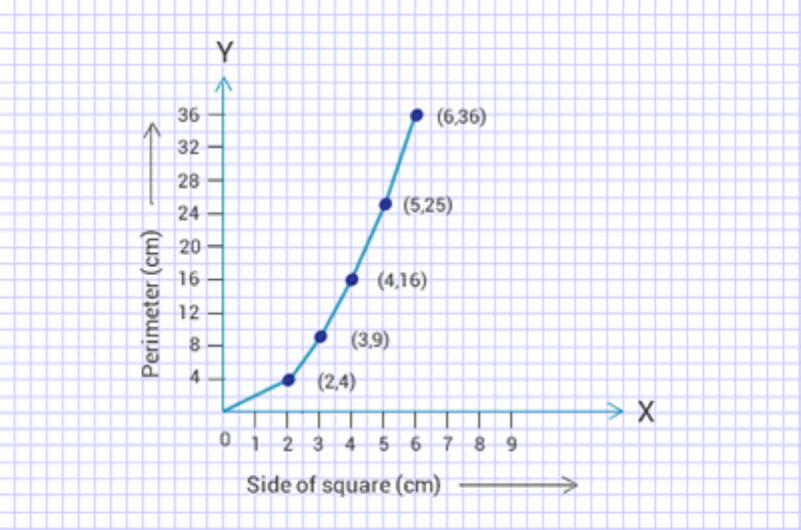
(ii) No, it is not a linear graph.