Lesson: Factorisation

Exercise 14.1

Question 1

Find the common factors of the given terms.

(i) 12x, 36

(ii) 2y, 22xy

(iii) 14pq, 28p

2

q

2

(iv) 2x, 3x

2

, 4

(v) 6abc, 24ab

2

, 12 a

2

b

(vi) 16x

3

, – 4x

2

, 32x

(vii) 10pq, 20qr, 30rp

(viii) 3x

2

y

3

, 10x

3

y

2

, 6x

2

y

2

z

Answer:

(i) 12 (ii) 2y (iii) 14pq (iv) 1

(v) 6ab (vi) 4x (vii) 10 (viii) x

2

y

2

Solution:

(i) 12x, 36

12 2 2 3xx   

36 2 2 3 3   

So, the common factor

2 2 3 12   

(ii) 2y, 22xy

22yy

22 2 11xy x y   

So, the common factor

22yy  

(iii) 14pq, 28p

2

q

2

14 2 7pq p q   

22

28 2 2 7p q p p q q      

So, the common factor

2 7 14p q pq    

(iv) 2x, 3x

2

, 4

22xx

2

33x x x  

4 2 2

We find that there is no common factor except one, as 1 is a factor of every term.

(v) 6abc, 24ab

2

, 12 a

2

b

6 2 3abc a b c    

2

24 2 2 2 3ab a b b      

2

12 2 2 3a b a a b     

The common factor

23ab   

6ab

.

(vi) 16x

3

, – 4x2, 32x

3

16 2 2 2 2x x x x      

 

2

4 2 2 1x x x      

32 2 2 2 2 2xx     

The common factor

22x  

4x

.

(vii) 10pq, 20qr, 30rp

10 2 5pq p q   

20 2 2 5qr q r    

30 2 3 5rp r p    

The common factor

25

10

(viii) 3x2y3, 10x

3

y

2

, 6x

2

y

2

z

23

33x y x x y y y     

32

10 2 5x y x x x y y      

22

6 2 3x y z x x y y z      

The common factor

22

xy

Question 2

Factorize the following expressions.

(i) 7x – 42

(ii) 6p – 12q

(iii) 7a

2

+ 14a

(iv) –16z + 20z3

(v) 20l

2

m + 30alm

(vi) 5x

2

y – 15 xy

2

(vii) 10a

2

– 15b2

+ 20c2

(viii) – 4a

2

+ 4ab – 4ca

(ix) x

2

y z + xy

2

z + xyz

2

(x) ax

2

y + bxy

2

+ cxyz

Answer:

(i) 7(x – 6)

(ii) 6(p – 2q)

(iii) 7a (a + 2)

(iv) 4z (– 4 + 5z2)

(v) 10 lm (2l + 3a)

(vi) 5xy(x – 3y)

(vii) 5(2a

2

– 3b

2

+ 4c

2

)

(viii) 4a (– a + b – c)

(ix) xyz (x + y + z)

(x) xy (ax + by + cz)

Solution:

(i)

7 42x 

   

7 7 6x   

 

76x  

 

76x

.

(ii)

6 12pq

   

6 6 2pq    

 

62pq

.

(iii)

2

7 14aa

   

7 2 7a a a     

   

72aa   

 

72aa

.

(iv)

3

16 20zz

   

2 2 2 2 2 2 5z z z z           

     

2 2 2 2 5z z z



       





 

2

4 4 5zz

(v)

2

20 30l m alm

   

2 2 5 2 3 5l l m a l m           

   

2 5 2 3l m l a       

 

10 2 3lm l a

(vi)

22

5 15x y xy

   

5 5 3x x y x y y        

   

53x y x y



    



 

53xy x y

.

(vii)

2 2 2

10 15 20a b c

     

2 5 3 5 2 2 5a a b b c c            





 

5 2 3 2 2a a b b c c          

 

2 2 2

5 2 3 4a b c  

.

(viii)

2

4 4 4a ab ca  

     

2 2 2 2 2 2a a a b c a            

   

22a a b c      

 

4a a b c   

.

(ix)

2 2 2

x yz xy z xyz

     

x x y z x y y z x y z z           

   

x y z x y z     

 

xyz x y z  

.

(x) ax

2

y + bxy

2

+ cxyz

     

a x x y b x y y c x y z           

 

xy ax by cz  

Question 3

Factorize.

(i) x

2

+ xy + 8x + 8y (ii) 15xy – 6x + 5y – 2 (iii) ax + bx – ay – by

(iv) 15pq + 15 + 9q + 25p (v) z – 7 + 7xy – xyz

Answer:

(i) (x + 8) (x + y) (ii) (3x + 1) (5y – 2) (iii) (a + b) (x – y)(iv) (5p + 3) (3q + 5)

(v) (z – 7) (1 – xy)

Solution:

(i)

2

88x xy x y  

2

( ) (8 8 )x xy x y   

(Grouping the first two and the last two terms)

   

8x x y x y   

  

8x y x  

.

(ii)

15xy – 6x + 5y – 2

 

(15 6 ) 5 2xy x y   

(Grouping the first two and the last two terms)

   

3 5 2 1 5 2x y y    

  

5 2 3 1yx  

.

(iii) ax + bx – ay – by

Grouping the first two terms,

ax bx

 

x a b

Hence,

ax bx ay by  

 

()ax bx ay by    

(Grouping the first two and the last two terms)

   

x a b y a b



    



 

()x a b y a b   

  

a b x y  

(iv)

15 15 9 25pq q p  

   

15 25 15 9pq p q   

(Rearranging and grouping the terms)

       

5 3 5 5 5 3 3p q p q

   

          

   

   

   

5 3 5 3 5 3p q q   

  

5 3 3 5pq  

(v) z – 7 + 7xy – xyz

   

77z xy xyz   

(Grouping the first two and the last two terms)

   

77z xy z   

   





7 1 1z xy   

  

71z xy  

.

Exercise 14.2

Question 1

Factorise the following expressions.

(i) a

2

+ 8a + 16 (ii) p

2

– 10p + 25 (iii) 25m

2

+ 30m + 9

(iv) 49y

2

+ 84yz + 36z

2

(v) 4x

2

– 8x + 4

(vi) 121b

2

– 88bc + 16c

2

(vii) (l + m)

2

– 4lm (Hint: Expand ( l + m)

2

first)

(viii) a

4

+ 2a

2

b

2

+ b

4

Answer:

(i)

  

44aa

(ii)

 

2

5p 

(iii)

 

2

53m 

(iv)

 

2

76yz

(v)

 

2

41x 

(vi)

 

2

11 4bc

(vii)

 

2

lm

(viii)

 

2

22

ab

Solution:

(i) a

2

+ 8a + 16













2

2 4 4aa    

Applying the identity

 

2

22

2a ab b a b   

,

The given expression reduces to

 

2

4a 

  

44aa  

.

(ii)

2

10 25pp









22

2 5 5pp    

 

2

5p

(Applying the identity

 

2

22

2a b a ab b   

)

(iii)

2

25 30 9mm









2

5 2 5 3 3mm    

 

2

53m

.

(iv)

22

49 84 36y yz z

















22

7 2 7 6 6y y z z    

 

2

76yz

.

(v)

2

4 8 4xx

 

2

4 2 1xx  









22

4 2 1 1xx



  



 

2

41x

.

(vi)

22

121 88 16b bc c

















22

11 2 11 4 4b b c c  

 

2

11 4bc

.

(vii)

 

2

4l m lm

22

24l lm m lm   

22

2l lm m  

 

2

lm

.

(viii)

4 2 2 4

2a a b b

      

22

2 2 2 2

2a a b b  

 

2

22

ab

.

Question 2

Factorize.

(i) 4p

2

– 9q

2

(ii) 63a

2

– 112b

2

(iii) 49x

2

– 36

(iv) 16x

5

– 144x

3

(v) (l + m)

2

– (l – m)

2

(vi) 9x

2

y

2

– 16

(vii) (x

2

– 2xy + y

2

) – z

2

(viii) 25a

2

– 4b

2

+ 28bc – 49c

2

Answer:

(i)

  

2 3 2 3p q p q

(ii)

  

7 3 4 3 4a b a b

(iii)

  

7 6 7 6xx

(iv)

  

3

16 3 3x x x

(v)

4lm

(vi)

  

3 4 3 4xy xy

(vii)

  

x y z x y z   

(viii)

  

5 2 7 5 2 7a b c a b c   

Solution:

(i)

22

49pq









22

23pq

Applying the identity

  

22

a b a b a b   

,

The given expression becomes

  

2 3 2 3p q p q

.

(ii)

22

63 112ab

 

22

7 9 16ab









22

7 3 4ab







  

7 3 4 3 4a b a b  

.

(iii)

2

49 36x 









22

76x

  

7 6 7 6xx  

(iv)

53

16 144xx

 

32

16 9xx

 

3 2 2

16 3xx

  

3

16 3 3x x x  

(v)

   

22

l m l m  

   

2 2 2 2

22l m lm l m lm     

2 2 2 2

22l m lm l m lm     

4lm

.

(vi)

22

9 16xy 









22

34xy

  

3 4 3 4xy xy  

.

(vii)

 

2 2 2

2x xy y z  

 

2

x y z  

  

x y z x y z    

.

(viii)

2 2 2

25 4 28 49a b bc c  

 

2 2 2

25 4 28 49a b bc c   

















22

2

25 2 2 2 7 7a b b c c



   



 

2

25 2 7a b c  





 

2

5 2 7a b c  

  

5 2 7 5 2 7a b c a b c    

Question 3

Factories the expressions.

(i) ax

2

+ bx

(ii) 7p

2

+ 21q

2

(iii) 2x

3

+ 2xy

2

+ 2xz

2

(iv) am

2

+ bm

2

+ bn

2

+ an

2

(v) (lm + l) + m + 1

(vi) y (y + z) + 9 (y + z)

(vii) 5y

2

– 20y – 8z + 2yz

(viii) 10ab + 4a + 5b + 2

(ix) 6xy – 4y + 6 – 9x

Answer:

(i)

 

x ax b

(ii)

 

22

73pq

(iii)

 

2 2 2

2x x y z

(iv)

  

22

m n a b

(v)

  

11lm

(vi)

  

9y y z

(vii)

  

5 2 4y z y

(viii)

  

2 1 5 2ab

(ix)

  

3 2 2 3xy

Solution:

(i)

   

a x x b x   

 

x ax b

(ii)

22

7 21pq

   

7 7 3p p q q      

 

22

73pq

.

(iii)

3 2 2

2 2 2x xy xz

     

2 2 2x x x x y y x z z           

  

2 x x x y y z z      

 

2 2 2

2x x y z  

(iv)

2 2 2 2

am bm bn an  

   

22

m a b n b a   

  

22

m n a b  

(v)

 

1lm l m  

   

1 1 1l m m    

  

11ml  

(vi)

   

9y y z y z  

  

9y z y  

(vii)

2

5 20 8 2y y z yz  

     

5 5 4 2 4 2y y y z y z            

   

5 4 2 4y y z y    

  

5 2 4y z y  

.

(viii)

   

10 4 5 2ab a b  

   

2 5 2 5 2 1a b b    

  

5 2 2 1ba  

.

(ix)

   

6 4 6 9xy y x  

   

2 3 2 3 2 3y x x   

    

2 3 2 3 1 3 2y x x    

  

2 3 3 2yx  

.

Question 4

Factorise.

(i) a

4

– b

4

(ii) p

4

– 81 (iii) x

4

– (y + z)

4

(iv) x

4

– (x – z)

4

(v) a

4

– 2a

2

b

2

+ b

4

Answer:

(i)

   

22

a b a b a b  

(ii)

   

2

9 3 3p p p  

(iii)

 





  

2

x y z x y z x y z     

(iv)

  

22

2 2 2z x z x xz z  

(v)

   

22

a b a b

Solution:

(i)

44

ab

   

22

ab

  

2 2 2 2

a b a b  

Factorizing

 

22

ab

again, the above expression becomes

   

22

a b a b a b  

(ii)

4

81p 

 

2

22

9p

  

22

99pp  

   

2

9 3 3p p p   

(iii)

 

4

x y z

   





2

22

2

x y z  

 





 





22

x y z x y z    

 





 





 





2

x y z x y z x y z      

 





  

2

x y z x y z x y z     

.

(iv)

 

4

x x z

   





2

22

2

x x z  

 





 





22

x x z x x z    

 





 





 





2

x x z x x z x x z      

   

2 2 2

2x x z x x z x x xz z       

  

22

2 2 2z x z x xz z   

(v)

4 2 2 4

2a a b b

      

22

2 2 2 2

2a a b b  

 

2

22

ab

  

2

a b a b



  



   

22

a b a b  

.

Question 5

Factorise the following expressions.

(i) p

2

+ 6p + 8 (ii) q

2

– 10q + 21 (iii) p

2

+ 6p – 16

Answer:

(i)

  

24pp

(ii)

  

37qq

(iii)

  

82pp

Solution:

(i)

2

68pp

2

2 4 8p p p   

   

2 4 2p p p   

  

24pp  

.

(ii)

2

10 21qq

2

3 7 21q q q   

   

3 7 3q q q   

  

37qq  

.

(iii)

2

6 16pp

2

8 2 16p p p   

   

8 2 8p p p   

  

82pp  

.

Exercise 14.3

Question 1

Carry out the following divisions.

(i) 28x

4

÷ 56x (ii) – 36y

3

÷ 9y2 (iii) 66pq

2

r

3

÷ 11qr

2

(iv) 34x

3

y

3

z

3

÷ 51xy

2

z

3

(v)

 

8 8 6 4

12 6a b a b

Answer:

(i)

3

2

x

(ii)

4y

(iii)

6pqr

(iv)

 

2

3

xy

(v)

24

2ab

Solution:

(i)

4

28 56xx

28

28 2

xxxx

x







3

2

x



.

(ii)

32

36 9yy

49

9

yyy

yy

    





4y

.

(iii)

2 3 2

66 11pq r qr

11 6

11

p q q r r r

q r r

      



  

6 p q r   

6pqr

(iv)

3 3 3 2 3

34 51x y z xy z

2 2 3

23

17 2

17 3

x x y y z

x y z

     



   

2

3

xy



2

3

xy

.

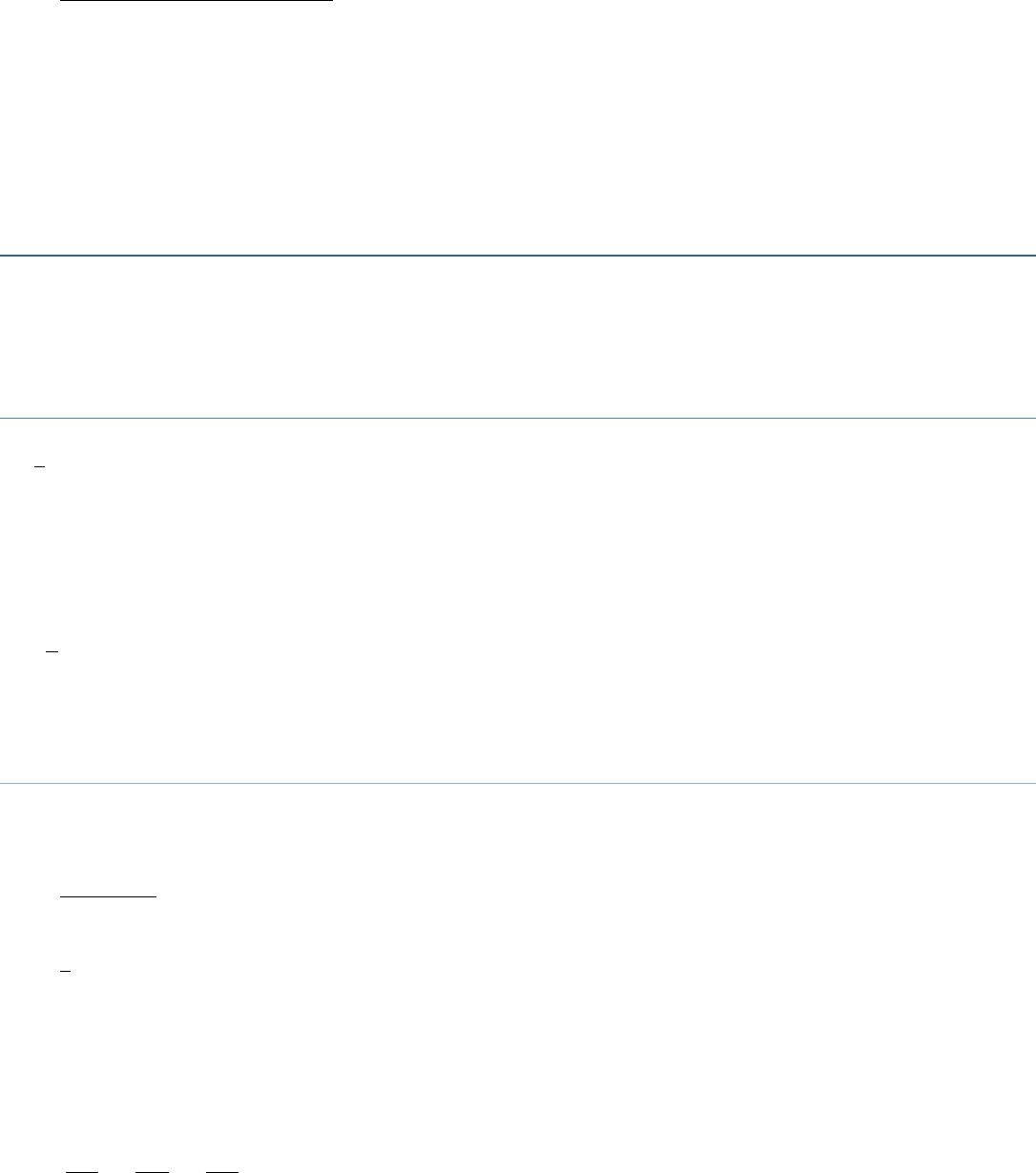
(v)

 

8 8 6 4

12 6a b a b

6 2 4 4

64

62

6

a a b b

ab

    



  

24

2 ab   

24

2ab

Question 2

Divide the given polynomial by the given monomial.

(i) (5x

2

– 6x) ÷ 3x (ii) (3y

8

– 4y

6

+ 5y

4

) ÷ y

4

(iii) 8(x

3

y

2

z

2

+ x

2

y

3

z

2

+ x

2

y

2

z

3

) ÷ 4x

2

y

2

z

2

(iv) (x

3

+ 2x

2

+ 3x) ÷ 2x

(v) (p

3

q

6

– p

6

q

3

) ÷ p

3

q

3

Answer:

(i)

 

1

56

3

x 

(ii)

42

3 4 5yy

(iii)

 

2 x y z

(iv)

 

2

1

23

2

xx

(v)

33

qp

Solution:

(i)

 

2

5 6 3x x x

 

56

3

xx

x





 

1

56

3

x

.

(ii)

 

8 6 4 4

3 4 5y y y y  

8 6 4

4 4 4

3 4 5y y y

y y y

  

42

3 4 5yy  

.

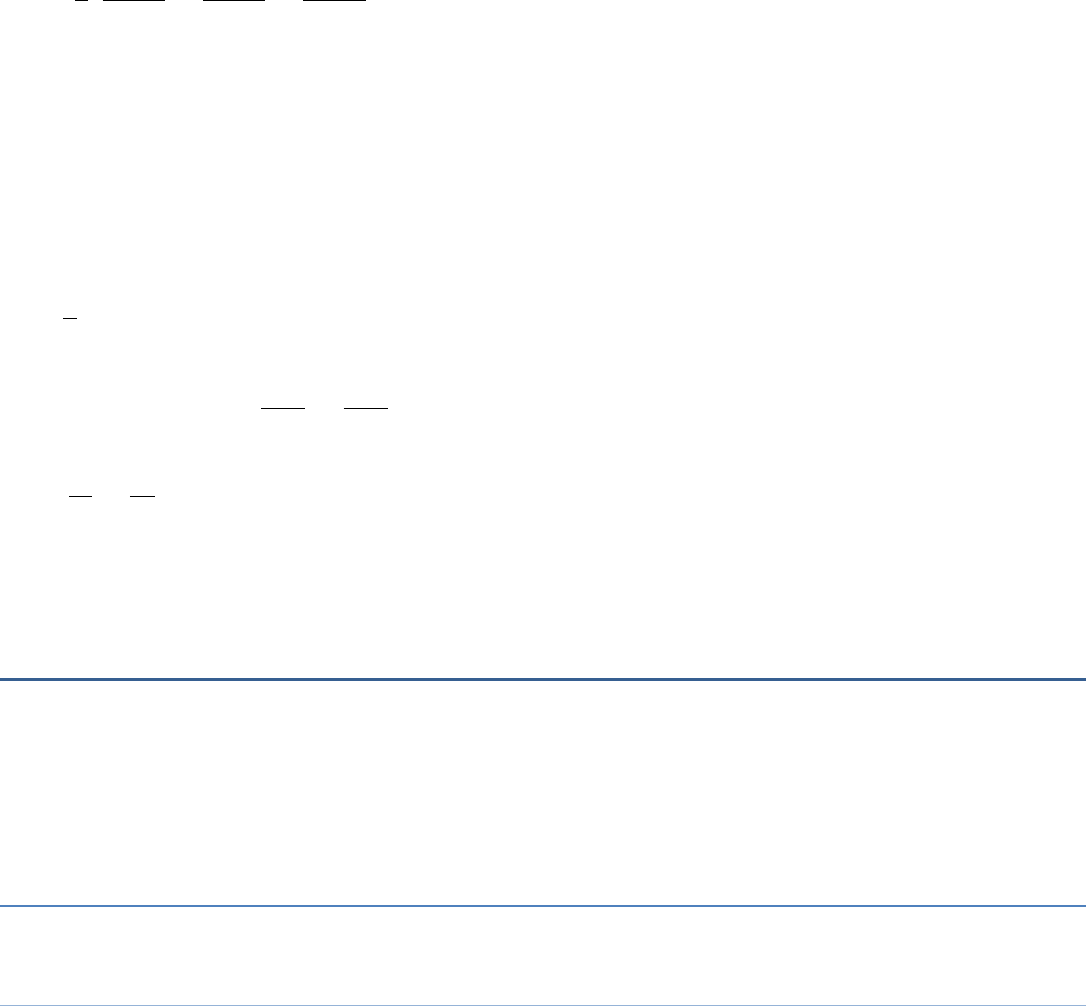
(iii) 8(x

3

y

2

z

2

+ x2y3z2 + x

2

y

2

z

3

) ÷ 4x

2

y

2

z

2

3 2 2 2 3 2 2 2 3

2 2 2 2 2 2 2 2 2

8

4

x y z x y z x y z



  





 

2 x y z  

.

(iv) (x

3

+ 2x

2

+ 3x) ÷ 2x

 

2

2 3 2x x x x   

 

2

1

23

2

xx  

.

(v) (p

3

q

6

– p

6

q

3

) ÷ p

3

q

3

3 6 6 3

3 3 3 3

p q p q



66

33

qp



33

qp

.

Question 3

Work out the following divisions.

(i) (10x – 25) ÷ 5

(ii) (10x – 25) ÷ (2x – 5)

(iii) 10y (6y + 21) ÷ 5(2y + 7)

(iv) 9x

2

y

2

(3z – 24) ÷ 27xy (z – 8)

(v) 96abc(3a – 12) (5b – 30) ÷ 144(a – 4) (b – 6)

Answer:

(i)

25x 

(ii) 5 (iii) 6y (iv) xy (v)

10abc

Solution:

(i)

10 25x 

 

5 2 5x

So, (10x – 25) ÷ 5 =

 

5 2 5 5x 

25x

(ii)

10 25x 

 

5 2 5x

So, (10x – 25) ÷ (2x – 5)

   

5 2 5 2 5xx   

5

(iii)

 

10 6 21yy

 

10 3 2 7yy  

So, 10y (6y + 21) ÷ 5(2y + 7)

 

10 3 2 7

52

yy







23y  

6y

.

(iv)

 

22

9 3 24x y z 

 

22

9 3 8x y z  

9x

2

y

2

(3z – 24) ÷ 27xy (z – 8)

 

9 3 8

27 8

x x y y z

x y z

    



   

xy

.

(v)

  

96 3 12 5 30abc a b

   

96 3 4 5 6abc a b    

96abc(3a – 12) (5b – 30) ÷ 144(a – 4) (b – 6)

   

  

96 3 4 5 6

144 4 6

abc a b

ab

   





96 3 5

10

144

abc





.

Question 4

Divide as directed.

(i) 5(2x + 1) (3x + 5) ÷ (2x + 1)

(ii) 26xy(x + 5) (y – 4) ÷ 13x(y – 4)

(iii) 52pqr (p + q) (q + r) (r + p) ÷ 104pq(q + r) (r + p)

(iv) 20(y + 4) (y

2

+ 5y + 3) ÷ 5(y + 4)

(v) x(x + 1) (x + 2) (x + 3) ÷ x(x + 1)

Answer:

(i)

 

5 3 5x 

(ii)

 

25yx

(iii)

 

1

2

r p q

(iv)

 

2

4 5 3yy

(v)

  

23xx

Solution:

(i)

    

5 2 1 3 5 2 1x x x   

   

 

5 2 1 3 5

21

xx

x

   





 

5 3 5x

(ii)

  

 

26 5 4

13 4

xy x y

xy





 

25yx   

 

25yx

.

(iii) 52pqr (p + q) (q + r) (r + p) ÷ 104pq(q + r) (r + p)

   

  

52

2 52

pqr p q q r r p

pq q r r p

  



   

 

1

2

r p q

.

(iv) 20(y + 4) (y

2

+ 5y + 3) ÷ 5(y + 4)

   

 

2

5 4 4 5 3

54

y y y

y

     





 

2

4 5 3yy  

.

(v) x(x + 1) (x + 2) (x + 3) ÷ x(x + 1)

     

 

1 2 3

1

x x x x

xx

     





  

23xx  

.

Question 5

Factorise the expressions and divide them as directed.

(i) (y

2

+ 7y + 10) ÷ (y + 5)

(ii) (m

2

– 14m – 32) ÷ (m + 2)

(iii) (5p

2

– 25p + 20) ÷ (p – 1)

(iv) 4yz (z

2

+ 6z – 16) ÷ 2y(z + 8)

(v) 5pq (p

2

– q

2

) ÷ 2p (p + q)

(vi) 12xy (9x

2

– 16y

2

) ÷ 4xy (3x + 4y)

(vii) 39y

3

(50y

2

– 98) ÷ 26y

2

(5y + 7)

Answer:

(i)

2y 

(ii)

16m 

(iii)

 

54p 

(iv)

 

22zz

(v)

 

5

2

q p q

(vi)

 

3 3 4xy

(vii)

 

3 5 7yy

Solution:

(i)

2

7 10yy

2

5 2 10y y y   

   

5 2 5y y y   

  

52yy  

(y

2

+ 7y + 10) ÷ (y +5)

  

 

52

5

yy

y







2y

.

(ii)

2

14 32mm

2

16 2 32m m m   

   

16 2 16m m m   

  

16 2mm  

(m

2

– 14m –32) ÷ (m + 2)

  

 

16 2

2

mm

m







16m

.

(iii)

 

2

5 25 20pp

2

5 20 5 20p p p   

   

5 4 5 4p p p   

  

5 5 4pp  

(5p

2

– 25p + 20) ÷ (p –1)

  

 

5 1 4

1

pp

p







 

54p

.

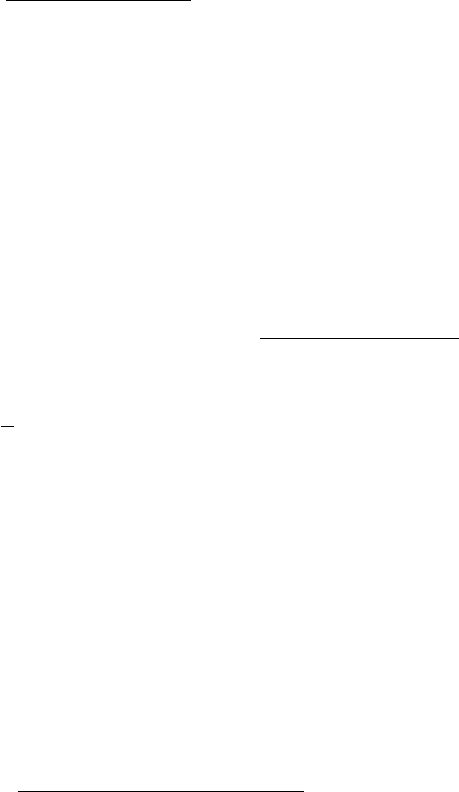
(iv)

 

2

4 5 16yz z z

 

2

4 8 2 16yz z z z   

   





4 8 2 8yz z z z   

  

4 8 2yz z z  

4yz(z

2

+ 6z – 16) ÷ 2y(z + 8)

  

 

4 8 2

28

yz z z

yz







 

22zz

.

(v)

 

22

5pq p q

  

5pq p q p q  

5pq (p

2

– q

2

) ÷ 2p (p + q)

  

 

5

2

pq p q p q

p p q







 

5

2

q p q

.

(vi)

 

22

12 9 16xy x y









 

22

12 3 4xy x y

  

12 3 4 3 4xy x y x y  

12xy (9x

2

– 16y

2

) ÷ 4xy (3x + 4y)

  

 

3 4 3 4 3 4

4 3 4

xy x y x y

xy x y

  





 

3 3 4xy

.

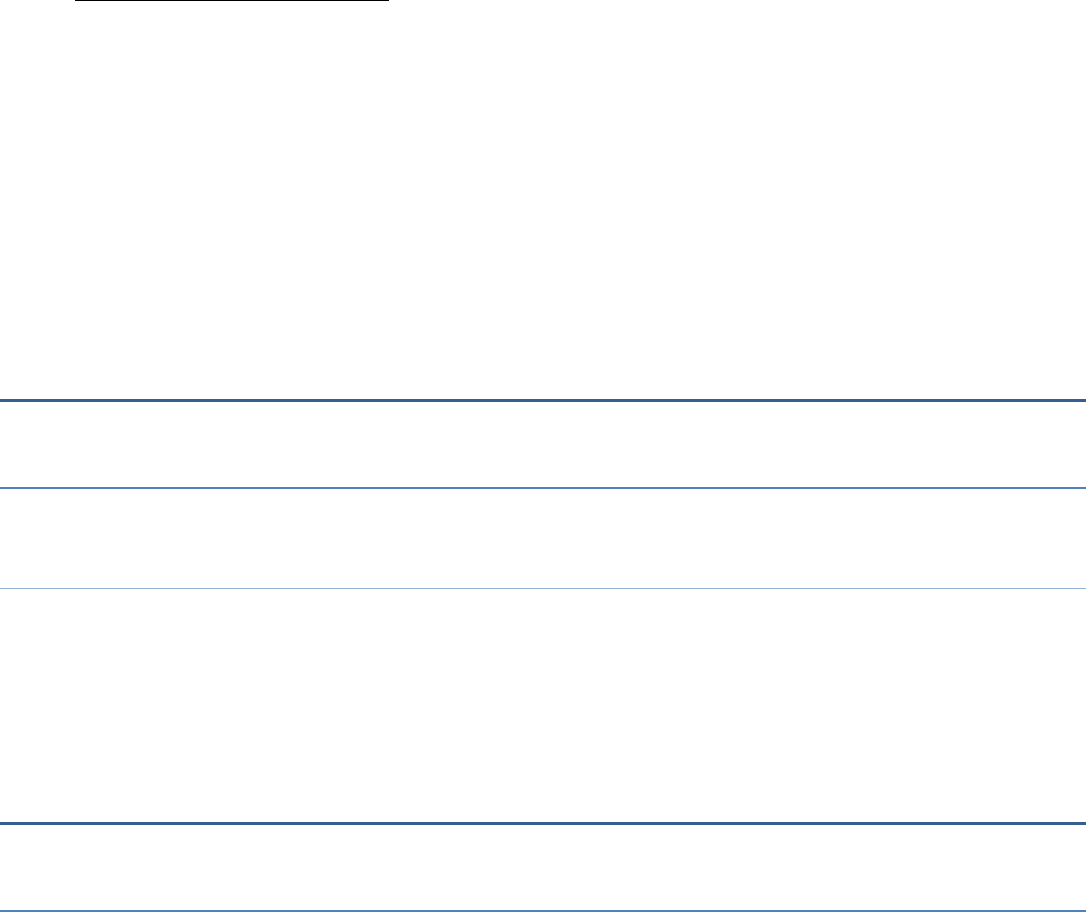
(vii)

 

32

39 50 98yy

 

32

39 2 25 49yy  





 

2

32

39 2 5 7yy  

  

3

39 2 5 7 5 7y y y   

39y

3

(50y

2

– 98) ÷ 26y2 (5y + 7)

  

 

3

2

13 3 2 5 7 5 7

13 2 5 7

y y y

yy

   





 

3 5 7yy

.

Exercise 14.4

Find and correct the errors in the following mathematical statements.

Question 1

4(x – 5) = 4x – 5

Answer:

4 20x 

Solution:

Error: The error occurs in the 2

nd

term on the RHS, which is incorrectly written as -5.

This should have been

4 ( 5) 20   

.

As per the distributive law,

()a b c ab ac  

Question 2

x(3x + 2) = 3x

2

+ 2

Answer:

 

2

3 2 3 2x x x x  

Solution:

Error:

The error occurs in the 2

nd

term on the RHS, which is incorrectly written as +2. This should have been

22xx   

.

As per the distributive law,

()a b c ab ac  

Question 3

2x + 3y = 5xy

Answer:

2 3 2 3x y x y

Solution:

Error:

The error occurs on the RHS, which is incorrectly written as 5xy.

In fact, the LHS cannot be simplified further as the two terms are unlike terms.

.

Question 4

x + 2x + 3x = 5x

Answer:

2 3 6x x x x  

Solution:

Error: The error occurs on the RHS, which is incorrectly written as 5x.

In fact, the LHS can be written as (1 + 2 + 3) x, which simplifies to 6x.

Question 5

5y + 2y + y – 7y = 0

Answer:

5 2 7y y y y y   

Solution:

Error:

The error occurs on the RHS, which is incorrectly written as 0. In fact, the LHS

can be written as

5 2 7 (5 2 1 7)y y y y y y       

Question 6

3x + 2x = 5x

2

Answer:

3 2 5x x x

Solution:

Error:

The error occurs on the RHS, which is incorrectly written as 5x

2

.

In fact, the LHS can be written as

 

3 2 5xx

Question 7

(2x)

2

+ 4(2x) + 7 = 2x

2

+ 8x + 7

Answer:









2

2 4 2 7 4 8 7x x x x    

Solution:

Error:

The error occurs on the RHS in the first term, which is incorrectly written as 2x

2

.

In fact





2

2 2 2

2 2 4x x x

Question 8

(2x)

2

+ 5x = 4x + 5x = 9x

Answer:





2

2 5 4 5x x x x  

Solution:

Error:

The error occurs on the RHS of the first equation in the first term, which is incorrectly

written as 4x.

In fact,





2

2 2 2

2 2 4x x x

second and the RHS of the first equation cannot be

further simplified to 9x.

Question 9

(3x + 2)

2

= 3x

2

+ 6x + 4

Answer:

 

2

3 2 9 12 4x x x   

Solution:

Error:

The error occurs on the RHS in the first term as well as in the second term, which

are incorrectly written as 3x

2

and 6x respectively.

In fact

 





2

2 2 2 2

3 2 3 2 3 2 2 3 12 4 9 12 4x x x x x x x           

The Correct formula/ identity, which is

 

2

ab

22

2a ab b  

,

should be applied.

Question 10

Substituting x = – 3 in

(a)x

2

+ 5x + 4 gives (– 3)

2

+ 5 ( – 3) + 4 = 9 + 2 + 4 = 15

(b)x

2

– 5x + 4 gives ( – 3)

2

– 5 ( – 3) + 4 = 9 – 15 + 4 = – 2

(c)x

2

+ 5x gives ( – 3)

2

+ 5 ( – 3) = – 9 – 15 = – 24

Answer:

(a)

2

(b) 28 (c)

6

Solution:

(a)

   

2

3 5 3 4   

9 15 4  

2

.

(b)

   

2

3 5 3 4   

9 15 4  

28

.

(c)

   

2

3 5 3 9 15    

6

Question 11

(y – 3)

2

= y

2

– 9

Answer:

 

2

3 6 9y y y   

Solution:

Error:

Here

 

2

ab

has been wrongly taken as

22

ab

, whereas

 

2

22

2a b a ab b   

.

Question 12

(z + 5)

2

= z

2

+ 25

Answer:

2

10 25zz

Solution:

 

2

2 5 10 25zz   

Error:

Here

 

2

ab

has been wrongly taken as

22

ab

, whereas

 

2

22

2a b a ab b   

.

Question 13

(2a + 3b) (a – b) = 2a

2

–3b

2

Answer:

22

23a ab b

Solution:

22

23a ab b  

Error:

  

22

2 3 2 3 2 3a b a b a ab ab b     

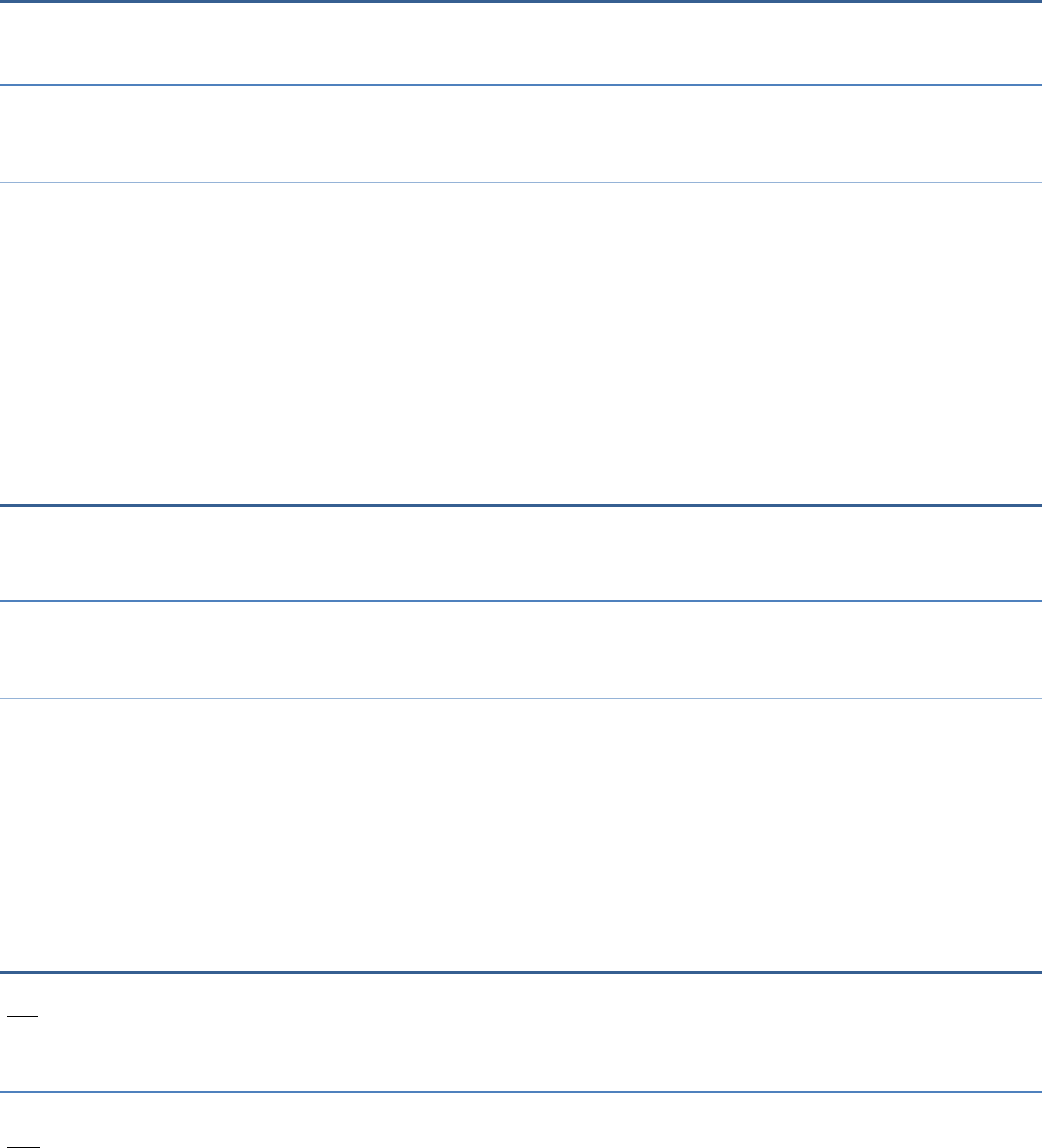
Here, when the brackets are opened, each term of one bracket has not been multiplied

by every term of the other bracket.

Question 14

(a + 4) (a + 2) = a

2

+ 8

Answer:

2

68aa

Solution:

  

2

4 2 4 2 8a a a a a     

2

68aa  

Error:

Here, when the brackets are opened, each term of one bracket has not been multiplied

by every term of the other bracket.

Question 15

(a – 4) (a – 2) = a

2

– 8

Answer:

2

68aa

Solution:

  

2

4 2 6 8a a a a    

Error:

Here, when the brackets are opened, each term of one bracket has not been multiplied

by every term of the other bracket.

Question 16

2

3

0

3

x



Answer:

2

3

1

3

x



Solution:

2

3

1

3

x



Error:

Here

 

0

a



has been incorrectly taken as 0.

In fact, the value is 1. Also, it must be mentioned that

0x 

Question 17

2

31

1 1 2

3

x





Answer:

2

22

3 1 1

1

33

x

xx





Solution:

2

22

3 1 1

1

33

x

xx





Error:

There has been a wrong splitting of

 

0

ab

a





as

a

b

a



In fact,

 

0

a b a b

a

a a a



  

Question 18

31

3 2 2

x





Answer:

33

3 2 3 2

xx





Solution:

33

3 2 3 2

xx





Error:

3 x and 3x have been wrongly canceled and in the numerator 3x has been wrongly

replaced by 1 and in the denominator 3x has been wrongly replaced by 0.

Question 19

31

4 3 4xx





Answer:

33

4 3 4 3xx





Solution:

33

4 3 4 3xx





Error:

3 & 3 have been wrongly canceled and in the numerator 3 has been wrongly replaced

by 1 and in the denominator 3 has been wrongly replaced by 0.

Question 20

45

5

4

x





Answer:

4 5 4 5 5

1

4 4 4 4

xx

x x x x



   

Solution:

4 5 4 5 5

1

4 4 4 4

xx

x x x x



   

Question 21

75

7

5

x





Answer:

7 5 7 5 7

1

5 5 5 5

x x x

   

Solution:

7 5 7 5 7

1

5 5 5 5

x x x

   

.