Lesson: Rational Number
Exercise 1.1
Question 1
Using appropriate properties, find:
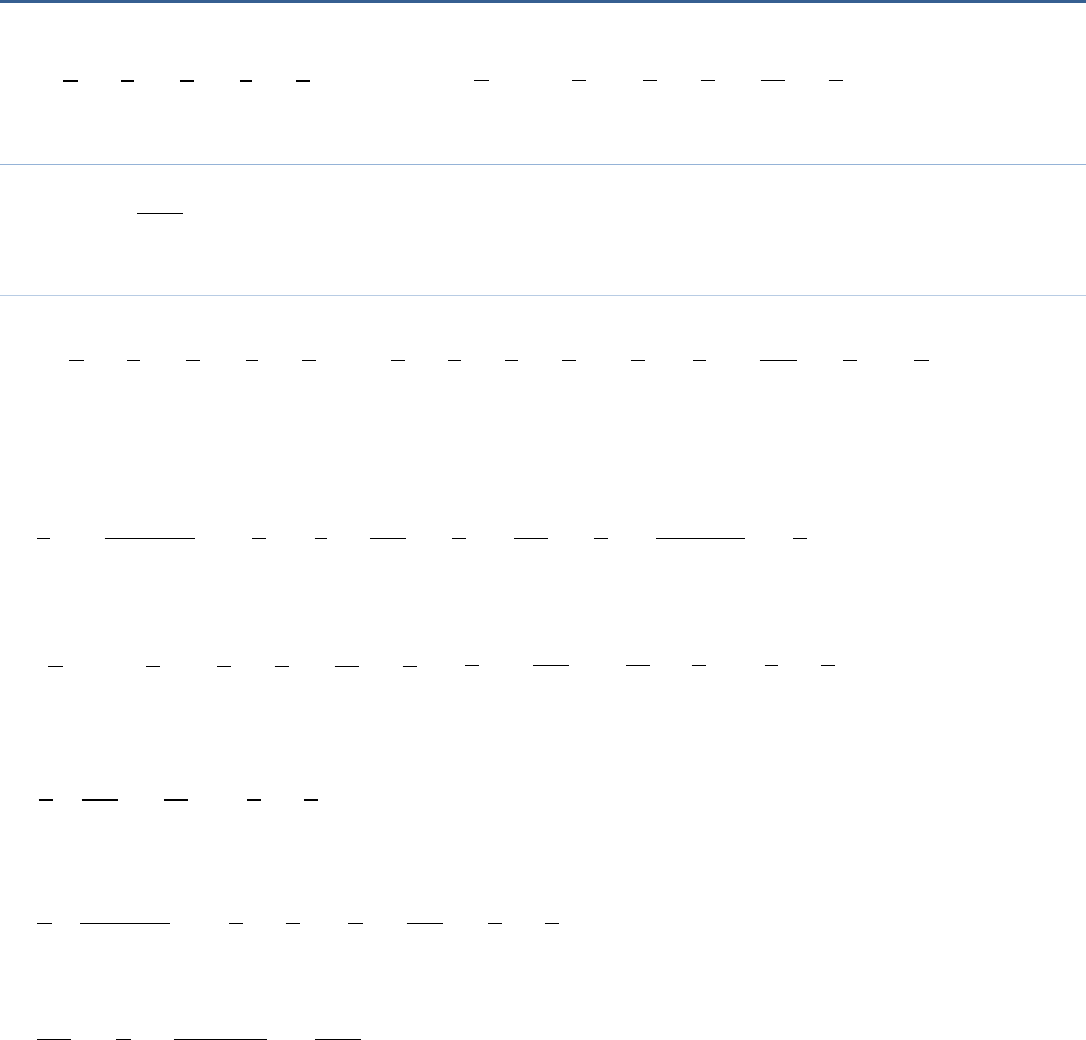
(i)
2 3 5 3 1
3 5 2 5 6
(ii)
2 3 1 3 1 2
5 7 6 2 14 5
Answer:
(i) 2 (ii)
11
28
Solution:
(i)
2 3 5 3 1
3 5 2 5 6
=
2 3 3 1 5 3 2 1 5
3 5 5 6 2 5 3 6 2
[Using a (b
c) = ab - ac]
3 4 1 5 3 5 5 1 5 1 5 4
2
5 6 2 5 6 2 2 2 2 2
(ii)
2 3 1 3 1 2
5 7 6 2 14 5
=
2 3 1 2 1 3
5 7 14 5 6 2
=
2 3 1 1 3
5 7 14 6 2
[Using a (b + c) = ab + ac]
2 6 1 1 3 2 5 1 3
5 14 6 2 5 14 6 2
1 1 4 7 11
7 4 28 28
Question 2
Write the additive inverse of each of the following:
(i)
2
8
(ii)
5
9
(iii)
6
5
(iv)
2
9
(v)
19
6
Answer:
(i)
2
8
(ii)
5
9
(iii)
6
5
(iv)
2
9
(v)
19
6
Solution:
(i) The additive inverse of
2
8
is
2
8
as
2 2 2 2 0
0
8 8 8 8
(ii) The additive inverse of
5
9
is
5
9
as
5 5 5 5 0
0
9 9 9 9
(iii) The additive inverse of
6
5
is
6
5
as
6 6 6 6 6 6 0
0
5 5 5 5 5
5
(iv) The additive inverse of
2
9
is
2
9
as
2 2 2 2 2 2 0
0
9 9 9 9 9
9
(v) The additive inverse of
19
6
is
19
6
as
19 19 19 19 19 19 0
0
6 6 6 6 6
6
Question 3
Verify that – (– x) = x for : (i) x =
11
15
(ii) x = –
13
17
Answer:
i.e, – (– x) = x. is verified
Solution:
(i) We have,
x =
11
15
The additive inverse of x =
11
15
is – x =
11
15
as
11
15
+
11
15
= 0
The same equality
11
15
+
11
15
= 0 shows that the additive inverse of
11
15
is
11
15
.
This
–
11
15
=
11
15
, i.e, – (– x ) = x. is verified.
(ii) We have,
x =
13
17
The additive inverse of x =
13
17
is – x =
13
17
as
13
17
+
13
17
= 0.
13
17
=
(
13
17
)
The same equality
13
17
+
13
17
= 0 shows that the additive inverse of
13
17
is
13
17
. This
13 13
( ( ))
17 17
i.e, – (– x) = x. is verified.
Question 4
Find the multiplicative inverse of the following
(i) – 13 (ii)
13
19
(iii)
1
5
(iv)
53
87
(v) – 1 ×
2
5
(vi) – 1
Answer:
(i) –
1
13
(ii)
19
13
(iii) 5 (iv)
56
15
(v)
5
2
(vi) – 1
Solution:
(i) The multiplicative inverse of – 13 is –
1
13
as
1
13 1
13
(ii) The multiplicative inverse of
13
19
is
19
13
as
13 19
1
19 13
(iii) The multiplicative inverse of
1
5
is 5 as
1
51
5
.
(iv) The multiplicative inverse of
5 3 8 7
is
87
53
=
56
15
as
5 3 8 7
1
87
53
(v) The multiplicative inverse of – 1 ×
2
5
is – 1 ×
5
2
=
5
2
as
(vi) The multiplicative inverse of – 1 is – 1 as
1 1 1
.

2
– 1 1
2
5
5
1
Question 5
Name the property under multiplication used in each of the following:
(i)
4
5
× 1 = 1 ×
4
5
= –
4
5
(ii)
13 2 2 13
17 7 7 17
(iii)
19 29
1
29
19
Answer:
(i) Existence of Multiplicative Identity (1 is the multiplicative identity)
(ii) Commutatively
(iii) Existence of Multiplicative Inverse
Solution:
(i)
4
5
× 1 = 1 ×
4
5
= –
4
5
as 1is the multiplicative identity.
(ii)
13 2 2 13
17 7 7 17
as multiplication is commutative.
(iii)
19 29
1
29
19
as
29
19
is the multiplicative inverse of
19
29
.
Question 6
Multiply
6
13
by the reciprocal of
7
16
.
Answer:
96
91
Solution:
Reciprocal of
7 16
is
16
7
.
Now,
6 16 96
13 91
7
Question 7
What property allows you to compute?
1 4 1 4
6 as 6
3 3 3 3
Answer:
Associativity of Multiplication
Solution:
For any three rational numbers a, b and c, a × (b × c) = (a × b) × c.
The multiplication is associative for rational numbers.
The associativity property allows us to compute
1 4 1 4
6 as 6 ,
3 3 3 3
1 4 1 24 8
× 6 ×
3 3 3 3 3
and
1 4 6 4 8
6
3 3 3 3 3
Here,
1 4 1 4
66
3 3 3 3
Question 8
Is
8
9
the multiplicative inverse of – 1
1
8
? Why or why not?
Answer:
No, because the product is not 1
Solution:
No, because the product of
8
9
and – 1
1
8
is not 1
Question 9
Is 0.3 the multiplicative inverse of
1
3
3
? Why or Why not?
Answer:
Yes, because
10 3 10
0.3 1
3 10 3
Solution:
Yes, because
1 10
3
33
and
10 3 10
0.3 1
3 10 3
Question 10
Write:
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
Answer:
(i) 0 (ii) 1 and
1 (iii) 0
Solution:
(i) Zero has no reciprocal.
(ii) 1 is equal to its reciprocal as
1 1 1
.
– 1 is also equal to its reciprocal as – 1 × (– 1) = 1
(iii) Zero is equal to its negative as
0 0 0
.
Question 11
Fill in the blanks:
(i) Zero has ____________ reciprocals.
(ii) The numbers ____________ and ____________ are their own reciprocals.
(iii) The reciprocal of – 5 is ____________
(iv) Reciprocal of
1
x
, where x
0 is ____________
(v) The product of two rational numbers is always a ____________
(vi) The reciprocal of a positive rational number is ____________
Answer:
(i) No (ii) 1, – 1 (iii)
1
5
(iv) x
(v) Rational number
(vi) Positive
Solution:
(i) No (ii) 1, – 1 (iii)
1
5
(iv) x (v) rational number
(vi) a positive rational number.
Exercise 1.2
Question 1
Represent these numbers on the number line (i)
7
4
(ii)
5
6
Answer:
(i)
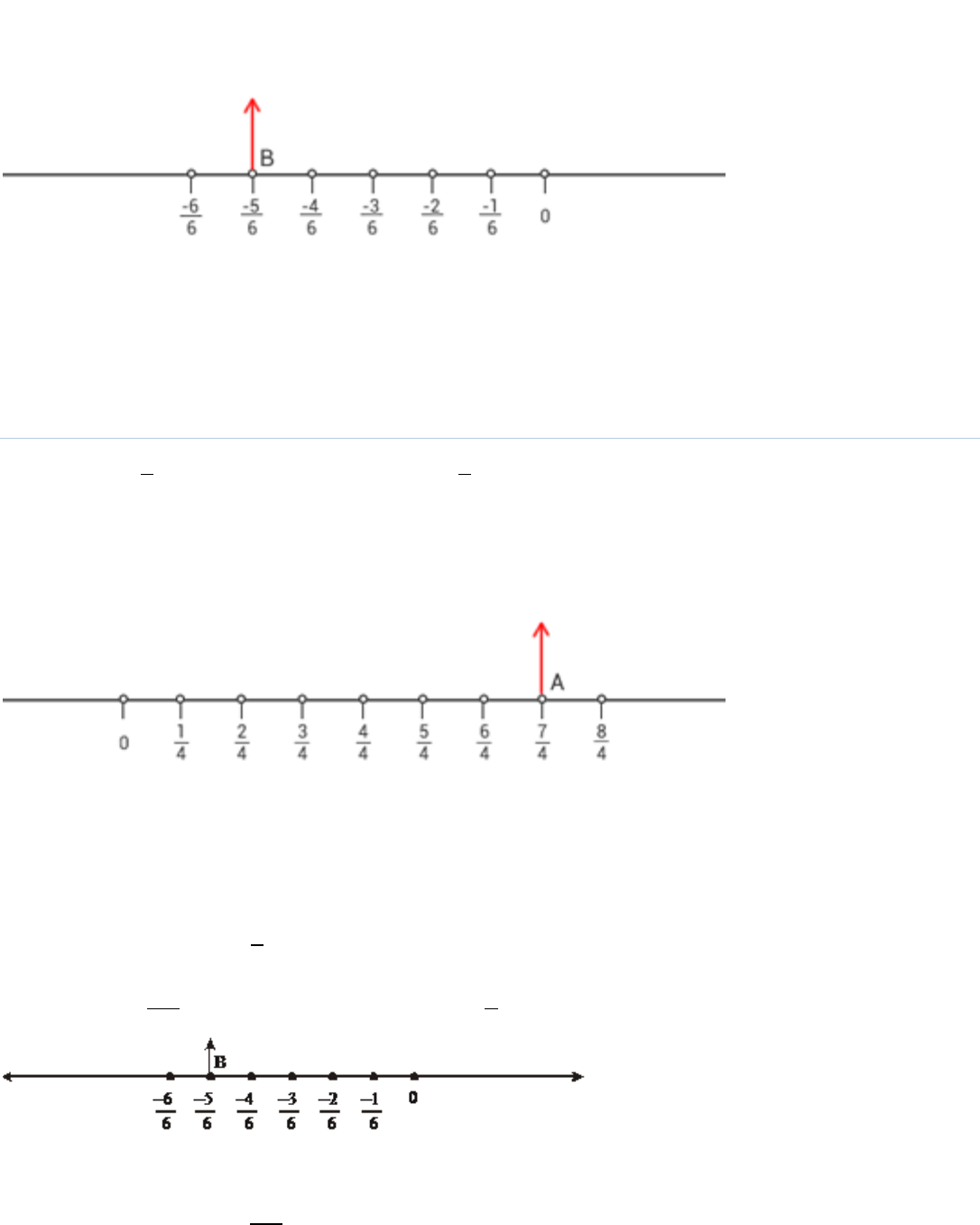
(ii)
Solution:
(i) To represent
7
4
, we make 7 markings of distance
1
4
each on the right of 0.
Thus, the point A represents
7
4
.
(ii) To represent
5
6
, we make 6 markings of distance
1
6
each on the left of zero.
Thus, the point B represents
5
6
.
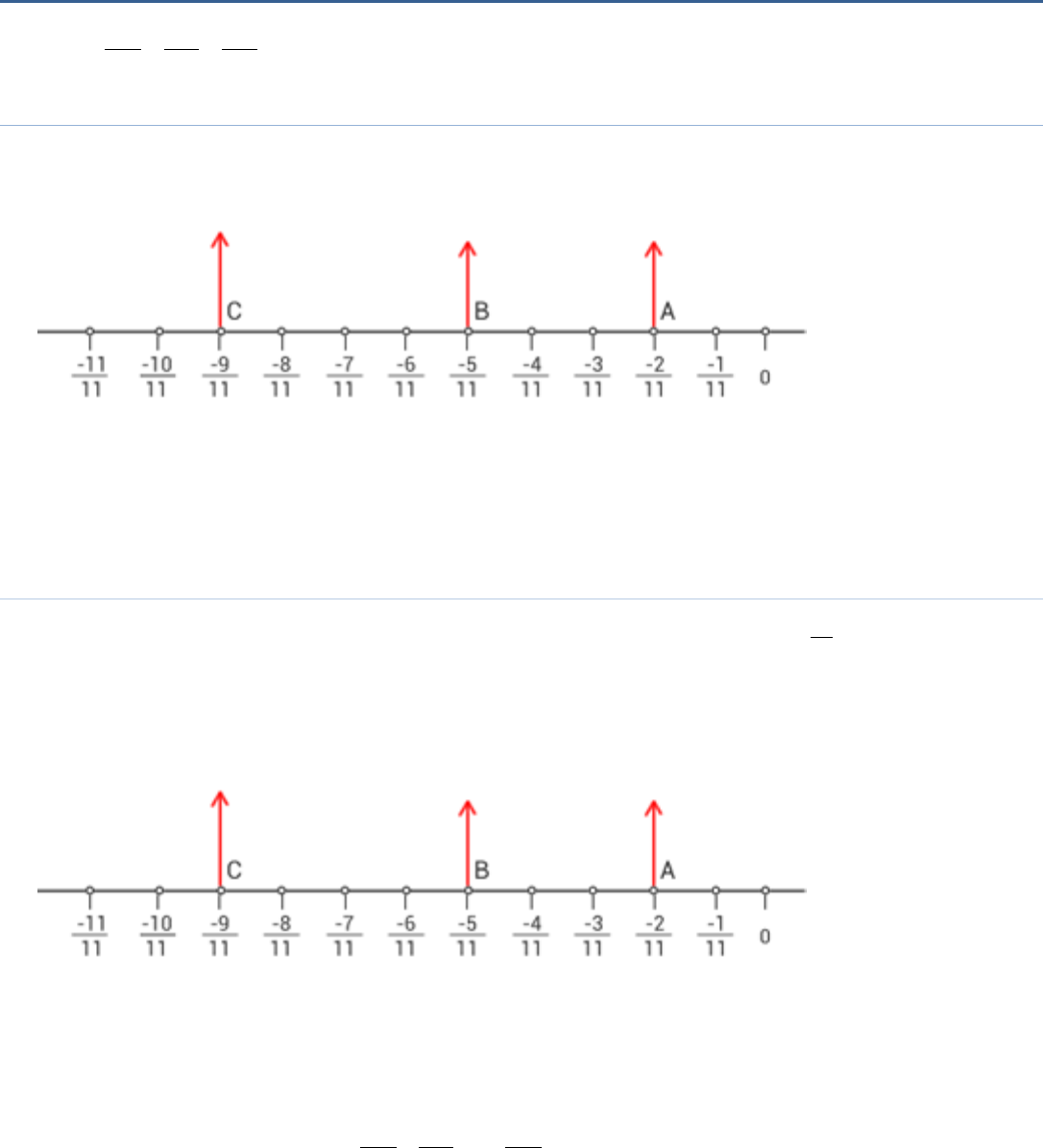
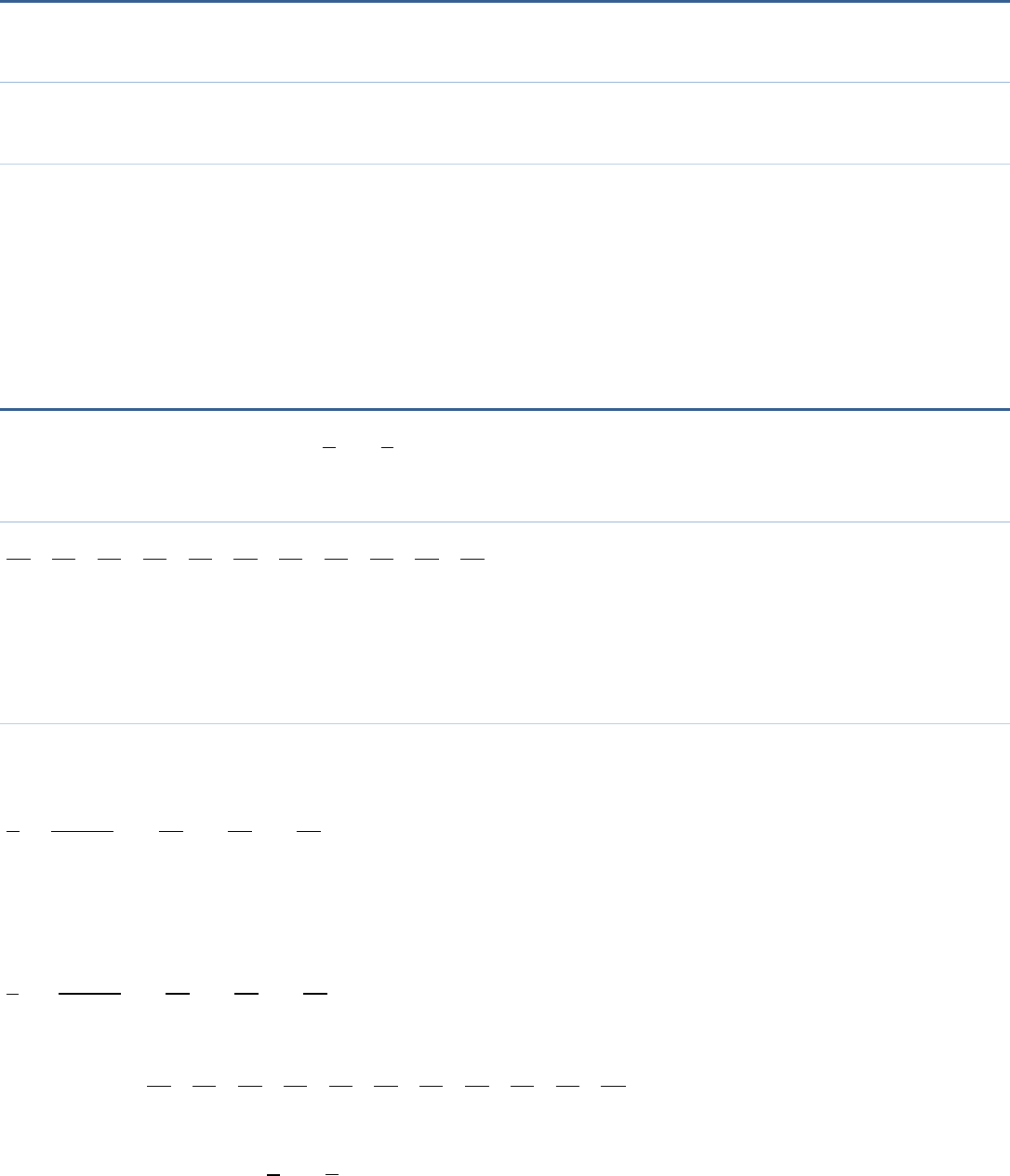
Question 2
Represent
2 5 9
,,
11 11 11
on the number line.
Answer:
Solution:
We draw a line l. We take a point O on it. From O, we mark 11 markings of distance
1
11
each on the left of O
(i.e., 0)
Thus, the points A, B and C represent
2 5 9
, and
11 11 11
respectively.

Question 3
Write five rational numbers which are smaller than 2.
Answer:
Some of these are
11
1, , 0, 1,
22
(There can be many more such rational numbers)
Solution:
Let’s take the two numbers 0 and 2. 0 is smaller than 2.
Now, 2 can be written as
20
10
and 0 as
0
10
.
Thus, we have
19 18 17 16 15 14 1
, , , , , .........
10 10 10 10 10 10 10
between 2 and 0.
We can take any five of these values.
Question 4
Find ten rational numbers between
2
5
and
1
2
.
Answer:
7 6 5 8 9
, , , ........ ,
20 20 20 20 20
(There can be many more such rational numbers)
Solution:
First, we make the same denominator of the given rational numbers.
2 2 2 4 4 2 8
5 10 20
5 2 10 2
and
1 1 5 5 5 2 10
2 10 20
2 5 10 2

Note: We make denominator 20 because when the denominator is 10, then we
can conveniently find out only 8 rational numbers.
Thus, we have
7 6 5 8 9
, , , ........ ,
20 20 20 20 20
We can take any ten of these values.
Question 5
Find five rational numbers between
(i)
24
and
35
(ii)
35
and
23
(iii)
11
and
42
Answer:
(i)
41 7 11 23
, , ,
60 10 15 30
(ii)
8 7 6 5 4 8 9
, , , , ..... ,
6 6 6 6 6 6 6
(iii)
11 10 9 8 7
,,,,
24 24 24 24 24
(There can be many more such rational numbers)
Solution:
(i)
24
and
35
First Method:
We first convert
2
3
and
4
5
to rational numbers with the same denominator i.e.
2 2 5 10 10 3 30
3 15 45
3 5 15 3
and
4 4 3 12 12 3 36
5 15 45
5 3 15 3
Thus, we have,
35 34 33 32 31
, , , and
45 45 45 45 45
as five ration numbers between
24
and
35
Another Method:
We know that, if a and b are two rational numbers, then
ab
2
is a rational
number between a and b such that a <
ab
2
< b.

We find the mean of the given rational numbers,
2 4 10 12 1 22 1 11
2
3 5 15 2 15 2 15
So,
2 11 4
3 15 5
We now find another rational number between
2 11
and
3 15
.
For this, we again find the mean of
2 11
and
3 15
, i.e.,
2 11 30 33 1 63 1 7 1 7
2
3 15 45 2 45 2 5 2 10
So,
2 7 11
3 10 15
or
2 7 11 4
3 10 15 5
Further, we find another rational number between
11
15
and
4
5
For this, we again find the mean of
11
15
and
4
5
i.e,
11 4 11 12 1 23 1 23
2
15 5 15 2 15 2 30
.
So,
11 23 4
15 30 5
or
2 7 11 23 4
3 10 15 30 5
Now, we find another rational number between
2
3
and
7
10
For this, we again find the mean of
2
3
and
7
10
,
i.e,
2 7 20 21 1 41 1 41
2
3 10 30 2 30 2 60
So,
2 41 7
3 60 10
or
2 41 7 11 23 4
3 60 10 15 30 5
Also, we find another rational number between
23
30
and
4
5

For this, we again find the mean of
23
30
and
4
5
, i.e.
23 4 1
30 5 2
23 24 1 47 1 47
30 2 30 2 60
So,
23 47 4
30 60 5
or
2 41 7 11 23 47 4
3 60 10 15 30 60 5
Thus, the five rational numbers between
2
3
and
4
5
are
41 7 11 23
, , ,
60 10 15 30
and
47
60
(ii)
35
and
23
We first convert
35
and
23
to rational numbers with the same denominator
i.e.,
3 3 3 9
26
23
and
5 5 2 10
36
23
Thus, we have
8 7 6 5 4 8 9
, , , , ..... ,
6 6 6 6 6 6 6
We can take any five of these values as rational numbers between
35
and
23
.
(iii)
1
4
and
1
2
We first convert
1
4
and
1
2
to rational numbers with the same denominator
i.e.,
1 1 6 6
4 24
46
and
1 1 12 12
2 24
2 12
.
Thus, we have,
11 10 9 8 7
, , , and
24 24 24 24 24
as rational numbers between
1
4
and
1
2
.
Question 6
Write five rational numbers greater than – 2.
Answer:
-1. 0. 1, 2, 3 (There can be many more such rational numbers)
Solution:
Since, every integer is a rational number, therefore, we can pick up any five integers
greater than -2.
Thus five rational numbers greater than -2 are -1, 0, 1, 2, 3.
Question 7
Find ten rational numbers between
3
5
and
3
4
.
Answer:
59 58 57 56 55 54 53 52 51 50 49
, , , , , , , , , ,
80 80 80 80 80 80 80 80 80 80 80
(There can be many more such rational numbers)
Solution:
First we make the denominator of the given rational numbers equal
3
5
=
3 4 12 24 48
20 40 80
54
and
3
4
=
3 5 15 30 60
20 40 80
45
Thus, we have,
59 58 57 56 55 54 53 52 51 50 49
, , , , , , , , , ,
80 80 80 80 80 80 80 80 80 80 80
as rational numbers between
3
5
and
3
4
.
We can take any ten of these values.