Lesson: Motion and time
Classify the following as motion along a straight
line, circular or oscillatory motion:
i)
Motion
of your hands while running.
ii)
Motion
of a horse pulling a cart on a straight road.
iii)
Motion
of a child in a merry-go-round.
iv)
Motion
of a child on a see-saw.
v)
Motion
of the hammer of an electric bell.
vi)
Motion of a train on a
straight bridge.
Solution:
i)
Motion
of your hands while running. - Oscillatory
motion
ii)
Motion
of a horse pulling a cart on a straight road. - Straight line motion
iii)
Motion
of a child in a merry-go-round. - Circular motion
iv)
Motion
of a child on a see-saw. - Oscillatory motion
v)
Motion
of the hammer of an electric bell. - Oscillatory motion
vi)
Motion of a train on a
straight bridge. - Straight line motion
Question: 2
Which of the following are not correct?
(i)
The
basic unit of time is second.
(ii)
Every
object moves with a constant speed.
(iii)
Distances
between two cities are measured in kilometers.
(iv)
The
time period of a given pendulum is not constant.
(v)
The speed of a train is
expressed in m/h.
Solution:
(i)
True
(ii)
False.
Different objects have different speed.
(iii)
True
(iv)
False.
The time period of a given pendulum is fixed.
(v)
False.
The speed of a train is expressed in km/h.
Question: 3
A simple pendulum takes 32 s to
complete 20 oscillations. What is the time period of the pendulum?
Solution:
No.
of oscillations =
20
Time
taken for 20 oscillations = 32
Time
period
Time
period
= 1.6 s
Question: 4
The distance between two stations is 240
km. A train takes 4 hours to cover this distance. Calculate the speed of the
train.
Solution:
Distance
between two stations is 240 km
Time
taken to cover the distance is 4 hours
=
60 km/h
Question: 5
The
odometer of a car reads 57321.0 km when the clock shows the time 08:30 AM. What is
the distance moved by the car, if at 08:50 AM, the odometer reading has changed
to 57336.0 km? Calculate the speed of the car in km/min during this time.
Express the speed in km/h also.
Solution:
Odometer
reading of car at 08:30 a.m. = 57321.0 km
Odometer
reading of car at 08:50 a.m. = 57336.0 km
Total
distance travelled by the car
=
57336.0 - 57321.0
Total
distance travelled by the car = 15 km
Time
taken to cover this distance
= 08:50 a.m. - 08:30 a.m. = 20 min
Speed
of the car in km/min =
= 0.75 km/h
Speed
of the car in km/hr =
Question: 6
Salma takes 15 minutes from her house
to reach her school on a bicycle. If the bicycle has a speed of 2 m/s,
calculate the distance between her house and the school.
Solution:
Speed
of Salma’s bicycle = 2 m/s
Time
taken by Salma to reach her school
=
15 min
Distance
= Speed × time
Distance
= 1800 m
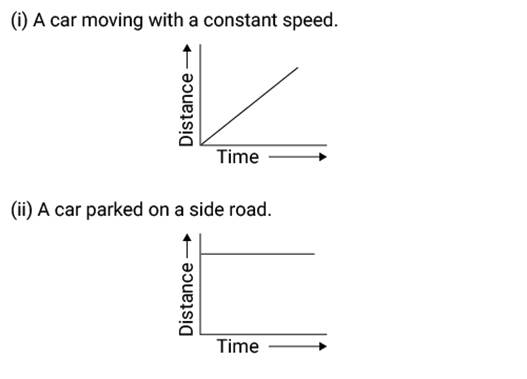
Question: 7
Show the shape of the distance-time graph for the
motion in the following cases:
i.
A
car moving with a constant speed.
ii.
A car parked on a side
road.
Solution:
Question:8
Which of the following relations is
correct?
(i)
(ii)
(iii)
(iv)
Solution:
(ii)
Question: 9
The basic unit of speed is:
(i)
km/min
(ii)
m/min
(iii)
km/h
(iv)
m/s
Solution:
(iv) m/s
Question: 10
A car moves with a speed of 40 km/h
for 15 minutes and then with a speed of 60 km/h for the next 15 minutes. The
total distance covered by the car is:
(i)
100 km
(ii)
25 km
(iii)
15 km
(iv)
10 km
Solution:
(ii) 25 km
Distance covered in first
=10.00 km
Distance
covered in next 15 min
= 15.00 km
Total
distance covered
= 25 km
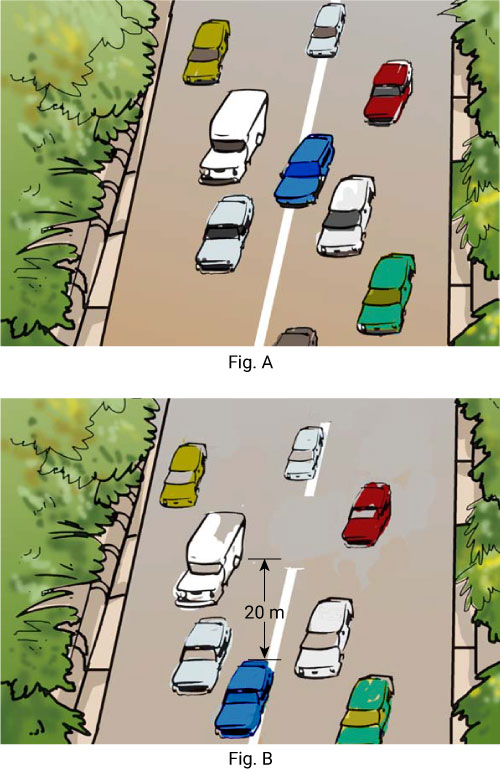
Question: 11
Suppose the two photographs, shown in
the figure A and figure B, had been taken at an interval of 10 seconds. If a
distance of 100 meters is shown by 1 cm in these photographs, calculate the
speed of the blue car.
Solution:
Distance
moved by the blue car in 10 seconds = 2 cm
Given
1 cm =100 m
Therefore,
Distance moved by the blue car in 10 seconds = 200 m
= 20 m/s
Question: 12
The figure below shows the
distance-time graph for the motion of two vehicles A and B. Which one of them
is moving faster?
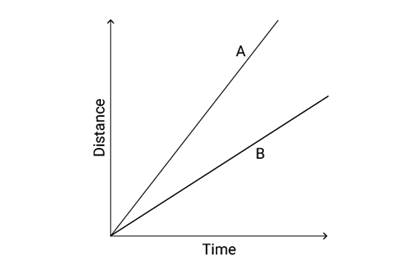
Figure: Distance-time
graph for the motion of two cars
Solution:
From the figure, the slope of vehicle A is steeper than slope
of vehicle B.
The steeper the line, greater the speed. Therefore vehicle A
is moving faster.
Question: 13
Which of the following distance-time
graphs shows a truck moving with speed which is not constant?
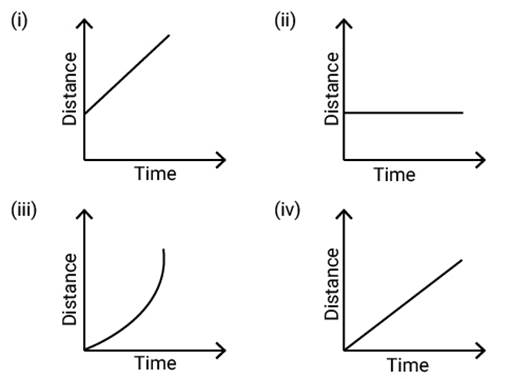
Solution:
(i)