Unit 4: Simple Equations

Complete the last column of the table.

S. No.	Equation	Value	Say, whether the equation is satisfied. (Yes/ No)
(i)	$x+3=0$	$x=3$
(ii)	$x+3=0$	$x=0$
(iii)	$x+3=0$	$x=-3$
(iv)	$x–7=1$	$x=7$
(v)	$x–7=1$	$x=8$
(vi)	$5x=25$	$x=0$
(vii)	$5x=25$	$x=5$
(viii)	$5x=25$	$x=-5$
(ix)	$\frac{m}{3}=2$	$m=-6$
(x)	$\frac{m}{3}=2$	$m=0$
(xi)	$\frac{m}{3}=2$	$m=6$

 

S. No.	Equation	Value	Say, whether the equation is satisfied. (Yes/ No)
(i)	$x+3=0$	$x=3$	No
(ii)	$x+3=0$	$x=0$	No
(iii)	$x+3=0$	$x=-3$	Yes
(iv)	$x–7=1$	$x=7$	No
(v)	$x–7=1$	$x=8$	Yes
(vi)	$5x=25$	$x=0$	No
(vii)	$5x=25$	$x=5$	Yes
(viii)	$5x=25$	$x=-5$	No
(ix)	$\frac{m}{3}=2$	$m=-6$	No
(x)	$\frac{m}{3}=2$	$m=0$	No
(xi)	$\frac{m}{3}=2$	$m=6$	Yes

 

Check whether the value given in the brackets is a solution to the given equation or not:

a.    $n+5=19\left(n=1\right)$

b.   $7n+5=19\left(n=–2\right)$

c.    $7n+5=19\left(n=2\right)$

d.   $4p–3=13\left(p=1\right)$

e.    $4p–3=13\left(p=–4\right)$

f.     $4p–3=13\left(p=0\right)$

a.    $n+5=19\left(n=1\right)$

Putting $n=1\text{ in L}\text{.H}\text{.S}\text{., }1+5=6$

$\because \text{ L}\text{.H}\text{.S}\ne \text{R}\text{.H}\text{.S}\text{.,}$

$\therefore n=1$ is not the solution of given equation.

b.   $7n+5=19\left(n=–2\right)$

Putting $n=-2\text{ in L}\text{.H}\text{.S}\text{., }7(-2)+5=-14+5=-9$

$\because \text{ L}\text{.H}\text{.S}\ne \text{R}\text{.H}\text{.S}\text{.,}$

$\therefore n=-2$ is not the solution of given equation.

c.    $7n+5=19\left(n=2\right)$

Putting $n=2\text{ in L}\text{.H}\text{.S}\text{., }7(2)+5=14+5=19$

$\because \text{ L}\text{.H}\text{.S}=\text{R}\text{.H}\text{.S}\text{.,}$

$\therefore n=2$ is the solution of given equation.

d.   $4p–3=13\left(p=1\right)$ 

Putting $p=1\text{ in L}\text{.H}\text{.S}\text{., }4(1)-3=4-3=1$

$\because \text{ L}\text{.H}\text{.S}\ne \text{R}\text{.H}\text{.S}\text{.,}$

$\therefore p=1$ is not the solution of given equation.

e.    $4p–3=13\left(p=–4\right)$ 

Putting $p=-4\text{ in L}\text{.H}\text{.S}\text{., }4(-4)-3=-16-3=-19$

$\because \text{ L}\text{.H}\text{.S}\ne \text{R}\text{.H}\text{.S}\text{.,}$

$\therefore p=-4$ is not the solution of given equation.

f.     $4p–3=13\left(p=0\right)$

Putting $p=0\text{ in L}\text{.H}\text{.S}\text{., }4(0)-3=0-3=-3$

$\because \text{ L}\text{.H}\text{.S}\ne \text{R}\text{.H}\text{.S}\text{.,}$

$\therefore p=0$ is not the solution of given equation.

Solve the following equations by trial and error method:

(i)             $5p+2=17$

(ii)          $3m–14=4$

(i)             $5p+2=17$

Putting $p=1\text{ in L}\text{.H}\text{.S}\text{. }5(1)+2=5+2=7$

$\because 7\ne 17\text{ Therefore, }p=1$ is not the solution.

Putting $p=2\text{ in L}\text{.H}\text{.S}\text{. }5(2)+2=10+2=12$

$\because 12\ne 17\text{ Therefore, }p=2$ is not the solution.

Putting $p=3\text{ in L}\text{.H}\text{.S}\text{. }5(3)+2=15+2=17$

$\because 17=17\text{ Therefore, }p=3$ is the solution.

(ii)          $3m–14=4$

Putting $m=1\text{ in L}\text{.H}\text{.S}\text{. }3(1)-14=3-14=-11$

$\because -11\ne 4\text{ Therefore, }m=1$ is not the solution.

Putting $m=2\text{ in L}\text{.H}\text{.S}\text{. }3(2)-14=6-14=-8$

$\because -8\ne 4\text{ Therefore, }m=2$ is not the solution.

Putting $m=3\text{ in L}\text{.H}\text{.S}\text{. }3(3)-14=9-14=-5$

$\because -5\ne 4\text{ Therefore, }m=3$ is not the solution.

Putting $m=4\text{ in L}\text{.H}\text{.S}\text{. }3(4)-14=12-14=-2$

$\because -2\ne 4\text{ Therefore, }m=4$ is not the solution.

Putting $m=5\text{ in L}\text{.H}\text{.S}\text{. }3(5)-14=15-14=1$

$\because 1\ne 4\text{ Therefore, }m=5$ is not the solution.

Putting $m=6\text{ in L}\text{.H}\text{.S}\text{. }3(6)-14=18-14=4$

$\because 4=4\text{ Therefore, }m=6$ is the solution.

Write equations for the following statements:

(i)             The sum of numbers $x$ and $4$ is $9$.

(ii)          The difference between $y$ and $2$ is $8$.

(iii)      Ten times $a$ is $70$.

(iv)       The number $b$ divided by $5$ gives $6$.

(v)          Three fourth of $t$ is $15$.

(vi)       Seven times $m$ plus $7$ gets you $77$.

(vii)    One fourth of a number minus $4$ gives $4$.

(viii)If you take away $6$ from $6$ times $y$, you get $60$.

(ix)       If you add $3$ to one third of $z$, you get $30$.

(i)             $x+4=9$

(ii)          $y-2=8$

(iii)      $10a=70$

(iv)       $\frac{b}{5}=6$

(v)          $\frac{3}{4}t=15$

(vi)       $7m+7=77$

(vii)    $\frac{x}{4}-4=4$

(viii)$6y-6=60$

(ix)       $\frac{z}{3}+3=30$

Write the following equations in statement forms:

(i)             $p+4=15$

(ii)          $m–7=3$ 

(iii)      $2m=7$ 

(iv)       $\frac{m}{5}=3$

(v)          $\frac{3m}{5}=6$

(vi)       $3p+4=25$

(vii)    $4p–2=18$

(viii) $\frac{p}{2}+2=8$

(i)             The sum of numbers $p\text{ and }4\text{ is }15.$

(ii)          7 subtracted from $m\text{ is }3.$

(iii)      Two times $m\text{ is }7.$ 

(iv)       The number $m$ is divided by $5$ gives $3$.

(v)          Three-fifth of the number $m$ is $6$

(vi)       Three times $p$ plus $4$ gives $25$.

(vii)    If you take away $2$ from $4$ times $p$, you get $18$.

(viii) If you add $2$ to the half of $p$, you get $8$.

Set up an equation in the following cases:

(i)             Irfan says that he has $7$ marbles more than five times the marbles Parmit has. Irfan has $37$ marbles. (Take $m$ to be the number of Parmit’s marbles.)

(ii)          Laxmi’s father is $49$ years old. He is $4$ years older than three times Laxmi’s age. (Take Laxmi’s age to be $y$ years.)

(iii)      The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus $7$. The highest score is $87$. (Take the lowest score to be $l$.)

(iv)       In an isosceles triangle, the vertex angle is twice either base angle. (Let the base angle be $b$ in degrees. Remember that the sum of angles of a triangle is $180$ degrees).

a.    Let $m$ be the number of Parmit’s marbles.

        $\therefore 5m+7=37$

b.   Let the age of Laxmi be $y$ years.

    $\therefore 3y+4=49$

c.    Let the lowest score be $l$.

    $\therefore 2l+7=87$

d.   Let the base angle of the isosceles triangle be $b$, so vertex angle $=2b$

        $\therefore 2b+b+b=180°$

        $\Rightarrow 4b=180°$      [Angle sum property of a $\Delta$ ]

 

Give first the step you will use to separate the variable and then solve the equation:

a.    $x–1=0$

b.   $x+1=0$

c.    $x-1=5$ 

d.   $x+6=2$

e.    $y-4=-7$

f.     $y-4=4$

g.   $y+4=4$ 

h.   $y+4=–4$

a.    $x–1=0$

$\Rightarrow x-1+1=0+1$        [Adding $1$ to both sides]

$\Rightarrow x=1$

b.   $x+1=0$

$\Rightarrow x+1-1=0-1$        [Subtracting $1$ from both sides]

$\Rightarrow x=-1$

c.    $x-1=5$ 

$\Rightarrow x-1+1=5+1$        [Adding $1$ to both sides]

$\Rightarrow x=6$

d.   $x+6=2$

$\Rightarrow x+6-6=2-6$       [Subtracting $6$ from both sides]

$\Rightarrow x=-4$

e.    $y-4=-7$

$\Rightarrow y-4+4=-7+4$    [Adding $4$ to both sides]

$\Rightarrow y=-3$

f.     $y-4=4$ 

$\Rightarrow y-4+4=4+4$      [Adding $4$ to both sides]

$\Rightarrow y=8$

g.   $y+4=4$ 

$\Rightarrow y+4-4=4-4$      [Subtracting $4$ from both sides]

$\Rightarrow y=0$

h.   $y+4=–4$

$\Rightarrow y+4-4=-4-4$    [Subtracting $4$ from both sides]

$\Rightarrow y=-8$

Give first the step you will use to separate the variable and then solve the equation:

a.    $3l=42$

b.   $\frac{b}{2}=6$

c.    $\frac{p}{7}=4$

d.   $4x=25$

e.    $8y=36$

f.     $\frac{z}{3}=\frac{5}{4}$

g.   $\frac{a}{5}=\frac{7}{15}$

h.   $20t=-10$

a.    $3l=42$

$\Rightarrow \frac{3l}{3}=\frac{42}{3}$           [Dividing both sides by $3$ ]

$\Rightarrow l=14$

b.   $\frac{b}{2}=6$

$\Rightarrow \frac{b}{2}\times 2=6\times 2$     [Multiplying both sides by $2$ ]

$\Rightarrow b=12$

c.    $\frac{p}{7}=4$

$\Rightarrow \frac{p}{7}\times 7=4\times 7$    [Multiplying both sides by $7$ ]

$\Rightarrow p=28$

d.   $4x=25$

$\Rightarrow \frac{4x}{4}=\frac{25}{4}$          [Dividing both sides by $4$ ]

$\Rightarrow x=\frac{25}{4}$

e.    $8y=36$

$\Rightarrow \frac{8y}{8}=\frac{36}{8}$          [Dividing both sides by $8$ ]

$\Rightarrow y=\frac{9}{2}$

f.     $\frac{z}{3}=\frac{5}{4}$

$\Rightarrow \frac{z}{3}\times 3=\frac{5}{4}\times 3$    [Multiplying both sides by $3$ ]

$\Rightarrow z=\frac{15}{4}$

g.   $\frac{a}{5}=\frac{7}{15}$

$\Rightarrow \frac{a}{5}\times 5=\frac{7}{15}\times 5$   [Multiplying both sides by $5$ ]

$\Rightarrow a=\frac{7}{3}$

h.   $20t=-10$

$\Rightarrow \frac{20t}{20}=\frac{-10}{20}$       [Dividing both sides by $20$ ]

$\Rightarrow t=\frac{-1}{2}$

Give the steps you will use to separate the variable and then solve the equation:

a.    $3n-2=46$

b.   $5m+7=17$

c.    $\frac{20p}{3}=40$

d.   $\frac{3p}{10}=6$

a.    $3n-2=46$

Step I: $3n-2+2=46+2$

$\Rightarrow 3n=48$                   [Adding $2$ to both sides]

Step II: $\frac{3n}{3}=\frac{48}{3}\Rightarrow n=16$     [Dividing both sides by $3$ ]

b.   $5m+7=17$

Step I: $5m+7-7=17-7$

$\Rightarrow 5m=10$                  [Subtracting $7$ from both sides]

Step II: $\frac{5m}{5}=\frac{10}{5}\Rightarrow m=2$    [Dividing both sides by $5$ ]

c.    $\frac{20p}{3}=40$

Step I: $\frac{20p}{3}\times 3=40\times 3$

$\Rightarrow 20p=120$               [Multiplying both sides by $3$ ]

Step II: $\frac{20p}{20}=\frac{120}{20}\Rightarrow p=6$   [Dividing both sides by $20$ ]

d.   $\frac{3p}{10}=6$

Step I: $\frac{3p}{10}\times 10=6\times 10$

$\Rightarrow 3p=60$                   [Multiplying both sides by $10$ ]

Step II: $\frac{3p}{3}=\frac{60}{3}\Rightarrow p=20$     [Dividing both sides by $3$ ]

Solve the following equations:

a.    $10p=100$

b.   $10p+10=100$

c.    $\frac{p}{4}=5$

d.   $\frac{-p}{3}=5$

e.    $\frac{3p}{4}=6$

f.     $3s=-9$

g.   $3s+12=0$

h.   $3s=0$

i.      $2q=6$

j.      $2q-6=0$

k.   $2q+6=0$

l.      $2q+6=12$

a.    $10p=100$

        $\Rightarrow \frac{10p}{10}=\frac{100}{10}$                      [Dividing both sides by $10$ ]

        $\Rightarrow p=10$

b.   $10p+10=100$

        $\Rightarrow 10p+10-10=100-10$  [Subtracting $10$ from both sides ]

        $\Rightarrow 10p=90$

        $\Rightarrow \frac{10p}{10}=\frac{90}{10}$                [Dividing both sides by $10$ ]

        $\Rightarrow p=9$

c.    $\frac{p}{4}=5$

        $\Rightarrow \frac{p}{4}\times 4=5\times 4$                    [Multiplying both sides by $4$ ]

        $\Rightarrow p=20$

d.   $\frac{-p}{3}=5$

        $\Rightarrow \frac{-p}{3}\times (-3)=5\times (-3)$ [Multiplying both sides by $-3$ ]

        $\Rightarrow p=-15$

e.    $\frac{3p}{4}=6$

        $\Rightarrow \frac{3p}{4}\times 4=6\times 4$                   [Multiplying both sides by $4$ ]

        $\Rightarrow 3p=24\Rightarrow \frac{3p}{3}=\frac{24}{3}$ [Dividing both sides by $3$ ]

        $\Rightarrow p=8$

f.     $3s=-9$

        $\Rightarrow \frac{3s}{3}=\frac{-9}{3}$                           [Dividing both sides by $3$ ]

        $\Rightarrow s=-3$

g.   $3s+12=0$

        $\Rightarrow 3s+12-12=0-12$ [Subtracting $12$ from both sides]

        $\Rightarrow 3s=-12\Rightarrow \frac{3s}{3}=\frac{-12}{3}$      [Dividing both sides by $3$ ]

        $\Rightarrow s=-4$

h.   $3s=0$

        $\Rightarrow \frac{3s}{3}=\frac{0}{3}$                             [Dividing both sides by $3$ ]

        $\Rightarrow s=0$

i.      $2q=6$

        $\Rightarrow \frac{2q}{2}=\frac{6}{2}$                             [Dividing both sides by $2$ ]

        $\Rightarrow q=3$

j.      $2q-6=0$

        $\Rightarrow 2q-6+6=0+6$              [Adding $6$ to both sides]

        $\Rightarrow 2q=6\Rightarrow \frac{2q}{2}=\frac{6}{2}$              [Dividing both sides by $2$ ]

        $\Rightarrow q=3$

k.   $2q+6=0$

        $\Rightarrow 2q+6-6=0-6$              [Subtracting $6$ from both sides]

        $\Rightarrow 2q=-6\Rightarrow \frac{2q}{2}=\frac{-6}{2}$         [Dividing both sides by $2$ ]

        $\Rightarrow q=-3$

l.      $2q+6=12$

        $\Rightarrow 2q+6-6=12-6$            [Subtracting $6$ from both sides]

        $\Rightarrow 2q=6\Rightarrow \frac{2q}{2}=\frac{6}{2}$              [Dividing both sides by $2$ ]

        $\Rightarrow q=3$

 

Solve the following equations.

a.    $2y+\frac{5}{2}=\frac{37}{2}$

b.   $5t+28=10$

c.    $\frac{a}{5}+3=2$

d.   $\frac{q}{4}+7=5$

e.    $\frac{5}{2}x=10$

f.     $\frac{5}{2}x=\frac{25}{4}$

g.   $7m+\frac{19}{2}=13$

h.   $6z+10=-2$

i.      $\frac{3l}{2}=\frac{2}{3}$

j.      $\frac{2b}{3}-5=3$

a.    $2y+\frac{5}{2}=\frac{37}{2}$

$\Rightarrow 2y=\frac{37}{2}-\frac{5}{2}$

$\Rightarrow 2y=\frac{37-5}{2}$

$\Rightarrow 2y=\frac{32}{2}$

$\Rightarrow 2y=16$

$\Rightarrow \frac{2y}{2}=\frac{16}{2}$    

$\Rightarrow y=8$

b.   $5t+28=10$

$\Rightarrow 5t=10-28$

$\Rightarrow 5t=-18$

$\Rightarrow t=\frac{-18}{5}$

c.    $\frac{a}{5}+3=2$

$\Rightarrow \frac{a}{5}=2-3$

$\Rightarrow \frac{a}{5}=-1$

$\Rightarrow a=-1\times 5$

$\Rightarrow a=-5$

d.   $\frac{q}{4}+7=5$

$\Rightarrow \frac{q}{4}=5-7$

$\Rightarrow \frac{q}{4}=-2$

$\Rightarrow q=-2\times 4$

$\Rightarrow q=-8$

e.    $\frac{5}{2}x=10$

$\Rightarrow 5x=10\times 2$

$\Rightarrow 5x=20$

$\Rightarrow x=\frac{20}{5}$

$\Rightarrow x=4$

f.     $\frac{5}{2}x=\frac{25}{4}$

$\Rightarrow 5x=\frac{25}{4}\times 2$

$\Rightarrow 5x=\frac{25}{2}$

$\Rightarrow x=\frac{25}{2\times 5}$

$\Rightarrow x=\frac{5}{2}$

g.   $7m+\frac{19}{2}=13$

$\Rightarrow 7m=13-\frac{19}{2}$

$\Rightarrow 7m=\frac{26-19}{2}$

$\Rightarrow 7m=\frac{7}{2}$

$\Rightarrow m=\frac{7}{2\times 7}$

$\Rightarrow m=\frac{1}{2}$

h.   $6z+10=-2$

$\Rightarrow 6z=-2-10$

$\Rightarrow 6z=-12$

$\Rightarrow z=\frac{-12}{6}$

$\Rightarrow z=-2$

i.      $\frac{3l}{2}=\frac{2}{3}$

$\Rightarrow 3l=\frac{2}{3}\times 2$

$\Rightarrow 3l=\frac{4}{3}$

$\Rightarrow l=\frac{4}{3\times 3}$

$\Rightarrow l=\frac{4}{9}$

j.      $\frac{2b}{3}-5=3$

$\Rightarrow \frac{2b}{3}=3+5$

$\Rightarrow \frac{2b}{3}=8$

$\Rightarrow 2b=8\times 3$

$\Rightarrow 2b=24$

$\Rightarrow b=\frac{24}{2}$

$\Rightarrow b=12$

Solve the following equations.

a.    $2\left(x+4\right)=12$

b.   $3\left(n-5\right)=21$

c.    $3\left(n-5\right)=-21$

d.   $3-2\left(2-y\right)=7$

e.    $-4\left(2-x\right)=9$

f.     $4\left(2-x\right)=9$

g.   $4+5\left(p-1\right)=34$

h.   $34-5\left(p-1\right)=4$

a.    $2\left(x+4\right)=12$

$\Rightarrow x+4=\frac{12}{2}$

$\Rightarrow x+4=6$

$\Rightarrow x=6-4$

$\Rightarrow x=2$

b.   $3\left(n-5\right)=21$

$\Rightarrow n-5=\frac{21}{3}$

$\Rightarrow n-5=7$

$\Rightarrow n=7+5$

$\Rightarrow n=12$

c.    $3\left(n-5\right)=-21$

$\Rightarrow n-5=\frac{-21}{3}$

$\Rightarrow n-5=-7$

$\Rightarrow n=-7+5$

$\Rightarrow n=-2$

d.   $3-2\left(2-y\right)=7$

$\Rightarrow -2(2-y)=7-3$

$\Rightarrow -2(2-y)=4$

$\Rightarrow 2-y=\frac{4}{-2}$

$\Rightarrow 2-y=-2$

$\Rightarrow -y=-2-2$

$\Rightarrow -y=-4$

$\Rightarrow y=4$

e.    $-4\left(2-x\right)=9$

$\Rightarrow -4\times 2-x\times (-4)=9$

$\Rightarrow -8+4x=9$

$\Rightarrow 4x=9+8$

$\Rightarrow 4x=17$

$\Rightarrow x=\frac{17}{4}$

f.     $4\left(2-x\right)=9$

$\Rightarrow 4\times 2-x\times (4)=9$

$\Rightarrow 8-4x=9$

$\Rightarrow -4x=9-8$

$\Rightarrow -4x=1$

$\Rightarrow x=\frac{-1}{4}$

g.   $4+5\left(p-1\right)=34$

$\Rightarrow 5(p-1)=34-4$

$\Rightarrow 5(p-1)=30$

$\Rightarrow p-1=\frac{30}{5}$

$\Rightarrow p-1=6$

$\Rightarrow p=6+1$

$\Rightarrow p=7$

h.   $34-5\left(p-1\right)=4$

$\Rightarrow -5(p-1)=4-34$

$\Rightarrow -5(p-1)=-30$

$\Rightarrow p-1=\frac{-30}{-5}$

$\Rightarrow p-1=6$

$\Rightarrow p=6+1$

$\Rightarrow p=7$

Solve the following equations.

a.    $4=5\left(p-2\right)$

b.   $-4=5\left(p-2\right)$

c.    $–16=-5\left(2-p\right)$

d.   $10=4+3\left(t+2\right)$

e.    $28=4+3\left(t+5\right)$

f.     $0=16+4\left(m-6\right)$

a.    $4=5\left(p-2\right)$

$\Rightarrow 4=5\times p-5\times 2$

$\Rightarrow 4=5p-10$

$\Rightarrow 5p-10=4$

$\Rightarrow 5p=4+10$

$\Rightarrow 5p=14$

$\Rightarrow p=\frac{14}{5}$

b.   $-4=5\left(p-2\right)$

$\Rightarrow -4=5\times p-5\times 2$

$\Rightarrow -4=5p-10$

$\Rightarrow 5p-10=-4$

$\Rightarrow 5p=-4+10$

$\Rightarrow 5p=6$

$\Rightarrow p=\frac{6}{5}$

c.    $-16=-5\left(2-p\right)$

$\Rightarrow -16=-5\times 2-(-5)\times p$

$\Rightarrow -16=-10+5p$

$\Rightarrow -10+5p=-16$

$\Rightarrow 5p=-16+10$

$\Rightarrow 5p=-6$

$\Rightarrow p=\frac{-6}{5}$

d.   $10=4+3\left(t+2\right)$

$\Rightarrow 10-4=3(t+2)$

$\Rightarrow 6=3(t+2)$

$\Rightarrow \frac{6}{3}=t+2$

$\Rightarrow 2=t+2$

$\Rightarrow 2-2=t$

$\Rightarrow 0=t$

$\Rightarrow t=0$

e.    $28=4+3\left(t+5\right)$

$\Rightarrow 28-4=3(t+5)$

$\Rightarrow 24=3(t+5)$

$\Rightarrow \frac{24}{3}=t+5$

$\Rightarrow 8=t+5$

$\Rightarrow 8-5=t$

$\Rightarrow 3=t$

$\Rightarrow t=3$

f.     $0=16+4\left(m-6\right)$

$\Rightarrow 0-16=4(m-6)$

$\Rightarrow -16=4(m-6)$

$\Rightarrow \frac{-16}{4}=m-6$

$\Rightarrow -4=m-6$

$\Rightarrow -4+6=m$

$\Rightarrow 2=m$

$\Rightarrow m=2$

a.    Construct $3$ equations starting with $x=2$

b.   Construct $3$ equations starting with $x=-2$

a.    $3$ equations starting with $x=2$.

(i) $x=2$

Multiplying both sides by $10$, $10x=20$

Adding $2$ to both sides

$10x+2=20+2=10x+2=22$

(ii)          $x=2$

Multiplying both sides by $5$,           $5x=10$

Subtracting $3$ from both sides

$5x-3=10-3\Rightarrow 5x-3=7$

(iii)      $x=2$

Dividing both sides by $5$,                $\frac{x}{5}=\frac{2}{5}$

b.   $3$ equations starting with $x=-2$.

(i) $x=-2$

Multiplying both sides by $3$,           $3x=-6$

(ii)          $x=-2$

Multiplying both sides by $3$,           $3x=-6$

Adding $7$ to both sides

$3x+7=-6+7\Rightarrow 3x+7=1$

(iii)      $x=-2$

Multiplying both sides by $3$,           $3x=-6$

Adding $10$ to both sides

$3x+10=-6+10=3x+10=4$

 

 

Set up equations and solve them to find the unknown numbers in the following cases:

a.    Add $4$ to eight times a number; you get $60$.

b.   One fifth of a number minus $4$ gives $3$.

c.    If I take three fourths of a number and count up $3$ more, I get $21$.

d.   When I subtracted $11$ from twice a number, the result was $15$.

e.    Munna subtracts thrice the number of notebooks he has from $50$, he finds the result to be $8$.

f.     Ibenhal thinks of a number. If she adds $19$ to it and divides the sum by $5$, she will get $8$.

g.   Anwar thinks of a number. If he takes away $7$ from $\frac{5}{2}$ of the number, the result is $\frac{11}{2}$.

a.    Let the number be $x$.

According to the question, $8x+4=60$

$\Rightarrow 8x=60-4$

$\Rightarrow 8x=56$

$\Rightarrow x=\frac{56}{8}$

$\Rightarrow x=7$

b.   Let the number be $y$.

According to the question, $\frac{y}{5}-4=3$

$\Rightarrow \frac{y}{5}=3+4$

$\Rightarrow \frac{y}{5}=7$

$\Rightarrow y=7\times 5$

$\Rightarrow y=35$

c.    Let the number be $z$.

According to the question, $\frac{3}{4}z+3=21$

$\Rightarrow \frac{3}{4}z=21-3$

$\Rightarrow \frac{3}{4}z=18$

$\Rightarrow 3z=18\times 4$

$\Rightarrow 3z=72$

$\Rightarrow z=\frac{72}{3}$

$\Rightarrow z=24$

d.   Let the number be $x$.

According to the question, $2x-11=15$

$\Rightarrow 2x=15+11$

$\Rightarrow 2x=26$

$\Rightarrow x=\frac{26}{2}$

$\Rightarrow x=13$

e.    Let the number be $m$.

According to the question, $50-3m=8$

$\Rightarrow -3m=8-50$

$\Rightarrow -3m=-42$

$\Rightarrow m=\frac{-42}{-3}$

$\Rightarrow m=14$

f.     Let the number be $n$.

According to the question, $\frac{n+19}{5}=8$

$\Rightarrow n+19=8\times 5$

$\Rightarrow n+19=40$

$\Rightarrow n=40-19$

$\Rightarrow n=21$

g.   Let the number be $x$.

According to the question, $\frac{5}{2}x-7=\frac{11}{2}$

$\Rightarrow \frac{5}{2}x=\frac{11}{2}+7$

$\Rightarrow \frac{5}{2}x=\frac{11+14}{2}$

$\Rightarrow \frac{5}{2}x=\frac{25}{2}$

$\Rightarrow 5x=\frac{25\times 2}{2}$

$\Rightarrow 5x=25$

$\Rightarrow x=\frac{25}{5}$

$\Rightarrow x=5$

Solve the following:

a.    The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus $7$. The highest score is $87$. What is the lowest score?

b.   In an isosceles triangle, the base angles are equal. The vertex angle is $40°$. What are the base angles of the triangle? (Remember, the sum of three angles of a triangle is $180°$ ).

c.    Smita’s mother is $34$ years old. Two years from now mother’s age will be $4$ times Smita’s present age. What is Smita’s present age?

d.   Sachin scored twice as many runs as Rahul. Together, their runs fell two short of a double century. How many runs did each one score?

a.    Let the lowest marks be $y$.

According to the question, $2y+7=87$

$\Rightarrow 2y=87-7$

$\Rightarrow 2y=80$

$\Rightarrow y=\frac{80}{2}$

$\Rightarrow y=40$

Thus, the lowest score is $40$.

b.   Let the base angle of the triangle be $b$.

Given, $a=40°,b=c$

Since, $a+b+c=180°$     [Angle sum property of a triangle]

$\Rightarrow 40°+b+b=180°$

$\Rightarrow 40°+2b=180°$

$\Rightarrow 2b=180°-40°$

$\Rightarrow 2b=140°$

$\Rightarrow b=\frac{140°}{2}$

$\Rightarrow b=70°$

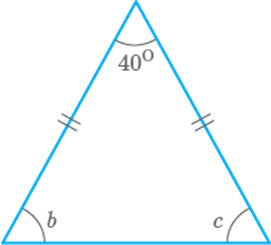
Thus, the base angles of the isosceles triangle are $70°$ each.

c.    Let Smita’s present age be $x$

$2$ years from now, Smita’s age $=x+2$

$2$ years from now her mother’s age $=4\left(x+2\right)$

i.e., $36=4\left(x+2\right)$

$\left(x+2\right)=\frac{36}{4}=9$

$\Rightarrow x=7$

Smita’s present age $=7$ years.

d.   Let the score of Rahul be $x$ runs and Sachin’s score is $2x$.

According to the question, $x+2x=198$

$\Rightarrow 3x=198$

$\Rightarrow x=\frac{198}{3}$

$\Rightarrow x=66$

Thus, Rahul’s score $=66$ runs

And Sachin’s score $=2\times 66=132$ runs.

Solve the following:

(i)             Irfan says that he has $7$ marbles more than five times the marbles Parmit has. Irfan has $37$ marbles. How many marbles does Parmit have?

(ii)          Laxmi's father is $49$ years old. He is $4$ years older than three times Laxmi's age. What is Laxmi's age?

(iii)      Maya, Madhura and Mohsina are friends studying in the same class. In a class test in geography, Maya got $16$ out of $25$. Madhura got $20$. Their average score was $19$. How much did Mohsina score?

(iv)       People of Sundargram planted a total of $102$ trees in the village garden. Some of the trees were fruit trees. The number of non-fruit trees were two more than three times the number of fruit trees. What was the number of fruit trees planted?

(i)             Let the number of marbles Parmit has be $m$.

According to the question, $5m+7=37$

$\Rightarrow 5m=37-7$

$\Rightarrow 5m=30$

$\Rightarrow m=\frac{30}{5}$

$\Rightarrow m=6$

Thus, Parmit has $6$ marbles.

(ii)          Let the age of Laxmi be $y$ year.

Then her father’s age $=(3y+4)$ years

According to question, $3y+4=49$

$\Rightarrow 3y=49-4$

$\Rightarrow 3y=45$

$\Rightarrow y=\frac{45}{3}$

$\Rightarrow y=15$

Thus, the age of Laxmi is $15$ years.

(iii)      Let the marks scored by Mohsina $=x$

According to the question scored by Maya $=16$

According to the question scored by Madhura $=20$

Total marks scored by all three $=16+20+x=36+x$

Average marks scored by all three $=19$

$\text{Average marks}=\frac{\text{total marks}}{3}$

$\frac{\text{Total marks}}{3}=19$

$\text{Total marks}=19\times 3=57$

Total marks scored by all three $=16+20+x=36+x$

$36+x=57$

Transposing $36$ will make it $-36$.

$x=57-36$

$x=21$

Hence the marks scored by Mohsina are $21$ out of $25$.

(iv)       Let the number of fruit trees be $t$.

Then the number of non-fruits tree $=3t+2$ 

According to the question, $t+3t+2=102$

$\Rightarrow 4t+2=102$

$\Rightarrow 4t=102-2$

$\Rightarrow 4t=100$

$\Rightarrow t=\frac{100}{4}$

$\Rightarrow t=25$

Thus, the number of fruit trees are $25$.

Solve the following riddle:

I am a number,

                                        Tell my identity!

Take me seven times over

                                        And add a fifty!

To reach a triple century

                                        You still need forty!

Let the number be $n$.

According to the question, $7n+50+40=300$

$\Rightarrow 7n+90=300$

$\Rightarrow 7n=300-90$

$\Rightarrow 7n=210$

$\Rightarrow n=\frac{210}{7}$

$\Rightarrow n=30$

Thus, the required number is $30.$