Unit
1: Integers
Exercise: 1.1 (10)
Question:
1
Following
number line shows the temperature in degree celsius ( ) at different places on a particular day.
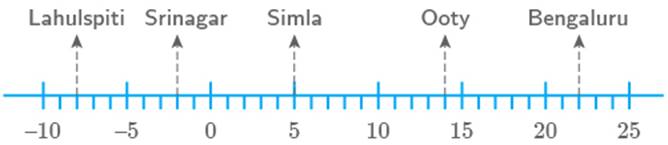
a.
Observe this number line and write the temperature of the places marked
on it.
b.
What is the temperature difference between the hottest and the coldest
places among the above?
c.
What is the temperature difference between Lahulspiti and Srinagar?
d.
Can we say temperature of Srinagar and Shimla taken together is less
than the temperature at Shimla? Is it also less than the temperature at
Srinagar?
Solution
a. The temperature
of the places marked on the given number line is given in the following table:
|
Places
|
Temperature
|
|
Bengaluru
|
|
|
Ooty
|
|
|
Shimla
|
|
|
Srinagar
|
|
|
Lahulspiti
|
|
b. The temperature
of the hottest place (Bengaluru)
The temperature of the
coldest place (Lahulspiti)
Difference
c. The temperature
of Srinagar
The temperature of Lahulspiti
Difference
d. Sum of the
temperatures of Srinagar and Shimla
The temperature at Shimla
So, the temperature of Srinagar and Shimla taken
together is less than the temperature at Shimla.
Now, temperature of Srinagar
So, temperature of is not less than the temperature at Srinagar.
Question:
2
In
a quiz, positive marks are given for correct answers and negative marks are
given for incorrect answers. If Jack’s scores in five successive rounds were and what was his total at the end?
Solution
Jack’s scores in five
successive rounds are and
Total marks got by Jack
Thus, marks are obtained by Jack in a quiz.
Question:
3
At
Srinagar temperature was on Monday and then it dropped by on Tuesday. What was the temperature of
Srinagar on Tuesday? On Wednesday, it rose by What was the temperature on this day?
Solution
On Monday, temperature at
Srinagar
On Tuesday, temperature
dropped by
Temperature on Tuesday
On Wednesday, temperature
rose up by
Temperature on Wednesday
Thus, temperature on Tuesday
and Wednesday was and respectively.
Question:
4
A
plane is flying at the height of above the sea level. At a particular point, it
is exactly above a submarine floating below the sea level. What is the vertical
distance between them?
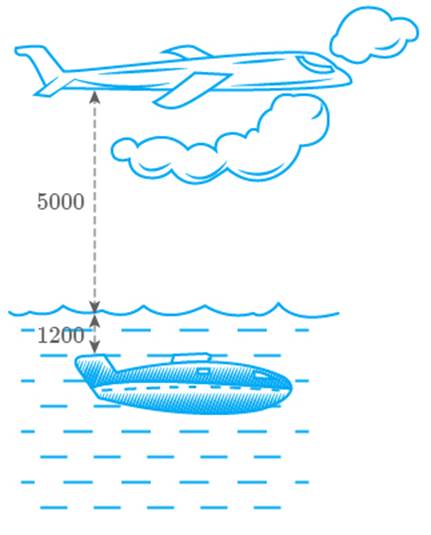
Solution
Height of a plane above the
sea level
Depth of a submarine below
the sea level
The vertical distance between the plane and
the submarine
Thus, the vertical distance
between the plane and the submarine is
Question:
5
Mohan
deposits in his bank account and withdraws from it, the next day. If withdrawal of amount
from the account is represented by a negative integer, then how will you
represent the amount deposited? Find the balance in Mohan’s account after the
withdrawal.
Solution
Amount deposited and Amount withdraw
Balance
Thus, the balance in Mohan’s
account after withdrawal is
Question:
6
Rita
goes towards east from a point A to the point B.
From B, she moves towards west along the same road. If the
distance towards east is represented by a positive integer then, how will you represent
the distance travelled towards west? By which integer will you represent her
final position from A?

Solution

According to the question distance
towards east is represented by a positive integer. So, the distance opposite of
east, that is west direction is represented by a negative integer.
On the given number line:
Distance from A to B
Distance from B to C
Thus, final position of Rita
from A
Question:
7
In
a magic square each row, column and diagonal have the same sum. Check which of
the following is a magic square.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(i) (ii)
Solution
(i)
Sum of numbers in each row:
Sum of numbers in each column:
Sum of numbers along each diagonal:
As the sum of numbers along a diagonal is not zero, the box is not a magic
square.
(ii)
Sum of numbers in each row:
Sum of numbers in each column:
Sum of numbers along each diagonal:
The given square is a magic
square as its
each row, column and diagonal have the same sum.
Question:
8
Verify
for the following values of and
(i)
(ii)
(iii)
(iv)
Solution
(i)
Given:
We have,
Put the values in L.H.S.
Put the values in R.H.S.
L.H.S. R.H.S.
Hence, verified.
(ii)
Given:
We have,
Put the values in L.H.S.
Put the values in R.H.S.
Thus, L.H.S. R.H.S.
Hence, verified.
(iii)
Given:
We have,
Put the values in L.H.S.
Put the values in R.H.S.
Thus, L.H.S. R.H.S.
Hence, verified.
(iv)
Given:
We have,
Put the values in L.H.S.
Putting the values in R.H.S.
Thus, L.H.S. R.H.S.
Hence, verified.
Question:
9
Use
the sign of in the box to make the statements true.
a.
b.
c.
d.
e.
Solution
a.
b.
c.
d.
e.
Question:
10
A water tank has steps
inside it. A monkey is sitting on the topmost step (i.e., the first step). The
water level is at the ninth step.
(i)
He jumps steps down and then jumps back steps up. In how many jumps will he reach the
water level?
(ii)
After drinking water, he wants to go back. For
this, he jumps steps up and then jumps back steps down in every move. In how many jumps
will he reach back the top step?
(iii)
If the number of steps moved down is represented
by negative integers and the number of steps moved up by positive integers,
represent his moves in part (i). and (ii) by completing the following; (a) (b)
In (a) the sum represents going down by eight steps. So, what
will the sum in (b) represent?
Solution
(i)
He jumps steps down and then jumps back steps up. Following number line shows the
jumps of monkey:
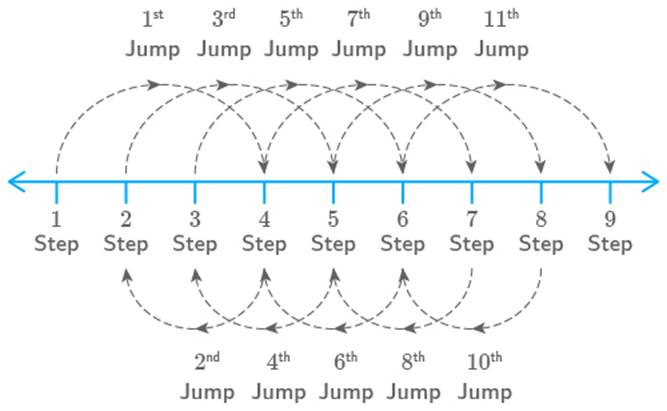
First jump steps,
Second jump steps,
Third jump steps,
Fourth jump steps,
Fifth jump steps,
Sixth jump steps,
Seventh jump steps,
Eighth jump steps,
Ninth jump steps,
Tenth jump steps,
Eleventh jump steps,
He will reach ninth steps in
jumps.
(ii)
Monkey jumps four steps up and then jumps down steps. Following number line shows the jumps
of monkey:
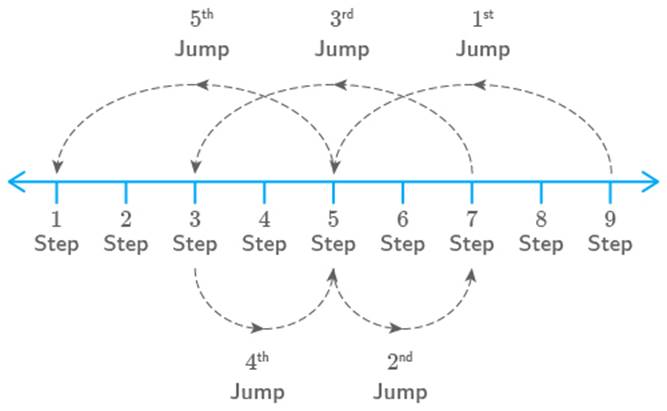
The money reaches back on
the first step in fifth jump.
(iii)
(a)
(b)
Thus, sum in (b) represents going up by eight steps.
Exercise: 1.2 (4)
Question:
1
Write
down a pair of integers whose:
a.
sum is
b.
difference is
c.
sum is
Solution
a. A pair of integers whose sum is
b. A pair of integers whose difference is
c. A pair of
integers whose sum is
Question:
2
a.
Write a pair of negative integers whose difference gives
b.
Write a negative integer and a positive integer whose sum is
c.
Write a negative integer and a positive integer whose difference is
Solution
a.
b.
c.
Question:
3
In
a quiz, team A scored and team B scored in three successive rounds. Which team scored
more? Can we say that we can add integers in any order?
Solution
Team A scored
Total score of Team A
Team B scored
Total score of Team B
Thus, scores of both the teams
are same.
Yes, we can add integers in
any order as per commutative property.
Question:
4
Fill
in the blanks to make the following statements true:
(i)
(ii)
(iii)
(iv)
(v)
Solution
(i)
(ii)
(iii)
(iv)
(v)
Exercise: 1.3 (9)
Question:
1
Find
each of the following products:
a.
b.
c.
d.
e.
f.
g.
h.
i.
j.
Solution
a.
b.
c.
d.
e.
f.
g.
h.
i.
j.
Question:
2
Verify
the following:
a.
b.
Solution
a.
Hence verified.
b.
Hence verified.
Question:
3
(i)
For any integer a, what is equal to?
(ii)
Determine the integer whose
product with is
(a)
(b)
(c)
Solution
(i)
where is an integer.
(ii)
(a)
(b)
(c)
Question:
4
Starting
from write various products showing some pattern to
show
Solution
This pattern shows the product of a negative integer and a positive
integer is a negative integer, whereas the product two negative integers is a
positive integer.
Question:
5
Find the product, using
suitable properties:
a.
b.
c.
d.
e.
f.
g.
h.
Solution
a.
[Distributive
property]
b.
[Associative property]
c.
[Commutative property]
d.
[Distributive property]
e.
[Distributive property]
f.
[Distributive property]
g.
[Distributive property]
h.
[Distributive property]
Question:
6
A certain freezing process
requires that room temperature be lowered from at the rate of every hour. What will be the room temperature hours after the process begins?
Solution
Present room temperature
Decrease in the temperature
every hour
Change in the temperature every hour
Room temperature after hours
Question:
7
In a class test containing questions, marks are awarded for every correct answer and
marks are awarded for every incorrect answer
and for questions not attempted.
(i)
Mohan gets four correct and six incorrect answers. What is
his score?
(ii)
Reshma gets five correct answers and five incorrect answers,
what is her score?
(iii)
Heena gets two correct and five incorrect answers out of
seven questions she attempts. What is her score?
Solution
(i)
Marks for four correct question
Marks for six incorrect question
Therefore, total score
Thus, Mohan gets marks in a class test.
(ii)
Marks for five correct question
Marks for five incorrect question
Therefore, total score
Thus, Reshma gets marks in a class test.
(iii)
Marks for two correct question Marks for five incorrect question
Therefore, total score
Thus, Reshma gets marks in a class test.
Question:
8
A cement company earns a
profit of per bag of white cement sold and a loss of per bag of grey cement sold.
a. The company sells
bags of white cement and bags of grey cement in a month. What is its
profit or loss?
b. What is the
number of white cement bags it must sell to have neither profit nor loss, if
the number of grey bags sold is bags.
Solution
Given, profit of bag of white cement
Loss of bag of grey cement
a. Profit on selling
bags of white cement
Loss on selling bag of grey cement
Since, Profit Loss
Therefore, total loss on selling grey cement bags Loss Profit
b. Let the number of
bags of white cement be
According to the question, Loss Profit
bags
Thus, he must sell white cement bags to have neither profit nor
loss.
Question:
9
Replace the blank with an
integer to make it a true statement.
a.
b.
c.
d.
Solution
a.
b.
c.
d.
Exercise: 1.4 (7)
Question:
1
Evaluate
each of the following:
a.
b.
c.
d.
e.
f.
g.
h.
i.
Solution
a.
b.
c.
d.
e.
f.
g.
h.
i.
Question:
2
Verify
that for each of the following values of and
a.
b.
Solution
a.
Given: and
On putting the given value
in L.H.S. L.H.S.
On putting the given value
in R.H.S. R.H.S.
Thus, L.H.S. R.H.S.
Hence verified.
b.
Given: and
L.H.S.
R.H.S.
Thus, L.H.S. R.H.S. Hence verified.
Question:
3
Fill
in the blanks:
a.
b.
c.
d.
e.
f.
g.
h.
Solution
a.
b.
c.
d.
e.
f.
g.
h.
Question:
4
Write
five pairs of integers such that One such pair is because
Solution
(i)
(ii)
(iii)
(iv)
(v)
So, five pairs of required integers are:
(–6, 2), (9, –3), (12, –4), (–9,
3) and (–15, 5)
Question:
5
The
temperature at noon was above zero. If it decreases at the rate of per hour until midnight, at what time would the temperature be below zero?
What
would be the temperature at mid-night?
Solution
Following number line represents the temperature.

The
temperature decreases
The temperature
decreases
The
temperature decreases
Total
time = .
Thus, at pm the temperature would be below
Time between mid-noon and mid-night hours
Temperature at mid-night
Question:
6
In
a class test marks are given for every correct answer and marks are given for every incorrect answer and
no marks for not attempting any question.
(i)
Radhika scored marks. If she has got correct answers, how many questions has she
attempted incorrectly?
(ii)
Mohini scores marks in this test, though she has got correct answers. How many questions has she
attempted incorrectly?
Solution
(i)
Marks given for one correct answer
Marks given for correct answers
Radhika scored marks.
Therefore, marks obtained
for incorrect answers
Now, marks given for one
incorrect answer
Therefore, number of incorrect
answers
Thus, Radhika has attempted questions incorrectly.
(ii)
Marks given for seven correct answers
Mohini’s score
Marks obtained for incorrect
answers
Now, marks given for one
incorrect answer
Therefore, marks given for incorrect
answers
Thus, Mohini has attempted questions incorrectly.
Question:
7
An
elevator descends into a mine shaft at the rate of If the descent starts from above the ground level, how long will it take
to reach
Solution
Starting position of mine shaft is above the ground but it moves in opposite
direction so it travels the distance below the ground.
So total distance covered by mine shaft
Now, time taken to cover a distance of minute
So, time taken to cover a distance of minute
Therefore, time taken to cover a distance of
[ ]
Thus, in one hour the mine shaft reaches m below the ground.






