Chapter 8: Comparing Quantities
Exercise 1:
(Multiple Choice Questions and Answers 1-23)
In questions 1 to 23, there are four options,
out of which one is correct. Write the correct one.
Question: 1
of is
a.
b.
c.
d.
Solution
(d)
of
Therefore, of is .
Question: 2
Gayatri’s income is per year. She pays of this as house rent and of the remainder on her child’s education. The
money left with her is
a.
b.
c.
d.
Solution
(c)
Given, Gayatri’s income
Money paid as house rent = of
Remaining amount
Money spent on child’s education of
Money left with Gayatri
Question: 3
The ratio of Fatima’s income to her savings is .
The percentage of money saved by her is
a.
b.
c.
d.
Solution
(a)
Given ratio of income to savings of Fatima
Here, we need to find out the percentage of money
saved by Fatima.
Let the income and her savings
Percentage of money saved by Fatima
Question: 4
is equal to
a.
b.
c.
d.
Solution
(b)
Question: 5
In a scout camp, of the scouts were from Gujarat State and of these were from Ahmedabad. The percentage
of scouts in the camp from Ahmedabad is:
a.
b.
c.
d.
Solution
(c)
Let the number of scouts in
scout camp
The number of scouts from Gujarat of
Number of scouts from Ahmedabad of
Percentage of scouts from Ahmedabad
Question: 6
What percent of is ?
a.
b.
c.
d.
Solution
(a)
Let the percentage
be
Option (a) is the correct one
Question: 7
is equal to
a.
b.
c.
d.
Solution
(c)
We have,
In percentage,
Question: 8
The ratio is equal to
a.
b.
c.
d.
Solution
(b)
Given, ratio
In percentage,
Question: 9
is equal to
a.
b.
c.
d.
Solution
(a)
We have, in fraction,
Required ratio
Question: 10
A bicycle is purchased for and is sold at a profit of .
Its selling
price is
a.
b.
c.
d.
Solution
(b)
Given, cost price of bicycle and profit
As we know, profit percentage can be calculated as,
Profit
Profit
SP CP Profit
Hence, selling price of bicycle is
Question: 11
A cricket bat was purchased for and was sold for .
Then profit
earned is
a.
b.
c.
d.
Solution
(a)
Given, cost price of bat
Selling price of bat
Profit SP CP
We know that profit percentage is given as,
Profit
Hence, profit earned is
Question: 12
A farmer bought a buffalo for and a cow for .
He sold the
buffalo at a loss of but made a profit of on the cow. The net result of the transaction
is
a.
loss of
b.
profit of
c.
loss of
d.
profit of
Solution
(c)
CP of buffalo
Loss
Loss
Loss
SP CP Loss
CP of cow
Profit
Profit
Profit
SP CP Profit
Total CP of buffalo and cow
Total SP of buffalo and cow
Net loss CP SP
Question: 13
If Mohan’s income is more than Raman’s income, then Raman’s income
is less than Mohan’s income by
a.
b.
c.
d.
Solution
(c)
Let the Raman’s income be .
Mohan’s income is more than Raman’s income.
Then, Mohan’s income of
Percentage of Raman’s income less than Mohan’s income
Question: 14
The interest on for years at the rate of per annum is
a.
b.
c.
d.
Solution
(d)
Given,
We know that,
Question: 15
Amount received on for years at the rate of per annum is
a.
b.
c.
d.
Solution
(b)
Given,
Now, amount
Question: 16
Interest on for month at the rate of per annum is
a.
b.
c.
d.
Solution
(c)
Given,
Question: 17
Rajni and Mohini deposited and in a company at the rate of per annum for years and years respectively. The difference of the
amounts received by them will be
a.
b.
c.
d.
Solution
(d)
Interest received by Rajni after 3 years,
I
And total amount received will be,
Interest received by Mohini after years,
I
And total amount received will be,
Difference in amounts
Question: 18
If of is then the value of
a.
b.
c.
d.
Solution
(b)
Given,
of
Question: 19
On selling an article for a dealer lost .
The cost price of the article is
a.
b.
c.
d.
Solution
(d)
Given, SP of an article is and loss per cent
We know that, loss per cent
Question: 20
is equal to
a.
b.
c.
d.
Solution
We have,
In percentage,
Question: 21
The sum which will earn a simple interest of in years at
per annum is
a.
b.
c.
d.
Solution
(c)
Given, and
Question: 22
The
per cent that represents the unshaded region in the figure.

a.
b.
c.
d.
Solution
(c)
Total parts
Shaded
parts
Percent
of shaded parts
Then,
percent of un-shaded parts
Hence,
the per cent that represents the un-shaded region is
Question: 23
The per cent that represents the shaded region in
the figure is

a.
b.
c.
d.
Solution
(a)
Total parts
Shaded parts
Percent of shaded parts
Hence, the per cent that represents the shaded region is
In each of the questions 24 to 59, fill in the blanks to make the
statements true.
Question: 24
______
Solution
Given ratio
In percentage
Question: 25
_______: ______
Solution
Given percentage
In fraction,
Ratio
Question: 26
of _____.
Solution
We have, of
Question: 27
of _____.
Solution
We have, of
Question: 28
_____
Solution
We have,
In percentage,
Question: 29
_____
Solution
We have,
In percentage,
Question: 30
A
________ with its denominator is called a per cent
Solution
A fraction
with its denominator is called a per cent.
Question: 31
is ______ of
Solution
Let of be
Then,
Hence, is of
Question: 32
Weight of Nikhil increased from to .
Then, the increase in weight is _____ .
Solution
Given, Initial weight of Nikhil
After increase in weight, weight became Increase in weight
Percentage
increase of weight
Question: 33
In a class of students, were absent on one day. The number of students
present on that day was ________.
Solution
Given, Total number of students in the class
Absent percentage on one day
Percentage of students present on that day
Number of students present on that day of
So, the number of students present on that day, was
Question: 34
Savitri obtained marks out of in an examination. She secured _______ marks in the examination.
Solution
Marks obtained by Savitri out of
Percentage of marks obtained
Hence, Savitri secured marks in the examination
Question: 35
Out of a total deposit of in her bank
account, Abida withdrew of the deposit. Now the balance in her account
is ______.
Solution
Total deposit
Amount withdrawn of
Balance in the account
Question: 36
________ is more than .
Solution
Let number be
It is given that is more than
Therefore, according to question
of
Question: 37
John sells a bat for and suffers
a loss of . The cost price of the bat is ________.
Solution
Given, SP of bat and loss
We know that, CP SP Loss
Hence, cost price of the bat is
Question: 38
If the price of sugar is decreased by then
the new price of sugar
originally costing will
be ________.
Solution
Original price of sugar
Given that, price of sugar is decreased by
So, new price of sugar Original price of original price
of
Question: 39
Mohini bought a cow for and
sold it at a loss of . The selling price of the cow is ________.
Solution
Given, CP of cow and loss
We know that, SP CP Loss
Hence, the selling price of the cow is
Question: 40
Devangi buys a chair for and
sells it for . She earns a profit of ________ in the
transaction.
Solution
Given, CP of a chair and SP of a chair
Since, SP CP
Profit SP CP
Now, Profit
Hence, Devangi’s profit is
Question: 41
Sonal bought a bed sheet for and
sold it for . Her ________ is
________.
Solution
Given, CP of a bed sheet and SP of a bed sheet
Since, SP CP
Profit SP CP
Now, profit
Hence, Sonal’s profit is
Question: 42
Nasim bought a pen for and
sold it for . His ________ is
________.
Solution
Given, CP of a Pen and SP of a pen
Since, SP CP
Loss CP SP
Now, Loss
Hence, Nasim’s loss is
Question: 43
Aahuti purchased a house for and
spent on its
repairs. To make a profit of , she should sell the house for ________.
Solution
Given, CP of house
And amount spent on repairing
So, total CP of house
Profit
Question: 44
If lemons
are bought for and
sold at for
three rupees, then ________ in the transaction is ________ .
Solution
CP of lemons
By applying unitary method,
If SP of lemons is
Then, SP of lemon
SP of lemons
Now, CP and SP
Since, SP CP
Profit SP CP
Now, profit
Hence, profit is
Question: 45
Narain bought oranges at each.
He sold of the
oranges at each
and the remaining at each.
His ________ is ________ .
Solution
CP of orange (given)
CP of oranges
Now, of oranges
SP of oranges
And SP of remaining oranges
Total SP of oranges
Since, SP CP
Profit SP CP
Now,
Profit per cent
Hence, profit is
Question: 46
A fruit seller purchased of
apples at . Out of these, of the
apples were found to be rotten. If he sells the remaining apples at , then his _________is _________ .
Solution
Price for per kg apples
Total weight of purchased apples
Since, were rotten, so weight of good apples of (rotten)
Also, he sells apples at per kg
Total SP
Cost price of apples
Profit SP CP
Now, Profit
So, his profit is
Question: 47
Interest on at per
annum for a period of years
is ________.
Solution
Given, and
Hence,
interest is
Question: 48
Amount obtained by depositing at per
annum for six months is ________.
Solution
Amount
deposited
Rate of interest
Time period months
Amount
received Principal Interest
Question: 49
Interest on at per
annum for a period of years
and months
is ________.
Solution
Given, and
months
We know that,
Question: 50
is
_________ per cent of litres.
Solution
Let be of
Then, of
[Converting litre into millilitre]
Hence, is of
Question: 51
If A is increased by it
equals B. If B is decreased by it
equals C. Then __________ of A
is equal to C.
Solution
Given, if is increased by then it is equal to
of
(i)
If B is decreased by then it is equal to C.
of
(ii)
On comparing eq. (i) and (ii), we get
In percentage
Hence, of A is equal to C.
Question: 52
Interest where
is
____________
is
____________ and
is
____________.
Solution
Here, T is time period, is rate of interest and P is Principal.
Question: 53
The difference of interest for years and years on a sum of at per annum is _________.
Solution
Given, and
For,
For
Difference between both interests
Question: 54
To convert a fraction into a per cent, we _________
it by .
Solution
To convert a fraction into a per cent, we multiple it by
Question: 55
To convert a decimal into a per cent, we shift the
decimal point two places to the _________.
Solution
To convert a decimal into a per cent, we shift the
decimal point into places to the right.
Question: 56
The _________ of interest on a sum of at the rate of per annum for years and years is .
Solution
Given, and
Now,
For
The sum of both interests is
Question: 57
When converted into percentage, the value of is _________ than .
Solution
In percentage,
When converted into percentage, the value of 6.5 is
more than
In questions 58 and 59 copy
each number line. Fill in the blanks so that each mark on the number line is
labelled with a per cent, a fraction and a decimal. Write all fractions in
lowest terms.
Question: 58
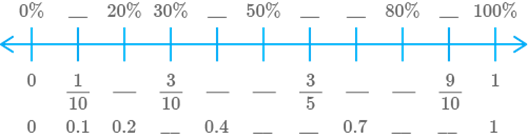
Solution
Percentage Fraction
Decimal
Now, according to the formula, we have
|
Percentage
|
Fraction
|
Decimal
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Question: 59
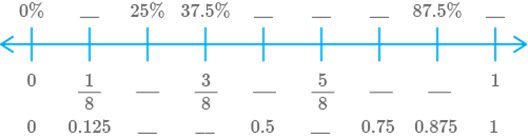
Solution
Percentage Fraction
Decimal
Now, according to the formula, we have
|
Percentage
|
Fraction
|
Decimal
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
True/False
In questions to state whether the statements are true of False.
Question: 60
Solution
True
Given fraction
In percentage,
Question: 61
When an improper fraction is converted into
percentage then the answer can also be less than .
Solution
False
Let’s consider, an improper fraction
In percentage,
Hence, when an improper fraction is converted into
percentage, then the answer is always greater than
Question: 62
hours
is of days.
Solution
False
Let be of days
Then, of days
Hence, is of days
Question: 63
The interest on at per annum for days is .
Solution
False
Given,
And days
Question: 64
The simple interest on a sum of for T years at per annum is given by the formula: Simple Interest
=
Solution
True
Simple Interest
It can also be written as, SI
Question: 65
Solution
False
In fraction, can be written as
Question: 66
of is .
Solution
False
of
Therefore, of is
Question: 67
If Ankita obtains marks out of then percentage of marks obtained by her is
Solution
False
Marks obtained by Ankita out of
Percentage of marks
Hence, Ankita got marks.
Question: 68
is
equivalent to
Solution
False
In percentage, can be written as,
Hence, is equivalent to
Question: 69
of is
Solution
True
Since, of
Hence, of is
Question: 70
is of
Solution
False
Now, of
Hence, of
Question: 71
Out of students of a school, go for a picnic. The percentage of students
that did not go for the picnic is
Solution
False
Total number of students in school
Number of students who went for picnic
Number
of students who did not go for picnic
Percentage of students who did not go for picnic,
Therefore, of students did not go for picnic.
Question: 72
By selling a book for ,
a shopkeeper suffers a loss of .
The cost price of the book is .
Solution
False
SP of book
Loss per cent on book
Loss per cent
Loss per cent
Hence, the cost price of the book is
Question: 73
If a chair is bought for and is sold at a gain of then selling price of the chair is .
Solution
False
Given, and Profit per cent
Profit per cent
Profit
10
Hence, SP of chair is
Question: 74
If a bicycle was bought for and sold for ,
then the percentage of profit is .
Solution
False
Given, CP of bicycle and SP of bicycle
Since, CP SP
Loss CP SP
Now, Loss per cent
Hence, Loss per cent is
Question: 75
Sushma sold her watch for at a gain of .
For earning a gain of she should have sold the watch for
Solution
True
Given, SP of watch
Profit on SP
CP SP Profit
Now, for earning profit ,
we need to find new SP.
Profit per cent
Profit
Profit per cent
Question: 76
Interest on for years at the rate of per annum is
Solution
False
Given, and
So, interest is
Question: 77
Amount received after depositing for a period of years at the rate of per annum is
Solution
False
Given, and
So, interest is
Hence, the amount received will be
A = P+ I
=
Question: 78
were
lent to Feroz and Rashmi at per annum for and years respectively. The difference in the
interest paid by them is
Solution
False
As per the question, Feroz borrowed for at per annum.
Here, and
Rashmi borrowed for at
Here,
Difference between interests
Hence, the difference in interest, paid by them is
Question: 79
A vendor purchased lemons at per hundred. of the lemons were found rotten which he sold
at per hundred. If he sells the remaining lemons
at per hundred, then his profit will be .
Solution
False
As per the question, cost price of lemons
Cost price of lemon
And cost price of lemons
Now, according to question, of the lemons were rotten.
of lemons lemons
Selling price of rotten lemons
Selling price of rotten lemon
And selling price of rotten lemons
Also, selling price of good lemons per hundred
& selling price of good lemons
Now, total selling price of lemons
As, SP CP
Therefore, vendor will bear loss.
Question: 80
Find the value of if
a. of is
of is
of is
of marks is
Solution
a. of is (given)
of is (given)
of is (given)
of marks is (given)
Question: 81
Imagine that, a grid has value and that this value is divided evenly among
the small squares. In other words, each small square is worth Use a new grid for each part of this problem
and label each grid “Value : ”.

a. Shade of the grid. What is of Compare the two answers.
What is the value of squares?
Shade of the grid. What is of Compare the two answers.
What is the value of of the grid?
Solution
a. We have to shade of the grid i.e., th part of grid th part of grid covers squares. Since, one square =
So,
total value of such squares
Now, of

Hence,
the above values are equal
Value of squares
of the grid means squares. So we will shade squares

Total
value these squares
Now,
of
Hence,
the above two values are equal.
Value
of grid
Value of of the grid
Question: 82
Express as a per cent.
Solution
In percentage, can be written as
Question: 83
Express as a per cent.
Solution
In percentage, can be written as
Question: 84
Express as a per cent.
Solution
In percentage, can be written as
Question: 85
Express as fraction in its lowest term.
Solution
In fraction, can be written as
Question: 86
Express as a ratio in the lowest term.
Solution
can be written as
For ratio in lowest term, can be
written as
Question: 87
Express as a ratio in the lowest form.
Solution
Given,
For ratio in lowest term,
Question: 88
Express as a ratio in the lowest form.
Solution
For the ratio in lowest term
Question: 89
Sachin and Sanjana are calculating of
Now calculate of using both the ways described above. Which way
do you find easier?
Solution
First way,
of
Second way,
of
Hence, second way is the easier to find the percentage.
Question: 90
Write as a percent.
Solution
In percentage, can be written as,
[to
convert in per cent, multiply by ]
Question: 91
Write as a percent.
Solution
In percentage, can be written as,
Question: 92
What is of
Solution
We need to
find, of ,
which can be written as,
Question: 93
What is of
Solution
We need to find of ,
which can be written as,
Question: 94
What is of
Solution
We need to find of ,
which can be written as,
Question: 95
What per cent of hour is minutes?
Solution
Let of h be min.
Then, min.
min min
Therefore, of hr. is min.
Question: 96
What per cent of day is minute?
Solution
Let of day is min
Then, day min
h min
min min
Therefore, of day is min
Question: 97
What per cent of is metres?
Solution
Let of km is m
Then, km m
m m
Therefore, of km is m
Question: 98
Find out of
Solution
We have to find, of kg, which can be written as,
kg
Hence, of is 2 kg
Question: 99
What percent of is
Solution
Let is
Then,
Hence, of is
Question: 100
of the
population of a town are men and are women. What is the percentage of children?
Solution
Given, percentage of men in town
Percentage of women in town
So, percentage of children in town will be
Hence, of the population of a town are children
Question: 101
The strength of a school is If of the students are girls then how many boys
are there in the school?
Solution
According to the question,
The strength of school
Percentage of girls in school
Percentage of boys in school
Number of boys in school of 2000, i.e
Hence, number of boys in school are
Question: 102
Chalk contains calcium, carbon and oxygen. Find the amount of carbon and calcium
(in grams) in of chalk.
Solution
Given, percentage of calcium in chalk
Percentage of carbon in chalk
Percentage of oxygen in chalk
Weight of chalk
Amount of carbon in chalk of
Amount of calcium in chalk of
Therefore, amount of carbon & calcium are and respectively.
Question: 103
of
mortar consists of sand, cement and rest lime. What is the mass of lime
in mortar?
Solution
Given, percentage of sand in mortar
Percentage of cement in mortar
So, percentage of lime in mortar
Weight of mortar
Mass of lime in mortar of
Therefore, weight of lime in mortar is
Question: 104
In a furniture shop, tables were bought at the rate of per table. The shopkeeper sold of them at the rate of per table and the remaining at the rate of per table. Find her gain or loss percent.
Solution
Buying cost
of the tables C.P
Selling cost of the tables
S.P
Gain or loss S.P C.P,
Therefore,
Gain S.P C.P
Gain
Question: 105
Medha deposited of her money in a bank. After spending of the remainder, she has left with her. How much did she originally
have?
Solution
Let the total money Medha had
Money deposited of
Remaining money
Money spended of
Money Remained
Question: 106
The cost of a flower vase got increased by If the current cost is ,
what was its original cost?
Solution
Let the original cost of flower vase be
Now, the cost of flower vase is increased by
So, of
Hence, original cost of the flower vase in
Question: 107
Radhika borrowed from her friends. Out of which were borrowed at and the remaining at rate of interest per annum. What is the total
interest after years?
Solution
For year interest, we have
and
For year interest, we have
and
Hence, after total interest
Question: 108
A man travelled by car and by train. Find what per cent of total journey
did he travel by car and what per cent by train?
Solution
Distance travelled by car
Distance travelled by train
Total journey
Let of
Let of
Therefore, distance is travelled by the car and distance is travelled by the train.
Question: 109
By selling a chair for a shopkeeper loses At what price did he buy it?
Solution
We have, SP of the chair and loss
Applying formula of Loss we have,
Loss
Loss
Hence, cost of the chair is
Question: 110
Dhruvika invested money for a period from May to April at rate of per annum. If interest received by her is find the money invested.
Solution
We have,
and
Time from May to April
Hence, the invested money is
Question: 111
A person wanted to sell a scooter at a loss of But at the last moment he changed his mind and
sold the scooter at a loss of If the difference in the two SP’s is then find the CP of the scooter.
Solution
Let CP of the scooter be
If he sells the scooter at a loss of then
SP of
& if he sells the scooter at a loss of then
SP of
It is given that the difference in the two SP’s is ,
Hence, cost price of scooter is
Question: 112
The population of a village is Out of these, are literate and of these literate people, are women. Find the ratio of the number of
literate women to the total population.
Solution
Given, total population of a village
Literate people of total population
Literate women of total population
Ratio of literate women to total population
Hence, the ratio of literate women to total
population is .
Question: 113
In an entertainment programme, tickets of and tickets of were sold. If the entertainment tax is on ticket of and on ticket of find how much entertainment tax was collected
from the programme.
Solution
Given, tickets of were sold,
Therefore, total amount received by selling these
tickets
Similarly, amount received by selling tickets of .
As per the question, entertainment tax on is and on tickets is respectively.
So total entertainment tax collected of total amount received by selling tickets of
of total amount received by selling tickets of
of of
Hence, the total collected entertainment tax was
Question: 114
Bhavya earns per month and spends of it. Due to pay revision, her monthly income
increases by but due to price rise, she has to spend more. Find her new savings.
Solution
Bhavya earn per
month
She spends per month of
Bhavya’s per month savings
Also, increment in monthly income of
Bhavya’s new income
Increase expenditure of
So, Bhavya’s new expenditure
Now, Bhavya’s new savings
Question: 115
In an examination, there are three papers each of marks. A candidate obtained marks in the first and marks in the second paper. How many marks must
the candidate obtain in the third paper to get an overall of per cent marks?
Solution
Let the marks of candidate in third paper be
Then, total marks secured in all three papers will
be
Total marks of three papers
Percentage of marks
But it is given that, he obtained overall of marks.
Hence, he needs to secure marks in the third paper to get an overall of marks.
Question: 116
Health Application
A doctor reports blood pressure in millimetres of
mercury (mm Hg) as a ratio of systolic blood pressure to diastolic blood
pressure (such as over ). Systolic pressure is measured when the
heart beats, and diastolic pressure is measured when it rests. Refer to the
table of blood pressure ranges for adults.
|
Blood
Pressure Ranges
|
|
|
Normal
|
Prehypertension
|
Hypertension
(Very
High)
|
|
Systolic
Diastolic
|
Under Hg
Under Hg
|
Hg
Hg
|
Hg
and above
Hg
and above
|
Manohar is a healthy years old man whose blood pressure is in the
normal category.
a. Calculate an approximate ratio of systolic to diastolic blood
pressures in the normal range.
If Manohar’s systolic blood pressure is Hg, use the ratio from part (a) to predict his
diastolic blood pressure.
Calculate ratio of average systolic to
average diastolic blood pressure in the prehypertension category.
Solution
a. Systolic blood pressure in the normal range mm Hg
Diastolic
blood pressure in the normal range mm Hg
Approximate
ratio of systolic to diastolic blood pressure
Hence,
approximate ratio is
Manohar’s systolic blood pressure mm Hg
Let
diastolic blood pressure mm Hg
As
per the question,
mm
Hg
Hence,
Manohar’s diastolic blood pressure is mm Hg
Average systolic blood pressure in
prehypertension category mm Hg
Average
diastolic blood pressure in prehypertension category mm Hg
Hence,
ratio of average systolic to average diastolic blood pressures
Hence,
required ratio is
Question: 117
a. Science Application: The king cobra can reach a length of .
This is only about per cent of the length of the largest
reticulated python. Find the length of the largest reticulated python.

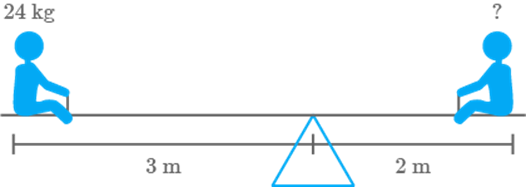
Physical
Science Application: Unequal masses will not
balance on a fulcrum if they are at equal distance from it; one side will go up
and the other side will go down.
Unequal
masses will balance when the following proportion is true:
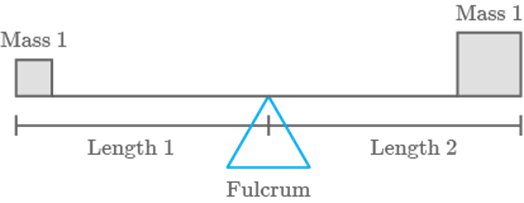
Two
children can be balanced on a see-saw when
The
child on the left and child on the right are balanced. What is the mass of the
child on the right?
Life
Science Application
A
DNA model was built using the scale If the model of the DNA chain is long, what is the length of the actual chain?
Solution
a. Length of the king cobra cm
As
per the question,
of
length of reticulated python cm
Length of reticulated python cm
It is given that, for balancing,
According
to the question,
Mass kg, Length m and Length m
Mass
kg
Let the length of the actual chain be mm.
Therefore,
mm
Question: 118
Language Application
Given below are few Mathematical terms.

Find
a.
The ratio
of consonants to vowels in each of the terms.
b.
The
percentage of consonants in each of the terms.
Solution
a. In term “Hypotenuse” consonants and vowels are there
In term
“Congruence” consonants and vowels are
there
In term
“Perpendicular” consonants and vowels are
there
In term
“Transversal” consonants and vowels are
there
In term
“Correspondence” consonants and vowels are
there
Percentage
of consonants
Total
number of letters Number of
consonants number of
vowels
In term
“Hypotenuse” total number of letters
In term
“Congruence” total number of letters
In term
“Perpendicular” total number of letters
In term
“Transversal” total number of letters
In term
“Correspondence” total number of letters
Question: 119
What’s the Error? An analysis showed that per cent of the T-shirts made by one company
were defective. A student says this is out of every What is the student’s error?
Solution
As per the question
Defective T-shirts made by the company
According to the student, number of defective
T-shirts out of every
Hence, student’s error is that, the defective
T-shirts are out of every 0 (not
Question: 120
What’s the Error? A student said that the ratios and were proportional. What error did the
student make?
Solution
As per the definition or rule:
Two ratios a : b and c : d are said to be
proportional, if or
But in the given ratios and
Hence, the ratios are not proportional. To make a
ratio proportional to another ratio, we just simply multiply both numerator and
denominator by same number. In our given case, student had multiplied numerator
by and denominator by which is incorrect.
Question: 121
What’s the Error? A clothing store charges for T-shirts. A student says that the unit price
is per T-shirt.
What is the error? What is the correct unit price?
Solution
By unitary method,
Cost of T-shirts
Cost of T-shirts
Hence, the correct unit price is
Question: 122
A tea merchant blends two varieties of tea in the
ratio of The cost of first variety is per and that of second variety is per .
If he sells the blended tea at the rate of per ,
find out the percentage of her profit or loss.
Solution
Ratio of
blended two varieties of tea (green tea: lemon tea)
Cost of green tea per kg.
Cost of lemon tea per kg
SP of blended tea per kg
As per the ratio,
Let green tea be kg and lemon tea be kg.
Then, cost of green tea
Cost of lemon tea
Total CP
Total quantity kg
So, for kg
SP of blended tea
CP SP
So, there is profit on blended tea.
Profit SP CP
Profit
Hence, there is profit on blended tea (new variety)
Question: 123
A piece of cloth long shrinks per cent on washing. How long will the cloth be
after washing?
Solution
Given,
Length of shrink cloth of
m m
Length of cloth after wash m
Question: 124
Nancy obtained marks out of and the marks obtained by Rohit are out of Whose performance is better?
Solution
Marks obtained by Nancy out of
Percentage marks
Rohit got marks out of
Percentage marks
Hence, Nancy’s performance is better, since she got
more than Rohit.
Question: 125
A memorial trust donates to a school, the interest on which is to be
used for awarding scholarships to students obtaining first three
positions in the school examination every year. If the donation earns an
interest of per cent per annum and the values of the
second and third scholarships are and respectively, find out the value of the
first scholarship.
Solution
Donation amount
Rate of interest for each year per annum
Time period yr
Interest received after yr
Scholarship amount for position
Scholarship amount for position
Remaining amount for position student
Hence, scholarship amount for position student
Question: 126
Ambika got per cent marks in Mathematics, per cent marks in Hindi, per cent in English, per cent in Science, and in Social Science. If each subject carries marks, then find the percentage of marks
obtained by Ambika in the aggregate of all the subjects.
Solution
Each subject
carries 100 marks
Marks
obtained by Ambika in,
Mathematics
Hindi
English
Science
Social science
Now, aggregate percentage of marks obtained
Question: 127
What sum of money lent out at per cent per annum simple interest would
produce as interest in years?
Solution
Here, yr and
Hence, sum of money lent out at per cent per annum simple interest would be
Question: 128
Harish bought a gas-chullah for and later sold it to Archana at a profit of per cent. Archana used it for a period of two
years and later sold it to Babita at a loss of per cent. For how much did Babita get it?
Solution
Harish
bought the chullah for and sold it to Archana at a profit of
Cost price of chullah for Archana of
Now, Archana sold it to Babita at a loss of
Cost price of chullah for Babita of
Hence, Babita got chullah at
Question: 129
Match each of the entries in Column I with the
appropriate entries in Column II:
|
|
Column I
|
Column II
|
|
(i)
|
|
(A)
|
|
|
(ii)
|
|
(B)
|
|
|
(iii)
|
|
(C)
|
|
|
(iv)
|
|
(D)
|
|
|
(v)
|
|
(E)
|
|
|
(vi)
|
|
(F)
|
|
|
(vii)
|
SP when CP and loss
|
(G)
|
|
|
(viii)
|
SP when CP and profit
|
(H)
|
|
|
(ix)
|
Profit when CP and SP
|
(I)
|
|
|
(x)
|
Profit when CP and SP
|
(J)
|
|
|
(xi)
|
Interest when principal ,
Rate of interest per annum and period years
|
(K)
|
|
|
(xii)
|
Amount when principal ,
Rate of interest per annum and period year
|
(L)
|
|
|
|
|
(M)
|
|
|
|
|
(N)
|
|
|
|
|
(O)
|
|
Solution
(i)
Matches with (E)
Ratio given
In Percentage,
(ii) Matches with (H)
Given,
In Percentage,
(iii) Matches with (O)
Given,
(iv) Matches with (J)
Given,
In Percentage,
(v) Matches with (G)
Given,
For Fraction,
(vi) Matches with (L)
Given,
For fraction,
For decimal,
(vii) Matches with (B)
Given,
(viii)
Matches with (A)
Given,
(ix) Matches with (F)
Given,
(x) Matches with (K)
Given,
(xi) Matches with (D)
Given,
(xii) Matches with (l)
Given,
Need to find out A
Question: 130
In a debate competition, the judges decide that per cent of the total marks would be given for
accent and presentation. per cent of the rest are reserved for the
subject matter and the rest are for rebuttal. If this means marks for rebuttal, then find the total marks.
Solution
Let be the total marks
Marks given for accent & presentation of
Remaining marks
Marks reserved for subject matter of rest marks
Now, remaining marks
According to question,
Hence, total marks are
Question: 131
Divide in two parts so that the simple interest on
the first part for years at per cent per annum may be equal to the simple
interest on the second part for years at per cent per annum.
Solution
Given, money
Now, we have divide in two parts such that SI on first part for yr at per annum may be equal to the SI on second
part for yr at
Let first part =
Then, second part
For part
For part,
yr,
Since
First part
Second part
Hence, two parts of the sum are and
Question: 132
becomes at simple interest in years. Find the rate per cent per annum.
Solution
Given, yr
We know that,
Hence, the rate of interest per annum is
Question: 133
In how many years will the simple interest on a
certain sum be times the principal at per cent per annum?
Solution
Let principal
times principal
yr
Question: 134
The simple interest on a certain sum for years at per cent per annum is more than the simple interest on the same sum
for years at per cent per annum. Find the sum.
Solution
Given,
yr,
According to question,
Hence, sum is
Question: 135
The simple interest on a certain sum for years at per cent per annum is less than the simple interest on the same sum
for years at per cent per annum. Find the sum.
Solution
Let the sum be
[given]
[given]
According to question,
Hence, sum is
Question: 136
Designing a Healthy Diet
When you design your healthy diet, you want to make
sure that you meet the dietary requirements to help you grow into a healthy
adult.
As you plan your menu, follow the following
guidelines
1. Calculate your ideal weight as per your
height from the table given at the end of this question.
2. An active child should eat around calories for each kilogram desired weight.
3. per
cent of calories should come from carbohydrates. There are calories in each gram of carbohydrates.
4. per
cent of your calories should come from proteins. There are calories in each gram of proteins.
5. per
cent of your calories may come from fats. There are calories in each gram of fat.
Following is an example to design your own healthy
diet.
Example
1. Ideal weight .
2. The number of calories needed
3. Calories that should come from carbohydrates
calories.
Therefore, required quantity of carbohydrates
(approx).
4. Calories that should come from proteins
calories.
Therefore, required quantity of protein
5. Calories that may come from fat
calories.
Therefore, required quantity of fat
Answer the Given Questions
1. Your ideal desired weight is __________ .
2. The quantity of calories you need to eat is
_______.
3. The
quantity of protein needed is ________ .
4. The quantity of fat required is ___________ .
5. The quantity of carbohydrates required is
________ .
|
Ideal Height and Weight Proportion
|
|
Men
|
Women
|
|
Height
|
Weight
|
Height
|
Weight
|
|
Feet
|
cm
|
Kilograms
|
Feet
|
cm
|
Kilograms
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
..
|
|
Solution
(i)
Let my
height be
ft.
Then, according to the table, my ideal weight kg
(ii)
The
quantity of calories needed calories
(iii)
Calorie
that should come from proteins calories
Therefore, required of protein
(iv)
Calories
that may come from fat calories
Therefore, required quantity of fats
(v)
Calorie
that should come from carbohydrate
Therefore required quantity of carbohydrate
Question:
137
students are studying English, Maths or both. per cent of students study English and per cent are studying Maths. How many students
are studying both?
Solution
Total students
Students who study English of
Students who study Math of
Total students studying English & Maths
Students who study English & Maths both
Question:
138
Earth Science: The table lists the world’s largest deserts.
|
Largest
Deserts in the World
|
|
Desert
|
Area
(km
)
|
|
Sahara (Africa)
|
|
|
Gobi (Asia)
|
|
|
Australian Desert (Australia)
|
|
|
Arabian Desert (Asia)
|
|
|
Kalahari Desert (Africa)
|
|
|
Chihuahuan Desert (North America)
|
|
|
Takla Makan Desert (Asia)
|
|
|
Kara Kum (Asia)
|
|
|
Namib Desert (Africa)
|
|
|
Thar Desert (Asia)
|
|
b. What are the mean, median and mode of the areas listed?
c. How many times the size of the Gobi Desert is the Namib Desert?
d. What percentage of the deserts listed are in Asia?
e. What percentage of the total area of the deserts listed is in Asia?
Solution
f. Mean
Median
Mode
Most frequent observation
Let the size of Gobi desert is times the Namib desert.
Gobi desert
Namib desert
Hence, the size of Gobi Desert is
times of Namib desert
Total number of desert
Number of deserts in Asia (Gobi,
Arabian, Takla Makan, Kum, Thar)
Hence, percentage of deserts in
Asia
Total area of all deserts
Total area of Asia’s deserts
Hence, percentage of the total
area of the deserts listed in Asia
Question:
139
Geography Application: Earth’s total land area is about .
The land area of Asia is about per cent of this total. What is the
approximate land area of Asia to the nearest square km?
Solution
Total land area of the earth
Land area of Asia of land area of Earth
Question:
140
The pieces of Tangrams have been rearranged to make
the given shape.

By observing the given shape, answer the following
questions:
a.
What percentage of total has been coloured?
i. Red
(R) _________
ii. Blue
(B) ________
iii. Green
(G) _______
b.
Check that the sum of all the percentages
calculated above should be
c.
If we rearrange the same pieces to form some
other shape, will the percentage of colours change?
Solution
a. Total coloured shape
i.
Red
coloured shape
Hence,
percentage of red coloured
ii.
Blue
coloured shape
Hence, Percentage of blue coloured
iii.
Green
coloured shape
Hence, percentage of green coloured
b.
Sum of all percentages
calculated Percentage of red coloured percentage of blue coloured percentage of green coloured
c.
No, the percentage of colours
will not change, because we just rearranging the parts and not changing the
percentage of colours.