Unit
4: Simple Equations
Exercise: 1 (Multiple Choice Questions and Answers 1-18)
In the Questions 1 to
18, there are four options, out of
which only one is correct. Write the correct one.
Question: 1
The solution of the equation is
a.
b.
c.
d.
Solution
(c)
Given equation
Question: 2
If and are positive integers, then the
solution of the equation will always be
a.
positive number
b.
negative number
c.
d.
Solution
(a)
Given equation
On dividing the
equation by a, we get
Now, if and are positive
integers, then the solution of the equation is also positive number as division
of two positive integers is also a positive number.
Question: 3
Which of the following is not allowed in a given
equation?
a.
Adding the same number to both sides of the
equation.
b.
Subtracting the same number from both sides of
the equation.
c.
Multiplying both sides of the equation by the
same non-zero number.
d.
Dividing both sides of the equation by the same
number.
Solution
(d)
Dividing both sides of the equation by the same
non-zero number is allowed in given equation, division of
any number by zero is not allowed as the division of number by zero
is not defined.
Note: If we add or subtract the same number to both
sides of the equation while adding or subtracting, then there
will be no change in the given equation.
Question: 4
The solution of which of the following equations
is neither a positive fraction nor an integer?
a.
b.
c.
d.
Solution
(d)
Let us solve the equations:
a.
Given equation is
b.
Given equation is
c.
Given equation is
d.
Given equation is
Which is neither a positive fraction nor an
integer.
Question: 5
The equation which cannot be solved in integers
is
a.
b.
c.
d.
Solution
(c)
Let us solve the equations
a.
Given equation is
b.
Given equation is
c. Given equation is
On
transposing to LHS & RHS respectively, we get
d. Given equation is
On
transposing to LHS & RHS respectively, we get
Question: 6
If then is equal to
a.
b.
c.
d.
Solution
(d)
Given equation is
On dividing the above equation by we get
Hence, the solution of the given eq. is
Question: 7
The solution of the equation is
a.
b.
c.
d.
Solution
(b)
Given equation is
Hence, the solution of eq. is
Question: 8
The value of for which the expressions and become equal is
a.
b.
c.
d.
Solution
(d)
It is given that both the equation are equal.
So, the equation is
Multiplying both sides by we get
Question: 9
If then the value of is
a.
b.
c.
d.
Solution
(a)
Given equation is
On transposing to RHS, we get
Put the value of in the equation we get
Question: 10
If then the value of m is
a.
b.
c.
d.
Solution
(a)
Given equation is
On dividing the given equation by we get
If we remove the decimal, we get in denominator
Question: 11
exceeds by can be represented as
a.
b.
c.
d.
Solution
The given statement means is more than
So, the equation is
We can also write it as
Question: 12
The equation having as a solution is:
a.
b.
c.
d.
Solution
(d)
Let us solve the equations:
a.
Given equation is
b.
Given equation is
c.
Given equation is
d.
Given equation is
Question: 13
The equation having as a solution is:
a.
b.
c.
d.
Solution
(c)
Let us solve the equations:
a.
Given equation is
b.
Given equation is
c.
Given equation is
Further,
there is no need to solve for option d as we have obtained correct option.
Question: 14
Which of the following equations can be formed
starting with
a.
b.
c.
d.
Solution
(c)
We have
On multiplying both the sides by we get
On adding to both sides, we get
Question: 15
Which of the following equations cannot be
formed using the equation
a.
b.
c.
d.
Solution
(b)
We have
On multiplying both the sides by we get
On adding both sides, we get
Question: 16
If then the value of is
a.
b.
c.
d.
Solution
(a)
Given
On multiplying both the sides by we get
Put in equation we get
Question: 17
Which of the following numbers satisfy the
equation
a.
b.
c.
d.
Solution
(c)
Let us put the values given in the options in equation
a. Put
LHS
RHS
b. Put
LHS
RHS
c. Put
LHS
RHS
(satisfied)
Now, there is no need
to check the next option.
Hence, satisfied the given
equation.
Question: 18
Shifting one term from one side of an equation
to another side with a change of sign is known as
a.
commutativity
b.
transposition
c.
distributivity
d.
associativity
Solution
(b)
Transposition means shifting one term from one
side of an equation to another side with a change of sign.
In Questions 19 to 48,
fill in the blanks to make the statements true.
Question: 19
The sum of two numbers is and their difference is
a.
If smaller number is the other number is ________.(use
sum)
b.
The difference of numbers in term of is ________.
c.
The equation formed is ________.
d.
The solution of the equation is ________.
e.
The numbers are ________ and ________.
Solution
a.
If the smaller number is then the other number is since the sum of both numbers is
b.
Given, one number
Then, other number
Difference
c.
Given, difference between two no. is
So, the equation
is
d.
Let us solve the equation for
On dividing the
equation by we get
Hence, the solution
of the equation is
e.
The numbers are
Now,
put the value of we get
First
number
Second number
Question: 20
Sum of two numbers is One is twice the other.
a.
If smaller number is the other number is ________.
b.
The equation formed is ________.
c.
The solution of the equation is ________.
d.
The numbers are ________ and ________.
Solution
a.
We are given that one number is twice the other.
If smaller number is then the other number is
b.
We are given that sum of two numbers is So, the equation will be
c.
Now, solve the equation for
Hence, the solution
of the equation is
d.
The two numbers are
Question: 21
In a test Abha gets twice the marks as that of
Palak. Two times Abha's marks and three times Palak's marks make
a.
If Palak gets marks, Abha gets ________ marks.
b.
The equation formed is ________.
c.
The solution of the equation is ________.
d.
Marks obtained by Abha are ________.
Solution
a.
If Palak gets marks, Abha gets twice the marks
as that of Palak, i.e.,
b.
Two times of Abha’s marks and three times the Palak marks
Now, two times Abha’s
marks and three times Palak’s marks make So, the equation formed is
c. Solve the equation for
Hence, the solution
of the equation is
d. Marks obtained by Abha are i.e.,
Question: 22
The length of a rectangle is two times its
breadth. Its perimeter is
a.
If the breadth of rectangle is the length of the rectangle is
________.
b.
Perimeter in terms of is ________.
c.
The equation formed is ________.
d.
The solution of the equation is ________.
Solution
a.
It is given that the length of the rectangle is
two times its breadth.
Length
b.
Perimeter of rectangle
c.
As we are given that perimeter of rectangle is
So, the equation
formed is
d.
On solving,
On dividing the equation by we get
Hence, the solution
of the equation is
Question: 23
In a bag there are and rupee coins. If they are equal in
number and their worth is then
a.
The worth of coins of each ________.
b.
The worth of coins of each ________.
c.
The equation formed is ________.
d.
There are ________ rupee coins and ________ rupee coins.
Solution
Let number of coins of
Then, number of coins of
a.
Number of coins of
So, the worth of of coins
b.
Similarly, the worth of of x coins
c.
As we are given that they are equal in number
& the worth is
So, the equation is
d.
On
solving,
Therefore, there
are 10 coins of both 5 rupee and 2 rupee.
Question: 24
In a Mathematics quiz, prizes consisting of and prizes only are to be given. and prizes are worth and respectively. If the total prize
money is then show that:
a.
If prizes are in number the number of prizes are ________.
b.
The total value of prizes in terms of are ________.
c.
The equation formed is ________.
d.
The solution of the equation is ________.
e.
The number of prizes are ________ and the
number of prizes are ________.
Solution
Given, number of prizes
Total prize money
and prizes are worth and respectively.
a.
prizes are in number, the number of prizes are because total number of prizes
are
b.
Total values of prizes in terms of are
c.
The equation formed is
d.
On
solving,
The solution of the equation is
e.
So, Number of prizes .
The number of prizes are & the number of prizes are
Question: 25
If then ________.
Solution
On solving the given equation, we get
Question: 26
_________ is the solution of the equation
Solution
On solving the equation for
Question: 27
__________ is the solution of
Solution
Solving the equation for
Question: 28
If then value of is __________.
Solution
Solving the equation for
Put the value of in we get
Question: 29
In integers, has __________ solution.
Solution
Solving the equation for
Since the solution of the equation is not an
integer, hence the equation has no solution.
Question: 30
In natural numbers, has ______ solution.
Solution
Solve the equation for
Since, the value of is not a natural number, hence equation has no solution in natural numbers.
Question: 31
In natural numbers, has ______ solution.
Solution
Solving the equation for
Since, natural numbers do not contain zero, hence the equation has no solution.
Question: 32
In whole numbers, has ______ solution.
Solution
Solving the equation for
Since, zero is in the range of whole numbers,
hence the equation has one solution.
Question: 33
If is added to three times a number,
it becomes the same as is subtracted from four times the
same number. This fact can be represented as __________.
Solution
Let the number be
Now, is added to times the number
It is same as is subtracted from times the number, i.e.
So, the equation formed is
Question: 34
has the solution _________.
Solution
Solving the equation for
Question: 35
when
Solution
Given,
Question: 36
when
Solution
Given,
Question: 37
when
Solution
Given,
Hence,
Question: 38
The solution of the equation is ________.
Solution
Solving the equation for
Hence, the solution of
the given equation is
Question: 39
Finding the value of a variable in a linear
equation that _______ the equation is called a _______ of the equation.
Solution
Finding the value of a variable in a linear
equation that satisfies the equation
is called a root of the equation.
Question: 40
Any term of an equation may be transposed from
one side of the equation to the other side of the equation by changing the
_______ of the term.
Solution
Any term of an equation may be transposed from
one side of the equation to the other side of the equation by changing the sign of the term.
Question: 41
If then
Solution
Given,
Question: 42
If then
Solution
Solving the equation for
Question: 43
If then
Solution
Given,
Question: 44
If then
Solution
Given,
Question: 45
If less than a number is then the number is _______.
Solution
Let the number be
Then, the equation
will be
Now, solving the
equation for
Hence, the number is
Question: 46
If a number is increased by it becomes Then the number is _______.
Solution
Let the number be
If it is increased by it becomes
So, the equation
formed is
Hence, the number is
Question: 47
If exceeds another number by then the other number is _______.
Solution
Equation formed:
Solving the equation for
Hence, the other
number is
Question: 48
If then
Solution
Given,
In Questions 49 to 55,
state whether the statements are True or False.
Question: 49
is the solution of the equation
Solution
True
Solving the equation for
Question: 50
is the solution of the equation
Solution
False
Solving the equation for
Question: 51
does not have an integer as its solution.
Solution
False
Given equation
Question: 52
One third of a number added to itself gives can be represented as
Solution
False
Let the number be
Then, the equation formed is
Question: 53
is the solution of the equation
Solution
True
Solving the equation for
Question: 54
If then
Solution
False
Solving the equation for
Question: 55
If is the solution of variable in the equation then the value of is
Solution
False
Given,
Put the value of in the equation, we get
Question: 56
Match each of the entries in Column I with the
appropriate entries in Column II.
|
Column I
|
Column II
|
|
i.
|
(a)
|
|
ii.
|
(b)
|
|
iii.
|
(c)
|
|
iv.
|
(d)
|
|
v. The value of which satisfies
|
(e)
|
|
vi.
If then the value of
|
(f)
|
|
|
(g)
|
Solution
i. (c)
Given,
ii. (e)
Given,
iii.
(f)
Given,
iv.
(d)
Given,
v. (b)
Given,
vi.
(a)
Given,
Put
the value of in the equation we get
In
Questions 57 to 67, express each of the given statements as an equation.
Question: 57
subtracted from twice of a number
gives
Solution
Let the number be
is subtracted from twice of a number i.e, and it results into
So, the equation
formed is
Question: 58
One-fifth of a number is less than that number.
Solution
Let the number be
Then of the number
Now, is less than
So, the equation
formed is
Question: 59
A number is more than one-third of itself.
Solution
Let the number be
Then, of the number
So, the equation
formed is
Question: 60
Six times a number is more than the number.
Solution
Let the number be
Then, times of the number
So, the equation
formed is
Question: 61
If is subtracted from half of a
number, the result is
Solution
Let the number be
Then, is subtracted from i.e, & its result into
So, the equation
formed is
Question: 62
Subtracting from the result is
Solution
Subtract from i.e., & result is
Hence, the equation
formed is
Question: 63
Five times a number increased by is
Solution
Let the number be Then, five times of number be
Since it is increased by i.e, & it gives result as
Hence, the equation
formed is
Question: 64
Mohan is years older than Sohan. The sum
of their ages is years.
Solution
Let age of Sohan be
Then, the age of Mohan is
Sum of their ages
So, the equation
formed is
Question: 65
If is subtracted from a number and
the difference is multiplied by the result is
Solution
Let the number be
Then, is subtracted from a number & the
difference multiplied by i.e., it gives result as
So, the equation
formed is
Question: 66
A number divided by and then increased by is
Solution
Let the number be
Then, is divided by & increased by i.e., & gives result as
So, the equation
formed is
Question: 67
The sum of twice a number and is
Solution
Let the number be .
Then, sum of twice of a number and gives result
Hence, is the equation.
Question: 68
The age of Sohan Lal is four times that of his
son Amit. If the difference of their ages is years, find the age of Amit.
Solution
Let be the age of Amit.
Then, age of Sohan Lal
According to question,
Hence, the age of Amit
is .
Question: 69
A number exceeds the other number by If their sum is find the numbers.
Solution
Let be a number, then another number will be .
According to question,
Hence, the number are & i.e.,
Question: 70
Seven times a number is less than thirteen times the same
number. Find the number.
Solution
Let the number be .
The, times of this number
times of this number
According to question,
Hence, the required
number is
Question: 71
The interest received by Karim is more than that of Ramesh. If the
total interest received by them is find the interest received by
Ramesh.
Solution
Let the interest received by Karim is Then interest received by
Ramesh will be So, the interest received by both will be
According to question,
So, the interest
received by Ramesh
Question: 72
Subramaniam and Naidu donate some money in a
Relief Fund. The amount paid by Naidu is more than that of Subramaniam. If
the total money paid by them is find the amount of money donated
by Subramaniam.
Solution
Let be the amount donated in a relief fund by Subramaniam. Then, the amount donated by Naidu will be
According to question,
Hence, the amount of
money donated by Subramaniam
is
Question: 73
In a school, the number of girls is more than the number of boys. The
total number of students is Find the number of girls.
Solution
Let be the number of boys in the school. Then the
number of girls in the school will be
According to question,
So, the number of boys in the school .
Then number of girls in the school .
Question: 74
Two times a number increased by equals Find the number.
Solution
Let the number be .
It is given that times this number increased by equals
Hence, the required
number is
Question: 75
added to twice a number gives Find the number.
Solution
Let the number be .
It is given that added to twice this number gives
Hence, the required
number is
Question: 76
subtracted from one-third of a
number gives Find the number.
Solution
Let the number be .
Then, one-third of the
number
According to question,
Hence, the required
number is
Question: 77
After years, Rama will be times as old as he is now. Find
his present age.
Solution
Let Rama’s present age be
Then, Rama’s age after
It is given that after Rama’s age will be times his present age.
Therefore, the equation is
Hence, the present age
of Rama is
Question: 78
After years, Manoj will be times as old as he is now. Find
his present age.
Solution
Let the present age of Manoj be
Then, Manoj’s age after
It is given that after Manoj’s age will be times his present age.
Therefore, the equation is
Hence, the present age
of Manoj is
Question: 79
My younger sister's age today is times, what it will be years from now minus times what her age was years ago. Find her present age.
Solution
Let age of my younger sister be
Then, her age after
Also, her age
It is given that her present age is times her age after minus times her age age.
Therefore, we obtain the following equation
Hence, her present age
is
Question: 80
If is added to half a number, the
result is triple the number. Find the number.
Solution
Let be the number.
Then, half of the
number is
According to question,
Hence, the number is
Question: 81
In a family, the consumption of wheat is times that of rice. The total
consumption of the two cereals is Find the quantities of rice and
wheat consumed in the family.
Solution
Given, total consumption of two cereals
Let be the consumption of rice.
Then, consumption of wheat
According to question,
Consumption of wheat
Hence, the consumption of rice & wheat are respectively.
Question: 82
In a bag, the number of one rupee coins is three
times the number of two rupees coins. If the worth of the coins is find the number of rupee coins.
Solution
Let the number of two rupee coins be Then, the number of one rupee
coins is
Total money by two rupees coins
Total money by one rupee coins
Total worth of coins
The equation formed is,
Number of two rupees coins & number of one rupee
coins
Question: 83
Anamika thought of a number. She multiplied it
by added to the product and obtained as the result. What is the number
she had thought of?
Solution
Let be the number thought by
Anamika.
If she multiplied it
by then the number would be
Added to it & obtained as result.
Hence, the number is thought by Anamika.
Question: 84
One of the two numbers is twice the other. The
sum of the numbers is Find the numbers.
Solution
Let be the number. Then, other
number is twice the first one
According to question,
Hence, the number are .
Question: 85
The sum of three consecutive integers is more than the smallest of the
integers. Find the integers.
Solution
Let one number be Then, the next two consecutive
numbers will be
Sum of these three
numbers
According to question,
Hence, the number are
Question: 86
A number when divided by gives the quotient What is the number?
Solution
Let the required no. be Then, divided by
Given, when is divided by gives quotient as
So, we obtain the following
equation,
Hence, the required
number is
Question: 87
The perimeter of a rectangle is The length of the rectangle is less than times its breadth. Find the
length of the rectangle.
Solution
Given, the perimeter of rectangle is
Let be the breadth of rectangle.
Then, length of rectangle
According to question,
Hence, the length of the rectangle
Question: 88
Each of the equal sides of an isosceles
triangle is twice as large as the third side. If the perimeter of the triangle
is find the length of each side of
the triangle.
Solution
Let third side of an isosceles triangle be
Then, two other equal sides are twice.
So, the both equal sides are
Perimeter of triangle is sum of all sides.
According to question,
Third side
So, the other equal sides are and .
Question: 89
The sum of two consecutive multiples of Find the numbers.
Solution
Let two consecutive multiplies of be .
According to question,
Hence, the required
numbers are and
Question: 90
Two complementary angles differ by Find the angles.
Solution
Let one of the angle be x, then other will be
According to question,
Hence, the required angles are and i.e., and .
Question: 91
has been divided into two parts
such that twice the first part is equal to the second part. Find the parts.
Solution
Let one part be & other part be
Since, has been divided into above two
parts.
According to question,
Hence, first part is & the second part is
Question: 92
In a class of students, the number of girls is
one third the number of boys. Find the number of girls and boys in the class.
Solution
Given, the total number of students in the class
Let be the number of boys in the
class. Then, the number of girls in the class
According to question,
Hence, the number of boys in the class is & the number of girls in the
class is .
Question: 93
Two-third of a number is greater than one-third
of the number by Find the number.
Solution
Let the no. be .
Two third of the number and one third of this number
According to question,
Hence, the required
number is
Question: 94
A number is as much greater than as it is less than Find the number.
Solution
Let number be ( greater than ) and ( less than ).
Now according to question,
So, Required number is
Alternatively,
The required number would be the average or mean
of and So Required number
Hence, the number is
Question: 95
A man travelled two fifth of his journey by
train, one-third by bus, one-fourth by car and the remaining on foot. What is the length of
his total journey?
Solution
Let his total journey length be .
Then, travelled by train
Travelled by bus
and travelled by car
Total journey
Remaining journey
According to question, remaining journey is
Hence, the total journey is of
Question: 96
Twice a number added to half of itself equals Find the number.
Solution
Let the no. be
Twice of this number
& half of this number
According to question,
Multiplying both sides by
Hence, the required number is
Question: 97
Thrice a number decreased by exceeds twice the number by Find the number.
Solution
Let the number be
Then thrice of this number
and twice of this number
If we decrease thrice of by we get
According to question,
Hence, the required number is
Question: 98
A girl is younger than her father. The sum
of their ages is Find the ages of the girl and her
father.
Solution
Let years be the age of girl.
Then, age of her father
According to question,
Hence, age of the girl is
& her father’s age is
Question: 99
The length of a rectangle is two times its
width. The perimeter of the rectangle is Find the dimensions of the
rectangle.
Solution
Let x be the width of rectangle. Then, length of
the rectangle will be
Perimeter of rectangle
According to question,
Hence, width of the rectangle is & length of the rectangle is .
Question: 100
Look at this riddle?
If she answers the riddle correctly however will
she pay for the pencils?

Solution
Let the cost of pencil be
Now, cost of such pencils will be and pencils will be .
Given, cost of pencils is more than cost of pencils. Therefore, we get
Since, cost of pencil
Cost of pencils
Thus, she have to pay for pencils.
Question: 101
In a certain examination, a total of students secured first division
in the years and The number of first division in exceeded those in How many students got first
division in
Solution
Let the number of students who got first
division in year be
Since, the number of first division in year exceeded those in year by therefore the number of
students who got first division in year will be
It is given that total number of students who
got first division in years and is
According to question,
Hence, students got first division in
year
Question: 102
Radha got as her monthly salary and
over-time. Her salary exceeds the over-time by What is her monthly salary?
Solution
Radha’s monthly salary & over-time
Let be the her monthly salary.
Then, overtime
Hence, her monthly salary is
Question: 103
If one side of a square is represented by and the adjacent side is
represented by find the length of the side of
the square.
Solution
Given, one side of a
square is and adjacent side is
We know that, all the
sides of a square are always equal
Hence, side of the
square is
Question: 104
Follow the directions and correct the given
incorrect equation, written in Roman numerals:
a. Remove two of these matchsticks to make a valid equation:

b.
Move one matchstick to make the equation valid.
Find two different solutions.

Solution
a. Given,
according
to question, we have to remove two matchsticks to make a valid equation.
Hence,
b. Given,
according
to question, we have to move one matchstick to make a valid equation.
i.
ii.
Question: 105
What does a duck do when it flies upside down?
The answer to this riddle is hidden in the equation given below:
For riddle answer :
substitute the number for the letter it equals
Solution
We have,
We have,
We have,
We have,
We have,
We have,
By substituting the number for the letter it
equals, we get
Question: 106
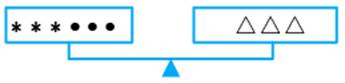
The three scales below are perfectly balanced if
What are the values of and
a. 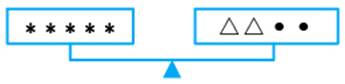
b. 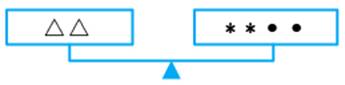
c.
Solution
Let the value of & be and & it is given that
From (a),
From (b),
From (c),
From eq.
On putting in eq. (i), we get
On putting in eq. (ii), we get
Value of & value of
Question: 107
The given figure represents a weighing balance.
The weights of some objects in the balance are given. Find the weight of each
square and the circle.
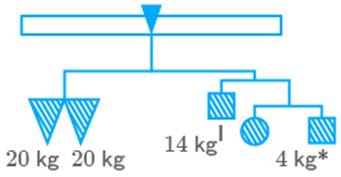
Solution
Weight on LHS kg
Weight on RHS kg
Weight should be equal,
Therefore, circle weight kg






