Practical
Geometry (Chapter 10), Symmetry (Chapter 14) and Visualising Solid Shapes
(Chapter 15)
Exercise: 1
(Multiple Choice Questions and Answers 1-26)
In each of the Questions 1 to 26, there are four options, out of which one
is correct. Choose the correct one.
Question: 1
A triangle can be
constructed by taking its sides as:
a.
b.
c.
d.
Solution
(b)
Condition for the formation of a triangle is that sum of two
sides should be greater than the third side.
Sum of two sides Third side,
Here, option (b) satisfies the given condition. i.e. ,
which holds true.
Question: 2
A triangle can be
constructed by taking two of its angles as:
a.
b.
c.
d.
Solution
(a)
For a triangle, the sum of all interior angles should be
equal to . So, sum of any two angles of a triangle should be
less than
For option (a)
i.e. less than .
For option
(b)
i.e. greater than .
For option (c)
i.e. equal
to .
For option
(d)
i.e. equal to .
So, the correct answer is (a).
Question: 3
The number of lines of
symmetry in the figure given below is:

a.
b.
c.
d. Infinitely many
Solution
(c)
The given figure has 6 lines of symmetry.

Question: 4
The number of lines of
symmetry in Fig. 12.14 is

Fig. 12.14
a.
b.
c.
d. Infinitely many
Solution
(b)
The given figure has lines of symmetry.

Question: 5
The order of rotational symmetry in the Fig. 12.15 given
below is

Fig. 12.15
a.
b.
c.
d. Infinitely many
Solution
(c)
Since, the number of times a figure fits onto
itself in one full turn is called order of rotational symmetry.
So, for the given figure the order of rotational symmetry is six.
So, the correct answer is (c).
Question: 6
The order of rotational symmetry in the Fig. 12.16 given
below is

Fig. 12.16
a.
b.
c.
d. Infinitely many
Solution
(b)
The
number of times a figure fits onto itself in one full turn is called order of
rotational symmetry. So, the given figure has rotational symmetry of order . Hence, the correct answer is (b).
Question: 7
The name of the given solid in Fig. 12.17 is:

Fig. 12.17
a. triangular pyramid
b. rectangular pyramid
c. rectangular prism
d. triangular prism
Solution
(b)
In the given figure the base of the pyramid is a rectangle. So,
the correct answer is (b).
Question: 8
The name of the solid in Fig. 12.18 is:
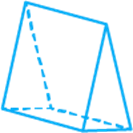
Fig. 12.18
a.
triangular pyramid
b.
rectangular prism
c.
triangular prism
d.
rectangular pyramid
Solution
(c)
A prism always consists of 2 bases which are polygons and
faces which are rectangular. This figure has
2 faces which are triangular in shape and can be considered as bases. The rest
of the faces are rectangular in shape.
So, the correct answer is (c).
Question: 9
All faces of a pyramid are always:
a. Triangular
b. Rectangular
c. Congruent
d. None of these
Solution
(d)
The faces of a pyramid can be triangular or rectangular. But we need to choose only one correct answer. So, the
correct answer is (d).
Question: 10
A solid that has only one vertex is
a.
Pyramid
b.
Cube
c.
Cone
d.
Cylinder
Solution
(c)
From the figure it is clearly seen that the cone shape has
only one
vertex.

So, the correct answer is (c).
Question: 11
Out of the following which is a 3-D figure?
a.
Square
b.
Sphere
c.
Triangle
d.
Circle
Solution
(b)
A 3-D figure is defined as the figure which can be specified
in all the three-dimensional axis. A 2-D figure can be represented only on a
plane. Hence,
square, triangle
and circle are 2-D figures
while sphere is the 3-D figure.
So, the correct answer is (b).
Question: 12
Total number of edges a cylinder has
a.
b.
c.
d.
Solution
(c)
The total number of edges of a cylinder are two.
The figure of cylinder is as follows:

So, the correct answer is (c).
Question: 13
A solid that has two opposite identical faces and other faces
as parallelograms is a
a.
prism
b.
pyramid
c.
cone
d.
sphere
Solution
(a)
Among the given shapes, prism is the only figure which has two opposite
identical faces and other faces
as parallelograms.

Question: 14
The solid with one circular face, one curved surface and one
vertex is known as:
a.
cone
b.
sphere
c.
cylinder
d.
prism
Solution
(a)
A cone has one
circular face, one curved surface and one vertex.

Question: 15
If three cubes each of edge are placed end to end, then the dimensions of
resulting solid are:
a.
b.
c.
d.
Solution
(a)
When three cubes are placed
end to end, then the resultant figure will be a cuboid. The length of this cuboid
is three times the length of the cube. The breadth and height of the cuboid
remains same as these are edge of the cube.
So, the cuboid will
have the dimensions
Hence, the correct answer is (a).
Question: 16
When we cut a corner of a cube as shown in the Fig.
12.19, we get the cut out piece as:

Fig. 12.19
a.
square pyramid
b.
trapezium prism
c.
triangular pyramid
d.
a triangle
Solution
(c)
If we cut a corner of a
cube, then we get cut-out
of a piece in the form of triangular pyramid. So, the correct answer
is (c).
Question: 17
If we rotate a right-angled triangle of height cm and base about its height a full turn, we get
a.
cone of height ,
base
b.
triangle of height ,
base
c.
cone of height ,
base
d.
triangle of height ,
base
Solution
(a)
If we rotate a right-angled triangle of height and base about its height a full turn, then we get a
cone of height and base
.
Question: 18
If we rotate a right-angled triangle of height and base
3 cm about its base, we get:
a.
cone of height cm and base cm
b.
cone of height cm and base cm
c.
cone of height cm and base cm
d.
cone of height cm and base cm
Solution
(d)
When we rotate a
right-angled triangle of height and base
about its
base,
we get a cone of height and
base .
Question: 19
When a torch is pointed towards one of the vertical edges of
a cube, you get a shadow of cube in the shape of
a.
square
b.
rectangle but not a square
c.
circle
d.
triangle
Solution
(b)
When a torch is
pointed towards one of the vertical edges of a cube, you
get a shadow of cube in the shape
of rectangle. Hence, the correct answer is (b).
Question: 20
Which of the following sets of triangles could be the
lengths of the sides of a right-angled triangle:
a.
b.
c.
d.
Solution
(c)
For a right-angled triangle,
minimum condition to be satisfied is the Pythagoras theorem which is stated
mathematically as below:
(Hypotenuse)2 (Base)2 (Perpendicular)2
So let us try each and every
option,
a.
b.
c.
(True)
d.
Hence, option (c) is the correct answer.
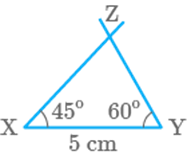
Question: 21
In which of the following cases, a unique triangle can be
drawn
a.
, and
b. , and
c. , and
d.
An isosceles triangle with the
length of each equal side cm.
Solution
(c)
Let us draw the
triangle according to measurements
given in respective options.
For (a), As we can see
triangle cannot be drawn
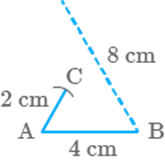
For (b), Triangle cannot
be
formed.
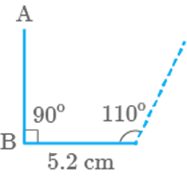
For (c), Unique
triangle can be drawn by these measurements.
For (d), Using given
data, we can form as many triangles as we want.
So, the correct answer is (c).
Question: 22
Which of the following has a line of symmetry?
a.

b.

c.

d.

Solution
(c)
The line of symmetry is a line which divides a figure into
two equal halves which are mirror image of each other.
The following
figure has one line of symmetry

Question: 23
Which of the following are reflections of each other?
a.

b.

c.

d.

Solution
(a)
Reflection means the figure should be just in opposite
orientation like the image in a mirror, that is the image is just flipped.
Since in the
figure (a) the image of one side of the figure is exactly same as the figure on the other side
of the line of symmetry.
So, the correct answer is (a).
Question: 24
Which of these nets is a net of a cube?
a.

b.

c.

d.

Solution
(b)
A net is 2-D figure which when folded in a
particular axis gives a 3-D figure.
So, for the net to form a cube, the shape of
the interlinking blocks of nets should be a square which is present only in
option ‘b’.

Question: 25
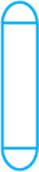
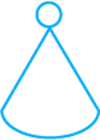
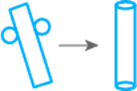
Which of the following nets is a net of a cylinder?
a.
b.

c.

d.
Solution
(c)
A net is 2-D figure which when folded in a
particular axis gives a 3-D figure. So for the net to form a cylinder,
the shape of the interlinking blocks of nets should contain a rectangle which
is present only in option C.
Question: 26
Which of the following letters of English alphabets have
more than lines of symmetry?
a.
Z
b.
O
c.
E
d.
H
Solution
(b) and
(d)


The letter O has more than
two lines of symmetry and letter H
has exactly two lines of symmetry.
Question: 27
Take a square piece of paper as shown in figure (1). Fold it
along its diagonals as shown in figure (2). Again fold it as shown in figure
(3). Imagine that you have cut off 3 pieces of the form of congruent isosceles
right-angled triangles out of it as shown in figure 4.
(1)

(2)
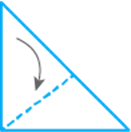
(3)
(4)

On opening the piece of paper which of the following shapes
will you get?
a.

b.

c.

d.

Solution
(a)
As per the given steps in the question, if we open the piece of paper, we will get the
figure as shown in option (a).
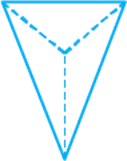
Question: 28
Which of the following 3-dimensional
figures has the top, side and front as triangles?
a.
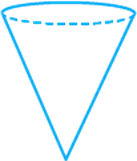
b.

c.
d.

Solution
(c)
Figure
in option (c) shows all (top, side and
front) views as triangle.
In
Questions 29 to 58, fill in the blanks to make the statements true.
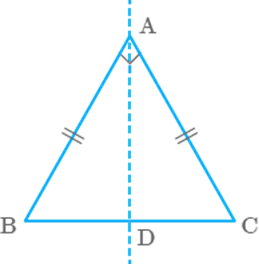
Question: 29
In
an isosceles right triangle, the number of lines of symmetry is ________.
Solution
One
Since, an isosceles triangle has one line of symmetry drawn from the
vertex touching the base as shown in the figure.
Question: 30
Rhombus
is a figure that has ______ lines of symmetry and has a rotational symmetry of
order _______.
Solution
two, two
A rhombus has two lines of symmetry along
the diagonal and has a rotational symmetry of order two.
Question: 31
__________ triangle is a figure that has a line of symmetry
but lacks rotational symmetry.
Solution
Isosceles
The triangle which has only one line of symmetry and no
rotational symmetry is the isosceles triangle.
An isosceles triangle is a figure
that has a line of symmetry but lacks rotational symmetry.
Question: 32
__________ is a figure that has neither a line of symmetry
nor a rotational symmetry.
Solution
Scalene
Triangle
Scalene
Triangle has all sides unequal and hence it has no lines of symmetry or
rotational symmetry.
Scalene
Triangle is a figure that has neither a line of symmetry nor a rotational
symmetry.
Question: 33
__________
and __________ are the capital letters of English alphabets that have one line
of symmetry but they interchange to each other when rotated through .
Solution
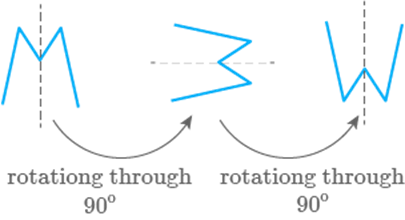
M, W
The only two letters which have only one line of symmetry
and those which interchange to each other when rotated through 180° are
M and W.
Question: 34
The
common portion of two adjacent faces of a cuboid is called __________.
Solution
Edge
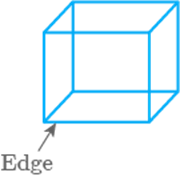
The common portion of two adjacent faces of a cuboid is called edge.
Question: 35
A
plane surface of a solid enclosed by edges is called __________ .
Solution
Face
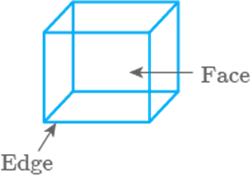
A plane surface of a solid enclosed by edges is called face.
Question: 36
The
corners of solid shapes are called its __________.
Solution
Vertices
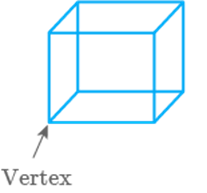
The corners of solid shapes are called its vertices.
Question: 37
A
solid with no vertex is __________.
Solution
Sphere
Since,
a sphere is a solid with vertex, edge and curved surface,
Question: 38
A
triangular prism has __________ faces, __________ edges and__________ vertices.
Solution

A triangular prism has faces, edges and
vertices.
Question: 39
A
triangular pyramid has __________ faces, __________ edges and __________vertices.
Solution

A triangular pyramid has faces, edges and vertices.
Question: 40
A
square pyramid has __________ faces, __________ edges and__________ vertices.
Solution

A square pyramid has faces, edges
and vertices.
Question: 41
Out
of __________ faces of a triangular prism, __________are rectangles and
__________ are triangles.
Solution
Out of faces of
a triangular prism, are
rectangles and are triangles.

Question: 42
The
base of a triangular pyramid is a __________.
Solution
Triangle
The base of a triangular pyramid is
a triangle.
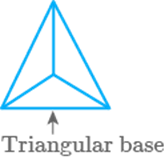
Question: 43
Out
of __________ faces of a square pyramid, __________ are triangles and
__________ is/are squares.
Solution
Out of faces of
a square pyramid, are
triangles and is square.

Question: 44
Out
of __________ faces of a rectangular pyramid __________ are triangles and base
is __________.
Solution
Out of faces of
a rectangular pyramid, are triangles and base is rectangle

Question: 45
Each
of the letters H, N, S and Z has a rotational symmetry of order__________.
Solution
2
Each
of the letters H, N, S and Z has a rotational
symmetry of order two.
Question: 46
Order
of rotational symmetry of a rectangle is __________.
Solution
Order
of rotational symmetry of a rectangle is two.

Question: 47
Order
of rotational symmetry of a circle is __________.
Solution
Order
of rotational symmetry of a circle is infinite.
The
number of times a figure fits onto itself in one complete rotation is called the order of rotational symmetry.
Question: 48
Each
face of a cuboid is a __________.
Solution
A
cuboid is a solid figure which is bounded by six rectangular faces.
Each face of a cuboid is a rectangle.
Question: 49
Line
of symmetry for an angle is its __________.
Solution
Line
of symmetry for an angle
is its bisector.
Question: 50
A
parallelogram has __________ line of symmetry.
Solution
A parallelogram has no line of symmetry.
Question: 51
Order
of rotational symmetry of  is _________.
is _________.
Solution
8
The
number of times a figure fits into itself in one full turn is called as order
of rotational symmetry.
Order of rotational symmetry of a given
figure is .
Question: 52
A
__________ triangle has no lines of symmetry.
Solution
Scalene
A scalene triangle has no lines of symmetry. Since, all of its angles and
sides are of unequal length.
Question: 53
Cuboid
is a rectangular_________ .
Solution
Prism
Rectangular prism and cuboid are same solids.
Question: 54
A
sphere has __________vertex, __________edge and __________curved surface.
Solution
A
sphere has zero vertex, zero edge and curved
surface.

Question: 55
 is a net of a ______.
is a net of a ______.
→ Circumference
of circle ______.
Solution
Cone

→ Circumference
of circle
Question: 56
 is a net of a __________.
is a net of a __________.
Solution

Question: 57
Order
of rotational symmetry of  is _____.
is _____.
Solution
For the given triangle, two sides are equal which means it
is an isosceles triangle.
Since,
isosceles triangle has rotational symmetry
of order .
Question: 58
Identical
cubes are stacked in the corner of a room as shown below. The number of cubes
that are not visible are _________.

Solution
The
number of cubes that are not visible are .
In
Questions from 59 to 92, state whether the statements are True or False.
Question: 59
We
can draw exactly one triangle whose angles are ,
and .
Solution
False
The
sum of the angles given is + + .Though
the angles are unique for the triangle, but the length of the sides can differ
and hence the number of triangles that can be drawn with these angles will also
be infinite.
Question: 60
The
distance between the two parallel lines is same everywhere.
Solution
True
The
distance between the two parallel
lines is always same everywhere.
Question: 61
A
circle has two lines of symmetry.
Solution
False
A
circle has infinite lines of symmetry.
Question: 62
An
angle has two lines of symmetry.
Solution
False
An
angle has only one line of symmetry i.e. its bisector.
Question: 63
A
regular hexagon has six lines of symmetry.
Solution
True
A
regular polygon has many lines of symmetry equal to the number
of its sides.
Question: 64
An
isosceles trapezium has one line of symmetry.
Solution
True
Isosceles
trapezium has only one line of symmetry along the
line segment joining the mid-points
of two parallel sides which is shown
in figure.
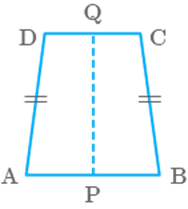
Question: 65
A
parallelogram has two lines of symmetry.
Solution
False
A parallelogram has no lines of symmetry. So the given
statement is false.
Question: 66
Order
of rotational symmetry of a rhombus is four.
Solution
False
Order
of rotational symmetry of a rhombus is two, so the given
statement is false.
Question: 67
An
equilateral triangle has six lines of symmetry.
Solution
False
Since,
in an equilateral triangle, there are three lines of symmetry along the three
medians of the triangle.
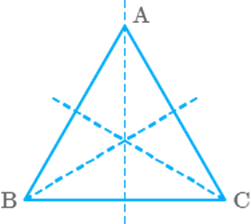
Question: 68
Order
of rotational symmetry of a semi-circle is two.
Solution
False
Order
of rotational symmetry of a semi-circle is one.
Question: 69
In
oblique sketch of the solid, the measurements are kept proportional.
Solution
False
In
oblique sketch of the solid, the measurements are not kept proportional.
So, the given statement is false.
Question: 70
An
isometric sketch does not have proportional length.
Solution
False
An
isometric sketch always has proportional length.
So,
the given statement is false.
Question: 71
A
cylinder has no vertex.
Solution
True
A
cylinder has faces, edges but
no vertex. Hence, the statement is
true.
Question: 72
All
the faces, except the base of a square pyramid are triangular.
Solution
True
A
square pyramid has triangular faces
and one square base. So, the given statement is true.

Question: 73
A
pyramid has only one vertex.
Solution
False
A
pyramid has at least vertices (in triangular pyramid). So,
the given statement is false.
Question: 74
A
triangular prism has faces, edges and vertices.
Solution
True

A
triangular prism has faces, edges and vertices.
Question: 75
If
the base of a pyramid is a square, it is called a square pyramid.
Solution
True

The
name of a pyramid is based
on the base of pyramid. So, if the base of a pyramid is a square, then it
is called a square pyramid.
Question: 76
A
rectangular pyramid has rectangular faces.
Solution
False

A
rectangular pyramid has rectangular face and triangular faces.
Question: 77
Rectangular
prism and cuboid refer to the same solid.
Solution
True

Rectangular prism and
cuboid refer to the same solid.
Question: 78
A
tetrahedron has triangular faces and rectangular face.
Solution
False

A
tetrahedron has 4 triangular faces.
Question: 79
While
rectangle is a 2-D figure, cuboid is a 3-D figure.
Solution
True
A
rectangle is a 2-D figure and cuboid is a 3-D figure.
Question: 80
While
sphere is a 2-D figure, circle is a 3-D figure.
Solution
False
Circle
is a 2-D figure and sphere is a 3-D figure
Question: 81
Two
dimensional figures are also called plane figures.
Solution
True
2-D
figures are also called plane figures. So, the statement is
true.
Question: 82
A
cone is a polyhedron.
Solution
False
A
cone is not a polyhedron.
Question: 83
A
prism has four bases.
Solution
False
A
prism has twobases.
Question: 84
The
number of lines of symmetry of a regular polygon is equal to the vertices of
the polygon.
Solution
True
The
number of lines of symmetry of
a regular polygon is equal to the vertices of the
polygon. So, the statement is true.
Question: 85
The
order of rotational symmetry of a figure is and the angle of rotation is only.
Solution
False
If
the order of rotational symmetry
of a figure is ,
then the angle of rotation must be .
Question: 86
After
rotating a figure by about its centre, the figure coincides with
its original position. This will happen again if the figure is rotated at an
angle of .
Solution
True
After
rotating a figure by about
its centre, the figure coincides with its original
position. This will happen again, if the figure is rotated at an
angle of .
Question: 87
Mirror
reflection leads to symmetry always.
Solution
False
Mirror
reflection does not always lead to
symmetry.
Question: 88
Rotation
turns an object about a fixed point which is known as centre of rotation.
Solution
True
Centre
of rotation turns an object about a fixed point.
Question: 89
Isometric
sheet divides the paper into small isosceles triangles made up of dots or
lines.
Solution
False
Isometric
sheet divides the paper into small equilateral triangles made up of dots or lines.
So, the statement is false.
Question: 90
The
circle, the square, the rectangle and the triangle are examples of plane
figures.
Solution
True
The
circle, the square, the rectangle
and the triangle are examples of
plane figures.
Question: 91
The
solid shapes are of two-dimensional.
Solution
False
The
solid shapes are of three-dimensional.
Question: 92
Triangle
with length of sides as cm, cm and can be constructed.
Solution
False
We
know that, in a triangle, sum of
any two sides is always greater
than the third side.
Here, the sum of two sides is equal to the
third side.
Hence,
these measurements do not
satisfy the basic condition of a triangle. Hence, the triangle cannot be
constructed.
Question: 93
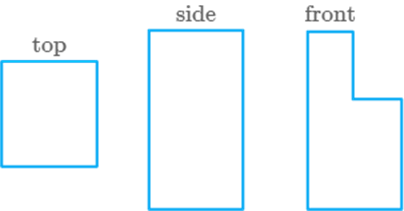
Draw
the top, side and front views of the solids given below in
(1)

(2)

Solution
For given Fig. (1)

For given Fig. (2)

Question: 94
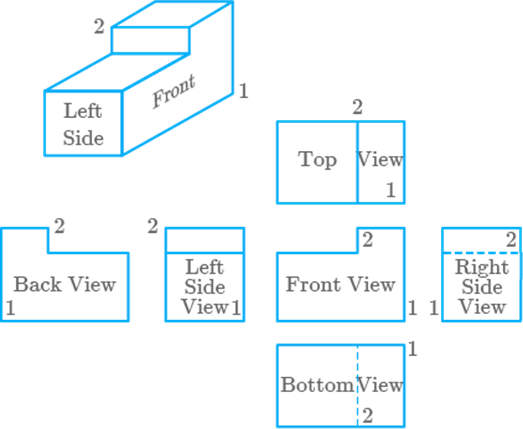
Draw
a solid using the top. side and front views as shown below. [Use Isometric dot
paper].
Solution
Question: 95
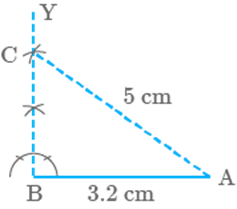
Construct
a right-angled triangle whose hypotenuse measures cm and one of the other sides measures cm.
Solution
Steps of construction
Step I: Draw a line
Step
II: Construct a right angle (
) at point B and draw a ray BY through it.
Step
III: From point A draw and arc of length
5 cm cutting BY at C.
Step
IV: Join AC
Step
V: ABCis the required triangle.
Question: 96
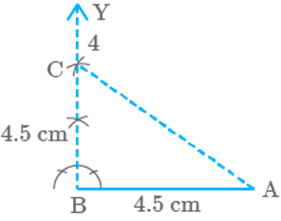
Construct a right-angled isosceles triangle with one side
(other than hypotenuse) of length cm.
Solution
Steps of construction
Step I: Draw a line AB of side
Step
II: Construct a right angle at point B and draw a ray BY through it.
Step
III: From point B, draw an arc of
length cutting BY at C.
Step
IV: Join AC
Step V: ABC is the required
triangle.
Question: 97
Draw
two parallel lines at a distance of cm apart.
Solution
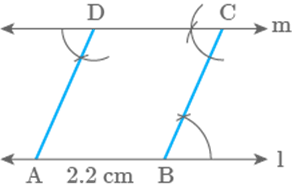
Steps of construction are as
follows:
Step
I: Draw a line of any length and mark a point outside
it.
Step II: Take a point B on line
and join BC.
Step III: Draw line parallel to line passing
through C.
Step IV: Mark a point D on line ,
at a distance of from C.
Step V: Through D draw Line
is parallel
to line .
Also,
Question: 98
Draw
an isosceles triangle with each of equal sides of length cm and the angle between them as .
Solution
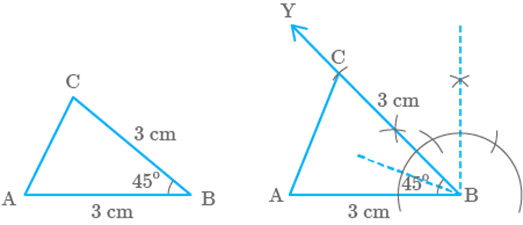
Steps
of construction
Step
I: Firstly, we draw a rough sketch
of triangle with given measures marked on it.
Step
II: Draw a line segment AB of length .
Step
III: Draw an angle of at point
B and produce it to form ray BY.
Step
IV: With B as centre, draw an arc of which intersects ray BY at C.
Step
V: Join AC.
Thus, is the required isosceles
triangle.
Question: 99
Draw
a triangle whose sides are of lengths and cm.
Solution
Let
us assume that given sides are and
Steps of construction
Step
I: Draw a line segment
Step
II: With centre B and radius cm draw
an arc.
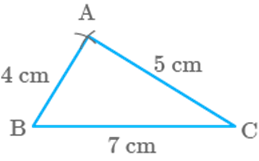
Step
III: With centre C and radius ,
draw an arc which cuts the previous arc at A.
Step
IV: Join AB and AC.
So, is the required triangle in which , and
Question: 100
Construct
an obtuse angled triangle which has a base of and base angles of and .
Solution
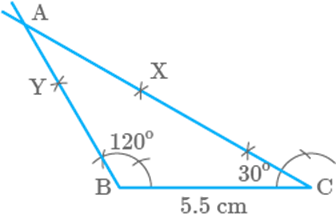
Steps of construction
Step
I: Draw a line segment BC of length .
Step
II: Draw an angle of at point B and
produce it to form ray BY.
Step
III: Draw an angle of at point C and
produce it to form ray CX.
Step
IV: Extend BY and CX in such manner that they intersect to get the third
point A.
Step
V: Join AC to complete the triangle.
Question: 101
Construct
an equilateral triangle ABC of side .
Solution
Steps of construction
Step
I: Draw a line segment AB cm
Step
II: Draw an arc of radius cm from point A.
Step
III: Now, draw another arc of radius cm from
point B to cut previous
arc at C.
Step
IV: Join A to C and B to C.
So, is the required triangle.
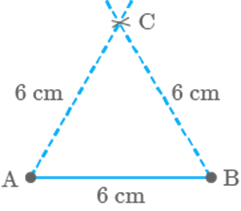
Question: 102
By
what minimum angle does a regular hexagon rotate so as to coincide with its
original position for the first time?
Solution
A
regular hexagon must be rotated through a minimum angle of .
So, that it can coincide with its original position for the first
time. Because the angle of rotation of hexagon
Question: 103
In
each of the following figures, write the number of lines of symmetry and order
of rotational symmetry.

Fig.
12.23
[Hint:
Consider these as 2-D figures not as 3-D objects.]
Solution
|
Figure
|
No. of lines of symmetry
|
Order of rotational symmetry
|
|
A
|
1
|
1
|
|
B
|
1
|
1
|
|
C
|
1
|
1
|
|
D
|
2
|
2
|
|
E
|
1
|
1
|
|
F
|
0
|
2
|
|
G
|
1
|
1
|
|
H
|
0
|
3
|
|
I
|
4
|
4
|
|
J
|
1
|
1
|
|
K
|
0
|
1
|
|
L
|
1
|
1
|
|
M
|
0
|
2
|
|
N
|
0
|
1
|
|
O
|
1
|
1
|
|
P
|
0
|
1
|
|
Q
|
5
|
5
|
|
R
|
0
|
1
|
|
S
|
3
|
3
|
|
T
|
1
|
1
|
|
U
|
0
|
10
|
|
V
|
3
|
3
|
|
W
|
0
|
1
|
Question: 104
In
the Fig. 12.24 of a cube,
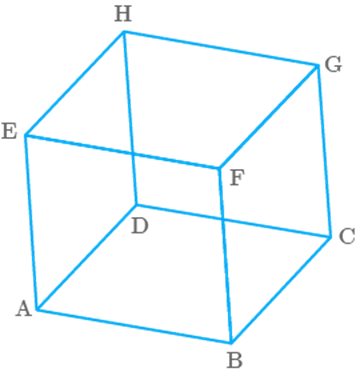
Fig.
12.24
(1) Which edge is the intersection of faces EFGH
and EFBA?
(2) Which faces intersect at edge FB?
(3) Which three faces form the
vertex A?
(4) Which vertex is formed by the faces ABCD,
ADHE and CDHG?
(5) Give all the edges that are parallel to edge
AB.
(6) Give the edges that are neither parallel nor
perpendicular to edge BC.
(7) Give all the edges that are perpendicular to
edge AB.
(8) Give four vertices that do not all lie in one
plane.
Solution
(1) From the given figure, we can observe that EF
is the intersection of faces EFGH and EFBA.
(2) From the given figure, we can observe that
faces EFBA and FBCG intersect at edge FB.
(3) Faces ABFE, ADHE and ABCD form the vertex A,
(4) Vertex D is formed by the faces ABCD, CDHG
and ADHE.
(5) The edges parallel to edge AB are CD, EF and
HG.
(6) From the given figure, we can observe that
edges AE, EF, GH and HD are neither parallel nor perpendicular to edge BC.
(7) From the given figure, we can observe that
edges AE, BF, AD and BC are perpendicular to edge AB.
(8) Vertices A, B, G and H do not lie in one plane.
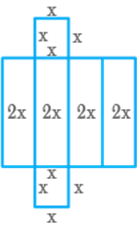
Question: 105
Draw
a net of a cuboid having same breadth and height, but length double the
breadth.
Solution
Required
net of a cuboid will be
Question: 106
Draw
the nets of the following:
(i)
Triangular prism
(ii)
Tetrahedron
(iii)
Cuboid
Solution
(i)
Net for triangular prism

(ii)
Net for tetrahedron,

(iii) Net for cuboid,

Question: 107
Draw
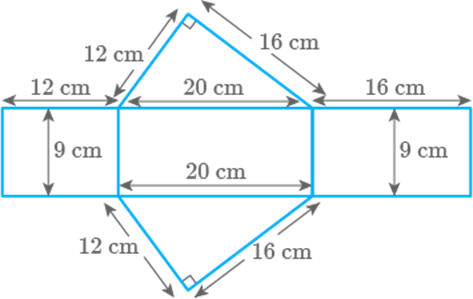
a net of the solid given in the Fig. 12.25:
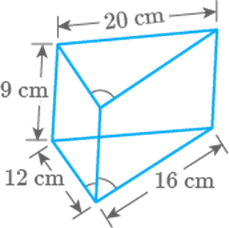
Fig.
12.25
Solution
The
net of the given solid figure will be
Question: 108
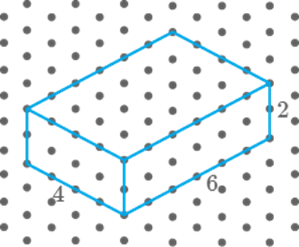
Draw an isometric view of a cuboid .
Solution
Isometric view of a cuboid
Question: 109
The
net given below in Fig. 12.26 can be used to make a cube.
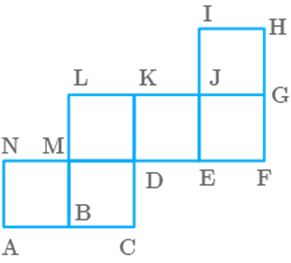
Fig.
12.26
(1)
Which edge meets AN?
(2)
Which edge meets DE?
Solution
(1) The given net of a cube shows that edge GH meets edge AN.
(2) The given net of a cube shows that edge DC meets edge DE.
Question: 110
Draw
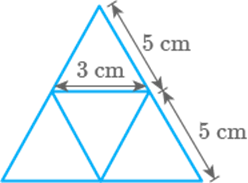
the net of triangular pyramid with base as equilateral triangle of side cm and slant edges cm.
Solution
The net of such triangular pyramid will be
Question: 111
Draw
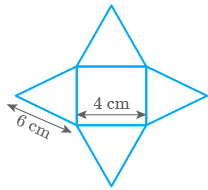
the net of a square pyramid with base as square of side cm and slant edges cm.
Solution
The
net of such square pyramid will be
Question: 112
Draw
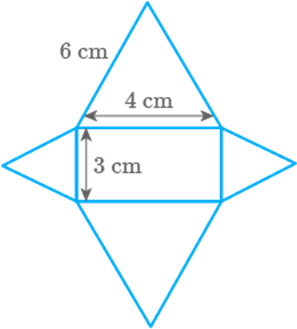
the net of rectangular pyramid with slant edge cm and base as rectangle with length cm and breadth cm.
Solution
The
net of such rectangular pyramid will be
Question: 113
Find
the number of cubes in each of the following figures and in each case give the
top, front, left side and right side view (arrow indicating the front view).
a. 
b. 
c. 
d. 
e. 
f. 
g. 
h. 
Solution
a. The no. of cubes in
the given figure is

b. The no. of cubes in the given figure is
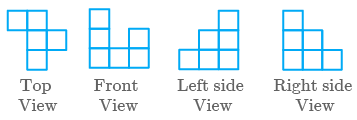
c. The no. of cubes in
the given figure is
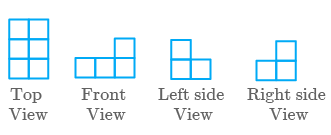
d.
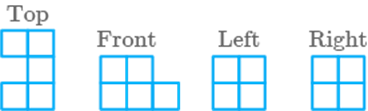
e.
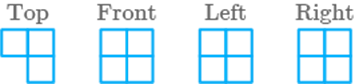
f.

g.

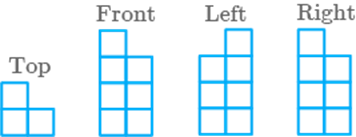
h.
Question: 114
Draw
all lines of symmetry for each of the following figures as given below:
a. 
b. 
c. 
Solution
a. 
1 line of symmetry
b. 
No line of symmetry
c. 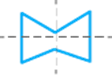
2 lines of symmetry
Question: 115
How
many faces does Fig. 12.27 have?

Fig.
12.27
Solution
There
are total faces in the given figure.
Question: 116
Trace
each figure. Then draw all lines of symmetry, if it has.
a. 
b. 
c. 
Solution
How
many faces does figure have?
a. 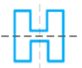
b. 
c. 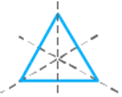
Question: 117
Tell
whether each figure has rotational symmetry or not.
a. 
b. 
c. 
d. 
e. 
f. 
Solution
a. Yes
b. No
c. No
d. Yes
e. Yes
f.Yes
Question: 118
Draw
all lines of symmetry for each of the following figures.
a. 
b. 
c. 
d. 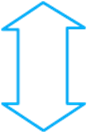
e. 
f. 
Solution
a. 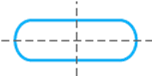
b. 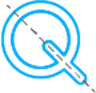
c. 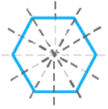
d. 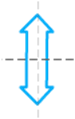
e. 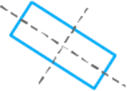
f. 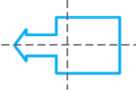
Question: 119
Tell
whether each figure has rotational symmetry. Write yes or no.
a. 
b. 
c. 
d. 
Solution
a. Yes
b. Yes
c. No
d. Yes
Question: 120
Does
the Fig. 12.28 have rotational symmetry?

Fig.
12.28
Solution
The
given figure does not show
rotational symmetry because one part of design is undarkened,
whereas other three part are darkened.
Hence, the design does not show
symmetry.

Question: 121
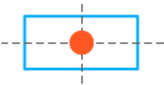
The
flag of Japan is shown below. How many lines of symmetry does the flag have?

Solution
The
given flag has 2 lines of symmetry
Question: 122
Which
of the figures given below have both line and rotational symmetry?
a.

b.

c.

d.

Solution
Only
(a) has both line & rotational symmetries.
In the given figure,

Also,
rotational symmetry will be shown as

i.e, rotational angel is
equal to
Question: 123
Which
of the following figures do not have line symmetry?
a.

b.

c.

d.

Solution
a. We observe that the given figure has 2
lines of symmetry

b. The given figure has one line of symmetry.
c. We observe that the given figure has 2 lines of symmetry.

d. The given figure has no line of symmetry.
Question: 124
Which
capital letters of English alphabet have no line of symmetry?
Solution
The
letters F, G, J, L, N,P, Q, R, S and Z have no line of
symmetry.

















![]()












![]()































 is _________.
is _________.
 is a net of a ______.
is a net of a ______. 
 is a net of a __________.
is a net of a __________.
 is _____.
is _____.


















































![]()
![]()

![]()
![]()













































