Unit: 13: Exponents and Powers
Exercise: 1
(Multiple Choice Questions and Answers 1-22)
In questions 1 to 22, there
are four options, out of which one is correct. Write the correct one.
Question: 1
is equal to
a.
b.
c.
d.
Solution
(b)
We have
studied that, if is a rational number, and are natural numbers, then
Question: 2
For a non-zero rational
number is equal to
a.
b.
c.
d.
Solution
(b)
We have
studied that, if is a rational number, are natural numbers
such
that then
Here,
we have
So,
Question: 3
is a non-zero rational number. Product of the
square of with the cube of is equal to the
a. second power of
b. third power of
c. fifth power of
d. sixth power of
Solution
(c)
Square
of
Cube
of
Product of
square with the cube of
i.e.
fifth power of .
Question: 4
For any two non-zero
rational numbers and ,
is equal to
a.
b.
c.
d.
Solution
(c)
It is given that,
We
have studied that,
Here,
Thus,
Question: 5
is equal to
a.
b.
c.
d.
Solution
(c)
As we have studied that, if is a rational number, and are
natural numbers, then
Question: 6
is equal to
a.
b.
c.
d.
Solution
(c)
As we
have studied that,
Question: 7
Value
of is
a.
b.
c.
d.
Solution
(c)
The given expression can be written as
Question: 8
The
standard form of the number is
a.
b.
c.
d.
Solution
(d)
A number in its standard form is written as ‘a where a
is a terminating decimal number such that and is any integer.
Thus,
the standard form of the number
Question: 9
If ,
then the value of K is
a.
b.
c.
d.
Solution
(c)
It is given
that
Thus,
the value of is
Question:10
Which
of the following is equal to 1?
a.
b.
c.
d.
Solution
(b)
Let
us solve all the expressions
one by one,
Option (a),
Option (b),
Hence,
option (b) is the answer.
Question: 11
In
standard form, the number is written as where is equal to
a.
b.
c.
d.
Solution
(c)
We have
studied that, if the given number is
greater than or equal to then the power of (i.e. ) is a positive
integer and is equal to the
number of places the decimal
point has been shifted.
Hence,
Question: 12
Square
of is
a.
b.
c.
d.
Solution
(d)
As
per question, square of
Thus,
Question: 13
Cube
of is
a.
b.
c.
d.
Solution
(c)
As
per question, cube of
Thus,
Question: 14
Which
of the following is not equal to ?
a.
b.
c.
d.
Solution
(c)
We have
studied that,
So,
Or
Hence,
option (c) is not equal to
Question: 15
Which
of the following is not equal to ?
a.
b.
c.
d.
Solution
(d)
Let
us solve each option one by one.
Option
a,
Option
b,
Option c,
Option
d,
Hence,
option (d) is not equal to .
Question: 16
is equal to
a.
b.
c.
d.
Solution
(c)
We have
studied that, if are rational numbers,
then
Here,
Thus,
Question: 17
In
standard form, the number is written as where K is equal to
a.
b.
c.
d.
Solution
(d)
We
know that, a number in a standard form is written as K where is a terminating
decimal such that
So,
there is only one option, where less then
Question: 18
Which
of the following has the largest value?
a.
b.
c.
d.
Solution
(a,
b)
Let
us solve each option one by one.
Option
a,
Option
b,
Option c,
Option
d,
The
fraction whose denominator is the smallest will be the largest
fraction.
Hence,
are the largest.
Question: 19
In
standard form crore is written as
a.
b.
c.
d.
Solution
(c)
We have
studied that, a number in standard form is written as K where
K is the terminating decimal such that and is any integer.
Thus,
crore
Question: 20
For
non-zero numbers a and b, ,
where ,
is equal to
a.
b.
c.
d.
Solution
(c)
We have studied that,
Thus,
Question: 21
Which
of the following is not true?
a.
b.
c.
d.
Solution
(c)
Let us solve each option one by one.
Option a,
(true)
Option b,
(true)
Option c,
(false)
Option d,
(true)
Hence, option (c) is not true.
Question: 22
Which
power of is equal to ?
a.
b.
c.
d.
Solution
(b)
Let
us suppose that the power of be .
According to the question, we have
Since, bases are equal,
by equating their exponents, we get
Hence, the power of is which is equal to .
In questions 23 to 39, fill in the blanks to make the statements true.
Question: 23
Solution
Here,
Question: 24
Solution
Here,
Question: 25
Solution
Let us
suppose that
Since, in
the above equation, the powers are same. Thus,
Hence,
Question: 26
Solution
Let us suppose that
Since
in the above equation the bases are equal. So, by equating the powers, we get,
Hence,
Question: 27
Solution
Here,
Question: 28
Solution
Question: 29
Solution
Here,
Question: 30
Solution
Let
us suppose that
Since
in the above equation, the powers are same.
Thus,
Hence,
Question: 31
Solution
The
expression can be written as
Question: 32
lakh
Solution
We know that,
Question: 33
1
million
Solution
We know that,
Question: 34
Solution
Here, we have to find out the factors of the given expression.
So,
|
3
|
729
|
|
3
|
243
|
|
3
|
81
|
|
3
|
27
|
|
3
|
9
|
|
3
|
3
|
|
|
1
|
Question: 35
Solution
Here, we are suppose to find out the factors of given expression.
So,
Question: 36
Solution
The given number =
In standard form, it can be written as
Also,
Question: 37
Solution
The given number =
In standard form, it can be written as
Also,
So,
Question: 38
Solution
The given number =
This number can be expressed in standard form as
Also,
So,
Question: 39
Solution
The given number can be written in
standard form as,
Also,
So,
Question: 40
Fill in the blanks with <,
> or = sign.
a.
b.
c.
d.
e.
Solution
a.
We can write,
So,
Therefore,
b.
We can write,
And
So,
Therefore,
c.
In the above expression, as base 7 is greater than base 5 and power is same,
Therefore,
d.
We can write,
So,
Therefore,
e.
We can write,
And
So,
Therefore,
In questions 41 to 65, state whether the given statements
are True or False.
Question: 41
One
million
Solution
False
We know that,
Hence,
Question: 42
One
hour seconds
Solution
True
We
know that,
Question: 43
Solution
False
We know that,
Question: 44
Solution
False
We
know that,
Question: 45
Solution
True
We know
that, and
Therefore,
Question: 46
Solution
True
Considering
left hand side of the equation, we have
Now,
taking RHS, we have
LHS
RHS
Hence,
Question: 47
Solution
False
Let us solve LHS,
Let
us solve RHS,
Now,
Hence,
LHS is not equal to RHS
Question: 48
is true for all non-zero values of .
Solution
True
As
we know that
and
Hence,
Question: 49
In
the standard form, a large number can be expressed as a decimal number between and ,
multiplied by a power of .
Solution
False
We
know that, a number in standard form
is written as where is any integer.
Question: 50
is greater than
Solution
False
and
Therefore,
Question: 51
where is a non-zero rational number and is a positive integer.
Solution
False
We have studied that
Also,
So,
Question: 52
,
where and are non-zero rational numbers and is a positive integer.
Solution
False
We
have studied that if are rational
numbers, then
Hence,
Question: 53
where and are non-zero rational numbers and is a positive integer.
Solution
True
We
have studied that, if are rational
numbers, then
Question: 54
where is a non-zero rational number and are positive integers.
Solution
True
We
have studied that, if is a rational
number and and are
positive integers, then
Question: 55
is greater than
Solution
True
Now,
in as powers
Question: 56
Solution
False
Taking
LHS we get,
Hence,
Question: 57
Solution
False
Taking
LHS we get,
And
As
the base is not same for LHS value,
So,
LHS RHS
Hence,
Question: 58
Solution
False
Taking
LHS we get,
Hence,
Question: 59
Solution
False
Taking
LHS we get,
Hence,
Question: 60
Solution
True
Taking
LHS we get,
Now,
taking RHS we get,
Hence,
Question: 61
Solution
True
Considering
the right hand side of the given equation, we get
Hence,
RHS LHS
Question: 62
Solution
False
Considering
the right hand side of the given equation, we get
Hence,
Question: 63
Solution
False
Considering
the left hand side of the given equation, we get
Hence,
Question: 64
Solution
True
Considering
the left hand side of the given equation, we get
Hence,
Question: 65
Solution
False
Considering
the left hand side of the given equation, we get,
and
Hence,
Question: 66
Arrange
in ascending order:
Solution
Ascending
order means arranging the numbers from least to greatest.
We
have,
and
Thus,
the required ascending order will be
Question: 67
Arrange
in descending order:
Solution
Descending
order means arranging the numbers from greatest to least.
We
have,
Thus, the required descending order will be
Question: 68
By
what number should be divided so that the quotient may be equal
to ?
Solution
In
order to find the number, that should divide to get the quotient we will divide by
Hence,
the required number is
Question: 69
Find
so that
Solution
We
have,
When the bases are same, we can equate the powers.
Therefore,
Hence,
Question: 70
If find the value of
Solution
Considering
the given equation,
Cubing
both sides, we get
Question: 71
Find
the reciprocal of the rational number
Solution
Considering the given expression
The reciprocal is
Question: 72
Find
the value of:
a.
b.
c.
d.
e.
f.
Solution
a. ,
as we know that any number to the power of zero is one.
b.
c.
d.
e.
f.
Question: 73
Find
the value of ,
where n is an integer and
Solution
Considering
the given equation,
Question: 74
Express
the following in usual form:
a.
b.
Solution
a.
The given number can be written as
b.
The given number can be written as
Question: 75
Find
the value of
a.
b.
c.
Solution
We have
studied that,
a.
b.
c.
Question: 76
Express
the following in exponential form:
a.
b.
c.
Solution
We have
studied that,
a.
b.
c.
Question: 77
How
many times of must be added together to get a sum equal to ?
Solution
Let
be the
number of times that must
be added together to get a sum
equal to
Therefore,
we can write the above statement as -
Hence,
if is added times, then
we get
Question: 78
Express
each of the following numbers using exponential notations:
a.
b.
c.
Solution
a. The number 1024 using prime
factorisation can be written as -
b.
The number 1029 using prime factorisation can be written as -
c.
The number using prime factorisation can be written as -
Question: 79
Identify
the greater number, in each of the following:
a.
b.
c.
Solution
a.
We know that, and
So,
b.
We know that,
and
So,
c.
We know that,
So,
Question:
80
Express
each of the following as a product of powers of their prime factors:
a.
b.
c.
Solution
The number 9000 using prime factorisation
can be written as -
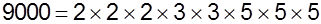
The number 2025 using prime factorisation
can be written as -
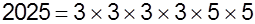
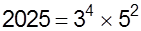
The number 800 using prime factorisation
can be written as -
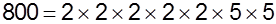
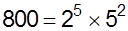
Question: 81
Express
each of the following in single exponential form:
a.
b.
c.
d.
e.
f.
Solution
a.
We have,
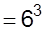
b.
We have,
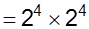
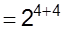
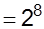
c.
We have,
d.
We have,
e.
We have,
f.
We have,
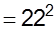
Question: 82
Express
the following numbers in standard form:
a.
b.
c.
d. billion
Solution
a. We have,
We
have studied that, a number in standard form is written as a
where is the terminating decimal such that is any
integer.
So,
Similarly,
b.
c.
d.
Question: 83
The
speed of light in vacuum is .
Sunlight takes about minutes to reach the earth. Express distance
of Sun from Earth in standard form.
Solution
It
is given that, speed of light m/s
Since
the speed is given in m/s, we need to convert the time taken into seconds.
Time
taken by light to reach the Earth
We have
studied that, Distance Speed Time
Hence,
the distance of Sun from the Earth is
Question: 84
Simplify
and express each of the following in exponential form:
a.
b.
c.
d.
e.
f.
Solution
a.
We have,
b. We have,
c. We have,
d. We have,
e.
We have,
f.We have,
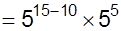
Question: 85
Evaluate
a.
b.
c.
d.
e.
f.
g.
Solution
a.
Considering the expression,
b. Considering the expression,
c.
Considering the expression,
d.
Considering the expression,
e.
Considering the expression,
f.
Considering the expression,,
g.
Considering the expression,,
Question: 86
Express
the given information in Scientific notation (standard form) and then arrange
them in ascending order of their size.
|
Sl.No.
|
Deserts of
the World
|
Area (Sq. Kilometres)
|
|
(1)
|
Kalahari, South Africa
|
|
|
(2)
|
Thar, India
|
|
|
(3)
|
Gibson, Australia
|
|
|
(4)
|
Great Victoria, Australia
|
|
|
(5)
|
Sahara, North Africa
|
|
Solution
1.
Area of Kalahari,
South Africa
[Since
we know that the standard form
is written as ]
2.
Area of Thar, India
3.
Area of Gibson,
Australia
4. Area of Great Victoria, Australia
5.
Area of Sahara,
North-Africa
We have studied that, to compare two numbers written in
scientific notation: The
number with the larger power
of is
greater than the number with
the smaller power of .
If the powers of ten are the
same, then the number with larger factor is the larger number.
Hence, the ascending order of the sizes of the deserts will be Gibson, Australia Thar,
India Great
Victoria, Australia Kalahari,
South-Africa Sahara, North-Africa.
Question: 87
Express
the given information in Scientific notation and then arrange them in
descending order of their size.
|
Sl.No.
|
Name
of the Planet
|
Mass
(in kg)
|
|
(1)
|
Mercury
|
|
|
(2)
|
Venus
|
|
|
(3)
|
Earth
|
|
|
(4)
|
Mars
|
|
|
(5)
|
Jupiter
|
|
|
(6)
|
Saturn
|
|
|
(7)
|
Uranus
|
|
|
(8)
|
Neptune
|
|
|
(9)
|
Pluto
|
|
Solution
We
have studied that, a number is written
in standard form as a ,
where a is terminating decimal and k is an integer.
|
Sl.No.
|
Name
of the Planet
|
Mass
(in kg)
|
|
(1)
|
Mercury
|
|
|
(2)
|
Venus
|
|
|
(3)
|
Earth
|
|
|
(4)
|
Mars
|
|
|
(5)
|
Jupiter
|
|
|
(6)
|
Saturn
|
|
|
(7)
|
Uranus
|
|
|
(8)
|
Neptune
|
|
|
(9)
|
Pluto
|
|
We
have studied that, to compare two numbers written
in scientific notation: the number with
the larger power of is
greater than the number with
the smaller power of .
If the powers of ten are the same, then the number with larger
factor
is the larger number.
Hence,
the size of the planets arranged in descending order will be Jupiter > Saturn > Neptune > Uranus > Earth > Venus > Mars > Mercury > Pluto
Question: 88
Write
the number of seconds in scientific notation.
|
Sl.
No.
|
Unit
|
Value
in Seconds
|
|
(1)
|
Minute
|
|
|
(2)
|
Hour
|
|
|
(3)
|
Day
|
|
|
(4)
|
1 Month
|
|
|
(5)
|
1 Year
|
|
|
(6)
|
10 Years
|
|
Solution
(1)
We know that, min
(2)
We know that, hour
(3)
We know that,
(4)
We know that,
(5)
We know that,
(6)
We know that,
Question: 89
In
our own planet Earth, square kilometer of area is covered with water
and square kilometer of area is covered by land.
Find the approximate ratio of area covered with water to area covered by land
by converting these numbers into scientific notation.
Solution
As per the
question, it is given that
Area covered by water
Area covered by land
In scientific
notation, these numbers are written as -
So,
Area covered by water
Similarly,
Also,
So,
Area covered by land
Let
and
Ratio of areas of water to land
Question: 90
If find the value of c.
Solution
Considering
the given expression,
[taking common in LHS]
[multiplying both
sides
by ]
Question: 91
A
light year is the distance that light can travel in one year.
1 light year km.
a.
Express one light year in scientific notation.
b.
The average distance between Earth and Sun is km. Is the distance
between Earth and the Sun greater than, less than or equal to one light year?

Solution
a.
As per question, it is given that 1 light year
for standard form
b.
As per question, it is given that - The average
distance between Earth &
sun
Distance between Earth & sun
Since,
So, the distance between Earth & sun is less than one light year.
Question: 92
Geometry
Application: The number of diagonals of an -sided figure is .
Use the formula to find the number of diagonals for a -sided figure (hexagon).

Solution
It
is given in the question that, a polygon
has sides, then number
of diagonals is
In
hexagon, there are 6 sides
Therefore,
put
in the above formula
Number
of diagonals
Hence,
a hexagon has 9 diagonals.
Question: 93
Life Science: Bacteria can divide in
every minutes. So bacterium can multiply to in minutes. in minutes, and so on. How many bacteria will
there be in hours? Write your answer using exponents, and
then evaluate.

Solution
We already
know that, min
Therefore,
min min.
As
per the question it is given that, a bacterium
doubles itself in every min. Number
of times it will double itself
Number of bacteria in
Question: 94
Blubber makes up per cent of a blue whale’s body weight. Deepak
found the average weight of blue whales and used it to calculate the average
weight of their blubber. He wrote the amount as kg. Evaluate this amount.
Solution
As per the question it is given that, weight
calculated by Deepak
Hence,
weight calculated by
Deepak was kg.
Question: 95
Life
Science Application: The major components of human blood are red blood cells,
white blood cells, platelets and plasma. A typical red blood cell has a
diameter of approximately metres. A typical platelet has a diameter of
approximately metre. Which has a greater diameter, a red blood cell or a
platelet?
Solution
As per the question it is
given that, diameter of red blood cell and diameter of platelet
We have studied that, two numbers written in
scientific notation can be compared.
The number with the larger
power of is greater than
the number with the smaller
power of .
If the powers of ten are the same, then
the number with the larger factor is the larger number.
Thus, >
Therefore, red blood cell has a greater diameter than a platelet
Question: 96
A
googol is the number followed by zeroes.
a.
How is a googol written as a power?
b.
How is a googol times a googol written as a power?
Solution
a.
1 googol
[as there are 100 zeroes after 1]
b.
Googol times googol means
multiply googol by googol
Required number = googol x
googol
Question: 97
What’s
the error?
A
student said that is the same as .
What mistake has the student made?
Solution
According
to the question, we have,
So,
is not same
as
Student
has multiplied the base by its exponent. This is an
error.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


