Unit 12: Algebraic Expression

In each of the questions 1 to 16, out of the four options, only one is correct. Write the correct answer.

An algebraic expression containing three terms is called a:

a.    Monomial

b.   Binomial

c.    Trinomial

d.   All of these

(c)

An algebraic expression containing three terms is called trinomial.

Number of terms in the expression $3x^{2}y-2y^{2}z-z^{2}x+5$ is

 

a.    $2$

b.   $3$

c.    $4$

d.   $5$

(c)

Total number of terms in the expression are $4$. They are  $3x^{2}y,-2y^{2}z,-z^{2}x$ and $5$.

The terms of expression $4x^2-3xy$ are:

a.    $4x^2\text{and}-3xy$

b.   $4x^2\text{ and }3xy$

c.    $4x^2\text{ and}-xy$

d.   $x^2\text{ and }xy$

(a)

Terms in the expression $4x^2-3xy$ are $4x^2\text{and}-3xy.$

Factors of $-5x^2{y}^{2}z$ are

a.    $-5\times x\times y\times z$

b.   $-5\times x^2\times y\times z$

c.    $-5\times x\times x\times y\times y\times z$

d.   $-5\times x\times y\times z^2$

(c)

$-5x^2{y}^{2}z$ Can be factorized as $-5\times x\times x\times y\times y\times z$.

Coefficient of $x$ in $-9x{y}^{2}z$ is

a.    $9yz$

b.   $-9yz$

c.    $9y^{2}z$

d.   $-9y^{2}z$

(d)

Coefficient of $x$ in $-9x{y}^{2}z$ is $-9y^{2}z$.

Which of the following is a pair of like terms?

a.    $-7x{y}^{2}z,-7x^{2}yz$

b.   $-10ay{z}^2$, $3ay{z}^2$

c.    $3xyz,3x^2{y}^2{z}^2$ 

d.   $4xy{z}^2,4x^{2}yz$

(b)

Like terms are those terms, having same algebraic factor.

Hence, $-10ay{z}^2$ and $3ay{z}^2$ are like terms.

Identify the binomial out of the following:

a.    $3x{y}^2+5y-x^{2}y$

b.   $x^{2}y-5y-x^{2}y$

c.    $xy+yz+zx$

d.   $3x{y}^2+5y-x{y}^2$

(d)

Taking option (d),

$\begin{array}{l}3x{y}^2+5y-x{y}^2\\ =2x^{2}y+5y\end{array}$ 

As it contains only two terms, hence it is binomial.

The sum of $x^4-xy+2y^2$ and $-x^4+xy+2y^2$ is

a.    Monomial and polynomial in $y$

b.   Binomial and Polynomial

c.    Trinomial and polynomial

d.   Monomial and polynomial in $x$

(a)

Required sum $=\left(x^4-xy+2y^2\right)+\left(-x^4+xy+2y^2\right)$

$=\left[(x^4+\left(-x^4\right)\right]+\left(-xy+xy\right)+\left(2y^2+2y^2\right)$

$=0+0+4y^2=4y^2$

$4y^2$ is a monomial and polynomial in $y$.

The subtraction of 5 times of $y$ from $x$ is

a.    $5x-y$

b.   $y-5x$

c.    $x-5y$

d.   $5y-x$

(c)

$5$ times of $y$ is $5y$. Now, subtraction of $5$ times of $y$ from $x$ is $x-5y$

$-b-0$ is equal to

a.    $-1\times b$ 

b.   $1-b-0$

c.    $0-\left(-1\right)\times b$

d.   $-55$

(a)

$-b-0$ is equal to $-1\times b$

The length of the top of square table is $x$. The expression for perimeter is:

a.    $4+x$

b.   $2x$

c.    $4x$

d.   $8x$

(c)

Given, length of a square table $=x$

$\therefore$ Perimeter of a square

$\begin{array}{l}=4\times \text{Side}\\ =4\times x\\ =4x.\end{array}$  

The number of scarfs of length half meter that can be made from $y$ meters of cloth is:

a.    $2y$

b.   $\frac{2y}{2}$

c.    $y+2$

d.   $y+\frac{1}{2}$

(a)

We have, length of 1 $\text{scarf}=1/2m$

So, number of scarfs which can be made from $y$ metres

$\begin{array}{l}=\frac{y}{1/2}\\ =2y.\end{array}$

$123x^{2}y-138x^{2}y$ is a like term of:

a. $10xy$

b.   $-15xy$

c. $-15x{y}^2$

d.   $10x^{2}y$

(d)

We have, $123x^{2}y-138x^{2}y=-15x^{2}y$

Hence, it is like term of $10x^{2}y$ as both contain $x^{2}y$.

The value of $3x^2-5x+3$ when $x=1$ is

a.    $1$

b.   $0$

c.    $-1$

d.   $11$

(a)

Put $x=1$ in given equation, we get

$\begin{array}{l}3x^2-5x+3\\ =3{(}^1-5\left(1\right)+3\\ =3-5+3\\ =1\end{array}$

The expression for the number of diagonals that we can make from one vertex of a $n$ sided polygon is:

a.    $2n+1$

b.   $n-2$

c.    $5n+2$

d.   $n-3$

(d)

Since, vertex is formed by joining two sides. Diagonal is line segment joining the two opposite vertex. So, number of diagonals formed by one vertex $=n-3$

The length of a side of square is given as $2x+3$. Which expression represents the perimeter of the square?

a.    $2x+16$

b.   $6x+9$

c.    $8x+3$

d.   $8x+12$

(d)

Side of the square $=\left(2x+3\right)$          [Given]

$\therefore$ Perimeter of square $\begin{array}{l}=4\times \left(\text{Side}\right)\\ =4\times \left(2x+3\right)\\ =8x+12\end{array}$

 

In questions 17 to 32, fill in the blanks to make the statements true.

Sum or difference of two like terms is ________.

Sum or difference of two like terms is a like terms.

In the formula, area of circle $=\pi r^2$, the numerical constant of the expression $\pi r^2$ is ________.

In $\pi r^2$, r is variable, so the numerical constant is $\pi$.

$3a^{2}b\text{ and }-7b{a}^2$ are ________ terms.

$3a^{2}b$ and $-7b{a}^2$ are like terms as both have same variable factor $a^{2}b$.

$-5a^{2}b\text{ and }-5b^{2}a$ are ________ terms.

$-5a^{2}b$ and $-5b^{2}a$ are unlike terms.

In the expression $2\pi r$, the algebraic variable is ________.

$r$ is algebraic variable in the expression $2\pi r$.

Number of terms in a monomial is ________.

Number of terms in a monomial is one.

Like terms in the expression $n\text{(}n+1\text{)}+6\text{(}n-1\text{)}$ are ___________and________.

We have, $n\left(n+1\right)+6\left(n-1\right)=n^2+n+6n-6$

Hence, like terms in the expression $n\left(n+1\right)+6\left(n-1\right)$ are $n$ and $6n$.

The expression $13+90$ is a ________.

$13+90=103$ is a constant term.

The speed of car is $55$ km/hrs. The distance covered in $y$ hours is________.

Given, speed of car $=55\text{km/hrs}$

We know that, Distance $=$ Speed $\times$ Time

$\therefore$ Distance covered in $y$ hours $=55xy$ km

 

$x+y+z$ is an expression which is neither monomial nor ________.

$x+y+z$ contains three terms, so it is trinomial.

Hence, $x+y+z$ is an expression which is neither monomial nor binomial.

If $\left(x^{2}y+y^2+3\right)$ is subtracted from $\left(3x^{2}y+2y^2+5\right)$, then coefficient of $y$ in the result is ________.

We have, $\left(3x^{2}y+2y^2+5\right)-\left(x^{2}y+y^2+3\right)$

$\begin{array}{l}=3x^{2}y+2y^2+5-x^{2}y-y^2-3\\ =2x^{2}y+y^2+2\end{array}$

$\therefore$  Coefficient of $y=2x^2$

$-a-b-c$ is same as $–a–$ ( ________ ).

$-a-b-c=-a-\left(b+c\right)$ 

So, $-a-b-c$ is same as $-a-\left(b+c\right)$.

The unlike terms in perimeters of following figures are ________ and ________.

Fig. (i)

Fig. (ii)

In above fig. (i), Perimeter = Sum of all sides

$=2x+y+2x+y=4x+2y$

In above fig. (ii), Perimeter = Sum of all sides

$\begin{array}{l}=x+y^2+x+y^2\\ =2x+2y^2\end{array}$

Unlike terms in perimeters are $2y$ and $2y^2$

On adding a monomial _____________ to $-2x+4y^2+z$, the resulting expression becomes a binomial.

We can add $2x$ to the expression to make it binomial.

$3x+23x^2+6y^2+2x+y^2+$ ____________ $=5x+7y^2.$

Assume

$\left(3x+23x^2+6y^2+2x+y^2\right)+\text{N}=5x+7y^2$

$\Rightarrow \text{N}=5x+7y^2-\left(3x+23x^2+6y^2+2x+y^2\right)$

$\Rightarrow \text{N}=5x+7y^2-3x-23x^2-6y^2-2x-y^2$

$\Rightarrow \text{N}=-23x^2$

If Rohit has $5xy$ toffees and Shantanu has $20xy$ toffees, then Shantanu has ___________ more toffees.

We have, Rohit’s toffees $=5xy$

Shantanu’s toffees $=20xy$

Difference:

$\begin{array}{l}=20xy-5xy\\ =15xy\end{array}$

Hence, Shantanu had $15xy$ more toffees.

--

In questions 33 to 52, state whether the statements given are True or False.

$1+\frac{x}{2}+x^3$ is a polynomial.

True

Expression with three or more than three terms is called a polynomial.

$\left(3a-b+3\right)-\left(a\text{+ }b\right)$ is a binomial.

False

We have, $\left(3a-b+3\right)-\left(a\text{+ }b\right)$

$=3a-b+3-a-b$

$=3a-a-b-b+3$

$=2a-2b+3$

The expression has three terms, it is a trinomial.

A trinomial can be a polynomial.

True

Trinomial is a polynomial.

A polynomial with more than two terms is a trinomial.

False

A trinomial have exact three terms.

Sum of $x$ and $y$ is $x+y$.

True

Sum of $x\text{and}y\text{is}x+y$

Sum of $2$ and $p$ is $2p$.

False

Sum of $2$ and $p$ is $2+p$

A binomial has more than two terms.

False

Binomial has exactly two terms.

A trinomial has exactly three terms.

True

A trinomial has exactly three unlike terms.

In like terms, variables and their powers are the same.

True

In like terms, variables and their powers are the same.

The expression $x+y+5x$ is a trinomial.

False

$\therefore x+y+5x=6x+y$ it is a binomial.

$4p$ is the numerical coefficient of $q^2\text{ in}-4p{q}^2$.

False

Numerical coefficient of $q^2$ in $-4p{q}^2=-4$.

$5a$ and $5b$ are unlike terms.

True

Both the terms have different algebraic factors.

Sum of $x^2+x$ and $y+y^2\text{ is }2x^2+2y^2$.

False

Sum $=\left(x^2+x\right)+\left(y+y^2\right)=x^2+x+y+y^2$

$=x^2+y^2+x+y$

Subtracting a term from a given expression is the same as adding its additive inverse to the given expression.

True

Additive inverse is the negation of a number or expression.

The total number of planets of Sun can be denoted by the variable $n$.

False

As, Sun has infinite planets around it.

In like terms, the numerical coefficients should also be the same.

False

e.g. $-3x^{2}y$ and $4x^{2}y$ are like terms as they have same algebraic factor $x^{2}y$ but have different numerical coefficients.

If we add a monomial and binomial, then answer can never be a monomial.

False

If we add a monomial and a binomial, then answer can be a monomial, e.g.

Add $x^2\&-x^2+y^2$

$=x^2+\left(-x^2+y^2\right)$

$\begin{array}{l}=x^2-x^2+y^2\\ =y^2\end{array}$

The answer is monomial.

If we subtract a monomial from a binomial, then answer is at least a binomial.

False

If we subtract a monomial from a binomial, then answer is at least a monomial.

When we subtract a monomial from a trinomial, then answer can be a polynomial.

True

When we subtract a monomial from a trinomial, then answer can be binomial or polynomial.

When we add a monomial and a trinomial, then answer can be a monomial.

False

When we add a monomial and a trinomial, then it can be binomial or trinomial.

Write the following statements in the form of algebraic expression and write whether it is monomial, binomial or trinomial.

a.    $x$ is multiplied by itself and then added to the product of $x$ and $y$.

b.   Three times of $5$ and two times of $q$ are multiplied and then subtracted from $r$.

c.    Product of $p$, twice of $q$ and thrice of $r$.

d.   Sum of the products of $a$ and $b$, $b$ and $c$ and $c$ and $a$.

e.    Perimeter of an equilateral triangle of
side $x$.

f.Perimeter of a rectangle with length $p$ and breadth $q$.

g.   Area of a triangle with base m and
height $n$.

h.   Area of a square with side $x$.

i.  Cube of $s$ subtracted from cube of $t$.

j.  Quotient of $x$ and 15 multiplied by $x$.

k.   The sum of square of $x$ and cube of $z$.

l.  Two times q subtracted from cube of $q$.

a.    $x^2+xy$

b.   $\begin{array}{l}r-\left(3p\times 2q\right)\\ =r-6pq\end{array}$

c.    $\begin{array}{l}p\times 2q\times 3r\\ =6pqr\end{array}$

d.   $ab+bc+ca$

e.    $3x$

f.$\begin{array}{l}2\left(p+q\right)\\ =2p+2q\end{array}$

g.   $\frac{1}{2}mn$

h.   $x^2$

i.   $t^3-s^3$

j.  $\begin{array}{l}\frac{x}{15}\times x\\ \text{or}\frac{x^3}{15}\end{array}$

k.   $x^2+z^3$

l.  $q^3-2q$

Write the coefficient of $x^2$ in the following:

(i)             $x^2-x+4$

(ii)         $x^3-2x^2+3x+1$

(iii)      $1+2x+3x^2+4x^3$

(iv)       $y+y^{2}x+y^3{x}^2+y^4{x}^3$     

(i)             $1$

(ii)         $-2$

(iii)      $3$

(iv)       $y^3$ 

Find the numerical coefficient of each of the terms:

(i)             $x^3{y}^{3}z,x{y}^2{z}^2,-3x{y}^2{z}^3,5x^3{y}^{3}z,-7x^2{y}^2{z}^2$

(ii)         $10xyz,-7x{y}^{2}z,-9xyz,2x{y}^{2}z,2x^2{y}^2{z}^2$

(i)             Coefficient of:

$x^3{y}^{2}z=1$

(ii)         Coefficient of:

$10xyz=10$

$-7x{y}^{2}z=-7$

$-9xyz=-9$

$2x{y}^{2}z=2$

$2x^2{y}^2{z}^2=2$

Simplify the following by combining the like terms and then write whether the expression is a monomial, a binomial or a trinomial.

a.    $3x^{2}y{z}^2-3x{y}^{2}z+x^{2}y{z}^2+7x{y}^{2}z$

b.   $x^4+3x^{3}y+3x^2{y}^2-3x^{3}y-3x{y}^3$

        $+y^4-3x^2{y}^2$

c.    $p^3{q}^{2}r+p{q}^2{r}^2+3p^{2}q{r}^2-9p^{2}q{r}^2$

d.   $2a+2b+2c-2a-2b-2c-2b$

        $+2c+2a$

e.    $50x^3-21x+107+41x^3-x+1$

       

a.    $3x^{2}y{z}^2-3x{y}^{2}z+x^{2}y{z}^2+7x{y}^{2}z$

By combining the like terms

         $\begin{array}{l}=3x^{2}y{z}^2+x^{2}y{z}^2-3x{y}^{2}z+7x{y}^{2}z\\ =4x^{2}y{z}^2+4x{y}^{2}z\end{array}$

The expression contains $3$ terms.
So, it is trinomial.

b.   $x^4+3x^{3}y+3x^2{y}^2-3x^{3}y-3x{y}^3$

          $+y^4-3x^2{y}^2$

         By combining the like terms

         $\begin{array}{l}=x^4+3x^{3}y-3x^{3}y+3x^2{y}^2\\ -3x^2{y}^2-3x^{3}y+y^3\\ =x^4-0+0-3x^{3}y+y^4\\ =x^4+y^4-3x^{3}y\end{array}$

The expression contains $3$ terms.
So, it is trinomial.

c.    $p^3{q}^{2}r+p{q}^2{r}^3+3p^{2}q{r}^2-9p^{2}q{r}^3$

By combining the like terms

$\begin{array}{l}=p^3{q}^{2}r+p{q}^2{r}^3+3p^{2}q{r}^2\\ -9p^{2}q{r}^2\end{array}$

$=p^3{q}^{2}r+p{q}^2{r}^3-6p^{2}q{r}^2$

The expression contains terms.
So, it is trinomial.

d.   $2a+2b+2c-2a-2b-2c$

$-2b+2c+2a$

By combining the like terms

$\begin{array}{l}=2a-2a+2a+2b-2b-2b\\ +2c-2c+2c\\ =2a-2b+2c\end{array}$

The expression contains $3$ terms.
So, it is trinomial.

e.    $50x^3-21x+107+41x^3-x+1-93$

$+71x-31x^3$

By combining the like terms

$\begin{array}{l}=50x^3+41x^3-31x^3-21x-x\\ +71x+107+1-93\\ =60x^3+49x+15\end{array}$

The expression contains $3$ terms.
So, it is trinomial.

Add the following expressions:

a.    $p^2-7pq-q^2\text{ and}-3p^2-2pq+7q^2$

b.   $x^3-x^{2}y-x{y}^2-y^3\mathrm{and}{x}^3-2x^{2}y+3x{y}^2+4y$

c.    $ab+bc+ca\mathrm{and}-bc-ca-ab$

d.   $p^2-q+r,q^2-r+p\mathrm{and}{r}^2-p+q$

e.    $x^3{y}^2+x^2{y}^3+3y^4\mathrm{and}{x}^4+3x^2{y}^3+4y^4$

f.$p^{2}qr+p{q}^{2}r+pq{r}^2\mathrm{and}-3p{q}^{2}r-2pq{r}^2$

g.   $uv-vw,vw-wu\mathrm{and}wu-uv$

h.   $a^2+3ab-bc,b^2+3bc-ca\text{ and}$ $c^2+3ca-ab$

i.  $\frac{5}{8}{p}^4+2p^2+\frac{5}{8};\frac{1}{8}-17p+\frac{9}{8}{p}^2\mathrm{and}$ $p^5-p^3+7a$

j.       $t-t^2-t^3-14;15t^3+13+9t-8t^2;$

a.    $p^2-7pq-q^2\text{and}$

$-3p^2-2pq+7q^2$

$=p^2-7pq-q^2-3p^2-2pq+7q^2$

By combining the like terms, we get

  $\begin{array}{l}=p^2-3p^2-7pq-2pq-q^2+7q^2\\ =-2p^2-9pq+6q^2\end{array}$

b.   $x^3-x^{2}y-x{y}^2-y^3\text{and}$

  $x^3-2x^{2}y+3x{y}^2+4y$

By combining the like terms, we get

  $=x^3+x^3-x^{2}y-2x^{2}y-x{y}^2+3x{y}^2-y^3+4y$

  $=2x^3-3x^{2}y+2x{y}^2-y^3+4y$

c.    $ab+bc+ca\text{and}-bc-ca-ab$

  $=ab+ac+bc-bc-ca-ab$

By combining the like terms,

  $\begin{array}{l}=ab-ab-bc+bc+ca-ca\\ =0+0+0=0\end{array}$

d.   $p^2-q+r,q^2-r+p\text{and}{r}^2-p+q$

  $=p^2-q+r+q^2-r+p+r^2-p+q$

By combining the like terms,

  $\begin{array}{l}=p^2+q^2+r^2-q+q+r-r+p-p\\ =p^2+q^2+r^2+0+0+0=p^2+q^2+r^2\end{array}$

e.    $x^3{y}^2+x^2{y}^3+3y^4\mathrm{and}{x}^4+3x^2{y}^3+4y^4$

  $=x^3{y}^2+x^2{y}^3+3y^4+x^4+3x^2{y}^3+4y^4$

By combining the like terms,

$\begin{array}{l}=x^3{y}^2+x^2{y}^3+3y^4+x^4+3x^2{y}^3+4y^4\\ =x^4+7y^4+x^3{y}^2+4x^2{y}^3\end{array}$

f.     $p^{2}qr+p{q}^{2}r+pq{r}^2\text{and}-3p{q}^{\text{2}}r-2pq{r}^2$

  $=p^{2}qr+p{q}^{2}r+pq{r}^2-3p{q}^{2}r-2pq{r}^2$

By combing the like terms,

  $\begin{array}{l}=p^{2}qr+p{q}^{2}r-3p{q}^{2}r+pq{r}^2-2pq{r}^2\\ =p^{2}qr-2p{q}^{2}r-pq{r}^2\end{array}$

g.   $\begin{array}{l}uv-vw,vw-wu\\ \text{and}wu-uv\end{array}$

  $=uv-vw+vw-wu+wu-uv$

By combining like terms,

= 0 

h.      $\begin{array}{l}{a}^2+3ab-bc,b^2+3bc-ca\\ \text{and}{c}^2+3ca-ab\end{array}$

$\left(a^2+3ab-bc\right)+\left(b^2+3bc-ca\right)+\left(c^2+3ca-ab\right)$

$a^2+b^2+c^2+2ab+2bc+2ca$

i.        $\begin{array}{l}\frac{5}{8}{p}^4+2p^2+\frac{5}{8};\frac{1}{8}-17p+\frac{9}{8}{p}^2\\ \text{and}{p}^5-p^3+7\end{array}$

  $=\frac{5}{8}{p}^4+2p^2+\frac{5}{8}+\frac{1}{8}-17p+\frac{9}{8}{p}^2+p^5-p^3+7$

By combining like terms,

  $=p^5+\frac{5}{8}{p}^4-p^3+\left(2+\frac{9}{8}\right)p^2-17p$

     $+\left(\frac{5}{8}+\frac{1}{8}+7\right)$

  $=p^5+\frac{5}{8}{p}^4-p^3+\left(\frac{16+9}{8}\right)p^2-17p$

      $+\left(\frac{5+1+56}{8}\right)$

  $=p^5+\frac{5}{8}{p}^4-p^3+\frac{25}{8}{p}^2-17p+\frac{62}{8}$

  $=p^5+\frac{5}{8}{p}^4-p^3+\frac{25}{8}{p}^2-17p+\frac{31}{4}$

j.        $t-t^2-t^3-14;15t^3+13+9t-8t^2;$

  $12t^2-19-24\mathrm{t}\text{and}4t-9t^2+19t^3$

  $=t-t^2-t^3-14+15t^3+13+9t-8t^2+12t^2$

  $-19-24t+4t-9t^2+19t^3$

By combining like terms,

  $=t+9t-24t+4t-t^2-8t^2+12t^2$

     $-9t^2-t^3+15t^3+19t^3-14+13-19$

  $\begin{array}{l}=-10t-6t^2+33t^3-20\\ =33t^3-6t^2-10t-20\end{array}$

Subtract

a.    $-7p^{2}qr\text{ from}-3p^{2}qr.$

b.   $-a^2-ab\text{ from }{b}^2+ab.$

c.    $-4x^{2}y-y^3\text{ from }{x}^3+3x{y}^2-x^{2}y.$

d.   $x^4+3x^3{y}^3+5y^4\text{ from }2x^4-x^3{y}^3+7y^4.$

e.    $ab-bc-ca\text{ from}-ab+bc+ca.$

f.$-2a^2-2b^2\text{ from }-a^2-b^2+2ab.$

g.   $x^3{y}^2+3x^2{y}^2-7x{y}^3\text{ from }{x}^4+y^4$

        $+3x^2{y}^2-x{y}^3.$

h.   $2(ab+bc+ca)\text{ from}-ab-bc-ca.$

i.   $4.5x^5-3.4x^2+5.7\text{ from }5x^4$

       

j.  $11-15y^2\text{ from }{y}^3-15y^2-y-11.$

a.    We have,

        $\begin{array}{l}-3p^{2}qr-\left(-7p^{2}qr\right)\\ =-3p^{2}qr+7p^{2}qr\\ =p^{2}qr\left(-3+7\right)\\ =4p^{2}qr\end{array}$

b.   We have,

$\begin{array}{l}{b}^2+ab-\left(-a^2-ab\right)\\ =b^2+ab+a^2+ab\end{array}$

By combining like terms,

$\begin{array}{l}=b^2+a^2+ab+ab\\ =a^2+b^2+2ab\end{array}$

c.    We have,

$x^3+3x{y}^2-x^{2}y-\left(-4x^{2}y-y^3\right)$

$=x^3+3x{y}^2-x^{2}y+4x^{2}y+y^3$

$=x^3+y^3+3x^{2}y+3x{y}^2$

d.   We have,

$\begin{array}{l}2x^4-x^3{y}^3+7y^4-\left(x^4+3x^3{y}^3+5y^4\right)\\ =2x^4-x^3{y}^3+7y^4-x^4-3x^3{y}^3-5y^4\end{array}$

By combining like terms,

$\begin{array}{l}=2x^4-x^4-x^3{y}^3-3x^3{y}^3+7y^4-5y^4\\ =x^4-4x^3{y}^3+2y^4\end{array}$

e.    We have,

$-ab+bc+ca-\left(ab-bc-ca\right)$

$=-ab+bc+ca-ab+bc+ca$

By combining like terms,

$\begin{array}{l}=-ab-ab+bc+bc+ca+ca\\ =-2ab+2bc+2ca\end{array}$

f.We have,

$\begin{array}{l}\left(-a^2-b^2+2ab\right)-\left(-2a^2-2b^2\right)\\ =-a^2-b^2+2ab+2a^2+2b^2\end{array}$

By combining like terms,

$\begin{array}{l}=-a^2+2a^2-b^2+2a^2+2ab\\ =a^2-b^2+2ab\end{array}$

g.   We have,

  $x^4+y^4+3x^2{y}^2-x{y}^3-\left(x^3{y}^2+3x^2{y}^2-7x{y}^3\right)$

  $=x^4+y^4+3x^2{y}^2-x{y}^3-x^3{y}^2-3x^2{y}^2+7x{y}^3$

By combining the like terms,

  $\begin{array}{l}=x^4+y^4+3x^2{y}^2-3x^2{y}^2-x{y}^3+7x{y}^3-x^3{y}^2\\ =x^4+y^4+6x{y}^3-x^3{y}^2\end{array}$

h.   We have,

  $\begin{array}{l}-ab-bc-ca-2\left(ab+bc+ca\right)\\ =-ab-bc-ca-2ab-2bc-2ca\end{array}$

By combining the like terms,

  $\begin{array}{l}=-ab-2ab-bc-2bc-ca-2ca\\ =-3ab-3bc-3ca\end{array}$

i.      We have,

  $\begin{array}{l}5x^4-32x^2-7.3x-\left(4.5x^5-3.4x^2+5.7\right)\\ =5x^4-3.2x^2-7.3x-4.5x^5+3.4x^2-5.7\end{array}$

By combining the like terms,

  $\begin{array}{l}=-4.5x^5+5x^4-3.2x^2+3.4x^2-7.3x-5.7\\ =-4.5x^5+5x^4+0.2x^2-7.3x-5.7\end{array}$

j.      We have,

  $\begin{array}{l}{y}^3-15y^2-y-11-\left(11-15y^2\right)\\ =y^3-15y^2-y-11-11+15y^2\end{array}$

By combining the like terms,

  $\begin{array}{l}=y^3-15y^2+15y^2-y-11-11\\ =y^3-y-22\end{array}$

a.    What should be added to

       

b.   What should be added to

       $3pq+5p^2{q}^2+p^3$ to get $p^3+2p^2{q}^2+4pq$

a.    Subtract: $x^3+3x^{2}y+3x{y}^2+y^3$ from $x^3+y^3$

        Required expression is

        $\begin{array}{l}{x}^3+y^3-\left(x^3+3x^{2}y+3x{y}^2+y^3\right)\\ =x^3+y^3-x^3-3x^{2}y-3x{y}^2-y^3\end{array}$

By combining like terms,

        $\begin{array}{l}=x^3-x^3+y^3-y^3-3x^{2}y-3x{y}^2\\ =-3x^{2}y-3x{y}^2\end{array}$

  So, if we add $-3x^{2}y-3x{y}^2$ in    

 $x^3+3x^{2}y+3x{y}^2+y^3$ we get $x^3+y^3$

b.   Subtract: $3pq+5p^2{q}^2+p^3$ from $p^3+2p^2{q}^2+4pq$

        Required expression is,

        $\begin{array}{l}{p}^3+2p^2{q}^2+4pq-\left(3pq+5p^2{q}^2+p^3\right)\\ =p^3+2p^2{q}^2+4pq-3pq-5p^2{q}^2-p^3\end{array}$

        By combining like terms,

        $\begin{array}{l}=p^3-p^3+2p^2{q}^2-5p^2{q}^2+4pq-3pq\\ =-3p^2{q}^2+pq\end{array}$

        So, if we add $-3p^2{q}^2+pq$ in $3p{q}^2+5p^2{q}^2+p^3$,

        we get $p^3+2p^2{q}^2+4pq$

a.    What should be subtracted from

        $2x^3-3x^{2}y+2x{y}^2+3y^3$ to get

       

b.   What should be subtracted from

        $-7mn+2m^2+3n^2$ to get

       

a.    Subtract: $x^3-2x^{2}y+3x{y}^2+4y^3$ from

        $2x^3-3x^{2}y+2x{y}^2+3y^3$

  Required expression is

  $\begin{array}{l}2x^3-3x^{2}y+2x{y}^2+3y^3\\ -\left(x^3-2x^{2}y+3x{y}^2+4y^3\right)\end{array}$   

  $\begin{array}{l}=2x^3-3x^{2}y+2x{y}^2+3y^3\\ -x^3+2x^{2}y-3x{y}^2-4y^3\end{array}$

By combining like terms,

  $\begin{array}{l}=2x^3-x^3-3x^{2}y+2x^{2}y+2x{y}^2\\ -3x{y}^2+3y^3-4y^3\end{array}$

  $=x^3-x^{2}y-x{y}^2-y^3$

  So, if we subtract $x^3-x^{2}y-x{y}^2-y^3$ from  

  $2x^3-3x^{2}y+2x{y}^2+3y^3$, then we get

  $x^3-2x^{2}y+3x{y}^2+4y^3$

b.   Subtract: $m^2+2mn+n^2$ from $-7mn+2m^2+3n^2$

  Required expression is,

  $-7mn+2m^2+3n^2-\left(m^2+2mn+n^2\right)$

  $=-7mn+2m^2+3n^2-m^2-2mn-n^2$

  By combining like terms,

  $=-7mn-2mn+2m^2-m^2+3n^2-n^2$

  $=-9mn+m^2+2n^2$

  So, if we subtract $m^2+2n^2-9mn$ from

  $-7mn+2m^2+3n^2$, then we get

  $m^2+2mn+n^2$

How much is $21a^3-17a^2$ less than $89a^3-64a^2+6a+16?$

Required expression is

$89a^3-64a^2+6a+16-\left(21a^3-17a^2\right)$

$=89a^3-64a^2+6a+16-21a^3+17a^2$

By combining the like terms,

$\begin{array}{l}=89a^3-21a^3-64a^2+17a^2+6a+16\\ =68a^3-47a^2+6a+16\end{array}$

So, $21a^3-17a^2\text{is}68a^3-47a^2+6a+16$ less than

$89a^3-64a^2+6a+16$.

How much is $y^4-12y^2+y+14$ greater than $17y^3+34y^2-51y+68?$

Required expression is

$y^4-12y^2+y+14-\left(17y^3+34y^2-51y+68\right)$

$=y^4-12y^2+y+14-17y^3-34y^2+51y-68$

By combining like terms,

$=y^4-12y^2-34y^2+y+51y+14-68-17y^3$

$=y^4-46y^2+52y-17y^3-54$

$=y^4-17y^3-46y^2+52y-54$

So, $y^4-12y^2+y+14$ is $y^4-17y^3-46y^2+52y-54$ greater than $17y^3+34y^2-51y+68$

How much does $93p^2-55p+4$ exceed $13p^3-5p^2+17p-90?$

Required expression is

$\begin{array}{l}93p^2-55p+4-\left(13p^3-5p^2+17p-90\right)\\ =93p^2-55p+4-13p^3+5p^2-17p+90\end{array}$

By combining the like terms,

$=93p^2+5p^2-55p-17p+4+90-13p^3$

$\begin{array}{l}=98p^2-72p+94-13p^3\\ =-13p^3+98p^2-72p+94\end{array}$

So, $93p^2-55p+4$ is $-13p^3+9p^2-72p+94$

more from $13p^3-5p^2+17p-90.$

To what expression must $99x^3-33x^2-13x-41$ be added to make the sum zero?

In order to find the solution, we will subtract $99x^3-33x^2-13x-41$ from 0.

Required expression is

$\begin{array}{l}0-\left(99x^3-33x^2-13x-41\right)\\ =0-99x^3+33x^2+13x+41\end{array}$

So, if we add $-99x^3+33x^2+13x+41$ to $99x^3-33x^2-13x-41$, then the sum is zero.

Subtract $9a^2-15a+3$ from unity.

In order to find the solution, we will subtract $9a^2-15a+3$ from unity, i.e. $1$.

Required expression is $1-\left(9a^2-15a+3\right)$

$\begin{array}{l}=1-9a^2+15a-3\\ =-9a^2+15a-2\end{array}$

Find the values of the following polynomials at $a=-2$ and $b=3$:

a.    $a^2+2ab+b^2$

b.   $a^2-2ab+b^2$

c.    $a^3+3a^{2}b+3a{b}^2+b^3$

d.   $a^3-3a^{2}b+3a{b}^2-b^3$

e.    $\frac{a^2+b^2}{3}$

f.$\frac{a^2-b^2}{3}$

g.   $\frac{a}{b}+\frac{b}{a}$

h.   $a^2+b^2-ab-b^2-a^2$

Given, $a=-2$ and $$$b=3$

Put $a=-2$ and $b=3$ in the given expressions, we get

a.    $a^2+2ab+b^2$

         $={\left(-2\right)}^2+2\left(-2\right)\left(3\right)+{\left(3\right)}^2$

        $\begin{array}{l}=4-12+9\\ =1\end{array}$

b.   $a^2-2ab+b^2$

        $={\left(-2\right)}^2-2\left(-2\right)\left(3\right)+{\left(3\right)}^2$

        $\begin{array}{l}=4+12+9\\ =25\end{array}$

c.    $a^3+3a^{2}b+3a{b}^2+b^3$

        $={\left(-2\right)}^3+3{\left(-2\right)}^2\left(3\right)+3\left(-2\right){\left(3\right)}^2+{\left(3\right)}^3$

        $\begin{array}{l}-8+36-54+27\\ =1\end{array}$

d.   $a^3-3a^{2}b+3a{b}^2-b^3$

        $={\left(-2\right)}^3-3{\left(-2\right)}^2\left(3\right)+3\left(-2\right){\left(3\right)}^2-{\left(3\right)}^3$

        $\begin{array}{l}=-8-36-54-27\\ =-125\end{array}$

e.    $\frac{a^2+b^2}{3}$

        $=\frac{{\left(-2\right)}^2+{\left(3\right)}^2}{3}$

        $\begin{array}{l}=\frac{4+9}{3}\\ =\frac{13}{3}\end{array}$

f.$\frac{a^2-b^2}{3}$

$=\frac{{\left(-2\right)}^2-\left(3\right)}{3}$

$\begin{array}{l}=\frac{4-9}{3}\\ =-\frac{5}{3}\end{array}$

g.   $\frac{a}{b}+\frac{b}{a}$

$=-\frac{2}{3}+\frac{3}{-2}$

$\begin{array}{l}=-\frac{2}{3}-\frac{3}{2}\\ =\frac{-4-9}{6}\end{array}$

$=-\frac{13}{6}$

h.   $a^2+b^2-ab-b^2-a^2$

$={\left(-2\right)}^2+{\left(3\right)}^2-\left(-2\right)\left(3\right)-{\left(-2\right)}^2-{\left(3\right)}^2$

$\begin{array}{l}=4+9+6-9-4\\ =6\end{array}$

Find the values of following polynomials at $m=1,n=-1$ and $p=2$:

a.    $m+n+p$

b.   $m^2+n^2+p^2$

c.    $m^3+n^3+p^3$

d.   $mn+np+pm$

e.    $m^3+n^3+p^3-3mnp$

f.$m^2{n}^2+n^2{p}^2+p^2{m}^2$

Given, $m=1,n=-1$ 

and $p=2$

Put $m=1,n=-1$ 

and $p=2$ in the expression, we get

a.    $\begin{array}{l}m+n+p\\ =1-1+2\\ =2\end{array}$

b.   $m^2+n^2+p^2$

$={\left(1\right)}^2+{\left(-1\right)}^2+\left(2\right)$

$=1+1+4$

c.    $m^3+n^3+p^3$

$={\left(1\right)}^3+{\left(-1\right)}^3+{\left(2\right)}^3$

$=1-1+8=8$

d.   $mn+np+pm$

$=\left(1\right)\left(-1\right)+\left(-1\right)\left(2\right)+\left(2\right)\left(1\right)$

$\begin{array}{l}=-1-2+2\\ =-1\end{array}$

e.    $m^3+n^3+p^3-3mnp$

$={\left(1\right)}^3+{\left(-1\right)}^3+{\left(2\right)}^3-3\left(1\right)\left(-1\right)\left(2\right)$

$\begin{array}{l}=1-1+8+6\\ =14\end{array}$

f.$m^2{n}^2+n^2{p}^2+p^2{n}^2$

$={\left(1\right)}^2{\left(-1\right)}^2+{\left(-1\right)}^2{\left(2\right)}^2+{\left(2\right)}^2{\left(1\right)}^2$

$\begin{array}{l}=1+4+4\\ =9\end{array}$

If $\begin{array}{l}\text{A}=3x^2-4x+1,\\ \text{B}=5x^2+3x-8\end{array}$ 

and $\text{C}=4x^2-7x+3,$ then find:

1.   (A + B) - C

2.   B + C - A

3.   A + B + C

Given, $\text{A}=3x^2–4x+1,$

$\begin{array}{l}\text{B}=5x^2+3x–8\\ \text{and C}=4x^2–7x+3\end{array}$

1.   $\text{(A}+\text{B)}-\text{C}$

$=(3x^2-4x+1+5x^2+3x-8)-(4x^2-7x+3)$

By combining the like terms,

$=\left(3x^2+5x^2–4x+3x+1–8\right)–\left(4x^2–7x+3\right)$

$=(8x^2-x-7)-(4x^2-7x+3)$

$=8x^2-x-7-4x^2+7x-3$

$=8x^2-4x^2-x+7x-7-3$

$=4x^2+6x-10$

2.   $\text{B}+\text{C}-\text{A}$

$=5x^2+3x-8+4x^2-7x+3-(3x^2-4x+1)$

By combining the like terms, 

$=(5x^2+4x^2+3x-7x-8+3)-\left(3x^2–4x+1\right)$

$=(9x^2-4x-5)-\left(3x^2–4x+1\right)$

$=9x^2-4x-5-3x^2+4x-1$

$\begin{array}{l}=9x^2–3x^2–4x+4x–5-1\\ =6x^2-6\end{array}$

3.   $\text{A}+\text{B}+\text{C}$

$=3x^2-4x+1+5x^2+3x-8+4x^2-7x+3$

By combining the like terms, 

$=3x^2+5x^2+4x^2-4x+3x-7x+1–8+3$

$=12x^2-8x-4$

If $\text{P }=-(x-2),\text{ Q }=-2(y+1)$ and

$\text{R }=-x+2y$, find $a$, when $\text{P}+\text{Q}+\text{R}=ax.$

Given, $\text{P}=-(x-2),$

$\begin{array}{l}\text{Q}=-2\left(y+1\right)\\ \text{and R}=-x+2y\end{array}$

Also given, $\text{P}+\text{Q}+\text{R}=ax$  

Put the values of P, Q and R on LHS, we get 

$-(x-2)+[-2\left(y+1\right)]+(-x+2y)=ax$

$-x+2+(-2y-2)-x+2y=ax$

$-x+2–2y–2–x+2y=ax$

By combining the like terms, 

$\begin{array}{l}-x–x–2y+2y+2–2=ax\\ -2x=ax\end{array}$

By comparing LHS and RHS, we get $a=-2$  

From the sum of $x^2-y^2-1,y^2-x^2-1$ and $1-x^2-y^2$ subtract $-(1+y^2)$.

Sum of $x^2-y^2-1,y^2-x^2-1$ and  $\begin{array}{l}1-x^2-y^2\\ =x^2-y^2-1+y^2-x^2-1+1-x^2-y^2\end{array}$

By combining like terms,

$\begin{array}{l}=x^2–x^2–x^2–y^2+y^2–y^2–1–1+1\\ =-x^2–y^2–1\end{array}$

Now, subtract $–\left(1+y^2\right)$ from $–x^2–y^2-1$

$=-x^2–y^2-1–\left[-\left(1+y^2\right)\right]$

$\begin{array}{l}=–x^2–y^2–1+1+y^2\\ =-x^2–y^2+y^2–1+1\\ =-x^2\end{array}$

Subtract the sum of $12ab-10b^2-18a^2$ and $9ab+12b^2+14a^2$ from the sum of $ab+2b^2$ and $3b^2-a^2$.

Sum of $12ab-10b^2-18a^2\text{ and }$

$9ab+12b^2+14a^2$

$=12ab–10b^2–18a^2+9ab+12b^2+14a^2$

By combining the like terms,

$\begin{array}{l}=12ab+9ab–10b^2+12b^2–18a^2+14a^2\\ =21ab+2b^2–4a^2\end{array}$

Sum of $ab+2b^2\text{ and }3b^2–a^2$

$\begin{array}{l}=ab+2b^2+3b^2–a^2\\ =ab+5b^2–a^2\end{array}$ 

Now, subtracting $21ab+2b^2–4a^2$ 
$\text{from }ab+5b^2–a^2,$ we get,

$=(ab+5b^2–a^2)–(21ab+2b^2–4a^2)$

$=ab+5b^2–a^2–21ab–2b^2+4a^2$

By combining the like terms,

$=ab–21ab+5b^2–2b^2–a^2+4a^2$

$\begin{array}{l}=–20ab+3b^2+3a^2\\ =3a^2+3b^2–20ab\end{array}$

Each symbol given below represents an algebraic expression:

  $=2x^2+3y,$  

  $=5x^2+3x,$  

  $=8y^2-3x^2+2x+3y$

 

The symbols are then represented in the expression:

        $+$                   $-$            

 

Find the expression which is represented by the above symbols.

Given,

  $=2x^2+3y,$  

  $=5x^2+3x,$  

  $=8y^2-3x^2+2x+3y$

$\therefore$          $+$               $-$           

 

$=(2x^2+3y)+(5x^2+3x)-(8y^2-3x^2+2x+3y)$

$=2x^2+3y+5x^2+3x-8y^2+3x^2-2x-3y$

By combining the like terms,

$=2x^2+5x^2+3x^2+3y-3y+3x-2x-8y^2$

$=10x^2-8y^2+x$

Observe the following nutritional chart carefully:

Food Item (Per Unit $=100$ g)	Carbohydrates
Rajma	$60$ g
Cabbage	$5$ g
Potato	$22$ g
Carrot	$11$ g
Tomato	$4$ g
Apples	$14$ g

 

Write an algebraic expression for the amount of carbohydrates in ‘g’ for

a. $y$ units of potatoes and 2 units of rajma

b. $2x$ units tomatoes and y units apples.

(a)

By unitary method,

$\therefore$ $1$ unit of potatoes contain carbohydrates

$=22\text{g}$

$y\text{ units}$ of potatoes contain carbohydrates

$\begin{array}{l}=22\times y\\ =22y\text{ g}\end{array}$ 

Similarly,

$\therefore$ $1$ unit of rajma contain carbohydrates

$=60\text{ g}$

$\therefore$ $2$ units of rajma contain carbohydrates

$\begin{array}{l}=60\times 2\\ =120\text{ g}\end{array}$

Hence, required expression is $22y+120.$

(b)

By unitary method,

$\therefore$ $1$ unit of tomatoes contain carbohydrates

$=4\text{ g}$

$\therefore$ $2x$ units of tomatoes contain carbohydrates

$\begin{array}{l}=2xx4\\ =8x\text{ g}\end{array}$ 

Similarly,

$\therefore$ $1$ unit apples contain carbohydrates

$=14\text{ g}$

$y$ units apples contain carbohydrates

$\begin{array}{l}=14\times y\\ =14y\text{ g}\end{array}$ 

Hence, the required expression is $8x+14y.$

Arjun bought a rectangular plot with length $x$ and breadth $y$ and then sold a triangular part of it whose base is $y$ and height is $z$. Find the area of the remaining part of the plot.

Given,

Arjun bought a rectangular plot with length $x$ and breadth $y$

$\therefore$ area of rectangular plot

$\begin{array}{l}=l\times b\\ =x\times y\\ =xy\end{array}$

Also, given triangular part of it whose base is $y$ and height is $z$ so, area of triangular part

$\begin{array}{l}=\frac{\text{1}}{2}\times y\times z\\ =\frac{\text{1}}{2}\times yz\end{array}$

Area of remaining part of the plot

$=$ Area of rectangular plot $–$ Area of triangular plot

$\begin{array}{l}=xy-\frac{\text{1}}{2}yz\\ =y\left(x-\frac{\text{1}}{2}z\right)\end{array}$

Amisha has a square plot of side m and another triangular plot with base and height each equal to m. What is the total area of both plots?

Given,
side of square plot $=m$ and
height & base of triangular plot $=m$

Area of square plot, ${(\text{side})}^2=m^2$

Area of triangular plot,

$\begin{array}{l}\left(\frac{1}{2}\times h\times b\right)\\ =\frac{1}{2}\times m\times m\\ =\frac{m^2}{2}\end{array}$

Total area of both plots

$=$ Area of square plot $+$ Area of triangular plot

$\begin{array}{l}=m^2+\frac{m^2}{2}\\ =\frac{2m^2+m^2}{2}\\ =\frac{3m^2}{2}\end{array}$   

[taking LCM of $1\&2$ is $2$ ]

A taxi service charges $Rs$ 8 per km and levies a fixed charge of $Rs$ 50.Write an algebraic expression for the above situation, if the taxi is hired for $x$ km.

As per the given information, taxi service charged $\text{Rs }8$ per km and fixed charged of 50. If taxi is hired for $x$ km. Then, algebraic expression for the situation $=8\times x+50=8x+50$

Hence, the required expression is $8x+50.$ 

Shiv works in a mall and gets paid $\text{Rs}$ 50 per hour. Last week he worked for 7 hours and this week he will work for $x$ hours. Write an algebraic expression for the money paid to him for both the weeks.

Given, money paid to shiv $=\text{Rs}50\text{per h}\text{.}$

$\therefore$ Money paid last week $\begin{array}{l}=\text{Rs}50\times 7\\ =\text{Rs}350\end{array}$

So, money paid this week $\begin{array}{l}=\text{Rs}50\times x\\ =\text{Rs}50x\end{array}$

Total money paid to shiv $\begin{array}{l}=\text{Rs}(350+50x)\\ =\text{Rs}50(x+7)\end{array}$

Sonu and Raj have to collect different kinds of leaves for science project. They go to a park where Sonu collects $12$ leaves and Raj collects $x$ leaves.

After some time Sonu loses $3$ leaves and Raj collects $2x$ leaves. Write an algebraic expression to find the total number of leaves collected by both of them.

According to the question,

Sonu collected leaves $\begin{array}{l}=12-3\\ =9\end{array}$

Raj collected leaves $\begin{array}{l}=x+2x\\ =3x\end{array}$

$\therefore$ Total leaves collected $=9+3x$

Hence, the required expression is $9+3x.$

A school has a rectangular play ground with length $x$ and breadth $y$ and a square lawn with side $x$ as shown in the figure given below.

What is the total perimeter of both of them combined together?

Given, Length of rectangular playground, $\text{AB}=x$

& breadth of rectangular playground, $\text{BC}=y$

FCDE is a square, i.e., $\text{FC}=\text{CD}=\text{EF}=\text{DE}=x$

ABCF is a rectangle, i.e., $\text{AB}=\text{FC}=x\text{and}\text{BC}=\text{AF}=y$

Now, perimeter of combined (playground $+$ lawn)
$=$ Sum of all sides

$=\text{AB}+\text{BC}+\text{CD}+\text{DE}+\text{EF}+\text{FA}$

$=x+y+x+x+x+y=4x+2y$

The rate of planting the grass is $\text{Rs}$$x$ per square meter. Find the cost of planting the grass on a triangular lawn whose base is $y$ meters and height is $z$ meters.

Given,
base of triangular lawn is $y$ meters and height $z$ meters.

Area of triangular lawn
$\begin{array}{l}=\frac{1}{2}\times y\times z\\ =\frac{1}{2}yz{\text{m}}^2\end{array}$

Cost of planting the grass on lawn
$\begin{array}{l}=\frac{1}{2}yz\times x\\ =\text{Rs}\frac{1}{2}xyz\end{array}$

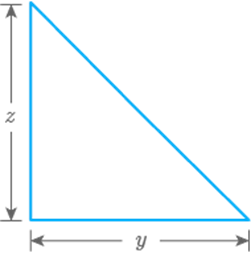
Find the perimeter of the figure given below:

 

We know that, perimeter is the sum of all sides. Perimeter of the given figure
$=\text{AB}+\text{BC}+\text{CD}+\text{DA}$

$=2(x+y)+(5x-y)+2(x+y)+(5x-y)$

$=2x+2y+5x-y+2x+2y+5x-y$

On combining the like terms,

$\begin{array}{l}=5x+2x+5x+2x-y+2y-y+2y\\ =14x+2y\end{array}$

In a rectangular plot, $5$ square flower beds of side $\left(x+2\right)$ meters each have been laid (see figure given below). Find the total cost of fencing the flower beds at the cost of $\text{Rs}50$ per $100$ meters.

Given,
side of one square flower bed
$=(x+2)\text{ m}$

Perimeter of one square flower bed $=4(\text{side})=4(x+2)\text{ m}$

Now, total perimeter of such square flower beds
$=5x$ perimeter of $1$ square

$=5\times 4(x+2)$

$=20(x+2)\text{ m}$

Cost of fencing of $100\text{ m}=\text{Rs}50$

Cost of $1\text{ m}=\text{Rs}\frac{50}{100}$

Cost of $20(x+2)\text{ m}$

$\begin{array}{l}=\frac{50}{100}\times 20(x+2)\\ =10(x+2)\end{array}$

$=Rs(10x+20)$

A wire is $(7x-3)$ meters long. A length of $(3x-4)$ meters is cut for use. Now, answer the following questions:

a.    How much wire is left?

b.   If this left out wire is used for making an equilateral triangle. What is the length of each side of the triangle so formed?

Given,
length of wire $=(7x-3)\text{ m}$ and wire cut for use has length $=(3x-4)\text{ m}$

a. Left wire $=(7x-3)-(3x-4)$

$\begin{array}{l}=7x-3-3x+4\\ =7x-3x-3+4\end{array}$

$=(4x+1)\text{ m}$

b. $\therefore$ Left wire $=(4x+1)\text{ m}$

$\therefore$ Perimeter of equilateral triangle $=$ Length of wire left

$\Rightarrow 3\times (\text{side})=4x+1$

$\Rightarrow \text{side}=\frac{4x+1}{3}=\frac{1}{3}(4x+1)\text{ m}$

Rohan's mother gave him $\text{Rs}3x{y}^2$ and his father gave him $\text{Rs}$$5\left(x{y}^2+2\right)$. Out of this total money he spent $\text{Rs}$$\left(10-3x{y}^2\right)$ on his birthday party. How much money is left with him?

Given,

Amount given to Rohan by his mother $=\text{Rs}3x{y}^2$ 

Amount given to Rohan by his father $=\text{Rs}5(x{y}^2+2)$

$\therefore$ Total amount Rohan has
$=\left[(3x{y}^2)+(5x{y}^2+10)\right]$

$\begin{array}{l}=\text{Rs}\left[3x{y}^2+5x{y}^2+10\right]\\ =\text{Rs}(8x{y}^2+10)\end{array}$

Total amount spent by Rohan
$=\text{Rs}(10-3x{y}^2)$

$\therefore$ After spending, Rohan have left money.

$\begin{array}{l}=\text{Rs}(8x{y}^2+10)-\text{Rs}(10-3x{y}^2)\\ =\text{Rs}11x{y}^2\end{array}$

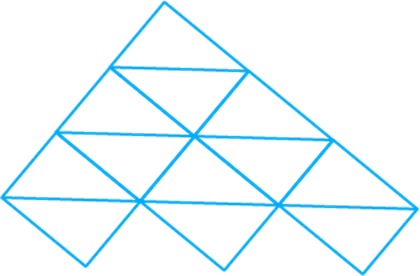
(i)       A triangle is made up of $2$ red sticks and $1$ blue stick. The length of a red stick is given by $r$ and that of a blue stick is given by $b$. Using this information, write an expression for the total length of sticks in the pattern given below:

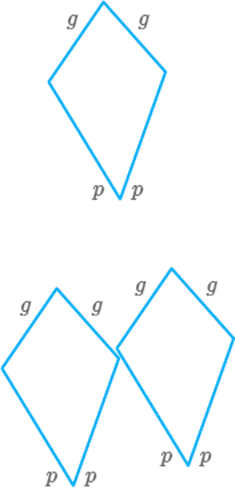
(ii)   In the given figure, the length of a green

side is given by g and that of the red side is given by $p$.

Write an expression for the following pattern. Also write an expression if $100$ such shapes are joined together.

(i)             Given length of a red stick $=2r$ and length of a blue stick $=b$, from the above given figure,

Total number of red sticks $=18$ and the total number of blue sticks $=6$

So, the total length of sticks
$=18r+6b=6(3r+b)$

Hence, the required expression is $6(3r+b)$

(ii)   Given length of green side $=g$ and of red side $=p$ when we take three figures,

      Total length of three figures $=3(2g+2p)=6g+6p$

      If 100 such shapes are joined together, then the expression becomes

      $=100(2g+2p)$

      $=200g+200p$

      $=200(g+p)$

      Hence, the required expression is $200(g+p)$

The sum of first n natural numbers is given by $\frac{1}{2}{n}^2+\frac{1}{2}n$. Find

(i)             The sum of first $5$ natural numbers.

(ii)         The sum of first $11$ natural numbers.

(iii)      The sum of natural numbers from $11$ to $30$.

Given, sum of first $n$ natural numbers $=\frac{1}{2}{n}^2+\frac{1}{2}n$

(i)             Sum of first $5$ natural numbers
$=\frac{1}{2}{(5)}^2+\frac{1}{2}(5)$                                         $[\text{put }n=5]$ 
$\begin{array}{l}=\frac{25}{2}+\frac{5}{2}\\ =\frac{30}{2}\\ =15\end{array}$

(ii)         Sum of $1\text{st }11$ natural numbers $=\frac{1}{2}{(11)}^2+\frac{1}{2}(11)$

$=\frac{1}{2}\times 121+\frac{11}{2}$                                  $[\text{put}n=11]$

$\begin{array}{l}=\frac{121}{2}+\frac{11}{2}\\ =\frac{132}{2}\\ =66\end{array}$

(iii)      Sum of natural numbers from $11$ to $30=$ Sum of $1\text{st}$ $30$ natural numbers $-$ Sum of $1^{\text{st}}$ $10$ natural numbers

$=\left[\frac{1}{2}{(30)}^2+\frac{1}{2}(30)\right]-\left[\frac{1}{2}{(10)}^2+\frac{1}{2}(10)\right]$

$=\frac{900}{2}+\frac{30}{2}-\frac{100}{2}-\frac{10}{2}$    [divide each term by $2$ ]

$\begin{array}{l}=450+15-50-5\\ =410\end{array}$

The sum of squares of first n natural numbers is given by $\frac{1}{6}n\left(n+1\right)\left(2n+1\right)\text{ or }\frac{1}{6}\left(2n^3+3n^2+n\right)$. Find the sum of squares of the first $10$ natural numbers.

Given, the sum of squares of first $n$ natural numbers

$\frac{1}{6}n\left(n+1\right)\left(2n+1\right)$

$\therefore$ The sum of square of first $10$ natural numbers $[\therefore \text{put}$$n=10]$

$=\frac{1}{6}(10)(10+1)(2\times 10+1)$

$\begin{array}{l}=\frac{1}{6}\times 10\times 11\times 21\\ =385\end{array}$

The sum of the multiplication table of natural number ‘ $n$ ’ is given by $55\times n$. Find the sum of

a.    Table of $7$

b.   Table of $10$

c.    Table of $19$

Given, the sum of multiplication table of $n$ natural numbers $=55\times n$

a.    Sum of table of $7=55\times 7=385$            $[\text{put}n=7]$

b.   Sum of table of $10=55\times 10=550$ $[\text{put}n=10]$

c.    Sum of table of $19=55\times 19=1045$       $[\text{put}n=19]$

If  $=2x+3$,        $=\frac{3}{2}x+7\text{ and }$    $=x-3,$ 
then find the value of:

(i)              2   $+$$-$

(ii)          $\frac{1}{2}$  $+$$-3$

Given,  $=2x+3$,        $=\frac{3}{2}x+7\text{ and }$    $=x-3,$

(i)             2   $+$$-$

$=2\times (2\times 6+3)+\left(\frac{3}{2}\times 3+7\right)-(1-3)$

$=2\times (12+3)+\left(\frac{9}{2}+7\right)-(-2)$

$\begin{array}{l}=2\times 15+\left(\frac{23}{2}\right)+2\\ =30+2+\frac{23}{2}\end{array}$

$\begin{array}{l}=32+\frac{23}{2}\\ =\frac{32\times 2+23}{2}\end{array}$

$\begin{array}{l}=\frac{64+23}{2}\\ =\frac{87}{2}\end{array}$

(ii)         $\frac{1}{2}$  $+$$-3$

$=\frac{1}{2}\left(\frac{3}{2}\times 2+7\right)+(8-3)-3(2\times 0+3)$

$=\frac{1}{2}(10)+5-3(3)$

$\begin{array}{l}=5+5-9\\ =1\end{array}$

If  $=\frac{3}{4}x-2\text{ and}$  $=x+6,$ then find the value of:

(i)              $-$

(ii)          $2$ $-\frac{3}{2}$

Given,

 $=\frac{3}{4}x-2\text{ and}$ 

 $=x+6,$ 

(i)             $-$

$=\frac{3}{4}\times 10-2-(4+6)$

$=\frac{30}{4}-\frac{12}{1}$

$\begin{array}{l}=\frac{30-48}{4}\\ =-\frac{18}{4}\\ =-\frac{9}{2}\end{array}$

(ii)         $2$ $-\frac{3}{2}$

$=2\times (12+6)-\frac{3}{2}\left(\frac{3}{4}\times 1-2\right)$

$=36-\frac{3}{2}\left(\frac{3-2\times 4}{4}\right)$

$=36-\frac{3}{2}\left(\frac{3-8}{4}\right)$

$=36-\frac{3}{2}\left(-\frac{5}{4}\right)$

$=36+\frac{15}{8}$

$=\frac{36\times 8+15}{8}$

$=\frac{288+15}{8}$

$=\frac{303}{8}$

Translate each of the following algebraic expressions Question 91 to 94 into words.

$4b-3$

Three subtracted from four times $b$.

$8\left(m+5\right)$

Eight times the sum of $m\text{ and }5.$ 

$\frac{7}{8-x}$

Quotient on dividing seven by the difference of eight and $x(x<8).$

$17\left(\frac{16}{w}\right)$

Seventeen times quotient of sixteen divided by $w$.

(i)             Critical Thinking Write two different algebraic expressions for the word phrase “ $\left(\frac{1}{4}\right)$ of the sum of $x$ and $7$.”

(ii)         What’s the Error? A student wrote an algebraic expression for “5 less than a number n divided by $3$ ” as $\frac{n}{3}-5$. What error did the student make?

(iii)      Write About it Shashi used addition to solve a word problem about the weekly cost of commuting by toll tax for $\text{Rs}15$ each day. Ravi solved the same problem by multiplying. They both got the correct answer. How is this possible?

(i)             First expression $=\frac{1}{4}(x+7)$

As we know, the addition is commutative.

So, it can also be written as $=\frac{1}{4}(7+x)$

(ii)         Since, the expression of $5$ less than a number $n=n-5$

so, $5$ less than a number $n$ divided by $3$ will be written $=\frac{n-5}{3}.$

So, students make an error of quotient.

(iii)      By addition method, total weekly cost

$\begin{array}{l}=(15+15+15+15+15+15+15)\\ =\text{ Rs}105\end{array}$

By multiplying method, total weekly cost
$=$ cost of one day $x$ Number of days in a week

$\begin{array}{l}=15\times 7\\ =\text{ Rs}105\end{array}$

Challenge Write an expression for the sum of $1$ and twice a number $n.$ If you let $n$ be any odd number, will the result always be an odd number?

Let the number be $n$. So, according to the statement, the expression can be written as $=2n+1.$ Yes, the result is always an odd number, because when a number becomes multiplied by $2,$ it becomes even and addition of $1$ in the even number makes it an odd number.

Critical Thinking Will the value of $11x$ for $x=-5$ be greater than $11$ or less than $11$? Explain

Expression given is $11x(-5)=-55$              [put $x=-5$ ]

clearly, $-55$

It is less than 11 because 11 is a positive number and -55 is a negative number

Match Column I with Column II in the following:

Column I	Column II
1. The difference of $3$ and a number squared	(a) $4-2x$
2. $5$ less than twice a number squared	(b) $n^2-3$
3. Five minus twice the square of a number	(c) $2n^2-5$
4. Four minus a number multiplied by $2$	(d) $5-2n^2$
5. Seven times the sum of a number and $1$	(e) $3-n^2$
6. A number squared plus $6$	(f) $2\left(n+6\right)$
7. $2$ times the sum of a number and $6$	(g) $7\left(n+1\right)$
8. Three less than the square of a number	(h) $n^2+6$

1  (e)

Let the no. be $n$, so, according to the statements, we can write the equation $=3-n^2$

2  (c)
Let the no. be $n$, so, according to the statements, we can write the equation $=2n^2-5$

3  (d)
Let the no. be $n$, so, according to the statements, we can write the equation $=5-2n^2$

4  (a)
Let the no. be x, so, according to the statements, we can write the equation $=4-2x$

5  (g)
Let the no. be $n$, so, according to the statements, we can write the equation $=7(n+1)$

6  (h)
Let the no. be $n$, so, according to the statements, we can write the equation $=n^2+6$

7  (f)
Let the no. be $n$, so, according to the statements, we can write the equation $=2(n+6)$

8  (b)
Let the no. be $n$, so, according to the statements, we can write the equation $=n^2-3$

At age of $2$ years, a cat or a dog is considered $24$ “human” years old. Each year, after age $2$ is equivalent to $4$ “human” years. Fill in the expression $\left[24+\boxed{}\left(a-2\right)\right]$ so that it represents the age of a cat or dog in human years. Also, you need to determine for what ‘ $a$ ’ stands for. Copy the chart and use your expression to complete it.

Age	$\left[24+\boxed{}\left(a-2\right)\right]$	Age (Human Years)
$2$
$3$
$4$
$5$
$6$

The expression is $[24+4(a-2)]$

Here $a$ represent the present age of dog or cat.

Age	$[24+4(a-2)]$	Age (human years)
$2$	$[24+4(2-2)]$	24
$3$	$[24+4(3-2)]$	28
$4$	$[24+4(4-2)]$	32
$5$	$[24+4(5-2)]$	36
$6$	$[24+4(6-2)]$	40

Express the following properties with variables $x$, $y$ and $z$.

(i)             Commutative property of addition

(ii)         Commutative property of multiplication

(iii)      Associative property of addition

(iv)       Associative property of multiplication

(v)          Distributive property of multiplication over additions

(i)             We know that, Commutative property of addition, $a+b=b+c$ 
$\therefore$ Required expression is $x+y=y+x$

(ii)         We know that, Commutative property of multiplication, $a\times b=b\times a$ 
$\therefore$ Required expression is $x\times y=y\times x$

(iii)      Associative property of addition    $a+(b+c)=(a+b)+c$

(iv)       We know that, Associative property of multiplication, $a\times (b\times c)=(a\times b)\times c$ 

$\therefore$ Required expression is $x\times (y\times z)=(x\times y)\times z$

(v)          We know that, Distributive property of multiplication over addition, $a\times (b+c)$ $=a\times b+a\times c$
$\therefore$ Required expression is $x\times (y+z)$ $=x\times y+x\times z$