Unit 11: Perimeter and Area
Exercise C:
(Multiple Choice Questions and Answers 1-37)
In the Questions to there are four options, out of which one is
correct. Choose the correct one.
Question: 1
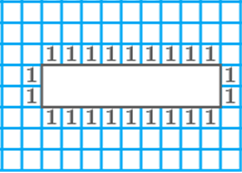
Observe the shapes and in the figures. Which of the following
statements is not correct?
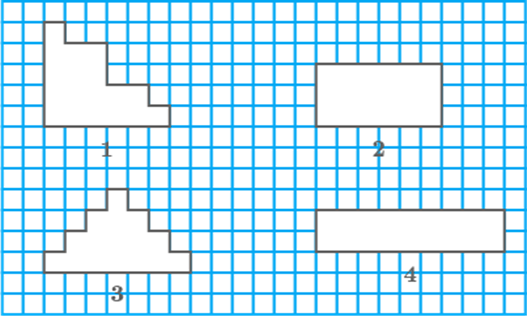
a. Shapes and have different areas and different perimeters.
b. Shapes and have the same area as well as the same
perimeter.
c. Shapes and have the same area.
d. Shapes and have the same perimeter.
Solution
(a)
Shape
:
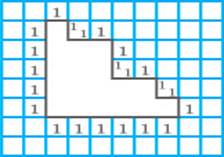
Area
sq.
units
Shape
:
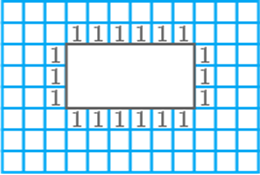
Area sq.
units
Shape :
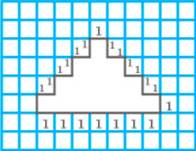
Area sq.
units
Shape :
Area sq.
units
So option (a) is incorrect.
Question: 2
A rectangular piece of dimensions was cut from a rectangular sheet of
paper of dimensions (Fig. 9.14).
Area
of remaining sheet of paper is
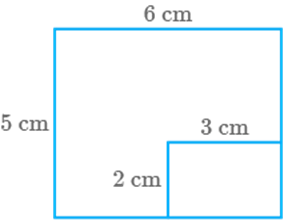
Fig. 9.14
a.
b.
c.
d.
Solution
(c)
Given, length and breadth of the bigger rectangle as and cm.
Area of bigger rectangle
Also given, length and breadth of the smaller rectangle as and .
Area of smaller rectangle
Area of remaining sheet Area of
bigger rectangle Area of
smaller rectangle
Question: 3
unit squares are joined to form a rectangle
with the least perimeter. Perimeter of the rectangle is
a. units
b. units
c. units
d. units
Solution
(b)
Area of rectangle formed square
units
We can write,
The possible pairs of sides can be:
1)
Length = 1, Breadth = 36
2)
Length = 2, Breadth = 18
3)
Length = 4, Breadth = 9
4)
Length = 12, Breadth = 3
5)
Length = 6, Breadth = 6
Now, for each pair of sides we will find the perimeter:
1)
Perimeter
2)
Perimeter
3)
Perimeter
4)
Perimeter
5)
Perimeter
So, the rectangle with sides 6 units and 6 units will have the
least perimeter which is 24 units.
Question: 4
A wire is bent to form a
square of side cm. If the wire is rebent to form a circle,
its radius is
a. cm
b. cm
c. cm
d. cm
Solution
(b)
Given, side of square
The wire has same length.
Perimeter of square circumference
of circle
Hence, the radius is
Exercise:
5
Area of the circle obtained
in Question 4 is
a.
b.
c.
d.
Solution
(c)
Area
of the circle
So,
the correct option is (c)
Question: 6
Area of a rectangle and the
area of a circle are equal. If the dimensions of the rectangle are 14 cm × 11 cm, then radius
of the circle is
a. cm
b. cm
c. cm
d. cm.
Solution
(d)
Given,
dimensions of rectangle
According
to the question,
Area
of rectangle Area of circle
Hence,
the radius of circle is .
Question: 7
Area of shaded portion in Fig. 9.15 is
a.
b.
c.
d.

Fig.
9.15
Solution
(d)
From
the given figure,
Length
of rectangle
Breadth
of rectangle
Area
of shaded portion
Question: 8
Area of parallelogram ABCD (Fig. 9.16) is not equal to
a. DE DC
b. BE AD
c. BF DC
d. BE BC
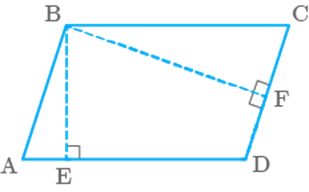
Fig. 9.16
Solution
(a)
We
know that, Area of parallelogram
Base Corresponding Height
So, Area
of parallelogram
Or, Area of parallelogram
Question: 9
Area of triangle MNO of Fig. 9.17 is
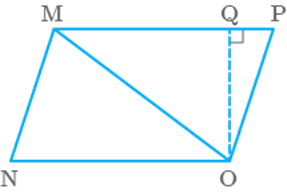
Fig. 9.17
a.
b.
c.
d.
Solution
(d)
We
know that,
Area
of triangle
Question:10
Ratio of area of to the area of parallelogram MNOP in the same figure
9.17 is
a.
b.
c.
d.
Solution
(c)
Area
of Area of parallelogram MNOP
Hence,
the required ratio is
Question: 11
Ratio
of areas of ,
and in Fig. 9.18 is
a.
b.
c.
d.
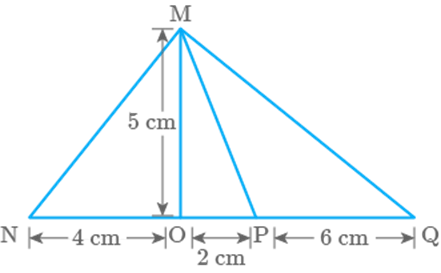
Fig. 9.18
Solution
(a)
From
the given figure,
Area
of
Hence,
required ratio is
Question: 12
In
Fig. 9.19, EFGH is a parallelogram, altitudes FK and FI are 8 cm and 4cm
respectively. If cm, then area of EFGH is
a.
b.
c.
d.
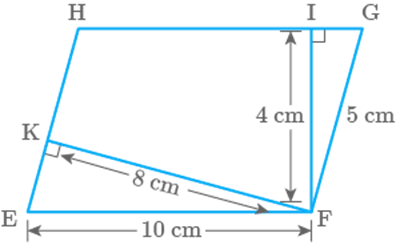
Fig. 9.19
Solution
(c)
In
parallelogram EFGH, EF HG [Given]
Area
of parallelogram EFGH
Base Corresponding height
=
HG IF
Question: 13
In
reference to a circle the value of is equal to
a.
b.
c.
d.
Solution
(c)
We
Know that,
Circumference
of a circle (r, the radius of circle)
Question: 14
Circumference
of a circle is always
a.
more than three times of its diameter
b.
three times of its diameter
c.
less than three times of its diameter
d.
three times of its radius
Solution
(a)
We
know that,
Circumference
of a circle
Circumference
Circumference
So,
circumference of circle is always more than three times of its diameter.
Question: 15
Area
of triangle PQR is (Fig. 9.20). If altitude QN is ,
then its base PR is
a.
b.
c.
d.
Fig. 9.20
Solution
(a)
Given,
area of
We
know that,
Area
of triangle
Area of
Question: 16
In
Fig. 9.21, if and then QM is -
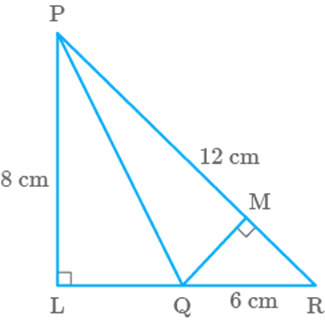
Fig. 9.21
a.
b.
c.
d.
Solution
(c)
Given
that, and
Now,
using Pythagoras theorem in right angled PLR,
Area
of
Area
of
Question: 17
In
Fig. 9.22 is a right-angled
triangle. Its legs are and long. Length of perpendicular NP on the side
MO is
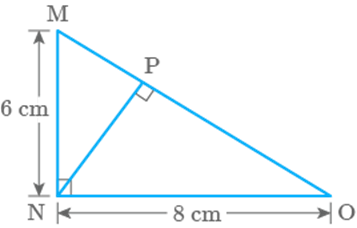
Fig. 9.22
a.
b.
c.
d.
Solution
(a)
Given,
is a right-angled triangle.
According
to Pythagoras theorem,
Question: 18
Area
of a right-angled triangle is If its smallest side is then its hypotenuse is
a.
b.
c.
d.
Solution
(b)
Given, area of right-angled triangle
and smallest side i.e., base
Area of right-angled triangle
Now, according to Pythagoras theorem,
Question: 19
Circumference of a circle of diameter is
a.
b.
c.
d.
Solution
(c)
Diameter of the given circle cm
Radius
Now, circumference of the circle
Question: 20
Circumference of a circle disc is 88 cm. Its radius is
a.
b.
c.
d.
Solution
(c)
Given, circumference of the circular disc
Hence, the radius of the disc is .
Question: 21
Length of tape required to cover the edges of a semicircular
disc of radius is
a.
b.
c.
d.
Solution
(b)
In order to find the length of tape required to cover the
edges of a semi-circular disc, we have to find the perimeter of semi-circle.
Perimeter of semi-circle circumference of semi-circle Diameter
Circumference of semi-circle
Length of tape required
Question: 22
Area of circular garden with diameter is
a.
b.
c.
d.
Solution
(c)
Given, diameter
So, radius
Area of circular garden
Question: 23
Area of a circle with diameter , radius and circumference is -
a.
b.
c.
d.
Solution
(d)
Given, diameter radius and circumference
We know that, area of circle
Question: 24
A
table top is semicircular in shape with diameter Area of this table top is -
a.
b.
c.
d.
Solution
(a)
Given, diameter
Now, radius
Area of table top Area of semi-circle
Question: 25
If then the value of is
a.
b.
c.
d.
Solution
(d)
Given,
[ ]
Question: 26
If squares of each side mm makes a square of side ,
then is equal to
a.
b.
c.
d.
Solution
(b)
Area of square of side mm
Area of square of side cm
Number of squares with side
According to question,
Area of square of side 1 mm
Question: 27
is the area of
a.
a square with side
b.
squares with side
each
c.
squares with side
each
d.
squares with side each
Solution
(b)
For option (a),
Area of a square with side
From option (b),
Area of squares with side each
For option (c),
Area of squares with side each
For option (d),
Area of squares with side Area of square side
Hence, option (b) is correct.
Question: 28
If each side of a rhombus is doubled, how much will its area
increase?
a.
times
b.
times
c.
times
d.
times
Solution
(b)
Let b
be the side and h be the height of a rhombus.
Area of rhombus
If side is doubled, then side of new rhombus
Now, area of new rhombus
Hence, the area of new rhombus will be increased by times.
Question: 29
If the sides of a parallelogram are increased to twice its
original lengths, how much will the perimeter of the new parallelogram?
a.
times
b.
times
c.
times
d.
times
Solution
(b)
Let the length and breadth of the parallelogram
be and respectively.
Then, perimeter
[ perimeter of parallelogram
(length breadth)]
If both sides are increased twice, then new
length and breadth will be respectively.
Now, new perimeter
times of original perimeter.
Hence, the perimeter of original parallelogram
will increase by times.
Question: 30
If radius of a circle is increased to twice its original
length, how much will the area of the circle increase?
a.
times
b.
times
c.
times
d.
times
Solution
(d)
Let be the radius of the circle.
Area of circle
If radius is increased to twice its original length, then new
radius will be So, area of new circle times of original area
Hence, the area of new circle will be increased
by times.
Question: 31
What will be the area of the largest square that can be cut
out of a circle of radius cm?
a.
b.
c.
d.
Solution
(b)
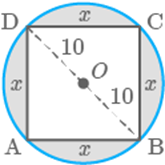
Given, radius of circle
The largest square that can be cut-out of a circle of radius
will have its diagonal equals to the diameter
of the circle.
Let the side of square be cm.
Area of the square is
Now, in right angled
Hence, the area of the largest square is .
Question: 32
What is the radius of the largest circle that can be cut out
of the rectangle measuring in length and in breadth?
a.
b.
c.
d.
Solution
(a)
The largest circle will have its diameter equal to the smaller
side of rectangle i.e., .
So, diameter
Radius
Question: 33
The perimeter of the figure ABCDEFGHIJ is
a.
b.
c.
d.
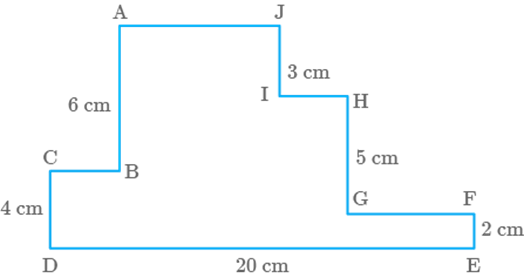
Fig. 9.23
Solution
(a)
We know that,
Perimeter of a closed shape sum of all its sides
So,
Question: 34
The circumference of a circle whose area is is
a.
b.
c.
d.
Solution
(b)
Let the radius of circle be R
Area of circle
Now, circumference of circle
Question: 35
The area of a square is The circumference (in cm) of the largest
circle cut of it is
a.
b.
c.
d.
Solution
(b)
Let the side of square be a cm.
Given, area of square

Area of square
Now, for the largest circle in the square, diameter of the
circle must be equal to the side of square.
Diameter side of square
Circumference of circle
Question: 36
If the radius of a circle is tripled, the area becomes
a.
times
b.
times
c.
times
d.
times
Solution
(a)
Let be the radius of a circle.
Area of circle
If radius is tripled, then new radius will be
Area of new circle times area of original circle
Hence, the area of new circle increases by times.
Question: 37
The
area of a semicircle of radius is
a.
b.
c.
d.
Solution
(a)
Given, radius of semi-circle
Area of semi-circle
In Questions 38 to 56, fill in the blanks to make the statements true.
Question: 38
Perimeter of a regular polygon Length of one side ___________.
Solution
Perimeter of regular polygon Length of one side Number
of sides.
Question: 39
If a wire in the shape of a square is rebent into a
rectangle, then the ___________ of both shapes remain same, but ___________ may
vary.
Solution
If
a wire in the shape of a square is rebent into a rectangle, then the perimeter of both shapes remain same,
but area may vary.
Question: 40
Area of the square MNOP of Fig. 9.24 is Area of each triangle is ___________.
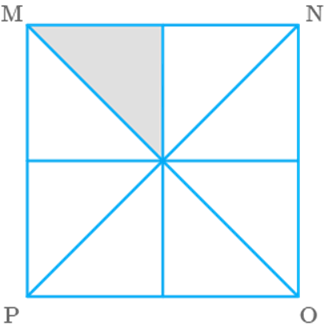
Fig. 9.24
Solution
Given, area of square MNOP
Since, there are identical triangles in the given square MNOP.
Hence, area of each triangle Area of square MNOP
Question: 41
In Fig. 9.25, area of parallelogram BCEF is ___________ , where ACDF is a rectangle.
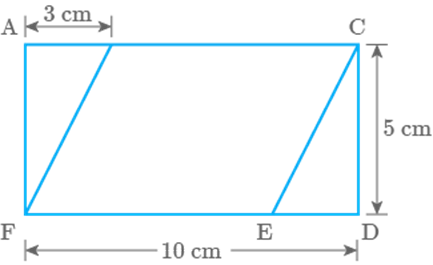
Fig. 9.25
Solution
Area of a parallelogram
BCEF Area of ACDF Area of
Question: 42
To find area, any side of a parallelogram can be chosen as ___________ of the parallelogram.
Solution
To find area, any side of a parallelogram can be chosen as base of the parallelogram.
Question: 43
Perpendicular dropped on the base of a parallelogram from
the opposite vertex is known as the corresponding ___________ of the base.
Solution
Perpendicular dropped on the base of a parallelogram from
the opposite vertex is known as the corresponding height/altitude
of the base.
Question: 44
The distance around a circle is its ___________.
Solution
The distance around a circle is its circumference.
Question: 45
Ratio of the circumference of a circle to its diameter is denoted
by symbol ___________.
Solution
Circumference of a circle r, the radius of circle
since,
Here, is the answer.
Question: 46
If area
of a triangular piece of cardboard is then the length of altitude corresponding to long base is ___________ cm.
Solution
We know that,
Area of triangle
Length of altitude
Question: 47
Value of is ___________
approximately.
Solution
We know that,
Thus, the approximate value of
Question: 48
Circumference of a circle can be found by multiplying
diameter with ___________.
Solution
Circumference of a circle ,
the radius of circle
Since, diameter
So,
Hence, is the answer.
Question: 49
Circumference of a circle is equal to ___________.
Solution
Circumference of a circle ,
radius of circle
Hence, is the answer.
Question: 50
___________
Solution
We know that,
On squaring both sides, we get
Question: 51
___________
Solution
We know that,
On squaring
both sides, we get
Question: 52
hectare ___________ .
Solution
Question: 53
Area of a triangle ___________.
Solution
Area of triangle
Question: 54
___________
Solution
We know that,
On squaring both sides, we get
Question: 55
Area of a square of side m is equal to the area of ___________ squares
of each side cm.
Solution
Let number of squares having side
According to the question,
Area of square with side Area of square with side
area of square (side)2
[ ]
Question: 56
___________
Solution
We know that m
In Questions 57 to 72, state whether the statements are True
or False.
Question: 57
In Fig. 9.26, perimeter of (ii) is greater than that of (i),
but its area is smaller than that of (i).

(i)
(ii)
Fig. 9.26
Solution
True
We know that, perimeter is the sum of all sides of any
polygon.
We also know that, area is the space covered in the polygon.
So, by observing the figures we can say that, perimeter of
(ii) is greater than (i) and area is less than that of (i).
Question: 58
In Fig. 9.27,
a.
area of (i) is the same as the area of (ii).
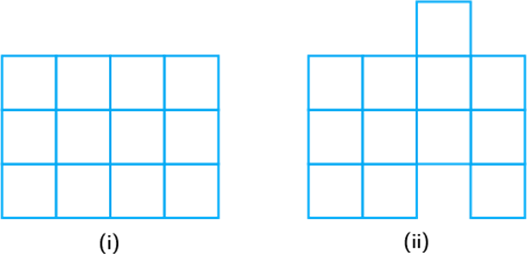
Fig. 9.27
b.
Perimeter of (ii) is the same as (i).
c.
If (ii) is divided into squares of unit length, then its area
is unit squares.
d.
Perimeter of (ii) is units.
Solution
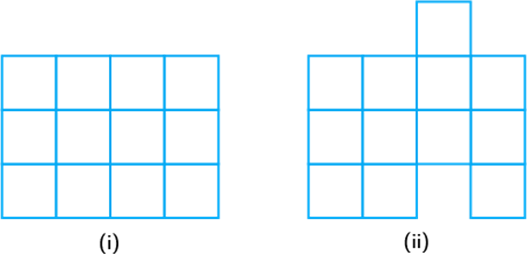
- True
Since the number of blocks in fig
(i) and fig (ii) are same, area of both figures is same.
- False
Because new sides are added in (ii).
So, the perimeter of (ii) is
greater than (i).
- False
Area of square unit squares
and number of squares
So, total area unit squares
- True
Perimeter is the sum of all sides.
When we add the sides of the
figure, we get 18 units.
So, the perimeter is units.
Question: 59
If perimeter of two parallelograms are equal, then their
areas are also equal.
Solution
False
Even if the perimeter of two parallelograms are equal, their
corresponding sides and height may be different. So, their area cannot be
equal.
Question: 60
All congruent triangles are equal in area.
Solution
True
Congruent triangles have equal shape and size. Hence, their
areas are also equal.
Question: 61
All parallelograms having equal areas have same perimeters.
Solution
False
It is not necessary that all parallelograms having equal
areas have same perimeters as their base and height may be different.
Observe the figure and answer the statements 62 to 65 as true or false:
Question: 62
Observe all the four triangles FAB, EAB, DAB and CAB as
shown in Fig. 9.28:
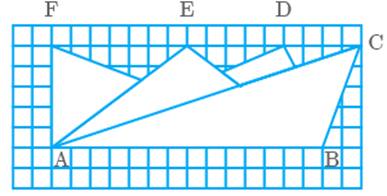
Fig. 9.28
All triangles have the same base and the same altitude.
Solution
True
It is clear from the figure that all triangles have same
base AB and all the vertices lie on the same line, so the distance between
vertex and base of triangle (i.e. length of altitude) are equal.
Question: 63
All triangles are congruent.
Solution
False
It is clear from the Fig. 9.28,that the lengths of sides
other than the base in all the triangles are not equal. Hence, not all triangles are congruent.
Question: 64
All triangles are equal in area.
Solution
True
This is true because the triangles on same base and between
same parallel lines have equal in area.
Question: 65
All triangles may not have the same perimeter.
Solution
True
It is clear from the Fig. 9.28,that the lengths of sides
other than the base in all the triangles are not equal. Hence, all triangles may not have the same perimeter.
Question: 66
In Fig. 9.29 ratio of the area of triangle ABC to the area
of triangle ACD is the same as the ratio of base BC of triangle ABC to the base
CD of triangle ACD.
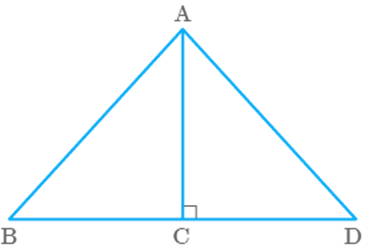
Fig. 9.29
Solution
True
Area of : Area of
Question: 67
Triangles having the same base have equal area.
Solution
False
Area of triangle
So, area of triangle does not only depend on base, it also
depends on height.
Hence, if triangles have equal base and equal height, then
only their areas are equal.
Question: 68
Ratio of circumference of a circle to its radius is always
Solution
True
We know that, the circumference C of a circle of radius r, is
Circumference : Radius
Question: 69
hectare
Solution
False
As we know that, hectare
So, hectare
Question: 70
An increase in perimeter of a figure always increases the
area of the figure.
Solution
False
Perimeter is the sum of sides of any polygon and area is
space covered by a polygon.
Question: 71
Two figures can have the same area but different perimeters.
Solution
True
Perimeter of (i)
Perimeter of (ii)
Area of figure (i)
Area of figure (ii)
So, two figures can
have the same area but different perimeters.
See the Q.58
Question: 72
Out of
two figures if one has larger area, then its perimeter need not to be
larger than the other figure.
Solution
True
Perimeter of figure (i) cm
Perimeter of figure (ii) cm
Though the first figure has the larger area, its
perimeter is less than the second one.
Out of two figures
if one has larger area, then its perimeter need not to be larger than the other
figure.
Question: 73
A hedge boundary needs to be planted around a rectangular
lawn of size If shrubs can be planted in a metre of hedge, how
many shrubs will be planted in all?
Solution
Given, length of rectangular lawn and breadth of rectangular lawn
Perimeter of rectangle
Perimeter of rectangular lawn
No. of shrubs to be
planted in 1 m of hedge
No. of shrubs to be
planted in m of
hedge
Question: 74
People of Khejadli village take good care of plants, trees
and animals. They say that plants and animals can survive without us, but we cannot
survive without them. Inspired by her elders Amrita marked some land for her
pets (camel and ox) and plants. Find the ratio of the areas kept for animals
and plants to the living area.
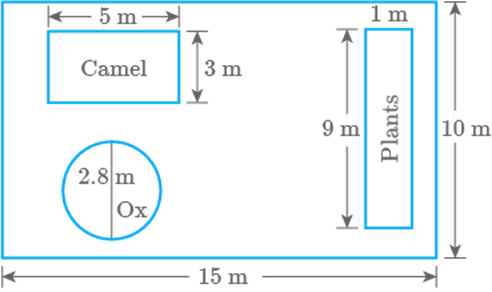
Fig. 9.30
Solution
Area of total rectangular land
Area of land covered by plants
Area of land covered by camel
Region of land covered by ox is circular area.
So, diameter,
Radius
Area of land covered by ox
Total area covered by plants, camel, and ox
Living area
Ratio of areas kept for animals & plants to the living
area
Question: 75
The
perimeter of a rectangle is Its length is four metres less than five times
its breadth. Find the area of the rectangle.
Solution
Let breadth of the rectangle
Then, length of the rectangle
Perimeter of the rectangle
So, breadth and length
Area of rectangle
Hence, the area of rectangle is
Question: 76
A wall of a room is of dimensions It has a window of dimensions and a door of dimensions Find the area of the wall which is to be
painted.
Solution
Length of the room
Breadth of the room
Area of the room
Also, length of the window and breadth of the window [given]
Area of the window
Now, length of the door and
breadth of the door
Area of the door
Now, area of the wall to be painted Area of the room (Area of the window Area of the door)
Question: 77
Rectangle MNOP is made up of four congruent rectangles (Fig.
9.31).If the area of one of the rectangles is and breadth is then find the perimeter of MNOP.
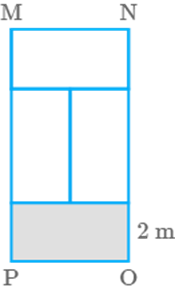
Fig. 9.31
Solution
Area of smaller rectangle
Breadth of smaller rectangle
We know that, Area of the rectangle
Perimeter of MNOP
So, the perimeter of MNOP is .
Question: 78
In Fig. 9.32, area of is equal to the area of parallelogram ABCD. If
altitude EF is long, find the altitude of the parallelogram
to the base AB of length What is the area of where O is the mid point of DC?
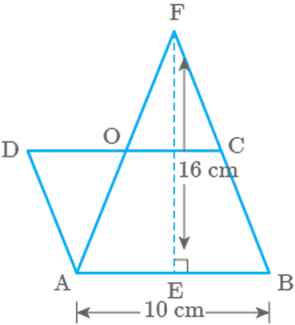
Fig. 9.32
Solution
Given,
Area of Area of parallelogram ABCD
Let corresponding height be
Then,
In
Area of
Question: 79
Ratio of the area of to the area of is (Fig. 9.33). If the area of is and WY cm, find the lengths of XY and
YZ.
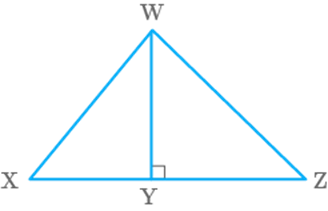
Fig. 9.33
Solution
We know that, area of a triangle
Given, area of
Area of
So,
Hence,
Question: 80
Rani bought a new field that is next to one she already owns
(Fig. 9.34). This field is in the shape of a square of side She makes a semi circular lawn of maximum area
in this field.
(i)
Find the perimeter of the lawn.
(ii)
Find the area of the square field excluding the lawn.
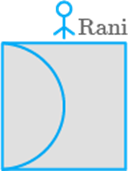
Fig.
9.34
Solution
(i)
Given, side of the square field
Diameter of semi-circular lawn
From the figure we understand
that, Diameter of semi-circle side of square
Therefore, Radius
Perimeter of lawn

(ii)
Area of square side side
Required area Area of square Area of semi-circle
Question: 81
In Fig. 9.35, find the area of parallelogram ABCD if the
area of shaded triangle is
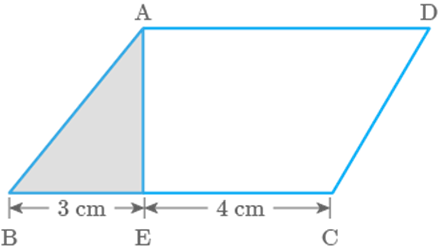
Fig. 9.35
Solution
Given, area of shaded triangle
And base of the triangle
We know that, Area of triangle
Therefore,
Area of parallelogram height base of parallelogram
Question: 82
Pizza factory has come out with two kinds of pizzas. A
square pizza of side costs and a circular pizza of diameter costs (Fig. 9.36). Which pizza is a better deal?
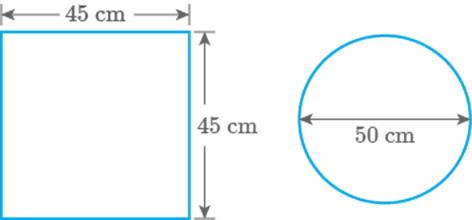
Fig. 9.36
Solution
Given, side of square pizza
Area of a square pizza
Diameter of circular pizza
Radius
Now, area of the circular pizza
Price of sq. cm. pizza
Price of cm circular pizza
Since price of of circular pizza is lesser, hence circular
pizza is a better deal.
Question: 83
Three squares are attached to each other as shown in Fig.
9.37. Each square is attached at the mid-point of the side of the square to its
right. Find the perimeter of the complete figure.

Fig. 9.37
Solution
Perimeter of the complete figure
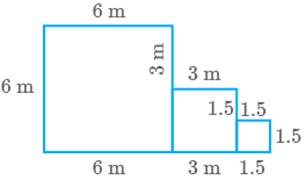
Side of first square
Side of second square
Side of third square
Question: 84
In Fig. 9.38, ABCD is a square with AB cm. Find the area of the square BDFE.
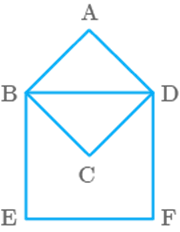
Fig. 9.38
Solution
Given, ABCD is a square and AB
Diagonal of square (a, the side of square ABCD)
Diagonal of square ABCD is the side of square BDEF
Area of the square
Question: 85
In the given triangles of Fig. 9.39, perimeter of perimeter of Find the area of
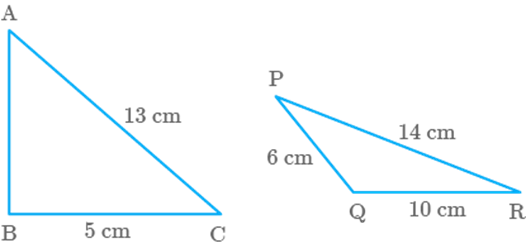
Fig. 9.39
Solution
Given, Perimeter of
Area of
Question: 86
Altitudes MN and MO of parallelogram MGHK are cm and cm long respectively (Fig. 9.40). One side GH
is cm long. Find the perimeter of MGHK.
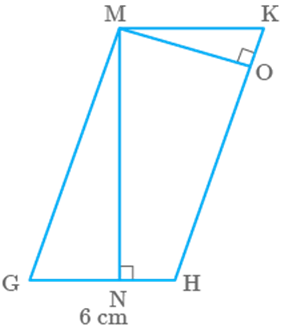
Fig. 9.40
Solution
Given, MGHK is a parallelogram where
We know that, area of parallelogram base height
Area of parallelogram MGHK, when base is GH
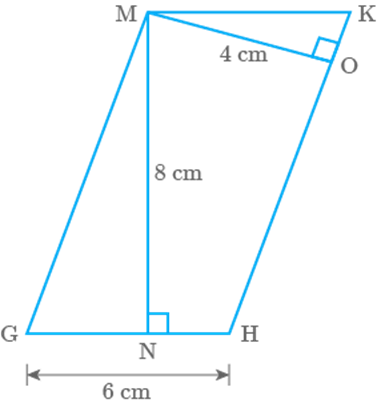
Area of parallelogram MGHK, when base is HK
In parallelogram, opposite sides are equal
So,
Perimeter of parallelogram
Question: 87
In Fig. 9.41, area of is and area of is Find the length RS, if PQ is perpendicular to
QS and QR is
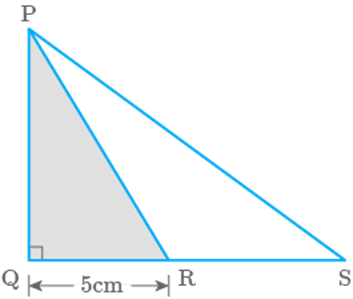
Fig. 9.41
Solution
Given, area of
area of
Area of triangle
Area of
Area of
Now,
Question: 88
Area of an isosceles triangle is If the altitudes corresponding to the base of
the triangle is find the perimeter of the triangle.
Solution
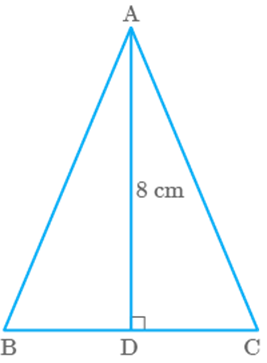
Given, area of and altitude
is an isosceles triangle, where
area of
In an isosceles triangle,
Using Pythagoras theorem in right angled
Perimeter of triangle
Question: 89
Perimeter of a parallelogram shaped land is and its area is square meters. If one of the sides of this
parallelogram is find the length of the other side. Also, find
the lengths of altitudes l and m (Fig. 9.42).
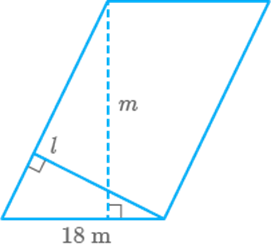
Fig. 9.42
Solution
Perimeter of parallelogram ABCD
Area of parallelogram
ABCD
Perimeter of parallelogram
So,
Now, area of parallelogram
Also, area of parallelogram
Hence, altitudes of parallelogram and
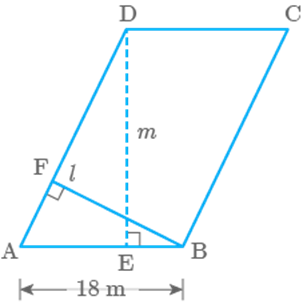
Question: 90
Area of a triangle PQR right-angled at Q is (Fig. 9.43). If the smallest side is long, find the length of the other two sides.
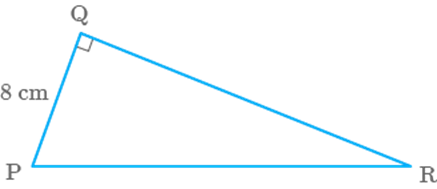
Fig. 9.43
Solution
Area of
Area of
In right angled (using Pythagoras theorem)
Hence, the length of two sides are and .
Question: 91
In Fig. 9.44 a rectangle with perimeter is divided into five congruent rectangles.
Find the perimeter of one of the rectangles.

Fig. 9.44
Solution
Let be the length of each smaller rectangle
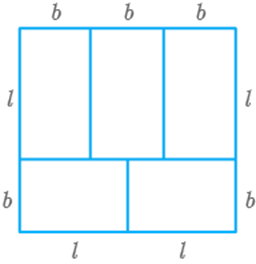
Given, perimeter of the bigger rectangle
According to the figure,
&
Put the value of from eq. (ii) in eq.(ii),
Perimeter of a rectangle
Hence, perimeter of smaller rectangle
Question: 92
Find the area of a square inscribed in a circle whose radius
is (Fig. 9.45).
[Hint: Four right-angled triangles joined at right angles to
form a square]
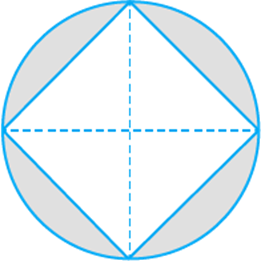
Fig. 9.45
Solution
ABCD is a square (given)
According to the question,
Area of square
Hence, area of inscribed square is
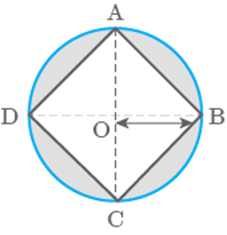
Question: 93
Find the area of the shaded portion in question
Solution
Area of shaded option area of circle area of square
In Questions 94 to 97 find the area enclosed by
each of the following figures:
Question: 94
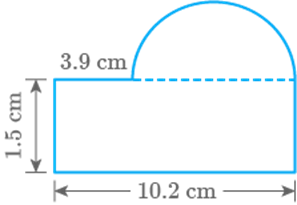
Fig. 9.46
Solution
Given shape contains a rectangle and a semi-circle.
Area of rectangle
Here, diameter of semi-circle
So, radius
Area of semi-circle
Total area area of rectangle area of semi-circle
Question: 95
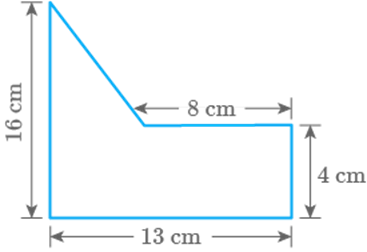
Fig. 9.47
Solution
For rectangle, and
Area of rectangle
For triangle, base
And height
Area of triangle
Total area enclosed by the shape
Question: 96
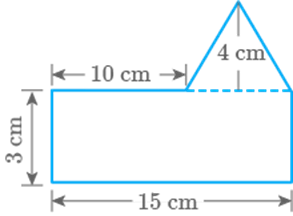
Fig. 9.48
Solution
For rectangle,
Area of rectangle
According to questions
Now, base of triangle
For triangle, base and height
Area of triangle
Total area enclosed by the shape
Question: 97
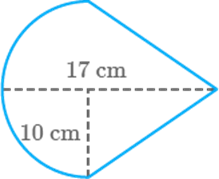
Fig. 9.49
Solution
Given shape contains a semi-circle and a triangle
Area of semi-circle
Area of triangle
Hence, total area enclosed by the shape = area of semicircle
+ area of triangle
Question: 98
Find the areas of the shaded region:
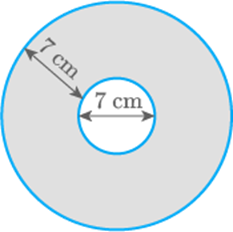
Fig. 9.50
Solution
Let the radius of smaller circle be and bigger circle be
From the figure, and
Area of the shaded region area of bigger circle – area of smaller circle
Hence, the area of shaded region is .
Question: 99
Find the area of the shaded region:
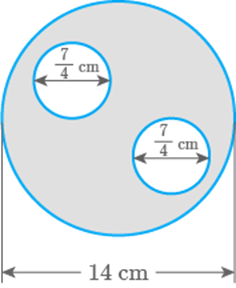
Fig. 9.51
Solution
Diameter of bigger circle
Radius of bigger circle
So, area of bigger circle
Diameter of smaller circle
Radius of the smaller circle
Area of two smaller circles
Area of shaded region area of bigger circle area of two smaller circles
Hence, area of shaded region is
Question: 100
A circle with radius is cut into four equal parts and rearranged to
form another shape as shown in Fig. 9.52: Does the perimeter change? If it does
change, by how much does it increase or decrease?
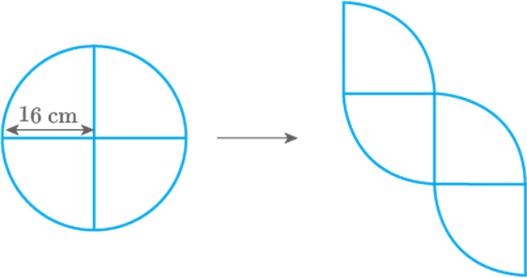
Fig. 9.52
Solution
Yes, the perimeter changes.
Perimeter of the circle in first fig includes 4 arcs of equal
length.
While in the second fig, perimeter includes 4 arcs as well as
radius twice.
So, The perimeter is increased by
Question: 101
A large square is made by arranging a small square
surrounded by four congruent rectangles as shown in Fig. 9.53. If the perimeter
of each of the rectangle is find the area of the large square.

Fig. 9.53
Solution
Let the length & breadth of rectangle be respectively
Given, perimeter of rectangle
Since, the side of large square is
Hence, area
Question: 102
ABCD
is a parallelogram in which AE is perpendicular to CD (Fig. 9.54). Also and the area of Find the perimeter and area of ABCD.
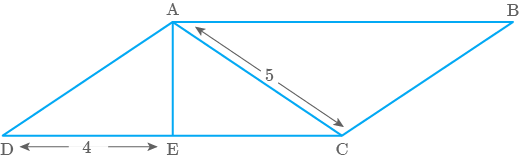
Fig. 9.54
Solution
Area of
Area of
In right angled
So, using Pythagoras theorem
Now, in right angled
Perimeter of parallelogram
Area of parallelogram
Question: 103
Ishika has designed a small oval race track for her remote
control car. Her design is shown in the figure 9.55. What is the total distance
around the track? Round your answer to the nearest whole cm.
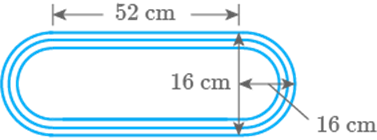
Fig. 9.55
Solution
Total distance around the track length of parallel strips length of two semi-circles
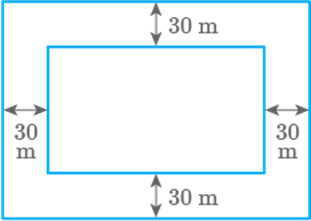
Question: 104
A table cover of dimensions is
spread on a table. If of the table cover is hanging all
around the table, find the area of the table cover which is hanging outside the
top of the table. Also find the cost of polishing the table top at per square metre.
Solution
Length of table cloth
Breadth of table cloth
Area of the table cloth
Area of the table cloth on the top of table
Area of hanging table cloth Area of the table cloth Area of the table cloth on the top of table
Since the area of the table top = 4.5050 sq. metre
Cost of polishing table top
Question: 105
The dimensions of a plot are A builder builds roads which are wide along the length on either side and one
in the middle. On either side of the middle road he builds houses to sell. How
much area did he get for building the houses?
Solution
Dimension of plot
& width of road
Total area available for houses area of plot area of roads

Question: 106
A room is long and wide. The floor of the room is to be covered
with tiles of size by Find the cost of covering the floor with tiles
at the rate of per tile.
Solution
Length of room width of room and size of tiles
Area of room
Area of tile
So, number of tiles
Cost of covering the floor with tiles at the rate of per tile
Question: 107
Find the total cost of wooden fencing around a circular
garden of diameter if of fencing costs
Solution
Given, diameter of the circular garden
Length of the fencing circumference of circle
Total cost of fencing
Question: 108
Priyanka
took a wire and bent it to form a circle of radius Then she bent it into a rectangle with one
side long. What is the length of the wire? Which
figure encloses more area, the circle or the rectangle?
Solution
Given, radius of circle and length of rectangle
Length of the wire circumference of the circle
Let be the width of rectangle
Since, the wire is re-bent in the form of rectangle,
Perimeter of rectangle circumference of the circle
Area of circle
Area of rectangle
Hence, the circle enclosed more area than rectangle.
Question: 109
How much distance, in metres, a wheel of radius will cover if it rotates times?
Solution
Radius of wheel
Distance travelled in rotation = circumference of circle
Distance travelled in rotation
Hence, the wheel covers a distance of m.
Question: 110
A circular pond is surrounded by a wide circular path. If outer circumference of
circular path is find the inner circumference of the circular
path. Also find area of the path.
Solution
Let and be the radius of outer circle and inner circle
respectively.
Circumference of outer circle is .
Since,
Inner circumference of the circular path
Area of the path area of outer circle area of inner circle
Question: 111
A carpet of size has wide red border. The inner part of the carpet
is blue in colour (Fig. 9.56). Find the area of blue portion. What is the ratio
of areas of red portion to blue portion?

Fig. 9.56
Solution
Length of the carpet m
Breadth of the carpet m
Given, size of carpet
& width of border
Area of carpet
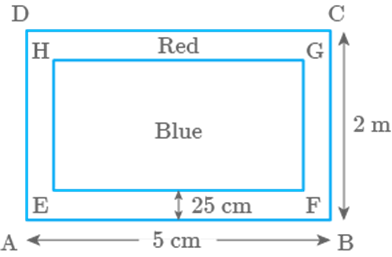
So, length of inner blue portion,
& breadth of inner blue portion
Area of blue portion area of rectangle
Now, area of red portion area of ABCD area of EFGH
Ratio of areas of red portion to blue portion
Question: 112
Use the Fig. 9.57 showing the layout of a farm house:
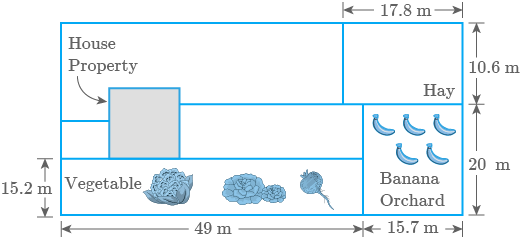
Fig. 9.57
a.
What is the area of land used to grow hay?
b.
It costs per to fertilise the vegetable garden. What is the total cost?
c.
A fence is to be enclosed around the house. The dimensions of the house are m. At least how many
metres of fencing are needed?
d.
Each banana tree required of ground space.
How many banana trees can
there be in the orchard?
Solution
a.
Area of land used to grow
hay
b.
Area of vegetable garden
cost to fertilise vegetable garden
cost to fertilise vegetable garden
c.
Since, fence is to be
enclosed around the house of dimensions
Perimeter of the house
Total
length of fence
- Area covered by banana
orchard
Since, area is required by banana tree
Therefore, number of banana trees
required to be covered in area trees
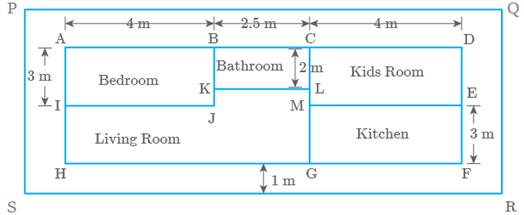
Question: 113
Study the layout given below in Fig. 9.58 and answer the
questions:
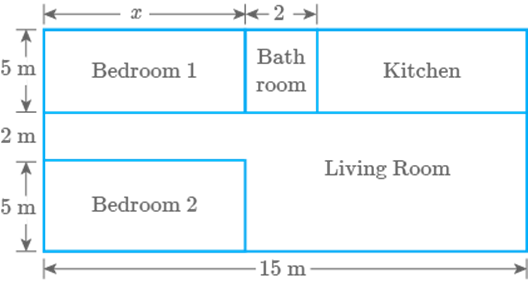
Fig. 9.58
a. Write an
expression for the total area covered by both the bedrooms and the kitchen.
b. Write an
expression to calculate the perimeter of the living room.
c. If the cost of
carpeting is write an expression for calculating the total cost of carpeting both the
bedrooms and the living room.
d. If the cost of
tiling is write an expression for calculating the total cost of floor tiles used for the bathroom
and kitchen floors.
e. If the floor area
of each bedroom is then find .
Solution
- Area of both bedrooms
& the kitchen
- Perimeter of the living room
- Total area of both the bedrooms & the living
room
area of bedroom 1 (area of bedroom 2
area of living room)
Total cost of carpeting
- Total area of bathroom & kitchen
Total cost of tilling
- Given, area of floor of each bedroom
Area of one bedroom
Question: 114
A long and wide rectangular lawn is in front of a house. Along
its three sides a wide flower bed is there as shown in Fig. 9.59.
Find the area of the remaining portion.
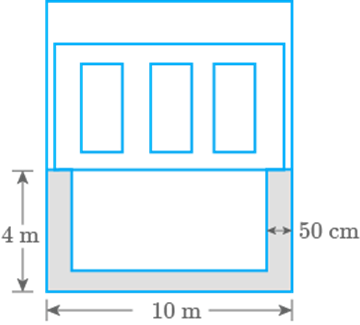
Fig. 9.59
Solution
Dimensions of the rectangular lawn and width of flower bed Length of remaining portion,
Breadth of remaining portion,
Area of the remaining portion of the lawn Area of portion
Question: 115
A school playground is divided by a wide path which is parallel to the width of
the playground, and a wide path which is parallel to the length of
the ground (Fig. 9.60). If the length and width of the playground are and respectively, find the area of the remaining
playground.
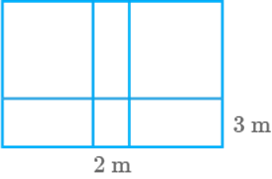
Fig. 9.60
Solution
Total area of the
playground
Area of the vertical road
lying above the horizontal road
Area of the horizontal road
Area of the remaining
playground
= 9086 m2
Question: 116
In a park of dimensions there is a L shaped wide flower bed as shown in Fig. 9.61. Find
the total cost of manuring for the flower bed at the rate of
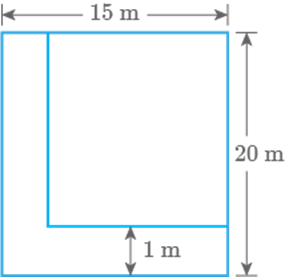
Fig. 9.61
Solution
Given, dimensions of the park and width of the flower bed
From the figure,
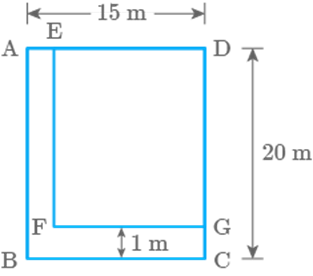
Area of flower bed Area of ABCD Area of EFGD
Cost of manuring of flower bed
Cost of manuring of the flower bed
Question: 117
Dimensions of a painting are Find the area of the wooden frame of width around the painting as shown in Fig. 9.62.
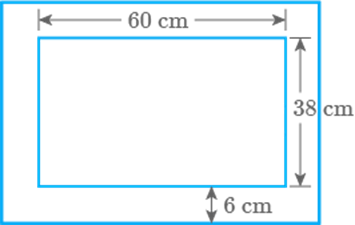
Fig. 9.62
Solution
Length of inner rectangle = 60 cm
Breadth of inner rectangle = 38 cm
Area of inner rectangle
Length of outer rectangle
Breadth of outer rectangle
Area of outer rectangle
Now, area of wooden frame
= area of outer rectangle – area of inner rectangle
Question: 118
A design
is made up of four congruent right triangles as shown in Fig. 9.63. Find the
area of the shaded portion.
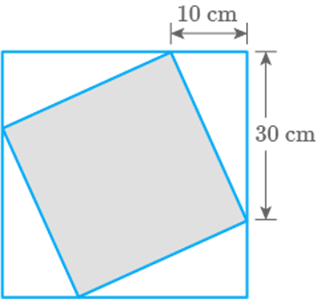
Fig. 9.63
Solution
Area of one right triangle
So, area of right angled triangles
Area of square
Area of square
Area of shaded portion
Question: 119
A square tile of length has four quarter circles at each corner as
shown in Fig. 9.64 (i). Find the area of shaded portion. Another tile with same
dimensions has a circle in the centre of the tile [Fig. 9.64 (ii)]. If the
circle touches all the four sides of the square tile, find the area of the
shaded portion. In which tile, area of shaded portion will be more? (Take )
(i) (ii)
Fig. 9.64
Solution
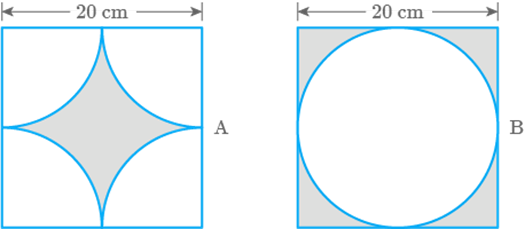
(i)
Area of shaded portion area of square
area of quarter circle
(ii) Area of shaded portion Area of square area of circle
Hence, area in both cases is equal is .
Question: 120
A rectangular field is long and wide. How many right triangular flower beds
can be laid in this field, if sides including the right angle measure and respectively?
Solution
Given, dimensions of the rectangular field .
Height of right-angled triangle = 2 m
Base of the triangle = 4m
Number of right triangular flower beds
[area of rectangle & area of a right-angled triangle ]
Question: 121
Ramesh grew wheat in a rectangular field that measured meters long and meters wide. This year he increased the area
for wheat by increasing the length but not the width. He increased the area of the
wheat field by square meters. What is the length of the expanded
wheat field?
Solution
Let the increase in
length be m.
Give, increase in area
of the field
Area of expanded wheat
field Area of
original wheat field
Length of expanded
wheat field
Question: 122
In Fig. 9.65, triangle AEC is right-angled at E, B is a
point on EC, BD is the altitude of triangle ABC, and Find the area of triangle ABC and the length
of DB.
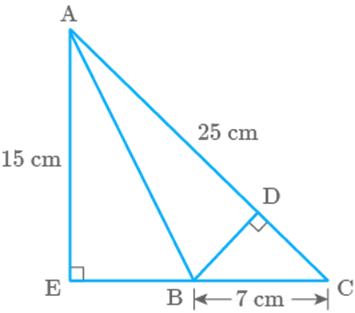
Fig. 9.65
Solution
Given, and
In using Pythagoras theorem
&
Area of
& Area of
Area of
Again, Area of
Hence, the area of is and the length of DB is
Question: 123

Solution
Number of pieces of chocolate
Question: 124
Calculate the area of shaded region in Fig. 9.66, where all
of the short line segments are at right angles to each other and long.

Fig. 9.66
Solution
Length of the larger rectangle
Breadth of the larger rectangle
Area of shaded region area of larger square area of small identical squares
Question: 125
The plan and measurement for a house are given in Fig. 9.67.
The house is surrounded by a path wide.
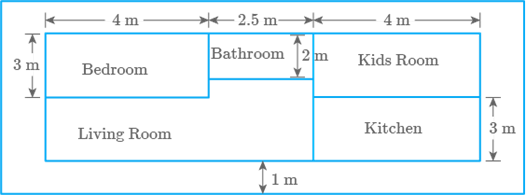
Fig. 9.67
Find the following:
(i)
Cost of paving the path with bricks at the rate
of per
(ii)
Cost of wooden flooring inside the house except
the bathroom at the cost of per
(iii) Area
of Living Room.
Solution
(i)
Area of path Area of rectangle PQRS Area of rectangle ADFH
Cost of paving the path with bricks
cost per unit Total area of path
(ii)
Area of the house with wooden flooring Area of house Area of bathroom
Area of rectangle ADFH Area of rectangle BCLK
Cost of wooden flooring cost per unit Total area
(iii) Area
of living room Area of rectangle ACGH Area of rectangle ABJI Area of rectangle BCLK
Question: 126
Architects design many types of buildings. They draw plans
for houses, such as the plan shown in Fig. 9.68:

Fig. 9.68
An architect wants to install a decorative moulding around
the ceilings in all the rooms. The decorative moulding costs
a.
Find how much moulding will be needed for each room.
(i)
family room
(ii) living room
(iii) dining room
(iv) bedroom
(v) bedroom
b.
The carpet costs Find the cost of carpeting each room.
c.
What is the total cost of moulding for all the five rooms.
Solution
a.
To install the decorative moulding around the ceilings in all rooms, we
need to find the perimeter of ceiling of each room.
(i) Given, breadth of the family room
& length of the family room
Perimeter of the family room
(ii) Given,
length of the living room
& breadth of the living room
Perimeter of the living room
(iii)Given, breadth of the dining room
& length of the dining room
Perimeter of dining room
(iv) Given, length of bedroom
& breadth of bedroom
Perimeter of the bedroom
(v) Given, breadth of bedroom
& length of bedroom
Perimeter of the bedroom
- To find the cost of
carpeting the rooms, we need to first find the area of the floor of each
room.
for bedroom
Given, length of bedroom
& breadth of bedroom
Area of bedroom
Area of bedroom
Cost of carpeting
Therefore, cost of carpeting 9.2416
sq m = 9.2416 200 = 1848.32
For bedroom ,
Given, length of bedroom
& breadth of bedroom
Area of bedroom
Cost of carpeting
Therefore, cost of carpeting
For living room,
Given, length of living room and breadth of living room
Area of living room
Cost of carpeting of living room
Therefore, cost of carpeting
For dining room,
Given, length of living room and breadth of living room
Area of living room
Cost of carpeting of living room
Therefore, cost of carpeting
For dining room,
Length of dining room
and breadth of dining room
Area of living room
Therefore, cost of carpeting
For family room,
Given, length of family room
& breadth of family room
Area of family room
So, cost of carpeting family room
c. Total
perimeter of all the rooms
Cost of moulding each room per m
Total cost of moulding all rooms
Question: 127
ABCD is a given rectangle with length as and breadth as P, Q, R, S are the mid points of sides AB, BC,
CD, DA respectively. A circular rangoli
of radius is drawn at the centre as shown in Fig. 9.69.
Find the area of shaded portion.
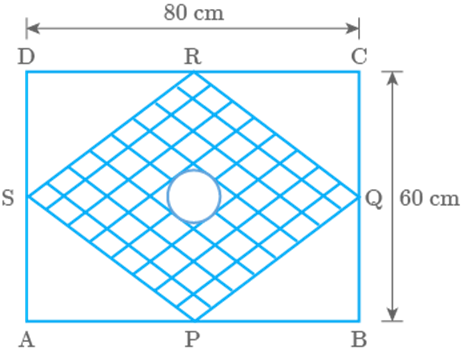
Fig. 9.69
Solution
Here,
Also,
Area of
Area of portion PQRS
Area of rectangle ABCD
Area of circular rangoli
Area of shaded region
Question: 128
squares each of side have been cut from each corner of a rectangular
sheet of paper of size From the remaining piece of paper, an
isosceles right triangle is removed whose equal sides are each of length. Find the area of the remaining part of
the paper.
Solution
Area of each square
[ area of square (side)2]
Area of rectangular sheet
[ area of rectangle length breadth]
Area of an isosceles right triangle
Area of remaining part of paper
Question: 129
A dinner
plate is in the form of a circle. A circular region encloses a beautiful
design as shown in Fig. 9.70. The inner circumference is mm and outer is mm. Find the width of circular design.

Fig. 9.70
Solution
Let the radius of inner & outer circle be and
Inner circumference
& outer circumference
Width of circular design =
Question: 130
The moon is about from earth and its path around the earth is
nearly circular. Find the length of path described by moon in one complete revolution. (Take )
Solution
Radius of the circular path = 384000 km
Length of path described by moon in one complete revolution =
Circumference of the circular path
[ radius distance of moon from the earth]
Question: 131
A photograph of Billiard/Snooker table has dimensions
as of its actual size as shown in Fig. 9.71:
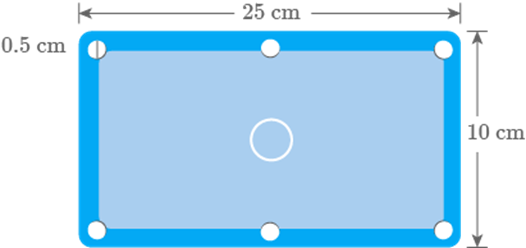
Fig. 9.71
The portion excluding six holes each of diameter needs to be polished at the rate of Find the cost of polishing.
Solution
Actual length of the table
Actual breadth of the table
Area of table
Radius of hole
Area of holes
Area of the portion of table excluding holes
Since, 1 m = 100 cm
Hence, Cost of polishing



















































































