Unit: 1: Integers

In Questions 1 to 25, there are four options, out of which only one is correct. Write the correct one.

When the integers $10,0,5,-5,-7$ are arranged in descending or ascending order, then find out which of the following integers always remains in the middle of the arrangement.

a.   $0$ 

b.   $5$

c.  $-7$

d. $-5$

(a)

Ascending order: $-7<-5<0<5<10$

Descending order: $10>5>0>-5>-7$

Hence the integer “ $0$ ”in the middle of both the arrangements remains the same.

By observing the number line (Fig. 1.2), state which of the following statements is not true.

Fig. 1.2

a. B is greater than $-10$

b. A is greater than $0$

c.  B is greater than A

d. B is smaller than $0$

(c)

As we know that, if a number lies on the right side to the other number, then the number is greater.

Here, B is greater than $-10$ but smaller than $0$ and A is greater than $0$ but smaller than $10.$ Also, B is smaller than A.

By observing the above number line (Fig. 1.2), state which of the following statements is true.

a. B is $2$

b. A is $-4$

c.  B is $-13$

d. B is $-4$

(d)

Since, B lies at the left side of $0$, so it will be negative and it is at 4^th place. So, $\text{B}=-\text{4}$ 

Similarly, A lies at the right side of $0$, so it will be positive and it is at 7^th place.

So, $\text{A}=7.$  and the value of $\text{B}=-4$

Next three consecutive numbers in the pattern 11, 8, 5, 2, --, --, -- are

a. $0,-3,-6$

b. $-1,-5,-8$

c.  $-2,-5,-8$

d. $-1,-4,-7$

(d)

By observing the pattern, difference between two consecutive numbers is $3$,

    $\begin{array}{c}11-8=3\\ 8-5=3\\ 5-2=3\end{array}$

So, next number will be $2-3=-1$

Similarly, next two numbers are:

$-1-3=-4$

$-4-3=-7$

The next number in the pattern $-62,-37,-12$ _______ is

a. $25$

b. $13$

c.  $0$

d. $-13$

(b)

By observing the series, the difference between two consecutive numbers is $25$, i.e. $-37-(-62)=-37+62=25$

$-12-(-37)=-12+37=25$

So, next number will be $-12+25=13$.

Which of the following statements is not true?

a. When two positive integers are added, we always get a positive integer.

b. When two negative integers are added we always get a negative integer.

c.  When a positive integer and a negative integer is added we always get a negative integer.

d. Additive inverse of an integer $2$ is $(-2)$ and additive inverse of $(-2)$ is $2$.

(c)

a. True, when two positive integers are added, the resultant number is also a positive integer.

b. True, while adding integers, if both the numbers have same sign, the resultant number also get that sign.

c.  False, while adding the integers of different signs, the resultant number get the sign of greater number.

d. True, additive inverse of an integer is the same integer value, with opposite sign.

On the following number line value ‘Zero’ is shown by the point

 

 

a. $\text{X}$

b. $\text{Y}$

c.  $\text{Z}$

d. $\text{W}$

(c)

All the points are equally spaced.

One division $=5$ units

So, $\text{X}=-15+5=-10$

$\begin{array}{l}\text{Y}=-10+5=-5\\ \text{Z}=-5+5=0\end{array}$

$\text{W}=0+5=5$

Hence, zero is shown by the point $\text{Z}.$

If $\otimes$,$◯$, $\varnothing$ and $•$  represent some integers on number line, then descending order of these numbers is

 

a. $•$ , $\otimes$, $\varnothing$, $◯$

b. $\otimes$, $•$ , $\varnothing$, $◯$

c.  $◯$, $\varnothing$, $\otimes$, $•$ 

d. $◯$, $•$ , $\otimes$, $\varnothing$

(c)

Descending order in number line, is from right to left.

Accordingly,

$◯$ comes first, $\varnothing$ comes second, $\otimes$ comes third and $•$ comes forth

Hence, descending order is $◯$, $\varnothing$, $\otimes$, $•$

On the number line, the value of $(-3)\times 3$ lies on right hand side of

a. $-10$

b. $-4$

c.  $0$

d. $9$

(a)

$(-3)\times 3$ equals to $-9.$

 

 

Above, it is shown on the number line that $-9$ lies on the right hand side of $-10$.

The value of $5÷\left(-1\right)$ does not lie between

a. $0$ and $-10$

b. $0$ and $10$

c.  $-4$ and $-15$

d. $-6$ and $6$

(b)

$5÷\left(-1\right)$ equals to $-5.$

On the number line, it is placed as

 

 

Now, as we see, $-5$ lies between ( $0$ and $-10$ ), ( $-4$ and $-15$ ) and ( $-6$ and $6$ ). But it does not lie between $0$ and $10.$

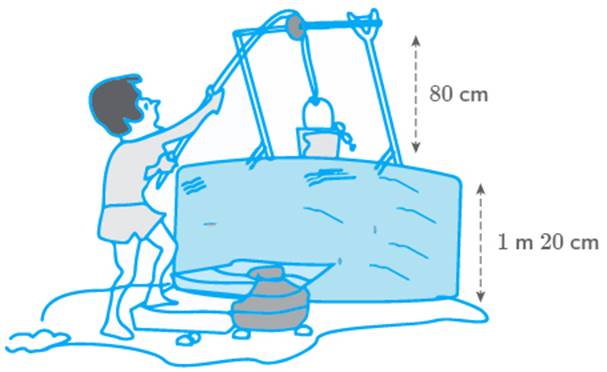
Water level in a well was $20\text{ m}$ below the ground level. During rainy season, rain water collected in different water tanks was drained into the well and the water level rises $5\text{ m}$ above the previous level. The wall of the well is $1\text{ m }20\text{ cm}$ high and a pulley is fixed at a height of $80\text{ cm}\text{.}$ Raghu wants to draw water from the well. The minimum length of the rope that he can use is

 

a. $17\text{ m}$

b. $18\text{ m}$

c.  $96\text{ m}$

d. $97\text{ m}$

(a)

Details given in the question, can be described in figure shown below

 

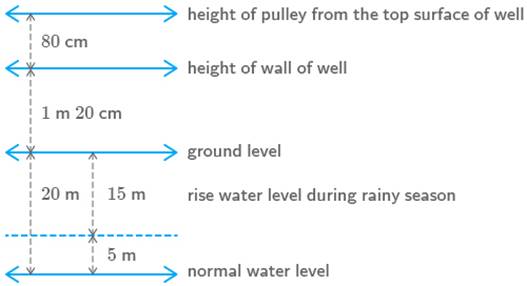
From the above figure, it is clear that minimum length of the rope required to draw the water during the rainy season $=$ Distance between pulley and wall of well $+$ Height of the wall of the well $+$ Distance between water level during rainy season and ground level

$=80\text{ cm}+1\text{ m }20\text{ cm}+15\text{ m}$

$\begin{array}{l}=\left(0.8+1.2+15\right)\text{ m}\mathrm{...}\\ \left[\because 1\text{ cm}=\frac{1}{100}\text{ m}=80\text{ cm}=\frac{80}{100}\text{m \& }1\text{ m }20\text{ cm}=1.20\text{ m}\right]\\ =17\text{ m}\end{array}$

$\left(-11\right)\times 7$ is not equal to

a. $11\times \left(-7\right)$

b. $-11\times 7$

c.  $\left(-11\right)\times \left(-7\right)$

d. $7\times \left(-11\right)$

(c)

Ex: $\left(-11\right)\times 7=\left(-77\right)$ (As we know, in multiplication, if sign of both numbers are different, then the sign of the resultant is negative and if sign of both numbers are same, then the sign of the resultant is positive.)

Option a. $11\times \left(-7\right)=-77$

Option b. $-11\times 7=-77$

Option c. $\left(-11\right)\times \left(-7\right)=77$

Option d. $7\times \left(-11\right)=-77$

$\left(-10\right)\times \left(-5\right)+\left(-7\right)$ is equal to

a. $-57$

b. $57$

c.  $-43$

d. $43$

(d)

$\begin{array}{c}\left(-10\right)\times \left(-5\right)+\left(-7\right)\\ =\left\{\left(-10\right)\times \left(-5\right)\right\}+\left(-7\right)\\ =50-7\\ =43\end{array}$

Which of the following is not the additive inverse of $a$?

a. $-\left(-a\right)$

b. $a\times \left(-1\right)$

c.  $-a$

d. $a÷\left(-1\right)$

(a)

Additive inverse of $a$ is $\left(-a\right).$ [additive inverse of an integer is the same integer value, with opposite sign] So,

Option a. $-\left(-a\right)=a$

Option b. $a\times \left(-1\right)=-a$

Option c. $-a$

Option d. $a÷\left(-1\right)=-a$

Which of the following is the multiplicative identity for an integer $a$?

a. $a$

b. $1$

c.  $0$

d. $-1$

(b)

Multiplicative identity for an integer a is $1.$ [a multiplicative identity is that identity in which any number is multiplied by that identity, it gives out the same number.]

$\left[\left(-8\right)\times \left(-3\right)\right]\times \left(-4\right)$ is not equal to

a. $\left(-8\right)\times \left[\left(-3\right)\times \left(-4\right)\right]$

b. $\left[\left(-8\right)\times \left(-4\right)\right]\times \left(-3\right)$

c.  $\left[\left(-3\right)\times \left(-8\right)\right]\times \left(-4\right)$

d. $\left(-8\right)\times \left(-3\right)-\left(-8\right)\times \left(-4\right)$

(d)

$\left[\left(-8\right)\times \left(-3\right)\right]\times \left(-4\right)$

$=\left[\left(-3\right)\times \left(-8\right)\right]\times \left(-4\right)$ $\dots$ as multiplication is commutative, i.e., $a\times b=b\times a$

$=\left(-3\right)\times \left(-8\right)\times \left(-4\right)$ $\dots$ (as multiplication is associative, i.e., $a\times \left(b\times c\right)=\left(a\times b\right)\times c$

$\begin{array}{l}=\left[\left(-8\right)\times \left(-4\right)\times \left(-3\right)\right]\\ =\left[\left(-8\right)\times \left(-4\right)\times \left(-3\right)\right]\\ =\left[\left(-8\right)\times \left(-3\right)\times \left(-4\right)\right]\end{array}$

Hence, $=\left[\left(-8\right)\times \left(-3\right)\times \left(-4\right)\right]$ is not equal to $\left(-8\right)\times \left(-3\right)-\left(-8\right)\times \left(-4\right)$

$\left(-25\right)\times \left[6+4\right]$ is not same as

a. $\left(-25\right)\times 10$

b. $\left(-25\right)\times 6+\left(-25\right)\times 4$

c.  $\left(-25\right)\times 6\times 4$

d. $-250$

(c)

$\left(-25\right)\times \left[6+4\right]=\left(-25\right)\times 10$

Also,

$\left(-25\right)\times \left[6+4\right]=-25\times 6+\left(-25\right)\times 4$

[using distributive property, i.e. $a\times \left(b+c\right)=a\times b+a\times c$ ] $=-150-100=-250$

Hence, $\left(-25\right)\times \left(6+4\right)$ is not same as $\left(-25\right)\times 6\times 4.$

$-35\times 107$ is not same as

a. $-35\times \left(100+7\right)$

b. $\left(-35\right)\times 7+\left(-35\right)\times 100$ 

c.  $-35\times 7+100$

d. $\left(-30-5\right)\times 107$

(c)

$-35\times 107=-35\times \left(100+7\right)$

$=\left(-35\right)\times 100+\left(-35\right)\times 7$ [using distributive property, i.e. $a\times \left(b+c\right)=a\times b+a\times c$ ]

$=\left(-35\right)\times 7+\left(-35\right)\times 100$ [as addition is commutative, i.e. $a+b=b+a$ ]

Also, $-35\times 107=\left(-30-5\right)\times \left(107\right)$

Hence, $-35\times 107$ is not same as $-35\times 7+100.$

$\left(-43\right)\times \left(-99\right)+43$ is equal to

a. $4300$

b. $-4300$

c.  $4257$

d. $-4214$

(a)

$\left(-43\right)\times \left(-99\right)+43=\left(-1\right)\left(43\right)\times \left(-99\right)+43$

$=43\left\{-\left(-99\right)+1\right\}$ (taking $43$ out as common)

$=43\left(99+1\right)=43\times 100=4300$

$\left(-16\right)÷4$ is not same as

a. $\left(-4\right)÷16$

b. $-\left(16÷4\right)$

c.  $16÷\left(-4\right)$

d. $-4$

(a)

$\begin{array}{l}\left(-16\right)÷4=-\left(16÷4\right)\\ =16÷\left(-4\right)\\ =\frac{16}{-4}\\ =-4\end{array}$

But division is not commutative, hence $\left(-16\right)÷4\ne \left(-4\right)÷16$

Which of the following does not represent an integer?

a. $0÷\left(-7\right)$

b. $20÷\left(-4\right)$

c.  $\left(-9\right)÷3$

d. $\left(-12\right)÷5$

(d)

An integer is a whole number (not a fractional number) that can be positive, negative or zero. So,

a. $\frac{0}{-7}=0$

b. $\frac{20}{-4}=-5$

c.  $\frac{-9}{3}=-3$

d. $\frac{-12}{5}$ (not an integer)

Which of the following is different from the others?

a. $20+\left(-25\right)$

b. $\left(-37\right)-\left(-32\right)$

c.  $\left(-5\right)\times \left(-1\right)$

d. $\left(45\right)÷\left(-9\right)$

(c)

Option a. $20+\left(-25\right)=20-25=-5$

Option b. $\left(-37\right)-\left(-32\right)=-37+32=-5$

Option c. $\left(-5\right)\times \left(-1\right)=5$

Option d. $\left(45\right)÷\left(-9\right)=\frac{45}{-9}=-5$

Which of the following shows the maximum rise in temperature?

a. $23°$ to $32°$

b. $-10°$ to $+1°$

c.  $-18°$ to $-11°$

d. $-5°$ to $5°$

(b)

Rise in temperature,

a. $32°-23°=9°$

b. $1°-\left(-10\right)°=1°+10°=11°$

c.  $-11°-\left(-18\right)°=-11°+18°=7°$

d. $5°-\left(-5°\right)=5°+5°=10°$

If $a$ and $b$ are two integers, then which of the following may not be an integer?

a. $a+b$

b. $a-b$

c.  $a\times b$

d. $a÷b$

(d)

Addition, subtraction and multiplication of two or more integers is always an integer. But, division of integers may or may not be an integer.

e.g. $2÷3=\frac{2}{3}$ (not an integer)

$3÷3=1$ (integer)

For a non-zero integer a, which of the following is not defined?

a. $a÷0$

b. $0÷a$

c.  $a÷1$

d. $1÷a$

(a)

Division of any number by zero is not defined, not defined $a÷0$.

 

Encircle the odd one of the following (Questions 26 to 30).

Encircle the odd one of the following

a. $\left(-3,3\right)$

b. $\left(-5,5\right)$

c.  $\left(-6,1\right)$

d. $\left(-8,8\right)$

(c)

Among all the options each pair of integers give the same value ( $–1$ ) of $a÷b$ except the option (c). So, odd one is option c.

Encircle the odd one of the following

a. $\left(-1,-2\right)$

b. $\left(-5,+2\right)$

c.  $\left(-4,+1\right)$

d. $\left(-9,+7\right)$

(d)

By observation, we can say that the sum of both values is same in options a, b and c. So, odd one is option d.

Encircle the odd one of the following.

a. $\left(-9\right)\times 5\times 6\times \left(-3\right)$

b. $9\times \left(-5\right)\times 6\times \left(-3\right)$

c.  $\left(-9\right)\times \left(-5\right)\times \left(-6\right)\times 3$

d. $9\times \left(-5\right)\times \left(-6\right)\times 3$

(c)

a. $\left(-9\right)\times 5\times 6\times \left(-3\right)=\left(-45\right)\times \left(-18\right)=810$

b. $9\times \left(-5\right)\times 6\times \left(-3\right)=\left(-45\right)\times \left(-18\right)=810$

c.  $\left(-9\right)\times \left(-5\right)\times \left(-6\right)\times 3=45\times \left(-18\right)=-810$

d. $9\times \left(-5\right)\times \left(-6\right)\times 3=\left(-45\right)\times \left(-18\right)=810$

So, odd one is option c.

Encircle the odd one of the following

a. $\left(-100\right)÷5$

b. $\left(-81\right)÷9$

c.  $\left(-75\right)÷5$

d. $\left(-32\right)÷9$

(d)

a. $-\frac{100}{5}=-20$

b. $-\frac{81}{9}=-9$

c.  $-\frac{75}{5}=-15$

d. $-\frac{32}{9}$

Here, option a, b and c are the negative integers, but option d is not the negative integer. So, odd one is option d.

Encircle the odd one of the following

a. $\left(-1\right)\times \left(-1\right)$

b. $\left(-1\right)\times \left(-1\right)\times \left(-1\right)$

c.  $\left(-1\right)\times \left(-1\right)\times \left(-1\right)\times \left(-1\right)$

d. $\left(-1\right)\times \left(-1\right)\times \left(-1\right)\times \left(-1\right)\times \left(-1\right)\times \left(-1\right)$

(b)

a. $\left(-1\right)\times \left(-1\right)=1$

b. $\left(-1\right)\times \left(-1\right)\times \left(-1\right)=-1$

c.  $\left(-1\right)\times \left(-1\right)\times \left(-1\right)\times \left(-1\right)=1$

d. $\left(-1\right)\times \left(-1\right)\times \left(-1\right)\times \left(-1\right)\times \left(-1\right)\times \left(-1\right)=1$

Hence, value of options a, c, d, is same but value of option b is different.

 

In Questions 31 to 71, fill in the blanks to make the statements true.

$\left(-a\right)+b=b+$ Additive inverse of _______.

Additive inverse of a number is the negative of that number.

As we know, addition is commutative for integers, i.e. $-a+b=b+\left(-a\right)$

Now, ‘ $-a$ ’ is the additive inverse of $a.$ So, ‘a’ will be the answer.

_______ $÷\left(-10\right)=0$

Division of $0$ by any number, result as zero. So, the answer is $0.$

$\left(-157\right)\times \left(-19\right)+157=$ _______

$\begin{array}{l}\left(-157\right)\times \left(-19\right)+157\\ =\left(-1\right)\times \left(157\right)\times \left(-19\right)+157\end{array}$

$=157\left\{-\left(-19\right)+1\right\}$    [taking $157$ out as common]

$\begin{array}{l}=157\left\{19+1\right\}=157\times 20\\ =3140\end{array}$

$\begin{array}{l}\left[\left(-8\right)+\_\_\_\_\_\_\_\right]+\_\_\_\_\_\_\_\\ =\_\_\_\_\_\_\_+\left[\left(-3\right)+\_\_\_\_\_\_\_\right]\\ =-3\end{array}$

$\left[\left(-8\right)+\left(-3\right)\right]+8=\left(-8\right)+\left[\left(-3\right)+8\right]$$=-3$

[addition is associative for integers, i.e. $[a+\left(b+c\right)]=[a+(b+c)]$ ]

On the following number line, $\left(-4\right)\times 3$ is represented by the point _______.

 

$\left(-4\right)\times 3=\left(-12\right)$

On the number line, each division has equal spacing of $2$ units.

So, $\text{A}=-20+2=-18$

$\begin{array}{l}\text{B}=-18+2=-16\\ \text{C}=-16+2=-14\\ \text{D}=-14+2=-12\end{array}$

Hence, $\left(-4\right)\times 3$ is represented by the point D.

If $x,y$ and $z$ are integers, then $(x+\_\_\_\_\_\_\_)+z=\_\_\_\_+(y+\_\_\_\_\_\_\_)$

Addition is associative for integers,

i.e. $\left(a+b\right)+c=a+\left(b+c\right)$

$\left(x+y\right)+z=x+\left(y+z\right)$

$(-43)+\_\_\_\_\_\_\_=-43$

Zero $\left(0\right)$ is an additive identity for integers, i.e. $a+0=0+a=a$ for any integer $a.$

So, $(-43)+0=-43$

$(-8)+(-8)+(-8)=\_\_\_\_\_\_\_\times (-8)$

Let $x$ be the missing number.

Then, $-8-8-8=x\times (-8)$

$\begin{array}{c}-24=x\times (-8)\\ =\frac{-24}{-8}=x\\ x=3\end{array}$

Hence, $(-8)+(-8)+(-8)=3\times (-8)$

$11\times \left(-5\right)=-\left(\_\_\_\_\_\_\_\times \_\_\_\_\_\_\_\right)=\_\_\_\_\_\_\_$

We can write the equation as, $11\times \left(-5\right)=-\left(11\times 5\right)=-55$

$\left(-9\right)\times 20=\_\_\_\_\_\_\_$

$\left(-9\right)\times 20=-180$

[In multiplication of integers, if both the numbers have different signs, then the result is a negative number.]

$(-23)\times (42)=\left(-42\right)\times \_\_\_\_\_\_\_$

$\begin{array}{l}(-23)\times (42)\\ =\left(-1\right)\times \left(23\right)\times \left(42\right)\end{array}$

$=\left(-1\right)\times \left(42\right)\times \left(23\right)$

[Multiplication is commutative, i.e. $a\times b=b\times a$ ] $=\left(-42\right)\times \left(23\right)$

While multiplying a positive integer and a negative integer, we multiply them as _______ numbers and put a _______ sign before the product.

When multiplying a positive integer and a negative integer, we multiply them as whole numbers and put a negative sign before the product.

If we multiply _______ number of negative integers, then the resulting integer is positive.

If we multiply even numbers of negative integers, then the resulting integer is positive.

If we multiply six negative integers and six positive integers, then the resulting integer is _______.

If we multiply six negative integers and six positive integers, then the resulting integer is positive. [Because the product of even negative integers is a positive integer]

If we multiply five positive integers and one negative integer, then the resulting integer is _______.

If we multiply 5 positive integers and one negative integer, then the resulting integer is negative.

_______ is the multiplicative identity for integers.

$1$ is the multiplicative identity for integers, i.e. $a\times 1=1\times a=a$ for any integer $a$.

We get additive inverse of an integer $a$ when we multiply it by _______.

Additive inverse of an integer is the same integer value, with opposite sign. So, we get additive inverse of integer $a$, when we multiply it by ‘ $-1$ ’.

$\left(-25\right)\times \left(-2\right)=$ _______

Two negative integers make the resultant integer, positive.

$\left(-25\right)\times \left(-2\right)=50$

$\left(-5\right)\times \left(-6\right)\times \left(-7\right)=$ _______

Odd negative integers make the resultant integer, negative.

$\left(-5\right)\times \left(-6\right)\times \left(-7\right)=30\times \left(-7\right)=-210$

$3\times \left(-1\right)\times \left(-15\right)=$ _______

Two negative integers and one positive integer make the resultant integer, positive.

$3\times \left(-1\right)\times \left(-15\right)=\left(-3\right)\times \left(-15\right)=45$

$\left[12\times \left(-7\right)\right]\times 5=\_\_\_\_\_\_\_\times \left[\left(-7\right)\times \_\_\_\_\_\_\_\right]$

Multiplication is associative for integers, i.e. $\left(a\times b\right)\times c=a\times \left(b\times c\right)$

So, $\left[12\times \left(-7\right)\right]\times 5=12\times \left[\left(-7\right)\times 5\right]$

$\begin{array}{l}23\times \left(-99\right)\\ =\_\_\_\_\_\_\_\times \left(-100+\_\_\_\_\_\_\_\right)\\ =23\times \_\_\_\_\_\_\_+23\times \_\_\_\_\_\_\_\end{array}$

We can write the equation as,

$23\times \left(-99\right)=23\times \left(-100+1\right)=23\times \left(-100\right)+23\times 1$

[Integers show distributive property of multiplication over addition, i.e. $a\times \left(b+c\right)=a\times b+a\times c$ ]

_______ $\times \left(-1\right)=-35$

$-35\times \left(-1\right)=35\left[i.e\frac{-35}{-1}=35\right]$

_______ $\times \left(-1\right)=47$

$\left(-47\right)\times \left(-1\right)=47\left[\because \frac{47}{-1}=-47\right]$

$88\times \_\_\_\_\_\_\_=-88\_\_\_\_\_\_\_$

$88\times \left(-1\right)=-88\left[\because \frac{-88}{88}=\left(-1\right)\right]$

_______ $\times \left(-93\right)=93$

$\left(-1\right)\times \left(-93\right)=93\left[\because \frac{93}{-93}=\left(-1\right)\right]$

$\left(-40\right)\times \_\_\_\_\_\_\_=80\_\_\_\_\_\_\_$

$\left(-40\right)\times \left(-2\right)=80\left[\because \frac{80}{-40}=\left(-2\right)\right]$

_______ $\times \left(-23\right)=-920$

$40\times \left(-23\right)=-920\left[\because \left(-\frac{920}{-23}\right)=40\right]$

When we divide a negative integer by a positive integer, we divide them as whole numbers and put a _______ sign before quotient.

When we divide a negative integer by a positive integer or a positive integer by a negative integer, we divide them as whole numbers and put a minus sign before quotient.

When $-16$ is divided by _________ the quotient is $4$.

$-4$

When $-16$ is divided by negative integer, i.e., $-4$ the quotient is $4$ as both signs are cancelled out.

Division is the inverse operation of _______

Division is the inverse operation of multiplication.

$65÷\left(-13\right)=$ _______

$65÷\left(-13\right)$

$=65\times \frac{1}{-13}$    [division is inverse of multiplication]

$=-5$

$\left(-100\right)÷\left(-10\right)=$ _______

$\left(-100\right)÷\left(-10\right)$

$=\left(-100\right)\times \frac{1}{-10}$    [division is inverse of multiplication]

$=\left(10\right)$

$\left(-225\right)÷5=$ _______

$\left(-225\right)÷5$

$=-225\times \frac{1}{5}$     [division is inverse of multiplication]

$=-45$

_______ $÷\left(-1\right)=-83$

$83÷\left(-1\right)=-83\left[\because \frac{-83}{-1}=83\right]$

_______ $÷\left(-1\right)=75$

$-75÷\left(-1\right)=75\left[\because \frac{75}{-1}=\left(-75\right)\right]$

$51÷\_\_\_\_\_\_\_=-51$

$51÷\left(-1\right)=-51\left[\because \frac{51}{-51}=\left(-1\right)\right]$

$113÷\_\_\_\_\_\_\_=-1$

$113÷\left(-113\right)=-1\left[\because \frac{113}{-1}=\left(-113\right)\right]$

$\left(-95\right)÷\_\_\_\_\_\_\_=95$

$\left(-95\right)÷\left(-1\right)=95\left[\because \frac{-95}{95}=\left(-1\right)\right]$

$\left(-69\right)÷\left(69\right)=$ _______

$\left(-69\right)÷\left(69\right)=\left(-1\right)$

$\left(-28\right)÷\left(-28\right)=$ _______

$\left(-28\right)÷\left(-28\right)=1$

 

In Questions 72 to 108, state whether the statements are True or False.

$5-\left(-8\right)$ is same as $5+8.$

True

$5-\left(-8\right)=5+8$

$\left(-9\right)+\left(-11\right)$ is greater than $\left(-9\right)-\left(-11\right).$

False

$\left(-9\right)+\left(-11\right)=-9-11=-20$

And $\left(-9\right)-\left(-11\right)=-9+11=2$

So, $\left(-9\right)-\left(-11\right)$ is greater than $\left(-9\right)+\left(-11\right).$

Sum of two negative integers always gives a number smaller than both the integers.

True

e.g. Taking two negative integers, i.e. $\left(-5\right)$ and $\left(-3\right).$

$\left(-5\right)+\left(-3\right)=-5-3=-8$

$=-8<-5$ and $-8<-3$

Difference of two negative integers cannot be a positive integer.

False

e.g. Taking two negative integers,

i.e. $-4$ and $-5.$

$-4-\left(-5\right)=-4+5=1$

We can write a pair of integers whose sum is not an integer.

False

Because, sum of two integers is always be an integer.

Integers are closed under subtraction.

True

Because, if we subtract two integers, we get another integer.

$\left(-23\right)+47$ is same as $47+\left(-23\right).$

True

Because, addition is commutative, i.e. $a+b=b+a$

$\left(-23\right)+47=47+\left(-23\right)$

When we change the order of integers, their sum remains the same.

True

Because, sum of two integers is commutative, i.e. $a+b=b+a$ for two integers $a$ and $b$

When we change the order of integers their difference remains the same.

False

Subtraction of two integers is not commutative, i.e. $a-b\ne b-a$ for two integers $a$ and $b$

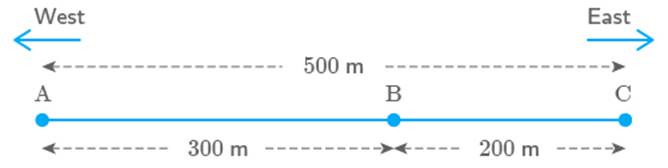
Going $500\text{ m}$ towards east first and then $200\text{ m}$ back is same as going $200\text{ m}$ towards west first and then going $500\text{ m}$ back.

True

Case I: Going $500\text{ m}$ towards East first, i.e. point A to C and then $200\text{ m}$ back, i.e. C to B.

Case 2: Going $200\text{ m}$ towards West, i.e. A to D and then $500\text{ m}$ back, i.e. D to B.

 

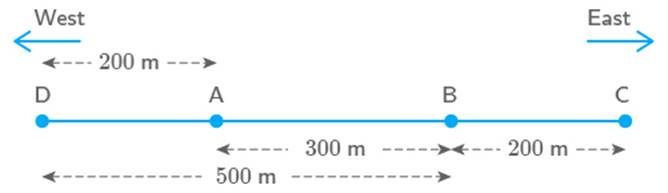
As per the above figures, final position is B, i.e., $300\text{ m}$ in East.

$\left(-5\right)\times \left(33\right)=5\times \left(-33\right)$

True

LHS $=\left(-5\right)\times 33=\left(-165\right)$ and

RHS $=5\times \left(-33\right)=\left(-165\right)$

Hence, LHS $=$ RHS

$\left(-19\right)\times \left(-11\right)=19\times 11$

True

Product of two negative integers is a positive integer, i.e. $\left(-a\right)\times \left(-b\right)=a\times b$.

$\left(-20\right)\times \left(5-3\right)=\left(-20\right)\times \left(-2\right)$

False

LHS $=\left(-20\right)\times \left(5-3\right)=\left(-20\right)\times 2=\left(-40\right)$

RHS $=\left(-20\right)\times \left(-2\right)=40$

Hence, $\text{LHS}\ne \text{RHS}$

$4\times \left(-5\right)=\left(-10\right)\times \left(-2\right)$

False

LHS $=4\times \left(-5\right)=-20$

RHS $=\left(-10\right)\times \left(-2\right)=20$

Hence, $\text{LHS}\ne \text{RHS}$

$\left(-1\right)\times \left(-2\right)\times \left(-3\right)=1\times 2\times 3$

False

$\because \text{LHS}=\left(-1\right)\times \left(-2\right)\times \left(-3\right)=\left(-6\right)$

RHS $=1\times 2\times 3=6$

Hence, $\text{LHS}\ne \text{RHS}$

$-3\times 3=-12-\left(-3\right)$

True

LHS $=\left(-3\right)\times 3=\left(-9\right)$

RHS $=\left(-12\right)-\left(-3\right)=\left(-12\right)+3=\left(-9\right)$

Hence, LHS $=$ RHS

Product of two negative integers is a negative integer.

False

Product of two negative integers is a positive integer,

i.e. $\left(-a\right)\times \left(-b\right)=ab$.

Product of three negative integers is a negative integer.

True

Product of three negative integers is a negative integer.

i.e. $\left(-a\right)\times \left(-b\right)\times \left(-c\right)=\left(-abc\right)$.

Product of a negative integer and a positive integer is a positive integer.

False

Product of a negative integer and a positive integer is a negative integer, i.e. $a\times \left(-b\right)=-ab$ 

When we multiply two integers their product is always greater than both the integers.

False

e.g. Let two integers be $\left(-5\right)$ and $2.$

So, $\left(-5\right)\times 2=-10$

$\left(-10\right)<\left(-5\right)$ and $\left(-10\right)<2.$

Integers are closed under multiplication.

True

If we multiply two integers, we get an integer.

e.g. $3\times 5=15$ 

3 and 5 are integers and their product 15 is also an integer.

Also, $-1\times 0=0$ 

Where, 0 is also an integer.

So, integers are closed under multiplication.

$\left(-237\right)\times 0$ is same as $0\times \left(-39\right)$.

True

When we multiply a number with $0\text{,}$ we always get $0.$

$\left(-237\right)\times 0=0$

$0\times \left(-39\right)$ = 0

Multiplication is not commutative for integers.

False

Multiplication is commutative for integers, i.e. $a\times b=b\times a$ 

Where $a\text{ and }b$ are integers.

$\left(-1\right)$ is not a multiplicative identity of integers.

True

$1$ is multiplicative identity of integers, i.e. $a\times 1=1\times a=a$ for any integer $a\text{.}$

$99\times 101$ can be written as $\left(100-1\right)\times \left(100+1\right)$

True

$\because 99\times 101=9999$ and $\left(100-1\right)\times \left(100+1\right)$

$=100\times \left(100+1\right)-1\times \left(100+1\right)$

$=100\times 100+1\times 100-1\times 100-1\times 1$   
    [using distributive property]

$=10000+100-100-1=9999$

If $a,b,c$ are integers and $b\ne 0$ then, $a\times \left(b-c\right)=a\times b-a\times c$

True

Multiplication can be distributive over subtraction, i.e. $a\times \left(b-c\right)=a\times b-a\times c$

where a, b and c are integers.

$\left(a+b\right)\times c=a\times c+a\times b$

False

Integers show distributive property of multiplication over addition, i.e. $\left(a+b\right)\times c=a\times c+b\times c$, where $a,b$ and $c$ are integers.

$a\times b=b\times a$

True

Multiplication is commutative for integers, i.e. $a\times b=b\times a$ where $a$ and $b$ are integers.

$a÷b=b÷a$

False

Division is not commutative for integers, i.e. $a÷b\ne b÷a$ where $a$ and $b$ are integers.

$a-b=b-a$

False

Subtraction is not commutative for integers, i.e. $a-b\ne b-a$ where $a$ and $b$ are integers.

$a÷\left(-b\right)=-\left(a÷b\right)$

True

Division of a negative integer and positive integer is always a negative integer i.e., $\frac{a}{-b}=\frac{-b}{a}=-\left(\frac{a}{b}\right)$ where $a$ and $b$ are integers.

$a÷\left(-1\right)=-a$

True

$a÷\left(-1\right)=\frac{a}{-1}=-a$ [as division of a negative and positive integer is always negative integer.]

Multiplication fact $\left(-8\right)\times \left(-10\right)=80$ is same as division fact $80÷\left(-8\right)=\left(-10\right)$

True

Integers are closed under division.

False

Because, when we divide two integers, we may or may not get an integer. e.g. $\frac{2}{1}=2$ (integer) and $\frac{2}{3}$ (not an integer).

$\left[\left(-32\right)÷8\right]÷2=-32÷\left[8÷2\right]$

False

LHS $=\left[\left(-32\right)÷8\right]÷2$

$\begin{array}{l}=\left[\frac{-32}{8}\right]÷2\\ =-4÷2\\ =-2\end{array}$

And RHS $=\left(-32\right)+\left[8÷2\right]$

$\begin{array}{l}=\left(-32\right)+\left[\frac{8}{2}\right]\\ =\left(-32\right)÷4\\ =\frac{-32}{4}\\ =-8\end{array}$

Hence, $\text{LHS}\ne \text{RHS}$

The sum of an integer and its additive inverse is zero $\left(0\right)\text{.}$

True

Additive inverse is the number that when added to a given number yields zero.

The successor of $0\times \left(-25\right)$ is $1\times \left(-25\right)$

False

We know that, successor means adding $1$ to the given number.

Here, given number is $0\times \left(-25\right)=0$ [On multiplying by $0$ to any number the result is zero]

Hence, the successor of $0=0+1=1$ but $1\ne 1\times \left(-25\right)$

Observe the following patterns and fill in the blanks to make the statements true:

a. $-5\times 4=-20$

$\begin{array}{l}-5\times 3=-15=-20-\left(-5\right)\\ -5\times 2=\_\_\_\_\_\_\_=-15-\left(-5\right)\\ -5\times 1=\_\_\_\_\_\_\_=\_\_\_\_\_\_\_\\ -5\times 0=0=\_\_\_\_\_\_\_\\ -5\times -1=5=\_\_\_\_\_\_\_\\ -5\times -2=\_\_\_\_\_\_\_=\_\_\_\_\_\_\_\end{array}$

b. $7\times 4=28$

$\begin{array}{l}7\times 3=\_\_\_\_\_\_\_=28-7\\ 7\times 2=\_\_\_\_\_\_\_=\_\_\_\_\_\_\_-7\\ 7\times 1=7=\_\_\_\_\_\_\_-7\\ 7\times 0=\_\_\_\_\_\_\_=\_\_\_\_\_\_\_-\_\_\_\_\_\_\_\\ 7\times -1=-7=\_\_\_\_\_\_\_-\_\_\_\_\_\_\_\\ 7\times -2=\_\_\_\_\_\_\_=\_\_\_\_\_\_\_-\_\_\_\_\_\_\_\\ 7\times -3=\_\_\_\_\_\_\_=\_\_\_\_\_\_\_-\_\_\_\_\_\_\_\end{array}$

a. $-5\times 2=-10=-15-\left(-5\right)$

$\begin{array}{l}-5\times 1=-5=-10-\left(-5\right)\\ -5\times 0=0=-5-\left(-5\right)\\ -5\times -1=5=0-(-5)\\ -5\times -2=10=5-(-5)\end{array}$

b. $7\times 3=21=28-7$

$\begin{array}{l}7\times 2=14=21-7\\ 7\times 1=7=14-7\\ 7\times 0=0=7-7\\ 7\times -1=-7=0-7\\ 7\times -2=-14=-7-7\\ 7\times -3=-21=-14-7\end{array}$

Science Application: An atom consists of charged particles called electrons and protons. Each proton has a charge of $+1$ and each electron has a charge of $-1.$ Remember number of electrons is equal to number of protons, while answering these questions:

a. What is the charge on an atom?

b. What will be the charge on an atom if it loses an electron?

c.  What will be the charge on an atom if it gains an electron?

a. Let ‘a’ be the number of electrons in an atom.

Number of protons in the atom, will also be equal to a. Since, an atom has equal number of protons and electrons.

$\therefore$ Charge on one electron $=\left(-1\right)$

$\therefore$ Total charge in a electrons $=a\times \left(-1\right)=-a$

$\therefore$ Charge on one proton $=\left(+1\right)$

$\therefore$ Total charge in a protons $=a\times \left(+1\right)=+a$

Hence, total charge on the atom

$=$ Charge of electrons $+$ Charge of protons $=-a+a=0$

b. If an atom loses an electron, it will have $\left(a-1\right)$ electrons and a protons.

$\therefore$ Charge in one electron $=\left(-1\right)$

$\therefore$ Charge in $\left(a-1\right)$ electrons $=\left(a-1\right)\times \left(-1\right)=-\left(a-1\right)=\left(1-a\right)$

$\therefore$ Charge in one proton $=\left(+1\right)$

Charge in a protons $=\left(+1\right)\times a=\left(+a\right)$

Hence, total charge on the atom $=$ Charge of electrons $+$ Charge of protons

                                $=1-a+a=+1$

c.  If an atom gains an electron, it will have $\left(a+1\right)$ electrons and a protons

$\therefore$ Charge in one electron $=-1$

Charge in $\left(a+1\right)$ electrons $=-1\times \left(a+1\right)=-\left(a+1\right)$

$\therefore$ Charge in one proton $=\left(+1\right)$

Charge in a protons $=\left(+1\right)\times a=\left(+a\right)$

Hence, total charge on the atom $=$ Charge of electrons $+$ Charge of protons

                                $=a-\left(a+1\right)=\left(-1\right)$

An atom changes to a charged particle called ion if it loses or gains electrons. The charge on an ion is the charge on electrons plus charge on protons. Now, write the missing information in the table given below:

a. For Hydroxide ion,

Proton charge $+$ Electron charge $=$ lon charge

Electron charge $=$ lon charge – Proton charge

Electron charge $=-1-9=-10$

Hence, the electron charge in a Hydroxide ion is $-10.$

b. For Sodium ion,

Electron charge $=$ lon charge — Proton charge $=+1-11=-10$

Hence, the electron charge in a Sodium ion is $-10.$

c.  For Aluminium ion,

lon charge $=$ Proton charge $+$ Electron charge

lon charge $=13-10=3$

Hence, the ion charge in an Aluminium ion is $3$

d. For Oxide ion,

lon charge $=$ Proton charge $+$ Electron charge lon charge $=8-10=-2$

Hence, the ion charge in an Oxide ion is $-2$

Social Studies Application: Remembering that $1\text{ AD}$ came immediately after $1\text{ BC}$, while solving these problems take $1\text{ BC}$ as $-1$ and $1\text{ AD}$ as $+1.$

a. The Greeco-Roman era, when Greece and Rome ruled Egypt started in the year $330\text{ BC}$ and ended in the year $395\text{ AD}$. How long did this era last?

b. Bhaskaracharya was born in the year $1114\text{ AD}$ and died in the year $1185\text{ AD}\text{.}$ What was his age when he died?

c.  Turks ruled Egypt in the year $1517\text{ AD}$ and Queen Nefertis ruled Egypt about $2900$ years before the Turks ruled. In what year did she rule?

d. Greek mathematician Archimedes lived between $287\text{ BC}$ and $212\text{ BC}$ and Aristotle lived between $380\text{ BC}$ and $322\text{ BC}\text{.}$ Who lived during an earlier period?

a. The era lasted for

$\begin{array}{l}395\text{ AD}-330\text{ BC}\\ =395-(-330)\\ =395+330\\ =725\text{ years}\end{array}$ 

b. Bhaskaracharya's age when he died was $1185-1114=71$ years.

c.  Queen Nefertis ruled Egypt in the year $1517-2900=-1383=1383\text{ BC}$

d. Aristotle lived earlier as $380\text{ BC}$ comes before $287\text{ BC}$.

The table shows the lowest recorded temperatures for each continent. Write the continents in order from the lowest recorded temperature to the highest recorded temperature.

 

Lowest to heights (ascending order) in a negative number, the number that has greater value of actually smaller and vice-versa. So, accordingly, we arrange them in ascending order as $-129°<-90°<-81°<-67°<-27°<-11°<-9°$ i.e.

Antarctica $<$ Asia $<$ North America $<$ Europe
$<$ South America $<$ Africa $<$ Australia.

Write a pair of integers whose product is $-12$ and there lies seven integers between them (excluding the given integers).

For a pair of integers, whose product is $-12$ and there lies seven integers between them excluding given integers, only two solutions are possible, i.e. $(-6$ and $2)$ and $(-2$ and $6)$.

$-6\times 2=-12,-2\times 6=-12$

1^st Pair: Let 1^st integer $=-6$ & 2^nd integer $=2$

$-6\times 2=-12$ & $7$ integers are lying between them.

2^nd Pair: Let 1^st integer $=-2$ & 2^nd integer $=6$

$-2\times 6=-12$ & $7$ integers are lying between them.

From given integers in Column I match an integer of Column II so that their product lies between $-19$ and $-6$:

$-5\times 3=\left(-15\right)$ which lies between $-19$ and $-6$

$6\times \left(-2\right)=\left(-12\right)$ which lies between $-19$ and $-6$

$-7\times 1=\left(-7\right)$ which lies between $-19$ and $-6$

$8\times \left(-1\right)=\left(-8\right)$ which lies between $-19$ and $-6$

Write a pair of integers whose product is $-36$ and whose difference is $15.$

For a pair of integers, whose product is $-36$ and whose difference is $15$, one possible solution is $\left(-3,12\right)\text{.}$

So, first integer $=-3$ and second integer $=12$

Their product $=\left(-3\right)\times 12=-\left(3\times 12\right)=-36$ and the difference between these two integers is $=12-\left(-3\right)=15.$

Match the following

a. vi. $a\times 1=a$

b. iii. $1$ is multiplicative identity

c.  v.  Both sign are cancelled with each other

d. vii. $a\times \left(-1\right)=-a$

e.  Viii. Any value which is multiplied by $0$ becomes $0$

f.   iv. $\left(-a\right)÷b=a÷\left(-b\right)$

g. ii.  $0$ is an additive identity

h. ix  $a÷\left(-a\right)=\frac{a}{-a}=-1$

i.   i.  $-a$ is additive inverse of $a$

You have $\text{Rs}500$ in your savings account at the beginning of the month. The record below shows all of your transactions during the month. How much money is in your account after these transactions?

According to the question, Already available amount $=\text{Rs}500$

On $\frac{4}{9}$ with cheque number $\text{384102}$ withdraw $\text{Rs}120.$

Also, with cheque number $\text{275146}$ on $\frac{12}{9}$ deposited amount was $\text{Rs}200.$

In the same way, on $\frac{22}{9}$ with cheque number $\text{384103,}$ $\text{Rs}240$ paid to LIC of India, also.

On $\frac{29}{9}$ with cheque number $\text{801351}$, deposited amount was $\text{Rs}150.$

Thus, net amount available in bank account will be $=$ Already saved amount $+$ Deposited amount $-$ Debited amount (paid amount) $=500+200+150-120-240=850+\left(-360\right)$

$=\text{Rs}490$

a. Write a positive integer and a negative integer whose sum is a negative integer.

b. Write a positive integer and a negative integer whose sum is a positive integer.

c.  Write a positive integer and a negative integer whose difference is a negative integer.

d. Write a positive integer and a negative integer whose difference is a positive integer.

e.  Write two integers which are smaller than $-5$ but their difference is $-5.$

f.   Write two integers which are greater than $-10$ but their sum is smaller than $-10.$

g. Write two integers which are greater than $-4$ but their difference is smaller than $-4.$

h. Write two integers which are smaller than $-6$ but their difference is greater than $-6.$

i. Write two negative integers whose difference is $7.$

j. Write two integers such that one is smaller than $-11\text{,}$ and other is greater than $-11$ but their difference is $-11.$

k. Write two integers whose product is smaller than both the integers.

l. Write two integers whose product is greater than both the integers.

a. A number of solutions can be possible. e.g.

Let first integer $=4$ and second integer $=\left(-6\right)$

Sum $=4+\left(-6\right)=-2$    [negative integer]

b. A number of solutions can be possible.

e.g. Let first integer $=8$ and second integer $=-2$

Sum $=8+\left(-2\right)=6$    [positive integer]

c.  A number of solutions can be possible.

e.g. Let first integer $=\left(-7\right)$ and second integer $=2$

Difference $=\left(-7-2\right)=\left(-9\right)$    [negative integer]

d. A number of solutions can be possible.

e.g. Let first integer $=4$ and second integer $=\left(-3\right)$    

Difference $=4-\left(-3\right)=7\left[\text{positive integer}\right]$

e.  For two integers, which are smaller than $-5$ but their difference is $-5.$

Let first integer $=-11$ and second integer $=\left(-6\right)[\because -11<\left(-5\right)$ and $-6<\left(-5\right)]$

Difference $=-11-\left(-6\right)=-11+6=\left(-5\right)$

f.   For two integers which are greater than $-10$ but their sum is smaller than $-10.$ Let first integer $=-4$ and second integer $=-7[\because -4>\left(-10\right)$ and $-7>-10]$

Sum $=-4+\left(-7\right)=-11<-10$

g. For two integers which are greater than $-4$ but their difference is smaller than $-4.$

Let first integer $=\left(-1\right)$ and second integer $=4[\because -1>-4$ and $4>-4]$

Difference $=-1-4=-5$

h. For two integers which are smaller than $-6$ but their difference is greater than $-6.$

e.g. Let first integer $=\left(-8\right)$ and second integer $=\left(-9\right)[\because -8<-6$ and $-9<-6]$

Difference $=-8-\left(-9\right)=-8+9=1>\left(-6\right)$

i. A number of solutions can be possible.

e.g. Let first integer $=\left(-3\right)$ and second integer $=\left(-10\right)$

Difference $=-3-\left(-10\right)=7$

j. For two integers, such that one is smaller than $-11$ and other is greater than $-11$.

Let first integer $=-20$ and second integer $=-9[\because -20<-11$ and $-9>-11]$

Difference $=-20-(-9)=\left(-11\right)$

k. A number of solutions can be possible.

e.g. Let first integer $=-3$ and second integer $=5$

Product $=-3\times 5=-15[\because -15<-3$ and $-15<5]$

l. A number of solutions can be possible. e.g.

Let first integer $=4$ and second integer $=6$

Product $=6\times 4=24[\because 24>6$ and $24>4]$

What’s the Error? Ramu evaluated the expression $-7-\left(-3\right)$ and came up with the answer $-10.$ What did Ramu do wrong?

Ramu went wrong in solving $-\left(-3\right)$ and took it as $-3$ only.

Correct answer $=-7-\left(-3\right)=-7+3=-4$

What’s the Error? Reeta evaluated $-4+d$ for $d=-6$ and gave an answer of $2.$ What might Reeta have done wrong?

Reeta went wrong in solving $+\left(-6\right)$ and took it as $+6.$

Correct answer $=-4+d$

$\begin{array}{l}=-4+\left(-6\right)\\ =-4-6\\ =-10\end{array}$

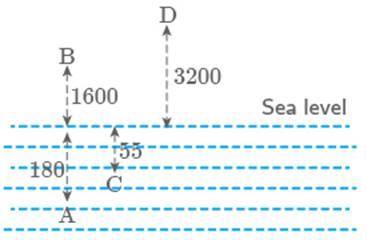
The table given below shows the elevations relative to sea level of four locations.

Taking sea level as zero, answer the following questions:

 

a. Which location is closest to sea level?

b. Which location is farthest from sea level?

c.  Arrange the locations from the least to the greatest elevation.

a. From the adjacent figure, we can clearly see that C is closest to sea level.

b. D is a farthest from sea level.

c.  Location from the least to the greatest elevation will be in the order A, C, B and D.

You are at an elevation $380\text{ m}$ above sea level as you start a motor ride. During the ride, your elevation changes by the following metres: $540\text{ m,}-268\text{ m,}$ $116\text{ m,}-152\text{ m, }490\text{m,}-844\text{m},94\text{m}\text{.}$ What is your elevation relative to the sea level at the end of the ride?

As per the given information, initial position of motor was $380\text{ m}\text{.}$

During the ride, changes in elevation was $540\text{ m,}$ $-268\text{ m,}$ $116\text{ m,}-152\text{ m, }490\text{ m,}-844\text{ m},94\text{m}\text{.}$ Net change in position $=540+\left(-268\right)+\left(116\right)$ $+\left(-152\right)+\left(490\right)+\left(-844\right)+\left(94\right)=-24\text{ m}$ Initial position was $380\text{ m}\text{.}$ So, at the end of the ride the position would be $=380+\left(-24\right)=356\text{ m}$

Evaluate the following, using distributive property.

a. $-39\times 99$

b. $\left(-85\right)\times 43+43\times \left(-15\right)$

c.  $53\times \left(-9\right)-\left(-109\right)\times 53$

d. $68\times \left(-17\right)+\left(-68\right)\times 3$

a. $-39\times 99$

$\left(-40+1\right)\times \left(100-1\right)$

Now, using distributive property

$\begin{array}{l}=\left(-40\times 100\right)+\left(-1\times -40\right)+\left(1\times 100\right)+\left(1\times -1\right)\\ =-4000+40+100-1\\ =-3861\end{array}$

b. $\left(-85\right)\times 43+43\times \left(-15\right)$

Taking $43$ out as common

$\begin{array}{l}=43\times \left(-85-15\right)\\ =43\times \left(-100\right)\\ =-4300\end{array}$

c.  $53\times \left(-9\right)-\left(-109\right)\times 53$

Taking $53$ out as common

$\begin{array}{l}=53\times \left[-9-\left(-109\right)\right]\\ =53\times \left(-9+109\right)\\ =53\times 100\\ =5300\end{array}$

d. $68\times \left(-17\right)+\left(-68\right)\times 3$

Taking $68$ out as common

$\begin{array}{l}=68\times \left(-17-3\right)\\ =68\times \left(-20\right)\\ =-1360\end{array}$

If $*$ is an operation such that for integers $a$ and $b$ we have

$a*b=a\times b+\left(a\times a+b\times b\right)$ then find

a. $\left(-3\right)*\left(-5\right)$

b. $\left(-6\right)*2$

a. We have, $a*b=a\times b+\left(a\times a+b\times b\right)$

Now, put $a=\left(-3\right)$ and $b=\left(-5\right)$

$=\left(-3\right)\times \left(-5\right)+\left[\left(-3\right)\times \left(-3\right)+\left(-5\right)\times \left(-5\right)\right]$

$\begin{array}{l}=15+\left(9+25\right)\\ =15+34=49\end{array}$

b. Now, put $a=-6$ and $b=2$

$\begin{array}{l}=\left(-6\times 2\right)+\left\{\left(-6\right)\times \left(-6\right)+2\times 2\right\}\\ =-6\times 2+\left(36+4\right)\\ =-12+40=28\end{array}$

If $\Delta$ is an operation such that for integers $a$ and $b$ we have $a\Delta b=a\times b-2\times a\times b+b\times b\left(-a\right)\times b+b\times b$ then find

a. $4\Delta \left(-3\right)$

b. $\left(-7\right)\Delta \left(-1\right)$

Also show that $4\Delta \left(-3\right)\ne \left(-3\right)\Delta 4$ and $\left(-7\right)\Delta \left(-1\right)\ne \left(-1\right)\Delta \left(-7\right)$

   i.    We have,

$a\Delta b=a\times b-2\times a\times b+b\times (b)(-a)\times b+b\times b$

Now, put $a=4\text{ and }b=(-3)$

$\begin{array}{l}4\Delta (-3)=4\times (-3)-2\times 4(-3)+(-3)\times (-3)\\ \times (-4)\times (-3)+(-3)\times (-3)\end{array}$

$=-12-2\times (-12)+(9)(12)+9=-12+24+108+9$

$=129$

Now, put $a=-3\text{ and }b=4$ 

$\Rightarrow (-3)\Delta 4=(-3)\times 4-2\times (-3)\times (4)+4\times 4\{-(-3)\}\times 4+4\times 4$

$=(-12)+24+16(3)\times 4+16$

$=(-12)+24+192+16$

$=220$

Clearly, $4\Delta (-3)\ne (-3)\Delta 4$

2. Now, put $a=(-7)\text{and }b=(-1)$

$\begin{array}{l}\Rightarrow (-7)\Delta (-1)=(-7)\times (-1)-2\times (-7)\times (-1)+(-1)\\ \times (-1)\{-(-7)\}\times (-1)+(-1)\times (-1)\end{array}$

$=7-14+1\times 7\times (-1)+1$

$=7-14-7+1\Rightarrow -13$

Now, put $a=(-1)\text{and }b=(-7)$

$\begin{array}{l}\Rightarrow (-1)\Delta (-7)=(-1)\times (-7)-2\times (-1)\times (-7)+(-7)\\ \times (-7)\{-(-1)\}\times (-7)+(-7)\times (-7)\end{array}$

$=7-14+49(1)\times (-7)+49$

$=7-14-343+49$

$=-301$

Clearly, $(-7)\Delta (-1)\ne (-1)\Delta (-7)$

Below $u,v,w$ and $x$ represent different integers, where $u=-4$ and $x\ne 1.$ By using following equations, find each of the values:

$\begin{array}{l}u\times v=u\\ x\times w=w\\ u+x=w\end{array}$

a. $v$

b. $w$

c.  $x$

Explain your reasoning using the properties of integers.

We have three equations

$u\times v=u$   (i)

$x\times w=w$  (ii)

$u+x=w$  (iii)

And   $u=-4$

a. By putting the value of $u$ in Eq. (i), we get

$(-4)\times v=(-4)$

$\Rightarrow v=\frac{(-4)}{(-4)}\Rightarrow v=1$

b. From Eq. (ii),

$x\times w=w\Rightarrow x=\frac{w}{w}\Rightarrow x=1$

But,     $x\ne 1$

Hence, $x\times w=w,$ (ii) is possible, when $w=0(x\ne 1).$

c.  From Eq. (iii), $u+x=w$

Put $u=-4\text{ and }w=0,$ we get

$\Rightarrow -4+x=0\Rightarrow x=4$

$\therefore v=1,x=4\text{ and }w=0$

Height of a place A is $1800\text{ m}$ above sea level. Another place B is $700\text{ m}$ below sea level. What is the difference between the levels of these two places?

As per the given information, we can draw the diagram,

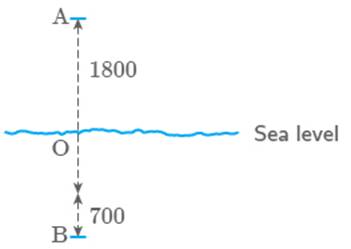
Let O be the point of level of sea.

Difference between these two point, A and B

$=$ Height between sea level and point A $+$ Height between point B and sea level

$\begin{array}{l}=\text{AO}+\text{OB}\\ =1800+700\\ =2500\text{ m}\end{array}$

The given table shows the freezing points in $°\text{F}$ of different gases at sea level. Convert each of these into $°\text{C}$ to the nearest integral value using the relation and complete the table,

$\text{C}=\frac{5}{9}\left(\text{F}-32\right)$

Gas	Freezing Point at Sea Level ( $°F$ )	Freezing Point at Sea Level ( $°C$ )
Hydrogen	$-435$
Krypton	$-251$
Oxygen	$-369$
Helium	$-458$
Argon	$-309$

For Hydrogen put $F=-435$

$\begin{array}{c}\text{C}=\frac{5}{9}\left[\left(-435\right)-32]\right]\\ =\frac{5}{9}\left(-435-32\right)\\ =\frac{5}{9}\times \left(-467\right)\\ =5\times \left(-51.888\right)\\ =259.44\\ =259°\text{C}\end{array}$

For Krypton put $F=-251$

$\begin{array}{c}\text{C}=\frac{5}{9}\left[\left(-251\right)-32\right]\\ =\frac{5}{9}\left(-251-32\right)\\ =\frac{5}{9}\times \left(-283\right)\\ =5\times \left(-31.444\right)\\ =157.22\\ =157°\text{C}\end{array}$

For Oxygen put $F=-369$

$\begin{array}{c}\text{C}=\frac{5}{9}\left[\left(-369\right)-32\right]\\ =\frac{5}{9}\left(-369-32\right)\\ =\frac{5}{9}\times \left(-401\right)\\ =5\times \left(-44.555\right)\\ =222.77\\ =223°\text{C}\end{array}$

For Helium put $F=-458$

$\begin{array}{c}\text{C}=\frac{5}{9}\left[\left(-458\right)-32\right]\\ =\frac{5}{9}\left(-458-32\right)\\ =\frac{5}{9}\times \left(-490\right)\\ =5\times \left(-54.444\right)\\ =272.22\\ =272°\text{C}\end{array}$

For Argon put  $F=-309$

$\begin{array}{c}\text{C}=\frac{5}{9}\left[\left(-309\right)-32]\right]\\ =\frac{5}{9}\left(-309-32\right)\\ =\frac{5}{9}\times \left(-341\right)\\ =5\times \left(-37.888\right)\\ =189.44\\ =189°\text{C}\end{array}$

Sana and Fatima participated in an apple race. The race was conducted in $6$ parts. In the first part, Sana won by $10$ seconds. In the second part she lost by $1$ minute, then won by $20$ seconds in the third part and lost by $25$ seconds in the fourth part, she lost by $37$ seconds in the fifth part and won by $12$ seconds in the last part. Who won the race finally?

Let difference in time denoted by positive, when Sana wins the race and negative, when Sana loses the race.

Total difference in time taken by Sana in all the six parts

$\begin{array}{l}=10-60+20-25-37+12\\ =-80\text{s }\left[\because 1\text{ min}=60\text{s}\right]\end{array}$

Hence, Fatima won the race by $80\text{s}\text{.}$

A green grocer had a profit of $\text{Rs}47$ on Monday, a loss of $\text{Rs}12$ on Tuesday and loss of $\text{Rs}8$ on Wednesday. Find his net profit or loss in $3$ days.

As per the given information,

Profit on Monday $=\text{ Rs}47$ and

loss on Tuesday $=\text{ Rs}12$ and loss on Wednesday $=\text{ Rs}8$

$\therefore$ Net profit $=$ Total profit $-$ Total loss

Now, total profit $=\text{ Rs}47$ and total loss $=12+8=20$

$\therefore$ Net profit $=47-20=\text{ Rs}27$

In a test, $+3$ marks are given for every correct answer and $-1$ mark are given for every incorrect answer. Sona attempted all the questions and scored $+20$ marks though she got $10$ correct answers.

a. How many incorrect answers has she attempted?

b. How many questions were given in the test?

Let $x$ be the correct answers and $y$ be the incorrect answers, given by Sona. It is given that, if she gives $10$ correct answers and her score is $20.$

Since, for every correct answer, $+3$ is given and for every incorrect answer, $-1$ is given.

Hence,

a. $3\times \left(\text{correct answer}\right)+\left(-1\right)\times \left(\text{incorrect answer}\right)=$ Total score

i.e. $3\times 10+\left(-1\right)\times y=20$

i.e. $30-y=20$

Hence $y=10$

b. Total number of questions $=$ correct answer $+$ incorrect answer

$\begin{array}{l}=x+y\\ =10+10\\ =20\end{array}$

In a true-false test containing $50$ questions, a student is to be awarded $2$ marks for every correct answer and $-2$ for every incorrect answer and $0$ for not supplying any answer. If Yash secured $94$ marks in a test, what are the possibilities of his marking correct or wrong answer?

Since, Yash scored $94$ marks.

So, Minimum correct answers $=\frac{\text{Total Marks}}{\text{Marks for }1\text{ correct answer}}$

$\begin{array}{l}=\frac{94}{2}\\ =47\end{array}$

Hence, there are two possibilities:

a. $47$ correct answers and $3$ unattempted.

b. $48$ correct answers, $1$ unattempt and $1$ wrong answer

A multistorey building has $25$ floors above the ground level each of height $5\text{ m}$. It also has $3$ floors in the basement each of height $5\text{ m}\text{.}$ A lift in building moves at a rate of $1\text{ m/s}\text{.}$ If a man starts from $50\text{ m}$ above the ground, how long will it take him to reach at $2^{\text{nd}}$ floor of basement?

Man covers the distance above the ground $=50\text{ m}$ and man covers the distance below the ground $=2\times 5=10\text{ m}$

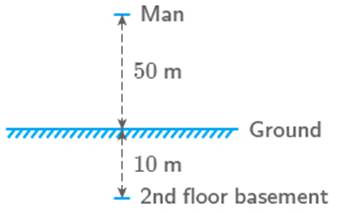
total distance $50\text{ m}+10\text{ m}=60\text{ m}$

speed of the lift $1\text{ m/s}$

Hence, time taken to reach second floor of the basement $=\frac{\text{Distance}}{\text{Speed}}$

$\begin{array}{l}=\frac{60\text{ m}}{1\frac{\text{m}}{\text{s}}}\\ =60\text{s or }1\text{ min}\end{array}$

Taking today as zero on the number line, if the day before yesterday is $17$ January, what is the date $3$ days after tomorrow?

If we take today as zero, then two days before today is $17$ January.

Hence, $3$ days after tomorrow will be at $4\text{th}$ place from zero on the number line.

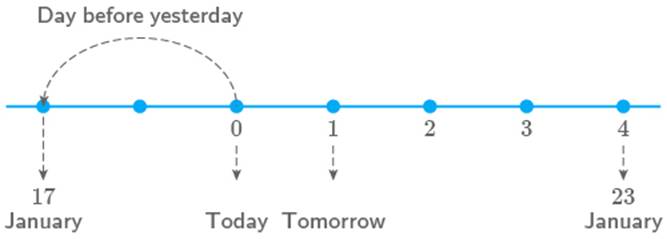
So, required date will be $\left(17+6\right)$ January

$=23$ January

The highest point measured above sea level is the summit of Mt. Everest which is $8,848\text{ m}$ above sea level and the lowest point is challenger Deep at the bottom of Mariana Trench which is $10911\text{ m}$ below sea level. What is the vertical distance between these two points?

As per the given information, we can draw the diagram,

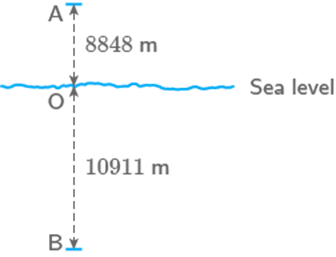
Let A be the point above the sea level and B be the point below the sea level.

$\therefore$ Vertical distance between points A and B $=$ Distance between point A and sea level $+$ Distance between point B and sea level

$=\text{AO}+\text{OB}=8848+10911=19759\text{ m}$